Phenomenological model-based study on electron beam welding process, and input-output modeling using neural networks trained by back-propagation algorithm, genetic algorithms, particle swarm optimization algorithm and bat algorithm

Abstract

High power density welding technologies are widely used nowadays in various fields of engineering. However, a computationally efficient and quick predictive tool to select the operating parameters in order to achieve the specified weld attribute is conspicuously missing in the literature. In the present study, a computationally efficient inverse model has been developed using artificial neural networks (ANNs). These ANNs have been trained with the outputs of physics-based phenomenological model using back-propagation (BP) algorithm, genetic algorithm (GA), particle swarm optimization (PSO) algorithm and bat algorithm (BA) separately to develop both the forward and reverse models. Unlike data driven ANN model, such approach is unique and yet based on science. Power, welding speed, beam radius and power distribution factor have been considered as input process parameters, and four weld attributes, such as length of the pool, depth of penetration of the pool, half-width of the pool and cooling time are treated as the responses. The predicted outputs of both the forward and reverse models are found to be in good agreement with the experimental results. The novelty of this study lies with the development and testing of five neural network-based approaches for carrying out both forward and reverse mappings of the electron beam welding process.

1 Introduction

Fusion welding is one of the most extensively used methods for various metal joining processes. The applications of high power density welding technologies, such as electron beam welding (EBW), laser beam welding (LBW), plasma arc welding (PAW) etc., are rapidly increasing in various fields of engineering. EBW, in particular, offers advantages, such as wide applicability, deep penetration, purity and many more, which are unmatched, and hence is gaining importance in various sectors. Moreover, several artificial neural network (ANN)-based models have been developed correlating inputs with the outputs for predicting both in the forward and backward directions. However, such models are of black-box types that do not explain the behaviors of the operating parameters based on science. Some literatures have also been reported on phenomenological models that are developed based on science, but final optimization of operating parameters has hardly been achieved using such a model employing with an optimization tool. Coupling phenomenological model with an optimization tool like either genetic algorithm (GA) or particle swarm optimization (PSO) algorithm or bat algorithm (BA) is very time consuming for running every individual of it by phenomenological model. For more than 1000 population (or swarm) in a generation and running several such generations (or iterations) before convergence, this approach will not be computationally efficient. On the other hand, if the ANN is trained based on the data collected from phenomenological model using either back-propagation (BP), GA, PSO or BA, its subsequent prediction will be very time efficient, yet based on science. Such ANN-based inverse model will form a quick predictive tool for practicing engineer to predict the operating parameters for a particular weld. Additionally, the development of a profound database through experiments alone is impractical because of the time, money and effort involved, but is feasible using such models.

The rest of the text is organized as follows. A detailed literature review has been carried out in Section 2. The gaps in the existing literature have been mentioned and the objectives of the present study have been stated in Section 3. A brief introduction to the phenomenological model is provided in Section 4. Section 5 deals with the data collection method adopted in the study. The developed neural networks-based approaches for the forward and reverse mappings are described in Section 6. Results are explained in Section 7. Some conclusions are drawn in Section 8.

2 Literature review

This section deals with the studies carried out on weld-pool modeling using phenomenological model and soft computing tools.

2.1 Studies on phenomenological models

David et al. [1] used a phenomenological model to study the dynamics of welding process including evolution of fluid flow, temperature profile and microstructure in order to avoid welding defects. Mundra et al. [2] combined phase transformation and thermo-fluid models for the prediction of microstructures in low alloy steel. A quasi-steady temperature distribution model having a linear heat source moving with a constant velocity was developed by Koleva et al. [3]. Their objective was to obtain a feasible range of optimal process parameters, and thereby, estimate the expected weld geometric characteristics. They also found considerable influences of turbulence and Marangoni force in the liquid weld-pool. He et al. [4, 5] studied the evolution of temperature and velocity fields, weld geometries, cooling rate and solidification using a 3D numerical heat transfer and fluid flow model for laser micro-spot welding of AISI 304 SS and also, compared the results with that of laser micro-linear welding. Experimental results were in agreement with the model predictions. Roy et al. [6] developed a model for pulsed laser welding (PLD) by conceptualizing PLD as a sequence of several tiny spot welds. The study described, in details, the evolution of velocity field, mushy zone and temperature profiles in the overlapped spots during pulsed laser welding. A computationally efficient model for keyhole mode welding without considering complex liquid, vapor cavity interaction and using a simple one equation turbulence model was developed by Rai et al. [7,8,9]. Their studies revealed a strong influence of convective heat transfer for low conductive materials. Solidification characteristics were included in their studies. Their predictions were validated with the experimental results for different materials having a wide range of properties in LBW [8]. They also reported that a change in working distance causes noticeable variation and influence on not only beam radius but also complete weld profile during EBW of SS304 plates [9]. In EBW, various possible outlines of the fusion zone geometry were expressed in terms of shape factor by Wang et al. [10]. Further analysis was carried out using non-linear curve fitting of two deduced parameters, obtained by combining different input parameters to find their effects on weld shape.

2.1.1 Study of cooling time and cooling rate

Energy input per unit length of the weld-pool (E)(kJ/mm) represents the combined effect of power (Q) and welding speed (U), which individually has contrasting effect on the weld-pool geometry and cooling time. The time required to cool from 800 ^∘C to 500 ^∘C, that is, the time taken to reduce the temperature by 300 ^∘C is called 800–500 cooling time (t _8/5). t _8/5 is metallurgically significant especially for mild steel, as it undergoes maximum phase transformation during this cooling period. The cooling time and energy per unit length of the high energy welding are considerably lower than that of conventional one, leading to overall reduction in the area of heating, hence improved properties. Another parameter is called cooling rate (C R)(^∘ C/s), which is a measure of amount of heat dissipated or lost in unit time. Increase in energy input per unit length increases the net heat input, resulting in reduction of cooling rate and increase in cooling time. These two parameters are inversely proportional, and are mentioned in (1) [11].

$$ CR=\frac{300^{\circ}}{t_{8/5}} $$

(1)

The cooling rate can also be defined as a product of solidification rate (R) and thermal gradient (G). It could be used as a reference to carry out further study on micro-structures [1, 2, 4,5,6,7,8]. The study of cooling rate had been carried out on different processes, such as electron beam (EB) hardening [12], Metal Active Gas (MAG) welding [13], laser welding [14,15,16] and EB welding [17].

2.2 Weld-pool modeling using various soft computing-based approaches

Bag et al. [18] combined a 3D convective heat transfer model with PCX G3 GA-based optimization tool for Gas Tungsten Arc Welding (GTAW) of SS304, for developing an improved forward model, for the prediction of weld geometries. An inverse model was also developed in order to predict the welding process parameters. Manvatkar et al. [19] developed ANN models following Bayesian approach for the determination of Friction Stir Welding (FSW) weld attributes. The training data were generated using phenomenological model and the model was validated with experimental results. Mishra and Debroy [20] studied a thermo-fluid physical model in order to predict heat transfer and fluid flow in GTAW of Ti-6Al-4V alloy. They used a GA to optimize the temperature and velocity fields. They found that by varying the set of welding parameters, such as speed, current and voltage etc., definite weld geometry could be achieved through multiple pathways. Andersen et al. [21] used an ANN to model the weld-pool in terms of input parameters of GTAW process. Karsai et al. [22] developed an ANN-based technique by using input-output relationships to model and control the static and dynamic behaviors of a GTAW process with limited errors. Lim and Cho [23] designed a 4-layer neural network to use surface temperature distributions on the work-piece to predict the weld-pool geometry. Dutta and Pratihar [24] mapped the input-output correlations of a welding process by utilizing conventional regression analysis, back-propagation neural network (BPNN) and genetic algorithm-tuned neural network (GANN), and found that the overall performance of GANN was better than that of the BPNN. Chokkalingham et al. [25] attempted to develop an ANN model to estimate the weld-pool geometry during an automated, robotic GTAW welding of SS316LN work-piece. Temperature distributions were measured separately by thermocouples and non-contact IR emission cameras, where the latter provided the better results. Reddy and Pratihar [26] developed BPNN and GANN-based expert systems separately to predict the temperature distributions of EBW of aluminum alloy. In their study, ANSYS was used to generate different sets of data regarding the temperature distributions by varying mesh refinement. GANN outperformed the BPNN in predicting the temperature distributions. Jha et al. [27] carried out regression analysis to map input-output relationships of electron beam (EB) butt welding of SS304 in both forward as well as reverse direction by utilizing the BPNN and GANN. The GANN outperformed the BPNN. Khorram et al. [28] employed Response Surface Methodology (RSM) to optimize weld-bead geometry in CO₂ laser welding of Ti-6Al-4V alloy in order to identify optimum weld conditions for the improved productivity. Srivastava and Garg [29] studied the effects of several input process parameters on the different weld attributes during gas metal arc butt welding of mild steel plates. RSM was used to obtain optimum weld geometries. Ronda and Siwek [30] developed a numerical model to investigate the interactions of keyhole and weld-pool. This model considered temperature dependent material properties. The material vaporization, occurring in the keyhole had also been simulated using the Volume of Fluid (VOF) method. They found that the shape and depth of melted zone depend on surface tension, pool surface temperature and presence of sulfur. They also found that convective heat loss had some effects on weld-pool shape. Gao and Zhang [31] used BPNN and Radial Basis Function Neural Network (RBFNN) to predict the weld-width during laser welding of SS304. They captured the dynamic variations of molten weld-pool morphology by using their shadows with an active vision system. The BPNN was reported to perform better than the RBFNN. A hybrid learning process was used to improve the performance of a RBFNN for the prediction of laser welding attributes [32]. The input-output modeling was done using ANN for Resistance Spot Welding (RSW) of Advanced High Strength Steel (AHSS) plates and EvoNorm algorithm was found to provide with a good Pareto-optimal front [33]. Buffa et al. [34] used an ANN model to predict the microstructure and strength of FSW welded titanium alloys. In another study, an ANN model was utilized to predict the strength of pulsed laser spot welded joints [35]. A fast and accurate Particle Swarm Optimization (PSO) algorithm was proposed as a good substitute of the GA [36]. Forward and reverse modeling of the EBW of zircaloy-4 had been carried out using different ANN models, such as BPNN, GANN and particle swarm optimization-tuned neural network (PSONN) [37]. The performance of ANN was seen to be data-dependent. ANN, with an intermediate feedback network from hidden neurons is the Elman Recurrent Neural Network [38]. PSO-tuned dynamic Elman Recurrent Neural Network (PSORNN) was also found to provide accurate results in predictions [39, 40]. Recently, a new nature-inspired algorithm has been developed from the prey locating behavior of bats using echoes [41]. Bat algorithm (BA) is a superset of some of the popular and efficient algorithms, such as PSO, Harmony search (HS), Simulated annealing (SA). This has resulted into the unification of the positive traits of these different algorithms into a single model along with unique hunting feature of bats [41, 42]. Moreover, Khan and Sahai [42] found the BA-tuned neural network (BANN) to outperform BPNN, GANN and PSONN. Still, the issues with convergence and inadequate performances are observed due to over-simplification of bat’s hunting nature and imbalance between exploration and exploitation [43, 44]. As a result, different modifications in the BA were proposed for improvement in the performances of ANN [43, 45, 46]. A novel bat algorithm (NBA) was developed by Meng et al. [43] having additional features of suitable habitat selection and echo adjustment.

3 Limitations of existing literature and objective of the present study

Although some input-output models exist based on ANN, these are valid for a specific range of inputs [21, 22, 24, 27, 33]. Besides this, such black-box models do not explain the behavior of the operating parameters based on science. Initially, it was thought that a phenomenological model will be coupled with an optimization tool named either GA, PSO or BA for inverse modeling. However, running such phenomenological model coupled with the GA, PSO, or BA will be very time consuming because to run each individual of the GA population/ PSO swarm/BA population, phenomenological model will consume around 20 min. Therefore, it is easily understandable that for a large population/swarm in a generation/iteration and several generations/iterations to converge the results, it may take several days to solve the optimization problem. On the other hand, if ANN is trained based on the data collected from the phenomenological model using either a GA, PSO or BA, it will be very time efficient. Such ANN-based inverse model will form a quick predictive tool for practicing engineer to predict the operating parameters for a particular weld attribute based on science. Such approach is conspicuously absent in the literature. Furthermore, while carrying out actual experiments in order to generate the test cases, there is no direct way to provide the beam diameter and power distribution factor (f) as input parameters in the experimental setup. In order to find the beam radius (r _b ), Elmer et al. [47] attempted to measure it experimentally, while Kar et al. [48] used the best-fit polynomial curve to predict it for different values of energy per unit length. However, the applicability of those methods is limited and only a rough estimation of beam radius could be obtained.

In the present study, the phenomenological model has been used to generate a large amount of input-output data by utilizing the material properties given in Appendix Table 2. Both forward and reverse modeling have been conducted to establish input-output relationships of the process using the BPNN, GANN, PSONN, PSORNN, and a novel BA-tuned dynamic Elman Recurrent Neural Network (NBARNN). The actual experiments have been carried out in order to obtain the data for test scenarios considering two separate cases. In case one, the current is kept constant, while the voltage has been varied in order to change the power. With the same range and values of power, the voltage is kept constant and the current has been varied in the second case of test scenarios. The experimental data, thus measured for the test cases, have been compared with the corresponding predicted values obtained from the above mentioned models.

4 Phenomenological model used

A pre-existing indigenous welding code [49], which is well-tested and validated against experimental data, is used to determine the thermal cycle. It is developed based on three dimensional steady heat, mass momentum balance equations. The code considers an incompressible, laminar and Newtonian fluid flow. All three driving forces for liquid flow, namely Marangoni force, Lorenz force and buoyancy force are considered for evolving the liquid flow pattern. Keyhole mode welding has been modeled by framing a keyhole by point by point heat balance on the keyhole surface and subsequently, putting it in the thermo-fluid code as a rigid wall at boiling temperature. Turbulence in the model is considered by a one dimension model [7, 8]. The model equations are discretized by control volume method and solved by SIMPLE algorithm. Non-uniform grids are utilized to make the code computationally efficient using only very fine grids at the location of steep gradients and coarse, otherwise. The code uses material property, heat source parameters as inputs and produces velocity, temperature profiles, cooling rates, cooling times as outputs. The circulation of liquid metal in the weld-pool can be represented by the following momentum equation given below.

$$ {\rho} \frac{\partial {u}_{{j}}} {\partial {t}}+{\rho} \frac{\partial \left( {{u}_{{i}} {u}_{{j}}} \right)}{\partial {x}_{{i}}} =\frac{\partial} {\partial {x}_{{i}}} \left( {{\mu} \frac{\partial {u}_{{j}}} {\partial {x}_{{i}}} } \right)+{S}_{{j}}, $$

(2)

where ρ represents the density, t indicates the time, x _i denotes the distance along the i direction, u _i and u _j are the velocity components along the i and j directions, respectively, μ represents the viscosity and S _j is the source term for the j-th momentum equation as given below.

$$\begin{array}{@{}rcl@{}} {S}_{{j}} &=&-\frac{\partial {P}}{\partial {x}_{{j}} }+\frac{\partial} {\partial {x}_{{j}}} \left( {{\mu} \frac{\partial {u}_{{j}}} {\partial {x}_{{j}}} } \right)-{C}\left( {\frac{\left( {\text{1}-{f}_{{L}}} \right)^{\text{2}}}{{f}_{{L}}^{\text{3}} +{B}}} \right){u}_{{j}}\\ &&+{\rho {g}\beta} \left( {{T}-{T}_{\text{ref}}} \right)-{\rho {U}}\frac{\partial {u}_{{j}}} {\partial {x}_{{j}} }\quad, \end{array} $$

(3)

where P represents pressure. In (3), the first term on the right hand side is the pressure gradient. The second term carries information of the viscosity. The third term denotes the frictional dissipation in the mushy zone according to the Carman- Kozeny equation for flow through a porous media, where f _L represents the liquid fraction. Here, C takes a high value for which the forces and velocity in the solid region become equal to zero, while a small value is assigned to B in order to avoid zero in the denominator. The fourth term corresponds to the buoyancy force, where g and β represent the acceleration due to gravity and coefficient of thermal expansion, respectively. T _{r e f} refers to any arbitrarily selected reference temperature. The last term indicates the source term due to welding velocity.

The following continuity equation is solved in conjunction with the momentum equation to obtain the pressure field:

$$ \frac{\partial \left( {{\rho {u}}_{{i}}} \right)}{\partial {x}_{{i}}} = 0 $$

(4)

The thermal energy transportation in the weld work-piece can be expressed by the following equation:

$$ {\rho} \frac{\partial {h}}{\partial {t}}+{\rho} \frac{\partial \left( {{u}_{{i}} {h}} \right)}{\partial {x}_{{i}}} =\frac{\partial} {\partial {x}_{{i}}} \left( {\frac{{k}}{{C}_{{p}}} \frac{\partial {h}}{\partial {x}_{{i}}} } \right)+{S}_{{h}}, $$

(5)

where k indicates the thermal conductivity, C _p is the specific heat, and S _h represents the source term due to latent heat content, h denotes the sensible enthalpy. The heat flux at the top surface is given by the following equation:

$$\begin{array}{@{}rcl@{}} {k}\left. {\frac{\partial {T}}{\partial {z}}} \right|_{\text{top}}&=&\frac{{{fQ}\eta}} {{r}_{{b}}^{\text{2}}} {\exp}\left( {-\frac{{f}\left( {{x}^{\text{2}}+{y}^{\text{2}}} \right)}{{r}_{{b}}^{\text{2}}} } \right)-{\varepsilon \sigma} \left( {{T}^{\text{4}}-{T}_{{a}}^{\text{4}}} \right)\\ &&-{h}_{{c}} \left( {{T}-{T}_{{a}}} \right) \end{array} $$

(6)

In (6), the first term on the right hand side is the heat input from the source, defined by a Gaussian heat distribution, where r _b , Q and f have been defined previously. Here, η is the power efficiency, ε represents emissivity, σ denotes the Stefan Boltzmann constant, h _c indicates the heat transfer coefficient and T _a is the ambient temperature. The second and third terms represent the heat loss by radiation and convection, respectively.

The weld-top surface is assumed to be flat. The Marangoni convection is initiated through the velocity boundary condition as given below.

$$ {\mu} \frac{\partial {u}}{\partial {z}}={f}_{{L}} \frac{{{d}\gamma} }{{dT}}\frac{\partial {T}}{\partial {x}};{\mu} \frac{\partial v}{\partial {z}}={f}_{{L}} \frac{{{d}\gamma} }{{dT}}\frac{\partial {T}}{\partial y};w = 0, $$

(7)

where u,v and w are the velocity components along the x,y and z directions, respectively, and $\frac {d\gamma } {dT}$ is the temperature coefficient of surface tension. Symmetrical vertical plane contains the direction of welding. The boundary conditions indicate no flux across the symmetric surface as mentioned below.

$$ \frac{\partial {u}}{\partial {y}}= 0;{v}= 0,\frac{\partial {w}}{\partial {y}}= 0;\frac{\partial {h}}{\partial {y}}= 0. $$

(8)

At all the surfaces, temperatures are kept equal to ambient temperature (T _a ) and velocities are set to be equal to zero.

5 Data collection

5.1 Collection of training data

The ranges of input parameters, used in the current study (refer to Table 1) have been selected on the basis of literature survey and experiences [12, 27, 48]. The phenomenological model has been used to generate input-output data according to a full-factorial design, considering four input and four output parameters, and each having six levels. Therefore, a set of 6⁴ = 1296 input-output data has been generated. The thus generated input-output data set has been used to train the BPNN, GANN, PSONN, PSORNN and NBARNN for the forward and reverse models separately.

Table 1 Ranges of process parameters for Phenomenological Model [12, 27, 48]

5.2 Collection of data for testing the models

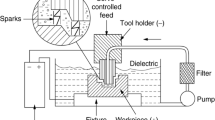
The input-output data for the test cases have been obtained after carrying out real experiments. The experiments are carried out in a 12 kW EBW machine developed by Bhabha Atomic Research Centre (BARC), Mumbai at IIT Kharagpur, India. It has the maximum voltage and current ratings of 80 kV and 150 mA, respectively. A photograph of the EBW setup is shown in Fig. 1.

Fig. 1

Photograph of 12 kW EBW Machine Setup at IIT Kharagpur, India

The ranges of the test data have been kept the same with that of the training data. In the existing facility, there is a provision for selecting power and welding speed as input parameters. The power and welding speed are varied in the range of (3.2, 5.6) kW and (900,1800) mm/min, respectively. The test data have been sub-divided into two separate cases. In case one of the test data, the current is kept fixed to 80 mA and voltage is varried from 40 kV to 70 kV (refer to Appendix Table 3). In case two, the voltage is kept constant at 60 kV by varrying the current from 54 mA to 94 mA (refer to Appendix Table 4). In the present study, a total of sixteen test scenarios have been considered for both the above two cases. Bead-on-plate welding has been carried out on AISI 304 Stainless Steel plate of dimensions 150 mm × 50 mm × 20 mm. Figure 2 depicts two weld passes.

Fig. 2

Bead-on-plate welded samples

After carrying out the welding, the required weld-pool dimensions for the different experimental conditions have been obtained by carrying out proper cutting, polishing and etching of the welded samples. Then, the weld geometries have been measured under a microscope and thereby, documented.

The two input parameters, namely power and welding speed are known from the real experiments. However, the other two input parameters considered in this study, such as beam radius and power distribution factor are not known beforehand. In order to find these two unknown input parameters, trial and error runs using the phenomenological model have been carried out. Along with the two known parameters (power and welding speed), the two unknown parameters have been varied in their respective ranges, as provided in Table 1. The combinations of four input parameters, for which the predicted depth and half-width of the pool by the phenomenological model almost match with the experimentally measured results are identified. The two unknown input parameters are, thus, determined. The beam radius is found to vary from 220 to 400 μ m (refer to Appendices Tables 3 and 4), which matches with the range for the same reported in the literature [50, 51].

The corresponding phenomenological model predicted data on length of the pool (L _p ) and cooling time, are also documented along with the experimentally measured outputs. The input-output data, consisting of four inputs and four outputs are, thus, obtained for all the test scenarios (refer to Appendices Tables 3 and 4), and have been used to check the performances of the BPNN, GANN, PSONN, PSORNN and NBARNN developed for the forward and reverse modeling.

6 Developed artificial neural network models

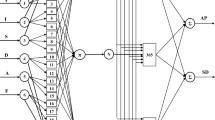
Figure 3 shows the schematic view of an ANN used in forward modeling. It consists of three layers, namely input, hidden and output layers. Four inputs and four outputs have been considered for the forward model. The symbols: [V] and [W] are used to represent the connecting weights between input and hidden layers and that between the hidden and output layers, respectively. The input, hidden and output layers are considered to have linear, log-sigmoid and log-sigmoid transfer functions, respectively. A total of 1296 input-output data generated using phenomenological model according to full-factorial design have been used for training of the network.

Fig. 3

Schematic view of an ANN used in forward modeling

The performances of the trained ANN have been tested using 16 test scenarios as discussed above. The average absolute percent deviation in predicting the outputs has been calculated, as shown in (9) [52].

$$ f_{d} =\frac{1}{L}\frac{1}{P_{o}} \sum\limits_{l = 1}^{L} {\sum\limits_{k^{\prime}= 1}^{P_{o}} {\left| {\frac{T_{ok^{\prime}l} -O_{ok^{\prime}l}} {T_{ok^{\prime}l}} \times 100} \right|}}, $$

(9)

where P _o denotes the number of outputs of the network, L represents the number of training scenarios, $O_{ok^{\prime }l}$ is the predicted output corresponding to l th training scenario and k ^′th neuron of the output layer.

The connecting weights have been updated with the aid of back-propagation algorithm employing the generalized delta rule in order to minimize the predicted error as shown in (10) and (11) [53].

$$ {\Delta} V(t_{i} )=-\eta_{l} \frac{\partial f}{\partial V}(t_{i} )+\alpha^{\prime}{\Delta} V(t_{i} -1), $$

(10)

$$ {\Delta} W(t_{i} )=-\eta_{l} \frac{\partial f}{\partial W}(t_{i} )+\alpha^{\prime}{\Delta} W(t_{i} -1), $$

(11)

where η _l ,α ^′ and t _i represent the learning rate, momentum constant and number of iterations, respectively.

Figure 4 displays an ANN to be used for reverse modeling. Here, the inputs and outputs of the forward model have been inter-changed. To train the network, both back-propagation algorithm and GA have been used as discussed above.

Fig. 4

Schematic view of an ANN used in reverse modeling

A parametric study is carried out to decide the number of hidden neurons in the network, learning rate, momentum constant, coefficients of transfer function of the hidden and output layers, maximum number of iterations and bias value. The details of the parametric study have been discussed in the result section. A batch mode of training has been used in the BPNN.

Figure 5 shows the flowchart of GANN used in the present study. In order to update the connecting weights, the back-propagation (BP) algorithm of the BPNN has been replaced by a real-coded genetic algorithm (GA). To develop the trained network, a parametric study has been carried out by varying the number of hidden neurons in the network, probability values of crossover and mutation, population size and maximum number of generations. In GANN, the fitness function of the GA has been calculated using (9). This percent deviation in predictions has been selected as the performance criterion for updating the connecting weights.

Fig. 5

Flow-chart of GANN [53]

PSO is an evolutionary computation tool, developed through the study of particles’ behavior in a swarm. The best solution is obtained through simultaneous local and global upgrading of the velocity and position of the particles, as given below.

$$\begin{array}{@{}rcl@{}} v_{id} \left( {t_{i} + 1} \right)&=&w_{I} v_{id} \left( {t_{i}} \right)+c_{1} r_{1} \left( {p_{id} -x_{id} \left( {t_{i}} \right)} \right)\\ &&+c_{2} r_{2} \left( {p_{gd} -x_{id} \left( {t_{i}} \right)} \right), \end{array} $$

(12)

$$ x_{id} \left( {t_{i} + 1} \right)=x_{id} \left( {t_{i}} \right)+v_{id} \left( {t_{i} + 1} \right), $$

(13)

where v _{i d} and x _{i d} denote the velocity and position of i th particle in d th dimension. p _{i d} represents the previous best position of the i th particle in d th dimension, and p _{g d} indicates the global best position in d th dimension . Moreover, w _I denotes a constant inertia weight, c ₁ represents a cognitive parameter, and c ₂ indicates a social parameter. r ₁ and r ₂ are the random numbers lying in the range of 0 to 1.

It is to be noted that the GA shown in Fig. 5 has been replaced by the PSO in order to develop the PSONN algorithm.

Unlike the previously discussed ANNs, a PSO-tuned Recurrent Neural Network (PSORNN) has also been employed in the said analysis. The effect of feedback on the network improvement is analyzed. Figure 6 displays the schematic view of an Elman recurrent neural network used in this study.

Fig. 6

Schematic view of recurrent neural network used in forward and reverse modeling

The PSO of PSORNN has been replaced by a recently reported novel bat algorithm (NBA) [43]. This NBA is an upgradation of the standard BA [41], where additional bat behaviors, such as selection of a proper habitat through quantum behavior and mechanical behavior like echo adjustment in the form of Doppler effect have also been taken into account. Thus, the developed NBARNN is used in the present study. The equations used for the standard bat algorithm have been stated below.

$$ f_{i} =f_{\min} +(f_{\max} -f_{\min} )\times \beta_{0,} $$

(14)

$$ v_{bid} \left( {t_{i}} \right)=v_{bid} \left( {t_{i} -1} \right)+\left( {x_{bid} \left( {t_{i}} \right)-x_{\ast} } \right)\times f_{i}, $$

(15)

$$ x_{bid} \left( {t_{i}} \right)=x_{bid} \left( {t_{i} -1} \right)+v_{bid} \left( {t_{i}} \right), $$

(16)

where f _i and β ₀ are the frequency and random number (0, 1), respectively. v _{b i d} and x _{b i d} denote the velocity and position of i th bat in d th dimensional search space. x _∗ represents the present best result. An additional local search through random walk method is employed using the following equations:

$$ x_{new} =x_{old} +\varepsilon_{0} A_{mean} \left( {t_{i}} \right), $$

(17)

where ε ₀ is a random number varying in the range of (− 1, 1). The average loudness of bats is represented by A _{m e a n} (t _i ). With the iterations, the decrease in loudness and increase in pulse rate are given as follows:

$$ A_{i} (t_{i} + 1)=\alpha_{b} \times A_{i} (t_{i} ), $$

(18)

$$ r_{i} (t_{i} + 1)=r_{i} (0)\times \left[ {1-\exp \left( {-\gamma_{b} \times t_{i}} \right)} \right], $$

(19)

where A _i and r _i are the loudness and pulse rate in each iteration. Here, α _b and γ _b have been set equal to 0.90 each. The modifications implemented in the standard BA, and the values of the parameters have been taken from the literature [43].

7 Results and discussion

Results of the forward and reverse models developed in this study are stated and discussed in this section. During forward modeling, the deviations in predictions of the depth of penetration and half-width of the weld pool, as obtained by the phenomenological, BPNN, GANN, PSONN, PSORNN and NBARNN models have been compared with the experimental results. Since the length of the pool and cooling time have not been determined experimentally, the results of the trained BPNN, GANN, PSONN, PSORNN and NBARNN models have been compared with that of the phenomenological model. The experimentally measured depth of penetration and half-width, along with the phenomenological model-predicted length of the pool and cooling time have been used as inputs of the reverse model. During the reverse modeling, the welding process parameters are predicted utilizing the trained BPNN, GANN, PSONN, PSORNN and NBARNN models. In addition, the effects of energy per unit length of weld-pool on weld attributes, namely depth of the pool, half-width of the pool, cooling time and cooling rate have also been studied.

7.1 Results of forward modeling

The parametric studies of the BPNN, GANN, PSONN, PSORNN and NBARNN have been carried out to decide their optimal parameters, as discussed below.

7.1.1 Parametric study of BPNN

The results of BPNN parametric study are shown in Fig. 7a–g. During this study, the number of hidden neurons in the network, learning rate, momentum constant, coefficient of transfer function of the hidden and output layers, maximum number of iterations and bias value have been kept in the ranges of (2, 20), (0.1, 1.0), (0.1, 1.0), (0.5, 5.0), (100, 10,000) and (0.00001, 0.00010), respectively. Here, one parameter has been varied at a time, keeping the others unaltered. The optimum values of the number of hidden neurons in the network, learning rate, momentum constant, coefficient of transfer function of the hidden layer, coefficient of transfer function of the output layer, maximum number of iterations and bias value are found to be equal to 19, 0.9, 0.10, 4.50, 2.50, 6000 and 0.00007, respectively.

Fig. 7

Results of the parametric study of BPNN: Average absolute Percent Deviation vs. a Number of Hidden Neurons, b Learning Rate, c Momentum Constant, d Coefficient of Transfer Function of Hidden Layer, e Coefficient of Transfer Function of Output Layer, f Maximum Number of Iterations, g Bias Value

7.1.2 Parametric study of GANN

Figure 8a–e display the results of the parametric study for GANN. The parameters like the number of hidden neurons, probability of crossover (p _c ), probability of mutation (p _m ), population size (N) and maximum number of generations $\left ({G_{\max }^{\prime }} \right )$ have been varied in the ranges of (2, 20), (0.5, 1.0), (0.001, 0.011), (1160, 2320) and (100, 3900), respectively. After carrying out the parametric study, the optimum values of the number of hidden neurons in the network, p _c , p _m , N and $G_{\max }^{\prime }$ are obtained as 14, 0.6, 0.004, 2204 and 3900, respectively.

Fig. 8

Results of the parametric study of GANN: a Fitness vs. Number of Hidden Neurons, b Fitness vs. Probability of Crossover $\left ({p_{c}} \right )$, c Fitness vs. Probability of Mutation $\left ({p_{m}} \right )$, d Fitness vs. Population size $\left (N \right )$, e Fitness vs. Maximum Number of Generations $\left ({G_{\max }^{\prime }} \right )$

7.1.3 Parametric study of PSONN

A parametric study has also been carried out by following the above procedure in order to obtain an optimized PSONN network. The parameters, namely the number of hidden neurons of the network and the maximum number of iterations have been varied in the ranges of (2, 20) and (5000, 30,000), respectively. The optimum results are obtained with 6 neurons and 30,000 iterations. The values of w _I , c ₁ and c ₂ are kept fixed to 0.722, 1.193 and 1.193, respectively.

7.1.4 Parametric study of PSORNN

The parametric study of PSORNN is carried out by following the similar procedure adopted in Section 7.1.3. In addition, the weights in the feedback mechanism have been varied in the range of 0.1 to 1.0 with an increment of 0.05. The optimum number of hidden neurons, maximum number of iterations and feedback weights are found to be equal to 7, 30000, and 0.4, respectively.

7.1.5 Parametric study of NBARNN

A parametric study has also been conducted in order to obtain an optimized NBARNN. The parameters of NBA have been taken from the literature [43]. The parameters, namely the number of hidden neurons of the network, number of bats, maximum number of iterations and feedback weight for the recurrent network have been varied in the ranges of (2, 20), (20, 200), (1000, 7000) and (0.1, 1.0), respectively. The optimized results are obtained with 15 hidden neurons, 110 number of bats, 5000 iterations and 0.6 as feedback weight.

7.1.6 Validation of experimental results with phenomenological and neural networks-based models during forward modeling

Experimental results have been compared with that of phenomenological and neural networks-based models for the two cases, as stated below.

Results of case one

The current is kept constant and the voltage has been varied. The percent deviation values in predictions of depth of penetration and half-width of the pool using different models with respect to the experimentally obtained results are plotted in Fig. 9a, b. Figure 10a, b display the values of precent deviation in predicting the length of the pool and cooling time by the BPNN, GANN, PSONN, PSORNN and NBARNN models, as obtained through the comparison of the results with that of the phenomenological model.

Fig. 9

Percent deviation of Phenomenological model-, BPNN, GANN, PSONN, PSORNN and NBARNN- predicted outputs from the corresponding experimentally obtained outputs for case one test scenarios: a Depth of penetration of the pool, b Half-Width of the pool

Fig. 10

Percent deviation of BPNN, GANN, PSONN, PSORNN and NBARNN- predicted outputs from the corresponding Phenomenological model predicted outputs for case one test scenarios: a Length of the pool, b Cooling Time

It is clear from Fig. 9a, b that the values of percent deviation in prediction of the depth of penetration and half-width for most of the test cases are found to be in the range of (− 7%, + 7%) and (− 5%, + 7.5%), respectively. Similarly, it is observed from Fig. 10a, b that the values of percent deviation in predicting the length of the pool and cooling time vary in the range of (− 7.5%, + 6%) and (− 17.5%, + 20%), respectively, for most of the test cases. It is to be noted that a high value of percent deviation in prediction of cooling time has been obtained for 11-th test scenario of the Appendix Table 3 (refer to Fig. 10b). It has happened so, as a low value of cooling time, that is, 0.283 s has been obtained from the phenomenological model for this test scenario. This may have occurred due to inherent limitations of the phenomenological model to analyze the highly complex process.

The values of average absolute percent deviation in predicting the depth of penetration are found to be equal to 4.14%, 8.73%, 6.81%, 5.02%, 4.54% and 4.49% for the phenomenological model, BPNN, GANN, PSONN, PSORNN and NBARNN, respectively. Similarly, these values have been calculated for the predictions of half-width of the weld pool by the phenomenological model, BPNN, GANN, PSONN, PSORNN and NBARNN, which are seen to be equal to 6.54%, 6.34%, 7.81%, 6.34%, 8.19% and 6.10%, respectively. The BPNN, GANN, PSONN, PSORNN and NBARNN models have predicted the lengths of the weld pool with an average absolute percent deviation of 6.81%, 4.74%, 6.40%, 6.81% and 7.31%, respectively. Similarly, cooling time has been predicted with an average absolute percent deviation of 19.50%, 15.54%, 13.03%, 10.78% and 10.43% by the BPNN, GANN, PSONN, PSORNN and NBARNN models, respectively. The phenomenological model is able to predict the responses with reasonable accuracy and PSORNN is seen to perform slightly better than the PSONN, GANN and BPNN. This may be attributed to the presence of a feedback mechanism. Moreover, PSONN has outperformed GANN because of preservation of the previous best solutions, while carrying out the global and local searches simultaneously. Being a gradient-based method, the chance of back-propagation (BP) algorithm for getting stuck at the local minima is more, and consequently, BPNN has yielded a slightly worse performance compared to the GANN. The performances of NBARNN and PSORNN, both having the feedback loop have been compared. It is observed that the former distinctly outperforms the latter for most of the cases. This may be because of an efficient local search mechanism used by the NBARNN. Moreover, the performance of the conventional BA has been improved in the present study by an addition of proper selection of habitat through quantum and mechanical behaviors of the bats. The quantum behavior of bats facilitates the search in a wide range of habitats. The Doppler effect considered under mechanical behavior of a bat, takes into account the self-adaptive capabilities to automatically adjust its velocity and position, depending upon the relative velocity and position of the prey by either increasing or decreasing its speed.

Two experimentally measured outputs, namely depth of penetration and half-width of the pool, phenomenological model-predicted cooling time, and cooling rate deduced from (1), have been plotted in Fig. 11a–d against the energy input per unit length of the weld-pool. The energy input per unit length has been varied from 0.107 kJ/mm to 0.373 kJ/mm. The power-welding speed combinations for the low and high energy input per unit length are considered to be 3200 W–1800 mm/min, and 5600 W–900 mm/min, respectively. With the increase in energy input per unit length, depth of penetration of the pool, half-width of the pool and cooling time are seen to increase, while the cooling rate is found to decrease. This has happened so, because with the increase in energy per unit length, the net heat input into the sample increases. It causes more melting, thereby affects both the deeper as well as wider part of the sample, and consequently, the depth of penetration and half-width of the weld-pool are found to increase. As the net heat input into the sample increases, the rate at which heat is dissipated is reduced, which results into the increased cooling time and decreased cooling rate.

Fig. 11

The effects of energy per unit length for case one test cases on a Depth of penetration of the pool, b Half -Width of the pool, c Cooling Time, d Cooling Rate

The variations of cooling time and cooling rate with the energy per unit length of weld-pool have been studied by various researchers. Results of the present study, as shown in Fig. 11c, d, are in close agreement with that of the literature [12,13,14,15,16,17].

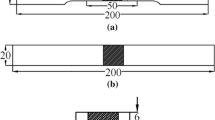
The bead-geometries corresponding to the minimum and maximum energy per unit length of the weld-pool have been considered for analysis. The experimentally measured bead-geometries (shown on left side) and the phenomenological model-predicted counterpart (displayed on right side) have been compared in Fig. 12a, b. The temperature distributions and fluid flow have also been shown in the phenomenological model-predicted weld-geometries. Both the depth of penetration as well as half-width of the weld-pool, corresponding to the higher energy per unit length, has been found to be higher than that of the lower counterpart. The dimensions of the weld-geometries for case one have been mentioned in the Appendix Table 3. The ratio of bead-width to depth of penetration, that is, the aspect ratio in Fig. 12a, corresponding to the highest energy per unit length is obtained as 0.683, while the same in Fig. 12b, corresponding to the lowest energy per unit length is found to be equal to 1.77. The trend matches with the pattern highlighted in Fig. 11a, b.

Fig. 12

Bead geometries in EBW corresponding to the highest and lowest heat input per unit length for case one of test scenarios: a power = 5600 W, welding speed = 900 mm/min, power distribution factor = 1.5, and beam radius = 400 μ m; b power = 3200 W, welding speed = 1800 mm/min, power distribution factor = 0.5, and beam radius = 400 μ m

Results of case two

Here, the current has been varied after keeping the voltage constant. The values of percent deviation in predictions of depth of penetration and half-width of the pool as obtained by different models with respect to the experimental results are displayed in Fig. 13a, b. Figure 14a, b show the percent deviation in predicting the length of pool and cooling time by the BPNN, GANN, PSONN, PSORNN and NBARNN models through the comparison with the results of phenomenological model for the test scenarios.

Fig. 13

Percent deviation of phenomenological model-, BPNN, GANN, PSONN, PSORNN and NBARNN - predicted outputs from the corresponding experimentally obtained outputs for case two test scenarios: a Depth of penetration of the pool, b Half-Width of the pool

Fig. 14

Percent deviation of BPNN, GANN, PSONN, PSORNN and NBARNN-predicted outputs from the corresponding phenomenological model predicted outputs for case two test scenarios: a Length of the pool, b Cooling Time

The phenomenological model, BPNN, GANN, PSONN, PSORNN and NBARNN models have predicted the depth of penetration of the weld-pool with an average absolute percent deviation value of 7.69%, 10.314%, 9.45%, 8.18%, 9.62% and 8.08%, respectively. Similarly, these models have been used for the predictions of half-width of weld-pool, and the values of average absolute percent deviation in predictions are found to be equal to 7.17%, 8.65%, 8.10%, 6.69%, 7.34% and 5.99%, respectively. The length of the weld-pool has been predicted with an average absolute percent deviation of 7.85%, 4.37%, 7.47%, 5.74% and 7.22% by the BPNN, GANN, PSONN, PSORNN and NBARNN -models, respectively. In a similar way, the BPNN, GANN, PSONN, PSORNN and NBARNN-models have predicted the cooling time with an average absolute percent deviation of 11.90%, 14.92%, 11.37%, 10.82% and 10.17%, respectively. It is important to mention that here again, NBARNN is seen to perform slightly better than PSORNN, PSONN, GANN and BPNN. The reason for this has been explained earlier.

Figure 15a and b display the variations of depth of penetration and half-width of the weld-pool, respectively with the energy input per unit length for the experimentally obtained and three model-predicted results. Figure 15c and d show the plots of cooling time and cooling rate vs. energy input per unit length of weld pool. It is important to mention that the similar trends of variations have been obtained as that of Fig. 11 and the reasons for the same have been explained above.

Fig. 15

The effects of energy per unit length on a Depth of the pool, b Half-Width of the pool, c Cooling Time, d Cooling Rate

It is also to be noted that the variations of cooling time and cooling rate with the energy input per unit length of weld-pool follow the same trends as that available in the literature [12,13,14,15,16,17].

The bead-geometries corresponding to the minimum and maximum energy input per unit length of weld-pool have been analyzed. Figure 16a and b compare the experimentally obtained (displayed on left side) and phenomenological model-predicted (shown on right side) bead-geometries corresponding to the maximum and minimum energy input per unit length of weld-pool, respectively. The temperature distributions and fluid flow patterns have also been shown in the phenomenological model predicted weld-geometries in Fig. 16. The depth of penetration and half-width corresponding to the higher energy per unit length of weld-pool are found to be more than that of the lower counterpart. The dimensions of the weld geometries are provided in the Appendix Table 4. The aspect ratio in Fig. 16a is found to be equal to 0.516, which corresponds to the highest energy per unit length. The same in Fig. 16b is obtained as 1.072, corresponding to the lowest energy per unit length. The trend follows the pattern shown in Fig. 15a, b. The aspect ratio of case two is found to be less than that of case one. This highlights the increase in depth of penetration in case two compared to case one, and thereby, the influence of current on the bead-geometry.

Fig. 16

Bead geometries in EBW corresponding to the highest and lowest heat input per unit length for case two of test scenarios: a power = 5600 W, welding speed = 900 mm/min, power distribution factor = 4.0, and beam radius = 400 μ m; b power = 3200 W, welding speed = 1800 mm/min, power distribution factor = 1.0, and beam radius = 370 μ m

7.2 Results of neural networks-based reverse modeling

Reverse modeling aims to predict the necessary welding input parameters in order to obtain the desired weld attributes. In the present study, BPNN, GANN, PSONN, PSORNN and NBARNN have been used for the reverse modeling, the results of which are explained below.

7.2.1 Parametric study of BPNN

For the reverse modeling, a parametric study has been conducted for the BPNN, for which the ranges of the number of hidden neurons, learning rate, momentum constant, maximum number of iterations, and bias value have been kept the same as that of the forward model (refer to Section 7.1.1). Through this parametric study, the optimum values of the number of hidden neurons in the network, learning rate, momentum constant, coefficient of transfer function of hidden layer, coefficient of transfer function of output layer, maximum number of iterations and bias value are found to be equal to 15, 0.8, 0.5, 8.5, 7.0, 8000, and 0.00006, respectively.

7.2.2 Parametric study of GANN

For the reverse modeling, during the GANN parametric study, the ranges of variation for the number of hidden neurons, probability values of crossover and mutation, and maximum number of generations have been kept the same as that of the forward model (refer to Section 7.1.2). The population size has been varied in the range of (1480, 2960). After carrying out the parametric study, the optimum values of the number of hidden neurons in the network, probability of crossover, probability of mutation, population size and maximum number of generations are seen to be equal to 18, 0.5, 0.001, 1776 and 3900, respectively.

7.2.3 Parametric study of PSONN

The ranges of variation of the number of hidden neurons and maximum number of iterations during the parametric study of PSONN used for reverse modeling are kept the same as that of the forward model (refer to Section 7.1.3). The optimum number of hidden neurons and maximum number of iterations are seen to be equal to 9 and 30000, respectively.

7.2.4 Parametric study of PSORNN

The ranges of different parameters used in the parametric study are kept the same as of the forward model (refer to Section 7.1.4). The optimum values of the number of hidden neurons, maximum number of iterations and feedback weights are obtained as 16, 30000 and 0.65, respectively.

7.2.5 Parametric study of NBARNN

During the parametric study, the ranges of different parameters have been kept the same as of the forward model (refer to Section 7.1.5). The following parameters are found to yield the best results: number of hidden neurons = 10, number of bats = 170, maximum number of iterations = 6000, feedback weights = 0.70.

7.2.6 Validation of experimental results with phenomenological and neural network-based models during reverse modeling

During reverse modeling, the process parameters of welding have been predicted. The results of the test scenarios are discussed below.

Results of case one

As previously mentioned, the current is kept constant and the voltage has been varied in this case. The percent deviations in predictions of power and welding speed using the BPNN, GANN, PSONN, PSORNN and NBARNN models with respect to the experimental inputs of the test scenarios are shown in Fig. 17a, b. Figure 18a, b display the percent deviation in the predicted values of beam radius and power distribution factor by the BPNN, GANN, PSONN, PSORNN and NBARNN models, in comparison with the inputs used in the phenomenological model.

Fig. 17

Percent deviation of BPNN, GANN, PSONN, PSORNN and NBARNN-predicted inputs from the corresponding inputs provided in the experimental setup for case one test scenarios: a Power, b Welding Speed

Fig. 18

Percentage deviation of BPNN, GANN, PSONN, PSORNN and NBARNN-predicted inputs from the corresponding inputs provided in the phenomenological model for case one test scenarios: a Beam Radius, b Power Distribution Factor

In Fig. 17a, b, the BPNN, GANN, PSONN, PSORNN and NBARNN-predicted percent deviation values of the power and welding speed for most of the test scenarios are found to lie in the ranges of (− 19%, + 15%) and (− 19%, + 27%), respectively. Likewise, the percent deviations in predicting the beam radius and power distribution factor are observed from Fig. 18a, b to vary in the ranges of (− 15%, + 20%) and (− 18%, + 25%), respectively, for most of the test cases.

The values of average absolute percent deviation in predictions of the power employing the BPNN, GANN, PSONN, PSORNN and NBARNN-models are seen to be equal to 11.85%, 10.44%, 10.65%, 10.02% and 9.92%, respectively. Similarly, the same have been obtained for the predictions of welding speed using the BPNN, GANN, PSONN, PSORNN and NBARNN and these are seen to be equal to 19.34%, 17.10%, 13.98%, 15.94% and 13.64%, respectively. The BPNN, GANN, PSONN, PSORNN and NBARNN-based models have been used to predict the beam radius with an average absolute percent deviation of 13.56%, 13.89%, 10.69%, 6.79% and 9.03%, respectively. Likewise, power distribution factor is predicted with an average absolute percent deviation of 16.26%, 11.29%, 12.23%, 12.35% and 10.86%, by the BPNN, GANN, PSONN, PSORNN and NBARNN, respectively. The overall average absolute percent deviations in predictions as obtained by the BPNN, GANN, PSONN, PSORNN and NBARNN models are found to be equal to 15.25%, 13.18%, 11.89%, 11.27% and 10.86%, respectively, thereby NBARNN is found to perform better than the PSORNN, PSONN, GANN and BPNN. The reason behind such observations has been discussed above.

It is important to mention that for some of the test scenarios, the percent deviation values are found to be high. It may be due to inherent deviation in predictions of the phenomenological model or neural network-based models, although a proper care has been taken.

Results of case two

In this case, the voltage is kept constant and the current has been varried. The percent deviations in predictions of power and welding speed as obtained by the BPNN, GANN, PSONN, PSORNN and NBARNN models with respect to the experimental inputs for the test scenarios are shown in Fig. 19a, b. Figure 20a, b display the percent deviation values in predicting the beam radius and power distribution factor by the BPNN, GANN, PSONN, PSORNN and NBARNN models, with respect to the inputs used in the phenomenological model.

Fig. 19

Percent deviation of BPNN, GANN, PSONN, PSORNN and NBARNN-predicted inputs from the corresponding inputs provided in the experimental setup for case two test scenarios: a Power, b Welding Speed

Fig. 20

Percent deviation of BPNN, GANN, PSONN, PSORNN and NBARNN-predicted inputs from the corresponding inputs provided in the phenomenological model for case two test scenarios: a Beam Radius, b Power Distribution Factor

BPNN, GANN, PSONN, PSORNN and NBARNN models are able to predict the power with an average absolute percentage deviation of 8.24%, 7.34%, 11.11%, 11.59% and 7.79%, respectively. Similarly, these values have been determined for the predictions of welding speed by the BPNN, GANN, PSONN, PSORNN and NBARNN-models as 18.04%, 16.92%, 12.51%, 13.36% and 11.89%, respectively. The BPNN, GANN, PSONN, PSORNN and NBARNN-models have predicted the beam radius with an average absolute percent deviation of 13.09%, 12.89%, 9.32%, 7.23% and 9.63%, respectively. Similarly, the power distribution factor has been predicted with an average absolute percent deviation of 14.37%, 13.98%, 11.82%, 11.65% and 11.04%, by the BPNN, GANN, PSONN, PSORNN and NBARNN models, respectively. The predicted results are found to be in the acceptable range. The values of overall average absolute percent deviation in predicting all the welding process parameters are obtained as 13.44%, 12.78%, 11.19%, 10.96% and 10.09% for the BPNN, GANN, PSONN, PSORNN and NBARNN-models, respectively. Once again, NBARNN is found to perform slightly better than other ANNs. The reason behind this fact has been explained above.

8 Conclusion

In the present study, a phenomenological model has been used to generate input-output welding data, according to a full-factorial design. Then, the collected data are used in the neural networks for the purpose of modeling the EBW process. The following conclusions are drawn from this study:

• 1. The physics behind the working of the phenomenological model is preserved in the developed ANN models, thereby acting as a quick and accurate predicting pseudo-phenomenological model.

• 2. Time, effort and money required for the development of a profound database are reduced due to the minimization of real experiments.

• 3. BPNN, GANN, PSONN, PSORNN and NBARNN-based forward and reverse models have been developed. The forward model predicts the different weld attributes, while the reverse model determines the welding process parameters. Even the hard-to-obtain beam radius has been predicted effortlessly. The predicted outputs by different models have shown very good agreement with the experimental results.

• 4. During forward modeling, the lower aspect ratio for case two (fixed voltage and varying current) than that of case one (fixed current and varying voltage) depicts the influence of current in the welding.

• 5. The experimentally measured and phenomenological model-predicted bead-geometries during forward modeling are found to be in good agreement.

• 6. Both the beam radius and power distribution factor are found to increase with the increase in energy per unit length of weld-pool.

• 7. GANN has provided better predictions compared to the BPNN in both forward as well as reverse modeling. It has happened so, as BPNN has a chance to get stuck at the local minima, whereas the GANN can provide globally minimum solution.

• 8. PSONN outperformed GANN through the preservation of the best fitness from the previous generations by carrying out the local and global searches simultaneously.

• 9. PSORNN has performed slightly better than the PSONN, which is expected because of the inclusion of a dynamic feedback system.

• 10. NBARNN has outperformed PSORNN because the former has a more efficient local search mechanism compared to that of the latter. It is important to mention that both the NBARNN and PSORNN are equally efficient in terms of their global search capability.

• 11. Neural network-based approaches are seen to establish input-output relationships of the EBW process efficiently. However, their performances are found to be data-dependent.

Appendix

Table 2 Material properties used in the phenomenological model [4, 7, 18, 54]

Table 3 Results of the test scenarios for case one

Table 4 Results of the test scenarios for case two