1 Introduction

In recent years, developing methods for the accurate estimation of sea-ice thickness has become an important issue due to its high importance for safe navigation in ice-infested waters, numerical prediction of climate change, and weather forecasting in ice-covered regions. The results of analyses by geoscientists indicate that if warming continues, there will be an increasing need to forecast accurate sea-ice information due to an increase in ship traffic in ice-covered regions [1]. Assessing thickness of sea-ice is important due to the fact that it has a direct effect on heat transfer between the atmosphere and the ocean. Furthermore, it is crucial to identify in which regions the accumulated ice has a high thickness to update the path of ships and icebreakers. In spite of the importance of developing accurate and practical prognostic models for estimating sea-ice thickness, it is known that it is very difficult to correctly estimate the ice thickness distribution [21, 34]. To cope with such a deficiency, some researchers have tried to improve the modeling results by incorporating observational data through statistical techniques such as data assimilation. Indeed, there exist several studies that assimilate sea-ice concentration information captured from passive microwave sensors to improve sea ice forecasts [6, 38]. However, there is a growing need to assimilate sea ice thickness observations, in addition to those of sea ice concentration [41].

So far, extensive research has been conducted to develop estimation tools that use information from satellite-borne sensors to calculate sea-ice thickness [20, 22, 29, 40]. Sea-ice thickness can be estimated at a spatial resolution of approximately 1 km with data obtained from visible/infrared (VIS/IR) sensors [42]. However, it is well known that information obtained from VIS/IR sensors cannot be used during cloudy conditions. To partially overcome this problem, data from passive microwave sensors can be taken into account [22, 29]. Such sensors are capable of returning surface information during both dark and cloudy periods.

To estimate sea ice thickness from satellite data, physics-based methods can be used, such as a radiative transfer model or a heat balance equation. However, such approaches are challenging, as several features, e.g. heat transfer between the ice and the environment may require the solution of nonlinear partial differential equations. Furthermore, when using physics-based approaches, several important issues may be neglected because of uncertainties and measurement errors [11, 26]. Such facts can be considered as provocative elements that have motivated researchers of geoscience to seek machine learning methods as an alternative to physics-based approaches that also allow the rate of human interference to be reduced [18].

In spite of the obvious computational power of intelligent techniques, there exist only a few reports in the literature addressing their successful application to sea-ice information processing. [37] proposed an intelligent system for satellite sea-ice image analysis. The developed intelligent framework was capable of performing both feature selection and rule-based classification based on the knowledge obtained from sensors. The results of the experiments clearly demonstrated the efficiency of the proposed intelligent framework. [16] developed an automated approach for determining sea-ice thickness from synthetic aperture radar (SAR) database. The results indicate that the method can adapt to varying ice thickness intensities in addition to regional and seasonal changes and is not subject to limitations from using predefined parameters. [3] proposed an in-situ learned and empirically forced neural network model for the estimation of fluctuating Arctic sea ice thickness. The results indicate that their neural network can predict sea-ice thickness under variety of conditions with a high accuracy. [24] proposed a hybrid algorithm based on chaos immune genetic algorithm and back-propagation neural network (BP-NN) to forecast sea-ice thickness in Bohai sea and north of the Yellow sea. Their study clearly proved the efficiency of the proposed method. In the light of such promising research, here, the authors intend to propose a novel hybrid intelligent system to automate both feature selection and estimation procedures for processing geophysical data and calculating sea-ice thickness along the Labrador coast. To the best knowledge of the authors, this is the first time that an intelligent approach is proposed for feature selection and processing of remote sensing data for estimation of sea-ice thickness along the Labrador coast. For the feature selection, an automated heuristic-based algorithm is proposed which uses a polynomial together with an objective function based on mean square error (MSE). The use of polynomials here is soley for the purpose of reducing the computational complexity of the algorithm. For the estimation part, a robust and accurate method called hierarchical selective ensemble randomized neural network (HSE-RNN) is developed. The hybrid intelligent model uses data from the moderate resolution imaging spectro-radiometer (MODIS), and advanced microwave scanning radiometer-earth (AMSR-E) observing system in addition to atmospheric and oceanic variables from forecasting systems. It is worth mentioning that to further ascertain the veracity of the proposed intelligent model; two different databases are considered which correspond to low and high frequency channels from AMSR-E.

In summary, the main motivation behind the current research are as below:

  1. (1)

    To demonstrate the potential of statistical machine learning techniques for sea-ice thickness estimation, as an intricate real-life problem,

  2. (2)

    To carry out a comparative study considering a number of powerful randomized and non-randomized neural networks to derive conclusions regarding the potential of stochastic learning for neural networks. In recent years, working on statistical machine learning has become a hot topic, and indicating the potential of such easy-to-train networks for tedious real-life applications has merit to the community of neurocomputing.

The rest of the paper is organized, as follows. Section 2 is devoted to the detailed description of the studied region as well as the characteristics of data collected from MODIS and AMSR-E sensors. The detailed steps required for the implementation of the hybrid intelligent system is given in Section 3. The experimental setup for conducting the simulations is scrutinized in Section 4. Section 5 is devoted to the results and discussions. Finally, the paper is concluded in Section 6.

2 Description of collected database

This section is given in three sub-sections. First, the characteristics of the sea-ice cover along the Labrador coast are described. Thereafter, the procedures required for estimating sea-ice thickness from MODIS and AMSR-E sensors are discussed.

2.1 Studied region

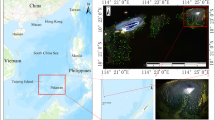
For this study, the chosen region is located along the east coast of Canada, which includes the sea-ice along the Labrador coast and the northern coast of Newfoundland.

For the current simulation, the available data over the period of 1st February to 28th February are considered. At this time of year the Labrador coast is ice-covered, yet the ice is not too thick to be measured by VIS/IR and passive microwave sensors. The sea-ice of the studied region is bounded to the east by the Labrador current, and is bounded to the west by the Labrador coast and Newfoundland. The observations indicate that the ice starts to appear along the Labrador coast in December and becomes thicker through January and February. The sea-ice cover includes a marginal ice zone composed of small ice floes near the open water, with the ice becoming thicker and more consolidated toward the land boundary. It is worth pointing out that sometimes there may be some coastal polynya between the consolidated ice region and the landfast ice.

2.2 AMSR-E data

The AMSR-E sensor uses six different frequencies, 6.9, 10.9, 18.9, 24.5, 36.5, and 89 GHz, to measure radiation in the passive microwave range of the electromagnetic spectrum. The footprint of each of these frequencies is approximately elliptical, with size ranging from 74 km × 43 km for 6.9GHz to 6 km × 4 km for 89GHz. To reduce uncertainty that can arise when data is averaged or resampled, in this study, swath data is used. Information associated with pixels with a distance of up to half of the sensor footprint away from the land boundaries are not considered due to the land contamination associated with the sensor footprint.

2.3 MODIS data

The MODIS sensor measures radiation in the VIS/IR range of electromagnetic spectrum. The sea-ice thickness is calculated using a heat balance equation [40]. The inputs to the heat balance are the sea-ice surface temperature from MODIS, and atmospheric variables from the Global Environmental Multiscale (GEM) model [9] as described in [36]. The sea-ice surface temperature is calculated using data from the infrared channels and the split window technique [13]. Here, the authors use MOD29 sea-ice surface temperature product which is prepared by the National Snow and Ice Data Center [14]. This product consists of swath data at 1 km resolution in which each pixel has been screened for cloud contamination. The reported results include surface temperatures ranging from 243K to 271K. The authors only select the nighttime images to suppress the undesired effects of uncertainty associated with the surface albedo and shortwave radiation [40]. Figure 1 depicts a sample image of the surface temperature calculated using data from the MODIS sensor.

Fig. 1
figure 1

Sea-ice surface temperature from MODIS for February 9, 0535 UTC

Full size image

2.4 Data from the forecasting system

The brightness temperature data from the higher frequency channels on the AMSR-E sensor (18.9 GHz and above) are influenced by atmospheric effects, such as cloud liquid water and water vapour. In addition, brightness temperatures at all frequencies are a function of the sea-ice or ocean surface temperature, the windspeed and the sea-ice surface conditions (e.g. salinity and roughness). While the surface conditions are difficult to take into account, data for the other variables is provided from an atmospheric weather forecasting model (GEM) and ice-ocean model, as described in a previous study [35]. These variables form the additional columns of the database used in the present study.

3 Methodology

The methodology is described in two sub-sections. First, the steps required for the implementation of the automatic feature selection mechanism are presented. Thereafter, the structure of the considered estimation technique, i.e. HSE-RNN, is scrutinized.

3.1 Automatic feature selection mechanism

The considered feature selection mechanism couples any given metaheuristic algorithm to a polynomial curve-fitting tool and tries to extract the most important features using an objective function based on mean-squared error (MSE) and complexity of the database. Prior to proceeding with the description of the considered metaheuristic, i.e. chaotic particle swarm optimization with adaptive inertia weight (CPSO-AIW) [27], the objective function used for feature selection is presented. The objective function should be devised such that a trade-off is created between the complexity of the final database and its accuracy for the prediction of the desired output. This enables CPSO-AIW to effectively explore the potential variables and select those having the highest impact on the output signal, i.e. sea-ice thickness. Suppose the training dataset is given by \(\mathfrak {D}=\lbrace (\mathbf {z}_{1},\,y_{1}),\,\dots ,\,(\mathbf {z}_{n},\,y_{n})\rbrace \), where \(\mathbf {z}_{i}=(z_{i,\,1},\,\dots ,\,z_{i,\,D})^{T}\) is a vector of D predictors from the database and y i is the respective response value, i.e. sea ice thickness from MODIS for the training data point i, and n is the training sample size. Let us indicate the number of features selected by CPSO-AIW by p, then, the following objective function is used at the heart of CPSO-AIW:

$$ J=\frac{1}{n}\sum\limits_{i=1}^{n}(y_{i}-f_{_{P}}(\mathbf{z}_{i}))^{2}+\lambda_{1}\,p\,, $$
(1)

where \(f_{_{P}}\) is a polynomial approximation for the target function f, and λ 1 is the tuning or penalizing parameter which is set to λ 1 = 0.1 in practice, to balance the effect of both terms in the objective function. The first part of the objective function represents the accuracy of the polynomial trained by the selected features, and the second term represents the complexity of the database. It is desirable in practice to reduce the number of features required for modelling for parsimony and interpretability of the final model.

The polynomial f P considered in (1) is a full-rank second order polynomial. This is an acceptable curve-fitting, and at the same time, has a very trivial complexity, and thus, can be used at the heart of CPSO-AIW for data-mining. In this paper, we consider \(f_{_{P}}\) to be a second-order polynomial

$$f_{_{P}}(\mathbf{z})=\beta_{0}+\boldsymbol{\beta}^{T}\mathbf{z}^{T}+\mathbf{z}^{T}\,\mathbf{B}\,\mathbf{z}=\beta_{0}+\sum\limits_{j=1}^{D}\beta_{j}\,z_{j} +\sum\limits_{k=1}^{D}\sum\limits_{\ell=1}^{D}\beta_{k,\,\ell}\,z_{k}\,z_{\ell}\,, $$

where β 0 is the intercept, \(\boldsymbol {\beta }=(\beta _{1},\,\dots ,\,\beta _{D})^{T}\) is the first order coefficients and

$$\mathbf{B}=\begin{array}{llll} \beta_{1,\,1} & \beta_{1,\,2}&{\cdots} &\beta_{1,\,D}\\ \beta_{2,\,1} & \beta_{2,\,2}&{\cdots} &\beta_{2,\,D}\\ {\ldots} & {\ldots} & {\ldots} & {\ldots} \\ \beta_{D,\,1} & \beta_{D,\,2}&{\cdots} &\beta_{D,\,D} \end{array} $$

represents the matrix of the second order coefficients in the polynomial f P .

In the rest of this section, the authors intend to explain the algorithmic structure of CPSO-AIW used for data mining. CPSO-AIW is a modified version of chaotic PSO (CPSO) proposed in [8]. CPSO is an agent-based stochastic optimizer that uses the concept of chaos and PSO for effective exploration/exploitation of the objective landscape. The efficacy of CPSO for feature selection and clustering tasks has been proven through several comparative numerical studies, as reported by [8] and [27]. The reported results are also in agreement with the authors’ own assessment. The subtle modification made in this paper is the adoption of well-known adaptive intertia weight (AIW) strategy to further balance the intensification/diversification properties of updating rule at the heart of CPSO. The steps required for the implementation of CPSO-AIW are given below:

  • Step 1. Randomly initialize a swarm (population) of m particles (candidate solutions), within the solution space. Suppose \(\mathbf {u} = (u_{1},\, u_{2},\,\dots ,\, u_{D})^{T}\), with \(0\le u_{j}\le 1,\,j=1,\,\dots ,\,D\), and \(\mathbf {v} = (v_{1},\, v_{2},\,\dots ,\,v_{D})^{T}\) represent the position and velocity of a particle in the swarm, respectively. Here, D is the dimension of particles which is equal to the dimensionality of the explanatory variables or predictors in the collected database \(\mathfrak {D}\). Since \(0\le u_{j}\le 1,\,j=1,\,\dots ,\,D\), by using a simple round command in Matlab, each of these variables is rounded to values 0 or 1. In this way, if the jth variable of a particle corresponds to 1, it means that jth feature z j in the database is considered for estimation of sea-ice thickness, and vice versa, the value 0 implies that jth feature z j of the database is neglected. It is clear that

    $$\sum\limits_{j=1}^{D}\text{round}(u_{j})=p\,.$$

  • Step 2. For each of these particles, train the second-order polynomial \(f_{_{P}}\) to have an estimation of sea-ice thickness \(\widehat {f}_{_{P}}\), and calculate the MSE of each polynomial using the observed values of sea-ice thickness measured by the MODIS sensor using the formula

    $$\frac{1}{n}\sum\limits_{i=1}^{n}(y_{i}-\widehat{f}_{_{P}}(\mathbf{z}_{i}))^{2}\,.$$

    Then, calculate the objective value of each particle using (1).

  • Step 3. Based on (1), determine the fitness of each particle (solution), and update the global best, denoted by g best, and particles best, denoted by p best vectors.

  • Step 4. Update the velocities and positions of all particles in each iteration using the following equations:

    $$\begin{array}{@{}rcl@{}} \text{Cr}(t)&=&\,K\cdot\text{Cr}(t-1)\cdot(1-\text{Cr}(t-1))\,, \\ \nu_{i,\,j}(t)&=&\,\eta(t)\cdot\nu_{i,\,j}(t-1)+c_{1}\cdot\text{Cr}(t)\cdot(\text{pbest}_{i,\,j}-u_{i,\,j}(t-1))\\ &+&c_{2}\cdot(1-\text{Cr}(t))\cdot(\text{gbest}_{j}-u_{i,\,j}(t-1))\,, \\ \eta(t)&=&\,\eta_{0}-\frac{t}{T}\,\eta_{0}\,,\\ u_{i,\,j}(t)&=&\,u_{i,\,j}(t-1)+v_{i,\,j}(t)\,, \end{array} $$

    where \(i=1,\,\dots ,\, m\) refers to the particle i, \(j=1,\,\dots ,\,D\) shows the jth dimension of each particle, and K is equal to 4. In addition, η 0 is the initial inertia weight equal to 1.45, and both c 1 and c 2 are equal to 2. It should be noted that the initial value of Cr(0) can be any value spanning the unity except {0, 0.25, 0.5, 0.75}. For a definition of the logistic map Cr(⋅), we refer to [27].

  • Step 5. Terminate the procedure if the stopping criterion, that is the maximum number of iterations for our case study, is met. Otherwise, return to Step 2 and repeat the procedure.

The flexibility of the proposed heuristic methodology lies in the fact that any given metaheuristic can be assigned for optimizing the objective function J given in (1). This will be shown in the results and discussion section.

3.2 Hierarchical selective ensemble RNN

The formulation of HSE-RNN is given in two different parts. Firstly, the mathematical formulation of RNN is provided, and thereafter, the architecture of HSE-RNN is explained.

3.2.1 Randomized neural network with Tikhonov regularization

In the literature of neural computation, there exists an interesting class of networks, known as random based neural networks, which have successfully been applied to function approximation and classification tasks. The potential of multi-layer feedforward neural network with random weights was initially investigated for regression tasks by Hornik [17]. The outcome of the study by Hornik has shown the power of randomized neural networks (RNNs) for estimation of nonlinear functions. The performance of randomized radial basis functions (RBFs) has also been examined in which the same width has been assigned to the basis functions [31]. The results clearly demonstrated the potential of RBF networks to serve as universal approximation tools. The results of the above primary investigations have been extended over the past two decades and a comprehensive investigation has been carried out which clearly demonstrated the potential of random based learning systems for designing feed-forward neural networks [33], radial basis neural networks [4, 25], extreme learning machines [19], and functional link nets [30]. Given the acceptable computational performance of feed-forward RNN [33], which is in good agreement with the authors own experiments, this network is used at the heart of the proposed hierarchical ensemble architecture.

Let us assume that after applying the feature selection in Section 3.1, the database \(\mathfrak {D}\) becomes \(\mathfrak {D}^{\ast }=\lbrace (\mathbf {x}_{1},\,y_{1}),\,\dots ,\,(\mathbf {x}_{n},\,y_{n})\rbrace \), where \(\mathbf {x}_{i}=(x_{i,\,1},\,\dots ,\,x_{i,\,p})^{T}\) represents the p dimensional (input) vector of the selected predictors and y i represents the response variable for the ith observation, respectively. Consider that RNN possesses N neurons in its hidden layer. Then, we assume the following relationship between the input vectors x i ’s and the target function f

$$ \sum\limits_{j=1}^{N}w_{j}\,g(\boldsymbol{\alpha}_{j}^{T}\,\mathbf{x}_{i}+b_{j})=f(\mathbf{x}_{i})\,,\qquad i=1,\,\dots,\,n,\, $$
(2)

where \(\boldsymbol {\alpha }_{j}=(\alpha _{j,\,1},\,\dots ,\,\alpha _{j,\,p})^{T}\) represents the synaptic weight vectors connecting the input nodes to the jth hidden node, w j shows the weight connecting the the jth hidden node to the output nodes, and g stands for a continuous activation function, which is the sigmoid function in this paper, i.e.

$$g(x)=\frac{e^{x}}{1+e^{x}} \qquad \text{ for} \quad x\in\mathbb{R}\,.$$

Let

$$\begin{array}{@{}rcl@{}} &&\mathbf{H}=\begin{array}{ccc} g(\boldsymbol{\alpha}_{1}^{T}\,\mathbf{x}_{1}+b_{1}) & {\dots} & g(\boldsymbol{\alpha}_{N}^{T}\,\mathbf{x}_{1}+b_{N})\\[-2pt] {\vdots} & {\vdots} & \vdots\\ g(\boldsymbol{\alpha}_{1}^{T}\,\mathbf{x}_{n}+b_{1}) & {\dots} & g(\boldsymbol{\alpha}_{N}^{T}\,\mathbf{x}_{n}+b_{N}) \end{array}\,,\quad \mathbf{y}=\begin{array}{c} y_{1}\\[-2pt] \vdots\\[-2pt] y_{n} \end{array}\,,\\[-2pt] \quad &&\mathbf{w}=\begin{array}{c} w_{1}\\[-2pt] \vdots\\[-2pt] w_{N} \end{array}\,. \end{array} $$

To fit the function f defined in (2), the RNN algorithm discussed in [33] allows the user to choose α j ’s and b j arbitrarily at random and apply the least square method to estimate the hidden output weight vector w, that is

$$ \min\limits_{\mathbf{w}}\|\mathbf{y}-\mathbf{H}\,\mathbf{w}\,\|_{_{2}}^{2}\,, $$

where \(\|\,\mathbf {a}\,\|_{_{2}}\) represents the Euclidean norm of an arbitrary vector a. It is known that if the matrix H T H is invertible, the least square solution is

$$\widehat{\mathbf{w}}=\left( \mathbf{H}^{T}\,\mathbf{H}\right)^{-1}\mathbf{H}^{T}\,\mathbf{y}\,.$$

Generally, in practice, the condition value of matrix H T H is close to zero and therefore the solution \(\widehat {\mathbf {w}}\) is not stable. To resolve this problem, [33] suggested using the Moore-Penrose generalized inverse. Based on the promising results obtained through this method, the RNN’s research community investigated other techniques to further increase the stability of the obtained results, and found that a better and more numerically stable solution is obtained by a penalized least square problem known as Tikhonov regularization or the ridge regression [5]. Therefore, in line with the recommendations given in [5], we do the following optimization to find the Tikhonov solution:

$$\min\limits_{\mathbf{w},\,\lambda_{2}}\left\lbrace\,\|\mathbf{y}-\mathbf{H}\,\mathbf{w})\,\|_{_{2}}^{2} +\lambda_{2}\,\|\mathbf{w}\,\|_{_{2}}^{2} \,\right\rbrace\,. $$

The solution to this optimization is given by the ridge regression estimate [15]:

$$ \widehat{\mathbf{w}}=(\,\mathbf{H}^{T}\,\mathbf{H}+\lambda_{2}\,\mathbf{I}\,)^{-1}\,\mathbf{H}^{T}\,\mathbf{y}\,, $$
(3)

where λ 2 ≥ 0 is the ridge or Tikhonov regularization parameter which is set to be λ 2 = 0.001, in this paper.

3.2.2 The overall architecture of HSE-RNN

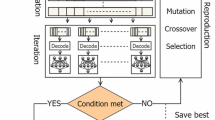
The main motivation behind the proposition of HSE-RNN lies in its capability to effectively cope with databases with blended information as well as yielding a computationally robust and accurate estimator. HSE-RNN retains a trade-off between complexity and accuracy. The hierarchical part of HSE-RNN is inspired based on the concept of deep learning. Deep-layer neural networks are composed of a hierarchy of networks, inspired based on hierarchical information processing of the human brain, and are capable of extracting different information layer-by-layer. This drastically increases the complexity of computations, which prevents the applicability of deep-learning networks for real-time applications as well as big data analysis [32]. To cope with such a challenge, HSE-RNN uses a 2 layer hierarchical ensemble, and thus, possesses a neat balance between deep and shallow networks. The experiments reveal that considering such a hierarchical architecture significantly increases the robustness of the resulting ensemble estimator and at the same time does not have a meaningful effect on the computational complexity of the system. Furthermore, our experiments have revealed that selecting a hierarchical structure with two layers prevents the resulting estimator from falling into the pit known as over-fitting. The architecture of HSE-RNN is shown in Fig. 2. In the first layer of HSE-RNN, a set of independent groups of ensembles are formed, and thereafter, a selection mechanism is used to extract the optimum components from each of those independent groups. The selected optimum RNN components are then transferred to the second layer, and another component selection is performed to select the most optimum values to form the final ensemble. It is worth pointing out that such a strategy is best suited for our case study in which a large database is collected from AMSR-E and MODIS sensors.

Fig. 2
figure 2

Procedure for designing HSE-RNN architecture

Full size image

For the implementation of HSE-RNN, four important parameters should be set. It is important to verify the number of independent ensembles in the first layer, the number of components in each ensemble, the number of optimum RNNs selected from each ensemble, and the number of optimum RNNs selected from the ensemble at the second layer. The training of each RNN component at the heart of HSE-RNN is performed using the analytical approach described in (3). Furthermore, most of the parameters defined above can be set based on trial and error. The only issue which should be considered pertains to providing a mathematical definition for the selection mechanism used in HSE-RNN. In a previous work by the authors’ research group, it was demonstrated that non-negative least learning method combined with negative correlation is an efficient approach for designing an ensemble of RNNs [28]. In this paper, an efficient method is used to select the fittest RNNs to form HSE-RNN, and the previous ensembling mechanism [28] is considered as a rival method. Assume that M base learners (RNNs) are considered to be combined for forming HSE-RNN. We treat all the individual learners equally by assigning the same weights

$$ \omega_{i}=\frac{1}{M} \qquad i=1,\,2,\,\dots,\,M\,. $$
(4)

Assume that the output of the ith RNN learner is indicated by \(\widehat {f}_{i}(\mathbf {x})\), then, the output of ensemble can be written as:

$$ \widehat{f}(\mathbf{x})=\sum\limits_{i=1}^{M}\omega_{i}\,\widehat{f}_{i}(\mathbf{x})\,. $$
(5)

Now, it is just needed to define the notions of training error and correlation. Suppose that the training inputs are randomly sampled from a distribution p(x), and the target value is indicated by f(x). Then, the training error of ith base RNN learner and the ensemble are measured by the square error loss, respectively, presented as follows:

$$ \begin{array}{ll} L(\widehat{f}_{i}(\mathbf{x}),\,f(\mathbf{x}))&=(\widehat{f}_{i}(\mathbf{x})-f(\mathbf{x}))^{2}\,,\\ L(\widehat{f}(\mathbf{x}),\,f(\mathbf{x}))&=(\widehat{f}(\mathbf{x})-f(\mathbf{x}))^{2}\,. \end{array} $$
(6)

Therefore, the global errors for the ith base learner \(\widehat {f}_{i}(\cdot )\) and the ensemble \(\widehat {f}(\cdot )\) are given by the following integrated square error losses

$$\begin{array}{@{}rcl@{}} L(\widehat{f}_{i},\,f)&=&\int(\widehat{f}_{i}(\mathbf{x})-f(\mathbf{x}))^{2}\,p(\mathbf{x})\,d\mathbf{x}\,,\\ L(\widehat{f},\,f)&=&\int(\widehat{f}(\mathbf{x})-f(\mathbf{x}))^{2}\,p(\mathbf{x})\,d\mathbf{x}\,. \end{array} $$
(7)

The correlation between ith and jth base learner RNNs, \(\widehat {f}_{i}\) and \(\widehat {f}_{j}\) can be defined as below:

$$ \widehat{\rho}_{i\,j}=\int(\widehat{f}_{i}(\mathbf{x})-f(\mathbf{x}))\,(\widehat{f}_{j}(\mathbf{x}) -f(\mathbf{x}))\,p(\mathbf{x})\,d\mathbf{x}\,. $$
(8)

On the other hand, from (4), (5) and (6), we have

$$\begin{array}{@{}rcl@{}} L(\widehat{f}(\mathbf{x}),\,f(\mathbf{x})) &=&\left( \sum\limits_{i=1}^{M}\omega_{i}\,\widehat{f}_{i}(\mathbf{x})-f(\mathbf{x})\right)\,\left( \sum\limits_{j=1}^{M}\omega_{j}\,\widehat{f}_{j}(\mathbf{x})-f(\mathbf{x})\right)\\ &=&\left( \sum\limits_{i=1}^{M}\omega_{i}\,\left( \,\widehat{f}_{i}(\mathbf{x})-f(\mathbf{x})\,\right)\right)\,\left( \sum\limits_{j=1}^{M}\omega_{j}\,\left( \,\widehat{f}_{j}(\mathbf{x})-f(\mathbf{x})\,\right)\,\right)\\ &=&\sum\limits_{i=1}^{M}\sum\limits_{j=1}^{M}\omega_{i}\,\omega_{j}\,\left( \,\widehat{f}_{i}(\mathbf{x})-f(\mathbf{x})\,\right)\,\left( \,\widehat{f}_{j}(\mathbf{x})-f(\mathbf{x})\,\right)\,, \end{array} $$
(9)

which in turn, we obtain the integrated error of (7) in terms of the correlations \(\widehat {\rho }_{i\,j}\)

$$ \begin{array}{ll} L(\widehat{f},\,f)&=\sum\limits_{i=1}^{M}\sum\limits_{j=1}^{M}\omega_{i}\,\omega_{j}\,\int\left( \,\widehat{f}_{i}(\mathbf{x})-f(\mathbf{x})\,\right)\,\left( \,\widehat{f}_{j}(\mathbf{x})-f(\mathbf{x})\,\right)\,p(\mathbf{x})\,d\mathbf{x}\\ &=\sum\limits_{i=1}^{M}\sum\limits_{j=1}^{M}\omega_{i}\,\omega_{j}\,\widehat{\rho}_{i\,j}\\ &=\frac{1}{M^{2}}\sum\limits_{i=1}^{M}\sum\limits_{j=1}^{M}\widehat{\rho}_{i\,j}\,. \end{array} $$
(10)

Presume that the k th base learner is omitted from the resulting ensemble, then, the error of the new pruned ensemble \(\widehat {f}^{(-k)}\), using (10), can be given as below:

$$L(\widehat{f}^{(-k)},\,f)=\frac{1}{(M-1)^{2}}\sum\limits_{{i=1} \atop {i\neq k}}^{M}\sum\limits_{{j=1} \atop {j\neq k}}^{M}\widehat{\rho}_{i\,j}\,. $$

Then, it can be easily shown that the necessary condition for omitting the k th base learner from the ensemble can be written as follows:

$$(2\,M-1)\,\sum\limits_{{i=1} \atop {i\neq k}}^{M}\sum\limits_{{j=1} \atop {j\neq k}}^{M}\widehat{\rho}_{i\,j}<2\,(M-1)^{2}\,\sum\limits_{{i=1} \atop {i\neq k}}^{M}\widehat{\rho}_{i\,k}+(M-1)^{2}\,L(\widehat{f}_{k},\,f)\,. $$

By using the above criterion, the eligibility of each of the base learners in the ensemble is checked, and finally, a set of base leaners with the highest fitness are retained in the ensemble. Then the selected RNNs are transferred to the second layer, and another selection procedure is carried out to select the base learners of the final ensemble. As the formulations required for ensemble selection is not too complicated, HSE-RNN can be executed in an acceptable period of time for our case study.

3.3 Aim of the resulting intelligent machine

As mentioned in the previous sub-sections, by putting the two intelligent methods, CPSO-AIW and HSE-RNN, together, a systematic structure is built-up which initially performs an unsupervised feature selection based on the objective function given in previous sections, and thereafter, tries to develop an efficient map to be used for analyzing the impact of input data on the output data. Apparently, these two algorithms work independently, and cannot affect each other. The point is that the feature selection conducted by CPSO-AIW technique can reduce the dimensionality of the input space which consequently makes it easier for the second algorithm, i.e. HSE-RNN, to create a map between input space and output space. It can be inferred that the two independent algorithms are working altogether for the same task, i.e. sparse and accurate modeling.

4 Experimental setup

Prior to proceeding with the simulations, a set of parameters should be set to make sure the rival techniques work properly. As it was mentioned, for both feature selection algorithm and the proposed estimator, a number of rival methods are taken into account. To check the efficacy of CPASO-AIW, some rival metaheuristics, i.e. genetic algorithm (GA) [7], artificial bee colony (ABC) [23], differential evolutionary algorithm (DEA) [10], and firefly algorithm (FA) [12], are adopted from the literature. For GA, the number of chromosomes of 40, the crossover probability (p c ) of 0.8, the mutation probability (p m ) of 0.02, and the number of elite chromosomes (e) of 1, are selected. In addition, the arithmetic graphical search (AGS), tournament selection, and simulated binary crossover operators are adopted to form the algorithmic structure of GA. For ABC algorithm, the number of onlooker and employed bees of 20, and the limit number of 10 are taken into account. In this way, the first bee which fails to update its position after 10 tries is fed to scout bee search phase to renew its solution vector. For DEA, the number of chromosomes of 40 is selected. Moreover, the scale factor of 0.6, and the crossover rate of 0.9 are taken into account. For FA, 40 fireflies are used for the optimization procedure. Also, the maximum attraction (\(\beta _{\max }\)) of 1 and the absorption rate (Υ) of 1 are selected for the sake of optimization. All algorithms are performed the optimization for 100000 function evaluations, and through 10 independent runs with random initial seeding of heuristic agents. To have a fair comparison of the performance of the considered rival techniques, the results of each algorithm are reported in terms of robustness (standard deviation (std.)), accuracy (mean), best (min), and worst (max) values through 30 independent runs. Let J i denote the value of objective function J at the ith run, therefore these metrics can be mathematically expressed as follows:

$$\begin{array}{@{}rcl@{}} \text{Mean fitness}&=&\bar{J}=\frac{1}{30}\sum\limits_{i=1}^{30}J_{i}\,,\\ \text{Best fitness}&=&\min\left\lbrace J_{i}\,\,|\,\,i=1,\,\dots,\,30\right\rbrace\,,\\ \text{Worst fitness}&=&\max\left\lbrace J_{i}\,\,|\,\,i=1,\,\dots,\,30\right\rbrace\,,\\ \text{Robustness}&=&\sqrt{\frac{1}{29}\sum\limits_{i=1}^{30}(J_{i}-\bar{J})^{^{2}}}\,. \end{array} $$

Also, to clarify the acceptable robustness and accuracy of HSE-RNN, several powerful estimation systems, i.e. randomized neural network (RNN) [33], optimally pruned randomized neural network (OP-RNN), Lasso-regularized randomized neural network (RNN-L1) [15], and back-propagation neural network (BPNN) [2], are considered. It is worth mentioning that OP-RNN is formed by the integration of RNN and a pruning methodology which retains the most influencial neurons in the hidden layer by means of multiresponse sparse regression neuron pruning. Furthermore, the pruning method uses leave-one-out cross-validation criterion to ensure the optimal selection of active neurons [15]. The performances of the rival estimators are compared in terms of accuracy and robustness. Through a trial and error procedure, it was observed that considering 4 independent ensemble groups with 4 sole RNN components in each of those ensembles is the optimal choice. For all of the methods, except HSE-RNN, 50 hidden nodes are considered at the hidden layer. To form the sole components of the ensemble architecture, RNNs of different number of hidden nodes within the range of 5 to 25 are considered.

For each of the sole RNN components, the parametrization involves the selection of the values of synaptic weights and biases for input-hidden nodes stochastically from a Guassian distribution. The sallient asset of using RNNs lies in the fact that there is no need for a computationally expensive effort to parametrize the model since the training process is stochastic. For BPNN, steepest descend optimization algorithm with learning rate of 0.1 is adopted to perform the gradient-based learning. The back propagation learning continues for 100 epochs.

In the collected input database, 8 different features are taken into account. These features are brightness temperature (x 1), wind speed (x 2), atmospheric water vapor (x 3), atmospheric cloud liquid water (x 4), sea-ice temperature (x 5), sea surface temperature (x 6), sea-ice concentration (x 7), and sea-ice thickness (x 8) from the ice-ocean model. The corresponding sea-ice thickness (y) for each data-pair in the database is captured from MODIS sensor. The considered data cover the measured values of both MODIS and ASMR-E sensors from 2nd February to 20th February, and contains 14639 and 17162 temporal data-pairs corresponding to low (6.9GHz) and high (36.5GHz) frequency AMSR-E channels, respectively. These two data sets will be referred to as the low and high frequency data bases. In the both databases only brightness temperatures from the vertically polarized AMSR-E channels are used as these channels are less sensitive to surface roughness than the horizontally polarized channels [39].

Figures 3 and 4 depict the characteristics of the features of the gathered database for the low and high frequencies, respectively. The forecasting model data used are the same for the both databases, the only difference being that for the low frequency database a spatial averaging operator is used to bring the spatial resolution of the model data to be the same as that of the AMSR-E data.

Fig. 3
figure 3

Features from the low frequency database. Top left is the brightness temperatures measured by ASMR-E sensor at low frequency (6.9GHz), while other panels are data from the atmospheric and ice-ocean models, interpolated to the time and spatial resolution of the AMSR-E data

Full size image
Fig. 4
figure 4

Features from the high frequency database. Top left is the brightness temperatures measured by ASMR-E sensor at high frequency (36.5GHz), while other panels are data from the atmospheric and ice-ocean models, interpolated to the time and spatial resolution of the AMSR-E data

Full size image

For all of the nodes, a log-sigmoid activation function is used. To work with a log-sigmoid activation function, all of the data should be normalized within the range of unity [0, 1], as below:

$$x_{i\,j}^{\ast}=\frac{x_{i\,j}-x_{j}^{\min}} {x_{j}^{\max}-x_{j}^{\min}}\quad\text{for} \, j=1,\,2,\,\dots,\,8\,, $$

where \(x_{j}^{\min }=\min \lbrace x_{i\,j}\,:\, i=1,\dots , n\rbrace \) and \(x_{j}^{\max }=\max \lbrace x_{i\,j}\,:\, i=1,\dots , n\rbrace \) for \(j=1,\,2,\,\dots ,\,8\,\).

To calculate the above function, the following relations should be taken into account:

  • a)    For the low frequency data:

    figure e

  • b)    For the high frequency data:

    figure f

It is also worth pointing out that to check the efficacy of the ensembling strategy, a rival selective ensembling strategy based on negatively correlated selection and non-negative least square learning is taken into account [26]. Furthermore, a regularized ensemble variant of RNN, proposed in a previous work of the authors, is adopted to check the power of the resulting bi-layer ensemble framework. The performances of all of the estimators considered are compared in terms of both accuracy and robustness.

All of the simulations are carried out using the Matlab software with Microsoft Windows 7 operating system on a PC with a Pentium IV, Intel core i7 CPU, and 4 GBs RAM.

5 Results and discussion

In this section, the results of the numerical simulations are given in different stages. In the first stage of the numerical simulations, different metaheuristics have been used at the heart of the considered feature selection algorithm to evaluate the computational potential of CPSO-AIW. In the second stage of the experiment, the selected features are used to train the considered rival estimators for measuring the sea-ice thickness. Finally, some characteristics of the obtained results are discussed.

Figures 5 and 6 depict the evolution of the objective function at the heart of rival metaheuristics for low frequency and high frequency scenarios, respectively. It should be pointed out that, in the both figures, distinct colors represent the evolution curves of metaheuristics over independent runs. As metaheuristic methods have stochastic instinct, their performance may vary over independent runs. Therefore, the provided plots indicate the evolution of the objective function for 10 independent simulations, with the same initial seeding. As it can be seen, the variation of the exploration/exploitation characteristics of CPSO-AIW is less than the other algorithms over 10 independent runs. Apparently, for each of those independent runs, a fast convergence can be observed in the first 100 iterations, and after that, exploitation is performed to search the nearby solutions in the objective landscape. However, for all of the other rival methods, different exploration/exploitation behavior can be observed over independent runs. Indeed, for some simulations, the rival metaheuristics fall into local pitfalls at the very beginning of the procedure, and fail to change their direction towards more qualified regions. By inspecting the performance of metaheuristics for high frequency scenario, it can be seen that the obtained results are different from the low frequency ones. It can also be observed that for all of the rival methods, except for DEA, the exploration/exploitation behavior of the rival metaheuristics is relatively the same. By taking a more precise look into the obtained results, it was observed that in this case at the very beginning of the procedure, more features have been selected from the database, and therefore, the approximation error of polynomial interpolator decreases significantly. Overall, the obtained convergence profiles indicate that CPSO is highly capable of balancing its exploration/exploitation capabilities, and thus, is acceptable to be used at the heart of the proposed feature selection algorithm.

Fig. 5
figure 5

Evolution of the objective function over 1000 iterations for low frequency scenario

Full size image
Fig. 6
figure 6

Evolution of the objective function over 1000 iterations for high frequency scenario

Full size image

To have clear insight into the performance of the rival methods for selecting a set of features, the values of MSE and n are presented. Table 1 lists the obtained values of MSE, n, and J, for all of the rival methods over 10 independent runs for the low frequency scenario. As can be seen, for all of the rival methods, the suggested number of selected features equals 2 or 3. It can be also seen that, when 3 features are selected, the estimation error of the polynomial interpolator decreases significantly. However, in some cases, for example the solutions suggested by FA, GA, and ABC, it can be seen that when the number of selected features equals 2, the estimation error of the interpolator increases significantly. By taking a look at the selected features suggested by the rival methods from Table 2, it can be seen that CPSO-AIW has selected wind speed, sea-ice temperature, and sea-surface temperature as effective features for low frequency database. This is in agreement with the fact that brightness temperatures at a low frequency (e.g. 6.9GHz) are not sensitive to the atmosphere, but are sensitive to windspeed, and also indicates the known link between ice thickness and ice temperature for thin ice (e.g. less than 50cm). It is obvious that all of the other rival algorithms also suggest wind speed as an effective feature. However, they fail to extract the most influential features. Table 3 indicates the obtained values of MSE, n, and J, for all of the rival methods over 10 independent runs for the high frequency scenario. It is apparent that, for this case, the number of selected features is more than that of low frequency scenario. Indeed, this time, all of the metaheuristics suggest 4 to 6 features for accurate estimation. It is obvious that most of the independent optimization procedures converge to 6 features, and thus, it is statistically concluded that this amount of features is reasonable for high frequency database. Table 4 lists the selected features for the rival metaheuristics. It can be seen that the brightness temperature is selected by all of the rival metaheuristics. However, this was not the case for the low frequency scenario. In this case, CPSO-AIW suggests brightness temperature, wind speed, water cloud, sea-ice temperature, sea-ice concentration, and sea-ice thickness from the ice ocean model as effective features which will be used for sea-ice thickness estimation.

Table 1 Objective value, MSE, and number of selected variables of different rival methods over 10 independent runs for the low frequency scenario (all of these values are obtained after 1000 iterations)
Full size table
Table 2 The features offered by the rival nature-inspired optimizers for the low frequency database
Full size table
Table 3 Objective value, MSE, and number of selected variables of different rival methods over 10 independent runs for the high frequency scenario (all of these values are obtained after 1000 iterations)
Full size table
Table 4 The features offered by the rival nature-inspired optimizers for the high frequency database
Full size table

To investigate the robustness and accuracy of the rival feature selection mechanisms, the statistical results of 10 independent runs are plotted in Fig. 7. As it can be seen, the length of the box plot of CPSO-AIW is shorter than those of the other rival methods. This implies that the variation of the solutions suggested by CPSO-AIW is less than the other algorithms. Furthermore, the mean value of the box plot of CPSO-AIW for objective function J is lower than the other techniques which implies that CPSO-AIW has a higher success for minimizing the objective function. The statistical results clearly verify the efficacy of CPSO-AIW at the heart of the feature selection algorithm.

Fig. 7
figure 7

Box plots for obtained MSE and n for the rival heuristics

Full size image

After selecting the features for low frequency and high frequency databases, the information is used for training the considered estimators for predicting sea-ice thickness. Tables 5 and 6 list the estimation error results for both training and testing phases of low and high frequency data, respectively. The interesting observation lies in the superior performance of both HSE-RNN and ERNN-NCL over the other rival techniques. It can be seen that both of the HSE-RNN and ERNN-NCL ensembling strategies appropriately improve the accuracy and robustness of the estimation. It can be also observed that the standard deviation of HSE-RNN is less than that of ERNN-NCL. This indicates that the selection mechanism of HSE-RNN can further improve the robustness of the resulting ensemble architecture, indicating the proposed method is a good choice for the considered case study. As mentioned previously, data for sea-ice estimation are from satellite-borne sensors and are subject to various types of noise with different unknown distributions. With this regard, a high priority of the research is to make sure the developed model has an acceptable robustness. The obtained results indicate that the weakest performances belong to RNN and BPNN. This in turn implies that considering regularization approaches, in the form of both Lasso and Ridge (Tikhonov), can improve the performance of the base RNN. It is also worth pointing out that the authors used the sole HSE-RNN without the features selection operator to determine the influence of the feature selection process. The observed results indicated that the performance of the sole HSE-RNN is very close to that of the ERNN-NCL, and thus using the feature selection (and the consequent sparse learning) can improve both the accuracy and robustness of estimation. Figures 8 and 9 depict the correlation of the sea-ice thickness estimated by HSE-RNN and those measured by MODIS sensor for testing and training phases, respectively when both low and high frequency AMSR-E data are used. It is clear that for the both testing and training phases, the results are in agreement. It is interesting to note that the correlation appears stronger for ice thickness less than 0.3m, and for data from the 6.9GHz channel. This is in agreement with results from previous studies [36], although to understand the reason for this in the present case would require further study.

Table 5 The estimation error of the rival estimators for the low frequency database
Full size table
Table 6 The estimation error of the rival estimators for the high frequency database
Full size table
Fig. 8
figure 8

Sea-ice thickness estimated by HSE-RNN and MODIS for the low frequency scenario. Left panel is training, right panel is testing

Full size image
Fig. 9
figure 9

Sea-ice thickness estimated by HSE-RNN and MODIS for the high frequency scenario. Left panel is training, right panel is testing

Full size image

After demonstrating the performance of HSE-RNN, the authors intend to describe how the considered hierarchical ensembling strategy works. As it was mentioned, at the first layer, several independent ensembles are trained, and a set of them are selected, and are sent to the second layer so that the final selection can be done to form HSE-RNN. Table 7 indicates which of sole RNNs have been selected to form the architecture of HSE-RNN for estimating sea-ice thickness of low frequency data. It can be seen that the final ensemble is composed of 4 RNNs of which two belong to the first ensemble, one belongs to the third ensemble, and one belongs to the forth ensemble. Figure 10 depicts the number of hidden nodes of each of the sole RNNs formed at the first layer of HSE-RNN. By adding the number of hidden nodes of the resulting ensemble, it can be seen that 42 neurons are used for estimation part which is less than those used for sole RNNs. This in turn indicates that the proposed ensembling mechanism is capable of performing the estimation with less hidden nodes, and at the same time, improves the robustness and accuracy of estimation. The results of the simulations clearly indicate that with the aid of computational statistics tools, it is possible to develop advanced machine learning methods to be used as knowledge-based sensors for estimating the sea-ice thickness along the Labrador coast. HSE-RNN can also be retrained to estimate sea ice thickness in a different region or season by using different input information to increase the accuracy of estimation.

Table 7 The architecture and construction procedure of HSE-RNN
Full size table
Fig. 10
figure 10

Number of hidden nodes of potential RNNs in HSE-RNN (selected RNNs are shown in gray)

Full size image

6 Conclusion

In this paper, a systematic hierarchical intelligent tool was developed to estimate sea-ice thickness along the Labrador coast in Canada. The proposed intelligent tool is comprised of two parts, a feature selection mechanism, and an estimation tool to create a nonlinear map between a set of inputs measured by sensors and sea-ice thickness. The feature selection part was done by a particle swarm optimization with adaptive inertia weight (PSO-AIW) which was coupled to a polynomial curve fitting tool. The estimation was performed with the aid of hierarchical selective ensemble randomized neural network (HSE-RNN). The conducted experiments included two main parts. On the one hand, a thorough comparative study was performed to elaborate on the efficacy of PSO-AIW and HSE-RNN. In this way, several rival estimation methods, i.e. randomized neural network (RNN), optimally pruned RNN (OP-RNN), Lasso-regularized RNN (RNN-L1), and back-propagation neural network (BPNN), were taken into account. Also, genetic algorithm (GA), artificial bee colony (ABC), differential evolutionary algorithm (DEA), and firefly algorithm (FA), were considered to evaluate the performance of PSO-AIW. The outcome of the comparative numerical study revealed the high potential of both HSE-RNN and PSO-AIW for feature selection and estimation tasks. Indeed, it was observed that PSO-AIW can outperform its rivals over independent runs and is much more reliable to be used at the heart of feature selection mechanism. In the feature selection phase, the results indicated that the number of input elements required for the estimation of low-frequency data is less than those required for the estimation of high frequency data. In the estimation phase, the results indicated that the two layer selective ensemble design mechanism can significantly improve the robustness of the estimation. In fact, it was observed that HSE-RNN has a higher robustness compared to RNN, OP-RNN and RNN-L1. In general, the outcome of the current study demonstrated the applicability of intelligent methods for estimating the sea-ice thickness. Based on the promising outcomes of the current study, in the future, the authors intend to test the efficacy of intelligent methods by exposing them to a more comprehensive database including information regarding spatio-temporal behavior of ice thickness on the Labrador coast.