1 Introduction

In optimization field, scientists and engineers are usually faced with problems with more than one objective function, which are called multi-objective problems(MOPs). Compared to single objective problems, MOPs are more difficult to be solved since no single solution is available for these problems. Quite often, objectives in MOPs are conflicting with each other, and the performance of each objective can’t be improved without sacrificing the performance of at least one of the other. Hence, the goal for settling MOPs is to find a set of solutions that represent a trade-off among the objectives[3].

Recently, evolutionary and swarm-based search methods have been widely used to solve problems with multiple objectives, and they can be classified into different categories such as aggregative, lexicographic, sub-population, Pareto-based, and hybrid methods[43, 56]. Among the multi-objective methods, the majority of research is concentrated on Pareto-based approaches[20]. Pareto-based methods select a part of individuals based on the Pareto dominance notion as leaders(or non-dominated solutions) which constitute the non-dominated set of the current iteration. These methods use different approaches to continually update the non-dominated set till the algorithms are terminated. Usually leaders are maintained in an external archive.

Many evolutionary algorithms have been extended to deal with multi-objective problems in recent years. The main issues of multi-objective evolutionary algorithms(MOEAs) are selecting and updating individuals using evolutionary operations. In 1985, Schaffer proposed the first multi-objective evolutionary algorithm named Vector Evaluated Genetic Algorithm (VEGA) [41]. After that, some other MOEAs were available, such as MOGA [17], NPGA [22] and NSGA [44]. During the time from 1994 to 2003, MOEAs got rapid development and many new methods were proposed by introducing the external archive. Typical MOEAs in this phase were: SPEA[59], NSGA [11], PAES[27], PESA[9] and SPEA2[58], etc. From the year 2003 until now, the study on MOEAs went into a new phase, with import of various of new notions, mechanisms and strategies. During this time period, Indicator-Based Evolutionary Algorithm(IBEA)[57], MOCell[36], cooperative multi-objective evolutionary algorithms such as DCCEA [45] and CO-MOEA [8], and dynamic MOEAs such as DMOEA [51], and parallel MOEAs as PSFGA[38] were reported in corresponding literatures. Meanwhile, Multi-Objective Evolutionary Algorithm based on Division (MOEA/D) [52],Generalized Differential Evolution 3 (GDE3) [29], Enhancing MOEA/D with Guided Mutation and Priority Update (MOEA/DGM) [6], improved MOEA/D with adaptive weight vector adjustment (MOEA/D-AWA)[40], Multiple Trajectory Search (MTS) [48], LiuLiAlgorithm [33], an improved version of Dynamical Multi-Objective Evolutionary Algorithm (DMOEA-DD)[34] and Archive-based Micro Genetic Algorithm (AMGA) [46] are some of other competitive methods aimed to obtain a true Pareto front for multi-objective problems by considering the main issues of multi-objective evolutionary algorithms.

Besides, several types of swarm-based algorithms for MOPs have been presented in the literature. Particle swarm optimization (PSO) algorithm, proposed by Kennedy and Eberhart [16, 26], was modified in recent years so as to deal with optimization problems with more than one objective. Some typical kinds of PSO-based multi-objective algorithms were available, such as Multi-Objective Particle Swarm Optimization (MOPSO)[7], OMOPSO[42], Multi-objective Algorithm based on Comprehensive Learning Particle Swarm Optimizer(MOCLPSO)[23], Time Variant Multi-Objective Particle Swarm Optimization (TV-MOPSO)[47], Interactive Particle Swarm Optimization (IPSO)[1], PSO-Based Multi-Objective Optimization With Dynamic Population Size and Adaptive Local Archives (DMOPSO)[31], Dynamic Multiple Swarms in Multi-Objective Particle Swarm Optimization (DSMOPSO)[50], Speed-constrained Multi-objective PSO (SMPSO)[35], Competitive and Cooperative co-evolutionary Multi-objective Particle Swarm Optimization (CCPSO)[19], Two Local Bests (lbest) based MOPSO (2LB-MOPSO)[54], Pareto-based particle swarm optimization [55] ,etc.

The Artificial bee colony (ABC) algorithm is one of the most recently introduced swarm-based methods [2, 25]. In the ABC, there are three kinds of bees who do different tasks to make the algorithm useful. The employed bees will be sent to food sources and try to improve them by using neighbor information. The onlookers will choose one of those food sources based on the quality of food sources shared by employed bees, and then try to improved it. At last, scout bees will find the food sources which have not been optimized in a limited number of cycles so as to reinitialize them to get rid of poor solutions. The ABC seems particularly suitable for multi-objective optimization mainly because of solution quality and the high speed of convergence that the algorithm presents for single-objective optimization[3].

However, only a few works that extend ABC for handling multi-objective problems were reported in recent years. Hedayatzadeh et al. proposed a multi-objective artificial bee colony (MOABC) which has adapted the basic ABC algorithm and a grid-based approach for maintaining and adaptively assessing the Pareto front[21]. Omkar et al. presented a method called the Vector-Evaluated ABC (or VEABC) for the multi-objective design of composite structures [39]. In the VEABC, multiple populations were used to concurrently optimize problem at hand. Also, a multi-objective variant of the ABC was used by Atashkari et al. for the optimization of power and heating system[5]. A Pareto-based discrete artificial bee colony algorithm was used by Li et al. for solving multi-objective flexible job shop scheduling problems in which a crossover operator was developed for the employed bees and an external Pareto archive set was designed to record the non-dominated solutions found so far, besides, several local search approaches were designed to balance the exploration and exploitation capability of the algorithm[32]. A multi-objective ABC was used in [4] for scheduling in grid environment. Zou et al. proposed a novel algorithm based on Artificial Bee Colony (ABC) to deal with multi-objective optimization problems which used the concept of Pareto dominance to determine the flight direction of a bee, and it maintained non-dominated solution vectors in an external archive[60]. Finally, Akbari et al. proposed a new type of MOABC utilizing different types of bees (i.e. employed bees, onlookers, and scouts) and a fixed-sized archive which was maintained by an ε-dominance method. In this algorithm, the social information provided by the external archive was used by the employed bees to adjust their flying trajectories. The diversity over the external archive was controlled using a grid. The onlookers evaluate the solutions provided by the employed bees to adjust their next position. Finally, the scout bees replaced the solutions who had reached trial limit with a new random solution in the search space [3].

In this paper, we are going to suggest a new multi-objective ABC algorithm by dividing the whole searching space S into two subspaces S 1 and S 2. We abbreviate this algorithm as dMOABC, and it uses three colonies: two basic colonies are searching in subspaces, while the synthetic colony explores in space S. They share information through a multi-colony communication model. An external archive is adopted to store and maintain non-dominated solutions found so far. For the purpose of diversity maintenance, the dMOABC utilizes a self-adaptive grid to divide the objective space and maintain the archive, thus the achieved solutions may distribute uniformly along the true Pareto front. For basic colonies, only neighbor information is used for generating new food sources, while, in the synthetic colony, both neighbor and social information (shared by the external archive) are employed to adjust the flying trajectories of bees. Finally, the scout bee for each colony will do a random search if the food source is abandoned. Just like basic ABC algorithm, only one scout bee is allowed for each colony in each cycle.

The rest of the paper is organized as follows: some preliminaries on multi-objective optimization and artificial bee colony algorithm are presented in Section 2. Section 3 describes the details of the proposed dMOABC algorithm for handling problems with multiple objectives. Next, the experimental study is presented in Section 4. Finally, Section 5 concludes the paper.

2 Preliminaries

2.1 Multi-objective problems

Multi-objective problems (MOPs) concerns optimizing problems with multiple and often conflicting objectives. Generally, a MOP with D decision variables, M objectives, p inequality constraints and q equality constraints could be formulated as below[30]:

$$ \begin{aligned}Min &~\mathbf{y} = \mathbf{f(x)} = [f_1(\mathbf{x}),f_2(\mathbf{x}),\ldots,f_M(\mathbf{x})],\\&s.t. \\&g_i(\mathbf{x})\leq 0,i=1,2,\ldots,p,\\&h_j(\mathbf{x})=0,j=1,2,\ldots,q,\\\end{aligned} $$
(1)

where x = (x 1, x 2,…, x D )∈S and y = (f 1, f 2,…, f M )∈Y are called decision and target vectors; S and Y denote the searching and target spaces, respectively.

Unlike single objective optimization, solutions of MOPs are in such a way that the performance of each objective cannot be improved without sacrificing the performance of at least another one. Hence, the solution to a MOP exists in the form of an alternate trade-off known as a Pareto optimal set. The Pareto optimal set is defined based on Pareto dominance[3]. A vecotor x 1 is said to dominate another vector x 2 (denoted as \(\mathbf {x}_1 \prec \mathbf {x}_2\)), if and only if

$$ \begin{aligned}&f_i(\mathbf{x}_1)\leq f_i(\mathbf{x}_2), i=1,2,\ldots,M, \\&f_j(\mathbf{x}_1)< f_j(\mathbf{x}_2), \exists j\in \{1,,2,\ldots,M \}.\end{aligned}$$
(2)

Considering Pareto dominance, a vector x 0 is called Pareto optimal if and only if ¬ ∃ x ∈ S such that \( \mathbf {x} \prec \mathbf {x}_0\). We call the set containing all Pareto optimal solutions the Pareto optimal set (PS), which is defined as:

$$ PS = \{ \mathbf{x}_0|\neg \exists \mathbf{x} \in S ~and~ \mathbf{x} \prec \mathbf{x}_0 \}. $$
(3)

Therefore, a Pareto front (PF) for a given multi-objective problem and the Pareto optimal set PS , is defined as:

$$ PF = \{ \mathbf{f(x)}=[f_1(\mathbf{x}),f_2(\mathbf{x}),\ldots,f_M(\mathbf{x})]| \mathbf{x} \in PS\}. $$
(4)

Given a set A and an element x ∈ A, x is called the non-dominated solution concerning set A if x is not dominated by any member in set A. And all non-dominated solutions will constitute a set, which is called the non-dominated set. A Pareto based mutli-objective method tries to find the optimal Pareto front by continually updating the current non-dominated set, so as to make it approximate the true Pareto front as close as possible. When the algorithm is terminated, the output will be the final non-dominated set. However, the determination of a true Pareto front is a difficult task due to a large number of suboptimal Pareto fronts, and difficulty may be increased due to the nature of the Pareto front. More precisely, for most MOP methods, a partially convex, concave, or discontinuous problem is harder to solve compared to convex ones[3]. Actually, MOPs can be divided into two types: constrained and unconstrained MOPs. The focus of this paper is studying the second type of MOPs with only boundary constraint.

2.2 Artificial bee colony algorithm

Artificial bee colony algorithm (ABC), proposed by Karaboga in 2005 for real parameter optimization, is a recently introduced optimization algorithm which was inspired by the method adopted from a swarm of honey bees trying to locate food sources[24]. In the ABC algorithm, the honey bee colony contains three different kinds of bees[2, 25], namely, employed bees, onlooker bees and scout bees. Half of the colony consists of employed bees, and the other half includes onlooker bees. Employed bees search the food around the food source in their memory, meanwhile they share information about the quality of the food source with onlooker bees. Onlooker bees tend to select good food sources from those founded by the employed bees, then further search the foods around the selected food source. The employed bee whose food source is exhausted will become a scout [18, 49].

The ABC algorithm starts with randomly producing food source sites that correspond to the solutions in the allowable domain. Initial food sources are generated randomly within the range of the boundaries of the parameters, formulated as below[49].

$$ {X_{ij}} = l{b_j} + rand(0,1)(u{b_j} - l{b_j}), $$
(5)

where i = 1, 2, ⋯ , S n ;j = 1, 2, ⋯ , D; S n is the number of food sources and D is the dimensions of the problem to be optimized. ub j and lb j are upper and lower boundaries of parameter j respectively. random(0,1) is a random number uniformly distributed over interval [0,1].

After initialization, each employed bee is sent to a food source site to find a neighboring food source using local information (visual information), and then its quality is evaluated. In ABC, the following equation is used to find a neighboring food source:

$$ {V_{ij}} = {X_{ij}} + {\phi_{ij}}({X_{ij}} - {X_{kj}}). $$
(6)

A neighboring food source V i is determined by changing one parameter of each food source X i .In (6), j is a random integer in the range [1, D] and D is the number of dimensions. ϕ ij is a random number uniformly distributed over the range [-1,1] and k is the index of a randomly chosen solution. A parameter value produced by this operation may exceed its predetermined boundaries. In standard ABC, the value of the parameter exceeding its boundary is set to its boundaries, i.e. if X ij > ub j , then X ij = ub j ; if X ij < lb j ,then X ij = lb j . Both V i and X i are then compared against each other and the employed bee exploits the better food source in terms of fitness value which is calculated by (7), and this is known as greedy selection mechanism.

$$ fi{t_i} = \left\{ {\begin{array}{*{20}{c}} {1/(1 + {f_i})} & {if\begin{array}{*{20}{c}} {{f_i} \ge 0} \\ \end{array}} \\ {1 + abs({f_i})} & {if\begin{array}{*{20}{c}} {{f_i} < 0} \\ \end{array}} \\ \end{array}} \right., $$
(7)

where f i is the objective value of solution V i or X i . Equation 7 is used to calculate fitness values for a minimization problem, while the objective function can be directly used as a fitness function for maximization problems[49].

In the next step, each onlooker bee randomly chooses a food source according to the probability given in (8) by using roulette wheel selection scheme. Then, each onlooker bee tries to improve the selected food source using (6):

$$ {p_i} = \frac{{fi{t_i}}}{{\sum\nolimits_{j = 1}^{{S_n}} {fi{t_j}} }}, $$
(8)

where fit j is the fitness value of ith food source.

Finally, if a certain food source i cannot be improved for a predetermined number of cycles, referred to as limit, this food source is then abandoned. The employed bee that was exploiting this food source becomes a scout that looks for a new food source by randomly searching the problem domain using (5). In basic ABC, it is assumed that only one source can be exhausted in each cycle, and only one employed bee can be a scout. The algorithm will be terminated after repeating a predefined max number of cycles, denoted as Max_Cycles.

3 Multi-objective artificial bee colony algorithm based on division of the searching space

Our dMOABC algorithm is designed by dividing the searching space S into two independent parts S 1 and S 2, and it uses a special multi-colony model which will be described in Subsection 3.7 in detail. In this model, three colonies are used: two of them are basic colonies and they search in S 1 and S 2, while the third one is called synthetic colony whose search space is S. In dMOABC, all control parameters that must be determined aforehand are:

  • depth, the number of recursive subdivisions of the objective space carried out in order to divide the objective space into a grid for the purposes of diversity maintenance. Values between 3 and 6 are useful, depending on number of objectives[28].

  • ColonySize, the number of colony size, namely, the sum of the numbers of employed bees and onlooker bees. In our algorithm, three colonies are with the same colony size.

  • FoodNumber, the number of food sources. Since the number of employed bees equals to that of onlooker bees in dMOABC algorithm, the value of FoodNumber will be the half of the ColonySize.

  • limit, the abandonment criteria. A food source which could not be improved through ”limit” trials will be abandoned by its employed bee.

  • MaxIterations, the termination criteria. The value of this parameter could be tuned according to the maximum number of function evaluations(max_FEs) and ColonySize.

  • ArchiveSize, the maximum number of non-dominated solutions stored in the archive.

The dMOABC is a Pareto based algorithm with an external archive to store non-dominated solutions. Since the length of the archive are usually limited, we need an updating method to maintain it so that solutions latest included are not dominated by other archive members or vice versa. The dMOABC uses a self-adaptive grid method that was used in PAES [27] to achieve and maintain diversity. This method will be described in Subsection 3.3. In our dMOABC method, all colonies share the same archive, and it should be initialized as null before the algorithm really goes into run.

There are 6 parameters in dMOABC, but ColonySize, MaxIterations and ArchiveSize are general parameters, i.e., they are involved in many multi-objective intelligent algorithms. FoodNumber is determined by ColonySize, i.e., FoodNumber=ColonySize/2. Hence, there are only two parameters depth and limit that should be tuned by the users. The value of depth is suggested to be set between 3 and 6[28]. The larger of this value, the better of the approximated fronts will be, and the longer the computation time is. The limit is an important parameter in ABC algorithm family. According to our empirical experiment[49], this parameter is recommended to be set at a value varying from 100 to 200 for generally usage.

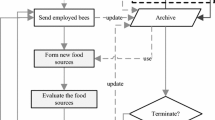
The flowchart of our dMOABC algorithm is shown in Fig. 1. The dMOABC method is constituted of the following main parts: Division, Initialization, Send Employed Bees, Send Onlooker Bees, Maintain archive, Send Scout Bees and Information Exchange. These parts are be explained in the following subsections respectively.

Fig. 1
figure 1

The flowchart of dMOABC algorithm

Full size image

3.1 Division

Each problem considered in this work has a number of decision parameters and these parameters, are continuous. Each parameter is limited to a span, between lower and upper bound values,which could be formulated as lb d ≤ x d ≤ ub d , where x d is the dth parameter or dimension, and lb d and ub d are lower and upper bounds of this dimension, respectively. Thus, for a D dimensional problem, the searching space S = [lb 1, ub 1]×[lb 2, ub 2]×...×[lb D , ub D ] will be a subset of R D. For each colony, each food source will be associated with a position vector x = (x 1, x 2,…, x D )∈S.

In our algorithm, the whole search space S is divided into two independent subsets, denoted as S 1 and S 2. This division is executed by equally dividing the first dimension of the problem, that is to say, the ranges of the first dimension of S 1 and S 2 are \([lb_1,\frac {(lb_1+ub_1)}{2}]\) and \([\frac {(lb_1+ub_1)}{2},ub_1]\), respectively. And the 2 to D dimensions of S 1 and S 2 keep the same as S. Mathematically, \(S_1=[lb_1,\frac {(lb_1+ub_1)}{2}]\times [lb_2,ub_2]\times ...\times [lb_D,ub_D]\) and \(S_2=[\frac {(lb_1+ub_1)}{2},ub_1]\times [lb_2,ub_2]\times ...\times [lb_D,ub_D]\), where ” ×” represents Cartesian product. It should be noted here that, except the first dimension, this division can be carried out according to any other dimensions. Two basic colonies will search in S 1 and S 2 independently, while the synthetic colony will seek solutions in the whole searching space S.

The division will enable more refined search for good solutions with less chances of missing some parts of the searching space S. Since the goal of multi-objective algorithms is to approximate a set instead of a single point, the performance of the algorithm is evaluated based on the closeness between the approximated and the true fronts, as well as the distribution of the computed non-dominated set. Thus, to achieve better approximated front, the algorithm can’t miss any part of the whole PF. When using only one colony, once it is dragged into a local minima, then there will be a higher chance that the algorithm may miss some parts of the whole true PF. But, if we use multi colonies, the probability of the occurrence of the above situation will be much lower. In our algorithm, as described before, basic colonies are independently searching in the subspaces, thus, the whole PF is divided into two parts and each part corresponds to a basic colony. Even if a basic colony is trapped, the synthetic colony could provide necessary remedy. This mechanism enhances the exploration abilities of the algorithm. Of course, more subspaces are feasible, but this may sacrifice the exploitation abilities of each colony, since the maximal number of function evaluations is fixed. To balance exploration and exploitation, we here use three colonies in the dMOABC algorithm.

3.2 Initialization

In the initialization phase, FoodNumber food sources will be randomly generated for each colony according to its corresponding searching space. Note again that the searching spaces for two basic colonies are S 1 and S 2, and that for synthetic colony is S. To be convenient for explanation, we will only take the synthetic colony as an example to show how to initialize it:

First, each food source will be initialized by a function named init(i, S),where i is the index of the food source and S is the searching space defined before. In this way, a D dimensional vector x i = (x i1, x i2,…, x iD ) will be assigned randomly to food source i through the following equation:

$$ x_{id}=lb_d + rand(0,1)\cdot(ub_d-lb_d), $$
(9)

where i = 1, 2, …, FoodNumber;d = 1, 2, …, D, and rand(0,1) is a random number distributed uniformly over the interval [0,1]; lb d and ub d are lower and upper bounds of the dth dimension respectively.

Second, a variable trial i will be assigned to each food source i in order to find food sources to be abandoned in the next iterations. A food source could not get optimized in a number of trials (i.e. limit), its related employed bee will turn into a scout bee and after doing a random search, it will turn back to be an employed bee again. Variable trial i is a counter of unsuccessful trials for food source i, and each trial i , i = 1, 2, …, FoodNumber is set to 0 in the initialization phase.

Finally, we calculate the objectives for each food source, and try to add it into the external archive. The global best food source gbest is initialized as a solution selected from the archive by using roulette wheel method. If the location of a solution is less crowded, then it will be chosen with higher probability. The following subsection will give details on archive maintenance.

3.3 Maintain archive

In dMOABC, an external archive is used to store and update all of the non-dominated solutions. The archive has a maximum size, ArchiveSize, which is set by the user to reflect the required number of final solutions desired. In order to make sure that solutions in the archive approximate the true Pareto front as close as possible, a self-adaptive grid is adopted for the purpose of diversity maintenance. Actually, maintaining archive involves two main tasks:

  • Update grid [27]. For a problem with m criterions, the whole objective space is divided by a m-dimensional grid which is used to keep track of the degree of crowding in different regions of the solution space. When a solution is generated its grid location is determined by using recursive subdivision and noted using a tree encoding. A map of the grid is also maintained, indicating for each grid location how many and which solutions in the archive currently reside there. When trying to add a candidate solution into the archive, the algorithm needs to first check whether the candidate exceeds the grid or not. If the candidate is located beyond the grid, the grid will be self-adaptively updated so as to make the new solution included. The objective space is then redivided, and grid locations for the new candidate and all solutions in the archive are recalculated. Besides, the degree of crowding(i.e., grid-location count) for each grid is also redetermined.

  • Add candidate solution into the archive [28]. After the grid is updated (if necessary), the new solution s will be added into the archive provided one of the following conditions is satisfied:

    a). the archive is empty ;

    b). the archive is not full and s is not dominated by or equal to any member in the current archive;

    c). s dominates any member in the archive ;

    d). the archive is full but s is non-dominated and is in a no more crowded square than at least one solution in the archive.

    In addition, the archive will be maintained such that all solutions are non-dominated. To be specific, all solutions that are dominated by s will be removed from the archive in case c.), and s will replace one of the archived solutions with the highest grid-location count in case d.).

3.4 Send Employed Bees

The pseudo code of Send_Employed_Bees() is given in Fig. 2. For each food source x i , its employed bee will explore a temporary position denoted as v i . The position v i is a copy of the food source with one randomly selected dimension d to be changed [3]. However, the updating equations for new positions are different for different types of colonies. Specifically, for basic colonies, one randomly selected neighbor k is used to generate new positions which could be formulated as follows:

$$ v_{id} = x_{id} + \phi_{id}\cdot(x_{id}-x_{kd}), $$
(10)
Fig. 2
figure 2

The pseudo code of Send_Employed_Bees

Full size image

where ϕ id is a real number randomly selected from interval [-1,1]. Although k is determined randomly, it has to be different from i. From (10) we can find that as the difference between x id and x kd decreases, the perturbation on the position x id gets decreased, too. Thus, as the search approaches the optimum solution in the search space, the step length is adaptively reduced.

For the synthetic colony, the updating equation becomes to

$$ v_{id} = x_{id} + \phi_{id}\cdot(x_{id}-x_{kd})+ \varphi_{id}\cdot(x_{id}-gbest_{d}), $$
(11)

where ϕ id and φ id are two different random numbers distributed uniformly over [−1,1], and k is the same as in (10). As mentioned before, gbest is called the global best food source. Equation 11 uses three parts to modify one dimension of the food sources which is analogous to the idea introduced in literature [49]. By introducing gbest position, it will attract the whole colony into a ”better” search region and this operation will also enable a precise local search around the neighborhood that gbest located at. Note that if the value produced by these operations overflows, then it will be shifted onto the bound value.

After the new position for a food source is generated, its objective values are then evaluated. If the new position v i can dominate the old one, then this food source will be replaced by the new position vector. If not, the update is deemed as unsuccessful and trial value of this food source will be incremented by one. If v i and x i are non-dominated with each other, then this trial is also successful if v i could be added into the archive.

If a trial for a food source is successful, then its new food source v i will be used to update the global best food source gbest. The logic for function gbest = update_gbest(gbest, v i ) (see Fig.2) is as follows:

If (v i dominates gbest)

              gbest = v i

Else If (v i and gbest are non-dominated with each other)

              If (The grid-location count of v i is smaller than that of gbest )

                            gbest = v i

              End If

End If

After all foods sources have been updated, their fitness values are calculated through function calculateFitness() (see Fig.2). In this paper, the method for calculating fitness value is the same as SPEA2[58]. Given an individual i, the fitness value F(i) contains two parts: raw fitness value R(i) and density information D(i), namely, F(i)=R(i) + D(i). The raw fitness is determined by the strengths of its dominators in both archive and colony, and it could avoid the situation that individuals dominated by the same archive members have identical fitness values. Density information is incorporated to discriminate between individuals having identical raw fitness values. Details of calculating this kind of fitness value are available in literature [58]. It is important to note that fitness in SPEA2 is to be minimized.

3.5 Send Onlooker Bees

The pseudo code of Send_Onlooker_Bees is shown in Fig. 3. After all employed bees optimized their food sources, they will come to the hive to share information with the onlooker bees about the quality of corresponding food sources, and onlooker bees will then choose one food source to be exploited. For this purpose, the probability for each food source k advertised by the corresponding employed bee will be calculated as follows:

$$ prob_k = 1-\frac{fit(\mathbf{x}_k)}{\sum\limits_{m=1}^{FoodNumber}fit(\mathbf{x}_m)}, $$
(12)
Fig. 3
figure 3

The pseudo code of Send_Onlooker_Bees

Full size image

where fit(x m ) returns the fitness value of x m . From (12) we can find that a food source with lower fitness value will be assigned with a higher selection probability, and this is because the fitness value used in dMAOBC is to be minimized.

Next, onlooker bees will choose a food source i based on the probability provided by its employed bee by using roulette wheel method. After that, they will randomly select one dimension of that food source and do same as employed bees to improve it. The updating equations for both basic and synthetic colonies are in accordance with those in employed bees phase given by (10) and (11), respectively. Note again that if the parameter value produced by those operations exceeds its predetermined limit, it will be set to its boundaries.

3.6 Send Scout Bees

The pseudo code of Send_Scout_Bees is given in Fig. 4. In this step, the algorithm will find abandoned food sources to replace them with new ones. A food source that can’t be improved by its employed or onlooker bee for limit cycles will be discarded, and be replaced with a vector which is generated similarly as in the initialization phase (see (9)). The scout bees phase could help the algorithm get rid of food sources that have been trapped in a local optimum. Just as basic ABC, only one scout is allowed in each cycle for each colony in our method.

Fig. 4
figure 4

The pseudo code of Send_scout_Bees

Full size image

3.7 Multi-colony model and information exchange

As previously stated, the dMOABC method employs three colonies: two are basic ones and the third one is synthetic. The schematic diagram of our multi-colony model is given in Fig. 5 which shows all possible relationships between colonies and the archive. Line (1) means that non-dominated solutions found by the synthetic colony are added into the archive. Basic colonies share information with synthetic colony by updating gbest, shown as line (2) and line (3). Non-dominated solutions found by two basic colonies are also added to the archive, so line (4) and line (5) exist. We can find line (6) and line (7) are dotted, this is because there exists no direct communication between two basic colonies.

Fig. 5
figure 5

Multi-colony model and communication mechanism

Full size image

4 Experimental study

This section contains the computational results obtained by the dMOABC algorithm compared to other 11 state-of-the-art multi-objective methods over a set of unconstrained test problems introduced in CEC09[53].

4.1 Performance Metrics

In this work, we use four indicators to provide quantitative assessments over all algorithms, and they are: Hypervolume (HV)[59], SPREAD [10], EPSILON [14], and IGD [14]. These metrics are computed by jMetalFootnote 1, an object-oriented Java-based framework for multi-objective optimization with meta-heuristics, which was developed by J.J. Durillo and A.J. Nebro[13, 14]. It is should be noted here that all indicators but Hypervolume are to be minimized.

4.2 Benchmarks and Experimental Setup

In this section, several test functions from the CEC09[53] are used in order to compare the performance of dMOABC against other multi-objective algorithms. The CEC09 benchmark presents a set of complex test problems, and ten unconstrained ones (UF1-UF10) are selected for the purpose of performance comparison. The mathematical representation of these test problems are given in Table 1. The UF1-UF7 are two objective test problems while UF8-UF10 are three objective ones. The Pareto fronts of these test problems have different characteristics (e.g. a part of them are convex while the other ones are concave or some of them are continuous while the other ones are discontinuous)[3].

Table 1 Mathematical representation of the unconstrained CEC09 test problems
Full size table

To observe the performance of the proposed dMOABC method in solving multi-objective problems, its performance is compared with MOEAD [52], SMPSO[35], GDE3 [29], AbYSS[37], CellDE[15], IBEA[57], MOCell[36], OMOPSO[42], NSGAII[11], PAES[27] and SPEA2[58]. In all experiments, the maximal number of function evaluations is set at 300, 000 for each problem and each algorithm. The maximum number of final solutions for computing indicators is 100 for both two and three objectives problems. Each algorithm is evaluated independently 30 times for each test problem. The dMOABC algorithm is tested with a colony of size 10, so MaxIterations is set at 300,000/10=30,000. Since there are three colonies, each colony iterates 30,000/3=10,000 cycles. According to our experience, we set the values of control parameter limit and depth at 100 and 6, respectively. The performance of the dMOABC is evaluated under this configuration over all test problems. dMOABC algorithm is implemented by our Java code, and other algorithms are executed by running jMetal software package.

4.3 Performance Analysis

The computational results on UF1-UF10 obtained by all algorithms are shown in Table 2-9. They include the mean and standard deviation, as well as the median and interquartile range (IQR) of all the independent runs for the indicators HV, SPREAD, EPSILON and IGD , respectively. To ease the analysis of these tables, some cells have a gray colored background in each row; particularly, there are two different gray levels: a darker one, pointing out the algorithm obtaining the best value of the indicator, and a lighter one, highlighting the algorithm obtaining the second best value of the indicator[14].

Table 2 HV. Mean and standard deviation
Full size table
Table 3 HV. Median and IQR
Full size table
Table 4 SPREAD. Mean and standard deviation
Full size table
Table 5 SPREAD. Median and IQR
Full size table
Table 6 EPSILON. Mean and standard deviation
Full size table
Table 7 EPSILON. Median and IQR
Full size table
Table 8 IGD. Mean and standard deviation
Full size table
Table 9 IGD. Median and IQR
Full size table

We start by describing the values obtained in the HV indicator. For this indicator, the higher the value the better the computed fronts. Thus, attending to Table 2 and Table 3, we see that the best indicator values are archived by dMOABC algorithm, and the second best is MOEAD. dMOABC has obtained the best or second best values in this indicator for all the problems but UF3 and UF9; MOEAD has computed the best fronts regarding to this indicator in four out of the ten evaluated problems. AbYSS is also a competitive algorithm which has gotten the second best values on three functions (UF5, UF8 and UF10) in terms of the mean value.

We turn now to analyze the computed fronts in terms of the diversity through the use of SPREAD indicator (Table 4 and Table 5). In this case, the first three best algorithms are distributed among MOEAD, SPEA2, SMPSO and dMOABC. Both MOEAD and SPEA2 have obtained the best values for this indicator on three evaluated problems: UF1, UF3 and UF7 for MOEAD; UF4, UF8 and UF9 for SPEA2. Another algorithm obtaining good results in this indicator has been dMOABC: it has computed the fronts with the best values of the indicator in two out of the ten evaluated problems, plus one second best value on test function UF1. For this indicator, no algorithm has obtained obviously better results than its competitors.

Next, we pay attention to the EPSILON values (Table 6 and Table 7). Regarding this indicator, dMOABC has been also the best algorithm; after it MOEAD has obtained the best values in three out of the ten problems in terms of the mean value. Another promising algorithm has been GDE3, which has archived the best value in one out of the ten problems and the second best values of the indicator in two cases (see Table 6). For the median values regarding this indicator, similar conclusion could be reached.

Finally, we compare algorithms in terms of IGD indicator (Table 8 and Table 9). Definitely, in this case, dMOABC has performed the best. Then it comes to MOEAD, archiving the best or second best values regarding to this indictor in five out of the ten evaluated problems in terms of both mean and median values.

The above conclusions are drawn just based on the number of the best or the second best results obtained by each algorithm . Average rankings of the algorithms will be given by using statistical test shown in Subsection 4.4. More detailed information can be obtained if we display the results by using boxplots, which constitutes a useful way of depicting groups of numerical data. In this case, the boxplot representing the distribution of values for the all indicators in the comparison carried out are showed in Fig. 6-9. Some interesting facts can be worked out by observing the figure. For example, in problems UF4, UF6 and UF10, we observe that dMOABC has clearly outperformed to the other algorithms in terms of HV indicator. Regarding indicator IGD, dMOABC has been the most salient on functions UF1,UF4, UF5, UF6, UF10. From these figures, we find dMOABC produces more stable results in most cases, that is to say, our algorithm has better robustness than other algorithms.

Fig. 6
figure 6

Boxplots of the HV obtained by the different algorithms in the evaluated problems

Full size image
Fig. 7
figure 7

Boxplots of the SPREAD obtained by the different algorithms in the evaluated problems

Full size image
Fig. 8
figure 8

Boxplots of the EPSILON obtained by the different algorithms in the evaluated problems

Full size image
Fig. 9
figure 9

Boxplots of the IGD obtained by the different algorithms in the evaluated problems

Full size image

4.4 Nonparametric Statistical Test

One of the most frequent situations where the use of statistical procedures is requested is in the joint analysis of the results achieved by various algorithms [12]. To determine whether the differences between the 12 involved algorithms introduced in Subsection 4.2 are significant or not, this section will perform multiple comparisons using Friedman test[12] which is one of the commonly used nonparametric statistical test procedures.

Average rankings of each algorithm for each indicator obtained by applying Friedman test are shown in Table 10. These rankings are also computed by jMetal software. The Friedman test assumes that the lower the values of the indicators the better. This is true in all the indicators but the hypervolume. It could be seen from Table 10 that the dMOABC is significantly better than other algorithms in terms of indicators HV, EPSILON and IGD. As for indicator SPREAD, SMPSO performs the best, and dMOABC is comparable to MOEAD algorithm.

Table 10 Average Rankings of the algorithms by applying Friedman test
Full size table

Summarizing, according to the problems, parameter settings and the quality indicators used, dMOABC has been the most salient algorithm in our study.

4.5 Distribution and convergence analysis

For each test function, the approximated fronts computed by dMOABC, together with the true fronts, are plotted in Fig 10. In this figure, the computed front is a combination of all archive members returned by dMOABC over 30 independent runs. It is shown by this figure that the Pareto fronts produced by dMOABC algorithm over the UF1 and UF2 test problems not only have good convergence but also has appropriate distribution along the true Pareto front in objective space.

Fig. 10
figure 10

The best Pareto fronts obtained by the dMOABC algorithm on the test problems UF1-UF10 (The blue and red lines represent the true and approximated Pareto fronts, respectively )

Full size image

For the UF3 test problem, the approximated fronts distribute uniformly in the middle part of the true front, but are not evenly distributed in the top-left and bottom-right corners of the Pareto front. Fig. 10 shows that dMOABC algorithm has the ability to produce the uniformly distributed Pareto front on UF4 test function.

It seems that the UF5 is a hard problem to be solved since it has a discontinuous Pareto front. Most of the algorithms have difficulties in approximating to its true Pareto front[3]. It is shown by Fig. 10 that the produced Pareto front by dMOABC is uniformly distributed along the true one.

The Pareto front of UF6 is also discontinuous. Hence, an optimization algorithm needs to pay more attention to the Pareto front and moves the archive members to the parts of solution space which contain the members of Pareto fronts. The results show that most of the algorithms have difficulty in optimizing this type of test problems[3]. Fig. 10 also shows that our algorithm could produce nearly uniformly distributed fronts for the problem.

For problem UF7, it could be seen from Fig.10 that the top-left corner of the Pareto front is not successfully covered by the dMOABC algorithm. Hence, the value of indicator SPREAD increases over the UF7 test problem.

The UF8 is the first three objective test problem investigated in this paper. Usually, the complexity of multi-objective problems increases by the number of objectives to be optimized. The quality of the approximated Pareto front is shown in Fig. 10. It is apparent from the results that the dMOABC produces a set of solution points which have an appropriate distribution in the 3 dimensional objective space.

For the test problem UF9, Fig. 10 shows that the dMOABC produces a set of non-dominated points which covers a large part of the objective space. However, small parts of the objective space are not covered by the approximated Pareto front.

It seems that UF10 is also a hard problem to be solved. Fig. 10 shows that the approximated Pareto front found by the dMOABC algorithm distributes nearly uniformly, but with a small number of non-dominated solutions.

Next, the behavior of the dMOABC in converging to the optimal Pareto front is studied. By setting the maximal number of function evaluations at 3K, 6K, 30K, 60K, 300K and 600K, we plot the approximated Pareto front of the UF4 test problem under different situations in Fig. 11. The results show that the dMOABC algorithm continuously improves its performance with the increase of the maximum number of function evaluations. From Fig. 11, we can find that the number of non-dominated solutions continuously increases and the distance between the true and the approximated Pareto front continuously decreases, with function evaluations varying from 3K to 600K. Although the dMOABC rapidly converges to the optimal Pareto front at the first function evaluations, it can produce a few solution points. As the number of function evaluations proceeds, the number of produced solutions increases and better distribution of them is achieved. An algorithm needs to provide appropriate balance between exploration and exploitation and mitigate the hard constriction on the flying trajectories of its individuals in order to avoid premature convergence [3]. The dMOABC algorithm uses some mechanisms to avoid itself being trapped into a local optimum: the use of both neighbor and social knowledge helps flying in the right trajectories toward food sources; the communication between basic and synthetic colonies also enables the algorithm to explore other optimal positions produced by basic colonies so as to avoid premature convergence.

Fig. 11
figure 11

The convergence behavior of dMOABC throughout maximal number of function evaluations (The blue and red lines represent the true and approximated Pareto fronts, respectively )

Full size image

4.6 Computational Complexity

The computational complexity is an important factor when evaluating an algorithm. Although, our dMOABC achieves good performance on CEC09 test functions, its space complexity is great since three colonies are used. The larger the number of colonies is, the greater the space complexity will be. However, we can find that there exists potential parallelism among the three colonies. That is to say, the dMOABC algorithm can be easily modified to a parallel algorithm with three processors, and each one for each colony. Hence, the running time of the dMOABC will decease significantly.

5 Conclusion

In this paper, we have presented a new multi-objective artificial bee colony algorithm by dividing the searching space. In our proposed method, three colonies are used: two of them are basic colonies and the third one is called the synthetic colony. These colonies search in different regions of the searching space and share information with each other, and the aim for that is to avoid being attracted into a local optimum. An external archive is adopted to store non-dominated solutions found by the algorithm, and the diversity of archived solutions is controlled by a self-adaptive grid. Besides neighbor information, social information shared by the external archive, called gbest, is also used to guide the flying of both employed and onlooker bees in the synthetic colony. Compared to other state-of-the-art algorithms considered in this work, the experimental study shows that our method achieves the first rank in terms of indicators HV, EPSILON and IGD. Some improvements and extensions are currently being investigated by the authors, including using ε dominance method to maintain the archive and extending it to be a parallel algorithm, or modifying it for handling multi-objective optimization problems. Practical applications of this algorithm would also be worth studying.