1 Introduction

Fuzzy Cognitive Maps (FCMs) constitute neuro-fuzzy systems, which are able to model complex systems [7, 8, 19]. Recently, Fuzzy Grey Cognitive Maps (FGCM) have been proposed as a FCM extension [26]. FGCM is based on Grey Systems Theory (GST), that has become a very worthy theory for solving problems within domains with high uncertainty, under discrete small and incomplete data sets [27, 29–31]. FGCMs model approximate knowledge on concepts grey state and the causal grey relationships among them being thus the generalization of FCMs.

FGCMs provide several improvements regarding to others similar techniques. First, FGCM models are designed specifically for multiple meanings (grey) problems. Second, the FGCM technique allows the defining of grey relationships between concepts. According to this, more reliable decisional models for interrelated environments are defined. Third, FGCM is able to quantify the grey influence of the relationships between concepts. Through this attribute, a better support in grey environments can be reached. Finally, with this FGCM model it is possible to develop a what-if analysis with the purpose of describing possible grey scenarios.

Recently, interest in control of nonlinear systems was ever increasing due to demands from practical applications, and many significant developments were achieved [1, 16–18, 40]. The main goal of control engineering is to apply knowledge about how to control a process so that the resulting control system will reliably and safely achieve high-performance operation.

In this sense, fuzzy logic is a well-known universal approximator [39]. That is, a fuzzy logic system can be used to approximate any nonlinear system with a required accuracy. Fuzzy control is a practical alternative for a variety of challenging control applications since it provides a convenient method for constructing nonlinear controllers using the heuristic information.

In the fuzzy control design methodology, we use to ask operators to write down a set of (fuzzy) rules on how to control the processes. Those rules are embedded into fuzzy controllers emulating the operator decision-making process. According to this, Fukami [6] proposed the first stable fuzzy adaptive controller, and many fuzzy adaptive control schemes have been reported with adaptive fuzzy logic systems [11–13, 35–39].

In this work, FGCMs and an unsupervised Hebbian-based learning algorithm for FGCMs were applied to analyze a well-known process control problem, where the FCMs and Hebbian-based learning approaches have been previously applied for [32, 34] and [24]. Many experiments, reproducible examples, were conducted to validate the proposed methods and the results were compared with those previously reported in the literature. The effectiveness of the proposed methodology is analyzed in the discussion of results.

The outline of this paper is as follows. Section 2 presents briefly the Grey System Theory. Section 3 describes the Fuzzy Grey Cognitive Maps technique with its learning capabilities. Section 4 introduces the experiments. In Sect. 5, the discussion of the results is presented and Sect. 6 concludes the paper.

2 Grey systems theory

Grey Systems Theory has become a worthy set of techniques within environments with high uncertainty, under discrete small and incomplete data sets [4]. GST requires only small data samples with poor information to be effective. It has been successfully applied in medicine, engineering, energy, computer science, agriculture, geology, meteorology, military science, transportation, business and so on [4, 9, 10, 23, 26, 28, 30, 43].

GST considers the data fuzziness, because it can flexibly deal with it [9, 10, 43]. Moreover, fuzzy mathematics holds some previous information (usually based on experience); while grey systems deal with objective data, they do not require any more information other than the data sets that need to be disposed [41]. Moreover, GST fits better with multiple meanings environments than fuzzy logic.

GST includes five major parts: grey prediction, grey relational analysis, grey decision, grey programming, and grey control [9]. In GST, according to the degree of known information, if the system information is fully known (a complete understanding), the system is called a white one, while the system information is completely unknown is called a black one. In addition, a system with partial information known and partial information unknown is grey system.

Let U be the universal set. Then a grey set G∈U is defined by both its mappings. Note that \(\{\overline{\mu}_{G} ( \cdot) \mid\underline{\mu}_{G} ( \cdot)\}\in [ 0,1 ]\), where \(\underline{\mu }_{G} ( \cdot)\) is the lower membership function, \(\overline{\mu}_{G} ( \cdot)\) is the upper one and \(\underline{\mu}_{G} ( \cdot) \leq \overline{\mu}_{G} ( \cdot)\). Also, GST extends fuzzy logic, since the grey set G becomes a fuzzy set when \(\underline{\mu}_{G} ( \cdot) = \overline{\mu}_{G} ( \cdot)\). The crisp value of a grey number is unknown, but the range within the value is known.

An interval grey number is a grey number with both a lower limit (\(\underline{x}\)) and an upper limit (\(\overline{x}\)) [10], and it is denoted as \(\otimes x \in [ \underline{x},\overline{x} ] | \underline{x} \leq\overline{x}\). If a grey number ⊗x has just lower limit is denoted as \(\otimes x \in [ \underline{x},+\infty )\), and if it has only upper limit is \(\otimes x \in ( -\infty, \overline {x} ]\). A black number is denoted as ⊗x∈(−∞,+∞), and a white number is \(\otimes x \in [ \underline {x},\overline{x} ],\underline{x} = \overline{x}\). There is not any information known about black numbers and the whole information is available about white ones.

The transformation of grey numbers in crisp ones is called whitenization [10], and the whitenization value is computed as follows

$$ \hat{g} = \alpha\cdot\underline{x} + ( 1 - \alpha) \cdot\overline {x} \;|\; \alpha\in[ 0,1 ] $$
(1)

when α=0.5 is called equal mean whitenization.

The length of a grey number is computed as \(\ell(\otimes x )=|\underline{x}-\overline{x}|\). In that sense, if the length of the grey number is zero (ℓ(⊗x)=0), then it is a white number. Otherwise, if ℓ(⊗x)=∞, the grey number is not necessarily a black number, because the length of a grey number with only one limit (lower or upper), \(\otimes g\in[\underline{x},+\infty)\) or \(\otimes x\in(-\infty ,\overline{x} ]\), is infinite but it is not a black number because we have information about one limit.

A deeper explanation of grey numbers, grey matrices and FGCMs can be found at [26].

3 Theoretical background

3.1 Fuzzy grey cognitive maps

Fuzzy Grey Cognitive Map is an emerging soft computing technique mixing FCMs and GST [26]. A FGCM models unstructured knowledge through causalities through vague concepts and grey relationships between them based on FCM [7, 8]. Furthermore, FGCMs provide an intuitive, yet detailed way of modeling concepts and analyzing them at their natural level of abstraction [29, 31].

By converting decision modeling into causal graphs, decision makers with no technical background can understand all of the components in a given situation. In addition, with a FGCM, it is possible to identify and consider the most relevant factor that seems to affect the expected target variable.

FGCMs are dynamical systems involving feedback, where the effect of change in a node may affect other nodes, which in turn can affect the node initiating the change [26].

The FGCM nodes are variables, representing concepts. The relationships between nodes are represented by directed edges. An edge linking two nodes models the grey causal influence of the causal variable on the effect variable.

Each relationship between FGCM nodes is measured by its grey intensity as

$$ \otimes w_{ij} \in[ \underline{w}_{ij}, \overline{w}_{ij} ] \mid \underline{w}_{ij} \leq \overline{w}_{ij}, \{ \underline{w}_{ij},\overline{w}_{ij} \} \in[ -1,+1 ] $$
(2)

where i is the pre-synaptic (cause) node and j the post-synaptic (effect) one.

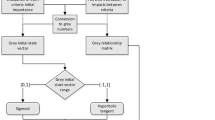
FGCM dynamics begins with the design of the initial grey vector state \(\otimes \vec{C}(0)\), which represents a proposed initial grey stimuli. We denote the initial grey vector state with n nodes as

$$ \begin{aligned}[b] &\otimes \vec{C}(0) \\ & \quad= \Bigl( \otimes {c}_{1}(0), \otimes {c}_{2}(0), \ldots, \otimes {c}_{n}(0) \Bigr) \\ & \quad= \bigl( \bigl[ \underline{c}_{1}(0), \overline{c}_{1}(0) \bigr], \bigl[ \underline{c}_{2}(0), \overline{c}_{2}(0) \bigr], \ldots, \bigl[ \underline{c}_{n}(0), \overline{c}_{n}(0) \bigr] \bigr) \end{aligned} $$
(3)

The updated nodes’ states [26] are computed in an iterative inference way with an activation function, which mapping monotonically the grey node state value into its normalized range {[0,+1]|[−1,+1]}. The unipolar sigmoid function is the most used one [3] in FCM and FGCM when the concept value maps in the range [0,1]. If f(⋅) is a sigmoid, then the i component of the grey vector state \(\otimes \vec{C}(t+1)\) after the inference would be update with Eq. (4).

$$ \begin{aligned}[b] \otimes {c}_{j}(t+1) & = f \Biggl( \otimes {c}_{i}(t) + \sum _{i=1}^{n} \otimes w_{ij}\cdot \otimes {c}_{i}(t) \Biggr) \\ & = f \Bigl(\otimes {c}_j \bigl(t^+ \bigr) \Bigr) \\ & = f \bigl( \bigl[{\underline{c}}_j \bigl(t^+ \bigr), { \overline{c}}_j \bigl(t^+ \bigr) \bigr] \bigr) \\ & = \bigl[f \bigl({\underline{c}}_j \bigl(t^+ \bigr) \bigr), f \bigl({ \overline{c}}_j \bigl(t^+ \bigr) \bigr) \bigr] \\ & = \biggl[\frac{1}{1+e^{-\lambda\cdot{\underline{c}}_j(t^+)}}, \frac {1}{1+e^{-\lambda\cdot{\overline{c}}_j(t^+)}} \biggr] \\ & = \bigl[{\underline{c}}_j(t+1), {\overline{c}}_j(t+1) \bigr] \end{aligned} $$
(4)

On the other hand, when the concepts’ states map in the range [−1,+1] the function used would be the hyperbolic tangent.

$$\begin{aligned} \otimes {c}_{j}(t+1) =& \biggl[\frac{e^{\lambda\cdot\underline {c}(t^+)} - e^{-\lambda\cdot\underline{c}(t^+)}}{e^{\lambda\cdot \underline{c}(t^+)} + e^{-\lambda\cdot\underline{c}(t^+)}}, \frac {e^{\lambda\cdot\overline{c}(t^+)} - e^{-\lambda\cdot\overline {c}(t^+)}}{e^{\lambda\cdot\overline{c}(t^+)} + e^{-\lambda\cdot \overline{c}(t^+)}} \biggr] \end{aligned}$$
(5)

The nodes’ states evolve along the FGCM dynamics. The FGCM inference process finish when the stability is reached. The steady grey vector state represents the effect of the initial grey vector state on the state of each FGCM node.

After its inference process, the FGCM reaches a steady state following a number of iterations in the same way of FCMs [2]. It settles down to a fixed pattern of node states, the so-called grey hidden pattern or grey fixed-point attractor. Furthermore, the state could to keep cycling between several fixed states, known as a limit grey cycle. Using a continuous activation function, a third state would be a grey chaotic attractor. It happens when, instead of stabilizing, the FGCM continues to produce different grey vector states for each iteration [26].

3.2 Building FGCMs

FGCMs, as FCMs [5, 14, 20, 22], can be built by experts or from raw data. We focus on a deductive approach based on experts’ knowledge about the system’s domain.

The experts’ team establish the number and categories of nodes (or concepts) relevant for the FGCM model. Furthermore, experts know which nodes influence others; for the corresponding nodes they determine the intensity of the influence and its sign (negative or positive). Each expert, indeed, determines the influence of a node to another one as negative or positive and then evaluates the degree of influence using a linguistic variable (such as strong influence, medium influence, weak influence, and so on). This is a procedure commonly used for FCM [25].

A grey causal weight should be determined for FGCMs. It is a little bit complex because it is not a fuzzy number, but a grey one. In this sense, we will use a class of grey numbers that vibrate around a base value, denoted as \(\otimes \hat{w}_{ij} \in [ a- \theta, a+\theta ]\), where a is the base value.

Moreover, the vibration value θ would be determined according with the uncertainty about the base value. If the base value has not uncertainty associated, then θ=0. This is the case for a white number. If the base value is completely unknown, then θ=∞ for the general case and θ≤{1|2} in FGCM models. The base value a is calculated as weights in FCM [25].

Equation (6) shows the computation of the \(\otimes \hat {w}_{ij}\) upper and lower limits.

$$\begin{aligned} \otimes \hat{w}_{ij} \in \left \{ \begin{array}{l@{\quad}l} [ a - \theta, +1 ] \\ \quad\mbox{if } (-1 \leq a - \theta\leq+1 ) \wedge (a + \theta> +1 ) \\ {} [ -1, a + \theta ] \\ \quad\mbox{if } (-1 \leq a + \theta\leq+1 ) \wedge (a - \theta< -1 ) \\ {} [ a - \theta, a + \theta ] \\ \quad\mbox{if } (-1 \leq a - \theta\leq+1 ) \wedge (-1 \leq a + \theta\leq+1 ) \\ {} [ -1, +1 ] \\ \quad\mbox{if } ( a + \theta> +1 ) \wedge (a - \theta< -1 ) \end{array} \right . \end{aligned}$$
(6)

3.3 FGCM’s advantages over FCM

FGCMs have several advantages over conventional FCM [23]. A FGCM compute the desired steady states of the models by handling uncertainty and hesitancy present in the experts’ judgments for causal relations among concepts as well as within the initial vector states.

FCM would need measures of the associated uncertainty in weights and concepts. The FGCM concepts have a greyness value to represent the degree of uncertainty associated to each node and each edge. Note that, even if the FCM dynamics would get the same steady state than FGCM after the whitenization process, the FGCM proposal handles the inner fuzziness and grey uncertainty.

Furthermore, it is possible to compute different whitenization state values. This paper uses the equal mean whitenization with α=0.5, but it would be possible to calculate an optimistic or pessimistic whitenization. The whitenization value vibrates between the grey number limits. The final whitenization value depends of the parameter α. Lower α values generate higher whitenization values closer to the upper limit.

Moreover, FGCM includes greyness as an uncertainty measurement. Higher values of greyness mean that the results have a higher uncertainty degree. It is computed as follows

$$ \phi\Bigl(\otimes c_{i}\Bigr) = \frac{\vert\ell(\otimes c_{i})\vert}{\ell (\otimes \psi)} $$
(7)

where |ℓ(⊗c i )| is the absolute value of the length of grey node ⊗c i state value, and ℓ(⊗ψ) is the absolute value of the range in the information space, denoted by ⊗ψ. FGCM maps the nodes’ states within an interval [0,1] or [−1,+1] if negative values are allowed. In this sense,

$$ \ell\Bigl(\otimes \psi\Bigr) = \left \{ \begin{array}{l@{\quad}l} 1 & \mbox{if } \{\otimes c_{i},\otimes w_{i}\} \subseteq [ 0,1 ] \\ 2 & \mbox{if } \{\otimes c_{i},\otimes w_{i}\} \subseteq [ -1,+1 ] \end{array} \right . $$
(8)

As an overview, FGCM proposal shows several advantages over the FCM [28], as the following:

  • It is a generalization and can be applied to closer approximate decision making in humans.

  • It allows modeling of the uncertainty and experts’ hesitancy associated to the description of the causal relations between the concepts and to the concept states.

  • FGCMs are able to model more kinds of relationships between nodes than FCM do. For instance, it is possible to run models with relations where the intensity is not known at all or just partially known.

  • The reasoning process’ output would incorporate the uncertainty degree (greyness) of the nodes expressed in grey values.

3.4 Nonlinear Hebbian learning in FGCMs

Recently, Nonlinear Hebbian (NHL) based algorithm has been applied to FGCM Learning [23]. The learning algorithm extracts hidden and worthy knowledge from experts. It can increase the FGCMs effectiveness and their implementation in real-world problems.

The unsupervised Hebbian learning rule improves the FGCM structure, eliminates the deficiencies in the usage of FGCM and enhances the flexibility and dynamical behavior of the FGCM model. The FGCM model and its updated FGCM structure after learning, guarantee the successful implementation of the proposed modeling procedure for real case problems.

The NHL algorithm is based on that all FGCM nodes are triggering at each iteration and updating their states grey values. During the FGCM dynamics the edges’ grey weights are updated and the new weight ⊗w ji (t) is derived for iteration step t.

The NHL rule for updating FGCM grey weights is computed as follows

$$\begin{aligned} \Delta \otimes w_{ji}(t) =& \eta_k \cdot \otimes c_j(t-1)\cdot \Bigl( \otimes c_i(t-1) \\ & {}- \otimes c_j(t-1) \cdot \otimes w_{ji}(t-1) \Bigr) \end{aligned}$$
(9)

Also, this proposal introduces three criteria for the NHL-FGCM algorithm. The first criterion is the maximization of the objective function J, which has been defined by Hebb’s rule

$$ \begin{array}{l@{\quad}l} \mbox{maximize} & J = E \{z^2 \} \\ \mbox{subject to:} & \|\mathbf{w} \|= 1 \end{array} $$
(10)

where \(J = \sum_{k=1}^{m} (O_{k})^{2}\), O are the output values, m the number of output nodes, z=f(⋅) where f(⋅) is the activation function.

The second one is the minimization of the difference between two subsequent value of the outputs values.

$$ \bigl| O_k(t+1) - O_k(t) \bigr|< \epsilon $$
(11)

where ϵ is the tolerance value (usually 0.001). Finally, the third criterion is the stability of the grey vector state.

4 Experiments

In order to investigate and demonstrate the performance of the proposed FGCM model, in comparison with conventional FCM, an industrial application, concerning a chemical process control problem has been considered.

FCMs were successfully applied to model control process [34] and in this study, our purpose is to show the functionality of FGCMs to effectively model and analyze a known chemical process control problems in industry.

4.1 Problem description

We consider the reference chemical process control system described in [32]. It consists of two tanks, three valves, one heating element and two thermometers for each tank, as depicted in Fig. 1.

Fig. 1
figure 1

An illustration of the chemical process example [21, 32, 33]

Full size image

Each tank has an inlet valve and an outlet valve. The outlet valve of the first tank is the inlet valve of the second tank. The objective of the control system is firstly to keep the height of liquid, in both tanks, between some limits, an upper limit H max and a low limit H min , and secondly the temperature of the liquid in both tanks must be kept between a maximum value T max and a minimum value T min .

The temperature of the liquid in tank 1 is regulated through a heating element. The temperature of the liquid in tank 2 is measured through a sensor thermometer; when the temperature of the liquid two decreases, valve 2 needs opening, so hot liquid comes into tank 2 from tank 1. The control objective is to keep values of these variables in the following range of values:

$$ \begin{aligned} &H1_{min} \leq H1 \leq H1_{max} \\ &H2_{min} \leq H2 \leq H2_{max} \\ &T1_{min} \leq T1 \leq T1_{max} \\ &T2_{min} \leq T2 \leq T2_{max} \end{aligned} $$
(12)

where, according to the experts, H1 min =0.55, H1 max =0.75, H2 min =0.75, H2 max =0.80, T1 min =0.75, T1 max =0.82, T2 min =0.65, and T2 max =0.75.

Three experts constructed the FCM and jointly determined the concepts of the FCM [25, 32]. Variables and states of the system such as the height of the liquid in each tank or the temperature, are the concepts of the FCM model, which describes the system. The values of the concepts correspond to the real measurements of the physical magnitude. Each concept of the FCM takes a value, which ranges in the interval [0,1] and it is obtained after threshold the real measurement of the variable or state, which each concept represent.

4.2 FGCM model

Based on the conventional FCM proposed in [20] for the considered problem we constructed a FGCM model sharing a similar structure. It consists of eight concepts, as illustrated in Fig. 2.

Fig. 2
figure 2

FGCM control model

Full size image

For the purposes of our paper, the three experts that participated in [32, 34] assigned new IF-THEN rules that describe the influences from concepts c i to concepts c j , where i=1,…,5 and j=1,…,5. The rules’ inference are linguistic weights described by grey weights as Eq. (2).

For the construction process of FGCMs, the experts were also assigned the vibration values of each one fuzzy relationship. Thus, grey weights with their vibration values as obtained from the experts for the construction of the FGCM model are apposed in Table 1. The greyness of each one weight is calculated following the mathematical formulation suggested by Salmeron [26] and described in Sect. 2.

Table 1 FGCM nodes and their descriptions
Full size table

The grey weights with their greyness, apposed in Fig. 2, are used for the simulation analysis of FGCM dynamics.

4.3 FGCM dynamics

A set of real measurements were provided as input to FGCM as in the case of conventional FCM model proposed in [34], where the initial vector state is

$$ \vec{C}(0) = (.48, .57, .58, .68, .59, .58, .59, .52) $$
(13)

The steady vector state for FCM is as follows

$$ \begin{aligned}[b] \vec{C}(t) = (&.6256, .7334, .7675, .8600, .7700, .7390, \\ &.6810, .7548) \end{aligned} $$
(14)

and the steady vector state of FCM with NHL learning is

$$ \begin{aligned}[b] \vec{C}(t) = (&.6197, .7632, 7857, .8717, .7620, .7510, \\ &.7094, .7441) \end{aligned} $$
(15)

In order to investigate and demonstrate the performance of the proposed FGCM model, in comparison with conventional FCM and the Hebbian learning of FCM, five different experimental setups have been considered.

The main aim of these experiments is not only the performance of FGCMs, but also their comparison with previous studies concerning the implementation of conventional FCMs and Hebbian-based learning algorithms for FCMs.

4.3.1 First case study

The first one aims to demonstrate the performance of FGCMs and its learning approach, on a real case scenario, whereas the other four are more general (using initial states with vibrations and more greyness) and aim to demonstrate their performance on a large randomized set of cases.

Thus, for the first case study, the initial white vector (expressed as a grey vector) is formed as follows

$$ \begin{aligned}[b] \otimes \vec{C}(0)_1 = \bigl(&[.48, .48], [.57, .57], [.58, .58], [.68, .68], \\ & [.58, .58], [.59, .59], [.52, .52], [.58, .58] \bigr) \end{aligned} $$
(16)

The results of the reasoning process obtained with FGCM without learning (Eq. (4)) and FGCM with NHL learning (Eq. (9)), at each iteration, till convergence at a steady state are apposed without NHL learning in Table 2. The results with NHL learning are shown in Table 3.

Table 2 First case study
Full size table
Table 3 Second case study
Full size table

The results in both cases (no learning and NHL learning) show that the four decision output nodes take values within the decision ranges. Especially in the case of FGCMs with NHL learning the values of concepts converge at a steady state which is the upper limit of the decision range with zero greyness.

The zero greyness in decision concepts shows that the system performs with an efficient way to the acceptable steady state.

4.3.2 Second case study

The second case study is a slightly more general scenario considering grey values with higher vibration of concepts as initial ones, in a measurement range that was considered. The initial grey vector state, formed with a vibration ±0.1, is the following

$$ \begin{aligned}[b] \otimes \vec{C}(0)_2 = \bigl(&[.38, .58], [ .47, .67], [.48, .68], [.58, .78], \\ & [.48, .68], [.49, .69], [.42, .62], [.48, .68] \bigr) \end{aligned} $$
(17)

The results of the reasoning process obtained with FGCM without learning (Eq. (4)) and FGCM with NHL learning (Eq. (9)), at each iteration, till convergence at a steady state are apposed without NHL learning in Table 2. The results with NHL learning are shown in Table 3.

The results in both cases show that the four decision output nodes take values within the decision ranges. Especially in the case of FGCMs with NHL learning the values of concepts converge at a steady state which is the upper limit of the decision range with zero greyness.

The zero greyness in decision concepts shows that the system performs with an efficient way to the acceptable steady state.

4.3.3 Third case study

In this case, a more general scenario considering grey values with higher vibration of concepts as initial ones, in a measurement range was considered.

For the second case study, the initial grey vector is formed by the initial white vector, but with a vibration ±0.2, and it is presented as follows

$$ \begin{aligned}[b] \otimes \vec{C}(0)_3 = \bigl(&[.28, .68], [.37, .77], [.38, .78], [.48, .88], \\ & [.38, .78], [.39, .79], [.32, .72], [.38, .78] \bigr) \end{aligned} $$
(18)

The results of the reasoning process obtained with FGCM without learning (Eq. (4)) and FGCM with NHL learning (Eq. (9)), at each iteration, till convergence at a steady state are apposed in Table 4.

Table 4 Third case study
Full size table

The results show that the four decision output nodes take values within the decision ranges. Especially in the case of NHL algorithm, the results show that the output values of four decision concepts reach the upper limit of the Eq. (12) with a zero greyness value.

The zero greyness means that there is no uncertainty in the decision concepts at the steady state. This is a meaningful result which shows that the decision concepts can be calculated with a zero uncertainty degree.

4.3.4 Fourth case study

In this scenario, we also considered the same initial set of measurements (white vector), but with a ±0.3 variation of the initial white values. Following the reasoning process of FGCM without learning (Eq. (4)) and FGCM with NHL learning (Eq. (9)), the results apposed in Table 5 were produced. For the fourth case study, the initial grey vector is formed as follows

$$ \begin{aligned}[b] \otimes \vec{C}(0)_4 = \bigl(&[.18, .78], [.27, .87], [.28, .88], [.38, .98], \\ & [.28, .88], [.29, .89], [.22, .82], [.28, .88] \bigr) \end{aligned} $$
(19)
Table 5 Fourth case study
Full size table

The results also show that the four decision output nodes take values within the decision ranges.

4.3.5 Fifth case study

In this case, a more generic scenario with large randomized cases is considered. Following the reasoning process of FGCM without learning (Eq. (4)) and FGCM with NHL learning (Eq. (9)), the results apposed in Tables 6 and 7 were produced.

Table 6 Fifth case study (No learning)
Full size table
Table 7 Fifth case study (NHL)
Full size table

For the fifth case study, a hundred random initial grey vectors (\(\otimes \vec{C}(t)^{(R)}\)) was computed using the Mersenne-Twister algorithm [15] with a period of 219937−1.

We compute the grey mean of 100 random vectors as follows

$$ \begin{aligned}[b] \mu_{g} \Bigl({\otimes c}_{i}(t)^{(R)} \Bigr) &= \bigl[\mu \bigl( \underline{c}_{i}(t)^{(R)} \bigr), \mu \bigl( \overline{c}_{i}(t)^{(R)} \bigr) \bigr] \\ &= \Biggl[\frac{1}{n}\cdot\sum_{j=1}^{n} \underline{c}_{i}(t)^{(R)}_{j}, \frac {1}{n} \cdot \sum_{j=1}^{n}\overline{c}_{i}(t)^{(R)}_j \Biggr] \end{aligned} $$
(20)

where n=100, and \(\underline{c}_{i}(t)^{(R)}_{j}\) is the i element of the random vector state j. The grey standard deviation is calculated as follows

$$ \begin{aligned}[b] \sigma_{g} \Bigl({\otimes c_{i}(t)}^{(R)} \Bigr) &= \sigma_{g} \bigl( \underline {c}_{i}(t)^{(R)} \bigr) + \sigma_{g} \bigl( \overline{c}_{i}(t)^{(R)} \bigr) \\ &= \frac{1}{n}\cdot\sqrt{\sum _{j=1}^{n} \bigl(\underline {c}_{i}(t)^{(R)}_j- \mu \bigl(\underline{c}_{i}(t)^{(R)} \bigr) \bigr)^{2}} \\ & \quad {}+ \frac{1}{n}\cdot\sqrt{\sum _{j=1}^{n} \bigl(\overline {c}_{i}(t)^{(R)}_j- \mu \bigl(\overline{c}_{i}(t)^{(R)} \bigr) \bigr)^{2}} \end{aligned} $$
(21)

Clearly, in all the examined cases, the output concepts take values with the accepted limits and with very small or zero greyness.

5 Discussion

The new FGCM model that copes with the inability of the current models to co-evaluate the greyness introduced into a complex system due to uncertainty and imperfect facts is explored in this work. The mathematical formalization of the grey systems theory has been considered instead of the conventional fuzzy sets theory. The applicability of the proposed FGCM model extends to a variety of domains. In this paper, we demonstrated its effectiveness with numeric, reproducible examples, on chemical process control for decision making.

In order to show the effectiveness of the proposed approach in the reference process control problem, the authors compare their results with those previously produced by conventional FCMs and their Hebbian-based approaches reported in the literature [21]. The previous results of conventional FCMs are gathered to be clearly compared with the new ones of FGCMs with and without NHL learning (Tables 8 and 9).

Table 8 FCM and FGCM (no learning) results comparison
Full size table
Table 9 FCM and FGCM (NHL learning) results comparison
Full size table

It is obvious, that in the initial set of measurements derived from a real case of the process control, the white values of the output concepts in the case of FGCMs without learning, are within the desired limits for the process behavior, indicating the acceptable operation of this new methodological proposal over the conventional FCMs.

In the case of conventional FCMs without learning, the model is not able to succeed desired behavior for the four decision concepts. Also, the white values of the output concepts in the case of FGCMs with NHL learning are in the upper level of the desired limits with very small or zero greyness indicating one more issue of handling uncertainty. It is one of the main advantages of the FGCMs with learning over the NHL FCM learning.

Thus, unlike conventional FCM, the proposed FGCM naturally expresses this inherent greyness at its outputs. FGCMs produce a length and greyness estimation of the outputs, exploring further the inherent uncertainty, which is not able to be assessed with the conventional FCMs.

It is important to highlight that in the case of using NHL learning in FGCMs, the outputs of the four decision concepts reach the upper limit for every input set of concept states with almost zero greyness. This is a significant result, as the proposed approach is able to succeed the desired behavior of the process control problems.

On the other hand, the most significant weaknesses of the FCMs, namely their dependence on the experts’ beliefs, and the potential convergence to undesired steady states, have been overcome by Hebbian-based learning procedures. However, in this work, we succeeded to produce desired equilibrium regions for the four decision-outputs of the process control problem even without learning algorithms in FGCMs. The results produced by the FGCM model without learning are acceptable and control the system without any learning process. Moreover, 100 runs were performed with random initial values with greyness and without greyness, and the results were the same with the ones presented in fifth case study. These facts proof the fitness of this proposal.

Also, in order to further advance the proposed approach, we implemented a Hebbian-based learning for FGCMs. We pinpoint that if the NHL learning process is used in the case of FGCMs, then the outputs continue to be within the desired limits having the advantage of zero greyness. The whitenization values reach the upper limit of the desired ranges (Eqs. (2), (3), and (4)).

It is proven that using the NHL algorithm in FGCMs we improve the conventional FCM model trained with NHL algorithm [21], which exhibit equilibrium behavior within the desired regions. With the proposed procedure the experts suggest the initial grey weights of the FGCM, and then using the NHL algorithm a new weight matrix is derived that can be used for any set of initial values of concepts.

The NHL algorithm is problem-dependent, starts using the initial weight matrix but all the process is independent from the initial values for grey concepts and the system succeeded to converge in desired equilibrium regions for appropriate learning parameters.

As a result, it is concluded that the FGCM and the FGCM with NHL learning affects the dynamical behavior of the system and the equilibrium values for decision concepts are within desired regions defined at Eq. (12).

The results of the FGCM dynamics show that the capability of FGCM to produce a length and greyness estimation at the outputs offers an advantage over FCM; the output greyness can be considered as an additional indicator of the decision’s quality, with respect to the information incompleteness at the input and model itself. This is an important cue regarding the quality of the decisions obtained from FGCM in the presence of uncertainty. One more advantage of FGCMs over conventional FCMs is their capability to succeed desired steady states for every set of initial concept states.

6 Conclusions

In this research, the FGCM model and the proposed NHL learning algorithm were applied for processing an industrial process control problem. The proposed mathematical formulation of FGCMs and the implementation of the NHL algorithm have been effectively applied. Experimental results based on simulations of a process control system, verify the effectiveness, validity and especially the advantageous behavior of the proposed grey-based approach of building and learning FCMs.

The benefits of FGCMs over conventional FCMs make evident the significance of developing a greyness-based cognitive model such as FGCM. The case studies presented in this paper are representative and facilitate both demonstration and benchmarking purposes.

The proposed NHL algorithm sustains a formal methodology for FGCMs training, improving the functional FCM reliability and providing the FCM practitioners with learning parameters to adjust the influence of concepts. This type of learning rule accompanied with the good knowledge of the given system, guarantee the successful implementation of the proposed process in industrial process control problems and in adaptive non-linear systems in general.

As a summary, FGCM model shows several advantages over the FCM one, as the following:

  • The model dynamics’ output includes a degree of uncertainty (greyness) expressed in grey numbers.

  • FGCMs model the uncertainty and experts hesitancy associated to the description of the causal relations between the concepts and within the description of the concept states.

  • FGCMs are able to model additional kinds of relationships than FCM. For instance, FGCMs usually run models with relations where the influence between nodes are unknown at all or just partially known.

  • FGCMs can be applied to closer approximate human decision making rather than FCM. It handles the uncertainty inherent in the complex systems by assessing greyness in nodes and edges.

Future research objectives include the exploration of even more challenging applications and improvements of the presented model towards further approximation of human cognition and intuition.