Scheduling operating rooms of multiple hospitals considering transportation and deterioration in mass-casualty incidents

Abstract

In mass casualty incidents, patients need to be evacuated to nearby hospitals as soon as possible, and a surge in demand for emergency medical services then occurs. It would result in ambulance offload delays, i.e., no emergency operating room is available when the ambulance arrives at a hospital, and thus the patients cannot be treated immediately. In this paper, we aim to solve a combinatorial problem of patient-to-hospital assignment and patient surgery sequence considering patient deterioration and ambulance offload delay during a mass casualty incident. A mixed-integer programming model is proposed. The objective is to minimize the completion time of all patients’ surgeries. For solving such a problem, some structural properties of our studied problem are derived, and a heuristic is developed to solve the single operating room scheduling problem considering ambulance offload delay and patient deterioration based on these structural properties. A hybrid Firefly Algorithm-Variable Neighborhood Search algorithm incorporating the heuristic method is proposed to solve it. Our proposed algorithm can solve the problem within a short computation time, and the computational results demonstrate the superiority of our proposed algorithm over the compared algorithms.

1 Introduction

A mass casualty incident (MCI), also called a multiple-casualty incident or multiple-casualty situation, means an incident in which the emergency medical service resources (e.g., human and facility) are overwhelmed by the number and severity of casualties. MCIs include disasters caused by natural catastrophes (such as earthquakes, hurricane, or volcanic activity) or man-made calamities (such as traffic accidents, terrorist attacks, or public health emergencies). Even an aircraft running off the end of a runway when landing at the airport (Dean & Nair, 2014), a bus fire, or an industrial explosion could almost instantly generate 10–125 severely injured casualties which is far more than the existing medical service resources can manage (Melton & Riner, 1981). A recent scientific framework has been developed using expert opinions, which defines an MCI as any event that results in more than 5 casualties (Kim et al., 2014). For example, under the circumstance when a two-person staff is responding to a motor accident with three critically injured casualties could be regarded as an MCI.

In China, due to the imbalanced development among rural areas and urban areas, there is usually few ambulances available in some rural areas (Yan et al., 2017). Some researchers point out that the number of negative pressure isolation ambulances is only 0.15 per health service institution on average (Ye, 2018). Especially for the mass casualty incidents, the available hospital emergency medical resources are limited and the ambulance utilization is very high (Repoussis et al., 2016). The injured must be rescued, triaged and dispersed to nearby hospitals The information available to medical resource owners, e.g., local hospitals, is often incomplete. In an emergency response time, ambulances and emergency operating rooms are in short supply beyond question. Usually, each hospital has its own ambulance site, while their ambulances are directed by the ambulance dispatching center. The decisions made by different medical resource owners/managers are based on partial and fragmented information, and thus affect the overall efficiency (Besiou et al., 2018). It would experience a high influx of patients and the hospitals would soon be overburdened. Investigators from Australia, Spain, and the United States find that patients experience higher mortality rates during periods of emergency operating room crowding (Bernstein et al., 2009).

It has been proved that having an effective real-time response in the aftermath of a disaster requires several inter-dependent decisions to be made and numerous coordinated operations to be arranged quickly (Farahani et al., 2020). Patients are supposed to receive surgeries as soon as possible, but their allocation is a complex problem. For example, one ambulance site may send their ambulances to the casualty collection area without the knowledge of other sites’ operations and the capabilities of hospitals’ admission, etc., which may cause rescue chaos and unbalanced load of resources. While one of the prerequisites for improving rescue efficiency is centralized coordination that can match limited medical resource capacity and urgent surgery demand. In a more efficient situation, the emergency medical resources are arranged in a united system by a centralized decision-maker, e.g., the government, which has the completed information about all the available emergency medical resources’ owners (Rachel Lu et al. 2011), with the knowledge of the patients’ situation, such as the rescue demand, severity, etc. The knowledge of the patients’ injury severity comes from diagnostics/physician assessments at the casualty collection site (Laan et al., 2016).

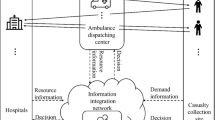
We consider such a rescue system under the centralized decision-making mechanism after an MCI. Integrating patient assignment and operating room scheduling presuppose centralized coordination that can match limited capacity and urgent demand. First, the patients’ information is collected from the casualty collection area to the government, which further gets the information of available medical resources from the hospitals and the ambulance dispatching center under govern. Then, the government makes decisions on ambulance transportation and operating room scheduling in an integrated way. The respective decisions will be transmitted to the corresponding hospitals and ambulance dispatching center, and they will act correspondingly, i.e., transport the patients, and treat them in the hospital following the decisions.

Under the setting of the above-centralized decision-making system, this paper considers two kinds of limited and reusable resources, i.e., ambulances and emergency operating rooms. Reusable resources mean that each ambulance is restored to available status after the previous patient has been transported to the target hospital and can continue to transport the next patient, and each emergency operating room is also available for the next patient after completing the previous patient’s surgery. The arrival times of patients at the hospitals and the trauma level will dictate the surgery order of the patients at the hospitals and the time required to treat all patients. We study the collaborative problem of ambulance scheduling and multi-hospital operating room scheduling in MCIs.

Although some models and decision support systems have been proposed for medical resource scheduling in the MCI response problem, there are still no generally accepted rules or principles to guide scheduling personnel on basic problems, such as which hospital ambulance should transport each patient to and how many patients should be transported to each hospital. Repoussis et al. (2016) formulate a mixed-integer model to integrate ambulance dispatching, transportation of patients and surgery order scheduling. It is assumed that one patient is assigned to an ambulance at a time. The impact of capacity-based bottlenecks on ambulances and hospital beds is quantified. Sung and Lee (2016) use a MIP formulation to model the problem as an ambulance routing problem, and the order and destination hospitals for patient evacuation are determined. The number of ambulances is not taken into consideration. Mills et al. (2018) propose two heuristic policies to determine how to allocate ambulances to patient and which hospital should be the destination for those ambulances. Dean and Nair (2014) determine which hospital ambulance should transport each patient to. A SAVE model is introduced to maximize the number of expected survivors from the MCI. While our paper solves the patient assignment problem and sequence of surgeries in hospital under the limitation of ambulances’ number and hospital capacity considering ambulance offload delay and patient deterioration.

Given the limited resources of ambulance, hospitals and operating rooms, the aim of our study is to determine the assignment of patients to multiple hospitals and exact surgery start times. The objective is to minimize surgery completion time of all patients. Figure 1 demonstrates the methods for our integrated problem in two stages.

Fig. 1

The methods for our integrated problems

The contributions of this paper are as follows: (1) We explicitly consider the combinatorial optimization problem of patient assignment and patient surgery sequence in MCIs, taking into account ambulance offload delay and the deteriorating condition of patients. Capacity limitation of operating rooms and ambulances are specially considered. An operating room would be released after one surgery. (2) Some structural properties of the studied problem are proposed, and a heuristic is developed to solve the single operating room scheduling problem considering ambulance offload delay based on these structural properties. (3) We also develop an effective novel hybrid Firefly Algorithm (FA)-Variable Neighborhood Search (VNS) algorithm incorporating the heuristic to solve our problem.

The remainder of the paper is organized as follows: Sect. 2 presents the literature review of ambulance scheduling and operating room scheduling problems. Section 3 describes our problem by a mixed-integer programming model. Section 4 develops a heuristic algorithm based on some structural properties and scheduling rules to solve the single operating room scheduling problem considering ambulance offload delays. In Sect. 5, a hybrid FA-VNS algorithm incorporating the proposed heuristic is developed to solve the combinatorial problem. Computational experiments are conducted in Sect. 6 to verify the correctness and rationality of the proposed model and evaluate the effectiveness of the proposed algorithm. The conclusions are presented in Sect. 7, and some future research directions are put forward.

2 Literature review

2.1 Ambulance dispatching and offload delay problem

A number of related papers determine transportation order to the hospital according to patient prioritization based on field triage in MCIs. A prevailing protocol of mass casualty triage is START protocol (Fiedrich et al., 2000; Frykberg, 2005; Jenkins et al., 2008; Mills et al., 2013; Sacco et al., 2005). Patients are triaged into four classes (e.g., minor, delayed, immediate, and expectant) by emergency medical technicians at the casualty collection location, and then evacuated following the priority. Patients with higher priority should receive surgeries ahead of those with lower priority, which is the standard practice. Wang et al. (2015) address the single operating room scheduling problem for one day. They consider two priority levels of patients: high-priority patients and low-priority patients. Patients with low priority can only be operated after the operations of high priority have been completed. They determine the surgery sequence in each level of patients by striking a balance between patient satisfaction and operating costs. Mills et al. (2013) present a model of patient triage and design prioritization policies considering multiple casualty locations and multiple receiving hospitals. Nevertheless, Garner (2003) mention that the only recorded incidents for which triage tags were considered useful are small incidents. In large incidents, triage tags were either not used, caused problems, or incidents were managed efficiently because triage tags were not used intentionally. It is noteworthy that little attention has been paid to preventing surges (e.g., avoiding over-triage) by better guiding patient distribution, and how to determine the minimum hospital capacity required to treat all MCI casualties. In this paper, these complex issues are incorporated, and thus we propose an optimal method that can be used to generate and assess emergency preparedness plans.

The transfer of patients from emergency medical service (EMS) providers to emergency department (ED) staff is an important bottleneck (Carter et al., 2014). Ambulance offload delays have recently emerged as one of the most significant challenges for EMS managers, which would increase both risks and surgery costs for patients. When the ambulance delivers the patient to the emergency department, the patient often cannot be admitted in time, resulting in the ambulance staying in the emergency department for a long time. It is called “ambulance offload delay”. Centers for Medicare & Medicaid Services (CMS) stated that it could be reasonable to require the EMS provider to accompany the individual until such time as there where ED resource available to provide care for that individual (Cooney et al., 2011). It takes much time to get ambulances back into service, severely affects the effective turnover of pre-hospital emergency resources, and thus leads to prolonged time on surgery and even compromise safety of casualties. Cooney et al. (2011) point out that it is important to monitor offload delays in evaluating inefficiency of EMS system. While recording this delay presents a serious challenge, most emergency medical services systems only measure the complete time at the hospital (Carter et al., 2014). Until now, there are many research papers that discuss on ambulance offload delay problem in medical services (Almehdawe et al., 2013, 2016; Carter et al., 2014; Cooney et al., 2011, 2013; Li et al., 2019; Majedi, 2008). Cone et al. (2012) found that 12.5% patients experience ambulance offload delay of 30–60 min, and 5% a delay of more than 60 min. In the report of (Crilly et al., 2015), ambulance offload time delay of more than 30 min was experienced by 15% of the 40,783 analyzable ambulance presentations. Carter et al. (2014) study how well the turnaround can act as a proxy for offload delay time, and verify the good correlation between turnaround and actual offload delay time. Although the health and family planning department has organized various hospitals to analyze and solve the problem of ambulance offload delay on many occasions, it has not been fundamentally alleviated because no effective operating mechanism has been established. There is still a lack of formal quantitative models for analyzing ambulance delay problem. Almehdawe et al. (2016) present a queueing network model to investigate the impact of patient routing decisions on ambulance offload delays. In their earlier research (Almehdawe et al., 2013), a queuing model is introduced, in which ambulance utilization is assumed to be not too high and thus travel durations of ambulances are negligible. While in our assumptions, the ambulance utilization is very high under the circumstance of MCIs.

2.2 Deterioration effect

One fundamental feature of trauma care after an MCI is the expectation that severely injured patients will deteriorate over time before receiving surgeries (Dean & Nair, 2014; Hupert et al., 2007; Kamali et al., 2017; L. Lei et al., 2015; Mills et al., 2013; Sung & Lee, 2016). The deteriorating condition of patients inevitably leads to increased care time for the casualties. Dean and Nair (2014) measure the care times by the number of periods for each patient class, and the number is incremental over time up to 7.5 h. Mills et al. (2013) build a fluid model in which patient deteriorate over time according to a survival probability function. The authors design an optimal policy to decrease critical mortality rate. Kamali et al. (2017) solve a optimal triage service order problem under a realistic assumption that patients would deteriorate and have decreasing survival probability. Eun et al. (2019) introduce a MIP model to optimize surgeries assignment considering patient health condition deterioration. They apply a tabu search (TS) to provide effective solutions. Different from the above papers, we consider the deteriorating condition of patients using time-dependent surgery durations. Incorporation of transportation times and deterioration over time makes our problem different from many well-studied problems. The comparison between existing studies and our study is shown in Table 1. We can see that many models and decision support systems have been proposed for medical resource scheduling in the MCI response problem. Most researchers are focused on the location and distribution of emergency response units (Fiedrich et al., 2000) and the supply and distribution of relief materials (Barbarosoǧlu & Arda, 2004; Mete & Zabinsky, 2010), while few papers consider the flow of patients between different locations.

Table 1 Key comparisons of the related papers and our study

2.3 Operating room scheduling problem

Operating room scheduling problems have also been widely discussed in the past decades year. Denton et al. (2007) propose a stochastic optimization model for a single operating room daily scheduling problem. They study the simultaneous effects of sequencing surgeries and scheduling start times with the goal of minimizing the weighted sum of surgeon waiting, operating room idling and tardiness. A simple sequencing rule is designed to solve the problem. Y. Sun and Li (2011) present a method to optimize surgery start times for a single operating room with stochastic operation duration. Xiao et al. (2018) propose models and exact combinatorial methods within the context of a single operating room on a single day. (Ito et al., 2018) present a stochastic programming model to minimize the conditional value-at-risk in a single operating room scheduling problem. Wang et al. (2015) solve surgery scheduling problem for single operating room in the single day.

Recently, Wilson et al. (2013) introduce a multi-objective model to decide rescue, surgery and transportation of casualties in major incident response. The model is established on a task scheduling framework, incorporating pre-rescue stabilization, rescue, pre-transportation stabilization and transportation consecutively. Each patient is assigned to a hospital. Variable neighborhood descent heuristic algorithm and a constructive heuristic method are applied. Different from them, the allocation of patients to ambulances is also considered in our paper. Repoussis et al. (2016) model the problem of allocating casualties to hospitals to improve patient outcomes. For each patient, there is a series of tasks, such as transportation, ambulance preparation, patient transfer and hospital service. Each patient is assigned to one of the trips of an ambulance and one of the beds in a hospital. The authors aim to minimize the overall response time and the total flow time for all patients’ surgeries. Exact and MIP-based heuristic methods are applied to address the problem. In their assumption, the number of beds in each hospital is fixed and non-recyclable. While in our problem, the operating room is recyclable, which means the operating room is available after the previous patient has completed the surgery. As far as we know, these are the only two work that provide clear task scheduling frameworks from the perspective of individual patient; nevertheless, our approach provides a more comprehensive response to the incidents, including patient surgery sequence in the operating room. In this paper, we combine transport time with operating room scheduling after completing assignment using a hybrid algorithm.

2.4 Heuristic algorithms

Facing the optimization problem, researchers first consider whether it can be solved by some exact algorithms. However, most of the problems in MCIs are proved to be NP-hard (Lee et al., 2013; L. Lei et al., 2015). In addition, solutions to operational problems need to be developed in a very limited time in an emergency. While Repoussis et al. (2016) point that when the number of patients is more than 12, exact algorithms cannot get the optimal solution in a reasonable time (2 h), and thus, the authors propose a TS algorithm to solve the problem. The traditional exact method is usually difficult to compute and its applicability is too limited. Considering the complexity of this class of problems, many researchers solve it by an intelligent algorithm. According to (Zheng et al., 2015), evolutionary algorithms are widely applied in disaster relief operation problems. Fiedrich et al. (2000) present an optimization model for the emergency medical resource allocation problem after earthquake disasters. Casualties are classified according to the level of injury severity and therefore the priorities are determined. The goal function consists of fatalities due to secondary disasters, lack of rescue attempts, duration of the rescue operation, delayed transport and duration of transport. Simulated annealing (SA) and tabu search (TS) are applied to address the problem. (Mills et al., 2018) design two heuristic policies to allocate ambulances for patients and determine destination hospitals for ambulances. Dean and Nair (2014) make decision on which hospital each casualty should be sent to. The authors introduce three implementations in common use: closest-first heuristic, furthest-first heuristic, and cyclical heuristic. Mills et al. (2013) introduce two heuristics for their model of patient triage. L. Lei et al. (2015) develop a rolling horizon heuristic based on mathematical programming to solve the problem of medical teams travelling and medical supplies distribution. Almehdawe et al. (2013) adopt heuristic routing policies to send patient to a specific hospital. Thus, it can be seen that heuristics are widely used in the related papers.

In this paper, a hybrid FA-VNS algorithm is proposed to address the problem. Firefly Algorithm (FA) is a nature-inspired algorithm, first proposed by (Yang, 2010). Since then, FA is developed by many researchers and shows its superiority over some traditional algorithms (Łukasik & Żak, 2009; Yang et al., 2012). Researchers then apply FA in many practical scheduling and optimization problems. FA is based on the flashing patterning of tropical fireflies. The positions of fireflies represent a set of solutions, and fireflies are attracted and move towards the brighter fireflies and thus find the new solutions. Variable neighborhood search (VNS) is a local search meta-heuristic, first proposed by Hansen and Mladenovic in 1997 (Hansen & Mladenović, 2001). The main idea is to systematically change the neighborhood structures in searching for a better solution. In this paper, we develop a novel hybrid FA-VNS algorithm combining the procedures and features of these two meta-heuristic algorithms.

3 Problem description and model

3.1 Problem description

We consider a situation where a large number of trauma patients from an MCI must be quickly transferred to multiple hospitals for surgery. After the disaster happens, emergency medical technicians have categorized patients into four groups according to the START triage protocol in an emergency response time ${t}_{0}$. Patients are all assumed ready for transportation to the hospital by ambulances in the casualty collection area, and all hospitals in the region can accept and provide appropriate quality care for immediate and delayed patients. Hospitals are distributed in different locations, and thus the casualty collection location and the transport time between each hospital is different. The number of available ambulances is assumed to be the number of total operating rooms, which is appropriate as long as the ambulance utilization is very high. The structure of this joint scheduling problem of multi-hospitals is shown in Fig. 2.

Fig. 2

Structure of joint scheduling problem of ambulances, hospitals, and operating rooms

Note that patients’ health conditions deteriorate over time (Hupert et al., 2007; Xiang & Zhuang, 2016), resulting in longer surgery time in the hospital. The problem is modeled by assuming that the actual surgery duration ${p}_{i}$ = $\overline{{p }_{i}}+{\upbeta }_{i}{t}_{i}$ (Wang et al., 2015), where ${\upbeta }_{i}$ is the deterioration rate for patient i, and $\overline{{p }_{i}}$ denotes the normal surgery duration of patient i. The normal surgery duration $\overline{{p }_{i}}$ of the patient in each class follows a known distribution of time based on empirical value.

Most studies on the resource-constrained triage problem focus on delayed patients and immediate patients among the four severity classes (e.g., minor, delayed, immediate, and expectant) in START triage (Dean & Nair, 2014; Jacobson et al., 2012; Mills et al., 2013; Sacco et al., 2005; Sung & Lee, 2016). The two classes of patients are in urgent need of surgeries and can endure long-distance transportation. In our problem, we only consider these two classes of patients, i.e., delayed patients and immediate patients. The low-priority patients (delayed patients) could only receive surgeries when surgeries of high-priority patients (immediate patients) have been completed. Let ${S}_{i}\in \{\mathrm{1,2}\}$ represents priority level of patient i. In our paper, the priority for immediate patients is set as “${S}_{i}=2$”, higher than the priority for delayed patients “${S}_{i}=1$”.

We assume that no new patients require admission in decision-making point. It is necessary for analyzing the problem since not all patients are ready for surgery at an emergency response time, some casualties may be still trapped at the disaster site and would be rescued and scheduled in the next time section. Considering that information is not timely updated about remaining capacity of EDs in nearby hospitals, and at the same time cannot interrupt the elective surgeries in progress, we limit hospital capacity to only one operating room available in each ED. The assumption is appropriate since under the circumstance of emergency incidents, only limited capacity is available for the current section of the patients.

To avoid frequent ambulance diversion episodes, we assume that each ambulance travels along a fixed route, which means that each ambulance can only transport patients between the casualty collection site and a fixed hospital. Since we focus on single operating room in each hospital, and only one ambulance travels on each fixed route, thus the order of patients to be transported in each specific ambulance is the same as the surgery order in the corresponding hospital. This simplification allows us to gain many insights without making the model too complex.

3.2 Mass casualty patient allocation model

Assuming I is the set of patients who need surgery, and H is the set of hospitals available at the response time ${t}_{0}$ (i.e., decision-making time section). The notations used in the formulation are shown in Table 2.

Table 2 Notations

Objective function: minimize the makespan

$$ Min\;C_{\max } $$

(1)

Subject to:

$$ \mathop \sum \limits_{{h \in H,b \in H_{b} }} x_{ihb} \le 1\quad \forall i \in I $$

(2)

$$ \mathop \sum \limits_{i \in I} x_{ihb} = 1\quad \forall h \in H,b \in B_{h} $$

(3)

$$ x_{ihb} = 1\quad l_{i} = T_{h} \quad \forall i \in I,b \in B_{h} $$

(4)

$$ \mathop \sum \limits_{i \in I} x_{{ih\left( {b - 1} \right)}} \ge \mathop \sum \limits_{i \in I} x_{ihb} \quad \forall h \in H,b \in B_{h} \backslash \left\{ 1 \right\} $$

(5)

$$ s_{i} \ge l_{i} \quad \forall i \in I $$

(6)

$$ p_{i} = \overline{{p_{i} }} + \upbeta_{i} *s_{i} \quad \forall i \in I $$

(7)

$$ x_{ih0} = 1 \Rightarrow a_{i} = T_{h} \quad \forall h \in H $$

(8)

$$ x_{ihb} = 1 \Rightarrow a_{i} = aa_{hb} \quad \forall i \in I,h \in H,b \in B_{h} $$

(9)

$$ x_{ihb} = 1 \Rightarrow s_{i} = as_{hb} \quad \forall i \in I,h \in H,b \in B_{h} $$

(10)

$$ c_{i} = s_{i} + p_{i} \quad \forall i \in I $$

(11)

$$ as_{hb} \ge as_{{h\left( {b - 1} \right)}} + \mathop \sum \limits_{i \in I} p_{i} x_{{ih\left( {b - 1} \right)}} \quad \forall h \in H,b \in B_{h} \backslash \left\{ 1 \right\} $$

(12)

$$ as_{hb} \ge as_{{h\left( {b - 1} \right)}} + \mathop \sum \limits_{i \in I} l_{i} x_{{ih\left( {b - 1} \right)}} ,\quad \forall h \in H,b \in B_{h} \backslash \left\{ 1 \right\} $$

(13)

$$ s_{i} \ge a_{i} \quad \forall i \in I $$

(14)

$$ aa_{hb} \ge as_{{h\left( {b - 1} \right)}} + T_{h} \quad \forall h \in H,b \in B_{h} \backslash \left\{ 1 \right\} $$

(15)

$$ a_{i} \ge l_{i} \quad \forall i \in I $$

(16)

$$ s_{{i^{\prime } }} \ge s_{i} \quad \forall i,i^{\prime } \in I,e_{i} \ge e_{{i^{\prime } }} $$

(17)

$$ C_{\max } \ge c_{i} \quad \forall i \in I $$

(18)

Constraint (2) ensures that each patient has been assigned exactly to one position in one hospital. Constraint (3) ensures that one position in one hospital can only be assigned to one patient. Constraint (4) defines the round-trip time for each patient. Constraint (5) limits that there must be a patient at position b − 1 if there is another patient assigned at position b in the same emergency operating room. Constraint (6) defines the start time of the first operation. Constraint (7) defines the actual surgery duration. Constraint (8) initializes the arrival time for the first patient to the hospital. Constraint (9) associates the auxiliary variables ${a}_{i}$ and ${aa}_{hb}$. Constraint (10) associates the auxiliary variables ${s}_{i}$ and ${as}_{hb}$. Constraint (11) defines the surgery complete time. Constraint (12) updates the surgery start time for each position in the emergency operating room. Constraint (13) updates the surgery start time at each position of the emergency operating room according to the surgery duration of the patient assigned to the same operating room at the previous position. Constraint (14–16) impose the lower bounds of the surgery start time. Constraint (17) ensure that the triage protocol is accepted by the patients. Constraint (18) determines the makespan, which is equal to the maximum of the surgery completion time of all patients.

4 Structural properties for single operating room sequence problem

In this paper, a hybrid FA-VNS algorithm is proposed (see Sect. 5) to assign patients to multiple hospitals. Based on the assignment results, we give an example of different arrangements in the single operating room (see Sect. 4.1) considering the ambulance offload delay. We also propose two lemmas in Sect. 4.2, based on which we design Algorithm 2 incorporated in the hybrid FA-VNS algorithm to determine the surgery sequence in each operating room and thus determine the transportation order in each ambulance.

4.1 An example of different arrangements in the single operating room

We can see that the surgery start time of the later patient depends on the round-trip transportation time ${T}_{h}$, and the actual surgery duration ${p}_{i}$ (${p}_{i}=\overline{{p }_{i}}+{\upbeta }_{i}{t}_{i}$) of patient who receives surgery earlier in the same operating room. Figure 3 gives an example of different schemes of patients’ surgeries in the operating room.

Fig. 3

An example of different arrangements for patients in the single operating room

In Fig. 3, we can see that three patients {${I}_{1},{I}_{2},$ and ${I}_{3}$} have been assigned to the same operating room. We give four cases to show different arrangements in the operating room. The blank squares denote the duration of each patient’s surgery, the arrows denote the round-trip transportation time between the casualty collection location and hospital location (${p}_{1}<{T}_{1}<{p}_{2}<{T}_{2}<{p}_{3}$), and the shadow squares denote the idle time of the operating room. Operating room’s idle time should be minimized to maximize the utilization of the operating room. The idle time depends on the difference between transportation time and the surgery duration. Round-trip transportation time depends on the hospital location. If there is a gap between the round-trip transportation time and surgery duration, the idle time is in-advisably prolonged.

In Case 1, we can see that since the surgery duration of patient ${I}_{1}$ is shorter than the round-trip transportation time ${T}_{1}$, patient ${I}_{2}$ receives the surgery after an idle duration in the operating room. In Case 2, we can see that since the surgery duration of patient ${I}_{3}$ is longer than the round-trip transportation time ${T}_{1}$, patient ${I}_{2}$ can receive the surgery without any idle time in the operating room. Also, patient ${I}_{1}$ can receive the surgery without any idle time in the operating room after patient ${I}_{2}$. Thus, the makespan in Case 2 is shorter than that in Case 1. While in Case 3, since the round-trip transportation time ${T}_{2}$ is very long, the surgery duration of patient ${I}_{1}$ and ${I}_{2}$ is shorter than ${T}_{2}$. Thus, there exits idle time before ${I}_{1}$ receives surgery, and so does ${I}_{2}$. While in Case 4, since the surgery duration of patient ${I}_{3}$ is longer than the round-trip transportation time ${T}_{2}$, there is no idle time before patient ${I}_{2}$ receives surgery. Thus, the makespan in Case 4 is shorter than that in Case 3. From the analysis above, we can see that Case 2 is better than Case 4, Case 1, and Case 3. In this case, the idle time for the operating room is perfectly minimized. Therefore, based on the results of different arrangements for surgeries of patients, we can sum up a set of dispatching rules for minimizing the idle time of the operating room under different situations of round-trip transportation time.

4.2 Structural properties for single operating room scheduling problem

To solve the single operating room scheduling problem considering ambulance offload delay, we give some properties of the makespan minimization problem for any given patient assignment list in a specific operating room.

Lemma 1

For the patients with the same priority (${\upbeta }_{1}={\upbeta }_{2}=\dots {\upbeta }_{i}={\upbeta }_{j}=\dots =\upbeta$) in the same operating room, if at time t, actual surgery durations of all remaining patients to be scheduled are not smaller than ${T}_{h}$ (i.e., ${p}_{i}$(t) ≥ ${T}_{h}$), they are ordered according to the smallest normal surgery duration first rule (SNSDF): $\overline{{p }_{1}}$ ≤ $\overline{{p }_{2}}$  ≤ … ≤ $\overline{{p }_{n}}$.

Proof

We prove the lemma by contradiction. If at $t=0$, all patients’ surgery durations are not smaller than ${T}_{h}$ (i.e., ${p}_{i}\ge {T}_{h}$). First we show that patients with the same priority are sequenced according to the SNSDF as a schedule ${\pi }^{^{\prime}}$, where patient ${I}_{j}$ is followed by ${I}_{i}$ ( $\overline{{p }_{i}}>\overline{{p }_{j}}$). At the same time, consider an optimal schedule ${\pi }^{*}$ of the OR where patients do not follow the SNSDF, where patient ${I}_{i}$ is followed by ${I}_{j}$ ($\overline{{p }_{i}}>\overline{{p }_{j}}$), leaving the remaining patients in their original positions of the sequence. We assume that the start time for ${I}_{i}$ in schedule ${\pi }^{*}$ is t.

For schedule ${\pi }^{*}$, ${C}_{i}({\pi }^{*})=t+{p}_{i}= t+(\overline{{p }_{i}}+\upbeta \mathrm{t})=\left(1+\upbeta \right)t+\overline{{p }_{i}}$, and then we have ${C}_{j}({\pi }^{*})={C}_{i}+{p}_{j}={C}_{i}+(\overline{{p }_{j}}+\upbeta {C}_{i})= \overline{{p }_{j}}+(1+\upbeta ) {C}_{i}=\overline{{p }_{j}}+(1+\upbeta )\left[(1+\upbeta )\mathrm{t}+\overline{{p }_{i}}\right]={(1+\upbeta )}^{2}\mathrm{ t}+(1+\upbeta )\overline{{p }_{i}}+\overline{{p }_{j}}$.

Similarly, for schedule ${\pi }^{^{\prime}}$, we can easily obtain ${C}_{j}({\pi }^{^{\prime}})=t+{p}_{j}= t+(\overline{{p }_{j}}+\upbeta \mathrm{t})=(1+\upbeta )\mathrm{t}+\overline{{p }_{j}}$, ${C}_{i}({\pi }^{^{\prime}})={(1+\upbeta )}^{2}\mathrm{ t}+(1+\upbeta )\overline{{p }_{j}}+\overline{{p }_{i}}$.

Thus we have ${C}_{j}\left({\pi }^{*}\right)-{C}_{i}({\pi }^{^{\prime}})=\upbeta (\overline{{p }_{i}}-\overline{{p }_{j}}) >0$. It implies that patient operated after ${I}_{i}$ and ${I}_{j}$ under ${\pi }^{*}$ has a later start time than that under ${\pi }^{^{\prime}}$. Thus, the makespan of patients under ${\pi }^{*}$ is strictly greater than that under ${\pi }^{^{\prime}},$ which conflicts with our assumption. It should be $\overline{{p }_{i}}<\overline{{p }_{j}}$. The proof is completed.

Lemma 2

For the patients with the same priority (${\upbeta }_{1}={\upbeta }_{2}=\dots =\upbeta$), if at time t, there is any patient to be scheduled whose actual surgery duration is smaller than ${T}_{h}$ (i.e., ${p}_{i}$(t) ≥ ${T}_{h}$), an optimized solution exists under different circumstances as shown in Table 3.

Table 3 Summary of the sequence rules in Lemma 2

The proof is presented in the Appendix.

Based on Lemma 2, the following Algorithm 1 is designed to solve patient sequence problem in a single operating room for patients with the same priority.

In this section, based on the above two lemmas for the single operating room scheduling problem, Algorithm 2 is proposed to determine the surgery sequence in each operating room, given that all patients with different priorities have been assigned to the destination hospitals. The framework of Algorithm 2 is as follows.

The time complexity of step 5 is O(n log n). The time complexity of step14-30 is O(${n}^{2}$), and the time complexity of the other steps is no more than O(${n}^{2}$). Thus, the total time complexity of Algorithm 1 is O(${n}^{2}$). The time complexity of Algorithm 2 is O(${n}^{2}$).

5 Metaheuristic-based hybrid approach

To solve our problem, we propose a hybrid Firefly Algorithm (FA)-Variable Neighborhood Search (VNS) algorithm incorporating the heuristic in this section. The critical procedures of the hybrid FA-VNS are introduced in Sects. 5.2, 5.3, 5.4.

5.1 Coding scheme

In our algorithm, a solution for the problem of assigning patients to the hospital is an array, of which the length is equal to the number of patients. Each position value stands for the index of the hospital that the patient is assigned to. We use an instance of six patients {${I}_{1}$, ${I}_{2}$, ${I}_{3}$, ${I}_{4}$,${I}_{5}$, ${I}_{6}$} and four hospitals {${H}_{1}$, ${H}_{2}$, ${H}_{3}$,${H}_{4}$}. An instance solution is showed in Fig. 4, and X = {2, 3, 4, 1, 2, 4} where the patients {${I}_{4}$}, {${I}_{1}$, ${I}_{5}$}, {${I}_{2}$}, {${I}_{3}$, ${I}_{6}$} are assigned to hospital ${H}_{1}$, ${H}_{2}$, ${H}_{3}$, and ${H}_{4}$ respectively.

Fig. 4

Illustration of a particle’s solution

5.2 Encoding correction

In the iterative processes, infeasible solutions may be generated under the following circumstances: (1) Hospital slots should be encoded with integers while searching operators may generate decimals. We adopt the coding correction strategy which takes integer approximate values. (2) All position values should be in the range of [1, ${n}_{H}$]. Set the numbers in X that are less than “1” to “1” and those greater than “${n}_{H}$” to “${n}_{H}$”. The initial feasible solution is obtained from the heuristic algorithm designed in Sect. 3 or randomly selected from a feasible solution set.

5.3 Neighborhood structures

In the following, three neighborhood structures are designed (see Fig. 5) and applied in a VNS-based local search procedure for improving the effectiveness of the traditional FA. These neighborhood structures are applied in order, and the local search process needs to be repeated until it finds a good set of base locations. ${N}_{k}(X)$ denotes the k-th neighborhood of solution X.

• (1) Insert Operator: In solution ${\mathrm{X}}_{i}$, randomly select two positions x and y. The x position value is taken from its current position and inserted after position y (see Fig. 5a).

• (2) Mutation Operator: In solution ${\mathrm{X}}_{i}$, randomly select a position x. Generate an integer number in [1, Q] and make it the substitute for the value of the position x, and thus, a neighbor of ${\mathrm{X}}_{i}$ can be obtained (see Fig. 5b).

• (3) Exchange Operator: In solution ${\mathrm{X}}_{i}$, randomly select position x and position y. A neighbor of ${\mathrm{X}}_{i}$ can be obtained by swapping the numerical values in position x and position y (see Fig. 5c).

Fig. 5

Local search operators

The detail of VNS-Based Local Search operation is designed as follows:

VNS-based local search operation:
Step 1	Define neighborhood structures ${N}_{s}(\mathrm{s}=1,\dots ,{s}_{max})$
Step 2	Get initial solution ${X}_{new}$ which is produced by FA
Step 3	Execute the s-th Local Search for $X_{new}$ to obtain a solution $X_{new}^{\prime }$
Step 4	If solution $X_{new}^{\prime }$ is better than $X_{new}$, then set$X_{new} = X_{new}^{\prime }$, s = 1 and go to step 5
Step 5	If s $< s_{max}$, then go to step 3; else, stop the iteration

5.4 Framework of the hybrid algorithm

The whole procedures of the hybrid FA-VNS to assign the patients to ambulances and hospitals and determine surgery sequence in each hospital based on the detailed description of our proposed algorithm are shown in Table 4 and Fig. 6.

Table 4 Procedures of FA-VNS algorithm

Fig. 6

The flow chart of the proposed FA-VNS algorithm

In the iterations, the time complexity of decoding steps is no more than O(${n}^{2}$), because the Algorithm 2 is incorporated. The time complexity of step 8 to step 29 is O(${n}^{2}$). The time complexity of other steps is no more than O(n). Thus, the total time complexity of FA-VNS is O(${n}^{2}$).

6 Computational experiments and comparison

We perform computational experiments to check the effectiveness and efficiency of our proposed methods. For this purpose, we have randomly generated small- and large-scale of instances based on realistic data. All experiments are conducted on a laptop with an Intel(R) Core (TM)2 Duo CPU @2.93 GHz and 8 GB RAM. Our methods are implemented by Python 2.7. Gurobi 9.0.2 (win64) is used as the MIP solver. 20 runs are performed for each case, and all computational times are recorded in the unit of second.

This section is organized as follows: In Sect. 6.1, we describe the data sets and the experimental parameter setting. In Sect. 6.2, the MIP model given in Sect. 3 is validated by Gurobi and the applicability of our proposed algorithm is examined. In Sect. 6.3, we compare our proposed algorithm with other three widely used algorithms. Section 6.4 is sensitivity analysis.

6.1 Experimental settings and data sets

We consider 24 possible cases reflecting different scales of the mass-casualty incidents. Referring to the actual situation of the hospital and other literature on surgical scheduling (Repoussis et al., 2016), the following experimental data were generated: the number of hospitals is ${n}_{H}$ = {4, 5, 6, 7}, and the number of patients is ${n}_{I}$ = {16, 18, 20, 30, 40, 50}. The proportion of immediate patients is 20–50% and the baseline is 35%. The distance from the disaster site is expressed in terms of round-trip time in minutes (see Table 2). We consider two hospitals that are included in regional disaster preparedness planning: a ‘‘local’’ hospital (5 min for a round-trip transport) and a ‘‘remote’’ one (20 min for a round-trip transport), and each has one available emergency operating room. One of the characteristics of our model is that it considers multiple hospitals in different geographical locations when making decisions. It should be noted that although only two types of hospitals are considered for illustrative purposes, our method is capable of handling more. The normal surgery times are normally distributed with a mean dependent on the severity class based on empirical value (Marques et al., 2012).

For immediate patients, ${\upmu }_{1}$= 40 and ${{\upsigma }_{1}}^{2}$=${18}^{2}.$ For delayed patients, ${\upmu }_{2}$=20 and ${{\upsigma }_{2}}^{2}$=${13}^{2}$. The deteriorating rate for patient surgery duration is set as ${\upbeta }_{i}=0.01$ for delayed patients and ${\upbeta }_{i}=0.05$ for immediate patients through the survey in (Wang et al., 2015). Table 5 shows the different levels considered.

Table 5 Parameter setting for the experiments

As mentioned in Sect. 1, there are no specific national or regional criteria for selection a patient’s destination hospital, and the results may vary with the location and incident. In the absence of any standard strategy to compare our algorithms, we compare our FA-VNS with three popular metaheuristic algorithms: FA (Marichelvam et al., 2013), VNS (D. Lei & Guo, 2016), and PSO (Taherkhani & Safabakhsh, 2016).

In our proposed FA-VNS algorithm, the parameters that may affect its performance include ${\upbeta }_{0}$, $\upgamma$, and $\mathrm{\alpha }$, the number of populations. According to the survey and a series of preliminary experiments, the parameter values are set as follows: ${\upbeta }_{0}$=1, $\upgamma =1,\mathrm{ \alpha }=2,$ popsize = 20.

6.2 FA-VNS VS Gurobi

In this section, the MIP model shown in Sect. 3.1 is solved by Gurobi with the time limitation of 1800s and is compared with our proposed algorithm. 17 randomly generated cases are tested, and the number of patients varies from 4 to 36.

Table 6 shows the results obtained by Gurobi and FA-VNS. Columns ${n}_{I}$ and ${n}_{H}$ represent the number of patients and hospitals, respectively. Columns Obj, GAP, and Runtime report the objective function value, GAP value, and run time obtained by Gurobi. Each case is run 20 times by FA-VNS. Columns Best, Avg, Worst, SD and Runtime report the best, average, worst objective function value, the standard deviation (SD) among the 20 times, and the run time by FA-VNS. The last column Impr. shows the improvement by the FA-VNS over Gurobi in terms of the solution’s objective value. The calculation formula of Impr. is as follows:

$$ Impr.\left( \% \right) = \frac{{Best Obj\left( {FA - VNS} \right) - Obj\left( {Gurobi} \right)}}{{Obj \left( {Gurobi} \right)}}*100\% $$

Table 6 Experimental results of Gurobi and TS-ALNS

As can be seen from Table 6, for most instances with the number of patients less than 12, the quality of the function values obtained by Gurobi is better than the best one obtained by FA-VNS, and Gurobi obtains the optimal solution in a shorter time than FA-VNS. When the number of patients is greater than or equal to 12, FA-VNS reports better results than Gurobi. In addition, FA-VNS takes much less time than Gurobi. The experiment verifies the correctness of the model in Sect. 3 and quality of the results obtained by our method. Meanwhile, the correctness of Algorithm 1 and Algorithm 2 designed in FA-VNS is also verified.

6.3 FA-VNS VS FA, VNS and PSO

The comparison of FA-VNS, FA, VNS and PSO are conducted in this section. The parameters are introduced in Sect. 6.1. We examine 24 cases with up to 50 patients for large-scale instances. The average objective value (Ave) and the minimization objective value (Best) are measured over 24 cases in Table 7. We also analyze and compare the performance of these four algorithms by Relative Percent Deviation (RPD) (Vallada and Ruiz 2011) defined as follows:

Table 7 Comparative results for the four algorithms

$$RPD\left( M \right) = \frac{Max\;Obj\left( F \right) - Ave\left( M \right)}{{Max\;Obj\left( F \right)}}*100\% $$

where $M$ denotes each algorithm, and $Ave\left( M \right)$ denotes the average fitness value for each algorithm. $Max\;Obj\left( F \right)$ denotes the best fitness value we have gotten.

In order to ensure the algorithms can converge to a good solution, the number of populations is set as 20, and the maximum of iteration is 200. The average fitness value (Ave) and the best fitness value (Min) obtained from 1 to 200 iterations are reported to analyze the performance of each algorithm in Table 7. Also, Relative Percent Deviation (RPD) (Vallada and Ruiz 2011) is calculated to evaluate and compare the performance of these four methods, defined as:

$$ RPD = \frac{{Method\left( {sol} \right) - Best\left( {sol} \right)}}{{Best\left( {sol} \right)}} \times 100\% $$

where $Method\left( {sol} \right)$ is the average fitness value obtained by and $Best\left( {sol} \right)$ is the lowest makespan obtained for that instance among the four algorithms. As the objective is minimizing the maximum makespan, the smaller the RPD, the better the performance. In order to ensure the reliability of experiments, each instance is run for 20 times. The initial solutions of each instance are the same for the algorithms to ensure that each algorithm starts at the same level to search for the optimized solutions. In Table 7, the last two rows show the best and average RPD (ARPD) values of instances 1–12 and instances 13–24 for each algorithm.

According to the experimental result for case 1 (${n}_{I}=16$, ${n}_{H}=4$) in Table 7, the obtained schedule scheme for patients (I1–I16) who are assigned among ambulances (A1–A4) and hospitals (H1–H4) is provided in Fig. 7. The length of ${T}_{i}$ and ${P}_{i}$ represent round -trip transportation time and surgery duration for each patient, respectively. For example, for A1 (i.e., Ambulance 1) and H1 (i.e., Hospital 1), the order of patients is P5, P6, P12, and P7. Following the scheme, the ambulance drivers and the doctors in the emergency department can prepare the relevant emergency medical resources and service the patients in an orderly manner.

Fig. 7

The obtained patients’ schedule scheme among ambulances and hospitals for case 1

From the values in bold, we can see that VNS can obtain as good objective values as FA-VNS in some cases. While in most cases, FA-VNS has the best performance in obtaining average makespan, lowest makespan, best RPD and average RPD compared with other three algorithms. In order to further verify the statistical validity of RPD values and find out the best algorithm, we design a series of experiments and variance analysis, in which we consider a different algorithm as a factor and set the response variable as the average RPD value.

By SPSS, the 20 results generated from each algorithm are analyzed with paired-samples t-test for all the 24 instances, shown in Table 8. Statistical significance is set at an alpha of 0.05, and a $\rho$-value of < 0.05 is deemed statistically significant. Compared with VNS, FA-VNS generates remarkably better results for 18 out of 24 instances and is competitive for the remaining instances where there is no statistical difference between the two algorithms. When compared to FA and PSO, FA-VNS achieves significantly better results in all instances, which proves the improvement of our proposed algorithm.

Table 8 The test results for the FA-VNS with the compared algorithms

Figure 8 intuitively shows the RPD of the compared algorithms. It shows that the RPD values of FA-VNS and VNS are maximal when the number of patients and hospitals is (50, 4). The RPD values of FA and PSO are maximal when the number of patients and hospitals is (50, 7). FA-VNS has more stable RPD values than the other three algorithms. The RPD values of VNS are smaller than those of FA and PSO. The RPD values of FA and PSO are similar. FA and PSO are especially unstable and VNS cannot converge to get a stable value. From Fig. 8 we can obtain the deduction that GWO-VNS is more stable and efficient compared with other three algorithms.

Fig. 8

RPD results in different instances for the algorithms (e.g., FA-VNS, FA, VNS, PSO)

Figure 9 shows the differences of RPD values among the four algorithms at 95% confidence level, where the minimum, the lower and upper quartiles, median, maximum and mean value for all 24 instances are shown. It can be seen that the confidence intervals of FA and PSO are overlapped, which proves that the performance of these two algorithms is at the same level, and they are not statistically different. VNS obtains smaller minimum, lower and upper quartiles, median, maximum and mean value than those of FA and PSO. Additionally, lower and upper quartiles, median, mean value, and the difference between the upper and lower quartiles of FA-VNS are much smaller than other three algorithms. This clearly shows the best performance of FA-VNS among the all four algorithms. Besides, this result is consistent with those in Table 7 and Fig. 8.

Fig. 9

The box-plot of RPD over the four algorithms (e.g., FA-VNS, FA, VNS, PSO)

Furthermore, the convergence curve graphs of FA-VNS, FA, VNS, PSO for the 24 instances are shown in Fig. 10 to verify the performance of convergence speed and solution qualify for the proposed algorithm. The average of fitness values in each iteration is shown in each figure. In Fig. 10, we can see that the differences of the best solutions among FA-VNS, FA, VNS, and PSO become greater with the number of hospitals increasing. VNS gets better solutions than FA and PSO. Compared with FA, VNS, and PSO, FA-VNS has the fastest convergence speed in all instances and it can always get better solutions than the other three algorithms. VNS also convergences sharply, but its results are worse than ours. In nearly all instances, fast convergence speed and best solutions are realized by our proposed FA-VNS algorithm.

Fig. 10

Convergence curves for 24 instances over the four algorithms

Based on above description and discussion, we can conclude that our FA-VNS is stable and effective in solution quality and performs well in convergence speed. In other words, our FA-VNS algorithm not only outperforms other algorithms in convergence speed and solution quality, but also maintains robust in all instances.

6.4 Sensitivity analysis

In addition to the number of patients, another important parameter that can affect the solution is the proportion critically injured. Therefore, we consider the proportion of critically injured patients ω, that is, the larger ω, the larger the proportion of immediate patients is. We also consider the distance between the casualty collection area and hospital ${T}_{h}$, that is, the larger ${T}_{h}$, the longer the time spent in delivering the patients.

To analyze the influence of two parameters, additional experiments are conducted. The three values of ω, i.e., 0.2, 0.4, and 0.6 are considered. The number of hospitals is 2, in which one is a local hospital and another is a remote hospital.

Table 9 records the Avg, Best, Worst, SD, the number of patients transferred to the local hospital, and the number of patients transferred to the remote hospital with different values of ω. Table 8 shows that the higher the proportion of critically injured patients, the longer the surgery completion time is needed, and the more patients are needed to transported to the remote hospital. When the proportion critically injured changes, it can guide the decision-makers to adjust the schedules and predict the time required for surgeries in MCIs.

Table 9 Solution values with different parameter setting $\omega$ ($n_{H} = 2$)

7 Conclusions

In this paper, we aim to improve the integrated problem of patient assignment and operating room scheduling considering ambulance offload delay and deteriorating condition in MCIs. A MIP model is proposed to effectively assign the limited ambulance and operating room resources for patients. The objective is to minimize the makespan. Because of the complexity of the model, only heuristic solution procedures may be used. Some structural properties of the studied problem are proposed, and a heuristic is developed to solve the single operating room scheduling problem based on these structural properties. Since the studied problem is proved to be NP-hard, a hybrid Firefly Algorithm (FA) - Variable Neighborhood Search (VNS) algorithm incorporating a heuristic method is proposed to solve it. The exact solver Gurobi is used to solve the model to verify the correctness and rationality of the established model and the known characteristics of the scheduling problem proposed in this paper. The applicability of the model is verified. Our proposed algorithm can solve the problem within a short computation time. A set of experiments is conducted to test our algorithm’s performance, compared with FA, VNS, and PSO. The computational results demonstrate the superiority of our proposed algorithm over the compared algorithms. In addition, the effects of the parameters, the proportion critically injured, on the problem are analyzed. The sensitivity analysis shows the higher the proportion of critically injured patients, the longer the surgery completion time is needed, and the more patients needed to transported to the remote hospitals. When the proportion critically injured changes, it can guide the decision-makers to adjust the schedules and predict the time required for surgeries in MCIs.

At the same time, we believe that our proposed model and algorithms can help decision-makers decrease the time spent on deciding destination hospital, transportation sequence and surgery sequence, and respond to MCIs more effectively and efficiently. Some readers would realize the limitations of our algorithm, including that we assume only one ambulance assigned to each fixed route, while the assumption is appropriate as long as the ambulance utilization is very high and the available ED resource is limited.

In our future work, we consider extending our model to accommodate multiple operating rooms and dynamic routing of ambulances. Also, take death possibility before receiving surgeries into consideration is of great value as it may arise in real-world applications. In addition, if demand is higher than all hospitals available, we could consider transferring stabilizing patients to more distant facilities and clear emergency departments to accommodate more casualties. It will also be of great value to extend the current model for stochastic environments and incorporate some uncertainty into the parameters of the model, like arrival rate, damaged road networks, transport cost and time to make the problem more realistic. Through further research, we would develop more effective algorithms to solve the practical problems and improve the health care systems’ surge capacity to handle more significant numbers of casualties.

Appendix

In this appendix, the proof of Lemma 2 in Sect. 4.2 is presented.

Proof

Given that an operating room has been assigned a set of patients, there exist two schedules for the operating room. We assume that ${\pi }^{*}$ is an optimized schedule where patient i precedes patient j to start the surgery, while in ${\pi }^{^{\prime}}$ schedule, patient j precedes patient i to start the surgery. That is, ${\pi }^{*}=(\dots ,{I}_{A},{I}_{i},{I}_{j},{I}_{B},\dots )$, and ${\pi }^{^{\prime}}=(\dots ,{I}_{A},{I}_{j},{I}_{i},{I}_{B},\dots )$.

For ${\pi }^{*}$ and ${\pi }^{^{\prime}}$ schedule, the surgery start time of patient A is given as ${S}_{A}({\pi }^{*})={S}_{A}({\pi }^{^{\prime}})={S}_{A}$, and the surgery duration of patient A is ${p}_{A}^{*}={p}_{A}^{^{\prime}}={p}_{A}$, and thus the complete time of patient A is ${C}_{A}({\pi }^{*})={C}_{A}({\pi }^{^{\prime}})={C}_{A}$.

For ${\pi }^{*}$, ${S}_{i}({\pi }^{*})=\mathrm{max}\{{S}_{A}({\pi }^{*})+{T}_{h},{C}_{A}({\pi }^{*})\}=\mathrm{max}\{{S}_{A}+{T}_{h},{C}_{A}({\pi }^{*})\}$. There exist two situations: (1) ${T}_{h}>{p}_{A}$; (2) ${T}_{h}<{p}_{A}$.

• (1) In situation (1), ${\mathrm{T}}_{\mathrm{h}}>{\mathrm{p}}_{\mathrm{A}}$:

  ${S}_{i}\left({\pi }^{*}\right)={S}_{A}+{T}_{h}$, ${C}_{i}\left({\pi }^{*}\right)={S}_{i}\left({\pi }^{*}\right)+{p}_{i}^{*}= {S}_{i}\left({\pi }^{*}\right)+\left(\overline{{p }_{i}}+\upbeta {S}_{i}\left({\pi }^{*}\right)\right) =\left(1+\upbeta \right){S}_{i}\left({\pi }^{*}\right)+\overline{{p }_{i}}=\left(1+\upbeta \right)\left({S}_{A}+{T}_{h}\right)+\overline{{p }_{i}}$, and ${S}_{j}({\pi }^{*})=\mathrm{max}\{{S}_{i}({\pi }^{*})+{T}_{h}, {C}_{i}({\pi }^{*})\}=\mathrm{max}\{{S}_{A}+2{T}_{h},\left(1+\upbeta \right)\left({S}_{A}+{T}_{h}\right)+\overline{{p }_{i}}\}$. There are two cases:

  • (a) When ${T}_{h}>\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-\upbeta }$:

  ${S}_{j}\left({\pi }^{*}\right)={S}_{A}+2{T}_{h}$, ${C}_{j}\left({\pi }^{*}\right)={S}_{j}\left({\pi }^{*}\right)+{p}_{j}^{*}={S}_{j}\left({\pi }^{*}\right)+\left(\overline{{p }_{j}}+\upbeta {S}_{j}\left({\pi }^{*}\right)\right)=\left(1+\upbeta \right){S}_{j}\left({\pi }^{*}\right)+\overline{{p }_{j}}=\left(1+\upbeta \right)({S}_{A}+2{T}_{h})+\overline{{p }_{j}}$. Then ${S}_{B}({\pi }^{*})=\mathrm{max}\{{S}_{j}({\pi }^{*})+{T}_{h},{C}_{j}({\pi }^{*})\}=\mathrm{max}\{{S}_{A}+3{T}_{h},(1+\upbeta )( {S}_{A}+2T) +\overline{{p }_{j}}\}$. If ${T}_{h}>\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-2\upbeta }$,${S}_{B}({\pi }^{*})={S}_{A}+3{T}_{h}$. Otherwise, ${S}_{B}^{*}=(1+\upbeta )( {S}_{A}+2{T}_{h}) +\overline{{p }_{j}}$.

  • (b) When ${T}_{h}<\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-\upbeta }$:

    ${S}_{j}({\pi }^{*})=(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}$, ${C}_{j}\left({\pi }^{*}\right)={S}_{j}\left({\pi }^{*}\right)+{p}_{j}^{*}={S}_{j}\left({\pi }^{*}\right)+\left(\overline{{p }_{j}}+\upbeta {S}_{j}\left({\pi }^{*}\right)\right)=\left(1+\upbeta \right){S}_{j}\left({\pi }^{*}\right)+\overline{{p }_{j}}=\left(1+\upbeta \right)\left[\left(1+\upbeta \right)\left( {S}_{A}+{T}_{h}\right)+\overline{{p }_{i}}\right] +\overline{{p }_{j}}$. Then ${S}_{B}({\pi }^{*})=\mathrm{max}\{{S}_{j}({\pi }^{*})+{T}_{h},{C}_{j}({\pi }^{*})\}=\mathrm{max}\{(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}+{T}_{h}, (1+\upbeta )\left[(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}\right] +\overline{{p }_{j}}\}$. If ${T}_{h}>\frac{\left({\upbeta }^{2}+\upbeta \right){S}_{A}+(1+\upbeta )\overline{{p }_{i}}+\overline{{p }_{j}}}{1-\upbeta -{\upbeta }^{2}}$, ${S}_{B}({\pi }^{*})=(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}+{T}_{h}$. Otherwise, ${S}_{B}({\pi }^{*})=(1+\upbeta )\left[(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}\right] +\overline{{p }_{j}}$.

• (2) In situation (2),${\mathrm{T}}_{\mathrm{h}}<{\mathrm{p}}_{\mathrm{A}}$:

  ${S}_{i}({\pi }^{*})={C}_{A}$,${C}_{i}({\pi }^{*})={S}_{i}({\pi }^{*})+{p}_{i}^{*}={S}_{i}({\pi }^{*})+\left(\overline{{p }_{i}}+\upbeta {S}_{i}\left({\pi }^{*}\right)\right) =(1+\upbeta ){S}_{i}({\pi }^{*})+\overline{{p }_{i}}=(1+\upbeta ){C}_{A}+\overline{{p }_{i}}$, and ${S}_{j}({\pi }^{*})=\mathrm{max}\{{S}_{i}^{*}+{T}_{h},{C}_{i}({\pi }^{*})\}=\mathrm{ max}\{{C}_{A}+{T}_{h},(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}\}$. There are two cases:

  • (a) When ${T}_{h}>\upbeta {C}_{A}+\overline{{p }_{i}}$:

    ${S}_{j}({\pi }^{*})={C}_{A}+{T}_{h}$, ${C}_{j}({\pi }^{*})={S}_{j}({\pi }^{*})+{p}_{j}^{*}=(1+\upbeta ){S}_{j}({\pi }^{*})+\overline{{p }_{j}}=(1+\upbeta )({C}_{A}+{T}_{h})+\overline{{p }_{j}}$. Then ${S}_{B}({\pi }^{*})=\mathrm{max}\{{S}_{j}({\pi }^{*})+{T}_{h}, {C}_{j}({\pi }^{*})\}=\mathrm{max}\{{C}_{A}+2{T}_{h},(1+\upbeta )( {C}_{A}+{T}_{h}) +\overline{{p }_{j}}\}$. If ${T}_{h}>\frac{\upbeta {C}_{A}+\overline{{p }_{j}}}{1-\upbeta }$, ${S}_{B}({\pi }^{*})={C}_{A}+2{T}_{h}$. Otherwise, ${T}_{h}<\frac{\upbeta {C}_{A}+\overline{{p }_{j}}}{1-\upbeta }$,${S}_{B}({\pi }^{*})=(1+\upbeta )( {C}_{A}+T) +\overline{{p }_{j}}$

  • (b) When ${T}_{h}<\upbeta {C}_{A}+\overline{{p }_{i}}$,

    ${S}_{j}({\pi }^{*})=(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}$, ${C}_{j}({\pi }^{*})={S}_{j}({\pi }^{*})+{p}_{j}^{*}=(1+\upbeta ){S}_{j}({\pi }^{*})+\overline{{p }_{j}}=(1+\upbeta )\left[(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}\right] +\overline{{p }_{j}}$. Then ${S}_{B}({\pi }^{*})=\mathrm{max}\{{S}_{j}({\pi }^{*})+{T}_{h}, {C}_{j}({\pi }^{*})\}=\mathrm{max}\{(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}+{T}_{h}, (1+\upbeta )\left[(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}\right] +\overline{{p }_{j}}\}$. If ${T}_{h}>\left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{i}}+\overline{{p }_{j}}$, ${S}_{B}({\pi }^{*})=(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}+{T}_{h}$. Otherwise, ${T}_{h}<\left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{i}}+\overline{{p }_{j}}$,${S}_{B}({\pi }^{*})=(1+\upbeta )\left[(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}\right] +\overline{{p }_{j}}$.

Similarly, we can obtain that for ${\pi }^{^{\prime}}$:

• (1) In situation (1),${T}_{h}>{\mathrm{p}}_{\mathrm{A}}$

  • (a) When ${T}_{h}>\mathrm{max}\{\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-\upbeta },\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-2\upbeta }\}$, ${S}_{B}({\pi }^{^{\prime}})={S}_{A}+3{T}_{h}$.

  • (b) When $\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-\upbeta }<{T}_{h}<\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-2\upbeta }$, ${S}_{B}({\pi }^{^{\prime}})=(1+\upbeta )( {S}_{A}+2{T}_{h}) +\overline{{p }_{i}}$.

  • (c) When $\frac{\left({\upbeta }^{2}+\upbeta \right){S}_{A}+(1+\upbeta )\overline{{p }_{j}}+\overline{{p }_{i}}}{1-\upbeta -{\upbeta }^{2}}<{T}_{h}<\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-\upbeta }$, ${S}_{B}({\pi }^{^{\prime}})=(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{j}}+{T}_{h}$.

  • (d) When ${T}_{h}<\frac{\left({\upbeta }^{2}+\upbeta \right){S}_{A}+(1+\upbeta )\overline{{p }_{j}}+\overline{{p }_{i}}}{1-\upbeta -{\upbeta }^{2}}$, ${S}_{B}({\pi }^{^{\prime}})=(1+\upbeta )\left[(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{j}}\right] +\overline{{p }_{i}}$.

• (2) In situation ${T}_{h}<{\mathrm{p}}_{\mathrm{A}}$, there are four cases:

  • (a) When ${T}_{h}>\mathrm{max}\{\upbeta {C}_{A}+\overline{{p }_{j}},\frac{\upbeta {C}_{A}+\overline{{p }_{i}}}{1-\upbeta }\}$, ${S}_{B}({\pi }^{^{\prime}})={C}_{A}+2{T}_{h}$.

  • (b) When $\upbeta {C}_{A}+\overline{{p }_{j}}<{T}_{h}<\frac{\upbeta {C}_{A}+\overline{{p }_{i}}}{1-\upbeta }$, ${S}_{B}({\pi }^{^{\prime}})=(1+\upbeta )( {C}_{A}+{T}_{h}) +\overline{{p }_{i}}$.

  • (c) When $\left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{j}}+\overline{{p }_{i}}<{T}_{h}<\upbeta {C}_{A}+\overline{{p }_{j}}$, ${S}_{B}({\pi }^{^{\prime}})=(1+\upbeta ) {C}_{A}+\overline{{p }_{j}}+{T}_{h}$.

  • (d) When ${T}_{h}<$ min{$\upbeta {C}_{A}+\overline{{p }_{j}}, \left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{j}}+\overline{{p }_{i}}$}, ${S}_{B}({\pi }^{^{\prime}})=(1+\upbeta )\left[(1+\upbeta ) {C}_{A}+\overline{{p }_{j}}\right] +\overline{{p }_{i}}$

By the analysis above, we conclude 14 cases in total:

• (1) When ${T}_{h}>\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-2\upbeta }$, ${S}_{B}({\pi }^{*})= {S}_{B}({\pi }^{\mathrm{^{\prime}}})={S}_{A}+3{T}_{h}$

• (2) When $\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-2\upbeta }<{T}_{h}<\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-2\upbeta }$,${S}_{B}({\pi }^{*})={S}_{A}+3T$, ${S}_{B}({\pi }^{\mathrm{^{\prime}}})=\left(1+\upbeta \right)\left( {S}_{A}+2{T}_{h}\right)+\overline{{p }_{i}}$

• (3) When $\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-\upbeta }<{T}_{h}<\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-2\upbeta }$, ${S}_{B}({\pi }^{*})=(1+\upbeta )( {S}_{A}+2{T}_{h}) +\overline{{p }_{j}}$, ${S}_{B}({\pi }^{\mathrm{^{\prime}}})=(1+\upbeta )( {S}_{A}+2{T}_{h}) +\overline{{p }_{i}}$

• (4) When $\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-\upbeta }<{T}_{h}<\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-\upbeta }$, ${S}_{B}({\pi }^{*})=(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}+{T}_{h}$, ${S}_{B}({\pi }^{\mathrm{^{\prime}}})=(1+\upbeta )( {S}_{A}+2{T}_{h}) +\overline{{p }_{i}}$

• (5) When $\frac{\left({\upbeta }^{2}+\upbeta \right){S}_{A}+(1+\upbeta )\overline{{p }_{i}}+\overline{{p }_{j}}}{1-\upbeta -{\upbeta }^{2}}<{T}_{h}<\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-\upbeta }$, ${S}_{B}({\pi }^{*})=\left(1+\upbeta \right)\left( {S}_{A}+{T}_{h}\right)+\overline{{p }_{i}}+{T}_{h}, {S}_{B}({\pi }^{\mathrm{^{\prime}}})=(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{j}}+T$

• (6) When $\frac{\left({\upbeta }^{2}+\upbeta \right){S}_{A}+(1+\upbeta )\overline{{p }_{j}}+\overline{{p }_{i}}}{1-\upbeta -{\upbeta }^{2}}<{T}_{h}<\frac{\left({\upbeta }^{2}+\upbeta \right){S}_{A}+(1+\upbeta )\overline{{p }_{i}}+\overline{{p }_{j}}}{1-\upbeta -{\upbeta }^{2}}$, ${S}_{B}({\pi }^{*})=(1+\upbeta )\left[(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}\right] +\overline{{p }_{j}}$, ${S}_{B}({\pi }^{\mathrm{^{\prime}}})=(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{j}}+{T}_{h}$

• (7) When ${\mathrm{p}}_{\mathrm{A}}<{T}_{h}<\frac{\left({\upbeta }^{2}+\upbeta \right){S}_{A}+(1+\upbeta )\overline{{p }_{j}}+\overline{{p }_{i}}}{1-\upbeta -{\upbeta }^{2}}$,${S}_{B}({\pi }^{*})=(1+\upbeta )\left[(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}\right] +\overline{{p }_{j}}$, ${S}_{B}({\pi }^{\mathrm{^{\prime}}})=(1+\upbeta )\left[(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{j}}\right] +\overline{{p }_{i}}$

• (8) When $\frac{\upbeta {C}_{A}+\overline{{p }_{i}}}{1-\upbeta }<{T}_{h}<{\mathrm{p}}_{\mathrm{A}}$, ${S}_{B}^{*}={S}_{B}^{\mathrm{^{\prime}}}={C}_{A}+2{T}_{h}$

• (9) When $\frac{\upbeta {C}_{A}+\overline{{p }_{j}}}{1-\upbeta }<{T}_{h}<\frac{\upbeta {C}_{A}+\overline{{p }_{i}}}{1-\upbeta }$, ${S}_{B}^{*}={C}_{A}+2{T}_{h}$, ${S}_{B}^{\mathrm{^{\prime}}}=(1+\upbeta )( {C}_{A}+{T}_{h}) +\overline{{p }_{i}}$

• (10) When $\upbeta {C}_{A}+\overline{{p }_{i}}<{T}_{h}<$ $\frac{\upbeta {C}_{A}+\overline{{p }_{j}}}{1-\upbeta }$, ${S}_{B}^{*}=(1+\upbeta )( {C}_{A}+{T}_{h}) +\overline{{p }_{j}}$, ${S}_{B}^{\mathrm{^{\prime}}}=(1+\upbeta )( {C}_{A}+{T}_{h}) +\overline{{p }_{i}}$

• (11) When $\upbeta {C}_{A}+\overline{{p }_{j}}<{T}_{h}<\upbeta {C}_{A}+\overline{{p }_{i}}$, ${S}_{B}^{*}=(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}+{T}_{h}$,${S}_{B}^{\mathrm{^{\prime}}}=(1+\upbeta )( {C}_{A}+{T}_{h}) +\overline{{p }_{i}}$

• (12) When $\left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{j}}+\overline{{p }_{i}}<{T}_{h}<\upbeta {C}_{A}+\overline{{p }_{j}}$, ${S}_{B}^{*}=(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}+{T}_{h}$,${S}_{B}^{\mathrm{^{\prime}}}=(1+\upbeta ) {C}_{A}+\overline{{p }_{j}}+{T}_{h}$

• (13) When $\left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{i}}+\overline{{p }_{j}}<{T}_{h}<\left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{j}}+\overline{{p }_{i}}$,${S}_{B}^{*}=(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}+{T}_{h}$,${S}_{B}^{\mathrm{^{\prime}}}=(1+\upbeta )\left[(1+\upbeta ) {C}_{A}+\overline{{p }_{j}}\right] +\overline{{p }_{i}}$

• (14) When ${T}_{h}<\left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{i}}+\overline{{p }_{j}}$, ${S}_{B}^{*}=(1+\upbeta )\left[(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}\right] +\overline{{p }_{j}}$,${S}_{B}^{\mathrm{^{\prime}}}=(1+\upbeta )\left[(1+\upbeta ) {C}_{A}+\overline{{p }_{j}}\right] +\overline{{p }_{i}}$

These 14 cases can be summarized as shown in Table 3 in the main body of the paper.