1 Introduction

Global awareness on environmental issues encourages researchers and practitioners to develop a green supply chain management (Sarkis, 2012). While focusing on improving the cooperation among parties, a further point promoted by green supply chain management is to improve operations by taking the emission reduction into account (Memari et al., 2016). Some important activities in the supply chain, such as transportation, production, and warehouse activities, generate carbon emissions (Ahmed & Sarkar, 2018). US-EPA (2018) reported that the largest carbon emissions generations are coming from industrial processes. In their efforts to restrict carbon emissions, some countries are issuing regulations (Tiwari et al., 2018). China and Canada have set target to reducing emissions 64% and 30%, respectively, below 2005 emission level. To achieve the target, some countries e.g. India, Sweden, Canada and Denmark have implemented carbon tax policy to reduce the emissions.

This policy will force the manufacturers to undertake initiatives to reduce emissions. One way of doing this is by opting for green production technology. Simons and Dell are the examples of manufacturers that adopt green production technology to reduce the emissions (Siberi et al., 2018). The manufacturer can operate green production system which is cleaner than the regular one. Although it generates lower emission, it is normally more expensive than the regular one (Gong & Zhou, 2013; Hong et al., 2016; Phouratsamay & Cheng, 2019). In addition, switching the production from regular system to green system in one swoop is uneconomical and leads to increasing the total operating cost (Entezaminia et al., 2020). Therefore, it is reasonable for the manufacturer to operate a hybrid production system that consists of both the regular and the green technology concurrently. The question then arise as to how much the production quantity should be allocated to each of these production technologies to achieve both the economic and environmental objectives.

Pulp and paper mills are examples of industries that face a problem with production cost and emission reductions. They commonly operate different production technologies in parallel. Each production technology requires different cost and generates different emission levels (Martin et al., 2000). To run the production process, the company often uses coal or natural gas as fuels to generate electricity. Coal is cheaper than natural gas but it generates more emissions. Other industries, such as cement also utilize different kiln technologies and may use coal or natural gas as alternatives to generate electricity (Drake et al., 2010; Hendriks et al., 2004).

In today’s competitive environment, besides focusing on the reduction of carbon emissions, supply chain needs to be efficiently managed. Customers are more demanding in terms of product quality which consequently force the companies to produce high quality products. In real life, however, the production system is imperfect due to process deterioration. In inventory management literature, there are models addressing the defective items (Daryanto et al., 2019; Manna et al., 2018; Mohanty et al., 2018; Rad et al., 2018; Sarkar et al, 2015). Previously, the models were concerned with considering defective rate as a constant parameter. Later, some researchers proposed a quality investment as a mechanism to control the defective rate (Dey & Giri, 2014; Kim et al., 2018; Mukherjee et al., 2019). However, treating the defective rate as a decision variable makes the model more complex and harder to solve. This is due to the need for investment in quality improvement so that the investment cost needs to be included in the model. In addition, the procedure to find the solution becomes more complex because it now includes new decision variables. However, the optimal value of the defect rate can be determined so that the policy makers can keep its level below a certain threshold value.

This paper deals with the joint economic lot size problem (JELP) that takes into account the use of hybrid production technologies. It concerns with jointly making lot sizing decisions for parties involved in the supply chain. The objective of JELP is to coordinate and collaborate the parties by synchronizing production and inventory decisions in order to minimize the joint total cost. Although many models have been developed to accommodate various situations, our review to JELP literature showed that no model has investigated the influence of adopting green technology on inventory decisions. In addition, the imperfect production system and quality investment have not been investigated in situation in which a manufacturer employs a hybrid production system containing a green and a regular production systems. Thus, by developing the proposed model, we intend to answer the following questions:

  1. (1)

    What would be the optimal production policy for manufacturer if a hybrid system consisting of a green production and a regular production is utilized to produce products?

  2. (2)

    What kind of decisions should be taken to minimize the defects generated from hybrid production system?

  3. (3)

    What kind of decisions should be taken to minimize the emissions and to deal with the trade-off between production cost and emissions?

To answer the questions above, we intend to develop a cooperative inventory model for vendor–buyer system by addressing carbon emission reduction, imperfect production and stochastic demand. The vendor’s manufacturing system consists of two types of production systems, one is the green production system that used green technology and the other one is a regular production system. The green production is more expensive to operate but results in lower level of emissions. Both production systems are imperfect, thus results in some percentage of defective items. The rework process is operated to improve the quality of defective items. In addition, the quality investment is proposed to improve the quality of production processes. The proposed model is developed under an assumption that both production systems work in parallel which means that they start and stop production at the same time.

The remainder of this paper is organized as follows. Section 2 presents the literature review. Section 3 describes the notations and assumptions used to develop the model. Section 4 presents a brief description about model development. Sections 5 and 6 provide solution methodology and numerical example, respectively. Sections 7 and 8 present discussion and conclusions, respectively.

2 Literature survey

2.1 Vendor–buyer inventory problem with imperfect production

A common unrealistic assumption used by authors when developing inventory models is that all items produced from the manufacturing system are of perfect quality. In reality, the production process is often imperfect and generates defective items. Therefore, it is worthwhile to study the impact of imperfect manufacturing system in inventory management. In order to surmount the unrealistic assumption of perfect quality, many researchers have attempted to develop various inventory models by taking into consideration the imperfections of manufacturing system. Porteus (1986) and Rosenblatt and Lee (1986) were among pioneer researchers who initiated the study of quality improvement in an Economic Production Quantity (EPQ) model. Afterwards, Schwaller (1988) added the screening process into EPQ model and assumed that there is a fixed proportion of defective rate in each lot produced by the system. A study regarding the effect of imperfect manufacturing has been extensively studied by other researchers with several different settings, including Lee and Park (1991), Ouyang and Chang (2000), Freimer et al. (2006), Wee et al. (2007) and Chiu et al. (2007).

The aforementioned models tackled imperfect items focused on determining optimal lot sizing policy from single side’s point of view. They ignored the interaction among parties in the supply chain. Thus, some researchers have discussed the effect of imperfect items in supply chain by forming an effective alliance among parties involved in the system. Huang (2002) was the first to introduce a single-vendor single-buyer inventory model under imperfect items and equal shipment policy. The number of defective items is formulated with a given probability and the defective items are treated as a single batch at the end of buyer’s screening period. Ouyang et al. (2006) developed a cooperative vendor–buyer model under imperfect production based on the basic model by Goyal and Nabebe (2000). The defective rate is presented with two models, crisp and fuzzy. Hsu and Hsu (2012) considered imperfect inspection and assumed that the screening process is not 100% error free. The model of Hsu and Hsu (2012) was further developed by Jauhari et al. (2016) by proposing a three-stage supply chain system consisting of a supplier, a manufacturer and a buyer with imperfect items and inspection errors.

The issue of imperfect production has also been widely discussed in a stochastic inventory problem. Ouyang et al. (2002) adopted a continuous review policy to formulate buyer’s inventory level in the joint economic lot sizing and proposed that the lead time can be reduced with an added cost. Lin (2010) investigated defective items in a supply chain inventory model under periodic review policy and assumed that the manufacturing system can go from in-control state to out of control state. During out of control state, the manufacturing system will produce some defective items. Lin and Lin (2016) proposed a recovery system used to recover the defective items generated from vendor’s manufacturing system. Priyan and Uthayakumar (2017) proposed a vendor–buyer system with defective items, inspection errors and setup cost reduction. Pal and Mahapatra (2017) considered a supplier-manufacturer-retailer system with rework and imperfect production. Marchi et al., (2019) studied the influence of energy usage and defective items in a cooperative inventory model with deterministic demand. Islam et al. (2020) investigated the impact of imperfect production and supplier reliability on inventory decisions in a three-echelon supply chain system with poisson demand.

An investment has also been proposed by several researchers to improve the quality of manufacturing process. This type of investment can be in the form of buying equipment, training the employee, or improving the maintenance. Dey and Giri (2014) used a logarithmic function to formulate the quality investment in order to reduce the defective rate. Kumar and Uthayakumar (2017) proposed two forms of quality investment. The first form is formulated using logarithmic function and the second using a power function. Mukherjee et al. (2019) considered a learning process and quality investment to reduce the defective probability in an integrated vendor–buyer problem. Kim et al. (2018) used an investment to reduce the probability of out-of-control and setup cost in a production process. Finally, Kim and Sarkar (2017) analyzed the impact of budget constraint on quality investment conducting in a complex multi-stage production system.

2.2 Vendor–buyer inventory problem with adjustable production rate

Production capacity is another concern in inventory management. In most published stochastic vendor–buyer models, the production rate is treated as a fixed constant. However, in reality, the production capacity can be flexibly determined by the decision makers. It is observed that the production output maybe affected by the adjustments of the performance of production machine or by the insertion of idle time between two successive units of production (Jauhari et al., 2017). Some benefits can be realized by the system by adjusting the production rate, such as reducing cost and increasing system’s flexibility.

The effect of adjustable production rate on inventory decisions was first studied by Khouja and Mehrez (1994). The production cost is formulated as a function of production rate and the quality of manufacturing process depends on the level of production rate. Khouja (1999) studied an EPQ model and assumed that the probability of the manufacturing process can go out of control is influenced by the production rate. Eiamkanchanalai and Banerjee (1999) proposed a model to simultaneously determine the optimal run length and the production rate of a single-stage inventory problem. The impact of increased unit cost generated from output deviation is studied with a quadratic function of production rate. Sarkar et al. (2010) suggested a new formulation of production cost, in which the function is depended on production rate and reliability parameter. Glock (2010) studied the effect of variable production rate on inventory build-up and total cost of a single production system. Furthermore, Glock (2011) extended the Glock (2010)’s model by proposing a multi-stage production system. He analyzed a situation where the production rate of each stage can be varied between a range of value.

A few studies have been conducted to explore the influence of adjustable production rate in a supply chain inventory model. Jauhari and Pujawan (2014) explored the impact of varying production rate on raw material’s procurement decisions. Jauhari and Saga (2017) developed a solution for vendor–buyer inventory model under adjustable production rate, fuzzy demand and setup cost reduction. Moreover, the effect of varying production rate on lead time and stochastic demand was discussed by AlDurgam et al. (2017).

2.3 Vendor–buyer inventory problem with environmental consideration

With an increasing awareness of sustainability, researchers have attempted to focus their studies on developing the inventory models by considering environmental impacts. Bonney and Jaber (2011) investigated the effect of vehicle emissions in a single -stage inventory problems. Later, Hua et al. (2011) considered carbon emissions generated from delivery and storage activities in an EOQ model. Carbon cap and trade is used as a mechanism to lessen the carbon emitted from the system. A study of the effect of carbon reduction in an international supply chain was also conducted by Wahab et al. (2011). They determined optimal production-delivery policy by taking the exchange rate between two countries, imperfect production and fixed and variable emission costs into account. Jaber et al. (2013) used three policies, namely carbon tax, carbon penalty and the combination of both to control the emissions in a deterministic vendor–buyer model.

In contrast to the above studies which considered the carbon reduction policy in a deterministic environment, some researchers explored the impact of carbon emission in an inventory problem under stochastic nature. Wangsa (2017) and Saga et al. (2019) proposed a penalty and incentive mechanism to control the emissions emitted from production and transportation activities. Turken et al. (2021) investigated various environmental regulations in a single vendor-multiple buyers supply chain system operated under vendor managed inventory (VMI). Tiwari et al. (2018) and Daryanto et al. (2019) developed a supply chain inventory models for deteriorating items by addressing carbon emissions resulting from transporting and warehousing. Jauhari et al. (2021) proposed a carbon tax regulation to control the emissions from a closed-loop supply chain system involved of a manufacturer and a retailer. Li and Hai (2019) proposed a warehouse-retailer inventory model and calculated carbon emissions from holding and replenishing inventory activities. Furthermore, Daryanto and Wee (2021) developed a three-echelon inventory model for deteriorating items with imperfect quality and used a carbon tax policy to reduce emissions from transportation and storing items in the warehouse.

2.4 Contributions of the proposed study

Although there are streams of research on a cooperative vendor–buyer model, little has been carried out to examine the effect of imperfect production, carbon emission reduction and varied production rate in a supply chain inventory system under two types of production technologies. In contrast to previous research which used a regular production, our model considers two production systems, namely green production and regular production. A green production employs a green technology which emits lower emissions than the technology used in a regular production. A parallel production system is proposed to synchronize the production runs of green and regular productions. We determine the optimal production-shipment policy by taking the trade-off between production cost and carbon emission level into account. In addition, both production processes are imperfect and generate a different rate of defective items. A reworking process is conducted to fix the defective items resulted from both productions. In addition, a quality investment formulated with logarithmic function is proposed to improve the quality processes of both systems. Quality investment could be in the form of adding facilities, equipment or trainings to enable the rework process. Table 1 compares the proposed model and the previous published models.

Table 1 A comparison between proposed model and previous published works
Full size table

3 Notations and assumptions

3.1 Notations

The main parameters and decision variables used to formulate the proposed mathematical model are given in Table 2.

Table 2 Notations used for model development
Full size table

3.2 Assumptions

The following assumptions are used to develop the proposed model:

  1. 1.

    An investigated system consists of a vendor who produces products and a buyer who purchases and then sells the products to the end customers.

  2. 2.

    The buyer’s demand is stochastic and follows a normal distribution with mean D and standard deviation \(\sigma \). A continuous review policy is employed to control the buyer’s inventories.

  3. 3.

    The lead time is variable, which depends upon the productive and non-productive times and is given by \(L = \sqrt {{\raise0.7ex\hbox{$Q$} \!\mathord{\left/ {\vphantom {Q P}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$P$}} + T_{s} }\)

  4. 4.

    The buyer orders nQ units whenever his inventory level reaches reorder point. The vendor will produce a batch of nQ units of product and delivers them to buyer at equal shipment size Q. The batch of nQ units consists of n \(\left( {1 - \alpha } \right)\) Q units and \(n\alpha Q\) units produced from green and regular production, respectively.

  5. 5.

    The production cost of green production is more expensive compared to the regular production. However, the green production emits lower emissions than the regular production.

  6. 6.

    The green and regular production will start and stop production at the same time. Therefore, the production batch allocated to green production depends on the ratio of green’s production rate to the sum of the whole system production rate and the production batch allocated to regular production depends on the ratio of regular’s production rate to the sum of system production rate that are \(nQ_{g} = nQ\frac{{P_{g} }}{P}\), \(nQ_{r} = nQ\frac{{P_{r} }}{P}\). The production rates of green and regular productions are defined by \(P_{g} = \left( {1 - \alpha } \right)P\) and \(P_{r} = \alpha P\), respectively.

  7. 7.

    The production rate is adjusted between \(P_{min} \le P \le P_{max}\).

  8. 8.

    The production cost per unit item and the emissions depend on production rate.

  9. 9.

    Once the production system goes out of control, it begins to produce defective items with the probability of γ until the remainder of batch is completed.

  10. 10.

    The vendor has an opportunity to conduct investment to improve the process quality, in terms of worker training, buying new equipment and improving machine maintenance. The quality investment follows a logarithmic function, which is \(I\left( \gamma \right) = \frac{\eta }{\delta }ln\left( {\frac{{\gamma_{0} }}{\gamma }} \right)\)

4 Model development

Suppose that the buyer uses a continuous review policy to manage the inventory level. It means that once the inventory level reaches the reorder point, an order should be placed with a quantity of nQ. Here, a formulation developed by Hadley and Within’s (1963), Q/2 + safety stock, is adopted to express the buyer’s inventory level. Thus, the buyer’s holding cost is given by the following expression

$$ Hold_{b} = h_{b} \left( {\frac{Q}{2} + k\sigma \sqrt {{\raise0.7ex\hbox{$Q$} \!\mathord{\left/ {\vphantom {Q P}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$P$}} + T_{s} } } \right) $$
(1)

By assuming that the shortages are fully backordered, the shortage cost per year is determined by Eq. (2)

$$ ESC = \frac{\pi D\sigma }{Q}\sqrt {{\raise0.7ex\hbox{$Q$} \!\mathord{\left/ {\vphantom {Q P}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$P$}} + T_{s} } \psi \left( k \right) $$
(2)

where

$$ \psi \left( k \right) = f_{s} \left( k \right) - k\left[ {1 - F_{s} \left( k \right)} \right] $$
(3)

\(f_{s} \left( k \right)\) and \(F_{s} \left( k \right)\) represent probability density function and the cumulative density function of standard normal distribution, respectively. Furthermore, the amount of emissions generated from transportation and storage is derived in Appendix A. The ordering and transportation costs incurred by the buyer are expressed in Eq. (4).

$$ OT = \frac{D}{nQ}\left( {A + nF} \right) $$
(4)

We use a term hybrid production to represent the system consisting of two different production systems which are a green and a regular production. They both work together to produce items to satisfy the buyer’s demand. The batch produced by the green production and regular production are \(\left( {1 - \alpha } \right)Q\) and \(\alpha Q\), respectively. The first delivery will be made in period \(\left( {1 - \alpha } \right)Q/P_{g}\) or \(\alpha Q/P_{r}\) and the next deliveries will be carried out in average of \(Q/D\). The average inventory level is calculated by subtracting the accumulative delivery from accumulated vendor’s production. Thus, the holding costs for green and regular production are given by Eqs. (5) and (6), respectively.

$$ INC_{g} = h_{g} \frac{{\left( {1 - \alpha } \right)Q}}{2}\left( {n\left[ {1 - \frac{D}{P}} \right] - 1 + \frac{2D}{P}} \right) $$
(5)
$$ INC_{r} = h_{r} \frac{\alpha Q}{2}\left( {n\left[ {1 - \frac{D}{P}} \right] - 1 + \frac{2D}{P}} \right) $$
(6)

The setup cost for green production and regular production are given by Eqs. (7) and (8), respectively.

$$ SC_{g} = \frac{{DK_{g} }}{nQ} $$
(7)
$$ SC_{r} = \frac{{DK_{r} }}{nQ} $$
(8)

It is assumed that the production costs per unit time depends upon the production rate (Khouja & Mehrez, 1994). The production costs for green and regular production are given by the following equations

$$ PC_{g} = \left( {\frac{{X_{g1} }}{{P_{g} }} + X_{g2} P_{g} } \right)\left( {1 - \alpha } \right)D $$
(9)
$$ PC_{r} = \left( {\frac{{X_{r1} }}{{P_{r} }} + X_{r2} P_{r} } \right)\alpha D $$
(10)

The amount of emissions generated from storage, production and rework is derived in Appendix A while the number of defective items resulted from production systems and rework costs are presented in Appendix B. Therefore, the joint total cost function for a proposed supply chain can be derived by summing up the costs incurred by the buyer and the costs incurred by the vendor, which is

$$ \begin{gathered} JTC = \frac{D}{nQ}\left( {A + nF} \right) + \left( {h_{b} + E_{b} W_{b} } \right)\left( {\frac{Q}{2} + k\sigma Y_{1} } \right) + \frac{\pi D\sigma }{Q}Y_{1} \psi \left( k \right) + E_{b} \left( {\frac{D}{Q}\vartheta_{T1} \varepsilon J_{b} + \vartheta_{T2} xD} \right) \hfill \\ + \frac{{DK_{g} }}{nQ} + \left( {h_{g} + E_{g} W_{g} } \right)\frac{{\left( {1 - \alpha } \right)Q}}{2}Y_{2} + E_{g} \left( {1 - \alpha } \right)DY_{3} + \left( {\frac{{X_{g1} }}{P} + X_{g2} P} \right)\left( {1 - \alpha } \right)D + s\left( {1 - \alpha } \right)D \hfill \\ + RW_{g} \frac{D}{nQ}E\left( {N_{g} } \right) + E_{g} \frac{D}{nQ}E\left( {N_{g} } \right)Y_{5} + \frac{{\eta_{g} }}{{\delta_{g} }}\ln \left( {\frac{{\gamma_{g0} }}{{\gamma_{g} }}} \right) + \frac{{DK_{r} }}{nQ} + \left( {h_{r} + E_{r} W_{r} } \right)\frac{\alpha Q}{2}Y_{2} + E_{r} \alpha DY_{4} \hfill \\ + \left( {\frac{{X_{r1} }}{{\left( {\frac{\alpha }{1 - \alpha }} \right)P}} + X_{r2} \left( {\frac{\alpha }{1 - \alpha }} \right)P} \right)\alpha D + s\alpha D + RW_{r} \frac{D}{nQ}E\left( {N_{r} } \right) + E_{r} \frac{D}{nQ}E\left( {N_{r} } \right)Y_{6} + \frac{{\eta_{r} }}{{\delta_{r} }}\ln \left( {\frac{{\gamma_{r0} }}{{\gamma_{r} }}} \right) \hfill \\ \end{gathered} $$
(11)

where

$$ Y_{1} = \sqrt {{\raise0.7ex\hbox{$Q$} \!\mathord{\left/ {\vphantom {Q P}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$P$}} + T_{s} } $$
(12)
$$ Y_{2} = \left( {n\left[ {1 - \frac{D}{P}} \right] - 1 + \frac{2D}{P}} \right) $$
(13)
$$ Y_{3} = a_{g} P_{g}^{2} - b_{g} P_{g} + c_{g} $$
(14)
$$ Y_{4} = a_{r} P_{r}^{2} - b_{r} P_{r} + c_{r} $$
(15)
$$ Y_{5} = a_{g} \left( {\varepsilon_{g} P_{g} } \right)^{2} - b_{g} \varepsilon_{g} P_{g} + c_{g} $$
(16)
$$ Y_{6} = a_{r} \left( {\varepsilon_{r} P_{r} } \right)^{2} - b_{r} \varepsilon_{r} P_{r} + c_{r} $$
(17)

5 Solution procedure

In this section, we present the mathematical formulations to determine the values of decision variables and the procedure to find the solutions. As described in the previous section that the objective of the proposed model is to obtain the optimal values of k, Q, P, \({\gamma }_{g}\) and \({\gamma }_{r}\) that minimizes the joint total cost (JTC). The derivation of JTC with respect to k, Q, P, \({\gamma }_{g}\) and \({\gamma }_{r}\) is provided in Appendix C. Equations (18)–(23) present the formulations for determining the values of k, Q, P, \({\gamma }_{g}\) and \({\gamma }_{r}\).

$$ F_{s} \left( k \right) = 1 - \frac{{\left( {h_{b} + E_{b} W_{b} } \right)Q}}{\pi D} $$
(18)
$$Q = \sqrt {\frac{{2D\left\{ {A/N + F + \pi \sigma \psi \left( k \right){Y_1} + {E_b}{\vartheta _{T1}}\varepsilon {J_b} + \frac{{{K_g}}}{n} + \frac{{{K_r}}}{n}} \right\}}}{{\begin{aligned}&\left( {{h_b} + {E_b}{W_b}} \right) + \frac{{k\sigma \left( {{h_b} + {E_b}{W_b}} \right)}}{{P{Y_1}}} + \frac{{\pi D\sigma \psi \left( k \right)}}{{PQ{Y_1}}} \\ &+ \left( {{h_g} + {E_g}{W_g}} \right)\left( {1 - \alpha } \right){Y_2} - \frac{{D{K_r}}}{{n{Q^2}}}\\ &+ \left( {{h_r} + {E_r}{W_r}} \right)\alpha {Y_2} + R{W_g}{\gamma _g}Dn\frac{{{G_1}}}{P}\\ & + {E_g}{\gamma _g}Dn\frac{{{G_1}{Y_5}}}{P} + R{W_r}{\gamma _r}Dn\frac{{{R_1}}}{P} + {E_r}{\gamma _r}Dn\frac{{{R_1}{Y_6}}}{P}\end{aligned}}}} $$
(19)
$$ {\begin{aligned}P & = \sqrt{\frac{\begin{array}{c}\frac{\left({h}_{b}+{E}_{b}{W}_{b}\right)k\sigma Q}{2D{Y}_{1}}+\frac{\pi \sigma \psi \left(k\right)}{2{Y}_{1}}+{X}_{g1}+{X}_{r1}-\left(n-2\right)\left({h}_{g}+{E}_{g}{W}_{g}\right)\frac{\left(1-\alpha \right)Q}{2}\\ -\left(n-2\right)\left({h}_{r}+{E}_{r}{W}_{r}\right)\frac{\alpha Q}{2}+{RW}_{g}{\gamma }_{g}\frac{nQ}{2}{G}_{1}+{E}_{g}\frac{nQ}{2}{\gamma }_{g}{G}_{1}{Y}_{5}\\ +{RW}_{r}{\gamma }_{r}\frac{nQ}{2}{R}_{1}+{E}_{r}{\gamma }_{r}\frac{nQ}{2}{R}_{1}{Y}_{6}\end{array}}{\begin{array}{c}{E}_{g}\left(1-\alpha \right)\left(2{a}_{g}{\left(1-\alpha \right)}^{2}P-\left(1-\alpha \right){b}_{g}\right)+{E}_{r}\alpha \left(2{a}_{r}{\alpha }^{2}P-{\alpha b}_{r}\right)\\ +{X}_{g2}{\left(1-\alpha \right)}^{2}+{X}_{r2}{\alpha }^{2}+{RW}_{g}nQ{\gamma }_{g}{\omega }_{g}{\left(1-\alpha \right)}^{3}\\ +\frac{{E}_{g}{\gamma }_{g}nQ{G}_{1}{G}_{2}}{2P}+{E}_{g}nQ{\gamma }_{g}{\omega }_{g}{\left(1-\alpha \right)}^{3}{Y}_{5}\\ +{RW}_{r}nQ{\gamma }_{r}{\omega }_{r}{\alpha }^{3}+\frac{{E}_{r}{\gamma }_{r}nQ{R}_{1}{R}_{2}}{2P}+{E}_{r}nQ{\gamma }_{r}{\omega }_{r}{\alpha }^{3}{Y}_{6}\\ \end{array}}} \\ & ={\sqrt{\theta}}\end{aligned}} $$
(20)
$$ \gamma_{g} = \frac{{2\eta_{g} P}}{{\delta_{g} DnQG_{1} \left\{ {RW_{g} + E_{g} Y_{5} } \right\}}} $$
(21)
$$ \gamma_{r} = \frac{{2\eta_{r} P}}{{\delta_{r} DnQR_{1} nQ\left\{ {RW_{r} + E_{r} Y_{6} } \right\}}} $$
(22)

By looking at Eq. (20), it is easy to show that if the value of \(\theta < 0\), the equation may result in an infeasible solution. So, we set \(P = P_{min}\) if \(\theta < 0\), hence Eq. (20) can be rewritten as

$$ P = max\left[ {P_{min}^{{}} ,\sqrt \theta } \right] $$
(23)

Here, we proposed a procedure adapted from Ben-Daya and Hariga (2004) and Dey and Giri (2014) to derive the optimal solution of the problem under hybrid production policy, that is.

Step 1:

Set \(\alpha = 0.01\), n = 1 and \(JTC\left( {P_{n - 1} ,Q_{n - 1} ,k_{n - 1} ,\gamma_{g,n - 1} ,\gamma_{r,n - 1} , \alpha } \right) = \infty\)

Step 2:

Set the initial values of Q, k, and P equal to zero and \(\gamma = \gamma_{0}\). Compute \(P\) by using Eq. (20)

Step 3:

Compute \(Q\) by inserting the previous value of \(P\) into Eq. (19)

Step 4:

Compute \(k\) by substituting \(Q\) into Eq. (18)

Step 5:

Compute \(\gamma_{g}\) and \(\gamma_{r}\) using Eqs. (21) and (22), respectively. If \(\gamma_{g} > \gamma_{g0}\) then set \(\gamma_{g} = \gamma_{g0}\) and if \(\gamma_{r} > \gamma_{r0}\) then set \(\gamma_{r} = \gamma_{r0}\)

Step 6:

Update the value of \(P\) by substituting the previous values of \(Q\), \(k \gamma_{g}\) and \(\gamma_{r} { } \) into Eq. (21)

Step 7:

Repeat steps 3–6 until the values of \(P\), \(Q\) \(k, \gamma_{g}\) and \(\gamma_{r}\) no longer change

Step 8:

Set \(P_{n} = P\), \(Q_{n} = Q\), \(k_{n} = k\), \(\gamma_{g,n} = \gamma_{g}\) and \(\gamma_{r,n} = \gamma_{r}\). Compute \(JTC\left( {P_{n} ,Q_{n} ,k_{n} ,\gamma_{g,n} ,\gamma_{r,n} , \alpha } \right){ }\) by using Eq. (11)

Step 9:

If \(JTC\left( {P_{n} ,Q_{n} ,k_{n} ,\gamma_{g,n} ,\gamma_{r,n} , \alpha } \right){ } \le JTC\left( {P_{n - 1} ,Q_{n - 1} ,k_{n - 1} ,\gamma_{g,n - 1} ,\gamma_{r,n - 1} , \alpha } \right)\) repeat steps 2–8 with n = n + 1, otherwise go to step 10

Step 10:

Compute \(JTC\left( {P,Q,k,\gamma_{g} ,\gamma_{r} ,\alpha } \right)\) = \(JTC\left( {P_{n - 1} ,Q_{n - 1} ,k_{n - 1} ,\gamma_{g,n - 1} ,\gamma_{r,n - 1} , \alpha } \right)\)

Step 11:

Repeat steps 1–10 for the set value of \(\alpha , (0 < \alpha < 1)\) with the change of \(\alpha = \alpha + 0.01\)

Step 12:

Find the solutions by searching the combination of \(P,Q,k,n ,\alpha\) which minimizes the value of \(JTC\)

It is observed that the joint total cost function is convex in k, \(\gamma_{g}\) and \(\gamma_{r}\) and may not be convex in P and Q (see Appendix D). Therefore, we cannot claim that the above proposed procedure will generate global optimal solutions. So, it is only guaranteed to local optimal solutions. This approach, however, has been widely used by many scholars (Ben-Daya and Hariga, 2004; Glock, 2011; Dey & Giri, 2014; Kumar & Uthayakumar, 2017; Mukherjee et al., 2019) to solve the JELP under stochastic demand and variable lead time.

To illustrate the above proposed iterative procedure, let us consider an integrated vendor–buyer system with the following data set: D = 1000, σ = 5, A = 100, F = 50, hb = 4, \(\pi\) = 50, Ts = 0.05, Wb = 8, Eb = 0.0618, \(\vartheta_{T1}\) = 2.6, \(\vartheta_{T2}\) = 2.5, \(\varepsilon\) = 0.3, JB = 400, x = 0.05, Kg = 400, Kr = 400, hg = 2, hr = 2, Wg = 5, Wr = 5, Eg = $0.0618, Er = $0.0618, Xg1 = 2500, Xr1 = 2000, Xg2 = 0.008, Xr2 = 0.004, ag = 0.0000007, bg = 0.0012, cg = 1.4, ar = 0.0000012, br = 0.0008, cr = 8.4, s = 1, \(RW_{g}\) = 3, \(RW_{r}\) = 2, \(\gamma_{g0}\) = 0.35, \(\gamma_{r0}\) = 0.35, \(\beta_{g}\) = 0.15, \(\beta_{r}\) = 0.25, \(\omega_{g}\) = 0.000001, \(\omega_{r}\) = 0.000001, \(\varepsilon_{g}\) = 1.2, \(\varepsilon_{r}\) = 1.2, \(\eta_{g}\) = 0.2, \(\eta_{r}\) = 0.2, \(\delta_{g}\) = 0.002, \(\delta_{r}\) = 0.002, \(P_{min}\) = 1000 \(P_{max}\) = 2000.

By utilizing the above procedure, the optimal solutions for the proposed problem are obtained. The optimal allocation factor (α), shipment quantity and number of deliveries are 0.66, 258.63 units and 10 times, respectively. Thus, the green production produces items with a batch of 879.34 units while the green production produces 1706.96 units. It seems that the regular production receives a greater production allocation than the green one. The total cost charged to the vendor and buyer are $8262.05 and $518.27, respectively. We further analyze the impact of the changes in key parameters, including D, \(\delta_{g}\), Eb, Xr2 and \(\omega_{r}\) on the model’s behaviour. The sensitivity analysis is performed by observing the optimal values of decision variables and their impacts on total cost, emissions, number of defects and quality investment.

6 Discussions

We first investigate how the demand’s changes affect the model’s behaviour. Table 3 clearly shows that the demand influences the optimal results. The system tends to balance the increasing of demand by increasing the inventory level. This is intuitively correct, because as the vendor is required to satisfy a greater demand, a considerable increase in production batch will lead to the increase in the inventory level. The defective rate of the both productions seems to decrease with the increase in demand. Consequently, the vendor incurs a greater investment to improve the quality of production process. In addition, facing a higher demand, the defective rate decreases which in turn increasing the amount of money invested by the vendor. Figure 1 shows that the total carbon emissions generated by green and regular production sharply increase due to the increase in demand. Facing an increased demand, the system needs to produce more items which results in generating more carbon emissions.

Table 3 The impact of the changes in the demand on model’s solution
Full size table
Fig. 1
figure 1

The impact of the changes in demand on total emissions, production batch and shipment quantity

Full size image

We further study how the changes in \({\delta }_{g}\) affect the model’s behaviour. The higher value of \({\delta }_{g}\) means that the quality investment made by vendor to improve the quality process of green production is getting more efficient. We may see from Table 4 that the production allocation to green production slightly increases due to the increase in \({\delta }_{g}\). We also observe that with the increase in \({\delta }_{g}\), there are decreases in the green production’s defective rates and the joint total cost. This makes sense from a practical point of view since an increase in \({\delta }_{g}\) results in the decrease of the number of defects which in turn reduces the rework cost (see Fig. 2). The figure shows that when \({\delta }_{g}\) increases by 300%, the rework cost of green production decreases by 79.99% while its investment cost increases by 128.74%.

Table 4 The impact of the changes in \(\delta_{g} \) on model’s solution
Full size table
Fig. 2
figure 2

Impact of the changes in \(\delta_{g}\) on the number of defective items and quality investment

Full size image

Table 5 summarizes the effects of the changes in the emission tax on the proposed model. When the regulation on carbon reduction becomes more stringent, a greater carbon tax maybe applied by the regulator to restrict such emissions. Facing this situation, the manager should shift more production allocation from the regular to the green production. From Table 5 we may see that the increase in carbon tax leads to the increase in the production allocation of the green production. If the carbon tax increases by 400%, the demand satisfied by the green production increases by 24%. This is intuitively correct, since if the vendor has to pay a higher carbon tax, it would be beneficial for him to reduce the emission generations by sharing more production to the greener one. Interestingly, the vendor needs to reduce the production rate to ensure that the emissions generating from the production process is at lower level and to control the number of defects resulting from the production. It is noted here that by adjusting the production rate at appropriate level, the vendor can also lengthen or shorten the time to out of control state which in turn reduces the defects. Moreover, the defective rate reduces due to the increase in carbon tax. This again makes sense, since a decrease in defective rate will give the opportunity to the vendor to lessen the emissions generated from reworking process. We also obtain that with the increase in carbon tax, there is an increase in investment needed to improve the quality of production process (see Fig. 3).

Table 5 The impact of the changes in the emission tax on model’s solution
Full size table
Fig. 3
figure 3

Impact of the changes in emission tax on total emissions, rework cost and investment

Full size image

The impact of the change in Xr2 on model’s behavior is also presented in Table 6. It is quite interesting that Xr2 significantly influences the decision variables and the total cost. In our model, Xr2 represents a marginal cost paid by the vendor to increase the production speed. When Xr2 increases by 100%, which means that the production cost of regular production become more expensive, the production allocation to green production increases. It is further seen that increase in regular’s production cost incurs a lower production rate. This is intuitively correct because, as the vendor is required to pay higher production cost, a considerable decrease in the production rate would reasonably be favourable for him. Figure 4 shows that an increase in Xr2 simultaneously decreases the number of defects generated from the regular production system. Having lower production rate, the mean time of the regular production system shifts to the out of control state is prolonged, which leads to the reduction of the number of defects. This facts show that by allowing that the production rate of the system to be adjusted flexibly and giving the vendor an opportunity to set the production allocation (α) appropriately, the mean time of the production system shifts to out of control state can be controlled by the system which in turn reduces the defects generated during production run.

Table 6 The impact of the changes in \(X_{r2} \) on model’s solution
Full size table
Fig. 4
figure 4

Impact of the changes in Xr2 on total cost and number of defects

Full size image

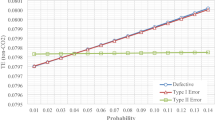
In this section, we also examine the effects of the changes in \({\omega }_{r}\) on optimal results. From Table 7, it is seen that defective rate of regular production decreases and the total costs of regular and green productions increase with the increase in \({\omega }_{r}\). Figure 5 presents how the production rate and percentage of defective items change against the change in \({\omega }_{r}\). The percentage defective items of regular and green productions decrease with the increase in \({\omega }_{r}\). We further see that the change in the value of \({\omega }_{r}\) does not give a significant influence on the production rate.

Table 7 The impact of the changes in \(\omega_{r} \). on model’s solution
Full size table
Fig. 5
figure 5

Impact of the changes in \(\omega_{r}\) on the percentage of defective rate and production rate

Full size image

Finally, Table 8 clearly shows how the adoption of quality investment in the model can reduce the joint total cost. We observe that the model with quality investment will achieve a lower production rate compared to the model without investment. In addition, by allowing the vendor to invest money to reduce the defects, the inventory level can be maintained at lower level which leads to the decreasing of joint total cost. However, the emissions generated from transportation sharply increase due to the increase of the shipment frequency. Furthermore, we may also observe that if the vendor makes an investment, the production allocation to the greener system gradually decreases which in turn reduces its cost. We may also note here that by conducting an investment, the vendor can control the appropriate level of defective rate at both systems to reduce the defect items.

Table 8 Comparison between proposed model and the model without quality investment
Full size table

7 Concluding remarks

This paper studied an integrated vendor–buyer model addressing imperfect production process and environmental impacts where a hybrid of regular and green production technologies is concurrently operated. The vendor’s manufacturing system encounters flawed production, thus generates defective items. Rework process is utilized to fix the defective items produced during production time. The vendor has an opportunity to make an investment to improve the quality of production process. Furthermore, the carbon tax is incorporated in the proposed model to elaborate environmental impact in the joint total cost. The green technology is adopted by the vendor to lessen the generations of emissions. In addition to utilizing this environmentally friendly technology, vendor also uses regular production to produce the items. The carbon emissions generated from production and rework processes and the production cost are influenced by the production rate. We developed a mathematical model which minimizes the joint total cost of the supply chain system. An iterative procedure is proposed to obtain the optimal production allocation factor, shipment size, number of deliveries, production rate, safety factor and defective rate.

The interesting findings obtained from a sensitivity analysis are summarized as follows. First, the vendor can control the defective items and the emissions generated from the production system by adjusting the production rate flexibly and setting the production allocation accurately. The results from the analysis proved that these actions can be used as a mechanism to control the mean time when the production system goes to out of control state, so the defects can be minimized. In addition, the emissions from the production and reworking processes can also be managed, thus reduces the total cost. Second, the number of defects resulted from the system also can be controlled and minimized by making a quality investment. Although this investment wouldn’t influence the mean time of the system will go to out of control state, it can control the number of defects during out of control state. Thus, we can conclude that by giving the vendor an option to adjust the production rate, set the production allocation level and make a quality investment, the number of defects generated during production run can be minimized.

Third, an increased demand requires an increased amount of money invested to improve the quality of production process. In addition, the system needs to increase the production batch in order to ensure that the existing inventories are adequate for satisfying the increased demand. Fourth, the increase in carbon tax leads to shifting more production allocation to the green production. It is also observed that the production rate and defective rate reduces since there is an increased carbon tax. This is reasonable, since keeping the production rate and defective rate at lower level, the vendor can control the cost associated with emissions. Fifth, an increase in the regular’s production cost component also encourages the manager to allocate more productions to the green production. We note that the regular’s production cost component has much more pronounced impact on the production allocation than that of other parameters discussed in this paper. Thus, the manager needs to pay more careful attention to controlling the parameter of production cost by adjusting the production rate.

Future research can look into incorporating human errors in the inspection process. During screening process, the inspector may misclassify good items as defective or vice versa. This type of error will consequently generates some costs incurred by both vendor and buyer. Furthermore, the model can be extended by exploring the other possible carbon reduction policies to restrict the carbon emissions. The policy such as carbon cap and trade and carbon penalty can be incorporated in the model to limit such emissions. Another potential research area is to develop an algorithm that can obtain the global optimal solutions. Although it will be more complex, the solutions obtained will be of benefit to the decision makers.