1 Introduction

Software system is embedded in most products applied in our daily life, such as consumer electronics, home appliances, network/grid systems, and computer systems (Rana et al. 2014). The smooth and friendly user-interface and increasing innovation of the embedded software system bring in more convenience and functionality in everyday life. At the same time, software system is becoming more sophisticated to meet various performance from different perspectives.

As discussed in the recent publication (Bosch 2010), both the size of software system built and the deployment speed of the new-built software system continue to evolve at a very enormous speed. Such evolvement requires software practitioner to continuously develop new approaches to manage the consequent implication of the environments. One of the major transitions is most software developments have shifted their attention from building the system toward composing system from the existing open source, commercial and internal developed components. Under such transition, the goal will be concentrated on the creation and functionality. Secondly, the lean and agile development approaches are commonly applied in many software development processes nowadays. Small team, short development iteration, and frequent deployment are the main elements of this approach. The third trend is the increasing adoption of software ecosystem. The development of new functionality can be occurred outside of the platform, not limited in the organization. App-store styled approaches are introduced by many companies to provide this feature to the market (Harman et al. 2012; Ghazawneh and Henfridsson 2013; Basole and Karla 2011).

Two issues are brought to our attention associated with these transitions in software industry: Software Reliability and Environmental Factors in development process. High software reliability must be demonstrated for each software release to assure it functions as designed in the operation environment (Palviainen et al. 2011). How to control and measure software quality is the most challenging issue faced by software industry (Hsu et al. 2011). Developing software and protecting against software failure contribute to the largest expenses of software industry (Chang and Liu 2009). Many software measurement metrics are developed to properly address software quality before its release. One of the most applied software measurement metrics is software reliability. Software reliability, not only helps manager with quantifying system behaviors, but allocating testing resource and optimizing release time. The commonest method to evaluate software reliability is to apply Software Reliability Growth Model (SRGM).

Since 1970s, many non-homogeneous Poisson process (NHPP) software reliability growth models in consideration of different assumptions have been proposed for the estimation of the number of remaining faults, failure rate, and software reliability for software products given a specific time horizon (Hsu et al. 2011; Goel and Okumoto 1979; Musa 1975; Kapur et al. 2011; Yamada et al. 1986; Zhu and Pham 2016; Ahmadi et al. 2016; Pachauri et al. 2015; Sukhwani et al. 2016; Yamada 2014; Jin and Jin 2014; Inoue et al. 2016; Fiondella and Zeephongsekul 2016; Zhu and Pham 2017a; Yamada and Tamura 2016; Zachariah 2015b; Özdamar and Alanya 2001). For example, incorporating testing effort into software reliability model has received lots of attention these years. Huang et al. (2007) incorporated logistic testing effort function into both exponential-type and S-type NHPP models. Lin and Huang (2008) discussed the multiple change-points into the flexible Weibull-type time dependent testing effort function. Later, Inoue et al. (2016) developed a bivariate software reliability growth model considering the uncertainty of the change-point. Additionally, the optimal release time and resource allocation is studied by many researchers (Xie and Hong 1998; Huang and Lyu 2005a; Lo et al. 2005; Huang and Lo 2006; Yang and Xie 2000; Huang and Lyu 2005b; Zachariah 2015a). These theoretical software reliability models have been effectively proven in a wide-range real application in industry and research institution (Almering et al. 2007; Jeske and Zhang 2005; Sukhwani et al. 2016). However, none of them has discussed the impact of environmental factor on software reliability during software development/operation and how to incorporate environmental factor into the modeling.

Zhang and Pham (2000) firstly defined 32 environmental factors during the software development process. These environmental factors not only included each phase of software development practice, but considered human nature, teamwork and the interactions amongst human, software system and hardware system. Later, Zhu et al. (2015) conducted another comparison study to address the impact level of each environmental factor on software reliability assessment and provided up-to-date critical environmental factors to software practitioners.

Only a few literatures incorporated the randomness of the environmental factors in software reliability model. Teng and Pham (2006) proposed a generalized random field environment software reliability model that linked both the testing phase and operation phase. The fault detection rate for testing and operation phase is not constant. Hsu et al. (2011) integrated fault reduction factor into software reliability modeling, where fault reduction factor is defined as the ratio of net fault reduction to the failure experienced. Recently, Pham (2014) considered the uncertainty of the operation environment into software reliability model.

In this paper, we consider one of the top 10 critical environmental factors (Zhu et al. 2015), Percentage of Reused Modules (PoRM), to be a random variable which has random effect on software fault detection rate. The real data collected from several industries is applied to obtain the distribution of PoRM in Sect. 2. We then introduce the martingale framework, specifically, Brownian motion and white noise process in the stochastic fault detection process to reflect the impact resulting from the randomness of environmental factor. The proposed NHPP software reliability model incorporating these considerations is presented in Sect. 3. Parameter estimation and model comparison criteria are discussed in Sect. 4. Two Open Source Software project data are analyzed in Sect. 5 to illustrate the effectiveness of the propose model. The reliability prediction and the significance of PoRM are also discussed in Sect. 5. Specifically, we are interested in the predictive accuracy comparison of the proposed model with and without considering PoRM. In Sect. 6, we conclude this study, discuss the directions for the future research and the limitations of the current study.

Notation

  • \( m\left( {t,\eta } \right) \): expected number of software failures by time \( t \), also mean value function

  • \( N\left( t \right) \): total fault content function in the software by time \( t \)

  • \( h\left( {t,\eta } \right) \): time-dependent fault detection rate per unit of time

  • \( G\left( {t,\eta } \right) \): impact of Percentage of Reused Modules (PoRM) on failure detection rate per unit of time

  • \( f\left( \eta \right) \): probability density function of PoRM

  • \( M\left( {t,w} \right) \): martingale with respect to the filtration

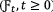
  • \( \dot{M}\left( {t,w} \right) \): derivative of \( M\left( {t, w} \right) \) with respect to time \( t \)

  • \( v\left( t \right) \): measures the impact of time on PoRM

  • \( F^{*} \left( s \right) \): Laplace transform of \( f\left( \eta \right) \)

  • \( \theta , \gamma \): parameters of gamma distribution

  • \( \eta \): random variable, which represents PoRM

  • \( \lambda \): coefficient along with \( G\left( {t,\eta } \right) \)

  • \( b, c,a,k \): coefficient in function \( h\left( t \right) \), \( v\left( t \right) \), and \( N\left( t \right) \)

  • \( y_{i} \): observed number of software failures at time \( t_{i} \)

2 Environmental factor (PoRM) distribution

Although some existing software reliability models have considered the environmental factors in the modeling, most of them assume the distribution of environmental factor based on their knowledge and model consideration. For example, Teng and Pham (2006) described the random environmental factor is 1 in in-house testing phase and a random variable in operation phase. They assumed that this random variable follows gamma distribution or beta distribution in reliability models. But, there is no real data to support this assumption.

In this study, the definition of Percentage of Reused Modules (PoRM), adopted from reference (Zhang and Pham 2000; Zhang et al. 2001; Zhu and Pham 2017b), is presented as follows

$$ PoRM = \frac{{S_{0} }}{{S_{N} + S_{0} }} $$
(1)

where \( S_{0} \) represents kiloline of code for the existing modules and \( S_{N} \) represents kiloline of code for new modules.

In this section, we employ the real data collected from several industries to illustrate the distribution of PoRM. Participants were asked to provide Percentage of Reused Modules in their industry based on the relevant working experience. All the participants are currently working in IT Department in different industry including computer software, banking, semiconductor, online retailing, IT service and research institution or working on software development in high-tech company in favor of the validity and reliability of the survey response. The collected Percentage of Reused Modules (PoRM) are shown in Fig. 1.

Fig. 1
figure 1

Data collection of Percentage of Reused Modules (PoRM)

Full size image

Eight different distributions commonly applied to model environmental factors are adopted in the model comparison to estimate the distribution of PoRM. Maximum likelihood estimation (MLE) is applied to compare the effectiveness of each model. The log-likelihood values for all models are shown in Table 1.

Table 1 Log-likelihood value comparison
Full size table

Gamma distribution will be employed to model the distribution of PoRM. The parameters of gamma distribution are also obtained from model comparison: \( \theta = 14.726, \gamma = 6.487. \)

$$ f\left( \eta \right) = \frac{{\theta^{\gamma } \eta^{\gamma - 1} e^{ - \theta \eta } }}{\varGamma \left( \gamma \right)} $$
(2)

3 Software reliability modeling

3.1 Related works

We first provide the definition of software fault and software failure in order to clearly address the software reliability models discussed below. Software fault is caused by an incorrect step, process, or data definition in a computer program (Radatz et al. 1990). Failure is defined as a system or component is not able to perform its required functions within specified performance requirements. Software failure is the manifestation of software fault (Radatz et al. 1990).

Many NHPP software reliability models have been proposed for the past four decades to address different assumptions. The failure processes are described by NHPP property with the mean value function (MVF) at time \( t \), \( m\left( t \right) \), and the failure intensity of the software, \( \lambda \left( t \right) \), which is also the derivative of the mean value function. Most existing NHPP software reliability models are developed based on the model given as follows

$$ \frac{d}{dt}m\left( t \right) = h\left( t \right)\left( {N\left( t \right) - m\left( t \right)} \right) $$
(3)

where \( m\left( t \right) \) is the expected number of software failures by time \( t \), \( N\left( t \right) \) is the total number of fault content by time \( t \), and \( h\left( t \right) \) is the time-dependent fault detection rate per unit of time. The underlying assumption of Eq. (3) is the failure intensity is proportional to the residual fault content in the software. Lots of NHPP software reliability models are developed based on Eq. (3). Some examples are given in Table 2.

Table 2 Some existing NHPP software reliability models
Full size table

The software reliability models presented in Table 2, along with other deterministic models, have not taken into account the effect of randomness from the development/operation environment. To capture the effect of random environments, a stochastic process can be incorporated in the fault detection process by imposing \( h\left( t \right) \) to be \( h\left( {t,\eta } \right) \), where \( \eta \) is the random effect. The Eq. (3) will be described as

$$ \frac{d}{dt}m\left( {t,\eta } \right) = h\left( {t,\eta } \right)\left( {N\left( t \right) - m\left( {t,\eta } \right)} \right) $$
(4)

For example, in Pham (2014), the author considered

$$ h\left( {t,\eta } \right) = h\left( t \right) \eta , N\left( t \right) = N $$
(5)

where \( \eta \) is a random variable and follows gamma distribution with parameter α and β. By substituting Eq. (5) to Eq. (4), the explicit solution of the mean value function can be expressed as (Pham 2014)

$$ m\left( t \right) = N\left( {1 - \left( {\frac{\beta }{{\beta + \mathop \int \nolimits_{0}^{t} h\left( s \right)ds}}} \right)^{\alpha } } \right) $$
(6)

The above formulation, \( h\left( {t,\eta } \right) = h\left( t \right) \eta \), proposed in Pham (2014) is referred as dynamic multiplicative noise model in recent publication from Pham and Pham (2017). They (Pham and Pham 2017) also proposed a dynamic additive noise model shown as follows

$$ h\left( {t,w} \right) = h\left( t \right) + \dot{M}\left( {t,w} \right) $$
(7)

where \( \dot{M}\left( {t,w} \right) \) denotes the derivative of \( M \) with respect to time \( t \). \( M\left( t \right) \) is defined as a martingale with respect to the filtration 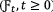in this function. One worth-noting martingale property (Mikosch 1998; Mörters and Peres 2010) applied in Eq. (7) is

$$ E\left( {\mathop \int \limits_{v}^{t} h\left( {s,w} \right)ds} \right) = \mathop \int \limits_{v}^{t} h\left( s \right)ds $$
(8)

Brownian motion (Mikosch 1998) is also a martingale. Let \( \left\{ {B\left( t \right) :\;t \ge 0} \right\} \) be Brownian motion, Mikosch (1998) mentioned that \( \left\{ {B\left( t \right) :\;t \ge 0} \right\} \) and \( \left\{ {B^{2} \left( t \right) - t :\;t \ge 0} \right\} \) are martingale with respect to the nature filtration 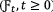. For the model consideration in this paper, we also choose \( M\left( t \right) \) to be Brownian motion since Brownian motion is deeply researched by many literatures.

A stochastic process \( \left\{ {B\left( t \right):t \ge 0} \right\} \) is called Brownian motion (Mörters and Peres 2010) with start in \( x \in {\mathbb{R}} \) if

  1. 1.

    \( B\left( 0 \right) = x \).

  2. 2.

    The process has independent increments. For example, the increments \( B\left( {t_{n} } \right) - B\left( {t_{n - 1} } \right), B\left( {t_{n - 1} } \right) - B\left( {t_{n - 2} } \right), \ldots , B\left( {t_{2} } \right) - B\left( {t_{1} } \right) \) are independent for all time \( 0 \le t_{1} \le t_{2} \le \cdots \le t_{n} \).

  3. 3.

    The increments \( B\left( {t + s} \right) - B\left( t \right) \) are normally distributed, for all \( t \ge 0, s \ge 0 \).

If \( B\left( 0 \right) = 0 \), i.e. the motion is started from the origins, this is called standard Brownian motion.

3.2 Proposed NHPP software reliability model

The proposed NHPP software reliability model in this study incorporates both the dynamic multiplicative and additive noise characteristics discussed in Sect. 3.1. Meanwhile, one of the top 10 environmental factors from the recent comparison survey study (Zhu et al. 2015), modeled as gamma distribution with parameter θ and r estimated from real-collected data from various industries, is incorporated in the model development. In sum, environmental factor (PoRM), described as gamma distribution from real data, and the randomness caused by PoRM, illustrated by the martingale, specifically, Brownian motion, are taken into account for the proposed software reliability model.

The assumptions for the proposed model are given as follows

  1. 1.

    The fault removal process follows the non-homogeneous Poisson distribution.

  2. 2.

    The failure of software system is subject to the manifestation of the remaining faults in the software program.

  3. 3.

    All faults in the software are independent.

  4. 4.

    The failure intensity is proportional to the remaining faults in the software.

  5. 5.

    The environmental factor, Percentage of Reused Modules (PoRM), is described as gamma distribution based on the real data collected from various industry, as discussed in the Sect. 2. The impact of PoRM is explained by an additive portion along with the traditional fault detection process.

  6. 6.

    The randomness caused by the environmental factor is explained as a martingale, particularly, Brownian motion in this study.

The proposed NHPP software reliability model is given as

$$ \frac{d}{dt}m\left( {t,\eta } \right) = \left[ {h\left( t \right) + \lambda G\left( {t,\eta } \right) + \dot{B}\left( t \right)} \right]\left[ {N\left( t \right) - m\left( {t,\eta } \right)} \right] $$
(9)
$$ m\left( 0 \right) = 0 $$
(10)

where \( m\left( {t,\eta } \right) \) is the expected number of failures by time \( t \), \( h\left( t \right) \) is the fault detection rate per unit of time without considering the effect of environmental factor, \( \eta \) is a random variable and represents the environmental factor, PoRM, \( G\left( {t,\eta } \right) \) is a time-dependent function and represents the impact of PoRM on failure detection rate per unit of time, \( \lambda \) is the coefficient along with \( G\left( {t,\eta } \right) \), and \( \dot{B}\left( t \right) \) denotes a standard Gaussian white noise, specifically

$$ \frac{d}{dt}B\left( t \right) = \dot{B}\left( t \right) $$
(11)

where \( B\left( t \right) \) is a Brownian motion.

The covariance of \( \dot{B}\left( t \right) \) is

$$ E\left( {\dot{B}\left( t \right)\dot{B}\left( u \right)} \right) = \delta \left( {u - t} \right), 0 < t < u $$
(12)

From (Pham and Pham 2017), similarly, we can obtain the general solution for Eq. (9) as follows

$$ m\left( {t,\eta } \right) = N\left( t \right) - N\left( 0 \right)e^{{ - \mathop \int \limits_{0}^{t} \left( {h\left( s \right) + \lambda G\left( {s,\eta } \right) + \dot{B}\left( s \right)} \right)ds}} - \mathop \int \limits_{0}^{t} e^{{ - \mathop \int \limits_{u}^{t} \left( {h\left( s \right) + \lambda G\left( {s,\eta } \right) + \dot{B}\left( s \right)} \right)ds}} N'\left( u \right)du $$
(13)

The detailed derivation can be found in “Appendix I”.

Since \( \dot{B}\left( t \right) \) denotes a standard Gaussian white noise, we can also have

$$ \begin{aligned} \mathop \int \limits_{0}^{t} \left( {h\left( s \right) + \lambda G\left( {s,\eta } \right) + \dot{B}\left( s \right)} \right)ds &= \mathop \int \limits_{0}^{t} \left( {h\left( s \right) + \lambda G\left( {s,\eta } \right)} \right)ds + B\left( t \right) - B\left( 0 \right) \\ & = \mathop \int \limits_{0}^{t} \left( {h\left( s \right) + \lambda G\left( {s,\eta } \right)} \right)ds + B\left( t \right) \\ \end{aligned} $$
(14)

The mean value function can be expressed as

$$ \bar{m}\left( t \right) = N\left( t \right) - N\left( 0 \right)e^{{ - \mathop \int \limits_{0}^{t} h\left( s \right)ds}} e^{{\frac{t}{2}}} e^{{ - \mathop \int \limits_{0}^{t} \lambda G\left( {s, \eta } \right)ds}} - \mathop \int \limits_{0}^{t} e^{{ - \mathop \int \limits_{u}^{t} h\left( s \right)ds}} e^{{\frac{t - u}{2}}} e^{{ - \mathop \int \limits_{u}^{t} \lambda G\left( {s, \eta } \right)ds}} N'\left( u \right)du $$
(15)

Let

$$ G\left( {t,\eta } \right) = \eta v\left( t \right) $$
(16)

where \( v\left( t \right) \) is a time-dependent function, measures the impact of time on PoRM.

The environmental factor, \( \eta \), has a gamma distribution with the parameter \( \theta \) and \( r \).

$$ f\left( \eta \right) = \frac{{\theta^{\gamma } \eta^{\gamma - 1} e^{ - \theta \eta } }}{\varGamma \left( \gamma \right)} $$
(17)

We apply the expectation on Eq. (15) with respect to \( \eta \). The mean value function can be obtained

$$ \begin{aligned} \bar{m}_{\eta } \left( t \right) & = N\left( t \right) - N\left( 0 \right)e^{{ - \mathop \int \limits_{0}^{t} h\left( s \right)ds}} e^{{\frac{t}{2}}} \mathop \int \limits_{0}^{\infty } e^{{ - \mathop \int \limits_{0}^{t} \lambda \eta v\left( s \right)ds}} f\left( \eta \right)d\eta\\ &\quad - \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{t} e^{{ - \mathop \int \limits_{u}^{t} h\left( s \right)ds}} e^{{\frac{t - u}{2}}} e^{{ - \mathop \int \limits_{u}^{t} \lambda \eta v\left( s \right)ds}} N'\left( u \right)f\left( \eta \right)dud\eta \\ & = N\left( t \right) - N\left( 0 \right)e^{{ - \mathop \int \limits_{0}^{t} h\left( s \right)ds}} e^{{\frac{t}{2}}} \mathop \int \limits_{0}^{\infty } e^{{ - \eta \mathop \int \limits_{0}^{t} \lambda v\left( s \right)ds}} f\left( \eta \right)d\eta \\ &\quad - \mathop \int \limits_{0}^{t} N^{\prime}\left( u \right)e^{{ - \mathop \int \limits_{u}^{t} \left( {h\left( s \right) - \frac{1}{2}} \right)ds}} \left[\mathop \int \limits_{0}^{\infty } e^{{ - \eta \mathop \int \limits_{u}^{t} \lambda v\left( s \right)ds}} f\left( \eta \right)d\eta \right]du \\ \end{aligned} $$
(18)

Compute the equations with Laplace transform

$$ \mathop \int \limits_{0}^{\infty } xe^{ - sx} f\left( x \right)dx = - \frac{{dF^{*} \left( s \right)}}{ds} $$
(19)

The Laplace transform of gamma probability density function is

$$ F^{*} \left( s \right) = \left[ {\frac{\theta }{\theta + s}} \right]^{\gamma } $$
(20)

Therefore

$$ \begin{aligned} \bar{m}_{\eta } \left( t \right) & = N\left( t \right) - N\left( 0 \right)e^{{ - \mathop \int \limits_{0}^{t} h\left( s \right)ds}} e^{{\frac{t}{2}}} F^{*} \left( {\mathop \int \limits_{0}^{t} \lambda v\left( s \right)ds} \right) - \mathop \int \limits_{0}^{t} N^{\prime}\left( u \right)e^{{ - \mathop \int \limits_{u}^{t} \left( {h\left( s \right) - \frac{1}{2}} \right)ds}} F^{*} \left( {\mathop \int \limits_{0}^{t} \lambda v\left( s \right)ds} \right)du \\ & = N\left( t \right) - N\left( 0 \right)e^{{ - \mathop \int \limits_{0}^{t} h\left( s \right)ds}} e^{{\frac{t}{2}}} \left[ {\frac{\theta }{{\theta + \mathop \int \nolimits_{0}^{t} \lambda v\left( s \right)ds}}} \right]^{\gamma } - \mathop \int \limits_{0}^{t} N^{\prime}\left( u \right)e^{{ - \mathop \int \limits_{u}^{t} \left( {h\left( s \right) - \frac{1}{2}} \right)ds}} \left[ {\frac{\theta }{{\theta + \mathop \int \nolimits_{0}^{t} \lambda v\left( s \right)ds}}} \right]^{\gamma } du \\ & = N\left( t \right) - N\left( 0 \right)e^{{ - \mathop \int \limits_{0}^{t} h\left( s \right)ds}} e^{{\frac{t}{2}}} \left[ {\frac{\theta }{{\theta + \mathop \int \nolimits_{0}^{t} \lambda v\left( s \right)ds}}} \right]^{\gamma } - \left[ {\frac{\theta }{{\theta + \mathop \int \nolimits_{0}^{t} \lambda v\left( s \right)ds}}} \right]^{\gamma } \mathop \int \limits_{0}^{t} N^{\prime}\left( u \right)e^{{ - \mathop \int \limits_{u}^{t} \left( {h\left( s \right) - \frac{1}{2}} \right)ds}} du \\ \end{aligned} $$
(21)

The Eq. (21) provides a general solution for the proposed NHPP software reliability model in consideration of PoRM and the randomness caused by this environmental factor. Different formulation for \( h\left( t \right) \), \( v\left( t \right) \) and \( N\left( t \right) \) with respect to different assumptions can be plugged in Eq. (21) to obtain the final solution. In this paper, we apply the formulation as follows.

Let

$$ h\left( t \right) = \frac{b}{{1 + ce^{ - bt} }} $$
(22)
$$ v\left( t \right) = e^{ - at} $$
(23)
$$ N\left( t \right) = \frac{1}{k}e^{kt} $$
(24)

As described in Melo et al. (1998), the application process of the reused module can be described as follows: (1) Reused module selection. (2) The adaption of the reused module to the new objective. (3) The integration to the new-developed software product. The impact of PoRM on the software fault detection rate will decrease as software development moves to the later phase. Thus, we use an exponentially decreasing function \( e^{ - at} \) to represent \( v\left( t \right) \) in this study. Meanwhile, \( \frac{1}{k}e^{kt} \) is employed to represent \( N\left( t \right) \) due to \( \frac{1}{k}e^{kt} \) is a monotonically increasing function, which can represent the nature growth of the software failures, and the inspiration from reference (Pham and Pham 2017).

Substitute Eqs. (22–24) to Eq. (21), the mean value function can be expressed as

$$ \begin{aligned} m\left( {t, \eta } \right) & = \frac{1}{k}e^{kt} - \frac{1}{k}\frac{c + 1}{{c + e^{bt} }}e^{{\frac{t}{2}}} \left[ {\frac{\theta }{{\theta + \frac{\lambda }{a}\left( {1 - e^{ - at} } \right)}}} \right]^{\gamma } \\ &\quad - \left[ {\frac{\theta }{{\theta + \frac{\lambda }{a}\left( {1 - e^{ - at} } \right)}}} \right]^{\gamma } \frac{{e^{{\frac{t}{2}}} }}{{c + e^{bt} }}\mathop \int \limits_{0}^{t} N^{\prime}\left( u \right)\left[ {ce^{{ - \frac{u}{2}}} + e^{{\left( {b - \frac{1}{2}} \right)u}} } \right]du \\ & = \frac{1}{k}e^{kt} - \frac{{e^{{\frac{t}{2}}} }}{{c + e^{bt} }}\left[ {\frac{\theta }{{\theta + \frac{\lambda }{a}\left( {1 - e^{ - at} } \right)}}} \right]^{\gamma } \\ &\quad \left( {\frac{c + 1}{k} - \frac{c}{{k - \frac{1}{2}}}e^{{\left( {k - \frac{1}{2}} \right)t}} - \frac{1}{{b + k - \frac{1}{2}}}e^{{\left( {b + k - \frac{1}{2}} \right)t}} + \frac{c}{{k - \frac{1}{2}}} + \frac{1}{{b + k - \frac{1}{2}}}} \right) \\ \end{aligned} $$
(25)

Given the definition of \( m\left( t \right) \) is the expected number of software failures by time t, we do know \( m\left( t \right) \) is an increasing function and we are also able to show \( when\; t \to \infty , m\left( t \right) \to \infty \) for Eq. (25) based on the numerical example.

We believe the behavior of Eqs. (21) and (25) mainly depends on the formulation of \( N\left( t \right) \). For example,

  1. 1.

    If \( N\left( t \right) \) is a constant, then \( m\left( t \right) \) converges to this constant.

  2. 2.

    If \( N\left( t \right) \) is a time-dependent function and can converge to a finite number, then \( m\left( t \right) \) converges to this finite number.

  3. 3.

    If \( N\left( t \right) \) is a time-dependent function and cannot converge, then \( m\left( t \right) \) cannot converge.

But in this paper, we are not going to cover the mathematical proof for the above description. The investigation of the function behavior will be further studied in the future research.

4 Parameter estimation and criteria

4.1 Parameter estimation

In practice, parameter estimation can be achieved by applying least square estimate (LSE) and maximum likelihood estimate (MLE). For example, minimizing Eq. (26) or maximizing Eq. (27).

$$ S = \mathop \sum \limits_{i = 1}^{n} \left( {m\left( {t_{i} } \right) - y_{i} } \right)^{2} $$
(26)
$$ LLF = \mathop \sum \limits_{i = 1}^{n} \left( {y_{i} - y_{i - 1} } \right){ \log }\left[ {m\left( {t_{i} } \right) - m\left( {t_{i - 1} } \right)} \right] - m\left( {t_{n} } \right) - \mathop \sum \limits_{i = 1}^{n} \log \left( {y_{i} - y_{i - 1} } \right)! $$
(27)

where \( y_{i} \) is the observed number of failures at time \( t_{i} \). We apply LSE to minimize Eq. (26) to estimate the parameters. Since the parameters of gamma distribution have already been estimated from the real data, thus, we need to estimate other five unknown parameters for Eq. (25), which are \( k \), \( b \), \( c \), \( \lambda \), and \( a \). The genetic algorithm (GA) is employed in order to solve the optimization function, as given in Eq. (26). Matlab and R software are used to solve the optimization function and estimate parameters.

4.2 Comparison criteria

  1. 1.

    Mean squared error (MSE)

$$ MSE = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\widehat{m}\left( {t_{i} } \right) - y_{i} } \right)^{2} }}{n - N} $$
(28)

where n is the total number of observations, N represents the number of unknown parameters in each model, and \( y_{i} \) is the observed number of failures at time \( t_{i} \). The mean squared error measures the distance of model estimate from the observed data.

  1. 2.

    Predictive-ratio risk (PRR) and predictive power (PP) (Pham 2007)

$$ PRR = \mathop \sum \limits_{i = 1}^{n} \left( {\frac{{\widehat{m}\left( {t_{i} } \right) - y_{i} }}{{\widehat{m}\left( {t_{i} } \right)}}} \right)^{2} $$
(29)
$$ PP = \mathop \sum \limits_{i = 1}^{n} \left( {\frac{{\widehat{m}\left( {t_{i} } \right) - y_{i} }}{{y_{i} }}} \right)^{2} $$
(30)

The predictive-ratio risk and predictive power are calculated to compare the predictive performance of different software reliability models. The predictive-ratio risk measures the distance of the model estimate from the actual data against the model estimate by assigning a larger penalty to the model that has underestimated the cumulative number of failures. The predictive power measures the distance of the model estimate from the actual data against the actual data.

  1. 3.

    Variation

The variation is defined as (Huang and Kuo 2002)

$$ Variation = \sqrt {\frac{1}{n - 1}\mathop \sum \limits_{i = 1}^{n} \left( {y_{i} - \widehat{m}\left( {t_{i} } \right) - Bias} \right)^{2} } $$
(31)

where

$$ Bias = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {\widehat{m}\left( {t_{i} } \right) - y_{i} } \right) $$
(32)

For all the criteria discussed above, the smaller of the criteria, the better fit of the model.

As the research problems become more complex, it is very nature to contain lots of parameters. The proposed software reliability model has five parameters, which is still reasonable to be applied in industrial application. We have also chosen some model evaluation criteria, for example, variation, to assign the penalty for the model contains more parameters and address possible overfitting issue. Additionally, we have applied two datasets collected from real world to compare the predictability as well as the practical applicability of the proposed model with other software reliability models in Sect. 5.

5 Applications

In the following experiments, we choose two applications, DS1 and DS2, to validate the proposed NHPP software reliability model and compare the performance with other existing software reliability models. The comparison criteria are discussed in the above section. DS1 and DS2 are both collected from Open Source Software (OSS) project. Open Source Software has attracted significant attention in the past decade. Some report shows that a few major Open Source Software products have surpassed their commercial counterparts in terms of the market share and quality evaluation (Wheeler 2007). Not only individuals are attracted by the features of Open Source Software, but many software companies and government-supported organizations (Zhou and Davis 2005). A research study conducted by CIO Magazine (Cosgrove 2003) found that IT community is growing better by using open source development model and open source software will dominate as the Web server application platform and server operating system. The majority of the companies are using open source today for web development. To align with the new transitions in software development, Open Source Software project data are employed to illustrate the performance of the proposed model.

5.1 Dataset 1 (DS1)

DS1 is extracted from Apache Open Source Software project. It was collected from Sep 2010 to April 2013. The collected data are described in Table 3. The column named Failure in Table 3 represents the number of software failures detected between time unit t − 1 and t. The column named Cumulative Failures in Table 3 represents the cumulative software failure by time t. The parameter estimate and model comparison are presented in Table 4. In this dataset, we use the first 24 time units to estimate the parameters.

Table 3 DS1 failure data
Full size table
Table 4 DS1 parameter estimate and model comparison
Full size table

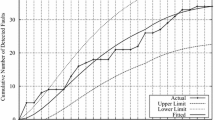
As presented in Table 4, we can see that the proposed model has the smallest MSE, PRR, and Variation. It is worth noting that MSE is the most critical criteria in terms of model selection. The PP value for the proposed model is 0.311, which is just slightly larger than the smallest PP value 0.228, however, all other three criteria for G-O model is significantly larger than the proposed model. Thus, we conclude that the proposed model has the best fit. Figure 2 also shows the comparison between the actual failure data and the predicted failure data from all the models discussed in Table 4. The proposed model yields very close fittings and predictions on software failure.

Fig. 2
figure 2

Comparison of actual failure data and predicted failure data (DS1)

Full size image

Other software reliability measures are also calculated to provide a comprehensive understanding of the prediction power for the proposed model. In this study, we are interested in the estimated software failures for each time unit, which can be obtained by \( m\left( t \right) - m\left( {t - 1} \right) \), and the estimated time to detect all the 136 actual software failures that have already appeared in the program, as seen in Table 3. Figure 3 shows the estimated software failures for 16 time units, ranging from time unit 25–40, which gives an estimate for software tester in terms of the number of software failures occurred in the operation field during each time unit and further helps software multiple release planning. Moreover, the estimated time unit to detect all the 136 actual software failures is 38.40 based on the proposed model. Software tester can use this information to estimate how much time will be spent on one project and assign the corresponding testing resource. In sum, these measures can help software testing team to optimally assign the available testing resource to each ongoing project, decide when to stop testing, and plan software multiple release.

Fig. 3
figure 3

Software failure prediction from time unit 25–40 (DS1)

Full size image

5.2 Dataset 2 (DS2)

DS2 is also one of Apache Open Source Software project data. It was collected from Feb 2009 to Feb 2014. 33 sets of failure data are presented in Table 5. The column named Failure in Table 5 represents the number of software failures detected between time unit t − 1 and t. The column named Cumulative Failures in Table 5 represents the cumulative software failure by time t. The parameter estimate and model comparison are described in Table 6.

Table 5 DS2 failure data
Full size table
Table 6 DS2 Parameter estimate and model comparison
Full size table

As seen from Table 6, the proposed model has the smallest MSE and Variation. Although PNZ model has the smallest PRR and PP, the MSE for PNZ model is much larger than the proposed model. Given MSE is the most critical for model selection, therefore, the best fitting model is still the proposed model. Figure 4 shows the comparison between the actual failure data and the predicted failure data from all the models discussed in Table 6. The proposed model subjects to a very close fittings and predictions on the cumulative software failures for DS2.

Fig. 4
figure 4

Comparison of actual failure data and predicted failure data (DS2)

Full size image

We also provide other software reliability measures for DS2. Figure 5 presents the estimated failures for each time unit, ranging from time unit 29 to 44. Moreover, the estimated time unit to detect all 185 software failures that have been already appeared in the program is 50.92.

Fig. 5
figure 5

Software failure prediction for time unit 29–44 (DS2)

Full size image

5.3 Reliability prediction

Once the parameters are obtained, the software reliability within \( \left( {t, t + x} \right) \) can be determined as

$$ R\left( {x |t} \right) = e^{{ - \left[ {m\left( {t + x} \right) - m\left( t \right)} \right]}} $$
(33)

Figure 6 presents the reliability prediction for DS1 and DS2 by varying \( x \) from time unit 0 to 1.2. All other models do not take into consideration of environmental factor (PoRM) and a dynamic fault detection process. As a result, they cannot present reliability prediction well since OSS projects are influenced by the randomness caused by environmental factors significantly than traditional projects. Thus, we did not incorporate reliability prediction from other models.

Fig. 6
figure 6

Reliablity predicton for DS1 and DS2

Full size image

During the testing phase, as the testing time increases, in general, software testing team can remove more software faults. In this case, software reliability will increase as the testing time increases. But after software released to operation phase (customers), the software reliability will decrease as the operation time increases if there is no updated version for the current release. First, it is impossible to remove all the software faults in the program due to the limitation of testing resource, programmer skill and constricted product development schedule (Zhu et al. 2015; Rana et al. 2014; Almering et al. 2007; Zhang et al. 2001; Zhu and Pham 2017a, b). Hence, even software product has already been released in the market, it still contains some software faults. Second, software users will also contribute incorrect/correct input during the operation phase, which can trigger the undetected software faults existed in the program. Thus, the total number of software failures will increase as the operation time increases if there is no updated version, then the software reliability tends to go zero in this case. The software reliability prediction shown in Fig. 6 also confirms this conclusion. Therefore, most software companies will release the updated version to fix the issues in the current release to increase software reliability in the operation phase and introduce some new features to improve user experience (Zhu and Pham 2017a).

5.4 Discussion of the impact of environmental factor (PoRM)

To emphasize the significance of incorporating PoRM in software reliability model, the comparison between the software reliability model with and without PoRM will be discussed in this section. Without considering PoRM and its impact, Eq. (9) will be formulated as

$$ \frac{d}{dt}m\left( {t,\eta } \right) = \left[ {h\left( t \right) + \dot{B}\left( t \right)} \right]\left[ {N\left( t \right) - m\left( {t,\eta } \right)} \right] $$
(34)

This formulation has detailed explanation in Pham and Pham (2017). Substitute Eqs. (10), (22) and (24) into Eq. (34), the new mean value function without considering environmental factor (PoRM) can be obtained as follows

$$ m\left( t \right) = \frac{1}{k}e^{kt} - \frac{{e^{{\frac{t}{2}}} }}{{c + e^{bt} }}\left( {\frac{c + 1}{k} - \frac{c}{{k - \frac{1}{2}}} - \frac{1}{{b + k - \frac{1}{2}}}} \right) - \frac{{ce^{kt} \left( {c + e^{bt} } \right)^{ - 1} }}{{k - \frac{1}{2}}} - \frac{{e^{{\left( {k + b} \right)t}} \left( {c + e^{bt} } \right)^{ - 1} }}{{b + k - \frac{1}{2}}} $$
(35)

As an illustration for the comparison, DS1 will be used to compare the mean value function with PoRM [Eq. (25)] and the mean value function without PoRM [Eq. (35)]. The parameter estimate for the mean value function without PoRM [Eq. (35)] are \( \widehat{k} = 0.109,\widehat{c} = 0.045, \widehat{b} = 0.501 \). Using the criteria described in Sect. 4, we have \( MSE = 103.238 \), which is significantly higher than the model considering PoRM, 35.173, as shown in Table 4. We also present Fig. 7, which compares the actual failure data, the failure prediction by the model with PoRM [Eq. (25)], and the failure prediction by the model without PoRM [Eq. (34)]. We can see that the failure prediction will be more accurate with considering PoRM for OSS project data. Therefore, incorporating PoRM in software reliability model will significantly improve the predictive accuracy.

Fig. 7
figure 7

Software failure prediction comparison of models with and without PoRM

Full size image

6 Conclusions and future research

To the best of our knowledge, the environmental factor, in particular, Percentage of Reused Modules (PoRM) and the martingale framework, specifically, Brownian motion and white noise process have not been simultaneously employed in NHPP software reliability model. Lots of software developments have shifted their attention from building a new system toward composing system from the existing open source platform. On the other hand, there is an increasing trend on the adoption of software ecosystem. The development of new functionality can be occurred outside of the platform. For example, App-store styled approaches are getting popular in software community (Bosch 2010). Therefore, it is of great importance to incorporate Percentage of Reused Modules in the software reliability model because it brings a significant impact on open source project compared with traditional software development. Pham and Pham’s (2017) recent publication concentrated on the application of martingale framework and provide a generalized solution for this type of problem, however, they did not include specific environmental factors and their distributions.

There are several research directions can be pursued in the next step. For instance, (1) we are currently investigating one environmental factor, PoRM, in this study. Two or more environmental factors can be studied in the future research. Correlation could also be considered between these environmental factors; (2) the total number of fault content is considered as a time dependent function in this study. The randomness caused by environmental factors may also affect this time dependent function; (3) the function [Eq. (21)] behavior can be further investigated.