Staff assignment policies for a mass casualty event queuing network

Abstract

We study parallel queuing systems in which heterogeneous teams collaborate to serve queues with three different prioritization levels in the context of a mass casualty event. We assume that the health condition of casualties deteriorate as time passes and aim to minimize total deprivation cost in the system. Servers (i.e. doctors and nurses) have random arrival rates and they are assigned to a queue as soon as they arrive. While nurses and doctors serve their dedicated queues, collaborative teams of doctors and nurses serve a third type of customer, the patients in critical condition. We model this queueing network with flexible resources as a discrete-time finite horizon stochastic dynamic programming problem and develop heuristic policies for it. Our results indicate that the standard $c \mu$ rule is not an optimal policy, and that the most effective heuristic policy found in our simulation study is intuitive and has a simple structure: assign doctor/nurse teams to clear the critical patient queue with a buffer of extra teams to anticipate future critical patients, and allocate the remaining servers among the other two queues.

1 Introduction

Mass casualty events (MCE) such as natural disasters and terror attacks are large scale incidents which create a sudden peak in demand for medical resources. For example, immediately after the Haiti earthquake in 2010 the Norwegian Red Cross set up their Rapid Deployment Emergency Hospital in Port-au-Prince. The outpatient department treated an average of 80 people per day and a total of 300 surgical procedures were performed during the 4-week mission of this hospital (Elsharkawi et al. 2010). It is clear that after a mass casualty event, the demand for medical response far exceeds the existing capacity to administer it. Thus dynamic allocation of limited resources such as doctors, nurses and operating rooms to cases will help ensure the survival of affected individuals (Merin et al. 2010).

Immediately after the event casualties arrive to hospitals (care facilities, field hospitals and alike), some on foot (also called walking wounded) and some in an ambulance. During their transport or on arrival, casualties are triaged and prioritized for treatment according to their medical situation (Bostick et al. 2008). There are several triage systems that distinguish between several classes of casualties but the probably the most commonly used one is Simple Triage And Rapid Transport (START) which classifies patients into five different groups (Lerner et al. 2008). Minor patients are the walking wounded. Delayed patients are those for whom treatment may be delayed by some time without risking their lives. Immediate patients need immediate care or their condition will get worse. Expectant patients are expected to die. And the last category includes the dead. Even though casualties classified as Immediates are prioritized for prompt treatment inadequate capacity may make it impossible to attend to all them within a reasonable time. The medical staff, especially the surgeons who are most frequently the bottleneck resource, simply cannot provide prompt treatment to all casualties (Hirshberg et al. 1999). Therefore, the main objective of mass casualty event management is to minimize the patients mortality (Cohen et al. 2014).

In general, patients in the minor category are attended by nurses. Patients triaged as delayed can be seen by nurses or doctors depending on their specific need. Patients who are in the immediate category will surely need a doctor, while some may need surgery. However, a doctor cannot perform surgery by himself/herself. A team of doctors, nurses and technicians is needed to perform a surgery. Limited resources means when a nurse attending minor patients is assigned to a surgery team, his/her patients have to wait. Holguín-Veras et al. (2013) suggest that after a disaster, casualties are deprived of basic needs, such as water, food and medical attention, and their suffering increases by the hour parallel to their deprivation. Thus the objective function of humanitarian operations should be to minimize this deprivation cost. The question investigated in this paper is how medical personnel could be allocated effectively to patient categories when all staff is already overwhelmed with a sudden increase in demand so that the total deprivation cost in the system could be minimized.

We model this problem as a queueing network where servers (i.e. medical staff) are assigned to queues of different triage groups. For example, nurses (resource A) are assigned to minor patients. Doctors (resource B) are assigned to delayed patients. But we need a team of doctors and nurses (resource A $+$ B) working together on immediate patients. The contribution of the paper is in the fact that we consider heterogeneous servers collaborating to make up a new server. To the best of our knowledge servers of heterogeneous team collaboration have not yet been studied in the queuing literature. We solve small instances of the model with dynamic programming but realistic size problems prove to be too large to handle. Therefore, we present three heuristics that produce reasonable solutions. We conclude the paper with future research directions.

Fig. 1

MCE queuing network considered in this study

2 Problem description

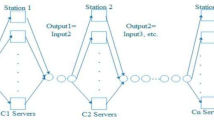
This paper is concerned with staff assignment decisions within the context of the queuing network shown in Fig. 1. The system represents a facility such as a hospital or emergency shelter where mass casualty event (MCE) survivors go to receive medical attention. At one end, random numbers of patients arrive over time where through triage, each is assigned to one of three priority classes based on the severity of his or her injuries: minor, serious, or critical. Distinct queues are designated for each patient class, and patients within each queue are treated on a first-come-first-serve basis. On the other side, medical staff enter the system, and they also arrive in random numbers over time. There are two types of medical workers, and for the purposes of this study, it is convenient to think of them as doctors and nurses. Patients with minor injuries are treated by nurses only, and those with serious injuries are only attended to by doctors.¹ However, both doctors and nurses are required to handle patients with critical injuries (e.g., these patients may need emergency surgery). Upon arrival, a healthcare administrator (i.e., the “controller” in Fig. 1) assigns the doctors and nurses to one of the three patient queues: Queue 1 for minor injuries, Queue 2 for major, or Queue 3 for critical. Of course based on the above-mentioned protocols for handling each type of injury, nurses can be assigned either to Queue 1 or Queue 3 and doctors to Queue 2 or Queue 3.

There are two characteristics that make this MCE queuing system unique from a research perspective. First, we consider random staff (i.e., server) arrivals within the context of a server assignment queuing control problem. To our knowledge, only two other studies examine random server arrivals and their subsequent service assignments in queuing systems: Mayorga et al. (2017) and Zayas-Caban and Lodree (2017). Our rationale for taking random server arrivals into account is motivated by the sudden surge in demand for medical services associated with MCEs, and the emergency response network’s attempts to meet these needs. In this situation, the facility’s capacity in terms of staff, supplies, equipment, and space is often exceeded by a significant amount. As such, medical facilities rely on external help from nearby healthcare service providers, and possibly other organizations such as Red Cross, for additional capacity. The availability of supplemental staff, materials, and space (e.g., mobile emergency tents) is uncertain. It takes time to identify and coordinate backup supply options with no guarantee that all of these alternatives will materialize, and some materials and volunteers may show up uninvited. Moreover, the additional capacity may not all come from the same place, which means that there is also variation in the time it takes to reach the facility from their respective origins. The crux of the matter is that various forms supplemental supply arrive in random quantities at random points in time. The other distinguishing feature of the queuing network shown in Fig. 1 is that for one class of patients (i.e., customers), a team of servers comprised of individuals with different skill sets is required to provide service (recall both a doctor and a nurse are required to serve the class of patients labeled as critical). This is in contrast to classical queuing models where customers are processed by one server at a time, or collaboratively by multiple identical servers.² We believe that this is the first paper to consider “mandatory collaboration” between two heterogeneous servers in a queuing control framework, and is one of only a few papers that investigates server assignment policies for servers who arrive randomly over time.

The performance of the MCE queuing network shown in Fig. 1 is evaluated based on a holding cost that is linearly proportional to the number of unserved patients from each priority class remaining at the end of each period during a finite horizon. This per unit holding cost is greatest for critical patients, and is the least for patients with minor injuries; the cost for those seriously wounded lies between these two extremes. We seek a series of decisions for the controller that minimizes the sum of expected holding costs over a finite number of periods. A stochastic dynamic programming model is developed whose solution gives an optimal server assignment policy. We propose logical heuristic methods to solve problem instances in an extensive computational study. The heuristics are related to the well-known $c \mu$ rule, but modified to accommodates the server collaboration requirement introduced in this study.

The remainder of this paper proceeds as follows. Related literature is discussed in Sect. 3 followed by the development of the stochastic dynamic programming model in Sect. 4. Next, our methodology is detailed in Sect. 5 which includes a description of heuristic methods, research questions, a simulation approach, and experimental design for a computational study. Results from the computational study are discussed in Sect. 6 followed by concluding remarks in Sect. 7.

3 Literature review

The problem studied in this paper consists of a queueing network in a MCE setting where servers (nurses, doctors and doctor and nurse teams) are allocated to queues with different priority settings and impatient jobs (i.e. the cost of delaying service increases with time similar to the idea of a deprivation cost). In the following paragraphs we review relevant research that applies to our case, namely, queues in MCE where tasks are impatient, servers are flexible and can be teamed up, and servers are assigned to queues rather than customers being assigned to servers.

Altay and Green (2006) first identified the need for more operations research approaches to problems in responding to disasters. Since then OR/MS research in the field of disaster management has been growing fast (Anaya-Arenas et al. 2014; Gupta et al. 2016). Most research on mass casualty events is focused on triage systems (Mills 2012). Triage is a mitigation strategy to limit the loss of life because it is well understood that an MCE would quickly overwhelm the service capacity and capability of a healthcare facility. Sacco et al. (2005) are first to explicitly consider resource constraints in a mathematical triage model. Hick et al. (2009) focus their attention on the response capacity of a hospital and propose adaptive strategies to deal with staff and supply shortages.

The problem of allocating scarce resources to different priority queues in a MCE scenario has been dealt by several researchers. Gong and Batta (2006) develop a two-priority, single-server queueing model for a disaster scenario with thousands of casualties. They propose a queue-length cutoff method to minimize the weighted average of customers in the system. Kilic et al. (2014) consider a two-priority non-preemptive S-server, and a finite capacity queueing system. They calculate optimal treatment rates for each priority class while minimizing both the expected value of the squared difference between the number of servers and patients in the system.

In a MCE scenario it is reasonable to assume that some patients condition (e.g. Immediates) will deteriorate as time passes. Even patients in the minor or delayed triage categories will get more and more uncomfortable if they do not receive timely service. This means that although they may not perish there exists a deprivation cost if casualties are not receiving treatment. In queuing theory, customers with deadlines or deterioration of task value are classified as impatient tasks. Since in our paper deprivation can be characterized as deterioration of task value, impatient task literature applies to our problem (Gaver and Jacobs 1999). Glazebrook et al. (2004) and discuss optimal resource allocation of services to impatient tasks. While the former develops multiple index heuristics the latter proposes improvements to these heuristics. Xiang and Zhuang (2016) extend Gong and Batta (2006) work by including the deterioration of the customers health condition into their model. Argon et al. (2009) develop a single-server clearing system with state-dependent prioritization policies. Jacobson et al. (2012) considered multiple resources and defined different mortality probabilities for different types of casualties.

In this paper we assign servers to queues rather than assigning customers to servers. Casualties are already assigned into queues during the triage process. Yang et al. (2013) study the structural properties of the optimal resource allocation policy for single-queue systems. Yang et al. (2011) generalizes the problem to multiple service facilities and shared pool of servers. In both cases the authors assume that there is no cost to switching resources.

Another aspect of our problem is that each server can serve customers in their respective triage category or below, making them somewhat flexible (e.g. doctors can serve the patients nurses could serve but not vice versa). A resource’s ability to process k different triage categories is referred to as level-k flexibility (Bassamboo et al. 2012). Resources may be flexible in the way they handle processes (Sethi and Sethi 1990), products (Fine and Freund 1990) or scope (Mieghem 2008). Ahn and Righter (2006) show that for dynamically allocating flexible resources to tandem queues the optimal policy is often either last-buffer-first-served or first-buffer-first-served. They also show that for exponential service times the optimal policy will have several resources assigned to the same server. Cohen et al. (2014) analyze a two-stage tandem queueing system with flexible resources, and time-varying arrivals using a fluid model that accounts for the transient nature of MCEs. Others investigated dynamic server assignment policies that maximize system capacity with flexible servers and random server switching times/costs (Andradóttir et al. 2001, 2003; Mayorga et al. 2009), or maximize throughput in serial systems (Arumugam et al. 2009).

Finally, in this paper we consider a “mandatory collaboration” between two heterogeneous resources working as team. Although there is a decent amount of research on server collaboration, most of the published work considers the collaboration of homogeneous servers, such as several technicians working together or multiple nurses forming a team, but not a team of doctors and nurses. Andradóttir et al. (2001) consider flexible servers collaborating on one customer to maximize average throughput in the system. Arumugam et al. (2009) study a two-station serial system in which servers may either work collaboratively or non-collaboratively. Only two papers we found deal with heterogeneous server collaboration (in that different server types have different service rates). Andradóttir et al. (2011) show when servers are homogeneous then synergistic servers should collaborate at all times. They add however that when servers are heterogeneous then “there is a tradeoff between taking advantage of server synergy on the one hand and of each servers training and abilities on the other hand” (Andradóttir et al. 2011, p. 2). Wang et al. (2015) generalize (Andradóttir et al. 2011) by considering task-dependent server synergy.

4 Model formulation

We represent the MCE queuing portrayed in Fig. 1 and corresponding server assignment control problem as a discrete-time finite horizon stochastic dynamic programming model (Table 1). A finite horizon framework is used because MCEs usually only last for a short time; hours, days or weeks. Also, even though the real world system evolves continuously in time, a technique known as uniformization is often applied to continuous-time stochastic dynamic programming models to create equivalent discrete time formulations that can be solved using standard techniques, viz. policy iteration, value iteration, or backward recursion. Servers arrive according to a stochastic process and are assigned to a queue by the controller. Similarly, customer arrivals are also based on a stochastic process. Customers are given a priority through triage upon arrival and are then routed to the appropriate queue. There are two types of servers $i \in \{1, 2\}$ and three classes of customers $j \in \{1, 2, 3\}$. Class 1 customers are routed to Queue 1 where they are served by Type 1 servers exclusively; Class 2 customers are only served by Type 2 servers at Queue 2. However, Class 3 customers require both Type 1 and Type 2 servers. Specifically, customers routed to the Class 3 customer queue (Queue 3) in triage cannot be served unless both a Type 1 server and a Type 2 server are available at that queue. Otherwise, Class 3 customers wait there until a server team becomes available. Put another way, let $z_{ik}$ be a binary variable that assumes the value 1 if Class j customers require Type i servers for processing, and zero if not. Then the service requirement $(z_{1j}, z_{2j})$ for each customer class j is (1, 0) for Class 1 customers, (0, 1) for Class 2 customers, and (1, 1) for Class 3 customers.

Table 1 Notations for stochastic dynamic programming model

4.1 Sequence of events in each period

We now explain the sequence of events that occurs during each period t of the finite horizon model, which is also illustrated in Fig. 2.

• 1. The state of the process, $(r_{it}, w_{jt})$, is observed. The state variable $r_{it}$ represents the total number of Type i servers in the system at the beginning of period t, and $w_{jt}$ is the number of Class j customers at Queue j prior to the arrival of any new customers during period t.

• 2. The controller decides how many Type i servers to assign to each Queue j. These are the control variables denoted $x_{ijt}$. In particular, $x_{ijt}$ is the number of Type i servers assigned to Queue j at epoch t which includes (i) the assignment of new servers who arrived during the previous period and (ii) the reassignment of servers currently working at one of the three customer queues. The control variables must chosen according to some restrictions, namely: only Type i servers can be assigned to Queue i for $i=1$ and 2; however, both Type 1 and Type 2 servers can be assigned to Queue 3. Also, the total number of servers assigned during the current period cannot exceed the total number of servers in the system at that time.

• 3. Customer arrivals occur throughout the period up to this point. The number of Class j customers who arrive during period t is a random variable $D_{jt}$, and its realization $\xi _{jt}$ is observed at this juncture, before the period ends.

• 4. Customers are served at all queues that have the capacity to do so, and served customers exit the system. For those customers who are not served, they remain in the system and incur holding costs. Since the event sequence is such that the actual number of customer arrivals in each period is observed prior to the initiation of the customer service process, it is possible for customers who arrive in period t to be served in period t provided enough capacity exists.

• 5. Servers arrive throughout the period up to this point. The number of servers of Type i who arrive during period t is a random variable $A_{it}$, and its realization $a_{it}$ is observed at this time. Note that servers who arrive in period t are not eligible for assignment during that period. As shown in Fig. 2, the server assignment decision takes place prior to observing the number of servers who arrive in the current period. From a practical standpoint, this can be interpreted to mean that each server is briefed during his or her arrival period and then assigned during a later period.

• 6. All state variables are updated based on the selected server assignments and realizations of random variables.

Fig. 2

Sequence of events during each period t of the finite horizon

4.2 Model assumptions

The sequence of events enumerated in Sect. 4.1 and stochastic dynamic programming model presented later in Sect. 4.3 are based on the following assumptions:

• A.1 There is no cost, time-lag, nor any other penalty associated with reassigning servers from one queue to another. Thus servers can begin serving customers immediately upon assignment or reassignment. Furthermore, the only costs considered in this study are the weighted holding costs for unserved customers at the end of each period.

• A.2 Just as the assignment of presently unassigned servers occurs at the beginning of a period, so too do server reassignments. This means that server reassignments cannot take place in the middle of a period, even if a server finishes serving customers at the queue he or she is assigned to and there are customers waiting for service at other queues. This is indeed a limitation of our model resulting from the discrete-time formulation. However, this limitation can be overcome from a practical perspective by restricting to length of each period to say, 5 or 10 min, and considering planning horizons with large values of T. That way, server reassignments can take place frequently if necessary.

• A.3 Service rates are deterministic; specifically, each individual server (or server team at Queue 3) has the ability to serve $\mu _j$ customers that belong to Class j during a single period. We introduce this assumption to make the process of computing the number of unserved customers at the end of each period straightforward within the context of our discrete-time formulation. This is also a limitation of our model, particularly given that nearly all queuing models in the research literature consider random service times. On the other hand, in addition to random customer arrivals for each customer class, our model also includes random server arrivals, which to our knowledge has only been addressed in two other papers.

• A.4 Service interruptions are allowed, but only at the end of a period. Consider, for example, a service rate of $\mu _j = 0.5$ customers per period, meaning that it takes two periods to serve a Class j customer. If a server spends the first of the two periods needed to complete the service process for a Class j customer, that server is still eligible for reassignment at the end of the period even though the customer has one service period remaining.

• A.5 Servers do not abandon the system until after the last decision epoch T. This may or may not be the case in practice depending on the length of the MCE; if it lasts, say, 12 h or so, servers will likely remain until the end. Otherwise for MCEs that span multiple days or longer, server vacations are inevitable. From this perspective, our model is appropriate for MCEs that go on for no more than 24 h.

An important implication of the above assumptions is that it is not necessary to distinguish between server assignments and reassignments. As such, there is no need to track the precise location of each server prior to an assignment decision; it is only necessary to know the total number of servers of each type present in the system and the number of customers at each queue. This is an important property from a modeling perspective because the number of states and actions would otherwise increase exponentially. If any of assumptions A.1, A.2, or A.4 were relaxed, then the location and status of each server would need monitoring and the corresponding state variables would be $r_{ijt}$, the number of Type i servers already assigned to Queue j when period t begins. Moreover, the control variables would have to include origin and destination queues and be defined as $x_{ijkt}$: the number of Type i servers assigned from Queue j to Queue k at epoch t. These additional variables represent increases in the dimensions of the state and action spaces and would make our problem significantly more difficult from a computational perspective.

4.3 Single period cost and optimality equations

The cost considered in this study is a holding cost that is linearly proportional to the expected number of customers remaining in the system at the end of each period. Let $h_j$ denote the holding cost per period for each unserved customer Type $j \in \{1,2,3\}$, where $h_1< h_2 < h_3$ is assumed. The interpretation is that Class 1 customers are the least critical, Class 3 customers are the most critical, and the Class 2 customers are in between these two extremes. Now let $L_{jt}$ be the expected number of unserved customers of Type j at the end of period t. Then the one period cost associated with Queue j is simply $h_{j}L_{jt}$, and the total cost we wish to minimize is

$$\begin{aligned} \sum _{t}\sum _{j}h_{j}L_{jt}. \end{aligned}$$

(1)

To derive an expression for $L_{jt}$, let $\mu _j$ denote the number of Class j customers that each server (or team of servers) can process in a single period (i.e., $\mu _j$ is the service rate for each server or server team at Queue j). Then the overall service rate of Queue j during period t is $\mu _j$ multiplied by the number of servers (or server teams) assigned to that queue. For queues $j=1$ and 2, this amounts to $\mu _j x_{jjt}$ since only Type j servers can serve class j customers (when $j = 1, 2$). However for Queue 3, the service rate is slightly different because of the stipulation that each Class 3 customer requires both a Type 1 server and Type 2 server. Specifically, the collective service rate at Queue 3 is based on the minimum of the number of Type 1 and Type 2 servers assigned there. Thus for $j=3$, the collective service rate is

$$\begin{aligned} \displaystyle \mu _3\min _{i \in \{1,2\}} x_{ijt}. \end{aligned}$$

For all queues $j=1,2,3$, the number customers served in a period is the minimum of the collective service rate of the queue and the number of customers at that queue, including those arriving during the period. So for $j=1,2$, $L_{jt} = \mathsf {E}\big [\min \{w_{jt} + D_{jt},~\mu _j x_{jjt}\}\big ]$, which is equivalent to

$$\begin{aligned} L_{jt} = \mathsf {E}\Big [w_{jt}+D_{jt} - \mu _j x_{jjt}.\Big ]^+ \end{aligned}$$

(2)

Similarly for $j=3$, the expected number of unserved customers at the end of a single period t is

$$\begin{aligned} L_{jt} = \mathsf {E}\Big [w_{jt}+D_{jt} - \mu _j \min _{i \in \{1,2\}}x_{ijt}\Big ]^+. \end{aligned}$$

(3)

The single period expected cost is the sum of the Eqs. (2) and (3) over all three queues:

$$\begin{aligned} C(\mathbf {r,w,x,D})= & {} \sum _{k=1}^{3} h_{k}L_{kt} \nonumber \\= & {} \sum _{k=1}^2 \mathsf {E}\Big [w_{jt}+D_{jt} - \mu _j x_{jjt}\Big ]^+ + \mathsf {E}\Big [w_{3t}+D_{3t} - \mu _3 \min _{i \in \{1,2\}}x_{i3t}\Big ]^+. \end{aligned}$$

(4)

The optimality equations take the standard form for $t = 1, \dots , T-1$:

$$\begin{aligned} V_t(\mathbf {r}_t, \mathbf {w}_t) = \min _{\mathbf {x}_t \in \chi (\mathbf {x}, \mathbf {r})}C(\mathbf {r_t,w_t,x_t,D_t}) + \mathsf {E}\Big [V_{t+1}(\mathbf {r}_{t+1}, \mathbf {W}_{t+1})\Big ]. \end{aligned}$$

(5)

Period $t=T$ includes the last decision epoch; thus the optimality equation in that period is the single period expected cost given by Eq. (4) with no future costs or decisions; i.e., $V_t(\mathbf {r}_T, \mathbf {w}_T) = C(\mathbf {r_T,w_T,x_T,D_T})$.

We seek a sequence of decisions $(\mathbf {x}_1^*, \mathbf {x}_2^*, \dots , \mathbf {x}_T^*)$ that satisfy the optimality Eq. (5), which gives the optimal assignment of servers to queues such that the expected weighted holding cost over a finite horizon is minimized. The control variables $\mathbf {x}_{t}$ that appear in Eq. (5) with components $x_{ijt}$ must be chosen such that the number of Type i servers assigned at epoch t does not exceed the existing number of Type i servers in the system at that time. In addition, the assignment of Type 1 servers to Queue 2, and Type 2 servers to Queue 1, are not permissable. Thus $x_{12t} = x_{21t} = 0$ for all t. Lastly, since servers can only work in pairs at Queue 3, there is nothing to be gained from an imbalance in the number of servers of each type. Hence the number of Type 1 servers and number of Type 2 servers at Queue 3 should always be equal, or symbolically, $x_{13t} = x_{23t}$ for all t. These restrictions constitute the action space for the stochastic dynamic programming model can be expressed as

$$\begin{aligned} \chi (\mathbf {x}_t, \mathbf {r}_t) = \bigg \{(\mathbf {x}_t, \mathbf {r}_t): \sum _{k=1}^{3}x_{ijt} \le r_{it};~~x_{12t} = x_{21t} = 0;~~x_{13t} = x_{23t}\bigg \}, \end{aligned}$$

(6)

where $i \in \{1,2\};~j \in \{1,2,3\}$, and $t \in \{1, \dots , T\}$.

The relationship between the state variables $(\mathbf {r}_t, \mathbf {w}_t)$ and $(\mathbf {r}_{t+1}, \mathbf {W}_{t+1})$ in Eq. (5) are specified by a transition function $\mathbf {f}: (\mathbf {r}_t, \mathbf {w}_t) \mapsto (\mathbf {r}_{t+1}, \mathbf {W}_{t+1})$, where the components of $\mathbf {r}_{t+1}$ and $\mathbf {W}_{t+1}$ for $t = 1, \dots , T-1$ are

$$\begin{aligned} R_{i,t+1}= & {} r_{it} + A_{it}~~i = 1,2; \end{aligned}$$

(7)

$$\begin{aligned} W_{j,t+1}= & {} \left[ w_{jt}+D_{jt} - \mu _j x_{jjt}\right] ^+,\;\;\qquad \qquad j = 1,2; \end{aligned}$$

(8)

$$\begin{aligned} W_{j,t+1}= & {} \left[ w_{jt}+D_{jt} - \mu _{j}\min _{i \in \{1,2\}}x_{ijt}\right] ^+,\quad j = 3. \end{aligned}$$

(9)

Equation (7) increments the total number of servers in the system by the number of servers who arrived during the previous period. Equations (8) and (9) reflect the number of customers in the system at the beginning of the next period, which is essentially the same as $L_{jt}$ in Eqs. (2) and (3), but without the holding cost and expectation operator. Finally, note that the upper case convention for $R_{i,t+1}$ and $W_{j,t+1}$ is deliberate to indicate that both are random variables. $R_{i,t+1}$ is a function of the random variable $A_{it}$ and $W_{j,t+1}$ is a function of the random variable $D_{jt}$.

In order to express the transitions (7) through (9) in vector form as they appear in the optimality Eqs. (5), we introduce a vector function $\mathbf {G}_{jt}$. Specifically, $\mathbf {G}_{jt}$ allows us to combine Eqs. (8) and (9) into a single equation. Define $\varvec{\mu } = (\varvec{\mu _1, \mu _2, \mu _3})$. Then we define $\mathbf {G}_{jt}$ as follows:

$$\begin{aligned} \mathbf {G}_{jt}= & {} {\left\{ \begin{array}{ll} \displaystyle x_{jjt}, &{}\quad \text {for}~ j = 1, 2\\ \displaystyle \min _{i \in \{1,2\}} x_{ijt}, &{}\quad \text {for}~ k = 3. \end{array}\right. } \end{aligned}$$

The vector form of the transition equations are

$$\begin{aligned} \mathbf {R}_{t+1}= & {} \mathbf {r}_{t} + \mathbf {A}_{t} \end{aligned}$$

(10)

$$\begin{aligned} \mathbf {W}_{t+1}= & {} \big [\mathbf {w}_{t} + \mathbf {D}_{t} - \varvec{\mu }^{\intercal }\mathbf {G}_t\big ]^+. \end{aligned}$$

(11)

Note the slight abuse of notation in Eq. (11). Here, $\mathsf {T}$ is the transpose of the vector $\varvec{\mu }$ whereas elsewhere in the paper, T refers to the number of decision epochs. Also, the superscript “+” in Eq. (11) is interpreted here, and here only, to mean $\mathbf {z}^+ = \max \{z_i, 0\}$ for each component $z_i$ of the vector $\mathbf {z}$. Finally, $\mathbf {G}_t \equiv (\mathbf {G}_{1t},\mathbf {G}_{2t},\mathbf {G}_{3t})$ in Eq. (11).

5 Methodology

Unfortunately, the stochastic dynamic programming model presented in the previous section is intractable from a computational standpoint, even for extremely small problem instances. This is a direct consequence dynamic programming’s infamous curse of dimensionality, which refers to exponential growth in the state space as its dimension increases. As such, a computational study that examines properties of the optimal policy is not possible. Instead, we conduct a simulation study in which the performance of heuristic policies based on the well known $c \mu$ rule are analyzed under a variety of experimental conditions.

5.1 Illustrating the curse of dimensionality

Recall that the state variables for our problem are $(\mathbf {r},\mathbf {w})$, where $\mathbf {r} = (r_{1}, r_{2})$ represents the number of servers of each type in the system at the beginning of a period, and $\mathbf {w} = (w_{1}, w_{2},w_{3})$ is the number of customers at each queue, also at the beginning of a period. So the state space as five dimensions. Now let ${\varOmega }_s$ denote the support of a discrete random variable S, and |S| its cardinality. Then the number of possible states associated with a single period t is at most³

$$\begin{aligned} \Big (|{\varOmega }_{A_1}| \cdot |{\varOmega }_{A_2}|\Big )^{t} \times \Big (|{\varOmega }_{D_1}| \cdot |{\varOmega }_{D_2}| \cdot |{\varOmega }_{D_3}|\Big )^t. \end{aligned}$$

(12)

To see this, consider that the state vector $\mathbf {r}$ depends on the random vector $\mathbf {A} = (A_1,A_2)$ and control vector $\mathbf {x} = (x_{11},x_{22},x_{13},x_{23})$, where the former denotes the number of servers of each type that arrive during s single period, and the latter represents the assignment/reassignment of servers to queues. Since servers never leave the system, the number of possible combinations of Type 1 and Type 2 servers in the system at the beginning of each period $t = 1, \dots , T$ is $\Big (|{\varOmega }_{A_1}| \cdot |{\varOmega }_{A_2}|\Big )^{t}$. Similarly, the state vector $\mathbf {w}$ depends on the random vector $\mathbf {D} = (D_1,D_2,D_3)$ and the control vector $\mathbf {x}$, where $\mathbf {D}$ is the number of customer arrivals from each class in a period. Since each Queue j consists of Class j customers exclusively, the number of customers across all queues $j=1,2,3$ can occur in $(|{\varOmega }_{D_1}| \cdot |{\varOmega }_{D_2}| \cdot |{\varOmega }_{D_3}|)^t$ ways. Therefore, the number of possible states $(\mathbf {r}_t, \mathbf {w}_t)$ in a single period t is given by Eq. (12). As an example, consider a scenario where the maximum arrivals in any period are 3 nurses, 1 doctor, 10 patients with minor injuries, 5 patients with serious injuries, and 2 patients with critical injuries. Applying Eq. (12), the number of possible states in period t is

$$\begin{aligned} (4 \times 2)^{t} \times (11 \times 6 \times 3)^{t} = (1,568)^{t}. \end{aligned}$$

(13)

If we interpret t as a 1-h time block and consider an 8-h planning horizon, the number of states (just in period $t=8$) would be $(1,568)^8 = 3.65 \times 10^{25}$.

In addition, we attempted to solve an unrealistically small problem instance to optimality in order to get a sense computation time requirements. For this smaller problem instance, we considered only $t=2$ periods and allowed maximum arrivals per period of 2 nurses, 1 doctor, 3 Type 1 patients, 2 Type 2 patients, and 1 Type 3 patient. According to Eq. (12), there could be up to $(3 \times 2 \times 4 \times 3 \times 2)^2 = 20{,}736$ states in period 2. This problem instance was executed on a computer with 3.6 GHz processing speed and 64GB of RAM. The computer code was written in the Python programming language and included multi-threading for parallel processing. The computation time for this small example was over 1 h.

5.2 Heuristic policies

We examine the performance of heuristic policies based on the well-known $c \mu$ rule. Within the context of a generic discrete-time parallel queuing system, the $c \mu$ rule can be described as follows: if $c_j$ is the unit holding cost for each customer at Queue j not served by the end of a period, and $\mu _j$ the average rate at which an individual server can process Type j customers, then the $c \mu$ rule prioritizes the queue with the largest value of $c_j \mu _j$. More generally, the $c \mu$ rule clears the highest priority queue if enough servers are available, and only assigns servers to lower priority queues when the highest priority queue is empty. The $c \mu$ rule is an optimal server assignment policy for various queuing systems, such as the “N-network”, which is somewhat similar to the queuing system addressed in this paper. The N-network consists of two types of servers and two classes of customers. One server type is fully flexible and can process both customer classes; the other is dedicated and can serve only one of the two customer types. Bell and Williams (2001) and Saghafian et al. (2011) show that the $c \mu$ rule is an optimal server assignment policy for the N-network if certain conditions hold. Given the optimality of the $c \mu$ rule in a related queuing system (the N-network), we expect that it would perform well within the context of the MCE queuing control problem introduced in Sect. 2 of this paper. We test this theory by simulating the MCE queuing network shown in Fig. 1 using the following variations of the $c \mu$ rule as server assignment policies.

Clear Queue 3 rule (CQ3) This policy always prioritizes Queue 3, logic being that critical patients endure the highest degree of suffering and should never be kept waiting if at all possible. The CQ3 assignment policy is a special case of the $c \mu$ rule with $c_j=1$ for each queue j, in which case Queue 3 is prioritized because the Class 3 customers there have the highest unit holding cost as mentioned at the beginning of Sect. 4.3. In essence, the CQ3 rule attempts to clear Queue 3 and will assign servers to queues 1 or 2 only if (i) Queue 3 is empty at the beginning of a period, (ii) not all available servers are needed to clear Queue 3’s current customers, or (iii) the system has more of one server type than the other. To illustrate (iii), suppose the number of Class 3 customers is 20 and there are 12 nurses and 8 doctors in the system. Then 8 doctor/nurse teams can be sent to Queue 3, which leaves 4 nurses to be assigned to the lower priority Queue 1. It is important to note that the CQ3 rule only tries to clear the customers who are present at the beginning of a period; customers who arrive at random during the period are not taken into account. This is perhaps a limitation of the CQ3 rule which we attempt to improve upon with the next heuristic.

Clear Queue 3 with Buffer rule (CQ3B) This policy extends the CQ3 rule by assigning extra servers to Queue 3 in anticipation of critical patients who might arrive later in the period. These extra servers form a buffer of excess capacity to hedge against the uncertainty of additional critical patient arrivals. The size of the buffer, denoted b, is the number of additional server teams assigned to Queue 3 beyond the total number of servers teams needed there. That is, $\displaystyle b = \min _{i}(x_{i3t} - w_{3t})^+$. We only consider b a buffer if it is at the expense of serving customers at Queue 1 or Queue 2. Otherwise, CQ3B is equivalent to CQ3 because CQ3 assigns excess servers to Queue 3 by default. Also, note that b does not change with t; for each individual problem instance solved later in this study, the buffer size will remain the same throughout the finite horizon. Lastly, we will use the CQ3B rule to find the best buffer size and examine how it changes under a variety of experimental scenarios. This will be done by enumerating all buffer sizes between zero and the minimum of $w_{3t}$ and $N_t$, the latter of which is the total number of server teams in the system at the beginning of each period t.

Clear Queue j rule (CQj) As mentioned previously, the CQ3 policy described above is a special case of the $c \mu$ rule with $c_j=1$ for all queues j and Queue 3 is prioritized. Similarly, policy CQj prioritizes one of the queues $j \not =3$, that is, either Queue 1 or Queue 2 has the highest priority under this policy. The reason for the distinction is that the algorithms for these two policies are quite different, which is evident from their pseudocodes shown in the “Appendix”.

Clear Queue j with Buffer rule (CQjB) This rule adds a buffer of size b to the CQj rule in exactly the same way that the CQ3B policy adds a buffer to the CQ3 rule. In fact, b is calculated the same way (see the above commentary on the CQ3B rule for the equation), and we will also find the best buffer size by enumerating different values for b.

These four rules can be thought of as four different policies, or alternatively, as distinct pieces of the $c \mu$ rule. To see this, consider (again) that the CQ3 and CQj rule are implementations of the $c \mu$ rule when Queue 3 and Queue $j \not =3$, respectively, are prioritized. So if the largest $c_j \mu _j$ comes from Queue 3, the $c \mu$ rule is the CQ3 rule. Otherwise if Queue 1 or Queue 2 yields the largest $c_j \mu _j$ value, then rule CQj must be implemented in order to apply the $c \mu$ rule. In either case, both are the $c \mu$ rule. The relationship between the CQ3 and CQ3B rules, and the CQj and CQjB rules are even more obvious. In particular, the CQ3 and CQj policies are special cases of the CQ3B and CQjB policies, respectively, with the buffer size b set to zero. The general structure of the algorithm for applying the $c \mu$ rule to the MCE queuing control problem is shown as Algorithm 1, with more details described in the “Appendix”. The steps for finding the best buffer size $b^*$ within this context is also shown in the “Appendix”.

5.3 Research questions

Since the $c \mu$ rules with buffer capacity (CQ3B and CQjB) include the standard $c \mu$ rules (CQ3 and CQj) as special cases, the former policies will obviously outperform the latter. So instead of designing a computational study to identify which heuristic policies perform best under different experimental conditions, our simulation analysis will be guided by questions related to the size of the buffer. Specifically, we look for insights into the following research questions:

Question 1

Under which conditions is the buffer most and least beneficial?

As mentioned earlier, the $c \mu$ is an optimal policy for several different queuing control problems, including the N-network which, similar to this study, concerns the assignment of heterogeneous servers in a priority parallel queuing system. Up to this point, we have subtlety deduced that the $c \mu$ rule is not optimal for the MCE queuing network addressed in this paper; we think it can be improved upon by adding a buffer of additional server capacity at higher priority queues to anticipate the random arrival of higher priority customers. However, this may or may not be the case; if the $c \mu$ rule is an optimal policy for our MCE queuing control problem, then the buffer would never be beneficial. If on the other hand our findings reveal at least one scenario in which a buffer leads to a lower expected cost, we can conclude that the $c \mu$ rule is not an optimal server assignment policy within the context of MCE queuing network considered in this study.

Question 2

What effects do changes in model parameters have on buffer size?

Sensitivity analysis will be used to explore what happens to the best buffer size $b^*$ as model parameters change. Although a limitation of the sensitivity analysis approach is that the effect of each parameter is examined one at a time, our hope is that the results lead to practical insights. On the other hand, the previous research questions lends itself to a response that requires an experimental design where the effects of changing multiple parameters simultaneously can be assessed.

Question 3

Is the difference in expected cost between the heuristic policies with the buffer and those without one more pronounced as $b^*$ increases?

$b^*$ represents the pseudo-optimal buffer size resulting from the process of enumerating all feasible buffer sizes for the CQ3B and CQjB policies. We refer to $b^*$ as “pseudo-optimal” because even though all possible buffer sizes are considered, the entire analysis takes places in a simulation environment; thus no rigorous claim of optimality can be made. Nonetheless, intuition suggests that the heuristic policies with buffer are more different than those that don’t have a buffer when the buffer size that serves as a basis for comparison is large. Therefore we would expect the answer to Question 3 to be “yes”.

5.4 Simulation analysis

To address the research questions posed in Sect. 5.3, we randomly generate sample paths using Monte Carlo simulation. A sample path through the network over a finite horizon of length T is a sequence of random variates $(\tilde{a}_{1t},\tilde{a}_{2t},\tilde{\xi }_{1t},\tilde{\xi }_{2t},\tilde{\xi }_{3t})$ for $t = 1, \dots , T$ sampled from the distributions of the random variables

$$\begin{aligned} (A_{1t},A_{2t},D_{1t},D_{2t},D_{3t}). \end{aligned}$$

For the purposes of this study, it is assumed that the stochastic process

$$\begin{aligned} (A_{1t},A_{2t},D_{1t},D_{2t},D_{3t}) \end{aligned}$$

is homogenous and stationary, thus independent of t. Consequently, the random variates generated each period are drawn from the same distributions. The performance metrics of interest are (i) the total expected weighted holding cost over the finite horizon and (ii) the best buffer size $b^*$. In order to derive an estimate of the total expected holding cost, let $\tilde{c}_{tk}(\cdot )$ denote the one period cost in period t associated with the sample path from the $k^{th}$ replication of a simulation run, where $k \in \{1, \dots , \rho \}$ and $\rho$ is the total number of simulated replications. Also let $\mathbf {x}^{\pi }$ represent the assignment of servers to queues based on an assignment policy $\pi : (\mathbf {r,w}) \mapsto \mathbf {x}$, where $\pi$ is one of the heuristic policies from Sect. 5.2. Then similar to the single period expected cost given by Eq. (4), we have

$$\begin{aligned} \tilde{c}_{tk}\left( \mathbf {r}_{tk}, \mathbf {w}_{tk}, \tilde{\varvec{\xi }}_{tk},\tilde{\mathbf {a}}_{tk}, \mathbf {x}_t^{\pi }\right)&= \sum _{j=1}^{2}h_j\left( w_{jtk} + \tilde{\xi }_{jtk}-\mu _jx_{jjtk}^{\pi }\right) ^+ \end{aligned}$$

(14)

$$\begin{aligned}&\quad + h_{3}\left( w_{3tk}+\tilde{\xi }_{3tk} - \mu _{3}\min _{i\in \{1,2\}}x_{ijtk}^{\pi }\right) ^+, \end{aligned}$$

(15)

and the total cost of one replication k from one sample path is

$$\begin{aligned} \tilde{tc}_k = \sum _{t=1}^T \tilde{c}_{tk}\left( \mathbf {r}_{tk}, \mathbf {w}_{tk}, \tilde{\varvec{\xi }}_{tk},\tilde{\mathbf {a}}_{tk}, \mathbf {x}_t^{\pi }\right) . \end{aligned}$$

(16)

To go from one period t to the next in Eq. (16), the transition equations are very similar to (7), (8), and (9). For $t=1, \dots , T$ and $k = 1, \dots , \rho$, they are

$$\begin{aligned} r_{i,t+1,k}&= r_{itk} + \tilde{a}_{itk}\quad i = 1,2; \end{aligned}$$

(17)

$$\begin{aligned} w_{j,t+1,k}&= \left[ w_{jtk}+\tilde{\xi }_{jtk} - \mu _j x_{jjt}^\pi \right] ^+,\qquad \;\;\; \qquad j = 1,2; \end{aligned}$$

(18)

$$\begin{aligned} w_{j,t+1,k}&=\left[ w_{jtk}+\tilde{\xi }_{jtk} - \mu _{j}\min _{i \in \{1,2\}}x_{ijtk}^{\pi }\right] ^+,\quad j = 3. \end{aligned}$$

(19)

An estimate of the total expected cost, which is one of our metrics of interest, is then

$$\begin{aligned} \tilde{TC} = \frac{1}{\rho } \sum _{k=1}^{\rho }\tilde{tc}_{k}. \end{aligned}$$

(20)

The expected cost will be estimated using Eq. (20) over a range of admissible buffer sizes, and $b^*$ is the buffer size that yields the lowest estimated average cost within this range.

All of the problem instances described later in Sects. 5.6 and 5.5 are based on $\rho = 1000$ replications and $T=32$ decision periods. The 1000 replications will achieve sufficient statistical significance for the results, and $T=32$ represents 15 min intervals over the course of a MCE that lasts 8 h. All numerical examples also assume a Poisson distribution for each of the random variables $A_{1t}, A_{2t}, D_{1t}, D_{2t}$, and $D_{3t}$ in each period $t=1, \dots , T$, where the rate of each Poisson variable is varied according to the experimental design and sensitivity analyses defined in Sects. 5.5 and 5.6, respectively.

5.5 Experimental design

The above Monte Carlo framework for estimating expected cost and the pseudo-optimal buffer size will be used to generate problem instances according to the experimental design shown in Table 2, then solved using the heuristic policies described in Sect. 5.2. The scenarios in Table 2 constitute a series of experiments in which the effects of changing multiple problem parameters at once can be examined, and are based on a modified $2^k$ factorial design. There are four parameters; three of them to be examined at two levels, and the other at three. Thus the number of problem instances is $(2^3)(3) = 24$. At Level 1, we set values within each parameter class equal to each other. Parameter values are taken to be different at Level 2 and are functions of the base values shown in Table 2. The reason for a third level of customer arrivals is that we want to consider scenarios where customer arrival rates differ from each other in two ways, namely $\lambda _1> \lambda _2 > \lambda _3$ and $\lambda _1< \lambda _2 < \lambda _3$. The first inequality represents the scenario in which the majority of customers have minor injuries, while the second inequality means that most customers have critical injuries. We believe that both scenarios are possible depending on the nature of the mass casualty event, and that each will have different effects on the system’s performance metrics. So the three levels of customer arrival rates considered in the experimental design are $\lambda _1 = \lambda _2 = \lambda _3$, $\lambda _1> \lambda _2 > \lambda _3$, and $\lambda _1< \lambda _2 < \lambda _3$.

Table 2 Experimental design for simulation study

5.6 Sensitivity analysis

Additional problem instances will be generated in order to conduct sensitivity analysis around model parameters. These parameters include (i) server arrival rates, (ii) customer arrival rates, (iii) customer service rates, and (iv) customer holding costs. Since there are two categories of servers and three classes of customers, each of the four above-mentioned parameters actually represent classes of parameters. So not only should the effects of varying entire parameter classes be taken into account, but changes within each parameter class should also be considered. For example, increasing the overall arrival rate of servers may effect performance metrics in a certain way, but increasing the arrival rate of one type of server but not the other is likely to have a different effect.

Table 3 Sensitivity analysis experiments where most patients have minor injuries

Table 4 Sensitivity analysis experiments where most patients have critical injuries

The range of values for each parameter considered in this study for the purpose of sensitivity analysis is shown in Tables 3 and 4. For the 11 experiments in Table 3, the customer arrivals rates satisfy $\lambda _1> \lambda _2 > \lambda _3$, which means that are most are patients with minor injuries. In Table 4, patients with critical injuries are the most prevalent and the arrival rates are such that $\lambda _1< \lambda _2 < \lambda _3$. We believe that both scenarios are possible depending on the nature of the mass casualty event, and that each will have different effects on the system’s performance metrics.

The 22 sensitivity analysis experiments will be carried out by varying each of the parameters shown in Tables 3 and 4 one by one within their respective ranges, while holding the other parameters to their base values. In Experiment 1 for example, $\gamma _2$ is varied from 1 to 10, and the other 10 parameters are fixed at values shown in the “Base” column of Table 3. Notice how both $\gamma _1$ and $\gamma _2$ vary in Experiment 1 since $\gamma _1$ is defined as a function of $\gamma _2$. Generally, experiments 1, 3, 6, and 9 (Table 3) and 12, 14, 17, and 20 (Table 4) reflect changes in parameter classes. For example, Experiment 1 captures the effects of varying the overall server arrival rate since both $\gamma _1$ and $\gamma _2$ are varied. The other 14 experiments represent changes within each parameter class.

6 Results

In this section, findings with regard to the research questions posed in Sect. 5.3 are provided.

Question 1

Under which conditions is the buffer most and least beneficial?

All of the possible “conditions” considered in this study are defined by the experimental design shown in Table 2 of Sect. 5.5, and the results pertaining to these experiments are presented in Table 5. The details of the simulation environment in which the values in Table 5 are obtained, including how the average costs are computed, are given in Sect. 5.4. Before discussing the results, we first explain the meaning of each column heading in Table 5. The first column heading is the experiment number, which ranges from 1 to 24. The other column headings are

$\varvec{\gamma } = (\gamma _1, \gamma _2)$::

Arrival rates for Type 1 and Type 2 servers, with two levels each considered.

$\varvec{\lambda } = (\lambda _1, \lambda _2, \lambda _3)$::

Arrival rates for class 1, 2, and 3 customers, each at three levels.

$\varvec{\mu } = (\mu _1, \mu _2, \mu _3)$::

Service rates for class 1, 2, and 3 customers, each at two levels.

$\mathbf {h} = (h_1,h_2,h_3)$::

Holding cost for class 1, 2, and 3 customers, each at two levels.

Priority Sequence::

is a list of the queues from the highest priority to the lowest. For example, the sequence 3–2–1 means that Queue 3 has the highest priority, Queue 2 is next, and Queue 1 has the lowest priority. Each queue’s priority is determined by the product of h and $\mu$—the queue with the largest value of $h \mu$ is the highest priority, and the queue with the smallest value is the lowest. For several of the experiments, the product of h and $\mu$ is the same for all three queues, which means that all sequences have the same priority. This is indicated by “All” in the Priority Sequence column of Table 5, where the sequence in parentheses gives the lowest average cost for that experiment. There are also several experiments in which two of the three queues (Queue 1 and Queue 3) tie for having the highest priority because they have equal $h \mu$ values that are larger than that of Queue 2. For each such case, the priority sequence is either 3–2–1 or 1–3–2. One final comment regarding the Priority Sequence column before moving on to explaining the subsequent columns of Table 5: the sequences 3–2–1 and 3–1–2 are equivalent. In both, all that matters is that Queue 3 has the highest priority relative to queues 1 and 2, and is assigned all available servers that can collectively clear the current demand at Queue 3 as soon as possible. The remaining servers are assigned to queues 1 and 2, but it doesn’t matter which of the two have the higher priority because all Type 1 servers not assigned to Queue 3 can only be assigned to Queue 1, and all Type 2 servers not assigned to Queue 3 can only go to Queue 2.

$b^*$::

is the best buffer size. The $b^*$ in Column 7 is the best buffer size associated with the $c \mu$ rule, and Column 11 is the best buffer size based on the CQ3B rule. Similarly, the values in columns 8 through 10 pertain to the $c \mu$ rule, and those in columns 12 through 14 to the CQ3B rule.

$b=0$:

is average cost of the heuristic policies ($c \mu$ rule in Column 8 and CQ3B rule in Column 12) with buffer $b=0$.

$b= b^*$:

is the average cost of the above-mentioned heuristic policies using a buffer of size $b^*$.

$\%{\varDelta }$ Cost::

is percentage increase in the average cost from using $b=0$ instead of $b = b^*$.

$c \mu$ versus CQ3 $\% {\varDelta }$ at $b^*$::

This is the percentage increase in average cost when using the $c \mu$ rule instead of the CQ3B rule, both at their respective best buffer sizes $b^*$. A negative value indicates that the $c \mu$ rule produces an average cost that is lower than the average cost of the CQ3B policy; otherwise, the CQ3B policy is at least as good as the $c \mu$ policy.

Table 5 Experimental design results

The results derived from Table 5 that pertain to Question 1 also require the following preliminary discussion. The first point is that we tested two different implementations of the CQ3B rule. In one, servers are assigned to Queue 3 in an attempt to clear it. If enough servers are present in the system to clear Queue 3, then Queue 3 is cleared using the minimum number of servers required (plus the buffer b), and the rest are assigned to queues 1 and 2. If not, all Type 1/Type 2 server teams are assigned to Queue 3 with servers only being assigned to Queue 1 or Queue 2 if there is an imbalance in the number of servers of each type in the system. The other implementation, like the first, attempts to clear Queue 3. In fact, the two implementations are equivalent if there is more work at Queue 3 than there is capacity to complete it. However, the two implementations diverge when there is server excess capacity in the system. Instead of assigning all additional servers to queues 1 and 2, our alternative implementation of CQ3B assigns only enough servers to queues 1 and 2 that would clear each of those queues, while the others that can be combined to form teams are assigned to Queue 3. The latter implementation truly prioritizes Queue 3 because all excess capacity that can form complete server teams is assigned to Queue 3, whereas in the former implementation, excess capacity beyond the buffer size b is assigned to queues 1 and 2.

Our preliminary discussion regarding the results in Table 5 continues by pointing out that we tested each of the five possible priority sequences⁴ against each other at various buffer sizes in order to find the best sequence/buffer size combination. This approach led to the discovery that the CQ3B policy generally outperformed the $c \mu$ rule, in 21 of the 24 experimental conditions to be exact. This is the reason that the performance of both the $c \mu$ rule and the CQ3B policy are reported, and compared, in Table 5.

The following observations are derived from the results shown in Table 5, which are based on the experimental design presented in Sect. 5.5. Observation O.1 is perhaps one of this paper’s most important findings, while observations O.2, O.3, and O.4 address Question 1 directly.

• O.1 The$c \mu$rule is not an optimal policy. There are several experimental scenarios where the $c \mu$ and CQ3B rules do not coincide, and CQ3B outperforms $c \mu$ (experiments 3, 11, 15, 19, and 23). Consequently, the $c \mu$ rule cannot be an optimal policy. Furthermore, whenever Queue 3 is the highest priority (i.e., the $c \mu$ and CQ3B rules are one in the same), a nonzero buffer at Queue 3 improves upon the performance of the $c \mu$ rule, which also confirms that the $c \mu$ policy is not an optimal one.

• O.2 The buffer is most beneficial when Queue 3 is prioritized. Column 11 in Table 5 shows that $b^* > 0$ in 22 of the 24 experimental conditions, which suggests that the buffer adds value in the majority of cases.⁵ Moreover, the benefit is often quite substantial; it can be deduced from the next to last column of Table 5 that on average, the expected cost increases by just under 90% if no buffer is used compared to using the pseudo-optimal buffer. In some cases (experiments 4 and 16), the increase is well over 300%.

• O.3 The buffer is least beneficial when Queue 3 is not prioritized. Column 7 of Table 5 shows that the pseudo-optimal buffer sizes is $b^* = 0$ for all but one experiment where Queue 3 is not prioritized. This occurs when Queue 1 has the highest priority, i.e., when the Priority Sequence column of Table 5 is 1–2–3, or when 3–2–1 and 1–3–2 tie for having the highest priority.

• O.4 For the few scenarios in which the$c \mu$and CQ3B rules do not coincide and$c \mu$is the better policy, the best buffer size associated with the CQ3B policy is always$b^*=0$. Put another way, the $c \mu$ rule outperforms the CQ3B policy only when the best buffer size associated with the CQ3B policy is $b^*=0$ (experiments 5, 7, and 17). On average, CQ3B improves upon the $c \mu$ rule by 52.32%, which is the average of the percentages shown in the last column of Table 5 (note that this percentage difference includes the cases where the 3–2–1 priority sequence ties with 1–3–2 in terms of having the highest priority, in which case the percentage difference is based on comparing the average costs of 3–2–1 and 1–3–2). For all of the experiments where CQ3B is equivalent to or better than $c \mu$, the pseudo-optimal buffer at Queue 3 is nonzero. It is only the three experiments where CQ3B has $b^*=0$ that it is outperformed by $c \mu$.

• O.5 While one implementation of the CQ3B rule produces the best results overall, the other consistently leads to the highest average cost of all the heuristic rules examined in this study. Although the results pertaining to Observation O.5 are not presented in Table 5, we mentioned earlier in this section two implementations of the CQ3B rule. In both, servers are first assigned to Queue 3 in an attempt to clear the current demand there, with extra servers assigned in anticipation of future customers according to a given buffer size b. The two approaches differ in the way they assign servers to the two lower priority queues, Queue 1 and Queue 2. The first approach (Implementation 1 hereafter) disperses all remaining servers among queues 1 and 2. The other, which will be referred to as Implementation 2, assigns only enough servers to clear the current demands at queues 1 and 2 (if the number of servers in the system is sufficient to do so), and any additional servers beyond that who can form teams are assigned to Queue 3. Referring to Algorithm 2 in the “Appendix”, Implementation 1 of CQ3B is represented by lines 1 through 8 and 19 through 22, and Implementation 2 by lines 1 through 12. By default, Implementation 1 includes buffers at queues 1 and 2; so in addition to a buffer of size b at Queue 3, Implementation 1 of CQ3B also has a built in buffer at queues 1 and 2. This perhaps explains why CQ3B (Implementation 1) performs so well; there is potentially a buffer at all three queues that can handle random customer arrivals in each period. Implementation 2, on the other hand, essentially starves queues 1 and 2 and never processes customers during their arrival periods, which may explain its poor performance. In summary, the best policy is to assign servers in a way that clears Queue 3, with a few extras to anticipate the random arrival of additional Class 3 customers. The worst policy is to assign just enough capacity to clear queues 1 and 2, and assign the rest to Queue 3.

Question 2

What effects do changes in model parameters have on buffer size?

To address Question 2, we turn to the 22 sensitivity analysis experiments presented in Tables 3 and 4 of Sect. 5.6. Representative results from these experiments are displayed in Figs. 3, 4, 5, 6, 7, 8, 9 and 10, and the details of the simulation environment in which these results were generated are discussed in Sect. 5.4. It is important to note that our entire analysis is based on prioritizing Queue 3, i.e., the CQ3B priority rule. More specifically, all buffer sizes shown in Figs. 3, 4, 5, 6, 7, 8, 9 and 10 were evaluated within the context of only the CQ3B rule; no attempt was made to ascertain the best buffer size/priority rule combination resulting in the lowest average cost. Although this approach can be construed as a limitation of the analysis, our rationale for doing so is based on the CQ3B rule’s superior performance (compared to the $c \mu$ rule in general) in nearly all of the scenarios examined in the experimental design study whose results are shown in Table 5. Furthermore, the buffer is likely to affect different priority rules in different ways, and we already have evidence that suggests it does (see observations O.2 and O.3). So for consistency, the effect that each parameter has on the best buffer size should be examined within the context on a single priority rule, and it makes sense to do so using the most robust heuristic policy.

We also point out that Figs. 3, 4, 5, 6, 7, 8, 9 and 10 each show the range of buffer sizes for each parameter value that produce the lowest average costs that do not differ from one another statistically at the 95% confidence level. So for example, the best buffer sizes in Experiment 12 (Fig. 3) are $b^* = 5,6,7,8$, and 9 for $\gamma _2 = 1$ because the average costs associated with these buffer sizes are statistically equivalent at the 95% confidence level.

Fig. 3

Effect of overall server arrival rate on the best buffer size $b^*$

Fig. 4

Effect of Type 1 server arrival rate on the best buffer size, $b^*$

Fig. 5

Effect of Class 1 customer arrival rate on the best buffer size, $b^*$

Fig. 6

Effect of Class 2 customer arrival rate on the best buffer size, $b^*$

Fig. 7

Effect of overall customer arrival rate on the best buffer size, $b^*$

Fig. 8

Effect of service rate on the best buffer size, $b^*$

Fig. 9

Effect of holding costs on the best buffer size, $b^*$

Fig. 10

Effect of service rates on the best buffer size, $b^*$

Observations O.6 through O.9 below appeal to Figs. 3, 4, 5, 6, 7, 8, 9 and 10 to address Question 2, while Observation O.10 identifies an important property of the model.

• O.6 The best buffer size appears to be an increasing function of$\gamma _2, \lambda _3$, and$h_3$. The graph in Fig. 3 shows how $b^*$ changes as a function of $\gamma _2$ for experiments 1 and 12, where $\gamma _2$ represents the arrival rate of Type 2 servers into the system. For the purposes of this discussion, it is convenient to think of Type 2 servers as doctors and Type 1 servers as nurses. Thus it is reasonable to assume $\gamma _1 > \gamma _2$ because doctors are presumably more scarce than nurses. In order to preserve this relationship as $\gamma _2$ increases, experiments 1 and 12 also have $\gamma _1$ increase proportionately to $\gamma _2$. So increasing $\gamma _2$ effectively increases the total number of server arrivals during a finite horizon. From this perspective, Observation O.6 says that the buffer size increases as the number of servers in the system increases. This relationship agrees with intuition; since more servers are in the system, more servers are available for anticipating future customer arrivals as opposed to only processing existing customers.

  Fig. 7 shows how the best buffer size is affected by $\lambda _3$, the arrival rate of critically injured patients who are all routed to Queue 3. In Experiment 3, $\lambda _3< \lambda _2 < \lambda _1$ whereas for Experiment 16, $\lambda _3> \lambda _2 > \lambda _1$. In each case, varying $\lambda _3$ affects the system in different ways. Similar to $\gamma _1$ and $\gamma _2$ in experiments 1 and 12, changes in $\lambda _3$ represents changes to the overall customer arrival rate in Experiment 3 in order to preserve the inequality among the $\lambda$ values. On the other hand, increasing $\lambda _3$ in Experiment 16 only increases the arrival rate of one class of customers; the arrival rates of the other two customer classes remain constant throughout. Because of the differing effects of $\lambda _3$ in these two scenarios, it seems quite odd that $b^*$ is affected in almost the same way. However, a closer look suggests that the effects are somewhat different. Not only does the range of $b^*$ values increase in Experiment 3, it also decreases. Thus as $\lambda _3$ increases, the $b^*$ range expands in both directions. The reasons for this can be explained as follows. First, observe in lines 6, 7, and 8 of Algorithm 2 in the “Appendix” that the number of servers of each Type i assigned to Queue 3 initially is the minimum of the current demand at Queue 3 (plus the buffer b) and the number of server teams in the system. If the number of servers is small relative to the number of customers, then all available server teams are assigned to Queue 3 in which case the buffer b has no effect. In Experiment 16, on the other hand, the $b^*$ range expands in one direction. Since only the arrival rate of Class 3 customers increases, there are enough servers in the system available to satisfy demand at Queue 3 by increasing its buffer size because the pool of servers is not as occupied with customers at queues 1 and 2 as they are in Experiment 3. Finally, Fig. 9 shows a slight upward trend as $h_3$ increases, which also agrees with intuition. As $h_3$, the penalty for unsatisfied demand at Queue 3, increases while the penalties at queues 1 and 2 stay the same, more servers should be assigned to the Queue 3 buffer to avoid the increasingly higher holding costs there.

• O.7 The best buffer size appears to be a decreasing function of$\lambda _2, \mu _3$, and$h_2$. Figs. 6, 8 and 9 show respectively how $b^*$ is impacted by $\lambda _2$, the arrival rate of Class 2 customers; $\mu _3$, the service rate per server at Queue 3; and $h_3$, the holding cost per customer, per period at Queue 3. All demonstrate decreasing trends, with the trend being more pronounced when Class 3 customers are the most prevalent (experiments 15, 17, and 22). For each of $\lambda _2, \mu _3$, and $h_3$, the results are intuitive. In the case of $\lambda _2$, the best buffer size at Queue 3 decreases because more servers are assigned to Queue 2 to accommodate the increased arrival of Class 2 customers, which means fewer are needed for the steady arrival of Class 3 customers at Queue 3. On the other hand, the reason fewer servers (including the buffer) are needed at Queue 3 as $\mu _3$ increases is that the overall service rate at Queue 3 can be maintained with fewer servers since each individual server team there becomes increasingly productive. Lastly, the growing unit holding cost at Queue 2, $h_2$, means that more servers are required there at the expense of fewer servers at Queue 3.

• O.8 The best buffer size is not sensitive to changes in$\gamma _1, \lambda _1, h_1, \mu _1$, nor$\mu _2$. For $\gamma _1$ (Fig. 4) and $h_1$ (figure not shown), there is no effect; but for $\mu _1$ and $\mu _2$ (not shown), the effects are minimal. Recall that $\gamma _i$ represents the arrival rate of Type i servers, and that $\gamma _1 > \gamma _2$ is assumed in all experiments. Thus for experiments 2 and 13 (Fig. 4), $\gamma _1$ increases while $\gamma _2$ remains constant. Since assignments to Queue 3 are restricted to only Type 1 and Type 2 server pairs, server assignments to Queue 3, including the buffer, are only affected by $\min \{\gamma _1, \gamma _2\} = \gamma _2$. Hence $\gamma _1$ does not influence $b^*$ because $\gamma _1 > \gamma _2$. As for holding costs, experiments 9 and 20 (figure not shown, but is the same as Fig. 4 with $1 \le h_1 \le 5$ on the horizontal axis) examine the effects of $h_1$, the holding cost per customer per period at Queue 1. Since $h_1< h_2 < h_3$ is assumed, $h_2$ and $h_3$ increase as $h_1$ increases in order to maintain the inequality. Experiments 9 and 20 are designed such that the ratio among $h_1, h_2$, and $h_3$ remain the same, which perhaps explains why the $b^*$ range does not change as $h_1$ increases.

  The service rates at queues 1 and 2 effect $b^*$ differently, and less dramatically, than the service rate at Queue 3. Experiments 7 and 18 are designed to examine the effects of $\mu _2$, and Experiments 8 and 19 the effects of $\mu _1$. Graphs for Experiments 7 and 8, where customer arrival rates satisfy $\lambda _1> \lambda _2> \lambda _3$, are not included in the paper because they are practically identical to the graph for Experiment 2 shown in Fig. 4. On the other hand, Fig. 10 shows that the graphs associated with Experiments 18 and 19, which have $\lambda _1< \lambda _2 < \lambda _3$, exhibit slight departures from the rectangular shape shown on the Experiment 13 side of Fig. 4. We first discuss why $\mu _1$ and $\mu _2$ do not affect $b^*$ for the $\lambda _1> \lambda _2 > \lambda _3$ case. As described above regarding $\gamma _1$, assignments to the Queue 3 buffer are driven by the number of Type 2 servers in the system because Type 2 servers are assumed to be scarce relative to Type 1 servers. So changes to the characteristics of Type 1 servers such as $\gamma _1$ above and $\mu _1$ here do not affect $b^*$ at Queue 3. However based on these arguments, it would seem that larger values of $\mu _2$ would cause $b^*$ to decrease as the productivity at Queue 2 could be maintained with fewer Type 2 servers who could in turn be assigned to the Queue 3 buffer. But keep in mind that $\mu _2$ does not increase beyond $\mu _3$ in Experiment 7; the goal is to examine what happens to $b^*$ as $\mu _2$ approaches $\mu _3$ (the effect of increasing values of $\mu _3$ is considered separately in Experiments 6 and 17). Furthermore, it is unlikely in practice that the service rate for patients with serious injuries $(\mu _2)$ would exceed that of the most critically injured patients $(\mu _3)$. Thus because $\mu _2 < \mu _3$ and Queue 2 is busier than Queue 3, the buffer at Queue 3 is not influenced by $\mu _2$.

  When $\lambda _1< \lambda _2 < \lambda _3$, $b^*$ essentially does not change as $\mu _1$ increases, except for an immediate and slight decrease in the range of $b^*$ values, which remains constant thereafter (Fig. 10, Experiment 19). Experiment 18 (Fig. 10) reveals that $\mu _2$ has somewhat an opposite effect: the range of $b^*$ values is the same throughout except that the lower bound increases by one unit at the two values of $\mu _2$ that are closest to $\mu _3$. Even though $\mu _2 < \mu _3$, larger buffers are beneficial at Queue 3 because it is the busiest of all the queues when $\lambda _1< \lambda _2 < \lambda _3$.

• O.9 The range of$b^*$values for the Experiments 12 through 22, which have$\lambda _1< \lambda _2 < \lambda _3$, is generally wider than the ranges associated with Experiments 1 through 11, where$\lambda _1> \lambda _2 > \lambda _3$. One of the reasons for this is that when $\lambda _1< \lambda _2 < \lambda _3$, the average holding cost is generally much larger then that of the experiments with $\lambda _1> \lambda _2 > \lambda _3$. For example, the expected holding costs used to produce the graphs shown in Fig. 6 are shown in Tables 6 and 7. For Experiment 4, the average of the expected holding costs in Table 6 is 287.20 whereas the corresponding average from Table 7 is 1293.34. Statistically significant differences are more difficult to achieve with larger values compared to smaller ones (e.g., 1 and 2 differ by 1 unit, and so do 1001 and 1002; but the latter values are much more likely to be statistically equivalent than the former). However, the wide range of $b^*$ values in Experiment 14 (Fig. 5), which depicts $b^*$ as a function of $\lambda _1$ for $\lambda _1< \lambda _2 < \lambda _3$, occurs for this reason and another. As described in the exposition that follows Observation O.6 regarding the effect of $\lambda _3$, when the number of customers in the system far exceeds the number of servers, all server teams are assigned to Queue 3 in which case no buffer is possible and b has no effect on the assignments.

• O.10 Average cost appears to be convex inb. For each of the eight experimental conditions presented in Tables 6 and 7, the average cost decreases for $b < b^*$ ($b^*$ is bold in Tables 6, 7), then steadily increases for $b > b^*$. This property was consistent across all 22 sensitivity analysis experiments; Tables 6 and 7 are representative. This finding has important implications for future analytical work. While the $c \mu$ rule is not optimal, perhaps there exists an optimal buffer size $b^*$ associated with the CQ3B heuristic that produces an optimal policy, at least under certain conditions.

Table 6 Average cost of CQ3B policy as a function of $\lambda _2$ in Experiment 4

Table 7 Average cost of CQ3B policy as a function of $\lambda _2$ in Experiment 15

Question 3

Is the difference in expected cost between the heuristic policies with the buffer and those without more pronounced as $b^*$ increases?

Let EC(b) denote the expected cost of applying the CQ3B priority rule with buffer size b. If the answer to Question 3 is “yes”, then $\displaystyle \% {\varDelta }(b^*) = \frac{EC(0) - EC(b^*)}{EC(b^*)}$ should be an increasing function. This, however, is not the case. Several counterexamples can be extracted from Table 5; here, we identify one. Consider experiments 2 and 24 in Table 5 with $b^*$ values of 2 and 7, and $\% {\varDelta }(b^*)$ values of 224.23 and 63.22%, respectively. Since $\% {\varDelta }(2) > \% {\varDelta }(7)$, $\% {\varDelta }(b^*)$ is not an increasing function, which shows that condition needed to answer Question 3 affirmatively is false. Therefore, the answer to Question 3 is “no”.

7 Conclusion

In this paper, we study the dynamic allocation of medical staff to casualties who have been assigned to triage categories after a mass casualty event. We model this queueing network with flexible resources as a discrete-time finite horizon stochastic dynamic programming problem. Our research contribution is twofold: first, we consider the collaboration of heterogeneous teams. While nurses attend to patients in the minor category, and doctors do the same for patients in the delayed category, the casualties in the immediate category need a team of one nurse and one doctor to serve them. Our second contribution lies in the fact that there is very little research that considers random server arrivals and their subsequent service assignments in queuing systems. Mostly, it has been assumed in the literature that the servers will be already in place when casualties (customers) arrive to the system. However, in MCE scenarios more resources may need to be pulled from other jurisdictions or systems to enhance capacity.

We first approach the problem with dynamic programming but end up developing heuristics due to the excessive computational times and tremendous demand for computational resources. We examine the performance of heuristic policies based on the well-known $c \mu$ rule. We specifically develop two heuristics each of which have two options, with or without a buffer of additional server capacity, resulting in four heuristic policies. Our experimental results aim to answer three questions: (1) Under which conditions is the buffer most and least beneficial? (2) how do changes in model parameters affect buffer size? and (3) Is the difference in expected cost between the heuristic policies more pronounced as the pseudo-optimal buffer size resulting from the process of enumerating all feasible buffer sizes increases?

Our results indicate that the $c \mu$ rule is not an optimal policy, and that prioritizing Queue 3 (the queue that serves critical patients, each of which requires one doctor and one nurse for service) is the best option in most circumstances. Buffer capacity is most beneficial whenever Queue 3 is prioritized, and least beneficial when it is not. In fact, the best buffer size is zero when a queue other than Queue 3 is prioritized. We find that the best buffer sizes increases as (i) the number of servers in the system, (ii) number of critical patients, or (iii) holding cost at Queue 3 increase; and also that the best buffer size decreases when either (i) the arrival rate of serious patients, (ii) holding cost at Queue 2 (for serious patients), or (iii) service rate at Queue 3 increase. In addition, the best buffer size is not affected by parameters related to Queue 1 nor the service rate at Queue 2. Finally, we show that the answer to Question 3 above is no.

Our research can be taken further by including switching costs/times into the model. We assumed that reallocation or switching cost is zero because our focus was treating casualties in one hospital. However, if doctors are being sent from one system to another then travel times will play a significant role in reallocation decisions. Furthermore, the problem modelled in this paper can be extended into resource allocations in disaster response and recovery. For example, in disaster recovery one problem is debris removal. If we consider debris collection points as queues, a central decision maker can send heavy equipment and operators as server teams (e.g. a bulldozer plus its operator) to these queues. The assumption in such scenarios generally is that the equipment comes with its own operator but that may not always be true. This work can also be extended in a more technical direction by exploring issues related to optimality. Given the computational challenges we encountered even for small problem instances, the analysis would require an analytical approach. A promising effort in this direction would be to examine the CQ3B policy in which Queue 3 is prioritized and additional servers are assigned there as a buffer to anticipate uncertain demand. Our computational results suggest that the expected cost function associated with CQ3B is convex in the buffer size b, so it is likely that this result can be shown analytically and perhaps lead to a closed form expression for the optimal buffer size. More generally, the conditions under which the CQ3B policy is optimal could be identified.

Appendix A