Bi-objective emergency blood supply chain network design in earthquake considering earthquake magnitude: a comprehensive study with real world application

Abstract

This research proposes a new multi-objective mathematical model to design efficient and effective blood supply chain network in earthquakes. For the first time in this field of knowledge, the devastating impact of earthquake destruction radius is considered on blood supply chain network based on its magnitude. Two different transportation means, with variant speed and capacity, are employed to carry the blood from blood collection centers to blood centers. However, the number of available conveyors is limited in each site. To solve the proposed multi-objective mixed integer linear programming model, five multi-objective decision making methods as well as the lexicographic weighted Tchebycheff method are utilized to provide the decision maker with Pareto optimal solutions. Further, the application of the proposed multi-objective mathematical model is investigated in a real-world case study using data from the latest earthquakes in one of the recent activated faults of Iran’s capital, Tehran, which is considered to be a potential place for a severe earthquake. Using different solution approaches, various Pareto optimal solutions are obtained for the case study. The results indicated that the proposed mathematical model is able to design the most cost and time efficient blood supply chain in a severe earthquake. At the end, sensitivity analyses are performed to explore the effects of any changes in main parameters of the multi-objective mathematical model on the objective functions value to demonstrate the most critical parameter.

1 Introduction

Natural disasters such as earthquake, volcano, tsunami and typhoon greatly influence the human lives. Among these, Earthquake is the most common and destructive one. Earthquake is the perceptible vibrations in the earth’s crust caused by sudden energy release as a result of rocks rupture underground which leads to seismic waves. In the last century, earthquakes have caused a lot of damages, destructions and loss of human lives around the world as reported in (USGS; Doocy et al. 2013; see “Appendix A”).

A shared vision about the emergency zone and the availability of resources is required for emergency management to manage emergency situations. One of the most important factors is support of knowledge-based systems which is essential for managers to help them make the best decision in emergency situations (De Maio et al. 2011). Many organizations including blood transfusion service and Humanitarian Non-Governmental Organizations (NGOs) have prominent role in emergency situations such as natural disasters (Wang et al. 2016; Rodríguez et al. 2010). One of the best guidelines for practitioners is the International Federation of Red Cross and Red Crescent Societies (IFRC) Code of Conduct (CoC) for Disaster Operations. Which provides qualitative guidelines that are an excellent building block for operational theory. Due to importance of humanitarian operations during and after disasters, many researchers aimed to develop applicable models and guidelines (Pyakurel et al. 2017). For instance, to improve the International Federation of Red Cross and Red Crescent Societies Code of Conduct, Coles et al. (2017) proposed a framework that can be implemented as a stand-alone model to help practitioners to make both qualitative and quantitative decisions. Xiang and Zhuang (2016) proposed a new queueing network to formulate the deterioration in victims’ health conditions after a sever disaster. For a systematic review of humanitarian operations, humanitarian logistics and humanitarian supply chain performance refer to Banomyong et al. (2017) and Oloruntoba et al. (2017).

One of the main challenges of any blood transfusion service is managing the blood supply chain effectively during and after earthquake. A severe earthquake can result in a sudden increase in blood demand (Hess and Thomas 2003). Therefore, designing an efficient blood supply chain in an emergency situation is of great importance.

Several researches have been done in the literature to propose new mathematical models to design blood supply chain in emergency situations. In recent researches, Yang et al. (2016) developed a decision making programming model utilizing the data envelopment analysis approach in the construction of reserve network for China Red Cross. They considered three main factors including utility, cost and risk. Jabbarzadeh et al. (2014) proposed a new mathematical model for blood supply in earthquake. In their proposed model, they only aimed to minimize total supply chain costs which is far from a real-world application in an emergency situation. Fahimnia et al. (2015) proposed a stochastic bi-objective mathematical model for blood supply in disasters. They considered delivery time to develop more realistic mathematical model. Kohneh et al. (2016) proposed a bi-objective mathematical model for the problem. They aimed to minimize total costs and maximize coverage of the donor groups. Zahiri and Pishvaee (2017) developed a bi-objective mathematical programming model to minimize the total supply chain costs and maximize unsatisfied demand. (for more information about the existing models in the literature see literature review section).

Although, several mathematical models were proposed in the literature to design an efficient blood supply chain network, the existing models in the literature can be further improved to propose more applicable and realistic models. For instance, none of the existing models in the literature considered how to transfer blood from collection centers to blood centers. How the earthquake can cause disruption in the blood supply chain network?

Consider an example which highlights the importance of these two vacuities in the literature.

On 26 December 2003, a 6.6 $\hbox {M}_{\mathrm{W}}$ earthquake destroyed the city of Bam in southeastern Iran, in which, 26,271 people were killed and 30,000 were injured (USGS). Since, the number of injured people were enormous, the hospitals called for emergency supply of blood. Unfortunately, due to an ineffective blood supply chain, from almost 108,000 donated blood units about only 21,000 units (almost 23%) arrived the hospitals. In the first four days after the earthquake, only 1231 (1.3%) of the donated blood units reached the disaster area. The experiences such as Bam disaster revealed the importance of an efficient transportation system in the blood supply chain during and after a severe natural disaster. Therefore, a new mathematical model is needed to fill this vacuity.

This motivated us to extend the mathematical model presented by Jabbarzadeh et al. (2014) to propose more realistic and applicable model. For this purpose, a new bi-objective mathematical formulation is proposed to design an efficient blood supply chain during and after earthquake. The proposed bi-objective mathematical model considers a three-echelon blood supply chain that consists of donor groups, blood collection facilities and blood centers. The goal of the mathematical model is to answer decisions related to the location of permanent and mobile blood collection facilities, allocation of donor groups to the blood collection facilities, the optimal number of located temporary and permanent blood collection facilities, blood inventory level at each blood center and the optimal number of required vehicles and helicopters in each blood collection facility to transfer collected blood to blood centers. Two objective functions are considered which aim to minimize total blood supply chain costs as well as total transportation time. To propose more realistic model, different transportations means are considered in the blood supply chain. Also, the destruction effect of the earthquake is considered in the model to design a robust and resistant blood supply chain during earthquake.

The remainder of this paper is organized as follows. Section 2 presents a brief review of the relevant literature. In the Sect. 3 the problem is defined and the assumptions are presented. Then, the bi-objective mathematical model of the problem is proposed. In Sect. 3 two multi-objective solution orientations are considered to solve the problem. In Sect. 4, five multi-objective decision making (MODM) and lexicographic weighted Tchebycheff methods are applied to solve a real-world problem. In Sect. 5, the proposed model is implemented a real-world problem. In Sect. 6 sensitivity analyses are carried out to determine the effects of changes in the main parameters of the problem on objective functions value. Section 7 concludes the paper.

2 Literature review

Designing an efficient blood supply chain requires many strategic and operational decisions such as location of the blood collection facilities, transportation of the collected blood from collection centers to distribution centers and then to hospitals. Since, the blood demand rate after a disaster may vary over periods (for example within every 24 h), designing an efficient blood supply chain falls within the scope of dynamic network design (Jabbarzadeh et al. 2014).

In one of the first studies on joint facility location-inventory problems, Daskin et al. (2002) introduced a distribution center location model considering two types of inventory costs including working and stock costs. They developed a Non-Linear Integer-Programming (NLIP) model for the problem. A Lagrangian relaxation solution algorithm was proposed to solve the problem. In dynamic network design, the location and capacity of the facilities may vary over different periods of planning horizon to address variations in blood demand rate. The first study on dynamic facility location was done by Ballou (1968). Even though, the dynamic facility location has advantages over the static facility location in which the location of the facilities is fixed over the planning horizon; few researches have been conducted on dynamic network design of the supply chain. Melo et al. (2006) proposed a mathematical modeling framework which captures a lot of practical aspects of network design problems. They considered inventory, dynamic planning horizon as well as storage constraints. Hinojosa et al. (2000) studied a dynamic facility location problem with the aim of minimizing the total cost of the network. They proposed a mixed integer programming (MIP) model for the problem considering plant and warehouse capacities. In a more recent researches, Correia et al. (2013) suggested a multi-period two-echelon supply chain, where, the aim was to determine the optimal location of facilities in order to maximize the total profit. Bozorgi-Amiri and Asvadi (2015) proposed a decision support system to prioritize Relief Logistic Center’s locations to simplify emergency helps to disaster zones in natural disasters. They considered availability, risk, cost and coverage to determine the optimal locations of the Relief Logistic Centers. All the previous researches showed the applicability of the dynamic facility location problem in different fields of study.

Beliën and Forcé (2012) presented a literature review on inventory and supply chain management of blood products and showed that few researches have been carried out in this area, trying to design an efficient emergency blood supply chain network especially using dynamic facility location (Galindo and Batta 2013; Altay and Green 2006). Pierskalla (2005) did a comprehensive study on the blood supply chain network design by answering the following questions: (1) where to locate blood banks, (2) how to assign donor groups to the blood collection centers, (3) in which areas blood facilities can be located (4) how the collected blood in the blood facilities should be transported to the blood banking facilities and hospitals. In other related works, which aimed to design an efficient blood supply chain, Or and Pierskalla (1979) proposed a transportation location-allocation problem for blood supply in hospitals and emergency situations. They assumed that the required blood in hospitals is fulfilled by assigning the hospitals to a near regional blood bank. The aim of their proposed model was to minimize the total supply chain costs (Mole 1975). In more recent studies, Duhamel et al. (2016) presented a mathematical model for multi-period location-allocation problem in post-disaster operations. Their innovation was to consider the impact of distribution over the population. Yadavalli et al. (2015) proposed a continuous review perishable product disaster inventory model in which an adjustable joint reordering policy for replenishment was adopted. Ülkü et al. (2015) studied behavioral and decision making aspects of donors by presenting analytical models for how the behavior of donors can be influenced by soliciting a minimum amount of cash donation. Hosseinifard and Abbasi (2016) studied the impacts of centralization on sustainability of the blood supply chain. In a case study, the showed that centralization of hospitals’ inventory is one of the most important factors in the blood supply chain. The results of their study showed that reducing the number of hospitals that hold inventory can significantly reduce the shortages. Dillon et al. (2017) proposed a two-stage stochastic programming model for inventory management in the blood supply chain. By implementing the proposed model on realistic data, they showed that the current inventory control policies can be revised by reducing current target levels to diminish wastage and total cost without compromising the service level. Huang and Song (2016) proposed an emergency logistics distribution routing model based on uncertainty theory. To solve the problem, they developed a cellular genetic algorithm. Zhang and Li (2015) proposed a novel probabilistic model with chance constraints for locating and sizing emergency medical service stations. They transformed the model into a conic quadratic mixed-integer program by employing a conic transformation. Katsaliaki and Brailsford (2016) used discrete-event simulation to determine ordering policies which can significantly reduce shortages and wastage, increase service levels, and reduce costs by employing better system coordination. Osorio et al. (2016) presented a simulation-optimization model for production planning in the blood supply chain. They showed that the proposed approach can reduce shortages, outdated units and cost in the blood supply chain network. Cheraghi and Hosseini-Motlagh (2017) proposed a fuzzy-stochastic mixed integer linear programming model to design blood supply chain network. Their main contribution was to consider uncertainty of the main parameters of the mathematical model in the optimization process.

After severe earthquakes in Turkey 1999, Şahin et al. (2007) developed several location-allocation models in regionalizing of blood services. They solved various real world problems using proposed mathematical models. In another research, Sha and Huang (2012) offered a multi-period location allocation model for emergency blood supply in disasters as well as a Lagrangian relaxation based heuristic algorithm to solve a real-world problem. Nagurney et al. (2012) developed a network optimization model for blood supply chain. They considered a regionalized blood banking system including collection centers, storage facilities, distribution hubs and hospitals. Arvan et al. (2015) introduced a blood supply chain involving donation or collection sites, processing labs and blood banks. The aim of their proposed model was to determine the location and allocation of the blood bank components in the network. Şahinyazan et al. (2015) proposed a selective vehicle routing model for temporary blood collection facilities. In spite of the previous researches, assigning the service to emergency departments is very important (Leo et al. 2016). For this purpose, Leo et al. (2016) suggested a mixed-integer programming model to determine service assignment to emergency departments. They had implemented the proposed model in the Department of Epidemiology of the Regional Health Service of Lazio, Italy, to show the effectiveness of the proposed model. Jin et al. (2015) presented a new mathematical model for patient delivery and medical resource allocation with capacity restrictions considering different injuries and survival probabilities.

One of the main challenges that blood supply chain optimization faces is handling the parameters in real world conditions due to their unpredictability (Jabbarzadeh et al. 2014). In order to develop a robust model to control uncertainty in main parameters. Jabbarzadeh et al. (2014) suggested a robust supply chain network design model for blood supply in natural disasters such as earthquake. They showed the applicability of the robust optimization method in a real case study. Fahimnia et al. (2015) proposed a stochastic bi-objective supply chain network design model for blood supply in disasters. They used $\upvarepsilon$-constraint and Lagrangian relaxation methods to solve the bi-objective model.

As mentioned earlier, disasters can disrupt the supply chain. Disruptions in the supply chain may occur due to different reasons such as natural disasters including tsunami, earthquake and volcano, epidemics or man-made disruptions, for instance, wars and terrorist attacks (Jabbarzadeh et al. 2012). Disruptions can significantly affect the effectiveness of the blood supply chain. For instance, Sri Lanka faced an unexpected tsunami in 26 December 2004. The tsunami killed 30,000 people and injured 23,000. The National Blood Transfusion Service were overburdened with influx of injured people. Therefore, National Blood Transfusion Service had to design an efficient blood supply chain to handle the catastrophe and manage the large number of blood donors (Kuruppu 2010). On March 11, 2011, a great earthquake stroked east japan and the subsequent tsunami disrupted the blood supply chain on the Pacific coast of Tohoku (Nollet et al. 2013).

Considering disruption in blood supply chain can significantly increase its efficiency. Jabbarzadeh et al. (2012) developed a mixed-integer nonlinear programming model for a supply chain network design problem with the risk of disruptions. The aim of their proposed model was to maximize the total profit of the entire supply chain. Akgün et al. (2015) proposed a facility location model to determine the optimal location of facilities for prepositioning supplies considering disruption risk. The aim of their model was to minimize the response time in a disaster area. Liang et al. (2012) proposed an optional contract model for relief material management supply chain considering two steps in delivery where the aim was to reduce the impact of the disasters. In more recent researches, Kohneh et al. (2016) proposed a bi-objective mathematical model for blood supply chain network design. The proposed model aimed to minimize total supply chain costs and maximize coverage of the donor groups. They implemented the presented model in a case study from Iran and show the effectiveness of the mathematical model. Zahiri and Pishvaee (2017) developed a bi-objective mathematical programming model to minimize the total supply chain costs and maximize unsatisfied demand. They implemented the proposed model in a case study from northern Iran. Salehi et al. (2017) proposed a robust two-stage multi-period stochastic model for the blood supply network design. Their novelty was in considering the possibility of transfusion of one blood type as well as its derivatives to other types based on the medical requirements.

A literature comparison between the proposed model in this research and the previous researches is proposed in Table 1.

Table 1 Comparison between the proposed model and the previous researches’

As in presented in the Table 1, different models with conflicting objectives and assumptions have been proposed in the literature. However; still some vacuities remain in this field of knowledge. For instance, none of the existing models in the literature considered transportation in their proposed models. While, in real world applications different transportation means with different capacity, cost and speed can be utilized. Also, the destruction radius of the earthquake which can significantly affect the blood supply chain efficiency is ignored in the existing models in the literature.

The proposed model in this article is a direct extension of the model presented by Jabbarzadeh et al. (2014). The model consists of some assumptions that can be seen in the literature; however, none of the proposed mathematical models in the literature include transportation decisions and disruption in the blood supply chain. Motivated by the aforementioned examples of disruptions caused by disasters in real life situations, for the first time in this field of knowledge, the destruction radius of earthquake is considered in this research while permanent blood collection centers can be destroyed by the earthquake. The other main question in blood supply during disasters is the way of transporting the collected blood to the earthquake zone. In this research two transportation means with limited capacities are considered to carry collected blood to the earthquake area. Besides, there are limited numbers of available transportation equipment in each blood collection facility. Thus, the optimal number of needed transportation equipment is determined by solving the proposed multi-objective mathematical model.

Moreover, in all previous researches the objective is to design a blood supply chain which aims to minimize the total supply chain costs, however, in an emergency situation such as a severe earthquake the priority is providing blood as soon as possible far from considering the costs. Therefore, this research takes a second objective function into account that is minimizing total transportation time of collected blood from blood collection centers to blood centers. To solve the multi-objective mathematical model, two optimization orientations are considered. The first one is MODM methods which solve the multi-objective mathematical models with different point of views. The second one is lexicographic weighted Tchebycheff method that is used to solve the multi-objective mathematical model to obtain efficient Pareto optimal solutions of the problem. The Pareto optimal solutions can help the decision maker to choose the most proper solution.

3 Problem definition

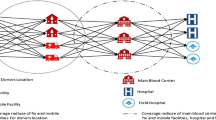
In this research, a three-echelon supply chain is made up of blood donors, blood collection facilities and blood centers which are essential to design the blood supply chain network. Two types of blood collection facilities include permanent and mobile blood collection facilities. A schematic view of the proposed blood supply chain is presented in Fig. 1.

Fig. 1

A schematic view of the proposed blood supply chain

Location of the permanent blood collection facilities are fixed while mobile (temporary) blood collection facilities can move within sites to collect more blood from donor groups in each period. Table 2 presents the responsibility of each facility in the blood supply chain.

Table 2 Responsibility of each facility in the blood supply chain

The collected blood in blood collection facilities are transported to blood centers using blood transportation vehicles and helicopters with fixed and variable cost, speed and capacity. The number of available blood transportation vehicles and helicopters are limited in each site at each period and the optimal number of required vehicles in each site will be determined by solving the multi-objective mathematical model. The following assumptions are used in this research.

• 1. Maximum blood supply of each donor is known.

• 2. Number of available transportation equipment in each site is limited.

• 3. Capacity of the blood collection facilities and blood centers is limited.

• 4. Demand rate of each blood center is known.

  By solving the proposed multi-objective mathematical model, following decisions are made at each period.

• (1) Allocation of donor groups to the blood collection facilities.

• (2) The flow of blood from donor groups to blood facilities and to the blood centers.

• (3) The optimal number of located temporary and permanent blood collection facilities.

• (4) The optimal location of temporary and permanent blood collection facilities.

• (5) Blood inventory level at each blood center in specific period.

• (6) Optimal number of needed vehicles in each blood collection facility to transfer collected blood to blood centers.

• (7) Amount of transferred blood from each collection center to each blood center by vehicles.

In this study the following parameters are used to develop the multi-objective mathematical model of the problem:

Sets
i	Donor groups
j	Potential location of blood facilities (permanent and temporary collection centers)
k	Blood centers
t	Periods of time
v	Transportation modes
Parameters
$ac_{jkv}$	Transportation cost of blood from blood collection facility j to blood center k using transportation mean v
$b_{jt}$	Capacity of temporary blood collection center j at period t
$c_{jt}$	Capacity of the permanent blood collection center j at period t
$ca_v$	Maximum capacity of transportation mean v to transport collected blood from collection centers to blood centers
$\hbox {cov}$	Coverage radius of blood collection centers
$d_{kt}$	Demand of blood center k at period t
$dis_j$	Distance between blood collection center j and the epicenter of the earthquake
EM	Earthquake magnitude
$f_j$	Fixed cost of establishment of permanent blood collection centers
$h_k$	Blood storing cost at blood center k
$m_i$	Maximum blood supply of donor group i
$na_{jv}$	Number of available transportation mean type v at blood collection center j
$o_{ijt}$	Cost of collecting blood from donor group i at blood collection facility j in period t
$r_{ij}$	Distance of donor group i from blood collection center j
$t_{jktv}$	Time needed to transport blood from blood collection facility j to distribution center k at period t using transportation mode v
$toc_v$	Fixed cost of transportation mode v
$u_k$	Maximum capacity of blood center k
$v_{jlt}$	Fixed cost of moving temporary blood collection facilities from location l to location j at period t
$\alpha$	The destruction radius of an earthquake with 5–6 Richter magnitude
$\beta$	The destruction radius of an earthquake with 6–7 Richter magnitude
$\eta$	The destruction radius of an earthquake with 7–8 Richter magnitude
$\xi$	The destruction radius of an earthquake with 8–9 Richter magnitude
$\psi$	The destruction radius of an earthquake with 9–10 Richter magnitude
Decision variables
$in_{kt}$	Inventory level of blood at blood center k at period t
$n_{jktv}$	Number of transportation mean v needed at blood collection center j at period t to transport collected blood to blood center k
$Q_{ijt}$	Amount of blood collected from donor group i at blood collection center j at period t
$Qa_{jktv}$	Amount of transported blood from blood collection center j to blood distribution center k at period t using transportation mode v
$vc_{jktv}$	Binary variable, equal to 1 if transportation mode v is used to transport collected blood from blood collection center j to blood center k at period t otherwise 0
$x_j$	Binary variable, equal to 1 if permanent blood collection center is established at location j, otherwise 0
$y_{ijt}$	Binary variable, equal to 1 if donor group i is allocated to blood collection center j at period t, otherwise 0
$z_{jlt}$	Binary variable, equal to 1 if temporary blood collection center is moved from location l to location j at period t, otherwise 0
$\delta _{kt}$	Amount of shortage in blood center k at period t
$\omega _1$	Binary variable, equal to 1 if earthquake magnitude is 5–6 Richter, otherwise 0
$\omega _2$	Binary variable, equal to 1 if earthquake magnitude is 6–7 Richter, otherwise 0
$\omega _3$	Binary variable, equal to 1 if earthquake magnitude is 7–8 Richter, otherwise 0
$\omega _4$	Binary variable, equal to 1 if earthquake magnitude is 8–9 Richter, otherwise 0
$\omega _5$	Binary variable, equal to 1 if earthquake magnitude is 9–10 Richter, otherwise 0

$$\begin{aligned} Min~{z_1} =&\sum \limits _j^{} {{f_j}} {x_j} + \sum \limits _j^{} {\sum \limits _l^{} {\sum \limits _t^{} {{v_{jlt}}} } } {z_{jlt}} + \sum \limits _i^{} {\sum \limits _j^{} {\sum \limits _t^{} {{o_{ijt}}} } } {Q_{ijt}} \nonumber \\&+ \sum \limits _j^{} {\sum \limits _k^{} {\sum \limits _t^{} {\sum \limits _v^{} {a{c_{jkv}}Q{a_{jktv}}} } } } \nonumber \\&+ \sum \limits _k^{} {\sum \limits _t^{} {{h_k}} } i{n_{kt}} + \sum \limits _j^{} {\sum \limits _k^{} {\sum \limits _t^{} {\sum \limits _v^{} {to{c_v} \times {n_{jktv}}} } } } + \sum \limits _k^{} {\sum \limits _t^{} {M \times {\delta _{kt}}} } \end{aligned}$$

(1)

$$\begin{aligned} Min~{z_2} =&\sum \limits _j^{} {\sum \limits _k^{} {\sum \limits _t^{} {\sum \limits _v^{} {v{c_{jktv}}{t_{jktv}}} } } } \end{aligned}$$

(2)

$$\begin{aligned}&\hbox {s.t}\nonumber \\&i{n_{kt - 1}} + \sum \limits _j^{} {\sum \limits _v^{} {Q{a_{jktv}}} } - i{n_{kt}} + {\delta _{kt}} = {d_{kt}} \quad \forall k,t \end{aligned}$$

(3)

$$\begin{aligned}&in_{kt} \le in_{kt-1} +\sum _j^{} {\sum _{v}^{} {Qa_{jktv} } } \quad \forall k,t \end{aligned}$$

(4)

$$\begin{aligned}&x_j +\sum _l^{} {z_{jlt} } \le 1 \quad \forall j,t \end{aligned}$$

(5)

$$\begin{aligned}&\sum _l^{} {z_{ljt} } \le \sum _l^{} {z_{jlt-1} } \quad \forall j,t \end{aligned}$$

(6)

$$\begin{aligned}&y_{ijt} \le x_j +\sum _l^{} {z_{jlt} } \quad \forall i,j,t \end{aligned}$$

(7)

$$\begin{aligned}&r_{ij} y_{ijt} \le \hbox { cov } \quad \forall i,j,t \end{aligned}$$

(8)

$$\begin{aligned}&Q_{ijt} \le m_i y_{ijt} \quad \forall i,j,t \end{aligned}$$

(9)

$$\begin{aligned}&\sum _j^{} {\sum _t^{} {Q_{ijt} } } \le m_i \quad \forall i \end{aligned}$$

(10)

$$\begin{aligned}&\sum _i^{} {Q_{ijt} } \le c_{jt} x_j +b_{jt} \sum _l^{} {z_{jlt} }\quad \forall j,t \end{aligned}$$

(11)

$$\begin{aligned}&in_{kt} \le u_k \quad \forall k,t \end{aligned}$$

(12)

$$\begin{aligned}&EM\ge 5\omega _1 +6\omega _2 +7\omega _3 +8\omega _4 +9\omega _5 \end{aligned}$$

(13)

$$\begin{aligned}&EM\le 6\omega _1 +7\omega _2 +8\omega _3 +9\omega _4 +10\omega _5 \end{aligned}$$

(14)

$$\begin{aligned}&\omega _1 +\omega _2 +\omega _3 +\omega _4 +\omega _5 =1 \end{aligned}$$

(15)

$$\begin{aligned}&dis_j \ge \left( {\alpha \omega _1 +\beta \omega _2 +\eta \omega _3 +\xi \omega _4 +\psi \omega _5 } \right) x_j \quad \forall j \end{aligned}$$

(16)

$$\begin{aligned}&\sum _k^{} {\sum _v^{} {Qa_{jktv} } } =\sum _i^{} Q_{ijt} \quad \forall j,t \end{aligned}$$

(17)

$$\begin{aligned}&Qa_{jktv} \le vc_{jktv} \times \sum _i^{} {Q_{ijt} }\quad \forall j,k,t,v \end{aligned}$$

(18)

$$\begin{aligned}&n_{jktv} \ge \left( {\frac{Qa_{jktv} }{ca_v }} \right) \quad \forall j,k,t,v \end{aligned}$$

(19)

$$\begin{aligned}&\sum _k^{} {n_{jktv} } \le \sum _k^{} {na_{jv} } vc_{jktv}\quad \forall j,t,v \end{aligned}$$

(20)

$$\begin{aligned}&vc_{jktv} \le (x_j +\sum _l^{} {z_{jlt} } )\quad \forall j,t \end{aligned}$$

(21)

$$\begin{aligned}&\sum _k^{} {\sum _v^{} {Qa_{jktv} } } \le (x_j +\sum _l^ {z_{jlt} } )\times \sum _i^{} {Q_{ijt} }\quad \forall j,t,v \end{aligned}$$

(22)

$$\begin{aligned}&Q_{ijt} \ge 0\quad \forall i,j,t \end{aligned}$$

(23)

$$\begin{aligned}&in_{kt} \ge 0\quad \forall k,t \end{aligned}$$

(24)

$$\begin{aligned}&Qa_{jktv} \ge 0 \quad \forall j,k,t,v \end{aligned}$$

(25)

$$\begin{aligned}&n_{jktv} \ge 0,\textit{Integer }\quad \forall j,k,t,v \end{aligned}$$

(26)

$$\begin{aligned}&vc_{jktv} \in \left\{ {0,1} \right\} \quad \forall j,k,t,v \end{aligned}$$

(27)

$$\begin{aligned}&x_j \in \left\{ {0,1} \right\} \quad \forall j \end{aligned}$$

(28)

$$\begin{aligned}&y_{ijt} \in \left\{ {0,1} \right\} \quad \forall i,j,t \end{aligned}$$

(29)

$$\begin{aligned}&z_{jlt} \in \left\{ {0,1} \right\} \quad \forall j,l,t \end{aligned}$$

(30)

$$\begin{aligned}&\omega _1 , \omega _2 , \omega _3 , \omega _4 , \omega _5 \in \left\{ {0,1} \right\} \end{aligned}$$

(31)

$$\begin{aligned}&\delta _{kt} \ge 0\quad \forall k,t \end{aligned}$$

(32)

The first objective function aims to minimize total supply chain costs including establishing permanent blood collection centers, moving temporary blood collection facilities, collecting blood from donor groups, transporting collected blood to blood centers, storing blood at blood centers, fixed cost of transportation means and a penalty assigned to amount of blood shortage. The second objective function aims to minimize total transportation time of collected blood from blood collection centers to blood centers. Constraint (3) guarantees that the inventory level in each blood center at previous period plus total transported blood from collection centers to the blood center minus on-hand inventory in the blood center at the end of the current period plus blood shortage in the blood center at the current period is equal to total blood demand in the blood center at the current period. Constraint (4) ensures that the on-hand inventory level in the current period is less or equal to the on-hand blood level in previous period plus amount of collected blood from collection centers transported to the blood center at the current period. Constraint (5) ensures that in each location only one blood collection facility can be settled. Constraint (6) handles the movement of temporary collection centers. Constraint (7) guarantees that each donor group can be allocated to only one blood collection facility. Constraint (8) shows that to allocate a donor group to a blood collection facility, the distance between donor group and blood collection facility should be less or equal to the coverage radius of the blood collection facility. Constraint (9) affirms that to collect blood from a donor group, the donor group must be allocated to a blood collection facility. Constraint (10) ensures that the total collected blood from a donor group in a blood collection facility is less or equal to the maximum blood supply of the donor group. Constraint (11) presents the capacity constraints of the blood collection facilities. Constraint (12) shows the capacity constraint of the blood centers. Constraints (13–16) show the damages caused by the earthquake to the permanent blood collection centers based on its magnitude. Constraints (17) shows that the collection facilities send all the collected blood to the blood centers. Constraints (18–21) determine the number of vehicles to transport collected blood from blood collection centers to blood centers considering limited number of transportation means. Constraints (22) ensure that if a blood collection facility is established in a location then blood can be transported to the blood centers. Constraints (23–32) show the decision variables and their possible values.

4 Solution methods

The mathematical model developed in the previous section is a constraint bi-objective mixed integer linear programming (MILP) model. The optimal solution of the developed bi-objective model is an ideal solution which minimizes both objective functions simultaneously. Since, the objective functions are in conflict such a solution does not exist (Khalilpourazari and Khalilpourazary 2017; Khalilpourazari and Pasandideh 2016). In these cases, the multi-objective solution methods should be utilized to solve the model. There are two types of solution techniques to solve multi-objective optimization models as follows.

• 1. Multi-objective decision making (MODM) methods

• 2. Multi-objective optimization techniques

Multi-objective optimization techniques provide a set of Pareto solutions named Pareto frontiers. These Pareto optimal solutions provide a variety of alternatives to the decision maker (Khalilpourazari and Khalilpourazary 2017). In some cases, when the number of Pareto solutions are enormous, choosing a Pareto optimal solution from Pareto frontier is a cumbersome work. In these cases, MODM methods, which solve the multi-objective problems with different views such as minimizing the deviation of each objective function from its individual optimal point, can be utilized. Considering all the above-mentioned points, both MODM and Multi-objective optimization techniques have their own advantages.

4.1 Multi-objective decision making (MODM) methods

According to Hwang and Masud (2012) and Pasandideh et al. (2015) the MODM methods are classified in four categories. Methods in the first category solve the problem without any information given by the decision maker, in other words, in these methods the decision maker only accepts or rejects the obtained solution. Methods in the second category try to find the most effective optimal point which minimizes both objective functions based on the priority that is determined by the decision maker. Therefore, in this category the decision maker must determine the priority of the objective functions based on their importance. Methods in third category generally called interactive methods which means that in each iteration the decision maker is asked about preference of the obtained solutions to determine the next solution. In methods of the fourth category the decision maker needs to choose a solution based on his/her preference at the end.

In this paper five MODM methods including Max–Min, utility function, goal attainment, LP-metric and goal programming are applied to solve the bi-objective mathematical model of the proposed blood supply chain as presented in Table 3.

To evaluate the performance of the five MODM methods three measures are defined including first objective function value, second objective function value and CPU-time which presents the required computation time to solve the multi-objective model.

4.1.1 Numerical examples

In this section the proposed bi-objective mathematical model of the problem is solved in different sizes using the five aforementioned MODM methods. For each size, five different test problems with randomly generated parameters are solved using GAMS software implementing the five MODM methods. Table 4 presents the parameters of the model and their distribution. Note that the following distributions are considered based on the real data which are provided in the next section.

Table 3 Five MODM methods

Table 4 Parameters and distributions

Table 5 Computational results

In each size five different test problems with different parameters are solved. Mathematically speaking, 175 test problems are solved to evaluate the performance of the MODM methods to demonstrate the superior method. Table 5 presents the computational results.

To solve the test problems, a laptop with i7 CPU and 8 GB of ram is utilized. Figures 2, 3 and 4 present the average value of the objective functions (Z1 and Z2) and CPU-time of the MODM methods.

Fig. 2

Average first objective function value for five MODM methods

Fig. 3

Average second objective function value for five MODM methods

Fig. 4

Average CPU-time of five MODM methods

An ideal solution is a solution in which both objective functions are minimized simultaneously. Since, the two objective functions are in conflict, we can infer that all obtained solutions by MODM methods are effective solutions. To compare the efficiency, these five MCDM methods are compared using single factor ANOVA to determine significant differences in the average CPU-time among them at 95% confidence level (Khalilpourazari and Pasandideh 2017; Khalilpourazari et al. 2016; Khalilpourazari and Khalilpourazary 2016). Table 6 presents the results of the single factor ANOVA.

As is presented in Table 6, the p value is less than 0.05, which means there are significant differences between average CPU-time of the five solution methods. Therefore, a post hoc analysis is needed (Khalilpourazari et al. 2016; Pasandideh et al. 2015). To achieve this aim, Tukey’s multiple comparison test (Tukey’s HSD) is used. Tukey’s HSD simultaneously compares the means of different treatments to find out which treatments are significantly different. In this paper, MINITAB software is utilized to perform Tukey’s HSD test. Table 7 presents the results.

In Table 7 the p value of the rows which shows the comparison between LP-metric method and other solution methods, are less than 0.05, which are marked with (*). So, we can infer that there are significant differences between LP-metric method and other solution methods in term of average CPU-time. Thus, the solution method with less CPU-time performs better than other methods. Therefore, the LP-metric method is inefficient in term of CPU-time measure. Figures 5 and 6 present the results of the Tukey’s test.

The other important point is that, each method produces a different performance in terms of different predefined measures. For example, the Goal attainment method is the best method regarding the CPU-time measure, since its computation time is significantly less comparing to other MODM methods. Contrarily, the Goal attainment method cannot perform well in minimizing the second objective function value. As a result, each MODM method has its own priority in terms of different measure. Thus, more analyses are needed to determine the superior method.

Table 6 Single factor ANOVA for CPU-time measure

Table 7 Tukey simultaneous tests for CPU-time measure

4.1.2 Performance evaluation

Since determining an accurate weight for each comparing measure is practically impossible, in this subsection Entropy method is used to assign a weight for each measure. Then Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method is applied to demonstrate the superior MODM method. First of all, a decision matrix is designed based on the results of Table 5 as presented in Table 8.

Fig. 5

Boxplot of the CPU-times

Fig. 6

The results of the Tukey’s HSD for CPU-time measure

Table 8 Decision matrix

The Entropy method estimates the weight of each measure without receiving any information from the decision maker for a given decision matrix. It determines weights based on uncertainty and diversification of the measure vector. In this method, the decision matrix is normalized in linear form as presented in Eq. 33.

$$\begin{aligned} D_{ij} =\frac{y_{ij} }{\mathop \sum \nolimits _i y_{ij} } \end{aligned}$$

(33)

Then the parameter $d_j$ is calculated for each measure using the below formula.

$$\begin{aligned} d_j =1+T\mathop \sum \limits _{i=1}^n D_{ij} \ln D_{ij}, \quad T=\frac{1}{\ln n} ,0<d_j <1 \end{aligned}$$

(34)

Using above calculations, the weight of each measure is obtained using Eq. 35.

$$\begin{aligned} WE_j =\frac{d_j }{\mathop \sum \nolimits _{j=1}^n d_j } \end{aligned}$$

(35)

Table 9 presents the obtained weights of each measure using Entropy method.

Table 9 Weights determined by Entropy method

After assigning a proper weight for each measure, Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method is used to rank the five MODM methods. TOPSIS method first proposed by Hwang and Yoon (1981) and it aims to find the best alternative with longest distance from the negative ideal solution and shortest distance from the positive ideal solution. The results of utilizing TOPSIS method is presented in Table 10. The five MODM methods are ranked based on their similarity ratio.

Table 10 Results of the TOPSIS method

As in Table 10 the Utility function is the best MODM method to solve the developed bi-objective mixed integer linear programming (MILP) model.

4.2 Multi-objective optimization techniques

Since both of objective functions are in conflict in the proposed multi-objective mathematical model of the problem, developing a solution procedure to provide Pareto optimal solution is important. Because, in some cases the decision makers prefer to choose a solution from a given set of Pareto optimal solutions (Khalilpourazari and Khalilpourazary 2017; Khalilpourazari et al. 2016; Samanlioglu 2013). In this study, the lexicographic weighted Tchebycheff method is used to provide Pareto optimal solutions. Khalilpourazari and Khalilpourazary (2017) and Steuer (1986) and define the Pareto optimal solution as follows.

Definition A decision vector $\hbox {x}^{*}\in \hbox {S}$ or Pareto optimal solution for a multi objective program (MOP)is efficient if there does not exist $\hbox {x}\in \hbox {S}$ that $\hbox {f}_{\mathrm{i}} \left( \hbox {x} \right) \le \hbox {f}_{\mathrm{i}} \left( {\hbox {x}^{*}} \right)$ where $\hbox {f}_{\mathrm{i}} \left( \hbox {x} \right) <\hbox {f}_{\mathrm{i}} \left( {\hbox {x}^{*}} \right)$ is true for at least one index.

For a bi-objective minimization problem Pareto optimal solutions can be presented as in Fig. 7.

Fig. 7

Pareto optimal set source: Khalilpourazari and Pasandideh (2016)

Lexicographic weighted Tchebycheff (LWT) method is first proposed by Steuer (1986). LWT is one of the most effective methodologies in solving Multi-objective programs (MOP). Using dispersed weights, the LWT can provide efficient Pareto optimal solutions of a MOP (Khalilpourazari and Pasandideh 2016). The formulation of the lexicographic weighted Tchebycheff method is presented in Eq. 36.

$$\begin{aligned} \begin{array}{l} \textit{lex} \min \left\{ {\delta ,e^{t}\left( {f\left( x \right) -f^{*}\left( x \right) } \right) } \right\} \\ {\textit{subject}} \quad {\textit{to}} \\ \delta \ge \varepsilon _i \left( {f_i \left( x \right) -f_i^*\left( x \right) } \right) \\ \end{array} \end{aligned}$$

(36)

where $f_i \left( x \right)$ are the objective functions, $f^{*}\left( x \right)$ is the vector of the optimal solutions of objective functions where they are minimized individually satisfying all constraints. $\varepsilon _i \ge 0$ are the weights where $\mathop \sum \nolimits _{i=1}^n \varepsilon _i =1$ (Khalilpourazari and Khalilpourazary 2017).

5 Model implementation

Iran as one of the most earthquake-prone countries has faced many devastating earthquakes (Sabzehchian et al. 2006). Table 11 presents some of the most devastating earthquakes recorded in Iran.

Table 11 Most destructive earthquakes recorded in Iran

Fast and adequate distribution of blood after severe earthquakes is always a matter of concern (Abolghasemi et al. 2008). To handle the situation, the proposed bi-objective mathematical model for blood supply chain network design in earthquake is implemented on a real-world data set to evaluate the effectiveness of the proposed bi-objective mathematical model.

Iranian Blood Transfusion Organization (IBTO) founded in 1974, is a non-profit and public organization that provides hospitals with blood and blood components free of any charges. IBTO is the only organization responsible for all activities related to blood collection and distribution. National laws have banned all other organizations from any activities related to blood transfusion (Cheraghali 2012). Some major responsibilities of the IBTO are to (1) modifying standards for collecting, screening, delivery and storage of blood. (2) Designing blood supply chain network including blood collection centers and distribution centers. (3) Conducting necessary tests on donated blood to ensure its safety.

One-third of Iran’s blood demand originates from IBTO’s north key blood center (Jabbarzadeh et al. 2014). This blood demand is collected by permanent and temporary blood collection facilities such as donation buses. According to (American Association of Blood banks, 200) blood type O is the best and the most needed blood type in an emergency situation such as earthquake because of its compatibility with all other blood types. Therefore, in this study the proposed multi-objective mathematical model is utilized to design a cost and time effective blood supply chain network for Type-O RBC.

Tehran is the largest city and urban area of Iran, the 2nd-largest city in Western Asia, and the 3rd-largest in the Middle East with a population of over 16 million in the wider metropolitan area. Tehran is located on 13 active faults which make it one of the most probable places for a potential severe earthquake. The city is divided into 22 municipal districts each with its own administrative center, as presented in Fig. 8.

Fig. 8

Geographical representation of Tehran’s districts

In this study 22 donor groups are allocated to their corresponding district (Jabbarzadeh et al. 2014) and the blood supply of each district is estimated based on districts average blood donation rate of 22.05 units per thousand people. An average deferral rate of 13% is considered to show the donors who are rejected due to special reasons including medical reasons and diseases. The geographical coordination of donor groups in each district and their corresponding blood supply are presented in Table 12 which is obtained using Google Map and Google Earth (Jabbarzadeh et al. 2014).

Table 12 Geographical coordinates of donor groups

The distances are calculated using the following formula as Eq. 37 presents.

$$\begin{aligned} r_{ij}= & {} { Arccos}\left( \sin \left( {\hbox {Latitude}_i } \right) \times \sin \left( {\hbox {Latitude}_j } \right) +\cos \left( {\hbox {Latitude}_i } \right) \times \cos \left( {\hbox {Latitude}_j } \right) \right. \nonumber \\&\left. \times \cos \left( {\hbox {Longitude}_j -\hbox {Longitude}_i } \right) \right) \times 6371.1 \end{aligned}$$

(37)

where 6371.1 is the earth’s radius and Latitude and Longitude are the geographic coordinates of the donor groups multiplied by $\pi /180$. Table 13 presents the real data for the required parameters to solve the proposed multi-objective mathematical model as presented in Davoudi-kiakalayeh et al. (2012) and Shen et al. (2003).

Table 13 The values of main parameters

The fixed cost of each vehicle used to transfer collected blood from collection centers to blood center is 3000$ and 35,000$, respectively. The blood capacity of vehicles and helicopters are 100 and 300 units. Table 14 presents the cost of transportation between collection centers and the distribution centers for vehicles and helicopters in each district. Table 15 presents the cost of moving a temporary blood collection facility from one district to another at the second period (Jabbarzadeh et al. 2014).

Table 14 Cost of transportation between candidate facilities and the blood center ($)

Table 15 Cost of moving a temporary blood collection facility between sites ($)

The number of available vehicles and helicopters in each district is given in Table 16. Also, the travel times of vehicles are given in Table 17 which are obtained from Google Map and Google Earth considering average speed of vehicles.

Table 16 Number of available transportation equipment in each district

Table 17 Travel time from each district center to the blood center (min)

In recent years designing a reliable blood supply chain network after a catastrophe such as a major earthquake in Tehran is one of the most important concerns for the government. Therefore, in this study the proposed multi-objective mathematical model is applied on real data to design an effective blood supply chain network after a destructive earthquake in Tehran. Heydari and Babai (2015) performed a risk analysis on Tehran in an area enclosed between 51$^{\circ }$25$^{\prime }$40$^{\prime \prime }$ longitude and 35$^{\circ }$45$^{\prime }$30$^{\prime \prime }$ latitude. They showed that in every 475 years a 7.5 Richter magnitude earthquake can be expected with 96% probability. Based on the data from Iranian Seismological Center (ISC) Tehran’s southern fault is activated in recent years and it is one of the most potential places for an earthquake while no severe earthquake has occurred for a long time in Tehran. Therefore, in this study we considered that a destructive earthquake with 7.8 Richter magnitude has occurred in the southern fault that is the most active one in Tehran with 30 km destruction radius as presented in Fig. 9 Heydari and Babai (2015). The distance between the earthquake center and the center of each district is presented in Table 18.

Table 18 The distance between the earthquake center and the center of each district (km)

Fig. 9

7.8 Richter magnitude Earthquake in South Tehran fault with 30 km destruction radius

To show that the objective functions are in conflict, each objective function is minimized individually using the real data of Tehran and the results show that the two objective functions are not minimized simultaneously. Table 19 presents the results.

Table 19 The relation between the two objective functions

To solve the problem five MODM methods are utilized in order to solve the problem with different point of views. Table 20 presents the results.

Table 20 Results of the five MODM methods in solving the real case study

As in Table 20 the solutions obtained by the five MODM methods are completely competitive in terms of the first and second objective function values. In the test problems presented in previous sections, the utility function method ranked first among the five MODM methods, as well as an accepted performance in the real-world data by providing a solution which has a good tradeoff between first and second objective functions value and CPU-time.

In addition, providing Pareto optimal solutions for a multi-objective mathematical model can help the decision maker to choose the solution he/she prefers. Therefore, lexicographic weighted Tchebycheff method is applied to obtain effective Pareto solutions of the multi-objective mathematical model which are presented in Table 21.

Table 21 Pareto optimal solutions obtained by the lexicographic weighted Tchebycheff method

Figure 10 presents a schematic view of the obtained Pareto optimal solutions by lexicographic weighted Tchebycheff and the five MODM methods in solving the real case problem. The solutions encircled by green provide a good trade-off between the value of the two objective functions.

Fig. 10

Solutions of the Five MODM and lexicographic weighted Tchebycheff methods

These Pareto optimal solutions help the decision maker to choose the most proper solution. For instance, if the first objective function is prior, the decision maker can choose Max–Min or LP-metric approaches. Conversely, if the second objective function is prior, the decision maker can choose Goal programming method to solve the problem. In other cases, when the decision maker aims to make an appropriate trade-off between the two objective functions, he/she can use LWT method to obtain various Pareto optimal solutions.

Computation time of the lexicographic weighted Tchebycheff method and five MODM methods are presented in Fig. 11 which determines that the lexicographic weighted Tchebycheff method requires significantly less computation time comparing to the MODM methods.

Fig. 11

Computation time of the Five MODM and lexicographic weighted Tchebycheff methods

To illustrate the values of the decision variables in the solutions obtained by different solution methods, the third Pareto optimal solution obtained by lexicographic weighted Tchebycheff method is illustrated. Table 22 presents the allocation of the donor groups to the permanent blood collection centers in the first and the second periods, respectively.

Table 22 Allocation of the donor groups to the permanent blood collection centers

Figure 12 presents the location of permanent blood collection centers and the transportation of the collected blood from collection centers in the first two periods after the 7.8 Richter earthquake. In addition, the permanent blood collection centers in 9, 10, 11, 12, 15, 16, 17, 18, 19, 20, 21 districts are destroyed by the earthquake.

Fig. 12

The third Pareto optimal solution obtained by lexicographic weighted Tchebycheff method

The results of the model implementation show that in the first period (first 24 h), it is required to transport the collected blood from collection centers to the blood center as fast as possible due to significant increase in the blood demand in the first 24 h. Therefore, based on the results, using fast transportation means such as helicopters is essential in blood collection centers 2 and 5. Also, the results demonstrate that the on-hand inventory level at the blood centers plays a major role in blood supply chain effectiveness. Since, it can significantly reduce the increased blood demand at the first 24 h.

The other advantage of using the proposed model in this research is that the model determines which blood collection centers may be destruct by the earthquake, this gives the decision maker a vision to predict the destruction effect of the earthquake on supply chain and helps to design an efficient and robust blood supply chain. Since, the proposed model in this research is a multi-objective optimization model, Pareto optimal solutions, which make a proper trade-off among conflicting objectives, are of great importance. In this research, several multi-objective solution methodologies were utilized to obtain efficient Pareto optimal solutions, since, the decision maker might have different preferences based on importance of each objective function. The results of the case study revealed that the lexicographic weighted Tchebycheff approach is one of the best solution methods for the problem, since, it can obtain efficient Pareto optimal solutions for the problem which enables the decision maker to choose the best solution he/she prefers.

In order to design a supply chain network which performs well under different scenarios, it is essential to study effect of any change in the main parameters of the mathematical model on objective function value to determine the most critical parameter of the mathematical model. For this purpose, sensitivity analyses are carried out in the following section.

6 Sensitivity analyses

In this section sensitivity analyses are carried out to show the changes in objective functions value caused by variation in the main parameters of the multi-objective mathematical model. It includes changes in each parameter at $-50$, $-25$, $+25$, $+50$% rates. To do this, the GAMS software is utilized to solve a medium size test problem. Table 23 presents the results.

Table 23 Results of sensitivity analyses

An increase in $d_{kt}$ increases both objective function values and an increase to $+$50% rate makes the problem infeasible. In addition, a small change in $d_{kt}$ results in a significant change in both objective function values. An increase in $m_i$ decreases both objective function values and a decrease to −50% rate makes the problem infeasible. An increase in EM increases both objective function values. It is obvious that the earthquakes with bigger magnitude result in bigger casualties, thus, most of the permanent collection centers will be destroyed. This result in a significant increase in supply chain costs and time needed to deliver collected blood to blood centers. An increase in cov decreases both objective functions value. This means that more donor groups will be covered and there would be no need to establish new permanent collection centers to collect blood from donor groups. A schematic view of the effects of changes in main parameters of the problem on the objective functions value is presented in Table 24.

Table 24 Effect of any change in main parameters on the objective functions value

Figures 13 and 14 present the radar plot of the results of the sensitivity analyses.

Fig. 13

Radar plot for the results of sensitivity analyses (First objective)

Fig. 14

Radar plot for the results of sensitivity analyses (Second objective)

From the results, increasing the parameters $c_{jt}$ and cov can significantly decrease the both objective functions value. Therefore, by increasing the capacity and coverage of the of the permanent collection facilities the decision maker can decrease total supply chain costs as well as total transportation time.

7 Conclusion, limitation and future scope of research

In this study, a multi-objective mathematical model was developed for blood supply chain network design in earthquake. The model consists of some assumptions that can be seen in the literature; however, none of the proposed mathematical models in the literature considered transportation decisions and disruption in the blood supply chain. For the first time in this field of knowledge, the destruction radius of the earthquake was considered in the mathematical model to design a robust supply chain when a severe earthquake occurs. In addition, two blood transportation means were appointed to transport the collected blood from collection centers to blood centers. Also, speed, capacity and number of available vehicles were considered to be different at each site. The aim of this study was to answer questions related to location of the permanent and mobile blood collection centers, allocation of the donor groups to the blood collection centers, inventory level at each blood center as well as transportation of the collected blood from and to these sites, taking into consideration the destruction effect of the earthquake on supply chain. By nature, the blood supply chain network design is a multi-criteria decision making problem, since there are conflicting objectives in making decisions about location of sites and transportation between them. The proposed model in this research aimed to minimize total transportation time and cost in the blood supply chain network, simultaneously. In contrast to existing models in the literature, to obtain efficient Pareto optimal solutions, the lexicographic weighted Tchebycheff and five multi-objective decision making (MODM) methods were applied. Different Pareto optimal solutions were attained for the problem, since, the decision maker might have different preferences based on importance of each objective function.

The model was implemented in Tehran city, the capital of Iran. Although some assumptions were made due to lack of information, many real-life aspects of the blood supply chain network design problem were considered and implemented. 22 districts of Tehran city were considered in the case study. There 22 districts were assumed to be candidate location for permanent and mobile blood collection centers. Also, Tehran’s north blood center was considered as the main blood center in the implementation. For each site, different transportation means with different capacity and speed were considered to transport blood from collection centers to the blood center. The model was solved using GAMS software using different multi-objective optimization methods and various Pareto optimal solutions were attained. The results showed that in the first period (24 h), using fast transportation means such as helicopters are essential due to significant increase in demand parameter. Also, the results indicated that the initial inventory level at the blood center is of great importance to satisfy demand in the first 24 h. Besides, the mathematical model determined that some blood collection centers were destroyed by the earthquake which helps the decision maker and health services to design more robust blood supply chain. In addition, sensitivity analyses were carried out to determine the most critical parameters of the mathematical model. The results indicated that by increasing the coverage and capacity of the blood collection centers, the total transportation time and total supply chain costs can be significantly reduced.

Although, the presented mathematical model in this paper considered different real-life aspects, still some improvements can be considered. For instance, considering different levels in the blood supply chain can improve the blood transfusion between sites. For this purpose, new levels including hospitals and disaster zones can be considered. In addition, considering some of the main parameters of the proposed model under uncertainty can lead to design more realistic and robust blood supply chain. Also, based on the preference of the decision maker and health services, different objective functions such as safety, reliability, equity and risk can be included in the mathematical model.

Appendix

See Table 25.

Table 25 The most devastating earthquakes in the world