1 Introduction and literature review

Managing the inventory is one of the most important and challenging decisions for any firm. In the classic inventory models like classic EOQ model is implicitly assumed that the item is non-decaying and the payments of purchasing cost are settled at receiving time (Harris 1990). Optimal order quantity is affected by two factors: (1) timing of the payment, (2) customer’s reactions when the vendor faces shortage. Timing the payment of the purchasing cost influences the strategies of inventory management. We have three possible different situations with respect to paying time: (1) advanced payment, (2) payment at receiving time, and (3) delayed payment. We can expect that advanced payment strategy is suggested by vendors in exclusive markets and delayed or postponed payment can be offered in competitive markets. Advanced payment is one of the most secure and riskless methods of trading for exporters and, consequently the least attractive one for buyers. The powerful vendors for controlling the cash flow risks are interested to receive all of the payments in advance from the buyers. This strategy is used for financing the procurement of parts used in production or mitigating risk of canceling an order. In Iranian automobile industries, the full advanced payment strategy is widely used in practice in all sections (sale, service, spare part and survey) and the customers should prepay the entire payment to manufactures before delivery time. To persuade the buyers for full advanced payment, sometimes the vendors offer them a price discount. Indian brick and tile industry and steel factories in Iran are as the examples of this situation. Also many researchers studied the deterioration effects because of its importance and significant influences on costs of inventory and management.

Here an EOQ model for decaying item when the entire purchasing cost is paid before receiving the items is studied. For this problem, we can mention a distributer of drugs or other deteriorating materials who wants to import them from a foreign country. In this case, its exporter asks the distributer to pay the entire purchasing cost in advance prior to goods are being shipped.

Many studies investigated the inventory control models of deteriorating products. Ghare and Schrader (1963) developed the first model for perishable product with constant deteriorating rate and the ordering cost was paid at delivery time. Also for this purchasing payment strategy, Covert and Philip (1973), developed a model for perishable products in which the deterioration rate follows the Weibull function. Afterwards, the topic of deterioration has widely been developed and investigated in the literature. Wee and Yu (1997), studied an inventory model of perishable products by considering an impermanent discount from the vendor to the buyer. Liao et al. (2012) considered lot-sizing decision strategies with two warehouses under linked to order trade credit. Taleizadeh et al. (2013a) extended a lot sizing model for perishable item under special sale and shortage. Yu (2013) developed a collaborative inventory management model of decaying and defective items. Taleizadeh et al. (2013d) proposed a Bees Colony Optimization (BCO) algorithm for solving a fuzzy rough economic order quantity model for perishable items considering quantity discount and advance payment. Das et al. (2015) investigated an inventory model with multi items and multi warehouse for deteriorating items with price dependent demand and permissible delay in payment.

In the studies related to partial backlogging, Wee (1995) introduced an ordering strategy of decaying item under partial backlogging of unfilled demand and order cancelations. Yu et al. (2005) developed a model in an inventory-production environment for a deteriorating item with considering defective products and partial backordering. Lo et al. (2007) extended a two-level integrated production-inventory model for a decaying item under inflation, partial backlogging, multiple deliveries and imperfect manufacturing process. Ghosh et al. (2011) extended a lot sizing model for a decaying item in which demand depends on whole sale price and partial backordering rate depends on the lead time. Pentico and Drake (2011) presented a comprehensive survey on partial backordering in 2011. Taleizadeh et al. (2012) extended a lot sizing model with considering special sale and partial backordering, moreover this work later is developed under considering known price increase (Taleizadeh and Pentico 2013). In another work, Taleizadeh et al. (2015) studied the EOQ models with incremental discounts and considered both full and partial backordering cases for the first time. Wang et al. (2015) extended an EOQ model for imperfect quality items with partial backlogging and screening constraint. San-José et al. (2015) studied an EOQ model with partial backordering where the unit holding cost includes two important elements. Wee et al. (2014) developed an EPQ model with partial backlogging considering linear and fixed backordering costs. They also derived a critical backlogging rate to find the feasible optimal solution.

Some papers have considered combination of inventory control models with credit-financing strategies. Jaggi and Aggarwal (1994) investigated an EOQ model for decaying items without shortage. Sarker et al. (2000) developed an inventory control system for decaying items with backordering, inflation and trade credit. Sarkar et al. (2015) investigated a trade policy in a two echelon supply chain in which the vendor offers full trade-credit to the buyer but the buyer offers partial trade-credit to their customers. Chang (2004) developed an inventory model where the vendor offers a permissible delay in payment to the buyer, if orders become large. He discussed about the effect of inflation and deterioration rates and delayed payment tactic on total inventory cost. Wu et al. (2015) extended a three echelons supply chain model under both full upstream and partial downstream trade credits. Ouyang et al. (2015) studied an inventory control system with capacity constraint and linked to order permissible delay in payment.

In the field of advanced payment, Maiti et al. (2009) exerts the prepayment scheme and studied the effect of prepayment on inventory policies and total profit. Gupta et al. (2009) extended an inventory control system including partial lost sale and imprecise information of the cost and used a Meta heuristic algorithm to optimize the model and find solutions. Taleizadeh et al. (2011) developed an inventory management system for importing raw materials, where the buyer must pay a proportion of purchasing cost before receiving goods. Taleizadeh et al. (2013c) developed a mathematical model for an inventory system with multiple advanced payments and permitted shortage. Thangam (2012) developed an EOQ model for decaying item in a supply chain including a supplier, retailers and customers under both advanced and delayed payments. He assumed that the supplier offer a full trade credit to his retailers whereas the retailer provide the customers a partial trade credit. Also he considered that the retailer offers price discount to the customers who prepay the purchasing cost. Taleizadeh (2014a) extended an inventory management model for a decaying item in two cases: (1) no shortages and (2) shortages are allowed, under consecutive prepayments. Taleizadeh (2014b) introduced a lot-sizing model for an evaporating product with partial consecutive advanced payment and partial backordering. Zhang et al. (2014) considered an EOQ model without shortage with two types of prepayment including full and partial prepayments and derived the optimal inventory policies. In their model shortage and deterioration was not allowed. Our work is an extension of their work by considering deterioration and different shortage modes under full advanced payment. Moreover some related researches can be found in Taleizadeh et al. (2009, 2010, 2011, 2013b). The studies described above are briefly summarized in Table 1.

Table 1 Brief review of advanced payment papers
Full size table

According to Table 1, our paper is the first one which presents a comprehensive study on EOQ model with considering different shortage situations and full prepayment for deteriorating product. Advanced payment with multiple payments is another interesting area and there are a few studies in this field. In the case of deterioration, there are only three papers having been already studied advanced payment scheme for perishable products.

Here an EOQ model for a decaying item is extended in which ordering cost must be fully prepaid. Three different possible cases consisting of (1) shortage is not permitted, (2) backordering shortage is allowed and (3) partial backordering shortage is permitted, are developed. In this paper, the problem in hand and its assumptions are defined in Sect. 2. The notations with mathematical models and the solution algorithm are presented in Sect. 3. Numerical examples are performed in Sect. 4 and sensitivity analysis is done in Sect. 5, and at the end, in Sect. 6 the conclusions and suggested future research directions are discussed.

2 Problem description

Assume a vendor asks the buyers to pay the entire contract amount in advanced before delivering the goods. Moreover the retailer considers discount if the buyers prepay entire of purchasing cost in advanced. In order to supply the purchasing cost, the buyer requests loan from a financing instruments to finance their account and pay the retailer as the advanced payment. The example of these interactions in advanced payment scheme is presented in Fig. 1. In a full advanced payment system there is an increase in the capital cost of the buyer because of ordering cost of those products which are not delivered. In the next section, EOQ models for a decaying product with full advanced payment under different conditions are extended. Moreover the following assumptions are made.

  1. (1)

    Time horizon is infinite.

  2. (2)

    Complete and partial backlogging of shortages is allowed.

  3. (3)

    Demand for item is constant with elapsing time.

  4. (4)

    Replenishments are instantaneous.

  5. (5)

    The vendor offers price discount linked to advance payment to the buyer.

  6. (6)

    The buyer’s unit sell price is not as same as his purchasing price.

Fig. 1
figure 1

The example of interactions in advanced payment scheme

Full size image

3 Model development

The notations are used to model and solve the problem at hand are presented in the following subsection.

3.1 Notation

Parameters

d :

Demand rate per period (unit)

h :

Unit carrying cost (capital cost is not included) ($/unit/period)

\(\pi \) :

Unit backordering cost ($/unit)

P :

Unit purchasing price ($)

\(P^{{\prime }}\) :

The marginal cost of purchasing (capital cost of advanced payment in $ included)

g :

The lost sale goodwill cost ($)

\(\pi ^{\prime }\) :

The cost of lost sale \(\pi ^{\prime }=P-P^{{\prime }}+g\) ($)

\(P_s\) :

Unit selling price ($)

\(\beta \) :

Price discount factor for prepayment

A :

Fixed ordering cost ($/order)

\(t_0\) :

Length of prepayment (time)

\(\theta \) :

The constant deterioration rate

\(\alpha \) :

The fraction of backordering

\(I_c\) :

Interest charges rate per year ($/unit/period)

Decision variables

T :

Time interval between successive orders (time)

k :

The proportion of inventory cycle with positive inventory level

Q :

The order size (unit)

B :

The backordered quantity (unit)

I(t):

The inventory level at time t (unit)

B(t):

The backordered level at time t (unit)

CTC :

The total cost in each period ($)

ATC :

Average annual total cost ($)

3.2 Model development

In this section an EOQ model with full prepayment for a deteriorating item under different cases is developed. In the first case the model without any shortage is developed. In case 2 we assume that the entire shortages will be backordered and finally in case 3 a proportion of shortages will be backordered.

Case 1: Without shortages

Assume a situation where the buyer exerts a classic inventory model for a perishable item when shortages are forbidden. The inventory diagram is presented in Fig. 2.

Fig. 2
figure 2

Time-weighted inventory with full prepayment when shortage is not allowed

Full size image

The following differential equation shows the inventory level changes during the period length:

$$\begin{aligned} \frac{dI(t)}{dt}=-\theta I(t)-d; \quad 0\le t\le T \end{aligned}$$
(1)

Using the boundary condition, \(I(T)=0\), gives;

$$\begin{aligned} I(t)=\frac{d}{\theta }(e^{\theta (T-t)}-1); \quad 0\le t\le T \end{aligned}$$
(2)

Moreover the order quantity can be derived as follows:

$$\begin{aligned} Q=I(0)=\frac{d}{\theta }(e^{\theta T}-1). \end{aligned}$$
(3)

It should be mentioned that when \(\theta \) approaches zero by applying l’Hopital’s rule, it gives \(I(0)=dT\). In practice, usually the deterioration rate is not too large. So, using the Taylor expansion for \(e^{\theta T}\) we have \(e^{\theta T}=1+\theta T+\frac{1}{2}(\theta T)^{2}\) and the amount of order quantity can be approximated as follows:

$$\begin{aligned} Q^{*}=dT \left( 1+\frac{1}{2}\theta T\right) . \end{aligned}$$
(4)

The holding cost in each period is \(h\int _0^T {\frac{d}{\theta }} (e^{\theta (T-t)}-1)dt=\frac{1}{2}hdT^{2}\), ordering cost is A and also the cost of purchasing of items is \(P \, \beta dT(1+\frac{1}{2} \theta T)\). The buyer in order to pay the purchasing cost \(P \, \beta dT(1+\frac{1}{2}\theta T)\) must pay interest charge at rate of \(I_c\), which is \(P \, \beta dt_0 I_c T(1+\frac{1}{2}\theta T)\). Therefore:

$$\begin{aligned} CTC= & {} \overbrace{A}^{\textit{Fixed cost}}+\overbrace{\frac{1}{2}hdT^{2}}^{\textit{Holding cost}}+\overbrace{P \, \beta dT\left( 1+\frac{1}{2}\theta T\right) }^{\textit{Purchasing cost}}+\overbrace{P \, \beta dt_0 I_c T\left( 1+\frac{1}{2}\theta T\right) }^{\textit{Interes charges in prepayment}} \end{aligned}$$
(5)
$$\begin{aligned} ATC= & {} \frac{1}{T}\times CTC=\overbrace{\frac{A}{T}}^{\textit{Fixed cost}}+\overbrace{\frac{1}{2}hdT}^{\textit{Holding cost}}+\overbrace{P \, \beta d\left( 1+\frac{1}{2}\theta T\right) }^{\textit{Purchasing cost}} \nonumber \\&+\overbrace{P \, \beta dt_0 I_c \left( 1+\frac{1}{2}\theta T\right) }^{\textit{Interes charges in prepayment}} \end{aligned}$$
(6)

We take the first and also the second derivations of cost function respect to T as follows.

$$\begin{aligned} \frac{\partial ATC}{\partial T}= & {} \frac{-A}{T^{2}}+\frac{1}{2}hd+\frac{1}{2}\theta P \, \beta d+\frac{1}{2}\theta P \, \beta dt_0 I_c \end{aligned}$$
(7)
$$\begin{aligned} \frac{\partial ATC}{\partial T}= & {} \frac{2A}{T^{3}}\ge 0 \end{aligned}$$
(8)

From Eq. (8) one can conclude that the second derivative is always positive (\(T>0\)). So the convexity of objective function is proved and we can find the optimal solution, as shown in Eq. (9).

$$\begin{aligned} T^{*}=\sqrt{\frac{2A}{hd+\theta P \, \beta d(1+t_0 I_c )}} \end{aligned}$$
(9)

Case2: Full prepayment with deterioration and shortage

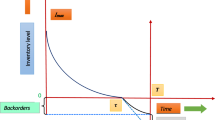
Assume a situation where the buyer exerts a classic inventory model for a perishable item in which the shortage items is fully backlogged. This situation is presented in Fig. 3.

Fig. 3
figure 3

Time-weighted inventory with full prepayment and full backordering

Full size image

The following differential equations show the inventory level changes during the period length:

$$\begin{aligned} I(t)= & {} \frac{d}{\theta }(e^{\theta (KT-t)}-1); \quad 0\le t\le kT \end{aligned}$$
(10)
$$\begin{aligned} B(t)= & {} dt; \quad kT\le t\le T \end{aligned}$$
(11)

Applying the boundary condition, \(I(kT)=0\), for Eqs. (10) and (11), gives:

$$\begin{aligned} I= & {} \frac{d}{\theta }(e^{\theta kT}-1) \end{aligned}$$
(12)
$$\begin{aligned} B= & {} d(1-k)T; \end{aligned}$$
(13)

Thus, the optimal order size will be:

$$\begin{aligned} Q=I+B=\frac{d}{\theta }(e^{\theta kT}-1)+d(1-k)T \end{aligned}$$
(14)

With exerting a brief Taylor series expansion, the following equation is derived:

$$\begin{aligned} Q=d \left( kT+\frac{1}{2}\theta k^{2}T^{2}\right) + d(1-K)T = dT \left( 1+\frac{1}{2}\theta k^{2}T\right) \end{aligned}$$
(15)

The holding cost in each period is \(h\int _0^{kT} {\frac{d}{\theta }} (e^{\theta (kT-t)}-1)dt=\frac{1}{2}hdk^{2}T^{2}\), the ordering cost is A and the purchasing cost is \(P \, \beta dT(1+\frac{1}{2}\theta k^{2}T)\). So the interest charge at rate \(I_c\), is \(P \, \beta dt_0 I_c T(1+\frac{1}{2}\theta k^{2}T)\). The backordering cost is \(0.5\pi d(1-k)^{2}T^{2}\), therefore, the cyclic and annual total costs are respectively:

$$\begin{aligned} CTC= & {} \overbrace{A}^{\textit{Fixed cost}}+\overbrace{\frac{1}{2}hdk^{2}T^{2}}^{\textit{Holding cost}}+\overbrace{P \, \beta dT\left( 1+\frac{1}{2}\theta k^{2}T\right) }^{\textit{Purchasing cost}} \nonumber \\&+\overbrace{P \, \beta dt_0 I_c T\left( 1+\frac{1}{2}\theta k^{2}T\right) }^{\textit{Interes charges in prepayment}}+\overbrace{\frac{1}{2}\pi d(1-k)^{2}T^{2}}^{\textit{Backordering cost}} \end{aligned}$$
(16)
$$\begin{aligned} ATC= & {} \frac{1}{T}\times CTC = \overbrace{\frac{A}{T}}^{\textit{Fixed cost}}+\overbrace{\frac{1}{2}hdk^{2}T}^{\textit{Holding cost}}+\overbrace{P \, \beta d\left( 1+\frac{1}{2}\theta k^{2}T\right) }^{\textit{Purchasing cost}} \nonumber \\&+\overbrace{P \, \beta dt_0 I_c \left( 1+\frac{1}{2}\theta k^{2}T\right) }^{\textit{Interes charges in prepayment}}+\overbrace{\frac{1}{2}\pi d(1-k)^{2}T}^{\textit{Backordering cost}} \end{aligned}$$
(17)

The objective function, represented in Eq. (17), can be rewritten as follows;

$$\begin{aligned} \Delta _1 (K,T)=\frac{\psi _1 }{T}+(\psi _2 k^{2}-2\psi _3 k+\psi _3 )T+\psi _4 \end{aligned}$$
(18)

where,

$$\begin{aligned} \psi _1= & {} A>0, \end{aligned}$$
(19)
$$\begin{aligned} \psi _2= & {} \frac{(h+\pi +p\,\beta \theta +P \, \beta t_0 I_c \theta ) d}{2}>0, \end{aligned}$$
(20)
$$\begin{aligned} \psi _3= & {} \frac{\pi d}{2}>0, \end{aligned}$$
(21)
$$\begin{aligned} \psi _4= & {} P \, \beta d+P \, \beta dt_0 I_c >0. \end{aligned}$$
(22)

Moreover Eq. (18) can be rewritten as;

$$\begin{aligned} \Delta _1 (K,T)=\frac{\psi _1 }{T}+T\gamma (k)+\psi _4 , \end{aligned}$$
(23)

where \(\gamma (k)=\psi _2 k^{2}-2\psi _3 k+\psi _3\) . The goal is to implement a condition in order to have a specific interior minimizer for Eq. (23). Differentiating \(\Delta _1 (k,T)\) with respect to T yields:

$$\begin{aligned} \frac{\partial \Delta _1 (k,T)}{\partial T}=-\frac{\psi _1 }{T^{2}}+\gamma (k). \end{aligned}$$
(24)

This equation equals to zero if T satisfies Eq. (25):

$$\begin{aligned} T^{*}=T^{*}(k)=\sqrt{\frac{\psi _1 }{\gamma (k)}.} \end{aligned}$$
(25)

The discriminate of \(\gamma (k), 4\psi _3^{2}-4\psi _2 \psi _3 =4(\frac{\pi d}{2})^{2}-4(\frac{(h+\pi +P \, \beta \theta +P \, \beta t_0 I_c \theta )d}{2})(\frac{\pi d}{2})= -h\pi d^{2}-P \, \beta \theta \pi d^{2}-P \, \beta t_0 I_c \pi \theta d^{2}\) is negative, therefore \(\gamma (k)\) has no root. Since \(\gamma (0)=\psi _3 =\frac{\pi d}{2}>0, \gamma (k)\) is more than zero within [0, 1], therefore Eq. (17) gives, for each k, a unique \(T^{*}=T^{*}(k)\) that minimizes the total cost in Eq. (23). So,

$$\begin{aligned} \hat{{\Delta }}_1 (k)=\Delta _1 (k,T(k))=\frac{\psi _1 }{\sqrt{\frac{\psi _1 }{\gamma (k)}}}+\sqrt{\frac{\psi _1 }{\gamma (k)}}\gamma (k)+\psi _4 =2\sqrt{\psi _1 \gamma (k)}+\psi _4 . \end{aligned}$$
(26)

This expresses show the minimum cost for each value of k. \(\hat{{\Delta }}_1 (k)\) is continuous and has at least one local minimum within [0,1], and its smallest one is the optimal value. To investigate these minimums, calculate the derivatives of \(\hat{{\Delta }}_1 (k)\) with respect to k. So we have:

$$\begin{aligned} \frac{d\hat{{\Delta }}_1 (k)}{dk}= & {} \sqrt{\psi _1 }\frac{{\gamma }^{\prime }(k)}{\sqrt{\gamma (k)}}, \end{aligned}$$
(27)
$$\begin{aligned} \frac{d^{2}\hat{{\Delta }}_1 (k)}{dk^{2}}= & {} \sqrt{\psi _1 }\frac{\left[ {2{\gamma }^{\prime \prime } (k)\gamma (k)-({\gamma }^{\prime }(k))^{2}} \right] }{2(\gamma (k))^{\frac{3}{2}}}, \end{aligned}$$
(28)

After some manipulations, it gives:

$$\begin{aligned} \frac{d^{2}\hat{{\Delta }}_1 (k)}{dk^{2}}= & {} \sqrt{\psi _1 }\frac{\left[ {2{\gamma }^{\prime \prime }(k)\gamma (k)-({\gamma }^{\prime }(k))^{2}} \right] }{2(\gamma (k))^{\frac{3}{2}}}=\sqrt{\psi _1 }\frac{\left[ {\psi _2^{2}k^{2}-2\psi _2 \psi _3 k+\psi _2 \psi _3 -\psi _3^{2}} \right] }{(\gamma (k))^{\frac{3}{2}}} \nonumber \\= & {} \sqrt{\psi _1 }\frac{\left[ {(\psi _2 k-\psi _3 )^{2}+\psi _2 \psi _3 } \right] }{(\gamma (k))^{\frac{3}{2}}}>0, \end{aligned}$$
(29)

Since \(\psi _1 ,\psi _2 ,\psi _3 ,\gamma (k),(\psi _2 k-\psi _3)^{2}\) are all positive. So \(\hat{{\Delta }}_1 (k)\) is convex and we find the global minimum with setting its first derivative equal to zero. Since \(\sqrt{\psi _1 }\) and \(\gamma (k)\) are always positive, \({\gamma }^{\prime }(k)=2\psi _2 k-2\psi _3\) should be equal to zero. Therefore, we have:

$$\begin{aligned} k^{*}=\frac{\psi _3 }{\psi _2 }=\frac{\pi }{h+\pi +P \, \beta \theta (1+t_0 I_c )} \end{aligned}$$
(30)

Substituting Eq. (30) into \(T^{*}=T^{*}(k)\), after some manipulations we have:

$$\begin{aligned} T^{*}=T^{*}(k)=\sqrt{\frac{2A(h+\pi +P \, \beta \theta (1+t_0 I_c ))}{\pi d(h+P \, \beta \theta (1+t_0 I_c ))}} \end{aligned}$$
(31)

Case 3: Full advanced payment with partial backordering

Assume that a buyer applies an EOQ model for a decaying product when shortage is partially being backordered. The diagram of inventory system is presented in Fig. 4. The inventory level at time t decreases because of both decaying and demand rates. So the inventory level changes at time t, can be presented as below:

$$\begin{aligned} I(t)= & {} \frac{d}{\theta }(e^{\theta (KT-t)}-1); \quad 0\le t\le kT \end{aligned}$$
(32)
$$\begin{aligned} B(t)= & {} \alpha dt; \quad kT\le t\le T \end{aligned}$$
(33)

Solving Eqs. (32) and (33) yield to:

$$\begin{aligned} I= & {} \frac{d}{\theta }(e^{\theta kT}-1) \end{aligned}$$
(34)
$$\begin{aligned} B= & {} \alpha d(1-k)T; \end{aligned}$$
(35)

And finally,

$$\begin{aligned} Q=I+B=\frac{d}{\theta }(e^{\theta kT}-1)+\alpha d(1-k)T \end{aligned}$$
(36)

using the Taylor series expansion, we have:

$$\begin{aligned} Q=dT\left( k+\frac{1}{2}\theta k^{2}T+\alpha (1-k)\right) \end{aligned}$$
(37)
Fig. 4
figure 4

Time-weighted inventory with full prepayment and partial backordering

Full size image

The holding cost per cycle is \(h\int _0^{kT} {\frac{d}{\theta }} (e^{\theta (kT-t)}-1)dt=\frac{1}{2}hdk^{2}T^{2}\), the ordering cost is A and the purchasing cost of product is \(P \, \beta dT(k+\frac{1}{2}\theta k^{2}T+\alpha (1-k))\). So because of borrowing the purchasing cost from a financial instrument the interest charge at rate \(I_c\), is \(P \, \beta dt_0 I_c T(k+\frac{1}{2}\theta k^{2}T+\alpha (1-k))\). The backordering and the lost sale costs are \(\frac{1}{2}\pi \alpha d(1-k)^{2}T^{2}\) and \({\pi }^{\prime }d(1-\alpha )(1-k)T\) respectively. Therefore, the cyclic and annual total costs are, respectively:

$$\begin{aligned} CTC= & {} \overbrace{A}^{\textit{Fixed cost}}+\overbrace{\frac{1}{2}hdk^{2}T^{2}}^{\textit{Holding cost}}+\overbrace{P \, \beta dT\left( k+\frac{1}{2}\theta k^{2}T+\alpha (1-k)\right) }^{\textit{Purchasing cost}} \nonumber \\&+\overbrace{P \, \beta dt_0 I_c T\left( k+\frac{1}{2}\theta k^{2}T+\alpha (1-k)\right) }^{\textit{Interest charged in prepayment}} \nonumber \\&+\overbrace{\frac{1}{2}\pi \alpha d(1-k)^{2}T^{2}}^{\textit{Backordering cost}}+\overbrace{{\pi }^{\prime } d(1-\alpha )(1-k)T}^{\textit{Lost sale cost}} \end{aligned}$$
(38)
$$\begin{aligned} ATC= & {} \frac{1}{T}\times CTC = \overbrace{\frac{A}{T}}^{\textit{Fixed cost}}+\overbrace{\frac{1}{2}hdk^{2}T}^{\textit{Holding cost}}+\overbrace{P \, \beta d\left( k+\frac{1}{2}\theta k^{2}T+\alpha (1-k)\right) }^{\textit{Purchasing cost}} \nonumber \\&+\overbrace{P \, \beta dt_0 I_c \left( k+\frac{1}{2}\theta k^{2}T+\alpha (1-k)\right) }^{\textit{Interest charged in prepayment}} \nonumber \\&+\overbrace{\frac{1}{2}\pi \alpha d(1-k)^{2}T}^{\textit{Backordering cost}}+\overbrace{{\pi }^{\prime } d(1-\alpha )(1-k)}^{\textit{Lost sale cost}} \end{aligned}$$
(39)

We can rewrite the objective function, represented in Eq. (39), as follows;

$$\begin{aligned} \eta (k,T)=\frac{\psi _1 }{T}+(\psi _2 k^{2}-2\psi _3 k+\psi _3 )T-\psi _4 k+\psi _5 \end{aligned}$$
(40)

where,

$$\begin{aligned} \psi _1= & {} A>0, \end{aligned}$$
(41)
$$\begin{aligned} \psi _2= & {} \frac{(h+\pi \alpha +{p}^{\prime }\theta )d}{2}>0, \end{aligned}$$
(42)
$$\begin{aligned} \psi _3= & {} \frac{\pi \alpha d}{2}>0, \end{aligned}$$
(43)
$$\begin{aligned} \psi _4= & {} (1-\alpha )d({\pi }^{\prime }-{P}^{\prime }), \end{aligned}$$
(44)
$$\begin{aligned} \psi _5= & {} {\pi }^{\prime }(1-\alpha )d+P \, \beta d\alpha +P \, \beta dt_0 I_c \alpha >0. \end{aligned}$$
(45)
$$\begin{aligned} {P}^{\prime }= & {} P \, \beta (1+t_0 I_c ) \end{aligned}$$
(46)

Equation (40) can be rewritten as;

$$\begin{aligned} \eta (k,T)=\frac{\psi _1 }{T}+T\gamma _1 (k)+\gamma _2 (k) \end{aligned}$$
(47)

where \(\gamma _1 (k)=\psi _2 k^{2}-2\psi _3 k+\psi _3 \) and \(\gamma _2 (k)=-\psi _4 k+\psi _5\). The aim is to implement the condition in order to Eq. (47) has a specific interior minimizer. With differentiate from \(\eta _1 (k,T)\) respect to T, we have:

$$\begin{aligned} \frac{\partial \eta (k,T)}{\partial T}=-\frac{\psi _1 }{T^{2}}+\gamma _1 (k). \end{aligned}$$
(48)

So,

$$\begin{aligned} T^{*}=T^{*}(k)=\sqrt{\frac{\psi _1 }{\gamma _1 (k)}.} \end{aligned}$$
(49)

The discriminate of \(\gamma _1 (k), 4\psi _3^{2}-4\psi _2 \psi _3 =4(\frac{\pi \alpha d}{2})^{2}-4(\frac{(h+\pi \alpha +P \, \beta \theta +P \, \beta t_0 I_c \theta )d}{2})(\frac{\pi \alpha d}{2})= -d(h+P \, \beta \theta (1+t_0 I_c ))(\pi \alpha d)\) is negative, thus \(\gamma _1 (k)\) has no roots. Since \(\gamma _1 (0)=\psi _3 =\frac{\pi d}{2}>0, \gamma _1 (k)\) is more than zero within [0,1]. Therefore, Eq. (49) gives, for each k, a unique \(T^{*}=T^{*}(k)\) that aims to minimize the cost in Eq. (47). We Substitute the expression for \(T^{*}(k)\) [Eq. (49)] into Eq. (47). So we have:

$$\begin{aligned} \hat{{\mu }}_1 (k)=\mu _1 (k,T(k))=\frac{\psi _1 }{\sqrt{\frac{\psi _1 }{\gamma _1 (k)}}}+\sqrt{\frac{\psi _1 }{\gamma _1 (k)}}\gamma _1 (k)+\gamma _2 (k)=2\sqrt{\psi _1 \gamma _1 (k)}+\gamma _2 (k). \end{aligned}$$
(50)

This equation expresses the minimum cost for each value of k. \(\hat{{\mu }}_1 (k)\) is continues and has at least one minimum within [0,1], which the global minimum of the cost function is the smallest one. To investigate these minimums, calculate the derivatives of \(\hat{{\mu }}_1 (k)\) respect to k, as below:

$$\begin{aligned} \frac{d\hat{{\mu }}_1 (k)}{dk}= & {} \sqrt{\psi _1 }\frac{{\gamma }^{\prime }_1 (k)}{\sqrt{\gamma _1 (k)}}+{\gamma }^{\prime }_2 (k), \end{aligned}$$
(51)
$$\begin{aligned} \frac{d^{2}\hat{{\mu }}_1 (k)}{dk^{2}}= & {} \sqrt{\psi _1 }\frac{\left[ {2{\gamma }^{\prime \prime }_1 (k)\gamma _1 (k)-({\gamma }^{\prime }_1 (k))^{2}} \right] }{2(\gamma _1 (k))^{\frac{3}{2}}}+{\gamma }^{\prime \prime }_2 (k), \end{aligned}$$
(52)

After some manipulations we have:

$$\begin{aligned} \frac{d^{2}\hat{{\mu }}_1 (k)}{dk^{2}}= & {} \sqrt{\psi _1 }\frac{\left[ {2{\gamma }^{\prime \prime }_1 (k)\gamma _1 (k)-({\gamma }^{\prime }_1 (k))^{2}} \right] }{2(\gamma _1 (k))^{\frac{3}{2}}} \nonumber \\= & {} \sqrt{\psi _1 }\frac{\left[ {2(\psi _2^{2}k^{2}-2\psi _2 \psi _3 k+\psi _2 \psi _3 )-2(\psi _2^{2}k^{2}-2\psi _2 \psi _3 k+\psi _3^{2})} \right] }{(\gamma _1 (k))^{\frac{3}{2}}} \nonumber \\= & {} 2\psi _3 \sqrt{\psi _1 }\frac{\left[ {(\psi _2 -\psi _3 )} \right] }{(\gamma _1 (k))^{\frac{3}{2}}}>0, \end{aligned}$$
(53)

Since \(\psi _1 ,\psi _2 ,\psi _3 ,\gamma _1 (k)\), are all positive and \(\psi _2 -\psi _3 =(\frac{d}{2})(h+P \, \beta \theta (1+t_0 I_c ))>0\). Thus \(\hat{{\mu }}_1 (k)\) is convex, so we set the first derivative of expression equal to zero and find the global minimum.

Therefore, we have:

$$\begin{aligned} k= & {} \frac{(1-\alpha )({\pi }^{\prime }-{P}^{\prime })+\pi \alpha T^{*}}{(h+\pi \alpha +{P}^{\prime }\theta )T^{*}} \end{aligned}$$
(54)
$$\begin{aligned} T^{*}= & {} \sqrt{\frac{2A}{hdk^{2}+\pi \alpha d(1-k)^{2}+{P}^{\prime }\theta dk^{2}}} \end{aligned}$$
(55)

Substituting Eq. (54) into Eq. (55) and after some simplification we have;

$$\begin{aligned} T^{*}=\sqrt{\frac{2A({P}^{\prime }\theta +h+\pi \alpha )}{\pi \alpha d(h+{P}^{\prime }\theta )}-\frac{\left[ {(1-\alpha )({\pi }^{\prime }-{P}^{\prime })} \right] ^{2}}{\pi \alpha (h+{P}^{\prime }\theta )}} \end{aligned}$$
(56)

It should be mentioned that when the shortages cost tends to infinity, Eq. (56) reduces to Eq. (57) which is equal to Eq. (9) and rewritten in Eq. (57).

$$\begin{aligned} T^{*}=\mathop {\lim }\limits _{\pi ,\pi ^{{\prime }}\rightarrow \infty } \sqrt{\frac{2A({P}^{\prime }\theta +h+\pi \alpha )}{\pi \alpha d(h+{P}^{\prime }\theta )}-\frac{\left[ {(1-\alpha )({\pi }^{\prime }-{P}^{\prime })} \right] ^{2}}{\pi \alpha (h+{P}^{\prime }\theta )}}=\sqrt{\frac{2A}{hd+\theta P \, \beta d(1+t_0 I_c )}} \end{aligned}$$
(57)

\(T^{*}= \lim \limits _{\pi ,\pi ^{{\prime }}\rightarrow \infty } \sqrt{\frac{2A({P}^{\prime }\theta +h+\pi \alpha )}{\pi \alpha d(h+{P}^{\prime }\theta )}-\frac{\left[ {(1-\alpha )({\pi }^{\prime }-{P}^{\prime })} \right] ^{2}}{\pi \alpha (h+{P}^{\prime }\theta )}}=\sqrt{\frac{2A}{hd+\theta P \, \beta d(1+t_0 I_c )}}\) Since \(T^{*}\) in partial backordering case must be larger than \(T^{*}\) in the basic EOQ model, according to Eq. (9) and Eq. (56) we have:

$$\begin{aligned} \sqrt{\frac{2A({P}^{\prime }\theta +h+\pi \alpha )}{\pi \alpha d(h+{P}^{\prime }\theta )}-\frac{\left[ {(1-\alpha )({\pi }^{\prime }-{P}^{\prime })} \right] ^{2}}{\pi \alpha (h+{P}^{\prime }\theta )}}>\sqrt{\frac{2A}{d(h+P \, \beta \theta (1+t_0 I_c ))}} \end{aligned}$$
(58)

After some simplification we have:

$$\begin{aligned} \alpha >\alpha ^{*}=1-\sqrt{\frac{2A({P}^{\prime }\theta +h)}{d({\pi }^{\prime }-{P}^{\prime })^{2}}} \end{aligned}$$
(59)

If \(\alpha >\alpha ^{*}\) is met and \(\alpha ^{*}>0\), so this solution is selected as the optimal one. If \(\alpha >\alpha ^{*}\) and \(\alpha ^{*}<0\), we must compare the cost of the not stocking and cost of optimal partial backordering in order to derive the optimal solution.

Solution method

The subsequent method can be applied to find the optimal values of decision variables:

  1. 1.

    calculate \({\pi }^{\prime }=P-{P}^{\prime }+g\), \(\alpha ^{*}=1-\sqrt{\frac{2A({P}^{\prime }\theta +h)}{d({\pi }^{\prime }-{P}^{\prime })^{2}}}\) and \({P}^{\prime }=P \, \beta (1+t_0 I_c )\).

  2. 2.

    If \(\alpha>\alpha ^{*}>0\), go to step 3. Otherwise, if \(\alpha <\alpha ^{*}\), calculate the cost of no backlogging and compare it with \({\pi }^{\prime }d\), to clarify either it is optimal to allow all backlogs or no backlogs. If \({\pi }^{\prime }d\ge \sqrt{2Ad(h+{P}^{\prime }\theta )}\) then \(k^{*}=1\), \(T^{*}=\sqrt{\frac{2A}{(d(h+{P}^{\prime }\theta )}}\), \(Q^{*}=dT^{*}\) and \(B^{*}=0\). If \({\pi }^{\prime }d<\sqrt{2Ad(h+{P}^{\prime }\theta )}\) then \(T^{*}=\infty \), \(k^{*}=Q^{*}=0\) and stop the algorithm.

  3. 3.

    Calculate \(T^{*}\) and \(k^{*}\) using Eqs. (54) and (56). If \(\alpha ^{*}<0\), determine \(\eta (k^{*},T^{*})\); if \(\eta (k^{*},T^{*})<{\pi }^{\prime }d\), go to step 4. If \(\eta (k^{*},T^{*})\ge {\pi }^{\prime }d\) then \(T^{*}=\infty \), \(k^{*}=Q^{*}=0\) and stop the algorithm.

  4. 4.

    Calculate the order and shortage quantities optimal values, respectively:

    $$\begin{aligned} Q^{*}= & {} \frac{d}{\theta }(e^{\theta k^{*}T^{*}}-1)+\alpha d(1-k^{*})T^{*} \\ B^{*}= & {} \alpha d(1-k^{*})T^{*} \end{aligned}$$

4 Computational and practical results

Our suggested model is supported on this idea that the vendor requests his buyers to pay the entire contract amount before receiving the purchased goods. Also the vendor suggests price discount if the buyers prepay the entire purchasing cost. The advanced payment mechanism is exerted for many unique items which are used and ordered by suppliers, manufacturers, distributers, retailers and customers. Usually, to order books, newspapers and periodicals items, including special items for trade and professional publications, this strategy is widely exerted. Moreover, in international trades, many exporters expected the full payment, prior the goods being shipped. All these examples show the necessity of investigating the full advance payment scheme.

To show the performance and usages of the proposed solution procedure and to investigate the impacts of model parameters on decision variables, we will use a numerical example. We set \(d=1000\), \(A=100\), \(h=10\), \(\pi =5\) (in case 2 and 3), \(P=30\), \(\beta =0.9\), \(t_0 =0.2\), \(I_c =0.25\) and \(\theta =0.1\).

Case 1: Without shortage

Using Eq. (9) we have;

$$\begin{aligned} T^{*}=\sqrt{\frac{2(100)}{10(1000)+0.1(30)(0.9)(1000)(1+(0.2)(0.25))}}=0.12483 \end{aligned}$$

And with exerting Eq. (3) we have;

$$\begin{aligned} Q^{*}=dT\left( 1+\frac{1}{2}\theta T\right) =125.608 \end{aligned}$$

Case 2: Full backordered with shortage

With exerting Eq. (30) we have;

$$\begin{aligned} k^{*}=\frac{5}{10+5+30(0.9)(0.1)(1+(0.2)(0.25))}=0.2803 \end{aligned}$$

By using Eq. (31) we have;

$$\begin{aligned} T^{*}=\sqrt{\frac{2(100)(10+5+30(0.9)(0.1)(1+0.2(0.25)))}{5(1000)(10+30(0.9)(0.1)(1+0.2(0.25)))}}=0.2357 \end{aligned}$$

Respect to Eqs. (13) and (15) the order and backordered quantities are:

$$\begin{aligned} Q= & {} dT\left( 1+\frac{1}{2}\theta k^{2}T\right) = 1000(0.2357)(1+0.5(0.1)(0.2803^{2})(0.2357))=235.977 \\ B= & {} d(1-k)T=1000(1-0.2803)0.2357=169.664; \end{aligned}$$

Case 3: Partial backordering case

Let \(\alpha =0.9\) and \(g=30\). The solution steps in this case are:

Step 1

$$\begin{aligned} {P}^{\prime }= & {} P \, \beta (1+t_0 I_c )=30(0.9)(1+0.2(0.25))=28.35 \\ {\pi }^{\prime }= & {} P-{P}^{\prime }+g=30-28.35+30=31.65 \\ \alpha ^{*}= & {} 1-\sqrt{\frac{2A({P}^{\prime }\theta +h)}{d({\pi }^{\prime }- {P}^{\prime })^{2}}}=1-\sqrt{\frac{2(100)(28.35(0.1)+10)}{1000(31.65-28.35)^{2}}}=0.5144 \end{aligned}$$

Step 2 since \(\alpha =0.9\) is more than \(\alpha ^{*}=0.5144\), move to step 3.

Step 3

$$\begin{aligned} T^{*}= & {} \sqrt{\frac{2A({P}^{\prime }\theta +h+\pi \alpha )}{\pi \alpha d(h+{P}^{\prime }\theta )}-\frac{\left[ {(1-\alpha )({\pi }^{\prime }-{P}^{\prime })} \right] ^{2}}{\pi \alpha (h+{P}^{\prime }\theta )}} \\= & {} \sqrt{\frac{2(100)(28.35(0.1)+10+5(0.9))}{5(0.9)(1000)(10+28.35(0.1))}- \frac{((0.1)(31.65-28.35))^{2}}{5(0.9)(10+28.35(0.1))}}=0.241 \\ k= & {} \frac{(1-\alpha )({\pi }^{\prime }-{P}^{\prime })+\pi \alpha T^{*}}{(h+\pi \alpha +{P}^{\prime }\theta )T^{*}} = \frac{(1-0.9)(31.65-28.35)+5(0.9)(0.241)}{(10+5(0.9)+28.35(0.1))(0.241)}=0.339 \end{aligned}$$

Step 4

$$\begin{aligned} Q= & {} dT\left( k+\frac{1}{2}\theta k^{2}T+\alpha (1-k)\right) \\= & {} 1000(0.241)(0.339+ 0.5(0.1)(0.339)^{2}(0.241)+0.9(1-0.339))=225.51 \\ B= & {} \alpha d(1-k)T=0.9(1000)(1-0.339)(0.241)=143.55 \end{aligned}$$

Also the average annual cost in this case is 29589.98.

5 Numerical analysis and insights

To investigate the impacts of changing in parameters on derived optimal values, a numerical analysis for each case is performed. The results of numerical analysis of the first case are presented in Table 2.

Table 2 Numerical analysis results of the case 1
Full size table

These conclusions can be drawn based on Table 2.

  • \(T^{*}, Q^{*}\) and \(ATC^{*}\) are moderately sensitive respect to \(\beta \). When \(\beta \) is decreased, \(T^{*}\) and \(Q^{*}\) increase, while \(ATC^{*}\) is reduced and vice versa.

  • \(T^{*}, Q^{*}\) and \(ATC^{*}\) are a little sensitive respect to \(I_c\). When \(I_c\) is decreased, \(T^{*}\) and \(Q^{*}\) increase, while \(ATC^{*}\) start to decrease and vice versa.

  • \(T^{*}, Q^{*}\) are moderately sensitive to the shifts in parameter \(\theta \), while \(ATC^{*}\) is a little sensitive to the changes in \(\theta \). When \(\theta \) starts to decrease, \(T^{*}\) and \(Q^{*}\) increase, but \(ATC^{*}\) is reduced and vice versa.

  • \(T^{*}, Q^{*}\) and \(ATC^{*}\) are a little sensitive respect to \(t_0\). When \(t_0\) is decreased, both \(T^{*}\) and \(Q^{*}\) increases, while \(ATC^{*}\) decreases and vice versa.

Table 3 Numerical analysis results of the case 2
Full size table

Table 3 presents the outcomes of sensitivity analysis of the second case. Also an analysis is done on shortages and holding costs per unit which is shown in Table 4. The following notes can be understood from Tables 3 and 4.

  • \(Q^{*}, T^{*}, B^{*}\) are slightly and \(ATC^{*}\) is moderately sensitive respect to \(\beta \). When \(\beta \) is reduced, both \(T^{*}\) and \(Q^{*}\) increases, while \(ATC^{*}\) and \(B^{*}\) decrease and vice versa.

  • \(T^{*}, Q^{*}, B^{*}\) and \(ATC^{*}\) are a little sensitive respect to \(I_c\). When \(I_c\) start to decrease, \(T^{*}\) and \(Q^{*}\) increase, while \(ATC^{*}\) and \(B^{*}\) decrease and vice versa.

  • \(T^{*}, Q^{*}, B^{*}\) and \(ATC^{*}\) are a little sensitive respect to \(\theta \). When \(\theta \) starts to decrease, \(T^{*}\) and \(Q^{*}\) increase, while \(ATC^{*}\) and \(B^{*}\) decrease and vice versa.

  • \(T^{*}, Q^{*}, B^{*}\) and \(ATC^{*}\) are a little sensitive respect to \(t_0\). When \(t_0\) is decreased, \(T^{*}\) and \(Q^{*}\) increase, while \(ATC^{*}\) and \(B^{*}\) decrease and vice versa.

  • \(T^{*}, Q^{*}, B^{*}\) are gently sensitive to \(\pi \), while \(ATC^{*}\) is a little sensitive to the changes in \(\pi \). When \(\pi \) starts to decrease, \(T^{*}\), \(Q^{*}\) and \(B^{*}\) increase, but \(ATC^{*}\) decreases and vice versa.

Table 4 Numerical analysis results of case 2 on shortage and carrying costs
Full size table
Table 5 The results of the case 3
Full size table

Table 5 shows the numerical analysis results related to the third case. The subsequent results can be drawn from Table 5.

  • \(T^{*}, Q^{*}, B^{*}, k\) and \(ATC^{*}\) are moderately sensitive to the changes in parameter \(\beta \). When \(\beta \) is decreased, \(T^{*}\), \(Q^{*}\), \(B^{*}\) and \(ATC^{*}\) decrease but k rises and vice versa.

  • \(T^{*}, Q^{*}, B^{*}, ATC^{*}\) and k are gently sensitive to \(I_c\). When \(I_c\) is reduced, \(T^{*}\), \(Q^{*}\), \(B^{*}\) and \(ATC^{*}\) decrease but k rises and vice versa.

  • \(T^{*}, Q^{*}, B^{*}\) and k are sensitive respect to \(\theta \). When \(\theta \) start to decrease, \(T^{*}\), \(Q^{*}\) and k increase while \(B^{*}\) decreases and vice versa. \(ATC^{*}\) is a little sensitive to the changes in \(\theta \). When \(\theta \) start to decrease, \(ATC^{*}\) reduces and vice versa.

  • \(T^{*}, Q^{*}, B^{*}, k\) and \(ATC^{*}\) are a little sensitive to \(t_0\). When \(t_0\) is decreased, \(T^{*}\), \(Q^{*}\), \(B^{*}\) and \(ATC^{*}\) decrease but k increases and vice versa.

We can conclude from the performed sensitivity analysis that with increasing in the length of advanced payment, the buyers’ total cost increases. Thus, choosing the smallest length of prepayment is recommended to the buyers. Also, with decreasing in price discount factor, the buyers’ total cost decreases. Therefore, discount policy can act as an incentive mechanism to persuade the buyers for full advance payment. Furthermore, perishable items with lower deterioration rate decreases the total cost of the buyers. With increasing in the capital cost, the buyers’ total cost increases. Thus, in advance payment scheme, it’s recommended to the buyers to choose the suppliers with lower capital cost rate.

In summary, according to all cases, the optimum situation of the buyer happens with the highest value of price discount for advanced payment, the lowest value of the length of prepayment, the least deterioration and capital cost rates.

6 Conclusion

Advanced payment scheme is an effective strategy widely used by firms especially in less developed countries. The advanced payment scheme is a reliable method for exporters and decreases the risk of cancelling orders from the international buyers. Although this strategy is not very interesting for buyers because of the capital cost, but in some cases the buyers don’t have any of other choices. To persuade the buyers to participate in this mechanism the vendors usually offer them a price discount related to full advanced payment.

In this paper three EOQ models for decaying products under full advanced payment and different conditions including; (1) without shortage, (2) full backordering, and (3) partial backordering. We considered that the decaying rate is fixed and the entire purchasing cost is paid before delivery time. Moreover, the vendor offered a price discount to persuade the buyer to participate in this payment scheme. We showed that the objective functions are convex and the closed form solutions are derived.

Numerical examples represented the performance of the models. Also sensitivity analyses investigate the impacts of changing in parameters on the decision variables and also the entire cost. The results show that the length of prepayment, the price discount linked to advance payment, the decaying rate and the capital cost rate influence the buyers’ decision variables and total costs. This paper can help the vendors and buyers to offer and select the best full advanced payment scheme.

For future directions, we suggest considering time dependent demand rate or considering partial advance-partial delayed payment scheme for perishable products. Furthermore, Involving inflation rates and uncertainty of some parameters, such as demand or perishable rate can make the problem more realistic. Also considering different conditional discount like linked to order quantity discount or more incentive mechanism for cooperation between members can be interesting which we left for future researches.