Individual optimal pension allocation under stochastic dominance constraints

Abstract

An individual investor has to decide how to allocate his/her savings from a retirement perspective. This problem covers a long-term horizon. In this paper we consider a 40-year horizon formulating a multi-criteria multistage program with stochastic dominance constraints in an intermediate stage and in the final stage. As we are dealing with a real problem and we have formulated the model in cooperation with a commercial Italian bank, the intermediate stage corresponds to a possible withdrawal allowed by the Italian pension system. The sources of uncertainty considered are: the financial returns, the interest rate evolution, the investor’s salary process and a considerable withdrawal event. We include a set of portfolio constraints according to the pension plan regulation. The objective of the model is to minimize the Average Value at Risk Deviation measure and to satisfy wealth goals. Three different wealth target formulations are considered: a deterministic wealth target (i.e. a comparison between the accumulated average wealth and a fixed threshold) and two stochastic dominance relations—the first order and the second order—introducing a benchmark portfolio and then requiring the optimal portfolio to dominate the benchmark. In particular, we prove that solutions obtained under stochastic dominance constraints ensure a safer allocation while still guaranteeing good returns. Moreover, we show how the withdrawal event affects the solution in terms of allocation in each of the three frameworks. Finally, the sensitivity and convergence of the stochastic solutions and computational issues are investigated.

1 Introduction

The pension system has become increasingly complex and structured throughout Europe in the last few decades. Because of the financial and social crisis, several countries have implemented strong reforms in their state welfare systems to reduce pension costs and improve the state budget balance. Furthermore, they have allowed, indeed encouraged, the establishment of private pension facilities. We have to consider three pillars. The first concerns the state pension system. The second concerns the relationship between the employer and the employee. The third pillar consists of individual investment plans issued mainly by insurance companies.

In general, a private pension fund is an investment fund which receives periodic contributions from a private investor and then provides an annuity during the person’s retirement. As a public pension does not always give pensioners a sufficient income, a reasonable aim for private pensions is to guarantee the integration of the public retirement pension so that the total income before and after retirement does not differ substantially. To satisfy this target, it is crucial to understand the difference between the Defined Benefit Fund (DBF) and the Defined Contribution Fund (DCF). DBFs are characterized by a mutual structure, meaning that the benefit during retirement is fixed and independent of the total amount of the contribution accumulated in the fund. This implies that if the final wealth is not sufficient to support the benefit, the fund draws money from the current contributions of younger investors. DCFs establish the level of the contribution. In this case, the benefit during retirement depends on the total accumulated wealth and on some actuarial considerations. DCFs thus become similar to private savings in the sense that the subscriber bears the risk (see e.g. Gerrard et al. 2004, 2006).

This research has been conducted in collaboration with a commercial Italian bank which offers a second pillar DCF pension plan to its employees. In particular, the bank would like to propose a tool for its employees that could suggest the optimal dynamic strategy from a pension perspective according to their specific characteristics. Therefore, some of the features of the model have been required directly by the bank managers. Such a model faces the individual investment issue. The individual asset allocation problem was first investigated by Merton (1969, 1971), who introduced the concept of consumption and optimal investment through a dynamic programming approach in order to maximize the utility for a private investor over a fixed time horizon. Richard (1975) introduces the concept of lifetime uncertainty, labour and insured wealth as further elements to be taken into account. Berger and Mulvey (1998) propose a tool named the Home Account Advisor, a multistage model which optimizes the investor’s financial objective considering jointly investments, savings and borrowings. Several contributions have addressed individual asset allocation, not necessarily from a pension perspective. However, they establish the common approaches for the description of all those variables that characterize the investor’s investment, i.e. the salary process, consumption, borrowings, etc. (see for example Consiglio et al. 2004, 2007; Consigli 2007; Medova et al. 2008). An individual investor typically has more than one goal, for instance to obtain suitable retirement wealth while minimizing risk. The models proposed in the literature consider this issue in different ways. A common approach is to split the portfolio into sub-portfolios and dedicate each of these to a specific target (e.g. Brunel 2003; Chhabra 2005). However, recent works propose multi-criteria models without sub-portfolios. For example Cai and Ge (2012) consider a loss-aversion objective which minimizes a loss risk measure and maximizes the final wealth, having as a constraint a minimum level of expected wealth in order to maintain the recipient’s lifestyle. Our model follows this approach, as well as that proposed in Kilianová and Pflug (2009), adopting a multi-criteria framework.

In the individual investment problem, the main features of a retirement perspective portfolio allocation are: a particular asset universe composed of pension funds, the definition of a long-term horizon strategy and the stochastic elements we address (see Milevsky and Young 2007; Horneff et al. 2008; Consigli et al. 2012; Gerrard et al. 2012). An overview of the individual pension problem can be found in Bertocchi et al. (2010).

The model we introduce considers as stochastic sources all the financial and monetary processes, i.e. returns on the pension funds and investor’s salary. Moreover, we also take into account the investor’s withdrawal decision which is one of the most effective investor behaviours in a pension strategy as it usually concerns an important part of the wealth accumulated in the pension plan. In determining an individual investor’s strategies, it is imperative to know the way in which the investor takes a decision (see Kahneman and Tversky 1979). Many works have addressed behavioural finance and proposed models which translate behaviours into constraints (see Blake et al. 2013).

To face sources of uncertainty and the bank’s request to define a dynamic strategy over a long-term horizon, we apply the instruments provided by Stochastic Programming. In particular, we formulate a multistage stochastic program that allows rebalancing and withdrawals at given time points. Moreover, in contrast to all previous papers, we enrich the model with stochastic dominance constraints which offer an attractive way of comparing the investment strategy (static or dynamic) with a given benchmark. Indeed, while mean-risk approaches compare portfolios only in terms of mean returns and measures of risk for the returns (losses), stochastic dominance relations employ the whole probability distribution of the returns. Finally, stochastic dominance relations are consistent with utility theory (see Levy 2016 and references therein); for example, a portfolio dominates a benchmark in the sense of second order stochastic dominance if and only if every non-satiable and risk-averse decision maker either prefers the portfolio to the benchmark or is indifferent between them.

The notion of stochastic dominance was introduced in statistics more than 50 years ago and it was first applied in the field of Economics and Finance in Quirk and Saposnik (1962), Hadar and Russell (1969) and Hanoch and Levy (1969). Later on, second order stochastic dominance constraints were applied to static stochastic programs in Dentcheva and Ruszczynski (2003) and Luedtke (2008) and to portfolio efficiency analysis (see Kuosmanen 2004; Dupačová and Kopa 2012 and, more recently, Kopa and Post 2015). Similarly, first order stochastic dominance constraints were used in Kuosmanen (2004), Dentcheva and Ruszczyński (2004) and Dupačová and Kopa (2014). In multistage stochastic programming, second order stochastic dominance constraints were applied to asset-liability modelling in Yang et al. (2010) and to mixed-integer programming in Escudero et al. (2016). Moving on from these works, our purpose is to apply first and second order stochastic dominance to portfolio allocation from a long-term horizon pension perspective and compare the results of three models (with expectation type constraints, first order stochastic dominance constraints and second order stochastic dominance constraints). Examining the pension problem with stochastic dominance constraints becomes much more complex and computationally demanding, but we show that the problem can remain tractable and be enhanced with more attractive results in terms of the reward/risk performance of the final wealth.

The paper is structured as follows. First, in Sect. 2, we define the objectives, the stochastic dominance constraints and the other elements of the model. Then, Sect. 3 describes the main settings of the problem, the stochastic tree structure and the generation of the stochastic processes. In particular we dedicate a paragraph to the short-term interest rate modelling and one to a heuristic historical extraction for the pension fund returns. Section 4 presents the results of the investment problem models, discussing the differences between the proposed formulations and the main improvements achieved by including stochastic dominance constraints. This is followed by sensitivity and convergence analysis (including computational issues) in Sect. 5. The paper concludes with Sect. 6.

2 Individual pension model

The aim of the model is to define the optimal allocation among pension funds for an employee from a retirement perspective. Thus, we face a multi-criteria problem in satisfying different investors’ targets. We deal with three main features: a long-term horizon with a fixed and given sequence of portfolio rebalancing stages, a comparison to a specific benchmark portfolio strongly required by the bank with which we cooperate, and an uncertain environment regarding: the returns on the pension funds, the salary process and the investor’s withdrawal choice. These elements naturally lead to a multistage stochastic programming approach involving policy constraints, inventory balance constraints and cash balance constraints. There are many approaches to comparing the optimal solution with a given benchmark. Of these, to consider the whole distribution of the wealth rather than a set of statistics, we adopt stochastic dominance constraints.

2.1 Stochastic dominance

The basic definition of first order stochastic dominance (FSD) is as follows: a random variable A first order stochastically dominates a random variable B if the cumulative probability distribution function of A is below that of B. Alternatively, A first order stochastically dominates B if and only if the expected utility of A is greater than or equal to the expected utility of B for all utility (non-decreasing) functions; hence, every non-satiated investor prefers A to B or is indifferent between them. Finally, using quantile functions, A first order stochastically dominates B if and only if the quantile function of A is above the quantile function of B. For further detail, see Levy (2016) and references therein. In this paper, we consider random variables (representing random wealth) having a discrete distribution with equiprobable scenarios (realizations). Under this assumption, it is useful to formulate the FSD conditions using a permutation matrix formulation as proposed in Kuosmanen (2004). The random wealth of the portfolio (with realizations ${\mathbf {w}}_{t_{int}} = ({w}_{t_{int},1},\ldots ,{w}_{t_{int},S})'$) first order stochastically dominates the random wealth of the benchmark (BM) portfolio (with realizations ${\mathbf {w}}_{t_{int}}^{BM} = ({w}_{t_{int},1}^{BM},\ldots ,{w}_{t_{int},S}^{BM})'$) at the intermediate stage if and only if

$$\begin{aligned} {\mathbf {w}}_{t_{int}} \ge {\mathbf {P}}_{t_{int}} \cdot {\mathbf {w}}_{t_{int}}^{BM} \end{aligned}$$

(1)

for at least one permutation matrix ${\mathbf {P}}_{t_{int}}$ and, similarly, at the final stage if and only if

$$\begin{aligned} {\mathbf {w}}_{T} \ge {\mathbf {P}}_T \cdot {\mathbf {w}}_{T}^{BM} \end{aligned}$$

(2)

for at least one permutation matrix ${\mathbf {P}}_T$ where all elements of the permutation matrices are binary variables satisfying conditions (3) and (4).

$$\begin{aligned} \sum _{i}P_{i,j}= & {} 1 \ \ \forall j \end{aligned}$$

(3)

$$\begin{aligned} \sum _{j}P_{i,j}= & {} 1 \ \ \forall i. \end{aligned}$$

(4)

Similarly, the basic definition of second order stochastic dominance (SSD) is as follows: a random variable A second order stochastically dominates a random variable B if the integrated cumulative probability distribution function of A is below that of B. Alternatively, A second order stochastically dominates B if and only if the expected utility of A is greater than or equal to the expected utility of B for all concave utility functions; hence, every non-satiated and risk-averse investor prefers A to B or is indifferent between them. Finally, using quantile functions, A second order stochastically dominates B if and only if the integrated quantile function of A is above the integrated quantile function of B. Assuming again discrete distributions of random wealth with equiprobable scenarios, following Kuosmanen (2004), the random wealth of the portfolio (with realizations ${\mathbf {w}}_{t_{int}} = ({w}_{t_{int},1},\ldots ,{w}_{t_{int},S})'$) second order stochastically dominates the random wealth of the benchmark portfolio (with realizations ${\mathbf {w}}_{t_{int}}^{BM} = ({w}_{t_{int},1}^{BM},\ldots ,{w}_{t_{int},S}^{BM})'$) at the intermediate stage if and only if

$$\begin{aligned} {\mathbf {w}}_{t_{int}} \ge {\mathbf {Q}}_{t_{int}} \cdot {\mathbf {w}}_{t_{int}}^{BM} \end{aligned}$$

(5)

and similarly at the final stage if and only if

$$\begin{aligned} {\mathbf {w}}_{T} \ge {\mathbf {Q}}_T \cdot {\mathbf {w}}_{T}^{BM} \end{aligned}$$

(6)

for some square double stochastic matrices ${\mathbf {Q}}_{t_{int}}$ and ${\mathbf {Q}}_T$, i.e. satisfying the following conditions

$$\begin{aligned} \sum _{i}Q_{i,j}= & {} 1 \ \ \forall j \end{aligned}$$

(7)

$$\begin{aligned} \sum _{j}Q_{i,j}= & {} 1 \ \ \forall i \end{aligned}$$

(8)

$$\begin{aligned} Q_{i,j}\ge & {} 0 \ \ \forall i,j. \end{aligned}$$

(9)

The only, very crucial, difference between matrices ${\mathbf {Q}}$ and matrices ${\mathbf {P}}$ is that the elements of ${\mathbf {Q}}$ do not have to be binary, but just have to belong to the interval [0, 1], so each row and each column represents a convex combination.

2.2 Objective function

According to the bank’s requirements, the problem needs to consider multiple criteria, which are:

• 1. to minimize a coherent risk deviation functional of the final wealth produced by the optimal allocation,

• 2. to maximize the expected wealth at an intermediate stage,

• 3. to maximize the expected wealth at the final stage (end horizon).

In many financial applications the risk is accounted as tail risk. In a similar application, Kilianová and Pflug (2009) suggests adopting the Average Value at Risk (${ AV}@R$), which is the average of the distribution below a certain threshold, computed according to a fixed confidence level, such threshold being the Value at Risk (V@R). More specifically, Kilianová and Pflug (2009) uses the distance between the expected value of the random wealth and its ${ AV}@R$, i.e. the ${ AV}@R$ Deviation of the random wealth at t-th stage $W_t$, ${ AV}@{ RD}(W_t)={\mathbb {E}}(W_t) - { AV}@R(W_t)$. Considering the discrete distribution of $W_t$ given by scenarios $w_{t,s}$ (where $t=t_0,\ldots ,T$ represents the stage and $s=1,\ldots ,S$ represents the scenarios) taken with probabilities $p_{s}$, the formulation of the minimization of the ${ AV}@{ RD}$ at the last stage T for a given confidence level $\alpha$ is

$$\begin{aligned}&\min \sum _{s=1}^{S} \left( w_{T,s}\cdot p_s \right) -a+\frac{1}{\alpha } \sum _{s=1}^{S}\left( z_s \cdot p_s\right) \end{aligned}$$

(10)

$$\begin{aligned}&\text {s.t.} -a+w_{T,s}+z_s \ge 0 , \ \ \ z_s \ge 0 \end{aligned}$$

(11)

As we are dealing with a discrete distribution, we implement the AV@R computation as suggested in Rockafellar and Uryasev (2000, 2002) and thus the discrete definition of ${ AV}@{ RD}$ needs inequalities (11) in order to define jointly the variables a and $z_s$.

As suggested in Dupačová et al. (2002), we adopt the $\epsilon$-Constrained Approach to include the other two criteria, i.e. the following wealth targets

$$\begin{aligned}&\sum _{s=1}^{S} w_{t_{int},s}\cdot p_s \ge \Pi _{t_{int}} \end{aligned}$$

(12)

$$\begin{aligned}&\sum _{s=1}^{S} w_{T,s}\cdot p_s \ge \Pi _T \end{aligned}$$

(13)

The first wealth target (12) forces the average of the accumulated wealth at an intermediate stage ($t_{int}$) to be greater than or equal to a fixed amount, $\Pi _{t_{int}}$. Similarly, the final wealth target (13) is fixed at the level $\Pi _T$.

Assuming we observe a benchmark portfolio the wealth $w^{BM}_{t,s}$ of which evolves through the stages t and along each scenario s, we define the values of $\Pi _{t_{int}}$ and $\Pi _T$ in (14) and (15) as the expected value of the benchmark portfolio’s wealth:

$$\begin{aligned} \Pi _{t_{int}}= & {} \frac{1}{S} \sum _{s=1}^{S}w^{BM}_{t_{int},s} \end{aligned}$$

(14)

$$\begin{aligned} \Pi _T= & {} \frac{1}{S} \sum _{s=1}^{S}w^{BM}_{T,s}. \end{aligned}$$

(15)

We refer to the model which includes (12) and (13) as the Deterministic Wealth Target (DWT) model . Furthermore, we propose two additional formulations using Stochastic Dominance (SD). In particular, we refer to the FSD model in which (12) and (13) are replaced with the FSD conditions as follows

$$\begin{aligned}&w_{t_{int},s} \succeq _{FSD} w^{BM}_{t_{int},s} \end{aligned}$$

(16)

$$\begin{aligned}&w_{T,s} \succeq _{FSD} w^{BM}_{T,s}. \end{aligned}$$

(17)

Also, we refer to the SSD model in which (12) and (13) are replaced with the SSD conditions as follows

$$\begin{aligned}&w_{t_{int},s} \succeq _{SSD} w^{BM}_{t_{int},s} \end{aligned}$$

(18)

$$\begin{aligned}&w_{T,s} \succeq _{SSD} w^{BM}_{T,s}. \end{aligned}$$

(19)

In these two distinct models, the SD constraints compare the whole distribution of the accumulated wealth of the optimal solution to that of the benchmark portfolio’s wealth at an intermediate and at the final stage.

2.3 Other constraints

We suppose that the decision times correspond to all stages except the last, in which we just compute the accumulated final wealth. The investment universe is composed of five different pension funds which are the sub-portfolios composing the pension plan. We define the following non-negative variables where the index $i=1,\ldots ,5$ represents the pension fund, $t=t_0,\ldots ,T$ represents the stage and $s=1,\ldots ,S$ represents the scenario:

• $c_{i,t,s}$ expresses the level of contribution saved by the investor in the pension fund i at stage t in scenario s;

• $x^{+}_{i,t,s}$ and $x^{-}_{i,t,s}$ are the rebalancing variables that allow the redistribution of the accumulated wealth among the chosen pension funds. These two variables quantify respectively how much the investor buys and how much he/she sells of each fund i in scenario s at the beginning of each stage t, i.e. before adding the contribution.

Finally, we can list the set of constraints in order to express the regulatory bounds and the cash balance conditions.

2.3.1 Salary process

Given an initial level ${sal}_{t_0,s}$ equal to the actual salary of the employee and having generated the salary growth rate $\rho ^{sal}_{t,s}$, we can easily describe the salary process as follows

$$\begin{aligned} sal_{t,s}=sal_{t-1,s}\cdot (1+\rho ^{sal}_{t,s}), \;\;\forall t>t_0, \forall s. \end{aligned}$$

(20)

2.3.2 Maximum contribution level

In each stage, the employee does not want to invest more than a certain maximum percentage of his/her salary. Therefore, we introduce the parameter propensity to save ($\lambda$) and the parameter employer contribution (e) which represents a supplementary contribution added by the employer as a percentage of the employee’s contribution. Moreover, the time structure of the problem defines the stages every $\varDelta t$ years, but in real life the contribution is added to the pension fund yearly (sometimes also monthly). Therefore, considering the growth rate of the salary to be constant over each period and equal to the discount rate and assuming that the contribution is paid at the beginning of each year, we compute the actual value of a growing annuity paying one euro for $\varDelta t$ years and multiplying by $\varDelta t$. Thus, the constraint describing the maximum contribution level is

$$\begin{aligned} \sum _{i=1}^n c_{i,t,s}\le sal_{t,s}\cdot \lambda \cdot (1+e) \cdot \varDelta t, \;\;\forall t, s. \end{aligned}$$

(21)

2.3.3 Total minimum contribution

The bank requires a minimum contribution m from the employee who decides to enter into the pension plan.

$$\begin{aligned} \sum _{i=1}^n c_{i,t,s}\ge m, \;\;\forall t, s. \end{aligned}$$

(22)

2.3.4 Portfolio balance

We define the set of constraints that describes the portfolio allocation, the rebalancing decisions and the wealth account. For this purpose, we introduce the returns $\rho _{i,t,s}$ on the pension funds and the holding variable $h_{i,t,s}$, which represents the amount we hold in each pension fund. Moreover, we define the initial cash parameter $w_0$ and the initial portfolio vector $h_{i,0}$. The choice to withdraw an amount of money from the pension fund is represented by the coefficient $d_{t,s}$. According to the Italian rules, the investor can withdraw a considerable amount of money only for specific reasons (e.g. housing or health) and only after a minimum period spent in the pension plan. Therefore, we assume that this decision can be made in one predetermined stage with a certain probability. In particular, $d_{t,s}=1-b$ for a given withdrawal percentage, b, at a certain stage with a certain probability and $d_{t,s}=1$ otherwise.

$$\begin{aligned}&h_{i,t_0,s}=h_{i,0}+c_{i,t_0,s}+x^{+}_{i,t_0,s}-x^{-}_{i,t_0,s}, \;\;\forall i, s \end{aligned}$$

(23)

$$\begin{aligned}&\sum _{i=1}^n x^{+}_{i,t_0,s}=\sum _{i=1}^n x^{-}_{i,t_0,s}+w_0, \;\;\forall s \end{aligned}$$

(24)

$$\begin{aligned}&x^{-}_{i,t_0,s}\le h_{i,0}, \;\; \forall i, s \end{aligned}$$

(25)

$$\begin{aligned}&\sum _{i=1}^n x^{-}_{i,t_0,s}\le \theta \sum _{i=1}^n h_{i,0}, \;\; \forall s \end{aligned}$$

(26)

$$\begin{aligned}&h_{i,t,s}=h_{i,t-1,s}\cdot (1+\rho _{i,t,s}) \cdot d_{t,s}+c_{i,t,s} +x^{+}_{i,t,s}-x^{-}_{i,t,s}, \;\; \forall t \in (t_0,T), \forall i, s \end{aligned}$$

(27)

$$\begin{aligned}&w_{t,s}=\sum _{i=1}^n (h_{i,t-1,s}\cdot (1+\rho _{i,t,s})), \;\; \forall t>t_0, \forall s \end{aligned}$$

(28)

$$\begin{aligned}&\sum _{i=1}^n x^{+}_{i,t,s}=\sum _{i=1}^n x^{-}_{i,t,s}, \;\; \forall t \in (t_0,T), \forall s \end{aligned}$$

(29)

$$\begin{aligned}&x^{-}_{i,t,s}\le h_{i,t-1,s} \cdot (1+\rho _{i,t,s}), \;\; \forall t \in (t_0,T), \forall s, i \end{aligned}$$

(30)

$$\begin{aligned}&\sum _{i=1}^n x^{-}_{i,t,s}\le \theta \cdot w_{t,s}, \;\; \forall t \in (t_0,T), \forall s \end{aligned}$$

(31)

$$\begin{aligned}&x^{+}_{i,t,s}\ge 0, \;\;x^{-}_{i,t,s}\ge 0, \;\;c_{i,t,s}\ge 0, \;\; \forall i, t, s. \end{aligned}$$

(32)

Equation (23) defines the holding in the first stage for each pension fund as the sum of the initial portfolio allocation $h_{i,0}$, the first period contribution $c_{i,t_0,s}$, the reallocation of purchased assets $x^{+}_{i,t_0,s}$ and sold assets $x^{-}_{i,t_0,s}$. Equation (24) is the cash balance of the initial wealth $w_0$. Equation (25) is the inventory balance of the first stage portfolio and (26) is its turnover constraint. For next stages, Eq. (27) defines the holding $h_{i,t,s}$ for each pension fund as the sum of the capitalization of the previous holding $h_{i,t-1,s}$ (reduced by the withdrawal $d_{t,s}$), the contribution $c_{i,t,s}$, the reallocation of the accumulated wealth $x^{+}_{i,t,s}$ and $x^{-}_{i,t,s}$. Equations (29), (30) and (31) describe the portfolio reallocation. Moreover, (26) and (31) define the turnover constraints through the parameter $\theta$ which states that we cannot sell more than a fixed percentage $\theta$ of the portfolio. Finally, Eq. (28) computes the accumulated wealth in each stage for each scenario. According to this wealth variable we build the target constraints and the objective function.

Using the stochastic tree structure, we must ensure that the decision variables depend only on the past values of the stochastic processes. Therefore, we include the following set of non-anticipativity constraints

$$\begin{aligned} c_{i,t,{\dot{s}}}= & {} c_{i,t,{\tilde{s}}}, \;\; \forall i, t \end{aligned}$$

(33)

$$\begin{aligned} x^+_{i,t,{\dot{s}}}= & {} x^+_{i,t,{\tilde{s}}}, \;\; \forall i, t \end{aligned}$$

(34)

$$\begin{aligned} x^-_{i,t,{\dot{s}}}= & {} x^-_{i,t,{\tilde{s}}}, \;\; \forall i, t \end{aligned}$$

(35)

for each couple of scenarios, ${\dot{s}}$ and ${\tilde{s}}$, which share the same history until stage t.

The formulation described produces a Linear Program (LP) in the DWT and SSD cases. The formulation with FSD produces a Mixed Integer Program (MIP) problem in which the computational complexity largely increases because of the high number of binary variables.

2.4 Benchmark portfolio definition

To make a proper comparison, the benchmark portfolio evolves in the same stochastic environment as the optimal dynamic strategy but with a fixed allocation which is the 1 / n suggested in DeMiguel et al. (2009), i.e. an equally distributed portfolio among the available asset. Indeed, the benchmark portfolio is assumed to be affected by the same withdrawal event and to return the average of the pension fund returns, i.e. $\rho _{t,s}^{BM}=1/n\sum _{i=1}^n \rho _{i,t,s}, \, \forall t, s$. Moreover, as in the optimal portfolio, the benchmark portfolio periodically receives contributions. Whereas for the optimal solution the contribution level is a decision variable controlled with Eq. (21), the benchmark rises according to the maximum allowed contribution, i.e. $C_{t,s}^{BM}= sal_{t,s}\cdot \lambda \cdot (1+e) \cdot \varDelta t, \,\forall t, s$. Starting from the initial wealth $w_{0}^{BM}=\sum _{i=1}^n h_{i,0}+w_0,\, \forall s$, the evolution of the benchmark portfolio wealth is given by the following conditions

$$\begin{aligned}&\displaystyle h_{t_0,s}^{BM} = w_{0}^{BM}+C_{t_0,s}^{BM} \, \;\; \forall s \end{aligned}$$

(36)

$$\begin{aligned}&\displaystyle h_{t,s}^{BM} = h_{t-1,s}^{BM}\cdot (1+\rho _{t,s}^{BM})\cdot d_{t,s} +C_{t_0,s}^{BM} \, \;\; \forall t>t_0, \forall s \end{aligned}$$

(37)

$$\begin{aligned}&\displaystyle w_{t,s}^{BM} = h_{t-1,s}^{BM} \cdot (1+\rho _{t,s}^{BM}) \, \;\;\forall t>t_0, \forall s. \end{aligned}$$

(38)

3 Numerical study

We implement the DWT, SSD and FSD models for the case of a 30-year-old Italian man with an expected working life of 40 years. The two wealth goals he wants to achieve are an intermediate objective after 8 years and a final pension benefit in 40 years. The 8-years target is due to the Italian rules, which allow the withdrawal of money only after 8 years following subscription to the pension plan contract. Then, the investor wants to have at least a minimum amount of expected wealth in case he will withdraw from his pension position at a given time $t_{int}$. For these reasons, we create a stochastic scenario tree with six stages, each equal to 8 years, i.e. $\varDelta t=8$ and then $t=0,8,16,24,32,40$ and $t_{int}=8$.

The asset universe is composed by one guaranteed capital and 4 risky pension funds. The stochasticity concerns the pension fund returns, the salary evolution and the investor’s withdrawal choice and it is represented by a discrete scenario tree composed of S paths and characterized by regular branching. The number of scenarios is chosen according to the trade-off between computational tractability and a reasonable representation of the stochastic variables as we discuss extensively in Sect. 5. The tree is generated assuming that the scenarios are equiprobable, i.e. $p_s=1/S$.

3.1 Short-term rate model

The first pension fund is a guaranteed capital investment with a risk-free return. We assume the risk-free rate to be represented by a short-term interest rate. In the European setting, the EURo InterBank Offered Rate (EURIBOR) represents the average interest rate at which banks in the eurozone lend funds to other banks. Therefore we adopt the EURIBOR 3-month rate as an approximation of the risk-free rate. To model short-term rate dynamics, several models have been proposed during the last decades. Their evolution has been linked to the evolution of economic theory, which through the second part of the last century hypothesized a long-term equilibrium rate and the impossibility of negative rates. Some of them, such as Rendleman and Bartter (1980) and Ho and Lee (1986), do not include a mean-reverting effect, while others do not allow negative interest rates, for instance Cox et al. (1985), Black et al. (1990) and Black and Karasinski (1991). Vasicek (1977) proposes a model which describes a mean-reverting process and allows the interest rate to become negative which is nowadays a common situation for real interest rates. The Vasicek model describes the interest rate dynamic as follows

$$\begin{aligned} dr_t=\alpha (\beta -r_t) dt +\nu dW_t, \;\; \forall t \end{aligned}$$

(39)

where $W_t$ is the Wiener process. There have been some extensions of the Vasicek model in order to describe a full yield curve, for instance Hull and White (1990). However, as we need to create scenarios only for the short-term interest rate, we adopt the Vasicek model to describe and forecast the EURIBOR 3-month interest rate.

We analyse the historical series of the EURIBOR 3-month rate from $1^{\text {st}}$ January 1999 to $31{\text {st}}$ December 2015. We perform a Maximum Likelihood Estimation for all the parameters and obtain the results reported in Table 1 according to three different estimation periods. In particular, we split the whole EURIBOR 3-month historical data into a pre-crisis period and one post-crisis period.

Table 1 Vasicek model estimation using the EURIBOR 3-month series

The estimations made for the post-crisis period and the whole period produce a very low parameter $\beta$. Then, as the Vasicek model parameters, we adopt those estimated for the pre-crisis period as an equilibrium interest rate equal to 2.5% seems more reasonable for a 40-year horizon problem.

The salary stochasticity is modelled assuming that its process follows the risk-free rate plus a constant risk premium. The salary stochastic process follows the risk-free rate process plus a constant premium of 2%. In this way, we account for a reasonable link between the evolution of the salary and economy growth approximated by the risk-free rate.

3.2 Risky asset returns

The other four pension funds are related to risky assets for which we have historical data series composed of daily observations of daily prices. As we want to avoid distribution assumptions but still want to consider the correlation structure and periodical changes in the return structures, we generate scenarios through an extraction from historical series. The extraction implies that for each node we draw the return of a single day for all the assets. In this way, we take care of the correlation structure. The drawing is not completely random and is differentiated between nodes in the second stage and nodes in the next stages. For the second stage nodes, i.e. the returns which describe the evolution between the here-and-now stage and the second stage we propose Algorithm 1. For further stages we suggest Algorithm 2.

By adopting these two algorithms, we consider that the financial markets show cycles and each path from the root node should correspond to a different point of the cycle. Then, within each cycle we consider good and bad scenarios by dividing the empirical distributions. The methodology described is designed for single asset scenario generation, but it is easily possible to extend it to a multiple asset scenario generation having as historical series the daily return observations of a set of assets. In summary:

• we consider the correlation drawing the return for each node from a single day’s observation;

• the whole historical series is split into sub-periods and the second stage nodes are drawn from different sub-periods considering the financial cycles;

• the descendant nodes consider the time path followed by the cycle;

• in splitting the empirical distribution, we consider all the parts of the distributions.

The described procedure is relatively easy in the case that the scenario tree follows regular branching. However, it could also be extended for non-regular branching. Moreover, the chosen window sizes and the compounding periods strongly depend on the time structure of the problem. Considering the features of our model and its time structure, from the observed daily prices we compute the 2-year returns and then the equivalent 8-year returns.

The four risky pension funds are related to: the Dow Jones Equal Weight US Issued Corporate Bond Index, the Merrill Lynch US High Yield BB Corporate Bond Index, the FTSE100 Index and the S&P500 Index, respectively. For each index, we have daily returns on a daily basis from 1st January 1999 to 31st December 2015. Thus, we have a dataset composed of 4178 price observations for each index. The chosen indices are well differentiated in terms of the risk/reward profile, as shown in Table 2.

Table 2 Statistics of the 2-year returns

3.3 Parameter and initial portfolio settings

In the Italian job market framework, the average initial net salary for a young employee is roughly 15,000 euros, i.e. ${sal}_{t_0,s}=15{,}000$. In (21) we assume that the propensity to save parameter is $\lambda = 7\%$, while the employer contribution is $e= 50\%$, in line with the usual Italian context. According to the regulation of the pension plan we are considering, the total minimum contribution in (22) is $m_2= 300$ euros. We suppose that the investor’s initial portfolio is composed as follows: $h_{i,0}=[0\;\; 1000\;\; 1000\;\; 5000\;\; 5000]$; we also suppose the investor has no initial wealth, i.e. $w_0=0$. Although the pension plan does not impose any turnover bound, we set the turnover coefficient to $\theta =50\,\%$ in order to make the solution smoother. These settings concern Eqs. (23)–(31).

In the objective function (10) the ${ AV}@{ RD}$ is computed using the confidence level $\alpha =5\,\%$. As already explained, in the Italian pension system, a huge percentage of money can be withdrawn after eight years following subscription to the pension plan. For this reason, we set the intermediate target after eight years, i.e. $t_{int}=8$, and in the case that the investor withdraws, the amount withdrawn corresponds to 70% of the accumulated wealth, i.e. $d_{t,s}= 0.70$. We assume that the withdrawal event occurs with probability 50% and that it is independent of the other stochastic sources.

4 Results

To compare the three formulations, DWT, FSD and SSD, we consider the following three models:

DWT::

(10)–(11), (12)–(13), (20)–(38);

SSD::

(10)–(11), (18)–(19), (20)–(38);

FSD::

(10)–(11), (16)–(17), (20)–(38).

For each of these models, we present in-sample results and we analyse the sensitivity of the optimal allocation with respect to the withdrawal event.

In the following sections, in the dynamic allocation and dynamic wealth figures, guaranteed capital is depicted in white, and each grade of the greyscale corresponds to a specific pension fund from the less risky one (light grey) to the most risky one (dark grey). For the comparison between the empirical distributions of the final wealth, the grey line stands for the benchmark portfolio and the black line for the optimal solution.

4.1 No-withdrawal case

4.1.1 Deterministic wealth target (DWT)

Figure 1 shows the solution of the DWT case in terms of the percentage optimal allocation. The solution presented for each stage is the average solution over all nodes of that stage.

Fig. 1

Dynamic allocation—DWT

The here-and-now solution is well diversified among the four risky assets. The dynamic strategy includes the guaranteed capital pension fund from the third stage. Getting closer to the final horizon the portfolio continues to have a diversified allocation, slightly enlarging the portion invested in the equity pension fund. This behaviour is not in conflict with the common result of decreasing risk exposure as the evolution of the pension fund follows the historical financial cycles of the last 15 years, in which, during some periods, equity assets were less risky than bond assets. In Fig. 2, we present the average optimal allocation, showing the increasing average wealth over all scenarios in each particular stage.

Fig. 2

Dynamic wealth—DWT

The wealth process shows a positive trend thanks to the long-term horizon, which induces a vast amount of contributions and financial gains. All the assets are proportionally enriched at each decisional stage (stages: 1, 2, 3, 4, 5, corresponding to times: 0, 8, 16, 24, 32). The final wealth distribution and its statistics are shown in Fig. 3. The statistics for the final wealth show that the optimal allocation is more risky than the benchmark portfolio in terms of the standard deviation, but is definitely better in terms of V@R and ${ AV}@R$, with values almost twice those of the benchmark portfolio. The mean values are equal, highlighting that the deterministic target constraint is active. In summary, the ${ AV}@{ RD}$ minimization under DWT constraints ensures a portfolio which is preferred to the 1 / N portfolio: the expected wealth achieved is equal and the tail risk is substantially reduced.

Fig. 3

Final wealth distribution and related statistics, DWT

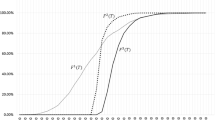
In Fig. 4 we propose a comparison between the quantile function of the benchmark wealth and of the final wealth accumulated by the investor. In Fig. 5 we show their integrated quantile functions. The figures show that the final wealth of the DWT model (black line) does not dominate the final wealth of the benchmark portfolio (grey line) either by FSD or by SSD.

Fig. 4

Quantile function—DWT

Fig. 5

Integrated quantile function—WT

The optimal strategy appears suitable according to the investor’s features. His young age allows an aggressive allocation in the here-and-now solution. The comparison between the empirical cumulative distribution functions in Fig. 4 shows that the DWT portfolio suffers in the right tail of the distribution. On the one hand, for these scenarios, the benchmark produces higher wealth. On the other hand, the minimization of the objective risk measure allows efficient control of the left tail in which the optimal portfolio reduces the huge losses of the benchmark portfolio.

4.1.2 Second order stochastic dominance (SSD)

In Fig. 6 we present the optimal solution of the SSD case as the percentage allocation. As in the previous case, the solution presented for each stage is the average solution over all the nodes of that stage.

Fig. 6

Dynamic allocation—SSD

The SSD here-and-now solution invests slightly more in the equity pension funds (33.4%) than the DWT option (30.8%). Through the stages, the optimal solution is well diversified and remains more aggressive than the DWT. However, the guaranteed capital pension fund is included from the second stage. In Fig. 7 we present the average optimal allocation showing the increasing wealth. The wealth evolution is aligned with the portfolio allocation. As in the DWT case the long-term horizon induces a high contribution level and remarkable financial gains, which increase the wealth accumulated in the pension plan. The final wealth distribution and its statistics are shown in Fig. 8. The final wealth distribution statistics show that the optimal portfolio reaches on average the same wealth as the benchmark portfolio. Moreover, the SSD leads the optimal portfolio to be far less risky than the benchmark portfolio and the DWT solution, having a lower standard deviation and a higher median. Thus, the final wealth for SSD is less volatile than for DWT, while V@R and AV@R are slightly smaller (worse) in the SSD case. In particular, as the SSD model’s feasible region is smaller than that of the DWT model, the ${ AV}@{ RD}$ has to be higher, but we observe only very small differences. To summarize, the solution for SSD has almost the same tail risk as for DWT and it reaches an equal expected wealth, but with a substantially higher median and a lower standard deviation. Moreover, of course, the SSD model guarantees that the portfolio dominates the benchmark in a specific and stronger sense than the DWT, that is, every non-satiated and risk-averse investor prefers the SSD optimal final wealth to the benchmark final wealth.

Fig. 7

Dynamic wealth—SSD

Fig. 8

Final wealth distribution and related statistics, SSD

In Fig. 9 we propose a comparison between the quantile function of the benchmark wealth and of the final wealth accumulated by the investor. In Fig. 10 we show their integrated quantile functions.

Fig. 9

Quantile function—SSD

Fig. 10

Integrated quantile function—SSD

The SSD relationship between the final wealth of the optimal SSD portfolio and of the benchmark portfolio is clearly satisfied, as shown in Fig. 10, while FSD is not requested and is therefore not fulfilled (see Fig. 9).

4.1.3 First order stochastic dominance (FSD)

In Fig. 11 we present the FSD optimal solution as a percentage allocation. As in the previous cases, the solution presented for each stage is the average solution over all the nodes of that stage.

Fig. 11

Dynamic allocation—FSD

Fig. 12

Dynamic wealth—FSD

The FSD allocation in the first stage is even more concentrated in the equity pension fund than in the DWT and the SSD cases. The portfolio is well diversified and the guaranteed capital pension fund is again included from the third stage (as in the DWT case), with a share consistently smaller than in the other two cases. The aggressive allocation of the FSD portfolio is induced by the FSD constraint. Indeed, the other two cases suffer a drawback in the right tail of the distribution but the FSD requires the optimal portfolio to beat the benchmark over all scenarios. Thus, the portfolio must look for higher returns and must opt for a riskier allocation. In Fig. 12 we present the average optimal allocation showing the increasing wealth. The wealth process takes advantage of the financial markets thanks to the equity pension funds which compose a remarkable part of the portfolio until the last decision stage. The final wealth distribution and its statistics are shown in Fig. 13. The strategy requires an increase in the right-tail of the distribution to fulfil the FSD constraint. Therefore, its average final wealth is the highest compared to the benchmark, DWT and SSD cases. However, both V@R and ${ AV}@R$ are lower than in the DWT and SSD cases, but still higher than the benchmark portfolio. The standard deviation is slightly lower than for the benchmark portfolio and remarkably lower than in the DWT case. Of course, as the feasible region is smaller than for the other models, the ${ AV}@{ RD}$ is larger than in the SSD and the DWT cases. To summarize, the FSD model achieves a higher average final wealth than the other models, the volatility is lower than in the DWT model and the tail risk is relatively high, but still smaller than that of the benchmark model. Of course, the FSD ensures the optimal portfolio beats the benchmark portfolio in a very strict sense, that is, every non-satiated investor has to prefer the FSD final wealth to the benchmark final wealth.

Fig. 13

Final wealth distribution and related statistics, FSD

In Fig. 14 we propose a comparison between the quantile function of the benchmark wealth and of the final wealth accumulated by the investor. In Fig. 15 we show their integrated quantile functions. Figure 14 confirms that the required FSD relationship is satisfied.

Fig. 14

Quantile function—FSD

Fig. 15

Integrated quantile function—FSD

4.2 Withdrawal case

In the following section, we develop the analysis of the optimal investment according to the three proposed formulations, also including the possibility that a withdrawal event might occur. Clearly, we assume that the same event occurs also for the benchmark portfolio wealth in order to make a fair comparison; otherwise, it would be impossible to reach the wealth targets. Moreover, the withdrawal event is assumed to be independent of the other stochastic processes and in particular of the salary.

4.2.1 Deterministic wealth target (DWT)

Figure 16 shows the DWT optimal solution as the percentage allocation considering the withdrawal event. The solution presented for each stage is the average solution over all the nodes of that stage.

Fig. 16

Dynamic allocation—WT withdrawal

The dynamic optimal allocation prefers the high-yield bond pension fund to the global bond fund. Thus, to achieve reasonable wealth in the case of withdrawal, the portfolio is more risky than in the no-withdrawal case. After the withdrawal stage, the portfolio shits more to the guaranteed capital pension fund in order to reduce the total riskiness. In Fig. 17 we present the average optimal allocation showing the increasing wealth.

Fig. 17

Dynamic wealth—DWT withdrawal

In the wealth process, the impact of withdrawal is demonstrated in the third stage. The dynamic is structured as follows: in the second stage, the investor makes the contribution and reallocation choice, taking account of the accumulated wealth and deciding whether to withdraw or not. Finally, in the case that the withdrawal is done at the end of the second stage, the wealth of the third stage is below its natural trend. We recall that the withdrawal consists of 70% of the wealth accumulated in the second stage and the event occurs with a probability of 50%. The remaining portfolio is invested primarily in the high-yield pension fund and its return partially mitigates the withdrawal. Therefore, in the third stage we observe a reduction in the wealth but the trend continues to be positive. The final wealth distribution and its statistics are shown in Fig. 18. The portfolio allocation guarantees an average return in line with the benchmark portfolio, i.e. the deterministic target constraint is active. The standard deviation of the DWT portfolio is slightly lower than that of the benchmark portfolio, and the V@R and ${ AV}@R$ of the DWT portfolio indicate the good quality of the solution compared to the benchmark portfolio.

Fig. 18

Final wealth distribution and related statistics, DWT withdrawal

In Fig. 19 we propose a comparison between the quantile function of the benchmark wealth and of the final wealth accumulated by the investor. In Fig. 20 we show their integrated quantile functions.

Fig. 19

Quantile function—DWT withdrawal

Fig. 20

Integrated quantile function—DWT withdrawal

The optimal solution does not guarantee either the FSD or the SSD relationship. In particular, it suffers some drawbacks both in the right part of the distribution and also in the central part.

4.2.2 Second order stochastic dominance (SSD)

In Fig. 21 we display the SSD optimal portfolio as the percentage allocation considering the withdrawal event. As in the previous case, the result presented for each stage is the average solution over all the nodes of that stage.

Fig. 21

Dynamic allocation—SSD withdrawal

The here-and-now solution makes a shift onto the high-yield bond pension fund, but not as strongly as for the DWT case. Then, through the stages, the allocation remains diversified but the portion invested in the guaranteed capital pension fund is slightly lower than in the DWT case and starts only from the third stage. In Fig. 22 we present the average wealth of the optimal allocation.

Fig. 22

Dynamic wealth—SSD withdrawal

The evolution of the wealth is again affected by the withdrawal event as for the DWT solution. However, as the target wealth is reached in the fifth stage (after 32 years), the last decision focuses mainly on risk reduction, making the final wealth less risky. The final wealth distribution and its statistics are shown in Fig. 23. The statistics for the final wealth distribution highlight a well-balanced portfolio which is able to beat the benchmark portfolio in all respects. The median is higher, the standard deviation is lower and the tail risk measures are also better than for the benchmark portfolio. The comparison between the SSD and the DWT illustrates that the two solutions are similar in terms of V@R and ${ AV}@R$, but the SSD portfolio is less risky in terms of the standard deviation and its median is higher. Thus, also for the withdrawal case, the SSD portfolio generally performs better than the DWT, guaranteeing the same expected return but with a much lower risk distribution.

Fig. 23

Final wealth distribution and related statistics, SSD withdrawal

In Fig. 24 we propose a comparison between the quantile function of the benchmark wealth and of the final wealth accumulated by the investor. In Fig. 25 we show their integrated quantile functions.

Fig. 24

Quantile function—SSD withdrawal

Fig. 25

Integrated quantile function—SSD withdrawal

The solution still shows some drawbacks with respect to the benchmark portfolio for the right tail of the distribution, but not as substantial as in the DWT case. In contrast to the DWT solution, the SSD option outperforms the benchmark portfolio also in the middle part of the distribution.

4.2.3 First order stochastic dominance (FSD)

In Fig. 26 we present the FSD optimal solution as the percentage allocation considering the withdrawal event. As in the previous cases, the solution for each stage is the average solution over all the nodes of that stage. The FSD optimal here-and-now allocation is equal to the here-and-now allocation of the no-withdrawal case. This means that the FSD constraints force the optimal solution independently of a possible withdrawal, which changes the solution in the subsequent stages. In particular the dynamic strategy appears more conservative than in the no-withdrawal case. In Fig. 27 we exhibit the average optimal allocation showing the increasing wealth. Again, the withdrawal effect is clear in the third stage. The final wealth distribution and its statistics are shown in Fig. 28. The optimal portfolio beats the benchmark portfolio in terms of average final wealth, standard deviation and tail risk measures. As in the no-withdrawal case, because of the smaller feasible region, the V@R and ${ AV}@R$ values are lower than in the DWT and SSD cases.

Fig. 26

Dynamic allocation—FSD withdrawal

Fig. 27

Dynamic wealth—FSD withdraw

Fig. 28

Final wealth distribution and related statistics, FSD withdrawal

In Fig. 29 we propose a comparison between the cumulative distribution function of the benchmark wealth and the final wealth accumulated by the investor. In Fig. 30 we show their cumulative distribution functions.

Fig. 29

Quantile function—FSD withdrawal

Fig. 30

Integrated quantile function—FSD withdrawal

It is hard to satisfy the FSD constraints from both a financial and a computational point of view. The optimal portfolio must be able to beat the benchmark in any scenario. Thus, the FSD solution guarantees a portfolio far better than the benchmark portfolio for any possible realization of the stochastic variables. Comparing the FSD solution to the DWT and the SSD solutions, it provides higher final wealth in terms of the mean and median, but at the cost of a substantially higher standard deviation and tail risk (no matter whether measured by V@R or ${ AV}@R$).

5 Sample size, convergence and sensitivity analysis

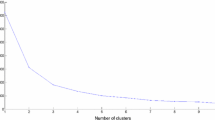
The definition of the problem instance and the generation of the stochastic tree were performed in MATLAB R2013b, while the optimal solution for both the linear problem and the mixed integer problem was estimated in GAMS using Cplex 12.1.0 algorithms. Using an Intel(R) Xeon(R) 2.40GHz with 8.00GB RAM virtual machine running Windows 8.1, we were able to solve FSD problems with a maximum of 200 scenario, i.e. 40025 binary variables and 6330 constraints. For more scenarios, both the DWT and the SSD can easily be solved, but we limited our research according to FSD limits. Then, to make a fair comparison, for all the formulations we adopted regular branching equal to 5-5-2-2-2 for the five periods. To support this branching choice, we performed an in-sample stability analysis for the no-withdrawal case.

Fig. 31

In-sample stability analysis of the optimal objective values for DWT (on the left), SSD (in the middle) and FSD (on the right) for each sample dimension. The stars represent the optimal solution of the selected cases described in Sect. 4

Fig. 32

In-sample stability analysis for DWT (on the left) and SSD (on the right) for each sample dimension

For each sample dimension, we generated 100 different scenario trees and solved the DWT, the SSD and the FSD models. In Fig. 31, we report the optimal values in box-plot form highlighting the minimum, the maximum and the 25th, 50th and 75th percentiles of the optimal value distribution. As a larger instance implies a smaller feasible region, we expect that by increasing the sample size the average solution increases. Moreover, a richer stochastic tree produces a more accurate solution and thus the spread between the minimum and the maximum decreases as the number of scenarios increases. The DWT and SSD solutions are very close for a large number of instances and only for a few of them is the SSD optimal solution slightly worse than the DWT solution. The FSD model has stronger stochastic dominance constraints and includes the complexity induced by the binary variables. Therefore, the FSD solutions are considerably worse than the other two models. However, for all three models, with an increase in the number of scenarios the box plots shrink, confirming the goodness of the convergence. Comparing the results of the box plots, we find that the branching choice 5-5-2-2-2, i.e. 200 scenarios, guarantees the good quality of the solution from a statistical point of view, producing a satisfactory reduction in the optimal value volatility for all cases. Moreover, the instance considered in Sect. 4 produces a value for the optimal solution of approximately $1.4\times 10^5$ for both DWT and SSD and approximately $1.5\times 10^5$ for FSD, which corresponds to the 75th percentile of the distribution. Therefore, it is reasonably representative of the other possible instances and is not an extreme case, as shown in Fig. 31. In Fig. 32, only for the DWT and the SSD cases, we extend the analysis to a larger sample dimension: 500 and 1000 scenarios. The convergence is strengthened. However, the choice of 200 scenarios forced by the tractability of the FSD case remains a well-balanced approximation.

In Table 3 we include the model statistics for the three formulations and for increasing bushiness of the stochastic tree. The DWT and the SSD models are linear programming problems and the execution time is relatively low for both. As shown in Sect. 2.1, the SD constraints require the definition of a double stochastic square matrix that implies a supplementary number of variables and constraints. For instance, for the 1000 scenarios case, the SSD formulation has more than 1 million variables and the execution time is significantly longer than in the DWT case. In the FSD model, the double stochastic matrix is also a permutation matrix, i.e. all its elements are binary. Thus, the total number of variables is equal to the SSD, but most of them are integers. Thus, the solver is not able to find a feasible solution in a reasonable time (less than one day) and for this reason we analysed the case with 200 scenarios.

Table 3 Computation statistics

Finally, we analyse the sensitivity of the here-and-now solution to changes in some of the model parameters. Some of these affect both the investor’s strategy and the benchmark portfolio. In particular, if we modify the propensity to save, the employer contribution and/or the total minimum contribution, we observe a consequent change in the accumulated total wealth but not in the optimal percentage allocations. A decrease in the turnover coefficient produces a slightly riskier here-and-now strategy, preferring the equity pension funds as the portfolio must satisfy the wealth benchmark at the expense of the riskiness of the portfolio. If the turnover is increased, the portfolio shifts clearly onto the high-yield bond pension fund. This is common to all models. In the proposed setting, the withdrawal event is assumed to be independent of the other stochastic processes. We also analysed two cases in which the withdrawal event is realized according to the salary level. First, in the scenarios in which the investor’s salary is not high enough to meet his/her goals, he/she decides to withdraw money from the pension plan. Second, contrary to the previous dependence, if the salary is relatively high, the investor decides on withdrawal because his/her classic savings will be sufficient to maintain his/her standard of living in the future. In both cases our analysis showed that the choice to link the withdrawal event to the salary has no relevant impact either on the here-and-now solution or on the dynamic strategy. However, our investigation concerns the framework of an Italian pension plan and therefore the regulations of other countries which allow for multiple withdrawals during such contracts or earlier than 8 years following subscription could highlight a sensitivity of the solution to the dependence of the withdrawal to other stochastic processes.

6 Conclusion

In this paper we have analysed the pension problem from the point of view of the individual investor who faces the issue of allocating his/her savings from a retirement perspective. The model has to consider a long-term choice and some elements of uncertainty. Therefore, we applied a stochastic programming approach.

Table 4 Here-and-now allocation and statistics for final wealth

The individual investor’s problem in the basic form (DWT, no-withdrawal) has already been introduced and analysed in the literature. Our contribution consists of: (i) the heuristic historical extraction for the risky pension fund returns over a long-term horizon, (ii) the comparison between the withdrawal and no-withdrawal cases and (iii) employing the stochastic dominance formulations in the model. Stochastic dominance constraints are more demanding in terms of modelling, formulation and time computation. However, the solutions highlight a tangible difference both in the allocation and in the quality of the risk/return profile of the portfolio. As shown in Table 4, for the no-withdrawal case the SSD model produces a less risky solution in terms of the standard deviation (1.78e$+$05) with respect to the other two models (3.99e$+$05 for DWT and 2.25e$+$05 for FSD) and it is almost equal to the DWT in terms of V@R (1.50e$+$05) and AV@R (1.35e$+$05). Moreover, every non-satiated and risk-averse investor prefers the final wealth of the SSD strategy to that of the benchmark, contrary to the DWT strategy already analysed in the literature. In the no-withdrawal case, the results are similar but the FSD strategy becomes more risky than the DWT as far as the standard deviation and tail risk of the final wealth are concerned. Since the SD conditions ensure that we obtain a portfolio that is preferred to the dominated one for a large class of investors and for this reason is automatically better than the DWT. Even if the SD relationships were not the sufficient reason to convince an investor to adopt the related portfolios, we can see directly from the statistics that the SSD model produces a solution that is less volatile than the DWT model and the FSD model identifies a solution slightly more risky but with higher final wealth in terms of the mean and median.

Once the preference for the SD conditions versus the expected wealth target has been shown, we can conclude that the choice to introduce SSD or FSD constraints depends mainly on what the investor is looking for in terms of risk/reward targets.

Alternatively, the investor may adopt higher order stochastic dominance relations as discussed in Post and Kopa (2013) and more recently in Branda and Kopa (2016) and Post and Kopa (2016). Moreover, a decreasing absolute risk aversion (DARA) stochastic dominance, as analysed in Post et al. (2015), may be employed. Finally, the analysis may be enriched by making the stochastic dominance relations more robust following Dentcheva and Ruszczynski (2010) or Kopa (2010). However, all these modifications would bring additional complexity and the problem would become computationally intractable for the number of scenarios considered.