Managing customer arrivals with time windows: a case of truck arrivals at a congested container terminal

Abstract

Due to increasing container traffic and mega-ships, many seaports face challenges of huge amounts of truck arrivals and congestion problem at terminal gates, which affect port efficiency and generate serious air pollution. To solve this congestion problem, we propose a solution of managing truck arrivals with time windows based on the truck-vessel service relationship, specifically trucks delivering containers for the same vessel share one common time window. Time windows can be optimized with different strategies. In this paper, we first propose a framework for installing this solution in a terminal system, and second develop an optimization model for scaling time windows with three alternative strategies: namely fixed ending-point strategy (FEP), variable end-point strategy and greedy algorithm strategy. Third, to compare the strategies in terms of effectiveness, numerical experiments are conducted based on real data. The result shows that (1) good planning coordination is essential for the proposed method; and (2) FEP is found to be a better strategy than the other two.

1 Introduction

Due to the increasing container traffic and the introduction of mega-ships, congestion becomes a big problem in many seaports, including truck congestion at terminal gate. The obvious reason is truck arrivals exceeding the gate capacity during peak hours. The gate capacity (also depending on yard operation efficiency) is relatively stable when resources and facilities are given. Even extending gate-opening hours is not possible in many seaports, e.g. seaports in Asia already open for $24\times 7$ h through the whole year. Therefore, it is essential to search for solution on the demand side. Conventionally, terminals place no constraint on arrival time, so a truck can schedule its arrival as preferred. With an effective and reliable method, it can be beneficial to control the arrival fluctuation. Different control methods have been developed and deployed in practice, e.g. terminal appointment system (TAS) (Morais and Lord 2006) and Toll/tariff policy (Chen et al. 2011). This study addresses on the method called vessel-dependent time windows (VDTWs).

The VDTWs method was originally used in some congested container terminals in China, where the storage space is insufficient to meet the high throughput. The solution was to assign time windows for outbound container deliveries: the truckers delivering outbound containers for a same vessel have to follow a specific time window of arrivals, which is appointed by the terminal operator. This solution can avoid trucks coming when storage space is fully occupied. As a side effect, truckers’ behavior gets influenced and forms an arrivals pattern that, the distribution of arrivals follows a Beta distribution within the time window (Yang et al. 2010). This arrival pattern makes VDTWs method capable of reducing gate congestion, hence we develop it into an arrival-management method for such a purpose. The economic feasibility of this proposed management method is addressed in a previous study (Chen and Yang 2010), but its practical application has not been systematically discussed. In this study we try to fill this gap, aiming to answer questions incl. how VDTWs method can fit into a terminal operation system and what strategies can maximize its effectiveness in reducing congestion?

This paper is organized as follows. The literature review on gate congestion and management of truck arrival demand at maritime container terminals is discussed in Sect. 2. Section 3 presents the three optimization strategies, i.e. fixed ending-point strategy (FEP), variable ending-point strategy (VEP) and greedy algorithm strategy (GRA). For each strategy, we develop an optimization model to minimize the total cost, incl. the cost of waiting time and fuel consumption, the cost of containerized cargo storage time and yard fee and the penalty of insufficient yard space. These optimization models are solved with Genetic Algorithm based solution heuristics, which are presented in Sect. 4. Computational experiments and analysis, as well as the results of numerical experiments are showed in Sect. 5. Conclusions and further directions are presented in Sect. 6.

The main contribution of this study is to develop the VDTWs method as an effective solution for customer arrival management in the context of container terminal operations. The VDTWs solution can be used not only to alleviate congestion and air pollution, but also to enhance the planning collaboration between seaside and landside operations in a seaport. This solution is especially useful when a container terminal faces challenge of limited capacity and has difficulties in promptly expanding its capacity. Due to time-consuming construction of port facilities and the continuously increasing container transportation volume, many container terminals can benefit from such a customer arrival management solution.

2 Literature review

During the last several years, a growing number of studies on gate congestion at maritime container terminals have been conducted. Most of them focus on the management of truck arrival demand. One of the major solutions of managing truck arrivals is terminal appointment system (TAS), which has received many research efforts. In a TAS system, the terminal operator announces opening hours and entry quota within each hour through a proprietary web-based information system, where truckers can choose an entry hour as they prefer. This TAS system was firstly proposed by the Californian local government as a means to reduce air pollution generated by heavy-duty truck engines. It was expected to save a significant number of truck-hours by spreading out the demand throughout a whole day (Huynh 2005). Huynh and Walton (2008) analyzed the effectiveness of this system on improving the efficiencies of both terminals and trucks, and developed a methodology to determine the optimal number of trucks the terminal can accept per time window. An improved concept of cooperative time window system is proposed by Ioannou et al. (2006) that terminal operators and trucking companies could communicate to generate an optimum time windows taking into account the objectives and constraints of both sides. Regarding the performance of this system, points of view in literature seem mixed, for example Giulianoa and O’Brienb (2007) found that ‘there is no evidence to suggest that the appointment system reduced queueing at terminal gates and hence heavy diesel truck emissions’, and quite oppositely, successful experience with appointment systems in Port of Vancouver has been reported (Morais and Lord 2006). In order to further develop the terminal appointment system, Zehendner and Feillet (2014) developed models for integrating the system with the allocation of straddle carriers, which can increase not only the service quality of trucks, but also of trains, barges and vessels. Phan and Kim (2015) focused on the process of negotiating truck arrival times among trucking companies and a container terminal, and proposed a decentralized decision-making model to support this negotiation considering the inconvenience of trucks from changing their arrival times and the waiting cost of trucks in peak hours.

Another approach for managing truck arrivals studied in the literature is the VDTWs method, which has been used at some container terminals in China. Its original purpose was to facilitate the operations inside terminals, enabling terminal operators to organize their production with as few interruptions of unplanned truck visits as possible. Yang et al. (2010) found that the distribution of truck arrivals with outbound containers follows a Beta distribution within a time window, which enables a prediction of truck arrivals given a vessel-calling schedule and a corresponding set of time windows. This finding sets up the foundation of managing truck arrivals by optimizing time windows. Chen and Yang (2010) developed a heuristic algorithm to find a near optimal time window assignment that can minimize the total cost of gate congestion. But some practical constraints were not included in their research, such as yard capacity and the impact of vessel delays. Besides, the proposed heuristic algorithm was not efficient enough for solving a real case problem and therefore needs improvement.

Toll charge can also be used for managing truck traffic in a port area. A time-of-day pricing is implemented by the Port Authority of New York and New Jersey. Ozbay et al. (2006) examined whether spreading weekday peak period traffic to the hours just before or after the peak toll rates might be successful for both cars and trucks. Chen et al. (2011) proposed a two-phase model to search for a desirable pattern of time varying tolls that can lead to optimal truck arrival pattern; the solution approach they use is to combine a fluid-based queueing model and a toll-pricing model.

Besides the above research on solutions of managing truck arrivals, there are some studies focusing on the supply aspect of gate capacity. A gate capacity depends on not only gate facilities (such as lanes and clerks), but also the utilization of yard cranes. Sometimes the bottleneck is at the yard, i.e. long waiting time for a yard crane to load the container (Huynh 2009). Huynh et al. (2004) developed a simulation model of container terminal yard operation to analyze truck turn time with respect to crane availability and deployment, which is applied to find the number of yard cranes needed to achieve a desired truck turn time. Guan and Liu (2009) used a multi-server queueing model to analyze maritime container terminal gate congestion and developed an optimization model to find the needed lanes for different truck arrival levels. Guan and Liu (2009) also stated that in practice the optimization of gate capacity is not always feasible because the land may not always be available, so optimization methods on the demand side could be more viable.

Lastly, the concept of time window optimization is also related to this paper. Time window has for many years been introduced into the transport research field, however in most cases it is considered as a constraint rather than a variable. Many studies focus on scheduling problems with time window constraint, e.g. transit network scheduling (Mesa et al. 2014), dock assignment problem (Berghman et al. 2014), airline scheduling problem (Erdmann et al. 2001), liner shipping scheduling (Boros et al. 2008) and vehicle routing problem as well (Potvin and Rousseau 1993; Desaulniers et al. 1998). To the best of the authors’ knowledge, very few studies have used time windows as a tool of managing traffic demand, Chen and Yang (2010) is one of them.

3 The models

In this section, we propose a framework to install VDTW in a terminal operation system, and then develop an optimization model for each time window strategy. These optimization models share the same mathematic basics and variables, but differ slightly in either objective function or constraints.

3.1 The VDTWs framework

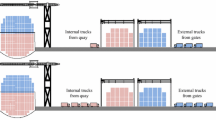
The general framework for assigning vessel-dependent time windows for outbound container entries can be described in Fig. 1. When a terminal operator receives an arrival announcement from an arriving vessel, a time window for the corresponding export/outbound container deliveries is considered. The starting point depends on the availability of yard capacity, and if there is not enough yard space it has to be postponed. The ending point usually depends on the estimated arrival time (ETA) of the vessel.

Given a set of time windows, one can predict truck arrivals in any time step using the method developed by Yang et al. (2010), which first calculates the probability of a truck arriving during a specific time step based on the Beta distribution, and then multiplies it with the total number of trucks to get an estimation of the level of truck arrivals. Next step is to estimate the congestion level based on the predicted truck arrivals using a queueing model. If the congestion is serious, the time windows should be modified, and hence the truck arrival prediction should also be updated; if the congestion is not serious, the terminal operator will likely implement this time window plan. After all handling operations are finished and the vessel departs, the occupied yard space will be released. During the whole process, there is a risk that the vessel comes later than its ETA. If this happens, the related truck entries operation will not be influenced but yard space will be occupied for longer time, which may trigger adjustment of time windows for the following vessels.

In this study, we propose three strategies for optimizing time windows. First is the GRA strategy, which aims to maximize the sum of time window lengths, based on the main constraint of the yard capacity. The basic idea of this strategy has been applied in some terminals, where the operators believe that long time windows can increase truckers’ satisfaction and reduce congestion. In this study, we will test this understanding in numerical experiments. The other strategies are FEP and VEP, and the difference between them is whether fixing the ending-point of a time window to the corresponding vessel ETA or not. If not, it is called VEP strategy, which has relatively higher variability and better ability to manage truck arrivals; on the other hand, VEP has a risk of too early ending points, which means long container storage time and low system efficiency. The FEP strategy keeps the ending-point fixed at the ETA, therefore is relatively simpler and easier to apply. Its effectiveness for reducing gate congestion is to be estimated and compared with the VEP strategy in the numerical experiments.

Fig. 1

The framework of optimizing vessel-dependent time windows

3.2 The optimization models

In this section, we propose an optimization model for each time window strategy. In most liner shipping markets, container lines provide weekly service; so a container terminal normally would have the same vessel-calling schedule for every week. To cope with this characteristic, we use a rolling horizon of one week in the following mathematical formulation.

Sets and Indices

i:

$1,\ldots , I\; \hbox {vessel index;}$

t:

$1,\ldots , T\; \hbox {time step}.$

Parameters

$\textit{ETA}_i$ :

the estimated arrival time of vessel i;

$\textit{ETD}_i$ :

the estimated departure time of vessel i;

$V_i$ :

the volume of export/outbound containers to be loaded onto vessel i;

Q :

the gate processing rate ( vehicles/hour);

W :

the unit value of waiting time per truck per hour;

F :

the unit cost of fuel consumption per truck per hour;

$\textit{YF}$ :

the hourly yard fee per container;

$\textit{VC}$ :

the average value of one container cargo;

$r_{hour}$ :

the hourly interest rate;

Y :

the total yard storage capacity.

Derived variables

$\textit{TC}$ :

the total cost;

$\textit{WFC}_{it}$ :

the cost of truck waiting and fuel consumption in time step t of vessel i;

$\textit{SYC}_{it}$ :

the yard fee and the storage time cost of cargos in time step t for vessel i;

$\textit{YC}_t$ :

the penalty for the insufficient yard space in time step t;

$a_{it}$ :

the number of truck arrivals for vessel i in time step t;

$a'_{it}$ :

the number of reallocated truck arrivals for vessel i in time step t;

$q_t$ :

the queue length in time step t (measured with the number of queueing vehicles );

$w_t$ :

the average waiting time of the trucks arriving in time step t (hour);

$s_{it}$ :

the average storage time of the containers arriving in time t for vessel i (hour);

S :

the value of the storage time per TEU cargo per hour;

$y_t$ :

the occupied yard space in time step t;

$L_i$ :

the length of time window i;

$\textit{TD}_{it}$ :

$\left\{ {{\begin{array}{l} {1 \hbox { if ship } i \hbox { departs at time step } t, \hbox {i.e.} \textit{ETD}_i =t} \\ {0 \hbox { otherwise} } \\ \end{array} }} \right. \!\!.$

Decision variables

$\textit{TS}_{it}$ :

$\left\{ {{\begin{array}{l} {1 \hbox { if the starting-point of time window } i \hbox { is at time step } t} \\ {0 \hbox { otherwise} } \\ \end{array} }} \right. \!\!;$

$\textit{TE}_{it}$ :

$\left\{ {{\begin{array}{l} {1 \hbox { if the ending-point of time window } i \hbox { is at time step } t} \\ {0 \hbox { otherwise} } \\ \end{array} }} \right. \!\!.$

3.2.1 GRA strategy model

The objective of GRA strategy is to maximize the sum of the length of all time windows, as defined in Eq. 1 that time window length is measured with $L_i =\sum \nolimits _t t\left( {\textit{TE}_{it} -\textit{TS}_{it} } \right)$. Equation 2 ensures that the occupied yard space should not exceed the total storage capacity in the terminal in any time step. The occupied yard space is calculated in the way that: a yard space of size $V_i$ will be reserved for vessel i when its time window starts (at time t that has $\textit{TS}_{it} =1)$, and released when the vessel departs (at time t that has $\textit{TD}_{it} =1)$. Equations 3–5 are the constraints for time window setting, which are formed based on the practical experience. Equation 3 indicates that the starting point of every time window should not be earlier than the corresponding ETA in the previous week, considering the weekly rolling schedule. Equation 4 indicates that the starting point of every time window should be at least 6 h earlier than the ending point, which is the minimal length of time window in practice. Equation 5 ensures the ending point of every time window being no later than the corresponding estimated vessel arrival time, and its earliest possible value is two days before the ETA.

$$\begin{aligned} max \sum \nolimits _i L_i =\sum \nolimits _i \sum \nolimits _t t\left( {\textit{TE}_{it} -\textit{TS}_{it} } \right) \end{aligned}$$

(1)

Subject to

$$\begin{aligned}&\displaystyle y_{t-1} +\sum \nolimits _i V_i \left( {\textit{TS}_{it} -\textit{TD}_{it} } \right) \le Y \quad \forall t \end{aligned}$$

(2)

$$\begin{aligned}&\displaystyle \textit{ETA}_i -24\times 7\le \sum \nolimits _t t*\textit{TS}_{it} \quad \forall i \end{aligned}$$

(3)

$$\begin{aligned}&\displaystyle L_i \ge 6 \quad \forall i \end{aligned}$$

(4)

$$\begin{aligned}&\displaystyle \textit{ETA}_i -48\le \sum \nolimits _t t*\textit{TE}_{it} \le \textit{ETA}_i \quad \forall i \end{aligned}$$

(5)

$$\begin{aligned}&\displaystyle \sum \nolimits _t \textit{TE}_{it} =1 \quad \forall i \end{aligned}$$

(6)

$$\begin{aligned}&\displaystyle \sum \nolimits _t \textit{TS}_{it} =1 \quad \forall i \end{aligned}$$

(7)

3.2.2 FEP and VEP strategy models

Different from GRA strategy, FEP and VEP strategies aim to minimize the total operational cost of export/outbound container delivery system, which includes the time cost of truck/driver waiting at a terminal gate, fuel consumption of engine idling, storage time of the containerized cargos, yard fee for container storage and the penalty for insufficient yard space, as shown in Eq. 8. For the VEP strategy, the constraints are modeled in Eqs. 9–13 and Eqs. 15–24. The constraints in Eqs. 9–13 are exactly the same as in Eqs. 3–7.

$$\begin{aligned} min\; \textit{TC}=\sum \nolimits _i \sum \nolimits _t \left( {\textit{WFC}_{it} +\textit{SYC}_{it} } \right) +\sum \nolimits _t \textit{YC}_t \end{aligned}$$

(8)

Subject to

$$\begin{aligned}&\displaystyle \textit{ETA}_i -24\times 7\le \sum \nolimits _t t*\textit{TS}_{it} \quad \forall i \end{aligned}$$

(9)

$$\begin{aligned}&\displaystyle L_i \ge 6 \quad \forall i \end{aligned}$$

(10)

$$\begin{aligned}&\displaystyle \textit{ETA}_i -48\le \sum \nolimits _t t*\textit{TE}_{it} \le \textit{ETA}_i \quad \forall i \end{aligned}$$

(11)

$$\begin{aligned}&\displaystyle \sum \nolimits _t \textit{TE}_{it} =1 \quad \forall i \end{aligned}$$

(12)

$$\begin{aligned}&\displaystyle \sum \nolimits _t \textit{TS}_{it} =1 \quad \forall i \end{aligned}$$

(13)

The model for FEP strategy has a minor difference from the VEP model: the ending point of each time window is fixed to the corresponding ETA, as shown in Eq. 14. So the FEP model is same to the VEP model, except Eq. 11, which should be replaced with Eq. 14.

$$\begin{aligned} \textit{TE}_{it} =\left\{ {{\begin{array}{l} {1\quad \hbox { when } t=\textit{ETA}_i } \\ {0\quad \hbox { when } t\ne \textit{ETA}_i } \\ \end{array} }} \right. \forall i \end{aligned}$$

(14)

The cost of waiting time and fuel consumption For each time step t and vessel i, the truck arrivals can be estimated with Eq. 15, where $a_{it}$ is positive only when the time step t is within the time window i, otherwise $a_{it}$ is 0. The parameters of the Beta distribution are obtained from the previous study (Yang et al. 2010). As above mentioned, it is assumed that a terminal has the same vessels calling each week. So for the vessel operation in the current week, if any workload is allocated to the former or the next week, then the same workload will be allocated back from the next or the former week. Therefore, truck arrivals should be updated with Eq. 16, to include this weekly rolling schedule condition. Given a constant gate progressing rate, queue length can be calculated with Eq. 17. It is noted that, this queueing calculation is handled in a deterministic way rather than a stochastic way. This is because the classical stochastic queueing models, e.g. M/G/s, are not the best option for studying terminal gate operations. Classical stochastic queueing models are based on the assumption of steady state, but in a terminal system the peak hours are usually too short to reach the steady state. So using stochastic queueing models may result in significant overestimation of queueing length for those peak hours (Chen and Yang 2014). Comparatively, slight underestimation of this deterministic queueing model is less risky. So we choose the deterministic queueing model for this study.

$$\begin{aligned}&a_{it} =\left\{ {{\begin{array}{ll} {V_{i_i} \times \frac{\int _c^{\mathrm{c+}\frac{1}{L_i }} u^{0.29}\left( {1{-}u} \right) ^{2.25}du}{\int _0^1 u^{0.29}\left( {1{-}u} \right) ^{2.25}du} \hbox { where } c=\frac{t{-}1{-}\sum \nolimits _{k=1}^{k=T} k*\textit{TS}_{ik} }{L_i },} &{}\quad {\textit{if}\,\, t\in \left[ {\sum \nolimits _{k=1}^{k=T} k*\textit{TS}_{ik} +1,\sum \nolimits _{k=1}^{k=T} k*\textit{TE}_{ik} } \right] } \\ 0&{}\quad { others} \\ \end{array} }} \right. \forall i , \quad \forall t \nonumber \\ \end{aligned}$$

(15)

$$\begin{aligned}&\displaystyle a'_{it} = a_{it} +a_{i\left( {t+24\times 7} \right) } +a_{i\left( {t-24\times 7} \right) } \quad \forall i ,\forall t \end{aligned}$$

(16)

$$\begin{aligned}&\displaystyle q_{t} = \max \left( {q_{{t - 1}} + \sum \nolimits _{i} a^{\prime }_{{it}} - Q,~0} \right) ~~~\forall t \end{aligned}$$

(17)

$$\begin{aligned}&\displaystyle w_t =\left( {q_t +q_{t-1} } \right) /2Q \quad \forall t \end{aligned}$$

(18)

$$\begin{aligned}&\displaystyle \textit{WFC}_{{it}} = \left( {W + F} \right) \times w_{t} \times a^{\prime }_{{it}} ~~~~\forall i~,\forall t \end{aligned}$$

(19)

When the queue length is known, the waiting time of a truck can be estimated by the number of trucks in front of it and the gate progressing rate, as shown in Eq. 18. Equation 19 calculates the cost of waiting time and fuel consumption of the trucks that arrived in time step t for vessel i.

The cost of containerized cargo storage time and yard fee All export/outbound containers are stored in the terminal before being loaded to the vessel, so the average storage time for the containers that arrived in time step t for vessel i can be estimated with Eq. 20. Then, the cost of containerized cargo storage time and yard fee can be calculated with Eq. 22. It is noted that the storage cost reduced in this optimization model (if any) is not necessarily the realized cost reduction. This is because in reality, cargos are usually produced according to production plan rather than logistics constraint, so if the terminal does not allow the cargo coming into its yard, the cargo owner has to find a place to store it temporarily before the gate opens. But this cost reduction can give an indication of the potential cost saving in this aspect.

$$\begin{aligned}&\displaystyle s_{it} =\textit{ETA}_i -t-w_t \quad \forall i ,\forall t \end{aligned}$$

(20)

$$\begin{aligned}&\displaystyle S=\textit{VC}\times r_{hour} \end{aligned}$$

(21)

$$\begin{aligned}&\displaystyle \textit{SYC}_{it} =\left( {S+\textit{YF}} \right) \times s_{it} \times a'_{it} \quad \forall i ,\forall t \end{aligned}$$

(22)

The cost of insufficient yard space Occupied yard space is calculated in Eq. 23, in the same way as in Eq. 2. If the yard space is not available in a specific time step, an operation halt will happen and all the trucks have to wait at the terminal gate until some storage space is released. In order to reduce this kind of operation halt, we add a penalty function (Eq. 24) into the model, to avoid infeasible solutions during the calculation.

$$\begin{aligned}&\displaystyle y_t = y_{t-1} +\sum \nolimits _i V_i \left( {\textit{TS}_{it} -\textit{TD}_{it} } \right) \quad \forall t \end{aligned}$$

(23)

$$\begin{aligned}&\displaystyle \textit{YC}_t =\left\{ {{\begin{array}{lll} 999,999 \quad \hbox {when} &{} y_t >Y \\ 0 \quad \hbox {when}&{} y_t \le Y \\ \end{array} }} \right. \forall t \end{aligned}$$

(24)

4 Solution heuristics

The above optimization model is nonlinear based on the discrete independent variables, therefore is a NP-hard problem. NP-hard problems are usually solved with evolutionary based algorithms. Evolutionary algorithms (EAs) are search methods inspired from natural selection and survival of the fittest in the biological world. Among the different EA options, GA is easy to implement and has been widely used to solve inherently intractable problems especially scheduling problems (Gen and Cheng 1997; Jones et al. 2002). GAs have the advantage of flexibility imposing no requirement for a problem to be formulated in a particular way, or that the objective function is differentiable, continuous, linear, separable, or of any particular data-type. Thus, they can be applied to any problem (e.g. single or multi-objective, single or multi-level, linear or non-linear) for which there is a way to encode and compute the quality of a solution. GA-based heuristics suffer from two main weaknesses (encountered by all (meta) heuristics): (a) there are no optimality guarantees, and (b) there is no formal selection of a search direction that guarantees global optimality. Considering the GA advantages (and common disadvantages), we propose a GA-based heuristic to solve the optimization models presented in Sect. 3.2. The GA-based heuristic is described in the rest of this section.

In this study, the GA is conducted with the following steps:

• Step 1: A population of M individuals (solutions) is initialized by randomly selecting start points and end points consistent with the constraint of Eqs. 3–5. These constraints are considered here in order to make sure every solution is feasible.

• Step 2: Evaluating the fitness value of each individual so as to give higher probability to better solutions to contribute to next generations. The fitness value of each individual can be computed as follows, where $F\left( {x_k } \right)$ is the fitness value and $Z\left( {x_k } \right)$ is the objective value of individual $x_k$.

  $$\begin{aligned} F\left( {x_k } \right) =\frac{\sum \nolimits _1^M Z\left( {x_i } \right) }{Z\left( {x_k } \right) } \end{aligned}$$

  (25)

• Step 3: Selecting two parent solutions for reproduction by the roulette wheel selection method.

• Step 4: Putting both of the parent solutions into the mutation operation, where each bit of them could be mutated. In order to get a reduced searching space, the mutation operation in this research has the following features:

  • (a) Time windows that are near to a peak traffic time are given a high probability to mutate, while the other time windows are given a low probability.

  • (b) For any time window, if chosen to mutate, both the start and end points can move forwards or backwards up to 48 h with uniform distribution. Of course, their movements must be under the constraint of Eqs. 3–5, so that the new solutions will be feasible.

  • (c) In order to reduce bad solutions generated in the mutation operation, a directional function is developed to guide the movement of start points. The principle is that a start point’s moving direction, forward or backward, depends on the available gate capacities on both sides. A start point is always more likely to move towards the side with higher gate capacity. For any start point, the possibility of a forward (or backward) movement, $D_i^f$ (or $D_i^d )$, can be calculated with Eq. 26 (or Eq. 27), where $g_t$ is the available gate capacity of time step t.

  $$\begin{aligned} D_i^f= & {} \frac{\sum \nolimits _{\sum \nolimits _{k=1}^{k=T} k*\textit{TS}_{ik} -48}^{\sum \nolimits _{k=1}^{k=T} k*\textit{TS}_{ik} } g_t }{\sum \nolimits _{\sum \nolimits _{k=1}^{k=T} k*\textit{TS}_{ik} -48}^{\sum \nolimits _{k=1}^{k=T} k*\textit{TS}_{ik} +48} g_t } \quad \forall i \end{aligned}$$

  (26)
  $$\begin{aligned} D_i^b= & {} 1-D_i^f \quad \forall i \end{aligned}$$

  (27)
  $$\begin{aligned} g_{t}= & {} \max \left( {Q - q_{{t - 1}} - \mathop \sum \limits _{i} a^{\prime }_{{it}} ,~0} \right) ~~\forall t \end{aligned}$$

  (28)

• Step 5: Then both the parent solutions are sent into a crossover operator. In this study, we try three different crossover methods: one-point crossover, two-point crossover and uniform crossover. These three methods will be compared with each other in the experiment analysis.

  • (a) One-point crossover: a point $p\in \left\{ {1,\ldots ,N} \right\}$ is randomly generated, and then a child solution will consist of the first p genes taken from the first parent, the rest $\left( {N-p} \right)$ genes taken from the second parent. The other child solution will consist of the remaining genes.

  • (b) Two crossover: points $p\in \left\{ {1,\ldots ,N-1} \right\}$ and $q\in \left\{ {p+1,\ldots ,N} \right\}$ are randomly generated, then a child solution will consist of the first p genes taken from the first parent, the next $\left( {q-p} \right)$ genes taken from the second parent, and the remaining $\left( {N-q} \right)$ genes taken from the first parent, or vice-versa.

  • (c) Uniform crossover: for each bit in a child solution, a random number is generation from uniform distribution: if it is smaller than 0.5, the corresponding gene from the first parent is taken into the child solution, otherwise the corresponding gene from the second parent will be taken. By doing so, approximately half of the genes from first parent and the other half from second parent. After the child solution is completed, the remaining genes will compose another child solution.

• Step 6: Evaluating the child solutions and determining the new generation from all child and parent solutions by elitism strategy, which allows the M best solutions to survive and copies them into the next generation.

• Step 7: Repeating steps 2–6 until the number of iteration reaches the pre-defined number.

5 Computational experiments and analysis

In this section, the proposed model and algorithm are applied in a real data test and a scenario test. The real data comes from a Chinese maritime container terminal, which has big throughput and serious road congestion as well. In a typical operation week, we collected the complete data set from this terminal, incl. the weekly vessel-calling schedule, truck traffic data, terminal system parameters and cost data. The vessel-calling schedule is shown in Fig. 2: 14 vessels called the terminal during the week and generated 4798 truck trips. Some other inputs are shown in Table 1.

Fig. 2

The vessel calling schedule. $V_i \left( n \right)$ means that the vessel i generates n truck trips for delivering export containers, and the numbers below the arrows are the vessels’ arrival times and departure times

Table 1 Input of the heuristic

The GA parameters are set to be 100 for population size, 1000 for iteration, 0.3 for high mutation probability, and 0.05 for low mutation probability. The number of iteration is determined by trying some pilot calculations, in which it is observed that normally the GA convergence is finalized at 200–300 generations, therefore 1000 iterations should be a sufficient number. In general the GA takes 29 s to complete the calculation of 1000 iterations.

First, we select best crossover operator for GA from the one-point, two-point and uniform operators, which have been introduced in step 5 of Sect. 4. These operators are run for 10 times and compared in terms of the objective value in Fig. 3. We can see that, for both VEP and FEP strategies, two-point operator slightly outperforms the other two operators. Therefore, we choose to use the two-point operator for the following experiment analysis. Furthermore, Fig. 3 also shows the VEP strategy is a little more competitive than the FEP strategy in minimizing the total cost.

Fig. 3

Boxplot of ten calculations under different crossover strategies

Fig. 4

The optimized time windows under different strategies

Second, we present the results of different strategies. The near optimal solutions under different strategies are shown in Fig. 4. Obviously, GRA strategy provides much longer time windows than the other strategies.

In the rest of this section, we illustrate the comparison of these strategies, in terms of truck arrivals, truck queue and required yard space. The comparison of truck arrivals is shown in Fig. 5, where FEP and VEP strategies have almost the same distribution of truck arrivals, but GRA strategy generates a very high arrival peak in the beginning of the week, which substantially exceed the gate capacity. The consequence of this high arrival peak can be observed in Fig. 6.

Fig. 5

Modeled hourly truck arrivals under different strategies

Fig. 6

Modeled hourly truck queue length and gate capacity residual under each strategy

Fig. 7

Occupied yard space under different strategies

The curves in Fig. 6 show both truck queue lengths and the surpluses of gate capacity. When a curve is above 0, it indicates the number of trucks waiting at the terminal gate each hour; when a curve is below 0, it indicates the number of extra trucks that can be accommodated in the hour, namely gate capacity surplus. We can see that both FEP and VEP strategies have a surplus of gate capacity during most of the time. However, the congestion under GRA strategy is quite serious as more than 200 trucks are waiting in queue at the gate at hour 36. This indicates, long time windows alone cannot prevent gate congestion, and a good planning coordination technique is necessary for assigning a good time windows plan.

Fig. 8

Performances of the strategies in the scenario test. S(i) means scenario i. From S(1) to S(6), the loading export container volume is increased/decreased by $-$20, $-$10, 10, 20, 30 and 40 % respectively. In diagram 3 and 4, the black lines show the ratio between GRA and FEP strategies

Figure 7 shows the occupied yard space of each strategy. Where GRA strategy almost uses up all yard space, FEP and VEP strategies save a significant percentage of the yard space. Surplus of yard capacity is essential for the issue of vessel delay, which needs extra container storage. In this test, keeping a yard capacity of 500 TEU free can help to deal with one 12-h delayed vessel each day. The rest surplus of the yard space provides the terminal operator with a large potential to increase the terminal throughput.

In brief, GRA strategy is not competitive because it can result in high utilization of yard capacity and high total cost (nearly twice higher than the other two strategies). VEP strategy, even though with more variability, does not perform significantly better than FEP strategy.

Additionally, in order to test the robustness of the strategies, six scenarios are created based on the real data set. Specifically, the loading export/outbound container volume from S(1) to S(6) is increased by $-$20, $-$10, 10, 20, 30 and 40 % respectively. In each diagram of Fig. 8, the three strategies are compared in one aspect. First, by comparing S(1) and S(2) in all the diagrams, we can see that when the loading volume is low, the GRA strategy seems competitive, especially in terms of maximum queue length and average truck waiting time. This can support the fact that GRA was applied successfully in practice. But we should be aware that, when the loading volume increases, the performance of GRA strategy goes down dramatically. Second, comparing FEP and VEP strategies in every scenario, we can see again that FEP is almost as competitive as VEP. Therefore FEP strategy outperforms thanks to its simplicity and effectiveness. Third, when we consider the robustness of FEP strategy, it can be seen that even in S(5) with 30 % increased demand FEP still has an acceptable performance, such as the maximum queue of 42 trucks, the average truck waiting time of 22.9 min and the yard capacity surplus of 1500 TEU. Therefore, time window optimization under FEP strategy is capable to cope with a demand growth up to 30 % at the sample terminal. To summarize, this VDTWs method can bring a big potential benefit to congested terminal systems.

6 Conclusion

Due to the increasing container traffic and the introduction of mega-ships, landside gate congestion has become a serious issue in many maritime container terminals. Most terminals in Asia already provide $24\times 7$ h service, so no room is left for extending the gate opening hours. One possible solution is to develop the vessel-dependent time windows as a method of managing truck arrivals. This paper proposes a framework to implement this method and three strategies to optimize time windows, namely FEP, VEP and GRA strategies. The result of numerical experiments indicates that, (a) GRA strategy has a good performance in the low loading volume scenarios, but is not a reliable choice when volume grows higher; (b) the FEP and the VEP strategies have almost same effectiveness in various loading volume scenarios, so the FEP strategies should be recommended due to its simplicity. There are some implications from this study:

• Terminal gate congestion problem should be given sufficient emphasis by terminal operators. As the container volume continuously increases, gate congestion grows significantly and generates more air pollution, which does not contribute to the greenness of port operations.

• To effectively manage gate congestion, it is necessary to adopt some solutions or methods that match the nature of terminal operations. For controlling truck arrival distribution, different options are available, including terminal appointment system, time-varying toll charge and VDTWs. In general the VDTWs method can be applied in any terminal, as long as all related parties would accept it. It is important to involve all parties in this change management, as subjective opinions may also matter for a successful implementation.

• Management of gate congestion should be addressed by careful assessment of its effectiveness and reliability. A typical example is GRA strategy, which works well in a low truck traffic condition, but not so well in high traffic condition.

• To assess a method of reducing gate congestion, understanding the pattern of truck arrival behaviour is indispensable. This pattern should be identified from the characteristics of local terminal operations, because truck traffic demand is generated by terminal operations.

There is a limitation in this study: the truck queueing phenomenon is modeled with fluid flow approach, which neglects the stochastic nature of gate service system and therefore slightly underestimates the queue length and waiting time. Queueing theory has been widely applied in container terminal operation research, e.g. Dragovic et al. (2012) and Zrnic et al. (1999). To improve the queueing estimation, recent developments in non-stationary queueing models can be used in this study, for example the PSA method by Green and Kolesar (1991) and PSFFA method by Wang et al. (1996).

There are some possibilities of future research, for example the planning collaboration between sea- and landside operations in a congested container terminal. Most research efforts have been spent on optimizing seaside operations, while the number of papers focusing on trucks and trailers at container terminals is relatively limited. ‘Improved terminal performance cannot necessarily be obtained by solving isolated problems but by an integration of various operations connected to each other’ (Stahlbock and Voß 2008, pp.33). Therefore in order to achieve the overall utilization of a container terminal, how to collaborate and integrate the seaside and landside operations becomes an important question.