On the impact of semidefinite positive correlation measures in portfolio theory

Abstract

In this paper potential usage of different correlation measures in portfolio problems is studied. We characterize especially semidefinite positive correlation measures consistent with the choices of risk-averse investors. Moreover, we propose a new approach to portfolio selection problem, which optimizes the correlation between the portfolio and one or two market benchmarks. We also discuss why should correlation measures be used to reduce the dimensionality of large scale portfolio problems. Finally, through an empirical analysis, we show the impact of different correlation measures on portfolio selection problems and on dimensionality reduction problems. In particular, we compare the ex post sample paths of several portfolio strategies based on different risk measures and correlation measures.

1 Introduction

The dependency structure of random sources plays a crucial role in portfolio theory and in several pricing and risk management problems. In particular, the classic Pearson linear correlation measure is regularly used to measure and optimize the dispersion of portfolio returns and to reduce the dimensionality of large-scale portfolio problems. It is well known that the Pearson linear correlation works well with Gaussian vectors. However, in practice the Gaussian distributional assumption of financial return series is mostly rejected, as was already proved by e.g. Mandelbrot (1963a, b) and Fama (1965); see also Rachev and Mittnik (2000) and the references therein.

It follows that many other correlation measures have been proposed in the literature to deal with the association among random variables, see, among others, Scarsini (1984), Joe (1997), Cherubini et al. (2004) or Nelsen (2006) and the references therein. However, in this paper we prove that most of these measures cannot be used directly to order investors’ choices, since they do not lead to a law invariant portfolio measure.

The first contribution of this paper is the discussion about models that has sufficient capacity to describe the dependence structure of financial returns. We first identify the most desirable characteristics of the Pearson linear correlation. In particular, we characterize the class of semidefinite positive correlation measures and we analyze their connection with deviation measures consistent with the preferences of risk-averse investors (see Rockafellar et al. 2006). In this context, we study the possibility of using portfolio risk measures that can be obtained by the contribution of different deviation measures and semidefinite positive correlation measures. Moreover, we show that other linear correlation measures can be used in portfolio selection problems as an alternative to the Pearson linear correlation. In particular, we introduce a sufficient condition to obtain a linear correlation measure and we suggest alternative linear correlation measures for stable sub-Gaussian distributed vectors.

The second contribution of this paper is an ex post empirical analysis on the use of different correlation measures in the portfolio theory. In particular, we propose to use the correlation measures for two distinct portfolio problems: (1) to reduce the dimensionality of large-scale portfolio selection problems; (2) to identify portfolio strategies that optimize the correlation between the portfolio and one or two market benchmarks. For both problems we perform an empirical analysis utilizing all the active stocks of the main US stock markets (NYSE and NASDAQ).

Regarding the first problem, we use different linear correlation measures to perform a principal component analysis (PCA) that identifies the main portfolio factors whose dispersion is significantly different from zero. These factors are used to approximate the portfolio returns in the large-scale portfolio selection problems. Therefore, using almost 1800 assets regularly traded on the US stock market, we compare the ex post performance of a portfolio selection strategy applied to the approximations of returns obtained by different specifications of principal component analysis.

As concerns the second problem, we propose new portfolio optimization models that respects two logical implications of investors’ behavior: (1) investors want to maximize the correlation with the upper stochastic bound of the market; (2) investors want to minimize the correlation with the lower stochastic bound of the market. Therefore, we compare ex post sample paths of wealth obtained using portfolio optimization strategies based on different correlation measures.

We proceed as follows. In Sect. 2 we summarize some of the basic characteristics of concordance/correlation measures and characterize the semidefinite positive correlation measures. In Sect. 3 we define new linear correlation matrices and their relationship with the deviation measures. In Sect. 4 we discuss when (and how) such correlation measures should be used within portfolio selection problems. In Sect. 5 we conduct empirical comparison among portfolio strategies based on the use of different correlation measures. We summarize our principal findings in Sect. 6, while a final “Appendix” contains the proofs of the main results.

2 Concordance and semidefinite positive correlation measures

One of the most essential tasks of financial decision-making is the measurement of the dependency among the realizations of particular random variables. Specifically, let us consider n risky assets with gross returns¹ $z=\left[ z_{1},z_{2},\ldots ,z_{n}\right] ^{\prime }.$ As a consequence of the Sklar theorem (Sklar 1959) the joint distribution function is given by:

$$\begin{aligned} F_{\mathbf {z}}(\mathbf {x})=\mathcal {C}(F_{z_{1}}(x_{1}),F_{z_{2}}(x_{2}), \ldots ,F_{z_{n}}(x_{n})), \end{aligned}$$

(1)

where $F_{z_{i}}(x_{i})=\Pr (z_{i}\le x_{i})$ is the marginal distribution function and $\mathcal {C}:[0,1]^{n}$ $\rightarrow [0,1]$ is the copula function. The copula function can therefore be defined by inverting (1):

$$\begin{aligned} \mathcal {C}(\mathbf {u})=F_{\mathbf {z} }\left( F_{z_{1}}^{-1}(u_{1}),F_{z_{2}}^{-1}(u_{2}),\ldots ,F_{z_{n}}^{-1}(u_{n})\right) . \end{aligned}$$

(2)

It follows that the dependency among particular variables is fully described by suitable copula function $\mathcal {C}$. Furthermore, the copula function can be regarded as the joint distribution function of the marginal distribution functions.

In the financial context it is often convenient to express the dependency between random variables by a single number (more generally, for n random variables we get an n-dimensional matrix). Most commonly used is the Pearson coefficient of correlation cor(X, Y). This measure is the inner product of standardized random variables in the Hilbert $L^{2}\left( \varOmega ,\mathfrak {I},\Pr \right) =\left\{ X|E(\left| X\right| ^{2})<\infty \right\}$ space and it derives most of its properties from this characteristic. In the next part of the paper, we assume that the random variables belong to a space of random variables (generally called H) that is closed with respect to the opposite, i.e., if X belongs to H also $-X$ belongs to H.

However, the Pearson coefficient of correlation is only one of possible measures of dependency. Generally, concordance (rank correlation) measures are used to measure the concordance/association/correlation between random variables. Given the random vector (X, Y) and given two joint distributions $F_{X,Y},$ $F_{X,Y}^{\prime }$ with the same marginal distributions we state that $F_{X,Y}^{\prime }$ is more concordant than $F_{X,Y}$ ($F_{X,Y} \le _CF_{X,Y}^{\prime }$), if $F_{X,Y}\le F_{X,Y}^{\prime }$. The concordance measures are easily definable by copula functions because they rely only on the ‘joint’ features, having no relation with the marginal characteristics. Formally, a concordance measure $\rho$ defined on a space of continuous random variables H is any functional that satisfies the following seven properties:

• (i) $\rho :H\times H\rightarrow [-1,1]$;

• (ii) for any random variable $X\in H:$ $\ \rho (X,X)=1;$ $\rho (X,-X)=-1;$

• (iii) $\rho (X,Y)=\rho (Y,X);$

• (iv) $\rho (-X,Y)=\rho (X,-Y)=-\rho (X,Y)$;

• (v) if X and Y are independent random variables, then $\ \rho (X,Y)=0;$

• (vi) if we consider two bivariate random vectors $\mathbf {X} =(X_{1},X_{2}),$ $\mathbf {Y}=(Y_{1},Y_{2}),$ ($X_{i},Y_{i}\in H$) with the same marginal distributions $(F_{1},F_{2})$ such that $F_{\mathbf {X}}(\mathbf {x})=\Pr (X_{1}\le x_{1},X_{2}\le x_{2})\le F_{\mathbf {Y}}(\mathbf { x})$ for any $\mathbf {x=(}x_{1},x_{2}\mathbf {)\in \mathbb {R}}^{2}$ (i.e. $\mathbf {X}$ dominates $\mathbf {Y}$ with respect to concordance ordering²) then $\rho (X_{1},X_{2})\le \rho (Y_{1},Y_{2})$ (or $\rho _{\mathcal {C}_{1}}\le \rho _{\mathcal {C}_{2}}$ where $\mathcal {C}_{1}$ and $\mathcal {C}_{2}$ are the copulas associated with bivariate vectors $\mathbf {X},$ $\mathbf {Y}$);

• (vii) given a sequence of continuous bivariate random vectors $\left\{ (X_{n},Y_{n})\right\} _{n\ge 1}$ with copulas $\mathcal {C}_{n}$ that converge pointwise to the copula $\mathcal {C}$, then $\rho _{\mathcal {C} _{n}}$ converge to $\rho _{\mathcal {C}}.$

Observe that $\rho (X_{1},X_{2})=\rho (h_{1}(X_{1}),h_{2}(X_{2}))$ for any concordance measure $\rho$, for any couple of continuous random variables $(X_{1},X_{2})$ and for any two strictly monotonic (either both increasing or both decreasing) functions $h_{1},h_{2}$. The Pearson coefficient of correlation is not a concordance measure, since it does not satisfy Property (vii). For further details on all properties of concordance measures and their proofs see Joe (1997), Cherubini et al. (2004) or Nelsen (2006).

The most popular concordance measures are Kendall’s tau, Spearman’s rho, Gini’s index of cograduation (Gini’s gamma), and Blomqvist’s beta. The concordance measure definition is given only for continuous random variables. Clearly, we can try to extend the definition to non-continuous random variables using the standard extension of the copula given by Schweizer and Sklar (1974). However, with the standard extension of the copula, the most interesting concordance measures (Kendall, Spearman etc.) do not satisfy axiom (vii) when non-continuous random variables are used, see Nešlehová (2007) and the references therein. In the next part of the paper, we continue to call ‘concordance measures’ their extended definitions to non-continuous random variables.

In order to consider a larger class of association measures, rather than concordance measures, we introduce the class of correlation measures.

Definition 1

The correlation measure defined on a given space of random variables H is any functional $\rho :H\times H\rightarrow [-1,1]$ that is law invariant (i.e. $\rho (X,Y)$ is uniquely determined by the joint distribution of (X, Y)) and satisfies the first five properties of concordance measures as given above. We say that a correlation measure $\rho$ is semidefinite positive on the space H if for any vector $X=(X_{1},X_{2},\ldots ,X_{N})^{\prime }$ with $X_{i}\in H$ the correlation matrix $Q=[\rho _{i,j}]$ (where $\rho _{i,j}=\rho (X_{i},X_{j}))$ is semidefinite positive. We call $\varphi$-correlation measure any correlation measure that satisfies the following additional property:

• (vi-bis) $\left| \rho (X,Y)\right| =1$ if, and only if, $Y=\varphi (X)$ almost surely (a.s.) for a given class of real monotonic functions $\varphi$.

Note that semidefinite positive correlation measures are generally used to determine uncorrelated factors with linear and non linear principal component analysis (PCA) that summarize most of the variability of functions applied to random variables. Clearly, the concordance measures and the Pearson correlation coefficient are correlation measures belonging to the class of continuous random variables. In particular, the Pearson correlation coefficient satisfies the property $\left| \rho (X,Y)\right| =1$ if and only if $Y=aX+b$ a.s. for certain real a and b. Similarly, for a pair of monotonic real functions $h_{1}$ and $h_{2}$ we can define a $\varphi$-correlation measure $\widetilde{\rho }(X,Y)=\rho (h_{1}(X),h_{2}(Y))$ where $\rho$ is the Pearson correlation coefficient. In this case $\left| \widetilde{\rho }(X,Y)\right| =1$ if and only if $Y=h_{2}^{-1}\left( ah_{1}(X)+b\right)$ a.s. for certain real a and b. Note, that the Spearman concordance measure $\rho _{S}(X,Y)=\rho (F_{X}(X),F_{Y}(Y))$ can be written as the Pearson correlation of the cumulative distribution functions and thus it is a $\varphi$-correlation measure.

Any correlation measure can be used to assess the dependence between random variables, but only some particular semidefinite positive correlation measures can be applied to reduce the dimensionality of statistical problems and to evaluate the dispersion of portfolios. For any couple of random variables X,  Y and for any correlation measure $\rho (X,Y)$ the correlation matrix

$$\begin{aligned} Q=\left[ \begin{array}{l@{\quad }l} 1 &{} \rho _{X,Y} \\ \rho _{X,Y} &{} 1 \end{array} \right] \end{aligned}$$

is semidefinite positive, since

$$\begin{aligned} 0\le \left( \left| x_{1}\right| -\left| x_{2}\right| \right) ^{2}\le x^{\prime }Qx=x_{1}^{2}+x_{2}^{2}+2x_{1}x_{2}\rho _{X,Y}\le \left( \left| x_{1}\right| +\left| x_{2}\right| \right) ^{2} \end{aligned}$$

for any $x=[x_{1},x_{2}]^{\prime }\in \mathbb {R} ^{2}.$ However, this property is not sufficient to guarantee that a correlation measure is semidefinite positive since simple counterexamples can be given. Semidefinite positive correlation measures are characterized by the following theorem.

Theorem 1

Let $\rho$ be a correlation measure defined on a space of real random variables H (closed with respect to the opposite). Then $\rho$ is a semidefinite positive correlation measure if and only if for any finite subspace of random variables $H_{1}\subseteq H$ the following two properties are satisfied:

• 1. there exists a vectorial space V, an inner vectorial product $\left\langle \cdot ,\cdot \right\rangle :V\times V\rightarrow R$ and a function $g:H_{2}\times H_{2}\rightarrow V\times V$, where $H_{2}=H_{1}\cup \left( -H_{1}\right)$, such that $\left\langle g(X,Y)\right\rangle =\left\langle g(Y,X)\right\rangle$ and $\left\langle g(-X,Y)\right\rangle =\left\langle g(X,-Y)\right\rangle =-\left\langle g(X,Y)\right\rangle$ and

  $$\begin{aligned} \rho (X,Y)=\frac{\left\langle g(X,Y)\right\rangle }{\sqrt{\left\langle g(X,X)\right\rangle \left\langle g(Y,Y)\right\rangle }}; \end{aligned}$$

• 2. if X and Y are independent random variables belonging to $H_{1}$, then $\left\langle g(X,Y)\right\rangle =0.$

Moreover, as a consequence of Cauchy–Schwarz inequality, we get that $\left| \rho (X,Y)\right| =1$ if and only if $(v_{1},v_{2})=g(X,Y)$ and $v_{1}=av_{2}$ for a given real a.

From the above results we easily deduce that Kendall, Spearman, and Blomqvist measures are semidefinite correlation measures on the space of the continuous random variables, since they satisfy properties (1) and (2) of Theorem 1. Moreover, for any $L^{p}\left( \varOmega ,\mathfrak {I},\Pr \right) =\left\{ X|\mathbb {E}(\left| X\right| ^{p})<\infty \right\}$ space of random variables defined in a probability space $\left( \varOmega ,\mathfrak {I},\Pr \right)$ we can introduce the following classes of semidefinite positive correlation measures.

Proposition 1

For any $p>0$ the following functionals defined on $L^{p}\left( \varOmega ,\mathfrak {I},\Pr \right)$ space are semidefinite positive correlation measures.

• M1
  $$\begin{aligned} \rho _{p}(X,Y)=\frac{\mathbb {E}\left( \left( X-V_{p/2}(X)\right) ^{\langle p/2\rangle }\left( Y-V_{p/2}(Y)\right) ^{\langle p/2\rangle }\right) ^{\langle \min (2/p,2)\rangle }}{\left\| X-V_{p/2}(X)\right\| _{p}\left\| Y-V_{p/2}(Y)\right\| _{p}}, \end{aligned}$$

  where $\left( x\right) ^{\langle q\rangle }= sign (x)\left| x\right| ^{q},V_{q}(X)$ is the unique real value such that $E\left( \left( X-V_{q}(X)\right) ^{\langle q\rangle }\right) =0$ and $\left\| X\right\| _{p}=E\left( \left| X\right| ^{p}\right) ^{\min (1,1/p)}$ is the classic metric in $L^{p}$. Moreover $\left| \rho _{p}(X,Y)\right| =1$ if and only if $Y=aX+b$ a.s. for some real a and b.

• M2
  $$\begin{aligned} \tau _{p}(X,Y)=\frac{\mathbb {E}\left( \left( X-X_{1}\right) ^{\langle p/2\rangle }\left( Y-Y_{1}\right) ^{\langle p/2\rangle }\right) ^{\langle \min (2/p,2)\rangle }}{\left\| \left( X-X_{1}\right) \right\| _{p}\left\| \left( Y-Y_{1}\right) \right\| _{p}}, \end{aligned}$$

  where $(X_{1},Y_{1})$ is an independent identically distributed (i.i.d.) copy of (X, Y).

• M3
  $$\begin{aligned} O_{p,\mathfrak {I}_{1}}(Z_{1},Z_{2})= cor (Z_{1},Z_{2})^{\langle \min (2/p,2)\rangle }, \end{aligned}$$

  where $Z_{1}=(X^{\langle p/2\rangle }-E(X^{\langle p/2\rangle }|\mathfrak {I}_{1}))$, $Z_{2}=(Y^{\langle p/2\rangle }-E(Y^{\langle p/2\rangle }|\mathfrak {I}_{1}))$, $\mathfrak {I}_{1}$ is a sub-sigma algebra of $\mathfrak {I}$ (i.e. $\mathfrak {I}_{1}\subset \mathfrak {I})$ and X,$Y\in L^{p}(\varOmega ,\mathfrak {I},\Pr )$ are not $\mathfrak {I}_{1}$ measurable. Measure $O_{p,\mathfrak {I}_{1}}$ is a correlation measure among all the random variables $Z_{i}$ (above defined) orthogonal to $L^{2}(\varOmega ,\mathfrak {I}_{1},\Pr )$ (when we use the scalar product $(U,V)\longrightarrow E(UV))$.

All these measures are logical extensions of the Pearson correlation measure. We obtain the Pearson correlation measure with measures of type M1, M2 and M3 when $p=2$ and $\mathfrak {I}_{1}=\left\{ \varnothing ;\varOmega \right\}$. In addition, if X and Y are continuous random variables, then $V_{0}(X)$ and $V_{0}(Y)$ are the medians of X and Y, respectively. Thus $\mathop {\lim }\nolimits _{p\rightarrow 0}\rho _{p}(X,Y)=\beta _{B}(X,Y)$ and measures of type M1 are extensions of the Blomqvist measure (which we obtain when $p=0$). Similarly, measures of type M2 are logical extensions of the Kendall correlation (which we obtain for $p=0$). Measure M3 is useful for identifying the variability of the part of each random variable³ which is ‘uncorrelated’ with $\mathfrak {I}_{1}.$ This variability is here represented by the correlation of random variables subtracted of their projection on the subspace of probability $\left( \varOmega ,\mathfrak {I}_{1},\Pr \right)$ (where $\mathfrak {I}_{1}\subset \mathfrak {I}$).

Working with semidefinite positive correlation matrices is fundamental in the case of several statistical problems. However, the estimator of semidefinite positive correlation matrices may not be semidefinite positive. In this case, we should approximate the estimates as suggested by Rousseuw and Molenberghs (1993).

Generally, the ordering properties of correlation measures are very useful in many financial problems. On the one hand, several semidefinite positive correlation measures, differently from concordance measures, are not necessarily isotonic with the concordance ordering. On the other hand, the most interesting correlation measures in the portfolio theory are those linked to investors’ choices. Since the investors are generally non-satiable and/or risk-averse, the optimal portfolio choices should be consistent with these investors’ preferences.

3 Deviation measures and linear correlation measures in portfolio selection problems

One of the most popular measures proposed to order admissible portfolios according to their risk is the standard deviation. Several papers in the recent literature discuss the possibility of using other measures of risk and variability to optimize investor’s choices. Typical examples of such variability measures are deviation measures that are defined axiomatically (Rockafellar et al. 2006; Rachev et al. 2008). A deviation measure is any positive functional D that is law invariant (i.e. $D(X)=D(Y)$ for any X and Y with the same distribution) and that satisfies the following properties:

• P1 $D(X+c)=D(X)$ for all X and constant $c>0$;

• P2 $D(0)=0$, and $D(aX)=aD(X)$ for all X and $a>0$;

• P3 $D(X)\ge 0$ for all X, with $D(X)=0$ if and only if X is constant;

• P4 $D(X+Y)\le D(X)+D(Y)$ for all X and Y.

All deviation measures that satisfy the Fatou property are consistent with concave ordering, see Bauerle and Müller (2006), i.e. if X dominates Y in the concave order $(X\ge _{cv}Y)$, the deviation measure of X is lower than or equal to the deviation measure of Y, $D(X)\le D(Y)$. Recall that we say portfolio $X\ge _{cv}Y$ if and only if every risk-averse investor prefers X to Y,  i.e. $E(u(X))\ge E(u(Y))$ for every concave (utility) function u. This is also considered as an implicit definition of risk-averse investors. Moreover, in a certain sense, semidefinite positive correlation matrices represent multivariate measures of dispersion, and they generally cannot be used to measure the dispersion of a given portfolio (except in special cases).

In practical terms, let us consider n assets with gross returns $z=[ z_{1},z_{2},\ldots ,z_{n}]^{\prime }$ and the vector of portfolio weights $x=[x_{1},x_{2},\ldots ,x_{n}]^{\prime }.$ Given a semidefinite positive correlation matrix $Q_{\rho }=[\rho _{i,j}]$ of gross returns, we may consider the following measure of portfolio dispersion:

$$\begin{aligned} d_{\rho ,\sigma }(x^{\prime }z)=\sqrt{x^{\prime }Q_{\rho ,\sigma }x}, \end{aligned}$$

(3)

where $Q_{\rho ,\sigma }=[\sigma _{z_{j}}\sigma _{z_{i}}\rho _{i,j}]$, $\rho$ is a semidefinite positive correlation measure and $\sigma _{z}$ is a deviation measure. When there is a riskless return among the asset returns (say, the first component), then $\rho _{1,j}=\rho _{j,1}=0$ for any j, since a constant is independent of any random variable. Therefore, the riskless asset does not make any contribution to the measure $d_{\rho ,\sigma }.$

The measure $d_{\rho ,\sigma }$ is a logical extension of portfolio variance and it takes into account different contribution of correlation $\rho$ and risk $\sigma _{z_{j}}$ of a given asset j. In the definition of portfolio dispersion (3), it is essential to use a semidefinite positive correlation measure $\rho ,$ since the semidefinite positiveness makes it possible to guarantee the convexity of $d_{\rho ,\sigma }^{2}.$ On the other hand, Bauerle and Müller (2006) prove the consistency with risk-averse preferences for several convex measures. In this section we mainly analyze the possibilities of using measures of type $d_{\rho ,\sigma }$ for portfolio problems. Firstly, we observe that measure $d_{\rho ,\sigma }$ does not always satisfy the law invariance property.

Example 1

Let us assume there are three assets with gross returns $z=(z_{1},z_{2},z_{3})^{\prime }$ and suppose that the third gross return has the same distribution as a suitable combination of $z_{1}$ and $z_{2}$, $xz_{1}+yz_{2}$, i.e. the portfolios [x, y, 0]z and [0, 0, 1]z have the same distribution. Since any deviation measure $\sigma _{z}$ is law invariant then $\sigma _{z_{3}}^{2}=\sigma _{xz_{1}+yz_{2}}^{2}$. Generally, however, unless $Q_{\rho ,\sigma }$ is the variance–covariance matrix, the following relation holds:

$$\begin{aligned} d_{\rho ,\sigma }([0,0,1]z)^{2}= & {} \sigma _{xz_{1}+yz_{2}}^{2}\ne x^{2}\sigma _{z_{1}}^{2}+y^{2}\sigma _{z_{2}}^{2} \\&+\,2xy\sigma _{z_{1}}\sigma _{z_{2}}\rho (z_{1},z_{2})=d_{\rho ,\sigma }([x,y,0]z)^{2}. \end{aligned}$$

This appears to be more evident if we suppose that the vector z is Gaussian with Pearson correlation $\rho (z_{1},z_{2})=0.5$ and that the portfolio $0.5z_{1}+0.5z_{2}$ has the same distribution as $z_{3}$, that is, Gaussian with variance $\sigma _{z_{3}}^{2}=0.5^{2}\sigma _{z_{1}}^{2}+0.5^{2} \sigma _{z_{2}}^{2}+0.5^{2}\sigma _{z_{1}}\sigma _{z_{2}}.$ Observe that for the two-dimensional Gaussian distribution with linear correlation coefficient $\rho ,$ the well-known relation $\tau =\frac{2}{\pi } \arcsin (\rho )$ between Kendall’s tau and the linear correlation coefficient holds. Now, if we consider an alternative dispersion matrix $Q_{\widetilde{ \rho },\sigma }=[\sigma _{z_{j}}\sigma _{z_{i}}\widetilde{\rho }_{i,j}]$, where $\sigma _{z_{j}}$ is the standard deviation of $z_{j}$ and $\widetilde{\rho } _{i,j}$ is the Kendall correlation measure between the i-th and the j-th components, then $\widetilde{\rho }_{1,2}=\tau (z_{1},z_{2})=\frac{2}{\pi } \arcsin (0.5)=0.3333$. Therefore $d_{\widetilde{\rho },\sigma }([0,0,1]z)^{2}= \sigma _{z_{3}}^{2}\ne d_{\widetilde{\rho },\sigma }([0.5,0.5,0]z)^{2}$ even if portfolios $0.5z_{1}+0.5z_{2}$ and $z_{3}$ have the same distribution. Thus the measure $d_{\widetilde{\rho },\sigma }(x^{\prime }z)=\sqrt{ x^{\prime }Q_{\widetilde{\rho },\sigma }x}$ is not law invariant.

On the one hand, the above example suggests that it can be guaranteed only for some particular correlation measures that the measure $d_{\rho ,\sigma }$ satisfies the law invariance property. In particular, as proved in Proposition 2, if $\rho$ is a semidefinite positive correlation measure different from the Pearson linear correlation and z is elliptically distributed with finite variance (or a more general two parametric family), then $d_{\rho ,\sigma }$ does not generally satisfy the law invariance property. On the other hand, if $\rho$ is the Pearson linear correlation measure, then $d_{\rho ,\sigma }$ is law invariant for any deviation measure $\sigma$ that we use (together with the mean) to characterize the family of elliptical distributions.

Proposition 2

Suppose that all the portfolios of returns belong to a translation- and scalar-invariant family of random variables (i.e. if the r.v. X belongs to the family also X+t and aX belong to the same family for any real a, t) that admits finite variance. Suppose that all the random variables of this family have a distribution identified by two parameters: the mean and a deviation measure (i.e. if two random variables have the same mean and deviation measure then they have the same distribution). Consider two different parameterizations $\left( m,std\right)$ and $\left( m,\sigma \right)$ for this family of random variables, where m is the mean, std is the standard deviation and $\sigma$ is a deviation measure. Let $\rho$ be a semidefinite positive correlation measure defined on this class of random variables. Then $d_{\rho ,\sigma }(x^{\prime }z)=\sqrt{ x^{\prime }Q_{\rho ,\sigma }x}$ satisfies the law invariance property if and only if $\rho$ is the Pearson correlation measure.

Therefore, for random variables depending on two parameters as in Proposition 2 (for example elliptical distributions), it makes sense to use the measure $d_{\rho ,\sigma }$, where we distinguish the contribution of the Pearson correlation measure $\rho$ and of the deviation measure $\sigma$. Moreover, all the portfolio returns belong to a translation- and scalar-invariant family depending on a finite number of parameters, which can be often seen as the union of translation- and scalar-invariant families depending on two parameters (see Ortobelli 2001). Thus, if we assume that all the returns admit finite variance, it makes sense to use the measure $d_{\rho ,\sigma }$ only if $\rho$ is the Pearson correlation measure and $\sigma$ is a deviation measure. However, the empirical evidence suggests that the return series are in the domain of attraction of a stable Paretian law that does not necessarily admit finite variance (see, among others, Grabchak and Samorodnitsky 2010). For this reason we study the most general case.

A sufficient condition guaranteeing that measure (3) is invariant in law is given by the following proposition.

Proposition 3

Suppose that $\rho$ is a semidefinite positive correlation measure defined on all possible portfolios of gross returns $x^{\prime }z$. Suppose that the functional $\rho$ can be represented for all portfolios as suggested by property (1) in Theorem 1, i.e. $\rho :H\times H\rightarrow [-1,1]$ and

$$\begin{aligned} \rho (X,Y)=\frac{\langle g(X,Y) \rangle }{\sqrt{\langle g(X,X) \rangle \langle g(Y,Y) \rangle } }, \end{aligned}$$

where H is the class of all admissible portfolios $x^{\prime }z$ and $\langle .,.\rangle :V\times V\rightarrow R$ is a vectorial inner product. Let us assume the function $g:H\times H\rightarrow V\times V$ such that g(X, Y) is bilinear, i.e. $g(aX+bZ,Y)=ag(X,Y)+bg(Z,Y)$ and $g(X,aY+bZ)=ag(X,Y)+bg(X,Z).$ If $\sigma _{X}=\sqrt{\langle g(X,X)\rangle }$ is a deviation measure, then $d_{\rho ,\sigma }(x^{\prime }z)=\sqrt{x^{\prime }Q_{\rho ,\sigma }x}$ is invariant in law.

More generally, we can define the semidefinite positive correlation measures that satisfy the properties of Proposition 3 as follows.

Definition 2

We say that $\rho$ is a linear correlation measure in the class of the random variables H if it satisfies the following properties:

• 1. $\rho$ is a semidefinite positive correlation measure defined on the class of random variables H;

• 2. for every vector $X=(X_{1},X_{2},\ldots ,X_{N})^{\prime }$ with $X_{i}\in H$ and a, $b\in R^{N}$ with $a=[a_{1},\ldots ,a_{N}]^{\prime }$ and $b=[b_{1},\ldots ,b_{N}]^{\prime }$, it holds $\rho \left( \sum _{i=1}^{N}a_{i}X_{i},\sum _{i=1}^{N}b_{i}X_{i}\right) =\rho \left( a^{\prime }X,b^{\prime }X\right) =\frac{a^{\prime }Qb}{\sqrt{ a ^{\prime }Qab^{\prime }Qb}}$, where $Q=\left[ v_{ij}\right]$ is a semidefinite positive matrix such that $v_{ij}=\left\langle g(X_{i},X_{j})\right\rangle ,$ where g and $\left\langle \cdot ,\cdot \right\rangle$ are defined by Theorem 1;

• 3. the functional $\sigma _{X}=\sqrt{\langle g(X,X)\rangle }$ is a deviation measure.

Therefore as a consequence of Proposition 3 we can guarantee that for any linear correlation measure there exists at least one deviation measure $\sigma$ (i.e. $\sigma _{X}=\sqrt{\langle g(X,X)\rangle }$) such that $d_{\rho ,\sigma }$ is invariant in law. Examples of linear correlation measures are all those that can be seen as an inner product of a Hilbert space of random variables. Typical examples of linear correlation measures on $L^{2}\left( \varOmega ,\mathfrak {I},\Pr \right)$ space are: the Pearson correlation, and correlation $O_{2,\mathfrak {I}_{1}}$ (which is still the Pearson linear correlation applied to all random variables orthogonal to $L^{2}\left( \varOmega ,\mathfrak {I}_{1},\Pr \right)$).

In order to find new invariant-in-law measures of the type (3) and new linear correlation measures, we consider correlation measures $\rho$ for elliptical random variables with infinite variance. In particular, several empirical financial investigations show that the returns $r_{i}$ ($i=1,\ldots ,n$) exhibit the following tail behavior

$$\begin{aligned} \Pr (\left| r_{i}\right| >u)\sim u^{-\alpha _{i}}L_{i}(u)\quad \text { as } u\rightarrow \infty , \end{aligned}$$

(4)

where $0<\alpha _{i}<2$ and $L_{i}(u)$ is a slowly varying function at infinity, i.e.

$$\begin{aligned} \underset{u\rightarrow \infty }{\lim }\frac{L_{i}(cu)}{L_{i}(u)}\rightarrow 1 \quad \text { for all }c>0, \end{aligned}$$

see Samorodnitsky and Taqqu (1994) and Rachev and Mittnik (2000).

From empirical evidence on stock returns (see, among others, Mandelbrot 1963a, b; Fama 1965; Grabchak and Samorodnitsky 2010; Nolan 2003) we always observe that the index of stability $\alpha _{i}$ belongs to interval (1,2), so that relation (4) implies that returns are in the domain of attraction of an $\alpha$-stable law that admits finite mean and not finite variance. This asymptotic behavior of data is generally approximated by assuming that the returns follow a stable Paretian law $S_{\alpha }(\gamma ,\beta ,\mu ).$ A stable Paretian law depends on four parameters: the index of stability $\alpha \in (0,2]$, the asymmetry parameter $\beta \in [-1,1]$, the dispersion parameter $\gamma >0$, and the location parameter $\mu$.

Typically, we can assume that the vector of returns r is $\alpha$-stable sub-Gaussian distributed. That is, the characteristic function of r has the following form:

$$\begin{aligned} \varPhi _{r}(u)=E(\exp (iu^{\prime }r))=\exp \left( -\left( u^{\prime }Qu\right) ^{\frac{\alpha }{2}}+iu^{\prime }\mu \right) , \end{aligned}$$

(5)

where $Q=\left[ v_{ij}\right]$ is a positive definite dispersion matrix and $\mu$ is the mean vector (when $\alpha >1).$ Note that an $\alpha$ stable sub-Gaussian distribution is an elliptical distribution symmetric around the mean (since $\beta =0$) and when $\alpha =2$ the vector r is Gaussian with mean $\mu$ and variance covariance matrix Q / 2. Since $\mu _{i}$ and $v_{ii}$ ($i=1,\ldots ,n$) are respectively the location parameter and the square scale parameter of the $\alpha$ stable distributed i-th component $r_{i}$, then we can estimate them either using the maximum likelihood estimator or other estimators.⁴ As noted by Kring et al. (2008), parameter $v_{ij}$ (also called covariation parameter) can be seen as the difference of square scale parameters, i.e.:

$$\begin{aligned} v_{ij}=\gamma _{\left( r_{i}+r_{j}\right) /2}^{2}-\gamma _{\left( r_{i}-r_{j}\right) /2}^{2}, \end{aligned}$$

(6)

where $\gamma _{\left( r_{i}\pm r_{j}\right) /2}^{2}$ are the square scale parameters of the random variables $\left( r_{i}\pm r_{j}\right) /2.$ Thus, to estimate the covariation parameters $v_{ij}$ (with $i\ne j$) of the stable vector we use the estimator $\widehat{v}_{ij}=\widehat{\gamma } _{\left( r_{i}+r_{j}\right) /2}^{2}-\widehat{\gamma }_{\left( r_{i}-r_{j}\right) /2}^{2}.$ Alternatively, to estimate the stable sub-Gaussian parameters, we can use the moment estimator considering the following relations

$$\begin{aligned} v_{jj}^{q/2}=A(\alpha ,q)E\left( \left| r_{j}-E(r_{j})\right| ^{q}\right) \end{aligned}$$

for any $q\in (-1,\alpha )$ where $A(\alpha ,p)=\frac{\varGamma \left( 1-\frac{p}{2}\right) \sqrt{\pi }}{2^{p}\varGamma \left( 1-\frac{p}{ \alpha }\right) \varGamma \left( \frac{p+1}{2}\right) }$ and

$$\begin{aligned} v_{ij}=v_{jj}^{\left( 2-p\right) /2}A(\alpha ,p)E\left( \left( r_{i}-E(r_{i})\right) \left( r_{j}-E(r_{j})\right) ^{\left\langle p-1\right\rangle }\right) \end{aligned}$$

(7)

for any $p\in [1,\alpha )$ (see Ortobelli et al. 2005). Moreover, under these distributional assumptions a linear correlation measure for the vector of returns r (or for the vector of gross returns z) is given by the following proposition.

Proposition 4

Suppose that the vector of gross returns z is $\alpha$ stable sub-Gaussian distributed ($\alpha >1$) and suppose that $\sigma$ is an alternative (to the stable scale parameter $\gamma$) deviation measure that, together with the mean, characterizes this elliptical family (i.e. if two stable distributed random variables have the same mean and deviation measure $\sigma$, then they have the same distributions). Let $\rho$ be a semidefinite positive correlation measure defined on the class of all these elliptically distributed returns. Then $\rho$ is a linear correlation measure and $d_{\rho ,\sigma }(x^{\prime }z)=\sqrt{x^{\prime }Q_{\rho ,\sigma }x}$ satisfies the law invariance property if and only if

$$\begin{aligned} \rho (x^{\prime }z,y^{\prime }z)=\frac{x^{\prime }Qy}{\sqrt{\left( x^{\prime }Qx\right) \left( y^{\prime }Qy\right) }} \end{aligned}$$

(8)

where $\left\langle g(x^{\prime }z,y^{\prime }z)\right\rangle =x^{\prime }Qy$ and Q is the matrix defined in (5).

We call stable correlation measure the linear correlation measure $\rho (z_{i},z_{j})=\frac{v_{ij}}{\sqrt{v_{ii}v_{jj}}}$ associated with a vector of $\alpha$-stable sub-Gaussian distributions. In particular, by using formula (7), the linear correlation can be defined by:

$$\begin{aligned} \rho (z_{i},z_{j})=\frac{v_{ij}}{\sqrt{v_{ii}v_{jj}}}=\frac{E\left( \left( z_{i}-E(z_{i})\right) sign \left( z_{j}-E(z_{j})\right) \right) }{E\left( \left| z_{i}-E(z_{i})\right| \right) } \end{aligned}$$

(9)

for all stable sub-Gaussian distributions that admit a finite first moment. Formula (9) produces an alternative definition of the Pearson linear correlation when the vector of returns is Gaussian distributed. On the other hand, if we use the standard method of the moments to estimate $\rho (z_{i},z_{j})$, we may get a nonsymmetric estimator of the linear correlation matrix. For this reason we can consider

$$\begin{aligned} \rho (X,Y)=\frac{E\left( \left( X-E(X)\right) sign \left( Y-E(Y)\right) \right) }{2E\left( \left| X-E(X)\right| \right) }+\frac{E\left( \left( Y-E(Y)\right) sign \left( X-E(X)\right) \right) }{2E\left( \left| Y-E(Y)\right| \right) } \nonumber \\ \end{aligned}$$

(10)

as a linear correlation measure of $\alpha$-stable sub-Gaussian laws with $\alpha >1$. As a matter of fact, formula (10) is always a linear correlation measure on the class of all admissible portfolios when the vector z admits an $\alpha$-stable sub-Gaussian distribution. We obtain an alternative linear correlation measure if we apply it to all random variables $X-E(X|\mathfrak {I}_{1}).$

Moreover, once we have some different types of correlation measures, we can produce further correlation measures as described in the following corollary.

Corollary 1

The convex combination of concordance measures (correlation measures, semidefinite positive correlation measures) is still a concordance measure (correlation measure, semidefinite positive correlation measure). Moreover, let $\rho _{i}$ ($i=1,\ldots ,m$) be m linear correlation measures defined for all random variables X, Y belonging to a space $H\subseteq L^{1}\left( \varOmega ,\mathfrak {I},\Pr \right)$ that we assume contains its centered random variables. Suppose that $\rho _{i}$ admits the representation $\rho _{i}(X,Y)=\frac{\langle g_{i}(X,Y)\rangle _{i}}{\sqrt{ \langle g_{i}(X,X)\rangle _{i}\langle g_{i}(Y,Y)\rangle _{i}}}$, where $\langle .,.\rangle _{i}:V_{(i)}\times V_{(i)}\rightarrow \mathbb {R}$, $i=1,\ldots ,m$, are vectorial inner products. Then $\langle X,Y\rangle =\sum _{i=1}^{m}a_{i}\langle g_{i}(X,Y)\rangle _{i}$ ($a_{i}\ge 0$; $\sum _{i=1}^{m}a_{i}=1$) is an inner product in the class of the centered random variables belonging to H and thus $\rho (X,Y)=\frac{\langle X,Y\rangle }{\sqrt{\langle X,X\rangle \langle Y,Y\rangle }}$ is a linear correlation measure.

The lack of invariance in law does not permit the use of measures $d_{\rho ,\sigma }(x^{\prime }z)$ within portfolio selection problems. When $d_{\rho ,\sigma }(x^{\prime }z)$ is invariant in law, we obtain the following proposition.

Proposition 5

Suppose that the matrix $Q_{\rho ,\sigma }$ does not depend on the portfolio weights x, and that all random variables are defined in a finite probability space where the probability is uniform. If $d_{\rho ,\sigma }(x^{\prime }z)$ is invariant in law, it is consistent with the preferences of risk-averse investors.

Clearly, the assumption that we are in a finite probability space $\varOmega =\left\{ \omega _{1},\omega _{2},\ldots ,\omega _{n}\right\} ,$ with uniform probability $\Pr \left( \left\{ \omega _{i}\right\} \right) =\frac{1}{n}$, is not very realistic. However, several consistent estimators $\widetilde{Q} _{\rho ,\sigma }$ of $Q_{\rho ,\sigma }$ are computed as if the gross returns were defined in a finite probability space with uniform probability and, also for this reason, the estimator $\widetilde{Q}_{\rho ,\sigma }$ is still semidefinite positive. Thus, for example, if $\sigma _{z_{i}}=\mathbb {E }(f(z_{i}))$ and $\rho _{i,j}=\mathbb {E}(v(z_{i},z_{j}))$ for some functions f and v,  then $\widetilde{\sigma }_{z_{j}}=\frac{1}{n} \sum _{k=1}^{n}f(z_{j}^{(k)}),$ $\widetilde{\rho }_{i,j}=\frac{1}{n} \sum _{k=1}^{n}v(z_{i}^{(k)},z_{j}^{(k)})$ (where $z_{j}^{(k)}$ is the k-th observation of $z_{j}$) are consistent estimators of $\sigma _{z_{i}}$ and $\rho _{i,j},$ and $\widetilde{Q}_{\rho ,\sigma }=[\widetilde{ \sigma }_{z_{j}}\widetilde{\sigma }_{z_{i}}\widetilde{\rho }_{i,j}]$ is a consistent estimator of $Q_{\rho ,\sigma }$.

Therefore, when $d_{\rho ,\sigma }(x^{\prime }z)$ is invariant in law (according to Bauerle and Müller 2006) and the estimated distribution of $w^{\prime }z$ is dominated in the convex order by the estimated distribution of $y^{\prime }z,$ then $w^{\prime }\widetilde{Q} _{\rho ,\sigma }w\le y^{\prime }\widetilde{Q}_{\rho ,\sigma }y$ . Moreover, as also pointed out by Bauerle and Müller (2006), when the probability space is non-atomic, we can guarantee that a measure D is consistent with the choices of risk-averse investors if D is an invariant-in-law, convex measure that satisfies the Fatou property. Thus the following corollary holds.

Corollary 2

Suppose that the matrix $Q_{\rho ,\sigma }$ does not depend on the portfolio weights x. If $d_{\rho ,\sigma }(x^{\prime }z)$ is invariant in law and satisfies the Fatou property, then it is consistent with the choices of risk-averse investors. In particular, under the assumption of Proposition 2 (4), $d_{\rho ,\sigma }(x^{\prime }z)$ is consistent with the choices of risk-averse investors only if $\rho$ is the Pearson correlation measure (stable correlation measure) and $\sigma$ is a deviation measure that (together with the mean) characterizes the distribution family.

Moreover, we can also prove that concordance measures cannot be used as linear correlation measures even if the linear correlation measures are not the only correlation measures related to functionals consistent with risk-averse preferences.⁵

4 Two distinct ways to use correlation measures in portfolio problems

We distinguish two possible directions for the application of correlation measures within portfolio theory. In particular, we use these measures either in optimization problems or in order to reduce the dimensionality of the problem. Let us briefly discuss both of them below.

4.1 The portfolio dimensional problem

Papp et al. (2005) and Kondor et al. (2007) have shown that the number of observations should increase with the number of assets in order to obtain a good approximation of the portfolio risk-reward measures. It is therefore necessary to find the right trade-off between a statistical approximation of the historical series depending only on a few parameters and the number of historical observations. In practice, there are two different ways to reduce the dimensionality of a large-scale portfolio selection problem: preselection or factor models. With preselection, only some assets are preselected with respect to one or more optimality criteria (see Ortobelli et al. 2011) to be used in the portfolio selection. On the other hand, portfolio managers reduce the dimensionality of the problem by approximating the gross return series with a k-fund separation model (or some other regression-type model, see Ross 1978) that depends on an adequate number (not too large) of parameters. As in the following empirical analysis, the two methodologies are often combined together. We first preselect two hundred assets and then reduce the randomness of the problem by approximating the preselected gross returns with a k-fund separation model.

In order to apply a k-fund separation model, we perform a principal component analysis (PCA) of the stock returns. In doing so, we identify the few factors (portfolios) with the highest return variability. We therefore replace the original n correlated time series $z_{i}$ with n uncorrelated time series $R_{i}$ assuming that each $z_{i}$ is a linear combination of the series $R_{i}$. This is always possible when we use a linear correlation measure $\rho$. We then implement a dimensionality reduction by choosing only those factors whose deviation measure $\langle R_{i},R_{i}\rangle$ is significantly different from zero. We call portfolio factors $f_{i}$ the s time series $R_{i}$ with a significant variability, while the remaining $n-s$ series with very small variability are summarized by an error. Thus, each series $z_{i}$ is a linear combination of the factors plus a small uncorrelated noise:

$$\begin{aligned} z_{i}=\sum _{j=1}^{s}a_{ij}f_{j}+\sum _{j=s+1}^{n}a_{ij}R_{j}= \sum _{j=1}^{s}a_{ij}f_{j}+\varepsilon _{i}. \end{aligned}$$

(11)

We can apply the PCA either to the Pearson correlation matrix or to any other linear correlation measure. For example, $Q=[\rho _{i,j}]$ could be the stable sub-Gaussian correlation measure or $\rho _{i,j}=O_{2,\mathfrak {I}_{1}}(z_{i},z_{j})$ for a suitable sigma algebra $\mathfrak {I}_{1}$. Once we have identified the s factors $f_{j}=\sum _{i=1}^{n}y_{i}z_{i}$ ($j=1,\ldots ,s$; such that $\sum _{k=1}^{n}y_{k}^{2}=1$), which explains most of the variability of the returns, we further reduce the variability of the error by regressing the series on the factors $f_{j},$ so that we get:

$$\begin{aligned} z_{i}=b_{i,0}+\sum _{j=1}^{s}b_{i,j}f_{j}+\varepsilon _{i}. \end{aligned}$$

(12)

We can then apply any portfolio optimization problem to the approximated portfolio:

$$\begin{aligned} x^{\prime }z\simeq x^{\prime }\widehat{\mathbf {b}}_{0}+\sum _{j=1}^{s}x^{ \prime }\widehat{\mathbf {b}}_{j}f_{j}, \end{aligned}$$

where $\widehat{\mathbf {b}}_{j}=[\widehat{b}_{1,j},\ldots ,\widehat{b} _{n,j}]^{\prime }$ is the vector of estimated coefficients $\widehat{b} _{i,j}$ ($j=0,1,\ldots ,s$). This procedure is computational efficient and can be applied using any linear correlation measure. Clearly, we can use a similar procedure to capture even a non-linear factor dependence. Indeed, if we consider a bijective non-linear function h that associates with any random gross return $z_{i}$ another random variable $u_{i}$ (i.e. $u_{i}=h(z_{i})$), we can apply the PCA to the random variables $u_{i},$ obtaining

$$\begin{aligned} u_{i}=\widetilde{b}_{i,0}+\sum _{j=1}^{s}\widetilde{b}_{i,j}\widetilde{f}_{j}+ \widetilde{\varepsilon }_{i}. \end{aligned}$$

(13)

We can therefore apply portfolio selection to the approximated gross returns: $x^{\prime }z\simeq \sum _{i=1}^{n}x_{i}h^{-1}( \widetilde{b}_{i,0}+\sum _{j=1}^{s}\widetilde{b}_{i,j}\widetilde{f}_{j}).$

4.2 Portfolio selection problems

The portfolio selection problem is generally studied by considering the reward and the risk of the admissible portfolios. In this context investors choose a portfolio that minimizes a given risk measure q provided that the reward measure v is constrained by some minimal value m; that is,

$$\begin{aligned} \begin{array}{c} \underset{x}{\min }\ q(x^{\prime }z-z_{b}) \\ \sum \limits _{i=1}^{n}x_{i}=1;\text { }x_{i}\ge 0; \\ v(x^{\prime }z-z_{b})\ge m, \end{array} \end{aligned}$$

(14)

where $z_{b}$ denotes the gross return of a given benchmark. In particular, as risk measure q we could use the measure $d_{\rho ,\sigma }$, where $\rho$ is a linear correlation measure and $\sigma$ is a deviation measure. The portfolio that yields the maximum reward per unit of risk is called the market portfolio. In particular, when the reward and risk are both positive measures, the market portfolio is the solution for the optimization problem:

$$\begin{aligned} \begin{array}{c} \underset{x}{\max }\frac{v(x^{\prime }z-z_{b})}{q(x^{\prime }z-z_{b})} \\ \sum \limits _{i=1}^{n}x_{i}=1;\text { }x_{i}\ge 0. \end{array} \end{aligned}$$

(15)

Generally, we can distinguish two different types of benchmarks: artificial benchmarks and traded benchmarks. Traded benchmarks are indices traded on the market that represent some sectors and/or markets. For these benchmarks we can obtain historical observations. Artificial benchmarks are not traded on the market, and they are artificially created by portfolio managers to represent the best/worst indicators of the assets used. Typical examples are the upper and lower market stochastic bounds (see, among others, Rachev and Mittnik 2000 or Ortobelli and Pellerey 2008).

The simplest upper and lower stochastic bounds are respectively given by $\max _{i}z_{i}$ and $\min _{i}z_{i}$ which satisfy the relation $\max _{i}z_{i}\ge x^{\prime }z\ge \min _{i}z_{i}$ for all vectors of portfolio weights x belonging to the simplex $S=\{ x\in \mathbb {R}^{n}| \sum _{i=1}^{n}x_{i}=1;x_{i}\ge 0\} .$ Thus, investors want to maximize the concordance and/or the correlation with the upper bound benchmark $\max _{i}z_{i}$ and to minimize the concordance and/or the correlation with the lower bound benchmark $\min _{i}z_{i}.$ Alternatively, with traded benchmarks, investors want to:

• 1. maximize the correlation between the portfolio $x^{\prime }z$ and the benchmark $z_{b}$, if the traded benchmark is on the right tail;

• 2. minimize the correlation between the portfolio $x^{\prime }z$ and the traded benchmark $z_{b}$, if the benchmark is on the left tail.

In particular, when the reward and risk are both positive measures, and there exists a portfolio $x^{\prime }z$ such that the difference between correlation measures is positive (i.e. $\rho _{1}\left( x^{\prime }z,\max _{i}z_{i}\right) -\rho _{2}\left( x^{\prime }z,\min _{i}z_{i}\right) >0$), we still call market portfolio the portfolio that yields the maximum reward per unit of risk, optimizing the differences between correlation measures. That is, the market portfolio is the solution of the following optimization problem:

$$\begin{aligned} \begin{array}{c} \underset{x}{\max }\frac{v(x^{\prime }z)}{q(x^{\prime }z)}\left( \rho _{1}\left( x^{\prime }z,\max \limits _{i}z_{i}\right) -\rho _{2}\left( x^{\prime }z,\min \limits _{i}z_{i}\right) \right) \\ \sum \limits _{i=1}^{n}x_{i}=1;\quad x_{i}\ge 0. \end{array} \end{aligned}$$

(16)

Generally, the optimization problem (16) admits more local optima and thus we should use a heuristic for the global optimization.

5 An empirical ex post analysis

In this section we first describe the data set and the methodology used to compare different models. Then we employ various deviation and correlation measures, as defined in Sects. 2 and 3, within the portfolio selection problem. Such empirical analysis is also useful because we cannot compare particular measures theoretically, but it somehow follows from the nature of the portfolio valuation process. We evaluate two distinct tasks: (i) dimensionality reduction of large-scale portfolio problems and (ii) portfolio performance optimization.

For both problems we use all active stocks on NYSE and NASDAQ from January 1, 2002 to August 20, 2014 (1791 stocks in total) as provided by DataStream. We first analyze their returns and then we compute the average of basic returns statistics over each month (20 trading days) from March 4, 2007 to August 20, 2014 using the previous 1300 daily observations.

Since central theories in finance assume that stock returns follow a Gaussian distribution, we consider the Jarque–Bera test for normality (with a 95 % confidence level) of the returns (see Table 1). We also report there the average values of minimum, maximum, mean, standard deviation, skewness, kurtosis, the maximum likelihood estimates of stable Paretian parameters $(\alpha ,\gamma ,\beta ,\mu )$ and percentage of rejections using the Kolmogorov–Smirnov statistic to test the stable Paretian assumption with a 95 % confidence level.

Table 1 Comparison of parameters computed on daily returns for the global dataset and preselected assets

The average results show us that the Gaussian distributional hypothesis is rejected (on average) for about 77.3 % of the stocks, and the stable Paretian hypothesis is rejected for about 14.7 % of the cases. The average values of the other parameters suggest the strong presence of heavy tails, since the average kurtosis is much higher than 3 and the stability parameter $\alpha$ is lower than 2. The average values of the other parameters do not suggest a strong presence of skewness, since the averages of asymmetry parameter $\beta$ and the skewness are around zero, and also the averages of the maximum and of the minimum are almost equal in absolute value. Therefore we deduce that the impact of heavy tails might be very strong using this data set.

We next examine the ex post impact of different correlation measures considering two portfolio problems: portfolio dimensionality reduction problems and portfolio performance ones.

We use a moving window of 1300 trading days (about 5 years) for the computation of each optimal portfolio and we compute it every month (20 trading days). Since the weights $x\in S$ represent the percentages of wealth invested in each asset, and since the values of the assets change every day, we should recalibrate the wealth daily, maintaining the percentage constant every day during each period $\left[ t_{k},t_{k}+20 \right] ,$ where $t_{k}$ is the time at which we compute the new portfolio composition, so that the computational time is kept at low level.

Then, considering an initial wealth $W_{t_{0}}=1$, which we have invested on March 4, 2007, we evaluate the ex post wealth sample path for both problems. Thus, at the k-th optimization ($k=0,1,2,\ldots ,m$), three main steps are performed to compute the ex post final wealth:

• Step 1 Apply the portfolio dimensionality reduction techniques and approximate the returns as suggested in Sect. 4.1.

• Step 2 Determine the market portfolio $x_{M}^{(k)}$ that optimizes the portfolio problem applied to the approximated returns.

• Step 3 During the period $[t_{k},t_{k+1}]$, where $t_{k+1}=t_{k}+20$, we must recalibrate the portfolio daily, maintaining the percentages invested in each asset equal to those of the market portfolio $x^{(k)}$. Thus, the ex post final wealth is given by:

  $$\begin{aligned} W_{t_{k+1}}=W_{t_{k}}\left( \prod \limits _{i=1}^{20}\left( x_{M}^{(k)}\right) ^{\prime }z_{(t_{k}+i)}^{(ex\text { }post)}\right) , \end{aligned}$$

  (17)

  where $z_{(t_{k}+i)}^{(ex\text { }post)}$ is the vector of observed daily gross returns between $( t_{k}+i-1)$ and $\left( t_{k}+i\right)$. The optimal portfolio $x_{M}^{(k)}$ is the new starting point for the $(k+1)$-th optimization problem.

Steps 1, 2 and 3 are repeated until the observations are available.

5.1 Portfolio dimensionality reduction of large scale portfolio problems

In order to reduce the dimensionality, at each recombination step we consider only those 200 assets that exhibit the highest Rachev ratio (RR).⁶ That is, we take returns $r_{i}$ with the highest $RR (r_{i})$:

$$\begin{aligned} RR (X)=\frac{ AVaR _{0.05}(-X)}{ AVaR _{0.05}(X)}, \end{aligned}$$

where $AVaR _{p}(X)=-\int \limits _{0}^{p}F_{X}^{-1}(u)du$ is the Average Value at Risk, and compute the average of the same basic statistics as for the global dataset. Obviously, the preselected assets are not always the same for all observation periods and thus we consider a dynamic data set where the final number of preselected stocks over the horizon of 7 years is 953 (among 1791). By doing so we guarantee a substantial turnover of the portfolio, since there are several new preselected stocks that are classified as the best ones (in the sense of RR) every month.

The average values of the statistics computed for the returns of the preselected assets reported in Table 1 suggest the presence of heavy tails (kurtosis greater than eight and stability index $\alpha$ lower than two) and positive skewness (skewness and asymmetry stable parameter $\beta$ are positive and the average value of the maximum is higher than the absolute value of the average of the minimum). A comparison between the statistics of the global data set and the preselected stocks also shows us that the average mean of preselected log returns is about 51 times the average mean of the global data set, even if the preselected stocks exhibit heavier tails since the kurtosis parameter is higher and the stability parameter is lower. Thus, it is not surprising that the Gaussian hypothesis is rejected for about 85 % of the stocks, while the stable Paretian hypothesis is rejected for about 17 % of the cases.

We apply a PCA based on the following correlation measures to the 200 preselected stocks:

P1 :

Pearson linear correlation of the gross returns $z_{i}$.

P2 :

Pearson correlation applied to the random variables $z_{i}-E(z_{i}|\mathfrak {I}_{1})$ orthogonal to $L^{2}\left( \varOmega ,\mathfrak {I}_{1},\Pr \right)$. As sigma algebra $\mathfrak {I}_{1}$ we consider a finite sub-sigma algebra of the sigma algebra generated by the upper stochastic bound $\max _{k}z_{k}$ given by

$$\begin{aligned} \mathfrak {I}_{1}=\mathfrak {I}_{(m)}=\left\langle \left\{ A_{i};i=1,\ldots ,m\right\} \right\rangle , \end{aligned}$$

where

$$\begin{aligned} A_{1}= & {} \left\{ \max _{k}z_{k}\le F_{\max _{k}z_{k}}^{-1}\left( \frac{1}{m} \right) \right\} ,\\ A_{i}= & {} \left\{ F_{\max _{k}z_{k}}^{-1}\left( \frac{1}{m}(i-1)\right) \langle \max _{k}z_{k}\le F_{\max _{k}z_{k}}^{-1}\left( \frac{1}{m}i\right) \right\} \end{aligned}$$

for $i=2,\ldots ,m-1;$ and

$$\begin{aligned} A_{m}=\left\{ \max _{k}z_{k}>F_{\max _{k}z_{k}}^{-1}\left( 1-\frac{1}{m} \right) \right\} . \end{aligned}$$

Observe that if m converges to infinity, $\mathfrak {I}_{(m)}$ converges to the sigma algebra generated by $\max _{k}z_{k}.$ In this sense, $\mathfrak {I}_{1}$ is a first trivial approximation of the sigma algebra generated by $\max _{k}z_{k}.$ In particular, in our empirical comparison we use $m=40.$ Under these assumptions, the conditional expectation can be easily estimated, since it is given by the simple function:

$$\begin{aligned} \mathbb {E}(X/\mathfrak {I}_{1})(w)=\sum _{i=1}^{n}I_{[X(w)\in A_{i}]}\frac{1}{\Pr (A_{i})}\int _{A_{i}}Xd\Pr { \ \ \ \ }\forall w\in \varOmega , \end{aligned}$$

where $I_{[X(w)\in A]}$ is equal to 1 if $X(w)\in A$, and it is equal to 0 otherwise.

P3 :

Pearson correlation applied to the bijective non-linear function of the returns $h(r_{i})= sign (r_{i})\left| r_{i}\right| ^{0.5}$ as suggested in formula (13). This correlation measure take into account non-linear dependence among returns, and it is finite for any sub-Gaussian stable distributed vector of returns with finite mean ($\alpha >1$).

P4 :

Pearson correlation applied to the function of the returns

$$\begin{aligned} h(r_{i})= sign (r_{i})\left| r_{i}\right| ^{(\alpha -0.001)/2} \end{aligned}$$

and $\alpha$ is the average of the MLE indices of stability (i.e. $\alpha = \frac{1}{n}\sum _{k=1}^{n}\alpha _{k})$. This correlation measure takes into account a non-linear dependence among returns, and it is finite even when the vector of returns admits sub-Gaussian $\alpha$ stable distribution.

S1 :

Stable approximated correlation $\rho (z_{i},z_{j})=\frac{ v_{ij}}{\sqrt{v_{ii}v_{jj}}}$. Here we use formula (6) to estimate $v_{ij}$ ($i\ne j$) and the MLE estimator of stable dispersion $v_{kk}$ once the index of stability $\alpha =\frac{1}{n}\sum _{k=1}^{n}\alpha _{k}$ has been fixed as the average of the indices of stability.

S2 :

Stable approximated correlation $\rho (X_{i},X_{j})=\frac{ v_{ij}}{\sqrt{v_{ii}v_{jj}}}$ applied to the random variables $X_{i}=z_{i}-E(z_{i}|\mathfrak {I}_{1})$, where $\mathfrak {I}_{1}$ is the finite sigma algebra of the point (ii) and the coefficients $v_{ij}$ are computed as for S1.

S3 :

Stable correlation given by formula (10) that is finite for all $\alpha$ stable distributed vectors with $\alpha$ greater than 1. In this case we estimate the correlation matrix using the moment estimator.

S4 :

Stable correlation given by formula (10) applied to the random variables $z_{i}-E(z_{i}|\mathfrak {I}_{1})$ where $\mathfrak {I}_{1}$ is the finite sigma algebra defined in P2.

As regards our choice of sigma algebra $\mathfrak {I}_{1},$ the random variable $E(z_{i}|\mathfrak {I}_{1})$ can be considered as a first approximation of the random variable $E(z_{i}|\max _{k}z_{k}).$ Thus, when we approximate the returns using factors derived from the principal component analysis on the correlation matrices of the random variables $z_{i}-E(z_{i}|\mathfrak {I}_{1}),$ we account the part of the returns which are ‘uncorrelated’ with the upper market stochastic bound.

In order to evaluate the impact of different PCAs on portfolio selection, we compare the ex post wealth sample paths obtained by maximizing a performance measure valued on the approximated preselected returns. In particular, we maximize the performance ratio

$$\begin{aligned} \frac{v(x^{\prime }z)}{q(x^{\prime }z)}=\frac{E(x^{\prime }z-1)}{E(\left| x^{\prime }z-\max _{k}z_{k}\right| )}, \end{aligned}$$

(18)

where the reward measure is the mean $E(x^{\prime }r)$ of the portfolio returns and the risk measure is the absolute distance between the portfolio and the upper market stochastic bound.

Observe that upper limit constraints are generally applied by financial institutions to guarantee a minimal diversification [see, for example, the discussion on diversified strategies (Pflug et al. 2012; DeMiguel et al. 2009)]. Thus we suppose that no short sales are allowed and that we cannot invest more than 5 % in a single asset, i.e. $0\le x_{i}\le 0.05$ for any $i=1,\ldots ,n$, to guarantee a diversification. Applying the principal component analysis at each optimization time, we observe that 25 factors are sufficient to explain on average more than 50 % of the variability for all the linear correlation matrices. Therefore, as suggested at the beginning of this section, at each optimization time (i.e. every 20 trading days) and for each correlation matrix we approximate the 200 preselected returns using 25 factors derived from the principal component analysis. We then regress the return series (or its functions, for the correlations of P3 and P4) on the 25 factors $f_{j}$ (or $\widetilde{f}_{j}$) and we approximate the portfolio of returns $x^{\prime }z\simeq x^{\prime }\widehat{ \mathbf {b}}_{0}+\sum _{j=1}^{s}x^{\prime }\widehat{\mathbf {b}}_{j}f_{j}$ (or $x^{\prime }z\simeq \sum _{i=1}^{n}x_{i}h^{-1}(\widetilde{b} _{i,0}+\sum _{j=1}^{s}\widetilde{b}_{i,j}\widetilde{f}_{j}))$ using OLS estimates of parameters $\mathbf {b}_{j}$ ($\widetilde{\mathbf {b}}_{j}$). Finally, at each optimization time and for each correlation matrix we solve the optimizationproblem:

$$\begin{aligned} \begin{array}{c} \underset{x}{\max }\frac{E(x^{\prime }z-1)}{E(\left| x^{\prime }z-\max _{k}z_{k}\right| )} \\ \sum \limits _{i=1}^{n}x_{i}=1;\quad x_{i}\ge 0;\quad x_{i}\le 0.05 \end{array} \end{aligned}$$

evaluated for the approximated returns. Since this problem admits a single optimum we use the standard solver in Matlab (that is, the function ‘fmincon’) to determine its solution.

In Fig. 1 we report the ex post comparison of the sample paths of wealth obtained with different portfolio approximation. In this figure we also consider the case when no PCA (noPCA) is applied to the 200 preselected stocks. The figure shows that:

• (a) If we do not apply any PCA, we get the worst ex post results; In particular we observe that all strategies that apply a PCA rise more than the noPCA strategy during the ‘bull’ market period from March 2009 till April 2010 and from October 2010 till August 2014, in the ‘bear’ market period from April 2010 till October 2010. While we do not observe very big differences during the US sub-prime mortgage crisis period before March 2009. This difference is a consequence of the effects of the pre-selection that is able to identify several stocks with very common behavior during the first bear market period (see also Ortobelli et al. 2011). As a matter of fact, we observe that during the bear market period before March 2009 the 25 principal components derived from all PCAs are able to explain a significant higher percentage of variability on average than the variability explained after March 2009.

  Fig. 1

  

  Ex post comparison of wealth obtained optimizing a performance ratio applied either to the original preselected returns (strategy noPCA) or to the approximated preselected returns. Approximation is obtained with factor models. Darker color of the curve indicates higher final value

• (b) The Pearson correlation does not give a particularly good performance, even if the ex post performance is much better than having no PCA reduction of dimensionality;

• (c) We get the best performance by maximizing the performance ratio applied to the approximated returns that uses one of the following correlation matrices in the principal component analysis: S4, S1, P4.

Thus, this analysis confirms that it is important to reduce the dimensionality of large-scale portfolio problems considering the heavy tails of the returns. Moreover, the empirical results show that in several cases we may obtain good portfolio approximations by applying a PCA to correlation matrices different from the Pearson linear correlation. In order to evaluate these results more precisely, we consider some empirical statistics on the ex post returns on the portfolio strategies.

Concerning the strategies based on different return approximations, we report in Table 2 the values of (1) two reward measures of the ex post returns (the empirical mean m(X) and AVaR$^{-}$, which is AVaR of the opposite random variable $AVaR _{0.05}(-X)$); (2) two deviation measures of the ex post returns (the standard deviation $\sigma (X)$ and AVaR$^{+}$, which is AVaR of the centered random variable $AVaR _{0.05}((X-E(X))$); (3) all possible reward risk ratios derived from these two measures, ie. Sharpe ratio, $mean/ AVaR (X-E(X))$ (PR2), $AVaR(-X)/AVaR(X-E(X))$ (PR3), $AVaR(-X)/(st.dev.(X))$ (PR4); (4) final wealth $W_T$ obtained on August 20, 2014 (at the end of the ex post period). A particular result indicates that the S4 strategy yields the highest ex post final wealth (about 3.33), the highest reward measures m(X), $AVaR _{0.05}^{-},$ and all the highest ex post reward/risk performances. However, the S2 strategy seems to be the less ex post risky one, since it presents the smallest risk measures $\sigma (X)$ and $AVaR _{0.05}^{+}$.

Table 2 Statistics computed for daily ex post returns obtained for particular strategies with different ex ante return approximations (all results multiplied by $10^2$)

5.2 Portfolio performance optimization

In this part of the empirical analysis we conduct an ex post comparison among several versions of optimization problem (16) based on different risk and correlation measures. Since in the previous analysis we obtained the best ex post results using the S4 strategy, in this analysis we reduce the dimensionality of the large-scale portfolio problem using the same techniques. Therefore, at each recombination step we consider 200 assets that present the highest Rachev ratio. We then approximate the preselected returns using 25 factors derived from the principal component analysis applied to the correlation matrix described as S4 in Sect. 5.1.

Finally, we solve the optimization problem (16) in order to examine the impact of different correlation measures on the US market. As performance ratios we consider the classic Sharpe ratio, SR (see Sharpe 1994):

$$\begin{aligned} SR(x^{\prime }z)=\frac{v(x^{\prime }z)}{q(x^{\prime }z)}=\frac{E(x^{\prime }r)}{E\left( \left( x^{\prime }z-E(x^{\prime }z)\right) ^{2}\right) ^{0.5}}, \end{aligned}$$

and a Modified Sharpe ratio, $MSR$

$$\begin{aligned} MSR (x^{\prime }z)=\frac{v(x^{\prime }z)}{q(x^{\prime }z)}=\frac{E(x^{\prime }r)}{d_{\rho ,\sigma }(x^{\prime }z)}, \end{aligned}$$

where as risk measure we use $d_{\rho ,\sigma }(x^{\prime }z)=\sqrt{ x^{\prime }Q_{\rho ,\sigma }x}$ instead of the standard deviation. In particular, as correlation measure $\rho$ we still use the Pearson linear correlation measure, while the deviation measure $\sigma$ is the AVaR of the centered random variable i.e. $\sigma _{X}= AVaR _{5\,\%}((X-E(X)).$

Moreover, we consider five different factors of the type:

$$\begin{aligned} \left( \rho _{1}\left( x^{\prime }z,\max _{i}z_{i}\right) -\rho _{2}\left( x^{\prime }z,\min _{i}z_{i}\right) \right) \end{aligned}$$

differently measuring the correlation of the portfolio return with the upper and lower bounds. For all the factors ($\rho _{1}-\rho _{2}$) we assume that the correlation $\rho _{i}$ is of the same type in order to guarantee that $(\rho _{1}-\rho _{2})>0$. In particular, we set $\rho _{1}$ and $\rho _{2}$ as follows:

Gini :

$\rho _{1}(X,Y)=\rho _{2}(X,Y)=\frac{1}{\lfloor n^{2}/2\rfloor }\left[ \sum _{i=1}^{n}|p_{i}+q_{i}-n-1|-\sum _{i=1}^{n}|p_{i}-q_{i}|\right]$ is the sample estimation of Gini’s index of cograduation, where $p_{i}$ and $q_{i}$ are the ranks of random variables X and Y, respectively;

Prs :

$\rho _{1}(X,Y)=\rho _{2}(X,Y)$ is the Pearson correlation measure;

Spr :

$\rho _{1}(X,Y)=\rho _{2}(X,Y)=\frac{\text {cov}\left( F_{X}(X),F_{Y}(Y)\right) }{\sqrt{\text {var}\left( F_{X}(X)\right) ,\text {var} \left( F_{Y}(Y)\right) }}$ is the Spearman concordance measure;

Knd :

$\rho _{1}(X,Y)=\rho _{2}(X,Y)=\mathbb {E} ( sign ((X_{1}-X_{2})(Y_{1}-Y_{2})))$ is the Kendall concordance measure, where ($X_{1},Y_{1}$) and ($X_{2},Y_{2}$) are independent replications of (X, Y);

Stb :

$\rho _{1}(X,Y)=\rho _{2}(X,Y)=\frac{v_{XY}}{\sqrt{v_{XX}v_{YY}}}$ is the stable correlation given by formula (10) that is finite for all $\alpha$ stable distributed vectors with $\alpha >1$.

Thus, every month we solve the optimization problem:

$$\begin{aligned} \begin{array}{c} \underset{x}{\max }\frac{v(x^{\prime }z)}{q(x^{\prime }z)}\left[ \rho _{1}\left( x^{\prime }z,\max \limits _{i}z_{i}\right) -\rho _{2}\left( x^{\prime }z,\min \limits _{i}z_{i}\right) \right] \\ \sum \limits _{i=1}^{n}x_{i}=1;\quad x_{i}\ge 0;\quad x_{i}\le 0.05 \end{array} \end{aligned}$$

(19)

evaluated on the preselected approximated returns. Since this optimization problem may present more local optima, we use the heuristic proposed by Angelelli and Ortobelli (2009) to approximate the global optimum.

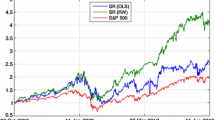
In Fig. 2 we report the ex post comparison of the sample paths of wealth obtained with the Sharpe ratio (SR) and the functionals based on different correlation measures. Figure 3 reports the same typology of results when we use the Modified Sharpe ratio (MSR) as the performance measure, i.e., $\frac{v(x^{\prime }z)}{ q(x^{\prime }z)}=\frac{E(x^{\prime }r)}{d_{\rho ,\sigma }(x^{\prime }z)}.$ In these figures we also consider:

• a) the case when we do not apply any PCA to the 200 preselected stocks and the factor $\rho _{1}-\rho _{2}=1,$ i.e. there is no correlation contribution ((M)SR1);

  Fig. 2

  

  Ex post wealth obtained optimizing portfolio strategies given by the Sharpe ratio multiplied by selected association factors. Darker color of the curve indicates higher final value

  Fig. 3

  

  Ex post wealth obtained optimizing portfolio strategies given by the Modified Sharpe ratio multiplied by selected association factors. Darker color of the curve indicates higher final value

• b) the case when we apply the PCA to the correlation matrix described in point 8 of Sect. 5.1, but there is no correlation contribution, i.e. $\rho _{1}-\rho _{2}=1$ ((M)SR2);

• c) the behavior of the S&P 500 index during the examined period.

Figures 2 and 3 show that:

• if we do not apply any PCA and do not use the correlation factor $\rho _{1}-\rho _{2}$ (i.e. $\rho _{1}-\rho _{2}=1$) we get the worst ex post results;

• if we do not use the correlation factor $\rho _{1}-\rho _{2}$ we get worst results than if we use it;

• the performances strategies that give the best results are those based on the Kendall correlation measure;

• all the strategies based on the maximization of the modified Sharpe ratio (multiplied with a correlation factor) generally present higher final wealth than the analogous strategies based on the maximization of the Sharpe ratio (except for the Spearman correlation factor where the ex post wealth difference is almost null);

• most strategies we proposed in the paper outperform the behavior of the S&P 500 index (see Fig. 2; Table 3).

Thus this analysis confirms that it is important to reduce the dimensionality of large-scale portfolio problems and to take into account the joint behavior of the portfolio of returns and the market stochastic bounds. Moreover, we also confirm that we can find performance strategies based on a different concept of risk (namely $d_{\rho ,\sigma }(x^{\prime }z))$ which outperforms the Sharpe ratio and the S&P 500 market index. Table 3 reports the values of the same statistics reported in Table 2 computed on the ex post returns on all these strategies.

Table 3 Statistics computed for daily ex post returns obtained for strategies with different performance ratios (SR and MSR) and different association measures of the portfolio and the market stochastic bounds (all results multiplied by $10^2$)

In particular, Table 3 shows that the Kendall strategy presents the highest ex post final wealth, mean, Sharpe ratio, and the highest ex post performance ratios, mean/$AVaR _{0.05}((X-E(X)),$ $AVaR _{0.05}(-X)/ AVaR _{0.05}(X-E(X)).$ In addition, for most strategies based on the maximization of the modified Sharpe ratio (except for those strategies where no correlation or no PCA is considered), we get higher mean and a lower risk (standard deviation and $AVaR _{0.05}((X-E(X))$) of the ex post returns) than when using those strategies obtained by maximizing the Sharpe ratio (multiplied with a correlation factor). This result confirms that it makes sense to use measures of the type $d_{\rho ,\sigma }(x^{\prime }z),$ where we distinguish the contribution of a linear correlation measure $\rho$ and of a proper deviation measure $\sigma$.

Comparing some results of Tables 2 and 3 (SR2 vs. S4 and SR1 vs. noPCA) we deduce that the strategies based on the maximization of the Sharpe ratio as well as its modification are more risk-averse and less aggressive than those based on the maximization of performance ratio (18). In fact, the SR1 strategy presents smaller risk measures ($\sigma (X)$ and $AVaR _{0.05}((X-E(X))$) and a higher ex post final wealth (2.27) than does noPCA strategy (1.26), while both SR1 and SR2 strategies presents smaller ex post final wealth (2.27, 1.5) than does the S4 strategy (3.33).

When we examine the turnover and diversification of the optimal portfolios, we observe that there is no strategy that invests in only twenty assets, even if we impose that more than 5 % cannot be invested in each asset. However, to better evaluate the portfolio diversification and the impact of different dispersion measures, we examine the ex post wealth we obtain optimizing the modified Sharpe ratio times the Kendall correlation factor (i.e. the previous ‘best’ strategy) using different portfolio constraints and different dispersion measure definitions.

In particular, we assume that problem (19) changes as follows:

• investors cannot invest more than 10, 50 and 100 % in each asset (i.e. $x_{i}\le 0.1;0.5;1)$

• deviation measure of modified Sharpe ration (MSR)$\sigma _{X}= AVaR _{u}((X-E(X))$ is based on $u=1\,\%;5\,\%;10\,\%$.

Results over the same horizon as in the basic case are apparent from Table 4.

Table 4 Sensitivity of the most profitable strategy (Table 3) with respect to MSR probability levels u and constraint on portfolio position $x_i$ (all results multiplied by $10^2$)

On the one hand we, observe that relaxing the portfolio constraints we generally reduce the diversification and we improve the ex post wealth. However, there is no strategy that invests in only ten (two, one) assets, even if we state that more than 10 % (50, 100 %) cannot be invested in each asset. In addition, we observe a strong turnover at each optimization time for all strategies that is also due to the preselection procedure. Thus, by using these portfolio strategies, we always observe a satisfying diversification and turnover in the optimal portfolios. Moreover, as we could expect, the risk of the strategy (see $\sigma (X)$ and $AVaR _{0.05}((X-E(X))$ of Table 4) also increases, when we relax the portfolio constraints and portfolio diversification decreases. On the other hand, we observe that the ex post wealth increases when the confidence level u of deviation measure $\sigma _{X}= AVaR _{u}((X-E(X))$ decreases for fixed portfolio constraints. Therefore, we proved that the optimal portfolios are very sensitive to different deviation measures used in optimization problem (19) in particular when these measures evaluate the portfolio distributional tails.⁷

6 Conclusion

This paper serves a twofold objective. First, the properties of association measures were theoretically discussed in order to characterize semidefinite positive correlation measures and their consistency with the investors’ choices. Secondly, two different ways of correlation measures usage in portfolio selection problems were proposed and their ex post empirical analysis on the US stock market was performed.

The empirical experiments show us (1) that the dimensional reduction of large-scale portfolio problems may have a substantial impact on the portfolio selection of the US stock market; (2) that it makes sense to distinguish the contribution of a correlation measure and a deviation measure in measuring risk; in this context it is important to consider proper correlation and deviation measures for returns with heavy tails; (3) that the (properly measured) joint behavior of the portfolio and the market stochastic bounds may have a substantial impact on the portfolio selection of the US stock market.

Since the empirical analysis has shown a strong impact of different correlation measures on the investor’s choices, it is evident that there must be reasons to investigate new linear correlation measures as suggested by our empirical analysis and motivated by the theoretical discussion conducted.

Appendix

Proof of Theorem 1 Suppose that properties 1 and 2 of the theorem are satisfied. Cauchy–Schwarz inequality applied to V guarantees property 1 and 2 of correlation measures, i.e. $\rho :H\times H\rightarrow [-1,1]$ and $\rho (X,X)=1;$ $\rho (X,-X)=-\rho (X,X)=-1.$ Consider $g(X,Y)=(v_{1,g},v_{2,g}).$ Properties 3 and 4 of correlation measures are logical consequences of $\langle g(X,Y)\rangle =\langle g(Y,X)\rangle$ and $\langle g(-X,Y)\rangle =\langle g(X,-Y)\rangle =-\langle g(X,Y)\rangle ,$ while Property 5 of the correlation measure follows by property 2 of the theorem. Moreover, since $\rho (X,Y)$ can be seen as an inner product of the vectors $\frac{v_{1,g}}{\sqrt{\langle g(X,X)\rangle }}$ and $\frac{v_{2,g}}{\sqrt{\langle g(Y,Y)\rangle }},$ we deduce from the Gram representation theorem that the correlation matrix that satisfies properties 1 and 2 of the theorem is semidefinite positive.

Viceversa, let $\rho$ be a semidefinite positive correlation measure. Then any correlation matrix $Q=[\rho _{i,j}]$ should be semidefinite positive. Consider the correlation matrix defined on the random variables belonging to $H_{1}=\left\{ X_{1},\ldots ,X_{n}\right\}$. From the Gram representation theorem we know that an n-dimensional correlation matrix $Q=[\rho _{i,j}]$ is semidefinite positive if, and only if, there exists n vectors $v_{1}$, $v_{2},\ldots ,v_{n}$, in a vectorial space V such that $\rho (X_{i},X_{j})=\rho _{i,j}=\langle v_{i},v_{j}\rangle$. Since $\rho :H_{1}\times H_{1}\rightarrow [-1,1]$ and $\rho (X_{i},X_{i})=1,$ then $\langle v_{i},v_{i}\rangle =1.$ Consider the function $g(\pm X_{i},\pm X_{j})=\left( \pm k_{i}v_{i},\pm k_{j}v_{j}\right)$ for some positive real $k_{i},k_{j}$ $\left( i,j=1,\ldots ,n\right) .$ Therefore we obtain $\rho _{i,j}=\frac{\langle g(X_{i},X_{j})\rangle }{\sqrt{\langle g(X_{i},X_{i})}\rangle \langle g(X_{j},X_{j})\rangle }.$ Since $\rho (-X_{i},X_{j})=\rho (X_{i},-X_{j})=-\rho (X_{i},X_{j})$ it follows that $\langle g(-X_{i},X_{j})\rangle =\langle g(X_{i},-X_{j})\rangle =-\langle g(X_{i},X_{j})\rangle$. If X and Y are independent random variables $\rho (X,Y)=0$ and thus $\langle g(X,Y)\rangle =0$.

Proof of Proposition 1 We first prove Case M1. Observe that $V_{p/2}(aX+b)=aV_{p/2}(X)+b$ holds for any constant a and b and the functional

$$\begin{aligned} \mathrm {cvp}(X,Y)=\mathbb {E}\left( \left( X-V_{p/2}(X)\right) ^{\langle p/2\rangle }\left( Y-V_{p/2}(Y)\right) ^{\langle p/2\rangle }\right) ^{\langle \min (2/p,2)\rangle } \end{aligned}$$

is an inner product in the $L^{p}$ space. Thus using the same notation of Theorem 1 we can assume that $\langle g(X,Y)\rangle =\mathrm {cvp}(X,Y)$ and then we easily prove that $\mathrm {cvp}$ satisfies the properties of Theorem 1. In particular, $\mathrm {cvp}(X,Y)=\mathrm {cvp}(Y,X)$ and $\mathrm {cvp}(aX+b,Y)= \mathrm {cvp}(X,Y)a^{\langle \min (p,1)\rangle }.$ Moreover, if X is independent of Y, then

$$\begin{aligned} \mathrm {cvp}(X,Y)^{\frac{1}{\langle \min (2/p,2)\rangle }}=\mathbb {E}\left( \left( X-V_{p/2}(X)\right) ^{\langle p/2\rangle }\right) \mathbb {E}\left( \left( Y-V_{p/2}(Y)\right) ^{\langle p/2\rangle }\right) =0. \end{aligned}$$

If $\left| \rho _{p}(X,Y)\right| =1$, then $\left| \mathrm {cvp} (X,Y)\right| =\left\| X-V_{p/2}(X)\right\| _{p}\left\| Y-V_{p/2}(Y)\right\| _{p}$, so that there exists a real c such that $\left( X-V_{p/2}(X)\right) ^{\langle p/2\rangle }=c\left( Y-V_{p/2}(Y)\right) ^{\langle p/2\rangle }$ and the thesis follows. Regarding Case M2, we can easily prove that $Y=X$ a.s. implies $X_{1}=Y_{1}$ a.s. and consequently $\tau _{p}(X,X)=1$. Since $(X_{1},Y_{1})\overset{d}{=}(X,Y),$ the assumption $Y=X$ a.s. implies that for any $x_{n}\in \mathbb {Q}$; $\Pr (X_{1}\le x_{n},Y_{1}>x_{n})+\Pr (X_{1}>x_{n},Y_{1}\le x_{n})=0.$ Consider $\widetilde{\varOmega }=\left( \cup _{n}\varOmega _{n}\right) ^{C}$ (where $\varOmega _{n}=\left\{ w|X_{1}(w)\le x_{n},Y_{1}(w)>x_{n}\text { or }X_{1}(w)>x_{n},Y_{1}(w)\le x_{n}\right\} )$. Then $\Pr (\widetilde{\varOmega })=1$ and $X_{1}(w)=Y_{1}(w)$ for any $w\in \widetilde{\varOmega }$ (otherwise if $X_{1}(w)>Y_{1}(w)$—or $X_{1}(w)\langle Y_{1}(w)$—there exists $x_{n}\in \mathbb {Q}$ such that $X_{1}(w)>x_{n}\ge Y_{1}(w)$—or $X_{1}(w)\le x_{n}\langle Y_{1}(w)$ contrary to the assumption that $w\in \widetilde{\varOmega }$ ). Moreover since $\left( X-X_{1}\right)$ and $\left( Y-Y_{1}\right)$ are symmetric random variables $\mathbb {E}\left( \left( X-X_{1}\right) ^{\langle p/2\rangle }\right) =\mathbb {E}\left( \left( Y-Y_{1}\right) ^{\langle p/2\rangle }\right) =0,$ when X and Y are independent random variables $\tau _{p}(X,Y)=0.$ All the other properties of Theorem 1 are satisfied by the measures $\tau _{p}(X,Y)$. Regarding Case M3, we observe that the random variable $Z=(X^{\langle p/2\rangle }-E(X^{\langle p/2\rangle }|\mathfrak {I}_{1})),$ where $X\in L^{p}(\varOmega ,\mathfrak {I},\Pr )$ is orthogonal to $L^{2}(\varOmega ,\mathfrak {I}_{1},\Pr )$ because for any $V\in L^{2}(\varOmega ,\mathfrak {I}_{1},\Pr )$ then $E(VZ)=E(VE(Z|\mathfrak {I}_{1}))=0.$ Since the measure $O_{p,\mathfrak {I}_{1}}$ is the Pearson measure applied to the space of the random variables of the type $Z=(X^{\langle p/2\rangle }-E(X^{\langle p/2\rangle }|\mathfrak {I}_{1}))$ orthogonal to $L^{2}(\varOmega ,\mathfrak {I}_{1},\Pr )$ the measure M3 is a correlation measure on this space. On the one hand, the measure M3 is not law invariant correlation measure on the whole space of random variables $L^{p}(\varOmega ,\mathfrak {I},\Pr ).$ As a matter of fact, if $X_{(1)},Y_{(1)}\in L^{p},$ $(X_{(1)},Y_{(1)})\overset{d}{=}\left( X_{(2)},Y_{(2)}\right)$ not necessarily$\ \left( Z_{1,(1)},Z_{2,(1)}\right) \overset{d}{=}\left( Z_{1,(2)},Z_{2,(2)}\right)$ where $Z_{1,(i)}=(X_{(i)}^{\langle p/2\rangle }-E(X_{(i)}^{\langle p/2\rangle }|\mathfrak {I}_{1}))$ and $Z_{2,(i)}=(Y_{(i)}^{\langle p/2\rangle }-E(Y_{(i)}^{\langle p/2\rangle }|\mathfrak {I}_{1}))$ ($i=1,2$) and it may be $O_{p,\mathfrak {I}_{1}}(Z_{1,(1)},Z_{2,(1)})\ne O_{p,\mathfrak {I}_{1}}\left( Z_{1,(2)},Z_{2,(2)}\right)$. On the other hand, measure M3 satisfies concordance property (v) on the whole space $L^{p},$ because if X is independent from Y then $O_{p,\mathfrak {I}_{1}}(Z_{1},Z_{2})=0.$

Proof of Proposition 2 Under the assumptions of the proposition every portfolio of returns is uniquely determined by the mean and the variance or the mean and by another deviation measure. Moreover, as a consequence of Theorem 5 in Ortobelli (2001), if we use another deviation measure $\sigma _{X}$ to characterize these distribution families then $\sigma _{X}=a\sqrt{var(X)}$ where a is a positive constant for all the random variables X of the two parametric family. Suppose that the vector of returns $z=(z_{1},z_{2},z_{3})^{\prime }$ is distributed with mean vector $\mu =[\mu _{1},\mu _{2},\mu _{1} \overline{x}+(1-\overline{x})\mu _{2}]$ for a given $\overline{x}\in (0,1)$ and a given variance covariance matrix

$$\begin{aligned} Q=\left[ \begin{array}{c@{\quad }c@{\quad }c} \text {var}(z_{1}) &{} \text {cov}(z_{1},z_{2}) &{} 0 \\ \text {cov}(z_{1},z_{2}) &{} \text {var}(z_{2}) &{} 0 \\ 0 &{} 0 &{} \text {var}(z_{3}) \end{array} \right] , \end{aligned}$$

where $\hbox {var}(z_{3})=\overline{x}^{2}\hbox {var}(z_{1})+(1-\overline{x})^{2}\hbox {var} (z_{2})+2\overline{x}(1-\overline{x})\hbox {cov}(z_{1},z_{2}).$ Then the distribution of portfolio $[\overline{x},(1-\overline{x}),0]z$ is equal to the distribution of $z_{3}.$ Therefore, if $\rho$ is a semidefinite positive correlation measure and $\sigma$ is a deviation measure, we obtain

$$\begin{aligned} d_{\rho ,\sigma }([0,0,1]z)^{2}=\sigma _{z_{3}}^{2}=a^{2}var(z_{3})=a^{2}var( \overline{x},(1-\overline{x}),0]z) \end{aligned}$$

and

$$\begin{aligned} d_{\rho ,\sigma }([\overline{x},(1-\overline{x}),0]z)^{2}= & {} \overline{x} ^{2}a^{2}var(z_{1})+a^{2}(1-\overline{x})^{2}var(z_{2}) \\&+\,2\overline{x}(1-\overline{x})a^{2}\sqrt{var(z_{1})var(z_{2})}\rho (z_{1},z_{2}), \end{aligned}$$

where a is the positive constant defined as a consequence of Theorem 5 in Ortobelli (2001) applied to the family of these distributions. Therefore $d_{\rho ,\sigma }([0,0,1]z)^{2}=a^{2}var(\overline{x},(1-\overline{x} ),0]z)=d_{\rho ,\sigma }([\overline{x},(1-\overline{x}),0]z)^{2}$ if and only if

$$\begin{aligned} \sqrt{var(z_{1})var(z_{2})}\rho (z_{1},z_{2})=\text {cov}(z_{1},z_{2}). \end{aligned}$$

Moreover, let $\rho$ be the Pearson correlation measure and let $z=\left[ z_{1},z_{2},\ldots ,z_{n}\right] ^{\prime }$ be the vector of the returns. If two portfolios $x^{\prime }z$ and $y^{\prime }z$ have the same distributions and $\sigma$ is a deviation measure, then $\sigma _{z_{i}}=a \sqrt{var(z_{i})}$ (where a is a positive constant) for any $i=1,\ldots ,n$ and

$$\begin{aligned} d_{\rho ,\sigma }(x^{\prime }z)^{2}= & {} \sum \limits _{i=1}^{n}x_{i}^{2}\sigma _{z_{i}}^{2}+2\sum \limits _{i=1}^{n}\sum \limits _{j=i+1}x_{i}x_{j}\sigma _{z_{i}}\sigma _{z_{i}}\rho _{i,j}=a^{2}var(x^{\prime }z) \\= & {} a^{2}var(y^{\prime }z)=\sum \limits _{i=1}^{n}y_{i}^{2}\sigma _{z_{i}}^{2}+2\sum \limits _{i=1}^{n}\sum \limits _{j=i+1}y_{i}y_{j}\sigma _{z_{i}}\sigma _{z_{i}}\rho _{i,j}=d_{\rho ,\sigma }(y^{\prime }z)^{2}. \end{aligned}$$

Proof of Proposition 3 Under these assumptions, the matrix $Q_{\rho ,\sigma }=[\sigma _{z_{j}}\sigma _{z_{i}}\rho _{i,j}]=[\langle g(z_{i},z_{j})\rangle ].$ Moreover, from bilinearity we deduce $x^{\prime }Q_{\rho ,\sigma }x=\langle g(x^{\prime }z,x^{\prime }z)\rangle .$ If we have two portfolios $x^{\prime }z$ and $y^{\prime }z$ with the same distribution

$$\begin{aligned} y^{\prime }Q_{\rho ,\sigma }y=\langle g(y^{\prime }z,y^{\prime }z)\rangle =\sigma _{y^{\prime }z}^{2}=\sigma _{x^{\prime }z}^{2}=\langle g(x^{\prime }z,x^{\prime }z)\rangle =x^{\prime }Q_{\rho ,\sigma }x, \end{aligned}$$

where we used the invariance in law of the variability measure $\sigma _{X}= \sqrt{\langle g(X,X) \rangle }$. Thus $d_{\rho ,\sigma }(x^{\prime }z)$ is invariant in law.

Proof of Proposition 4 As a consequence of (7) the measure (8) is defined on the marginals by:

$$\begin{aligned} \rho (z_{i},z_{j})=\frac{v_{ij}}{\sqrt{v_{ii}v_{jj}}}=\frac{ A(\alpha ,p)E\left( \left( z_{i}-E(z_{i})\right) \left( z_{j}-E(z_{j})\right) ^{\left\langle p-1\right\rangle }\right) }{A(\alpha ,1)A(\alpha ,p-1)E\left( \left| z_{i}-E(z_{i})\right| \right) E\left( \left| z_{j}-E(z_{j})\right| ^{p-1}\right) } \end{aligned}$$

for any $p\in [1,\alpha ).$ Moreover, considering that the matrix Q is semidefinite positive, we can easily verify that $\rho$ is a linear correlation measure (for further details on stable sub-Gaussian distributions see Samorodnitsky and Taqqu 1994). Under the assumptions of the proposition, every portfolio of gross returns $x^{\prime }z$ is uniquely determined by the mean $x^{\prime }\mu$ (since $\alpha >1$) and the dispersion $x^{\prime }Qx$ of this elliptical distribution or the mean and the deviation measure $\sigma _{x^{\prime }z}$. Therefore, as a consequence of Theorem 5 in Ortobelli (2001), we can essentially repeat the proof of Proposition 2 and the measure $d_{\rho ,\sigma }(x^{\prime }z)$ is invariant in law if and only if $\rho$ is defined by (8).

Proof of Corollary 1 Let us consider $\rho (X,Y)=\sum _{i=1}^{m}a_{i}\rho _{i}(X,Y)$ such that $a_{i}\ge 0; \sum _{i=1}^{m}a_{i}=1.$ Clearly, $\rho (X,Y)$ is a concordance (correlation) measure if all $\rho _{i}(X,Y)$ satisfy the seven (five) properties of concordance (correlation) measures. Similarly, if $\rho _{i}$ for $i=1,\ldots ,m$ are semidefinite positive correlation measures, then also $\rho =\sum _{i=1}^{m}a_{i}\rho _{i}$ is semidefinite positive because any correlation matrix $Q=\sum _{i=1}^{m}a_{i}Q_{i}$ derived from $\rho$ is the convex combination of the correlation matrices $Q_{i}$ derived from the measures $\rho _{i}.$ Observe that if $\rho _{i}(X,Y)$ $i=1,\ldots ,m$ are linear correlation measures $\langle g_{i}(X,X)\rangle _{i}\ge 0$ and $\langle g_{i}(X,X)\rangle _{i}=0$ if and only if X is a constant. Thus $\langle X-\mathbb {E}(X),X-\mathbb {E}(X)\rangle \ge 0$ and it is equal to zero if and only if $X-\mathbb {E}(X)=0$. Since $\langle g_{i}(X,Y)\rangle _{i}=\langle g_{i}(Y,X)\rangle _{i}$ then $\left\langle X-\mathbb {E}(X),Y- \mathbb {E}(Y)\right\rangle =\left\langle Y-\mathbb {E}(Y),X-\mathbb {E} (X)\right\rangle .$ In addition, for any $a,b\in \mathbb {R}$ and $X,Y,Z\in H$, $\langle g_{i}(aX+bZ,Y)\rangle _{i}=a\langle g_{i}(X,Y)\rangle _{i}+b\langle g_{i}(Z,Y)\rangle _{i},$ thus $\langle aX+bZ,Y\rangle =a\langle X,Y\rangle +b\langle Z,Y\rangle$ and $\langle X,Y\rangle$ is an inner product in the class of centered random variables belonging to H.

Proof of Proposition 5 The matrix $Q_{\rho ,\sigma }$ is still semidefinite positive since $x^{\prime }Q_{\rho ,\sigma }x=y^{\prime }Q_{\rho }y\ge 0$ where $y=(x_{1} \sigma _{z_{1}},x_{2}\sigma _{z_{2}},\ldots ,x_{n}\sigma _{z_{n}})^{\prime }.$ Moreover, Bauerle and Müller (2006) have proved that in a finite probability space where the probability $\Pr$ is uniform, any invariant in law, convex measure D (i.e. $D( aX+( 1-a) Y) \le aD(X)+(1- a )D(Y)$ for any $a\in [0,1])$ is consistent with the choices of risk-averse investors. The measure $x^{\prime }Q_{\rho ,\sigma }x$ (or its estimator $x^{\prime }\widetilde{Q}_{\rho ,\sigma }x$ with semidefinite positive matrix $\widetilde{Q}_{\rho ,\sigma }$) is convex in the class of portfolio returns $x^{\prime }z$ since the function $f(x)=x^{\prime }Q_{\rho , \sigma }x$ ($f(x)=x^{\prime }\widetilde{Q}_{\rho ,\sigma }x$) is a convex function because the Hessian of function f(x) is $Q_{\rho ,\sigma }$ ($\widetilde{Q}_{\rho ,\sigma }$). Then, for any $a\in [0,1]$:

$$\begin{aligned} \left( ax+(1- a )y\right) ^{\prime }Q_{\rho ,\sigma }\left( ax+(1- a )y\right) \le ax^{\prime }Q_{\rho ,\sigma }x+(1- a )y^{\prime }Q_{\rho ,\sigma }y. \end{aligned}$$

The measure $x^{\prime }Q_{\rho ,\sigma }x$ (or its estimator $x^{\prime } \widetilde{Q}_{\rho ,\sigma }x)$ is strictly convex when matrix $Q_{\rho ,\sigma }$ ($\widetilde{Q}_{\rho ,\sigma }$) is definite positive. According to Bauerle and Müller (2006), if $w^{\prime }z$ is dominated in the sense of the convex order by $y^{\prime }z,$ then $w^{\prime }Q_{\rho ,\sigma }w\le y^{\prime }Q_{\rho ,\sigma }y.$