Stochastic optimization models in forest planning: a progressive hedging solution approach

Abstract

We consider the important problem of medium term forest planning with an integrated approach considering both harvesting and road construction decisions in the presence of uncertainty modeled as a multi-stage problem. We give strengthening methods that enable the solution of problems with many more scenarios than previously reported in the literature. Furthermore, we demonstrate that a scenario-based decomposition method (Progressive Hedging) is competitive with direct solution of the extensive form, even on a serial computer. Computational results based on a real-world example are presented.

1 Introduction

In this paper, we consider the problem of medium term forest planning. A deterministic version of this problem has been proposed and solved for a real Chilean forest firm (Andalaft et al. 2003). The main decisions to be made involve which units (lots) to harvest in each period of the planning horizon and what roads need to be built in order to access the harvest units. This is a well-known problem, with difficulties for large-scale problems, due to computationally inefficient MIP formulations. Although current versions of CPLEX can solve the problem directly, Andalaft et al. (2003) introduce a solution approach based on Lagrangian relaxation and a strengthening of the LP formulation, enabling solution of an instance with 17 forests, which are linked by demand constraints at the firm level. This problem was solved considering deterministic demand and price conditions for each period. Quinteros et al. (2009) consider a variant of this problem with market uncertainty, represented through 16 sampled scenarios with both timber prices and upper and lower bounds on demand in each period. In this work each scenario represents all uncertain parameters in all periods, from period 1 to the final time period in the planning horizon. Periods in this problem were defined as semesters, to account for seasonal effects. Given the increased difficulty of solving stochastic models relative to their deterministic counterparts, the paper considered only one forest, the largest of the original 17.

The stochastic model developed by Quinteros et al. (2009) considered the objective of maximizing expected net present value, subject to the solution being feasible under all scenarios. This is a standard treatment of uncertainty in the objective of a stochastic optimization model. The constraints in this case need to include the well-known non-anticipativity constraints (Wets 1975), which state that, given 2 scenarios $S_i$ and $S_k$, if the representation (i.e., data) of scenarios $S_i$ and $S_k$ are identical up to period t, then the decisions taken in scenarios $S_i$ and $S_k$ must also be identical up to period t.

The non-anticipativity constraints in a stochastic optimization model can be expressed in two ways, to create a so-called extensive form. In an explicit formulation, the non-anticipativity constraints relate scenario-specific instances of the decision variables at each node in the scenario tree. In an implicit formulation, the non-anticipativity constraints are expressed by introducing shared, common decision variables at each node in the scenario tree. The implicit formulation is more compact and thus can lead to problems that are easier to solve (Quinteros et al. 2009). However, it is often difficult to solve stochastic optimization instances, even with an implicit formulation, given their typically large dimension. In Quinteros et al. (2009), the stochastic forest planning problem was solved by incorporating the non-anticipativity constraints in an implicit manner, by defining one path through the scenario tree for each scenario, but with variables shared by the all scenarios at a node of the tree. By branching in a coordinated way along all paths, the non-anticipativity constraints are satisfied automatically. Alonso-Ayuso et al. (2003) first developed this solution approach. This type of decomposition enabled more efficient solution of the stochastic optimization model. In Quinteros et al. (2009), a problem with 16 scenarios was solved considering several sources of uncertainty. In this paper, we present a different approach to handle the non-anticipativity constraints, to enable computationally efficient consideration of even larger numbers of scenarios.

We use the algorithm Progressive Hedging (PH) (Rockafellar and Wets 1991), which is based on the separation of the problem by scenarios, thus eliminating the need to explicitly introduce non-anticipativity constraints. In PH, each scenario is solved independently and iteratively. Naturally, the solutions obtained under each scenario do not initially satisfy non-anticipativity, and variables that should be equal by non-anticipativity take different values. The PH algorithm attempts to equalize the values of these variables by penalizing deviations from the average value in all scenarios, through augmentation of the objective function. In an iterative way, convergence to a solution ultimately satisfying the non-anticipativity constraints (without their representation, either in explicit or implicit form) can be developed. The advantage of PH lies in the possibility of solving problems with very large numbers of scenarios, such that an extensive form of the stochastic optimization problem is either too difficult to solve directly, requires too much memory (e.g., in the course of a branch-and-cut procedure), or both. PH and a few other methods have been proposed for multi-stage stochastic programming with integers in all stages, but applications are relatively scarce. For alternatives to PH, see, e.g., Caroe and Schultz (1999), Römisch and Schultz (2001), Guglielmo and Sen (2004), Escudero et al. (2009).

In this paper, we solve the same basic stochastic forest planning problem as (Quinteros et al. 2009). However, in order to render the model more realistic—in particular, to allow for a wide variety of potential undesirable scenarios—we focus on the need to consider a substantially larger number of scenarios. The scenarios for our test case additionally include uncertainty in timber growth and yield.

Forest planning problems have been solved over the past few decades using integer programming models, including an integrated approach that considers both harvesting and road construction decisions (Andalaft et al. 2003; Weintraub et al. 1994, 1995; Kirby et al. 1986, Weintraub and Navon 1976). Introducing binary decision variables into forest planning problems has become integral in the course of making these models more realistic over time. There are two components of these models where discrete decision have been widely leveraged: (a) Road building and (b) All-or-nothing decisions on harvesting areas (lots). Such discrete decisions warrant careful consideration, as they induce mixed-integer optimization models, which can be very difficult to solve in practice. Because our model considers such features, we now briefly review the literature related to the use of discrete decision variables in forest planning.

Road building decisions: Between the late 1970’s and 1990’s, the US Forest Service introduced explicit decision making related to road building (Weintraub and Navon 1976; Kirby et al. 1986). Originally, harvesting models were modeled as continuous optimization problems, which were solved independently of road building models. Jones et al. (1986) provide a thorough analysis showing the significant advantages of integrating the two types of decisions. Weintraub et al. (1995) describe an application involving several regions of the US Forest Service, in which planning was carried out using a mixed-integer programming (MIP) model to integrate road building and harvesting decisions. The primary challenge in this problem involved the fixed cost network flow portion of the model.

Given the computational power and algorithmic advances available at the time, heuristics were needed to find approximate solutions. Guignard et al. (1994) discussed model tightening to better solve these MIP problems. In Andalaft et al. (2003), a similar problem was applied to Forestal Millalemu, a forest company in Chile, which was used again for integrated planning of harvesting and road building decisions. In this case, the company managed 17 separate forests, linked by demand constraints. CPLEX 3.0 was used to solve the problem, and obtained a solution with a optimality bound of about 20 % in 6 h. Using Lagrangian relaxation and a strengthening of the formulation, a solution within 1 % of optimal was obtained in one hour. However, the same problem run years later, with CPLEX 9.0, could be solved to optimality in minutes. This paper presents a stochastic version of the (Andalaft et al. 2003) model, applied to one of the 17 forests (the largest) of the Forestal Millalemu problem. MIP models for forest road building problems have been solved by researchers in Scandinavia, in this case for road upgrade decisions (Frisk et al. 2006).

Harvesting decisions: Harvesting decisions are naturally modeled using 0–1 variables. The constraint that a cutting unit be harvested completely or not at all has been particularly important for environmental reasons, where adjacent units cannot be harvested in the same period. This constraint is based on what is referred to as the maximum opening size, which states that there is a maximum contiguous area (typically about 40 has). Contributing factors include wildlife concerns (elks will not feed in a clearing unless they are relatively near to the protection provided by grown trees), scenic beauty, and erosion factors. Thus, in the planning process, units are defined to be no larger than this maximum opening size area. Further, if one unit k is harvested, the neighboring units cannot be harvested until trees in unit k have reached a certain height. While in this paper we do not impose these adjacency constraints, it is important to have this option, which is now being applied in a deterministic problem. Second, for production and logistical reasons, given the size of the units, it makes economic sense that once a unit is intervened, it should be completely harvested. These concepts have proved critical, and have been used in forest planning for over 20 years. Additional conditions are often imposed, such as needing also to maintain large contiguous areas of mature trees for wildlife protection. In many cases, heuristics have been used to solve these problems (Murray and Church 1995). Exact algorithms have also been proposed for this problem class. However, for larger adjacency problems, even the latest version of CPLEX cannot solve these problems. More complex algorithms, including column generation, have performed better (Goycoolea et al. 2005; Richards and Gunn 2000; Constantino et al. 2008). Goycoolea et al. (2009) present a comparison of these methods. Another approach is presented by McNaughton and Ryan (2008).

The remainder of this paper is organized as follows. Section 2 presents the deterministic medium term forest planning model to be solved. Section 3 describes the uncertainties involved in our stochastic optimization model. Section 4 details the stochastic optimization model. In Sect. 5, we describe the PH algorithm and our specific implementation. Section 6 introduces and discusses the computational results. We conclude in Sect. 7 with a summary of our contributions.

2 The forest planning optimization model

We consider a tactical (medium-term) planning model first developed for a Chilean forest firm, Millalemu. The original problem considered the planning of 17 forests, spatially separated. The planning process horizon was 3 years, divided into summer and winter periods, to account for seasonal effects. The planning decisions involved which units to harvest in each period, and what roads to build to access the harvesting units not already connected to main public roads.

Additionally, stocking areas were used to store timber from summer to winter, and timber flows defined the movement of logs from origins in the forest to destinations. This problem was introduced by Andalaft et al. (2003), and was solved by using Lagrangian relaxation to decouple the forests—which are linked by global demand constraints. The addition of strengthening and lifting constraints to the initial formulation yielded significant improvements in the computational efficiency of the mixed-integer optimization solves. Such enhancements resulted in reductions of the optimality gap for the most difficult data set tested from 162 to 1.6 %, and for all data sets to 2.6 % or less.

In this paper, we work with a simplified version of the original deterministic optimization model. The additional complexities would only add to the computational burden, and are not needed to analyze the complexities of the stochastic optimization model and solution procedure. The specific simplifications we consider are as follows:

• (a) We only consider one type of timber, eliminating the possibility of downgrading (cutting) timber from higher diameters to lower diameters.

• (b) We do not consider stocking yards, eliminating the storing of timber from summer periods to winter periods.

• (c) We only define one type of road, thus eliminating the upgrading of roads.

Figure 1 shows a description of the forest we will analyze, consisting of 25 units to be harvested. Existing roads are depicted as blue arrows, potential roads are depicted as red arrows, and the access to each unit is depicted by green arrows. Finally, the point S represents the exit node of the forest, which links with a public road.

Fig. 1

Diagram of the Los Copihues forest

For the sake of brevity, we do not present the simplified deterministic optimization model here. Rather, we introduce the full stochastic optimization model in Sect. 4, with a scenario-based formulation, driven by parameter uncertainty as described next in Sect. 3.

3 Uncertainties in forest planning

Typical uncertainties occurring in forestry planning are documented by Martell et al. (1998), and summarized as follows:

• (a) Market uncertainties: These uncertainties are expressed mainly through prices for the different timber products, and in some cases also through bounds on demand. Lower demand bounds can reflect minimum amounts a firm needs to sell to keep a market, while upper demand bounds can reflect the maximum amount possible to sell in a market. These properties are a natural result of varying global market conditions as well as local realities in countries where the firm exports. Chile exports almost 90 % of its lumber and pulp products, so its forest firms are heavily dependent on global economic conditions.

• (b) Natural variations in future growth and yields: These uncertainties address the cubic volume ($\hbox {m}^{3})$ per hectare that will be harvested in the future from each unit. Regression and simulation models allow reasonable point predictions of the values of future volumes that will be harvested, but there is a variability that can be modeled though approximate probability functions, with estimates of the averages and standard deviations. One of the approaches that has been proposed is to incorporate this type of variability is chance constraint programming (Hof and Pickens 1991; Weintraub and Vera 1991), in the context of long range planning LP models. Note that if integer variables are incorporated, as is the case in our model, which includes road building, this approach is no longer a computationally practical alternative.

• (c) The effect of fires or pests. These uncertainties model the impact of fires and/or pests on the harvesting of particular units in each period, as described in Martell (2007).

We consider the first two types of uncertainties, expressed as scenarios that specify value for the uncertain parameters in each period through the planning horizon. This is a well known form for expressing uncertainty, in the form of a (sampled) scenario tree.

As discussed in Sect. 2, for the purpose of developing the stochastic model we will consider only one forest, the largest one of the 17 in the original problem, as was done by Quinteros et al. (2009). Details of the scenario generation process are provided in Sect. 6.

4 The stochastic optimization model

We present now our stochastic optimization model, where the deterministic optimization model is adapted for each scenario, and the scenarios are coupled by non-anticipativity constraints.

Sets

• $T:$ $Time\, periods\,in\,the\,planning\,horizon,\,\left\{ t \right\}$

• $O:$ $Origin\,nodes\,of\,harvests,\,\left\{ o \right\} .$

• $J:$ $Road\,intersection\,nodes,\,\left\{ j \right\}$

• $E:$ $Timber\,exit\,nodes,\,\left\{ e \right\}$

• $H:$ $Harvest\,units,\,\left\{ h \right\}$

• $H_{o}:$ $Units\,adjacent\,to\,origin\,node\,\left\{ o \right\}$

• $O_{h}:$ $Origin\,nodes\,adjacent\,to\,unit\,\left\{ h\right\}$

• $R^{E}:$ $Existing\,roads,\,arcs\,\left\{ {k,l} \right\}$

• $R^{P}:$ $Potential\,roads,\,arcs\,\left\{ {k,l} \right\}$

• $R=R^{E} \cup R^{P}:$ $All\,roads.\,arcs\,\left\{ {k,l} \right\}$

• $S:$ $Scenarios\,\left\{ s\right\}$

Deterministic parameters

• $A_h:$ $Area\,of\,unit\,h$ (ha)

• $U_{k,l}^{t}:$ $flow\,capacity\,on\,road\,(k,l)\,in\,period\,t\,\mathrm{{(m^{3})}}$

• $P_{h}^{t}:$ $Cost\,of\,harvesting\,one\,ha\,of\,unit\,h\,in\,period\,t\,\mathrm{{(USD/Ha)}}$

• $Q_o^t:$ $Cost\,of\,producing\,one\,\mathrm{{m^{3}}}\,at\,origin\,o\,in\,period\,t\,\mathrm{{(USD/m^{3})}}$

• $C_{k,l}^t :$ $Cost\,of\,building\,road\,( {k,l})\,in\,period\,t\,\mathrm{{(USD)}}$

• $D_{k,l}^t:$ $Cost\,of\,hauling\,one\,\mathrm{{m^{3}}}\,on\,road\,( {k,l})\,in\,period\,t\,\mathrm{{(USD/m^{3})}}$

• $\Pr ( s ):$ $Probability\,of\,the\,occurence\,of\,scenario\,s$

• $d^{t}:$ $Discount\,factor\,for\,period\,t$

Scenario-dependent parameters

• $R_e^{t,s} :$ $Sale\,price\,in\,period\,t\,under\,scenario\,s\,\mathrm{{(USD/m^{3})}}$

• $\underline{Z}^{t,s},\bar{Z}^{t,s}:$ $Lower\,and\,upper\,bounds\,on\,demand\,under\,scenario\,s\,in\,period\,t\,\mathrm{{({m^3})}}$

• $a_h^{t,s}:$ $Productivity\,of\,unit\,h\,in\,period\,t\,under\,scenario\,s \mathrm{{(m^{3}/ha)}}$

Decision variables

• $\delta _h^{t,s} \in \left\{ {0,1} \right\} :$ $\left\{ {{\begin{array}{ll} 1&{}if\,unit\,h\,is\,harvested\,in\,period\,t\,under\,scenario\,s \\ 0&{}otherwise \\ \end{array} }} \right.$

• $\gamma _{k,l}^{t,s} \in \left\{ {0,1} \right\} :$ $\left\{ {{\begin{array}{ll} 1&{}if\,road\,\left( {k,l} \right) \,is\,built\,in\,period\,t\,under\,scenario\,s \\ 0&{}otherwise \\ \end{array} }} \right.$

• $f_{k,l}^{t,s} \ge 0:$ $Flow\,of\,timber\,transported\,on\,arc\,\left( {k,l} \right) \,in\,period\,t\,under scenario\,s \mathrm{{(\hbox {m}^{3})}}$

• $z_e^{t,s} \ge 0:$ $Timber\,sold\,in\,period\,t\,at\,exit\,e\,under\,scenario\,s\, \mathrm{{(\hbox {m}^{3})}}$

Constraints

• $1.$ $Balance\,of\,flow\,at\,network\,nodes$

• $(a)$ $At\,harvest\,origin\,nodes$

  $$\begin{aligned} \sum \limits _{h\epsilon H_0 } a_h^{t,s} A_h \delta _h^{t,s} +\sum \limits _{\left( {k,o} \right) \epsilon \,K} f_{k,0}^{t,s} -\sum \limits _{\left( {o,k} \right) \epsilon \,K} f_{0,k}^{t,s} =0\,\,\,\forall \,o\,\epsilon \,O,t\,\epsilon \,T,\,s\,\epsilon \end{aligned}$$

• $(b)$ $At\,road\,intersection\,nodes$

  $$\begin{aligned} \mathop \sum \limits _{\left( {k,j} \right) \epsilon \,K} f_{k,j}^{t,s} -\mathop \sum \limits _{\left( {j,k} \right) \epsilon \,K} f_{j,k}^{t,s} =0\qquad \forall \,t\,\epsilon \,T,\,s\,\epsilon \,S,\,j\,\epsilon \,J \end{aligned}$$

• $(c)$ $At\,exit\,nodes$

  $$\begin{aligned} z_e^{t,s} =\mathop \sum \limits _{\left( {k,e} \right) \epsilon \,K} f_{k,e}^{t,s} -\mathop \sum \limits _{\left( {e,k} \right) \epsilon \,K} f_{e,k}^{t,s} \qquad \forall \,e\,\epsilon \,E,t\,\epsilon \,T,\,s\,\epsilon \,S \end{aligned}$$

• $(d)$ $No\,stocks\,are\,held\,between\,periods$

  $$\begin{aligned} \mathop \sum \limits _{h\,\epsilon \,H} a_h^{t,s} A_h \delta _h^{t,s} -\mathop \sum \limits _{e\,\epsilon \,E} z_e^{t,s} =0\qquad \forall \,t\,\epsilon \,T,\,s\,\epsilon \,S \end{aligned}$$

• $2.$ $Bounds\,for\,timber\,production$

  $$\begin{aligned} \underline{Z}^{t,s}\le \mathop \sum \limits _{e\,\epsilon \,E} z_e^{t,s} \le \bar{Z}^{t,s} \end{aligned}$$

• $3.$ $Building\,of\,potencial\,roads$

• $(a)$ $Flow\,up\,to\,capacity\,if\,road\,(k,l)\,is\,built$

  $$\begin{aligned} f_{k,l}^{t,s} \le U_{k,l}^{t,s} \mathop \sum \limits _{1\le m\le t} \gamma _{k,l}^{m,s} \qquad \forall \,\left( {k,l} \right) \,\epsilon \,R^{P},t\,\epsilon \,T,\,s\,\epsilon \,S \end{aligned}$$

• $(b)$ $Roads\,are\,built\,at\,most\,once$

  $$\begin{aligned} \mathop \sum \limits _{t\,\epsilon \,T} \gamma _{k,l}^{t,s} \le 1 \qquad \forall \,\left( {k,l} \right) \,\epsilon \,R^{P},\,s\,\epsilon \,S \end{aligned}$$

• $4.$ $Capacity\,of\,existing\,roads$

• $(a)$ $Respect\,the\,capacity\,of\,each\,road$

  $$\begin{aligned} f_{k,l}^{t,s} \le U_{k,l}^{t,s} \qquad \forall \,\left( {k,l} \right) \,\epsilon \,R^{E},t\,\epsilon \,T,\,s\,\epsilon \,S\, \end{aligned}$$

• $(b)$ $Upper\,bound\,of\,flow\,capacity\,for\,all\,roads$

  $$\begin{aligned} f_{k,l}^{t,s} \le \mathop \sum \limits _{w\,\epsilon \,O} \mathop \sum \limits _{h\,\epsilon \,H_w } a_h^{t,s} A_h \delta _h^{t,s} \qquad \forall \,(k,l)\,\epsilon \,K,t\,\epsilon \,T,\,s\,\epsilon \,S \end{aligned}$$

• $5.$ $Each\,cell\,is\,harvested\,at\,most\,once$

  $$\begin{aligned} \mathop \sum \limits _{t\,\epsilon \,T} \delta _h^{t,s} \le 1\qquad \forall \,h\,\epsilon \,H,\,s\,\epsilon \,S\, \end{aligned}$$

Objective function

$$\begin{aligned} \max \mathop \sum \limits _{s\,\epsilon \,S} \hbox {Pr}(s)\left( {TS^{s}-HC^{s}-PC^{s}-RC^{s}-TC^{s}} \right) \end{aligned}$$

where:

$$\begin{aligned}&\displaystyle TS^{s}=\mathop \sum \limits _{e\,\epsilon \,E} \mathop \sum \limits _{t\,\epsilon \,T} d^{t}R_e^{t,s} z_e^{t,s} \qquad \forall \,s\,\epsilon \,S&\\&\displaystyle HC^{s}=\mathop \sum \limits _{h\,\epsilon \,H} \mathop \sum \limits _{t\,\epsilon \,T} d^{t}P_h^{t,s} A_h \delta _h^{t,s}\qquad \forall \,s\,\epsilon \,S&\\&\displaystyle PC^{s}=\mathop \sum \limits _{o\,\epsilon \,O} \mathop \sum \limits _{t\,\epsilon \,T} d^{t}Q_o^t \left( {\mathop \sum \limits _{h\,\epsilon \,H_o } a_h^{t,s} A_h \delta _h^{t,s} } \right) \qquad \forall \,s\,\epsilon \,S&\\&\displaystyle RC^{s}=\mathop \sum \limits _{(k,l)\,\epsilon \,R^{P}} \mathop \sum \limits _{t\,\epsilon \,T} d^{t}C_{k,l}^{t,s} \gamma _{k,l}^{t,s} \qquad \forall \,s\,\epsilon \,S&\\&\displaystyle TC^{s}=\mathop \sum \limits _{(k,l)\,\epsilon \,K} \mathop \sum \limits _{t\,\epsilon \,T} d^{t}D_{k,l}^{t,s} f_{k,l}^{t,s} \,\,\,\,\forall \,s\,\epsilon \,S&\end{aligned}$$

The objective function specifies maximization of the net revenue, which is composed of the income from timber sales ($TS$) and four types of expenses: the harvesting cost ($HC$), the cost of the production at the origin nodes ($PC$), the road construction cost ($RC$), and the transportation costs ($TC$).

Additional constraints

$1.$ :

$Direct\,strengthenings$

We additionally include several strengthening constraints to improve mixed-integer solve times, first introduced by Andalaft et al. (2003). The following notation is used to express these constraints:

The specific constraints employed are given as follows:

$(a)$ :

$Do\,not\,build\,isolated\,roads$

$$\begin{aligned} \gamma _{k,l}^{t,s} \le \mathop \sum \limits _{q\le t} \mathop \sum \limits _{\left( {i,j} \right) \epsilon \,N(k,l)} \gamma _{i,j}^{q,s} \qquad \forall \,t\,\epsilon \,T,\,\left( {k,l} \right) \,\epsilon \,R^{P}\backslash SC,\,s\,\epsilon \,S \end{aligned}$$

$(b)$ :

$Do\,not\,harvest\,units\,unless\,a\,connecting\,road\,has\,been\,built$

$$\begin{aligned} \delta _h^{t,s} \le \mathop \sum \limits _{q\le t} \mathop \sum \limits _{\left( {i,j} \right) \epsilon \,N(h)} \gamma _{i,j}^{q,s} \qquad \forall \,t\,\epsilon \,T,\,s\,\epsilon \,S,\,h\,not\,connected\,to\,an\,existing\,road \end{aligned}$$

where $N\left( h \right) =\left\{ {\left( {i,j} \right) \epsilon R^{P}|\,i\,\epsilon \,O_h \,{\textstyle {\bigvee }} j\,\epsilon \,O_h } \right\}$. We observe that .

$2.$ :

$Liftings$

$(a)$ :

$Lifting\,on\,road\,capacities$, where flows in the LHS on all periods up to t are added up, considering that timber can be harvested at most once

$$\begin{aligned}&\mathop \sum \limits _{g\le t} f_{k,l}^{g,s} \le U_{k,l}^{t,s} \mathop \sum \limits _{1\le m\le t} \gamma _{k,l}^{m,s} \qquad \forall \,\left( {k,l} \right) \epsilon \,R^{P},\,t\,\epsilon \,T,\,s\,\epsilon \,S\\&\mathop \sum \limits _{g\le t} f_{k,l}^{g,s} \le U_{k,l}^{t,s} \qquad \forall \,\left( {k,l} \right) \epsilon \,R^{E},\,t\,\epsilon \,T,\,s\,\epsilon \,S \end{aligned}$$

$(b)$ :

$Lifting\,on\,not\,\,building\,isolated\,roads$

$$\begin{aligned} \mathop \sum \limits _{g\le t} \gamma _{k,l}^{g,s} \le \mathop \sum \limits _{g\le t} \mathop \sum \limits _{\left( {i,j} \right) \epsilon \,N(k,l)} \gamma _{i,j}^{g,s} \qquad \forall \,\left( {k,l} \right) \epsilon \,R^{P}\backslash SC,\,t\,\epsilon \,T,\,s\,\epsilon \,S \end{aligned}$$

$(c)$ :

$Lifting\,on\,the\,constraints\,of\,not\,harvesting\,unconnected\,units$

$$\begin{aligned}&\mathop \sum \nolimits _{g\le t} \delta _h^{g,s} \le \mathop \sum \nolimits _{g\le t} \mathop \sum \limits _{\left( {i,j} \right) \epsilon \,N(h)} \gamma _{i,j}^{g,s} \\&\quad \forall \,t\,\epsilon \,T,\,s\,\epsilon \,S, \; h\,not\,connected\,to\,an\,existing\,road \end{aligned}$$

$3.$ :

$New\,Strengthenings$

$(a)$ :

$Flow\,balance\,in\,the\,network$

$$\begin{aligned} \mathop \sum \limits _{h\in H} a_h^{t,s} A_h \delta _h^{t,s} -\mathop \sum \limits _{e\in E} z_e^{t,s} =0\,\,\,\forall \,t\,\epsilon \,T,\,s\,\epsilon \,S \end{aligned}$$

$(b)$ :

$Road\,flow\,capacity$

$$\begin{aligned} f_{k,l}^t \le \mathop \sum \limits _{h\in H} a_h^{t,s} A_h \delta _h^{t,s} \qquad \forall \left( {k,l} \right) \in R,\,t\,\epsilon \,T,s\,\epsilon \,S \end{aligned}$$

The new strengthening provided significant improvement in the efficiency of the runs.

5 The progressive hedging algorithm

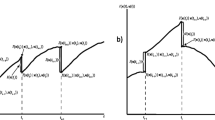
Consider a stochastic optimization problem such as that presented in Sect. 4, where scenarios have been pre-defined. Figure 2 presents an example problem with 4 time periods and 5 scenarios. Figure 2a shows the scenario tree in a standard form, while Fig. 2b shows the 5 scenarios in a disaggregated form, in which the non-anticipativity constraints on decision variables are represented by the circling of nodes. In period 1, all scenarios share identical decisions, as no knowledge of future uncertainty has been acquired yet. In contrast, we see in period 2 that node 2 represents scenarios 1, 2 and 3, while node 3 shares scenarios 4 and 5.

Fig. 2

Example of a scenario tree in standard (left figure) and disaggregated (right figure) forms

As the uncertainties can take only a finite number of values when a scenario tree is provided as input, the stochastic optimization problem can be stated as follows:

$$\begin{aligned}&\mathop {\min }\limits _x \mathop \sum \limits _{s\in S} \hbox {Pr}(s)f\left( {x,s} \right) \\&s.t.x_s \in C_s \quad \forall s\in S\\&x\in \mathcal {N} \end{aligned}$$

The model seeks to minimize the expected cost across all scenarios, weighted by their probabilities Pr(s). Solutions must satisfy feasibility for all scenarios when taken independently, and must satisfy the non-anticipativity constraints at each node in the scenario tree when taken together. We use $C_s$ to represent the constraints for each scenario. We use $\mathcal {N}$ to represent the set of non-anticipative solution vectors, i.e., those for which scenarios that share a node in the scenario tree have the same value for all those decision vector elements associated with that node..

The basic idea of the PH algorithm is to relax the non-anticipativity constraints and solve the scenario sub-problems independently. Solving these problems separately is naturally much easier than solving the extensive form directly. However, the non-anticipativity constraints will be satisfied only in very rare cases. That is, the values of the variables which should be equal to satisfy non-anticipativity are not equal. The PH algorithm then iteratively solves the scenario sub-problems, gradually enforcing equality. Note that if all variables are equal, they are also equal to their average. The PH algorithm incrementally enforces non-anticipativity by penalizing deviations from the average values of decision variables.

PH starts solving each scenario independently, as follows:

$$\begin{aligned}&\mathop {\min }\limits _x f\left( {x,s} \right) \\&s.t.x\in C_s \end{aligned}$$

PH then computes a solution average and a convergence value to determine if solutions are sufficiently non-anticipative. The convergence value quantifies the deviation of solutions from the “mean” solution. If the convergence value is sufficiently small, PH terminates because the non-anticipativity constraints are (approximately) satisfied. If not, then PH computes a penalization terms, w, for each decision variable, proportional to both the deviation from the average and a penalty factor $\rho$. Given these penalization terms that tend to force non-anticipativity, the scenario sub-problems are re-solved. The algorithm iterates until the non-anticipativity constraints are “practically” satisfied.

The following pseudo-code describes the PH algorithm:

$1.$ :

$Solve\,each\,scenario\,without\,penalizations$

$$\begin{aligned} k=0,\,w_k =0 \end{aligned}$$

$2.$ :

$Compute\,the\,average\,for\,each\,variable$

$$\begin{aligned} \bar{x} =\mathop \sum \limits _s \hbox {Pr}(s)x_s \end{aligned}$$

$3.$ :

$If\,solutions\,are\,sufficiently\,converged,\,then\,exit;\,\,else\,k=k+1$

$$\begin{aligned} g:=\Vert x-\bar{x} \Vert <\varepsilon \end{aligned}$$

$4.$ :

$Update\,penalization\,terms$

$$\begin{aligned} w=\rho \left( {x-\bar{x}} \right) +w \end{aligned}$$

$5.$ :

$Solve\,scenarios\,with\,penalization\,terms$

$$\begin{aligned} \overline{f_{s}} \left( {x_s } \right) {:=}f_s \left( {x_s } \right) +wx_s +\frac{\rho }{2}\Vert x_s -\bar{x}\Vert ^{2} \end{aligned}$$

$6.$ :

$Goto\,step\,2$

If all decision variables are continuous, the PH algorithm provably converges to an optimal solution (Rockafellar and Wets 1991). In the problem we consider, with integer variables, no such convergence proof exists. However, several enhancements to the basic PH algorithm have been introduced to ensure and accelerate convergence in the mixed-integer case (Watson and Woodruff 2010). Specifically, the following issues were carefully addressed in our implementation of PH:

• 1. The quadratic term complicates the solution procedure: In particular, quadratic mixed-integer programs are much more difficult to solve than linear mixed-integer programs. To address this issue, we linearized all quadratic penalty (proximal) terms. In the case of linear decision variables, the number of pieces used in the linearization must be determined. In the case of binary decision variables, the quadratic penalty terms simply reduce to linear penalty terms, because they only take on 0–1 values.

• 2. The value given to the parameter $\varvec{\rho }$ (Steps 4 and 5 in the PH pseudo-code): Computational experience has shown that the value given to $\rho$ has a major impact on the convergence of the PH algorithm, and the quality of the resulting solution.

• 3. Mipgap tolerance: When considering each scenario subproblem, there is no need to solve each problem to optimality, particularly in early PH iterations. Allowing the solves for each subproblem to terminate when the solution obtained is within a small optimality gap allows to solve these problems in a much faster way, without significant loss in the quality of final solution.

• 4. Hot starts: A well-known acceleration technique for PH is to use hot starts when re-solving scenario subproblems. Specifically, the solution obtained for sub-problem r in iteration k is used as a starting solution for sub-problem r in iteration k + 1. Feasibility is guaranteed, as only the optimization objective is modified.

• 5. Strengthening of the formulation. Several such strengthenings were implemented, as discussed above in Sect. 4. These strengthenings lead to significantly faster solution times for scenario subproblems.

• 6. Variable fixing. As noted, the PH algorithm is used as a heuristic for our problem due to the presence of 0–1 variables. To obtain solutions more quickly, our implementation fixes individual discrete variables when they have satisfied non-anticipativity for a number of iterations. Fixing variables in such a manner may lead to sub-optimal solutions, but computational experience supports the overall effectiveness of this strategy. Experiments were carried out to determine how many iterations should be considered with common values in the variables before fixing them.

• 7. Early termination of PH. There is no guarantee of convergence for the class of non-convex problems we consider, which include discrete decision variables. Furthermore, convergence of the last few variables often requires more computational effort than it is worth. Computational experience has shown it is valuable, after a number of PH iterations, to switch the solution algorithm to a regular branch and cut scheme. Specifically, a commercial code is used to solve the full extensive form of the stochastic optimization problem, subject to fixing variables whose values have converged. The solution time for the branch-and-cut approach applied to the extensive form is now considerably faster since a significant number of the 0–1 variables are already fixed.

The combination of these factors has enabled implementation of a PH algorithm that is efficient, with relatively good quality of solutions. The primary potential advantage of PH over direct solution of either the explicit or implicit extensive form lies in scalability, when very large numbers of scenarios are considered. In this case, the extensive form is often computationally intractable for commercial deterministic solvers, in terms of memory, run-time, or both.

6 The test case

The case we are dealing with is the Los Copihues forest, shown in Fig. 1. It has 25 stands, with a total area of 300 hectares, 150,000 $\hbox {m}^{3}$ of timber, 15 existing and 11 potential roads, 9 origins where timber is extracted, 3 road intersections, and one exit to a public road. A discount factor of 10 % was used because it is consistent with commonly used values in the Chilean forestry industry to capture the risk free rate and adjustments for risk. The experiments were done under Linux using a computer with Intel(R) Core(TM) 2 Quad CPU Q8200 @ 2.33GHz and four gigabytes of main memory.

To generate the scenarios we first consider market uncertainties. We represent the market uncertainty exactly as in Quinteros et al. (2009), with two random variables: prices and quantity demanded. First, price is simulated as a random walk, and second, the quantity demanded is assumed to have a positive correlation with the price considering the bounds on demand. Then, we also develop scenarios considering uncertainty in timber growth. To generate the timber growth component of the scenarios we considered an average of yearly growth of 3 % with a standard deviation of 0.15 %, which correspond to typical observed values in timber growth in this region of Chile based on conversations with foresters.

In general there are markets for timber products, and Chile has a small share of the world market, so it could be argued that uncertainty should only be expressed in terms of prices. However, for Chilean forest firms, the market is not completely fluid. There are contracts, existing and future ones that may be signed for given quantities. There are markets that need to be supplied with a minimum quantity to be retained, and others where the firm has saturated its ability to supply. In addition, future competitor producers may appear, like Russia increasing significantly its production, which might make some markets unavailable, due to shipping costs. These conditions influenced us to include also uncertainty in future demand. We modeled minimum quantities for retention of a customer and maximum quantities to avoid saturation by putting upper and lower bounds on production. A more complex scheme would be to have multiple prices and various demand breakpoints, but we lacked the data to set these values and this is beyond the scope of the present work.

For our problem, we added uncertainty in growth and yield, that is, the $\hbox {m}^{3}$ per hectare obtained when harvesting. Variability is assumed completely correlated between stands, (the case of less correlation does not alter the solution approach), and variation in timber production is assumed to be uniformly distributed over plus and minus 10 % of average value. Then, we combine the 16 market scenarios with production variability, creating up to 324 scenarios, which a significantly larger number than previously reported.

For example, a case with 144 scenarios in 4 periods, was created combining market and tree growth scenarios. The scenarios have a tree form, as shown in Fig. 2, with branches emerging from a root node that corresponds to the present period and then from continuing nodes in the tree. One example has (1,3,3,2) branchings for market price, and (1,2,2,2) branching for tree growth. In this case the total number of scenarios becomes 1$\times 3\times 3\times 2\times 1\times 2\times 2\times 2=$ 144 scenarios. In general the number of branches is chosen with a larger number of possibilities in the early periods.

As the number of scenarios grows, so does the dimension of the model. Table 1 shows the dimension for both the explicit and implicit formulations.

Table 1 Problem sizes for the implicit and explicit extensive forms (EF)

7 Results

Several options were considered in the problems runs.

• (a) Use of hot starts

• (b) Linearization of quadratic penalization

• (c) Strengthening of the formulation

• (d) Use of gaps for early termination of MIP problems

• (e) Value assigned to parameters $\rho$ and $\epsilon$ for termination

• (f) Fixing variables

The effect of strengthenings depends on the instance, the solver, other options, and other strengthenings used. When combined with the best set of options for our experiments, the best set of strengthenings we found to be Flow Balance in the Network, Lifting on Road Capacities, Road Flow Capacity.

Hot-starts provided 11 % faster solutions. After testing, a gap of 2  % was found to be the best compromise between computational effort and solution quality. The best results were found in linearizing the quadratic penalization term into just two segments, in V form. For binary variables, the quadratic term is simply approximated linearly. Fixing variables, setting $\rho$ as in Watson et al. (2012), and early termination proved to increase efficiency in solving the problems. We fixed $\epsilon =0.01$ and $k_{max} =10$, based on preliminary experiments. Figure 3 shows the convergence graph for 144 scenario case. Convergence is not always monotonic, but the graph gives the reader a sense of typical convergence behavior.

Fig. 3

Example of a convergence of PH; a 144 scenario example

The results for diverse instances are shown in Table 2, where a comparison between solving the extensive form in CPLEX 10.2 with default setting and solving the problem using PH with the same CPLEX as the subproblem solver. We see that for 18 scenarios EF alone obtains slightly better solutions in more time and for this particular set of 324 scenarios where PH+ is slightly dominated by the EF. For all other scenario sets, PH+ dominates the EF alone.

Table 2 Computational results obtained by varying the number of scenarios

Parallelization of PH shows promise for extremely large numbers of scenarios. Descriptions of parallel implementation and experimentation are beyond the scope of this paper. However, to give the reader a sense of the impact of parallel PH, we conducted an experiment on the 64-scenario case and obtained an objective function value of 5,347,334.56. For this experiment, we parallelized by forming bundles of 4 scenarios each, which we treated as “super-scenarios”. If these super-scenarios are solved in parallel, then only a couple of minutes of wall clock time is required for solution. A full study of parallelization on larger instances remains as future work.

8 Conclusions

Solutions for optimization models for medium-term forest management that combine road and harvest planning can be obtained for realistic sized problem instances, even in the face of uncertainty. In this paper we have described strengthening methods that enable solution of problems with many more scenarios previously reported in the literature. Without these strengthenings, solution of the extensive form was limited to very small instances. Furthermore, we have demonstrated that Progressive Hedging is competitive even on a modest serial computer (in our case, a standard laptop). This is important because PH can be parallelized to solve instances with even more scenarios where the attempts to solve the Extensive Form directly will run out of memory. Note that by fixing large numbers of integer variables, the PH algorithm produces a modified extensive form that is smaller and that can be solved with fewer branch and bound nodes. For a particular instance in practice, there is a tradeoff between using more scenarios to get better representations of the uncertainty and the need for more processors and more time for PH to reduce the number of variables so that the resulting modified EF can be solved.

The comparisons we made were done using the best version of CPLEX available at the time. Naturally, CPEX is constantly improving, so the number of scenarios that can be solved using the extensive form is increasing and so is the number of scenarios that can be solved using PH, which employs CPLEX as a sub-problem solver. In the meantime we have also been improving our code. In particular we are starting to test a parallel version, which has the very significant advantage in that the scenario problems can be run in parallel, rather than serially, which is the present case. All indications are that a parallel implementation will be far superior, in particular for a large number of scenarios. As parallel computers become ubiquitous, the ability of PH to immediately use large numbers of processors will be its chief advantage for practical applications in forestry.

An important avenue of ongoing research concerns improving the scenarios for price (Weintraub and Wets 2013). When generated rigorously, there can be a very large number of scenarios needed to capture a multi-stage progression of wood prices. This increases the importance of the work reported here.