Strategic Management Scheduling

Abstract

Strategic or long-term management planning plays a key role in the development of forest schedules as the temporal dimension is a determinant characteristic of all forestry production systems. In this chapter we address the representation of industrial forest strategic forest management problems as well as the interpretation of its solution. We start with a simple harvest scheduling model aiming at the maximization of economic returns while addressing concerns with the sustainability of a product flow. This policy scenario is expanded to reflect concerns with the volume in the ending inventory, with the average carbon stock, with the environmental impacts of clearcuts and with the integration of road building and maintenance decisions. Several modeling approaches are considered to represent and solve each problem. An example forest is used to illustrate all problems and how they may be addressed by each modeling approach. Several applications of the modeling approaches to strategic management planning of industrial plantations are briefly described in six Management Planning in Action boxes. A list of problems at the end of the chapter build from the same example forest to support model building, model solving and interpretation of results by readers.

1 Introduction

Strategic management planning plays a key role in the development of forest schedules as the temporal dimension is a determinant characteristic of all forestry production systems. Strategic or long-term management planning typically encompasses temporal horizons extending over more than 10 years so that forestry economic and biological processes may be adequately acknowledged (Chap. 2). The importance of this planning level was highlighted in a recent review of forest management problems that are prevalent world-wide (Borges et al. 2014b). Forest management experts representing 26 countries from Europe, North and South America, Africa and Asia involved in the FORSYS Cost Action (http://www.cost.eu/domains_actions/fps/Actions/FP0804) did include strategic management planning in the list of the most important problems that foresters have to face in their countries (Borges et al. 2014b).

Long term stand-level problems tend to be more important in countries where the forest is mostly privately owned and highly fragmented (Borges et al. 2014b). This spatial scale structures a problem with specific features and that requires specialized solution techniques (Chap. 6). In this chapter we will focus on long-term management planning at the regional and forest-level spatial scales (Chap. 2). The latter typically encompasses several contiguous stands and is more frequent in the case of industrial plantations. Nevertheless, in the case of the vertically integrated forest industry its land base is often dispersed over a region. Further, the industry is often concerned with the supply of raw material from other ownerships within a regional framework.

Socioeconomic development and demographic trends have led to an increasing awareness of the externalities that derive from the use of forests for commercial purposes over extended planning horizons. Strategic management scheduling of industrial forests is thus increasingly framed by demands other than by the forest industry (Chap. 2). As a consequence, the long term sustainability of an industrial forest is currently assessed by a set of indicators (Chap. 13) to characterize both the supply of industrial product flows and the ecological/economic features of its land base. Moreover, the forest industry competitiveness often depends on the success of certification processes where a wide range of ecological and socioeconomic indicators are considered (Chap. 15).

In this context, strategic or long term management scheduling of industrial forests has to address objectives that range from traditional products’ even-flow goals to stock control and landscape structure targets. Borges et al. (2014b) reported that even when strategic management planning addresses only market wood products thus excluding all other goods and services, forest managers often target multiple objectives rather than a single one. For that purpose, forest managers sometimes sequence land allocation and harvest scheduling decisions. For example, in Brazil, land allocation decisions in areas managed by the industry are often made prior to harvest scheduling decisions. The legal framework prescribes the amount of land that a rural property has to preserve for environmental purposes or to maintain uncultivated, protecting soils and water streams (usually referred in Brazil as APPs – Permanent Preservation Areas), or to reserve as a precautionary measure to maintain a constant stock of wood and forest resources (also referred in Brazil as RLs – Legal Reserves) (Rodriguez and Nobre 2013). Nevertheless, even when uses are segregated in space the management of the industrial plantation may still be framed by concerns other than with the sustainability of the product flow to the factory.

The spatial context of harvest scheduling decisions is typically addressed at tactical and operational planning scales (Chap. 2). The importance of locational specificity in a management plan, i.e. the definition of the spatial location where management options are actually to be implemented, grows when tactical and operational concerns are to be addressed (Chap. 7). Nevertheless the possibility of balancing strategic and tactical goals may be facilitated if long-term management planning does address locational specificity. The management of the industrial plantation is often framed by spatial considerations that require the acknowledgement of neighboring relations between stands. If these are totally ignored by strategic management planning it may even more difficult to reconcile the long-term and medium and short-term perspectives and schedules. Accordingly, in countries where strategic forest-level management planning targeting only wood products is reported as a prevalent problem, locational specificity of the long-term solution is typically required (Borges et al. 2014b). In fewer cases it was reported that neighborhood relations should also be fully acknowledged.

The practice of strategic management scheduling of industrial plantation thus focus on the structuring, the representation and the solution of a range of long-term planning problems. These may be classified according to dimensions that include the spatial scale, the number of objectives as well as of products and the spatial context. In any case, thoughtful development of all stages of the decision process requires information and knowledge about the structure of the planning process, the land base that is the object of the planning exercise, the models available to make projections of forest products and the models available to generate prescriptions that may be implemented in each stand (Chap. 2). Last but not the least it requires the application of forest economic and finance models (Chap. 5).

Problem structuring issues may be better addressed in the framework of the development of information systems that may encapsulate the data and the model base needed to support the integration of temporal planning levels (Chap. 9). In this chapter we will address the representation of industrial forest strategic forest management problems as well as the interpretation of its solution. We will start with a simple harvest scheduling model aiming at the maximization of economic returns while addressing concerns with the sustainability of a product flow (Problem 1). This policy scenario will be expanded to reflect concerns with the volume in the ending inventory and with the average carbon stock (Problem 2). Further concerns with the environmental impacts of clearcuts will be addressed in Problem 3. The integration of road building and maintenance decisions within strategic forest management scheduling will be discussed as Problem 4.

Several modeling approaches will be considered to represent and solve each problem. In the case of Problems 1 and 2 we will start with linear programming formulations, the technique most widely used in long-term forest management scheduling (Chap. 2). Mixed integer programming formulations will be used to ensure the locational specificity of the solutions to Problems 1 to 3. We will present a goal programming representation of the multiple objective policy scenarios in Problems 1 to 3. A meta-heuristic – simulated annealing – will be considered as an alternative integer solution approach in the case of Problems 1 to 3. Further, a Pareto frontier approach will be used to illustrate how the setting of management planning targets may benefit from a priori display of trade-offs between objectives. The reader is referred to Chap. 2 for an introduction to each modeling approach.

1.1 Example Forest and Applications

In this chapter, an example forest will be used to illustrate all problems and how they may be addressed by each modeling approach. Several applications of the modeling approaches to strategic management planning of industrial plantations will be briefly described in six Management Planning in Action boxes.

Our example forest encompasses a set of 16 stands from Leiria National Forest (LNF), a pine forest in Portugal (Fig. 6.1). Land classification led to stand areas that range from 28.5 to 31 ha (Table 6.1). Long-term planning typically extends over the number of years corresponding to 1.5 rotations (Chap. 2). In the case of LNF the planning horizon extends over 100 years (Tomé et al. 2010; Garcia-Gonzalo et al. 2013). Nevertheless, for illustration purposes we will consider a four 10-year period planning horizon.

Fig. 6.1

Example forest with 16 pine stands from Leiria National Forest in Portugal

Table 6.1 Current inventory in the 16 stands example forest

These stands were assigned LNF inventory plot information (Table 6.1). Stand age ranges from 23 to 53 years. The volume ranges from 107. 5 to 331.3 m³/ha in the case of younger and older stands, respectively. A prescription writer was used to generate 3–5 prescriptions for each stand. For simplicity, the prescriptions involve only clearcuts and it is assumed that stands regenerate naturally. Prescriptions are available that involve clearcuts in alternative years of the same planning period.

An empirical growth and yield model was used to estimate the values of volume harvested in each planning period and at the ending inventory as well as of the carbon stock, resulting from the assignment of each prescription to each stand (Table 6.2). The corresponding revenues were computed considering a constant price equal to 15.5 €/m³. Their present value in year 1 of the planning horizon was computed considering a discount rate equal to 3 % (Table 6.2).

Table 6.2 Prescription summaries for the 16 stands example forest

What You Will Learn in This Chapter

• The dimensions of strategic forest management planning in the case of industrial plantations.

• How to build a model that may represent a strategic forest management planning problem.

• How to analyze the potential of operations research techniques to address several long-term management planning problems.

• How to interpret the long-term schedules provided by several modeling approaches.

2 Volume and Area Control in Long Term Industrial Forest Management Planning (Problem 1)

The demand of timber has played a major role in defining strategic forest management planning problems as well as in early modeling approaches to address it (Chap. 2). Ecological and socioeconomic conditions prevailing in nineteenth century Europe, e.g. extensive deforestation of areas close to urban centers and limited transportation technology, prompted the development of management models emphasizing the stability of timber supply (Borges and Hoganson 1999). Theoretical concepts such as “sustainable yield” and “normal forest” (Alves 1984, Chap. 2) emerged in order to address that society economic requirements. Biological or financial parameters contributed explicitly to time the harvest (Chap. 5). Socioeconomic factors were implicitly considered by area or volume harvested control methods (Chap. 2) that targeted the sustainability of timber flows over extended planning horizons.

The area control method aims to get to the maximum sustainable timber even flow by balancing the age-class distribution as quickly as possible. It achieves this goal by simply harvesting A/r hectares each period where A is the forest area and r is the number of periods in the rotation. The area to be harvested in each period may be adjusted to take into account the productivity of each hectare in the forest. In the worst-case scenario, this will result in a regulated forest in r periods. The problem with area control is that during the periods where the age-class distribution of the initial forest is being regulated – which can be a long time if r periods is very long – the volume harvested each period can vary dramatically. The more unbalanced the initial age-class distribution, the larger this problem will be.

Volume control methods were developed to try to produce a more even flow of volume while still eventually producing a regulated forest. In area control, the forester cuts a constant area of forest each period and hopes to produce a steady flow of timber, sometimes not too successfully. With volume control, the forester cuts a certain volume each period and hopes to eventually produce a regulated forest. With area control, the question of how much area to cut each period is straightforward. With volume control, the problem of determining how much to cut each period is less obvious.

An approach that would be analogous to the area control solution would be to simply cut the long term sustainable yield (LTSY) each period. Unfortunately, depending on the initial age-class distribution of the forest, this approach could result in severe overcutting, eventually reducing the inventory of the forest to zero, or cut so little that it would take a very, very long time to regulate the forest. For example, the Hundeshagen method of determining the volume to cut adjusts the LTSY by the ratio of the current total forest inventory over the total forest inventory that will be present when the forest is regulated. The logic of this is that if the forest currently has more inventory than it will have once it is regulated, then more volume should be cut to reduce the excess inventory. Conversely, if the forest currently has less inventory than it will have once it is regulated, then less volume should be cut to allow the inventory to build up.

Mathematically, Let I ₀ be the current inventory (at time 0) and let I _Reg be the inventory that will be present in the forest when it is regulated. The volume to cut in the first period, H ₁ , according to the Hundeshagen method is:

$$ {H}_1=\frac{I_0}{I_{\mathrm{Re} g}} LTSY $$

(6.1)

In many cases, if this volume is harvested each period, one will achieve a fairly constant volume of timber over time and the forest will eventually be regulated. However, depending on the initial age-class distribution of the forest, this formula can lead to overcutting, followed by undercutting, followed by overcutting, until the age-class distribution approaches a somewhat balanced state, and the harvest level fluctuations settle into a more constant level. Other volume control formulas have been developed, some as general rules and others for very specific situations, but none of them ideal for all situations. The main problem with classical approaches, however, is that all of them, when confronted with the detailed inventory information and varied conditions and constraints of modern forestry, fail to handle the complexity of industrial forest management planning.

Furthermore, more sophisticated approaches are available that can handle much of this complexity. Management science and computational capacity developments enhance management planning processes by providing the ability to further analyze alternative strategies through the use of mathematical programming or simulation (Chap. 2). Automation provided the means to process huge amounts of data and enabled the use of these more sophisticated techniques. As a result, the potential for the definition of more sound strategic schedules for industrial forests has been increased. Therefore, we now turn our attention to the application of modern techniques introduced in Chap. 2 to address Problem 1.

2.1 Linear and Integer Programming

While many different objective functions can be defined for harvest scheduling models, and even combined in a single, multi-objective model, the two most common objectives are maximizing the discounted net revenues from the forest or minimizing the cost of managing the forest. We will consider the former for illustration purposes as most planning models developed for industrial forest plantations use the discounted net revenues objective function. Moreover, to enhance readability we will list a sub-set of the decision variables when describing each equation.

In the case of our example forest, a model to address sustainability concerns with the supply of volume through both volume and area control may be described by Eqs. 2.1, 2.2, 2.3, 2.4, 2.5, and 2.6 in Chap. 2. The LP formulation of Problem 1 (F1) will thus include (a) an objective function that expresses the management objective of maximizing the forest net present value subject to (b) a set of area constraints to ensure that the area managed in each stand does not exceed the area available, (c) a set of accounting equations to determine the volume harvested in each period, (d) a set of accounting equations to determine the area harvested in each period, (e) a set of volume control constraints, (f) a set of area control constraints and (g) a set of non-negativity constraints.

• (a) Objective function Z. In this abbreviated form it displays the decision variables x _kj, i.e. the area of stand k assigned to prescription j, for stands 1, 2 and 16:

$$ \begin{aligned} MAX \ Z&=5.0{x}_{11}+4.6{x}_{12}+4.2{x}_{13}{+}3.9{x}_{14}{+}3.5{x}_{15}{+}5.2{x}_{21}{+}4.8{x}_{22}{+}4.4{x}_{23}\\ {}& \quad +4.0{x}_{24}+3.6{x}_{25}+\dots +2.9{x}_{161}+2.7{x}_{162}+2.4{x}_{163}+2.3{x}_{164}\end{aligned} $$

(6.2)

(Eq. 2.1 in Chap. 2)

The coefficients of the decision variables c _kj correspond to the net present value per hectare associated with prescription j for stand k. They include the value of the ending inventory. For example the net present value resulting from the assignment of an hectare of stand 1 to its prescription 1 is equal to 5.0 × 10³ €/ha (c ₁₁ ).

This value was computed by adding the discounted return associated to the volume harvested in year 8 of planning period 1 to the value of ending inventory. The former was computed by multiplying the volume harvested – v ₁₁₁ (307.4 m³/ha) in Table 6.2 – by the stumpage price – 15.5 €/m³ – and by the discount factor – ((1/(1 + 0.03)⁷) – and is thus equal to, approximately, 3.9 × 10³ €/ha. The latter was computed assuming a perpetual series of optimal rotations. In the case of stand 1, the optimal rotation is 50 years. Thus the Soil Expectation Value (SEV) (Chap. 5) was computed by first multiplying v ₁₁₁ (30.7 × 10 m³/ha) in Table 6.2) – by the stumpage price – 15.5 €/m³ to get the revenue resulting from selling the stumpage from the second rotation in year 58. This was multiplied by the discount factor ((1/((1 + 0.03)⁵⁰ − 1)) to get the present value of a perpetual series of revenues occurring every 50 years (1.4 × 10³ €/ha). As the initial year of this series corresponds to the 8th year of the planning horizon that value must be discounted further 7 years. The present value of ending inventory is thus estimated as 1.4 × 10³ €/ha times 1/(1 + 0.03)⁷ = 1.1 × 10³ €/ha. In summary, approximately, c ₁₁  = 3.9 + 1.1 = 5.0 × 10³ €/ha (5019.4 €/ha in Table 6.2).

The maximization is subject to

• (b) The set of area constraints stating that the sum of the stand area assigned to each prescription cannot exceed the total stand area (Eq. 2.2 in Chap. 2) (6.3)

$$ \begin{aligned} {}&{x}_{11}+{x}_{12}+{x}_{13}+{x}_{14}+{x}_{15}=31 \\ {}&{x}_{21}+{x}_{22}+{x}_{23}+{x}_{24}+{x}_{25}=29.8 \\ {}&\dots \\ {}&{x}_{161}+{x}_{162}+{x}_{163}+{x}_{164}=30 \end{aligned} $$

(6.3)

• (c) The set of accounting equations to determine the volume harvested in each period H ₁ to H ₄ (Eq. 2.3 in Chap. 2). Each Eq. (6.4) includes all decision variables that involve a harvest in the corresponding period.

$$ \begin{array}{l}30.74{x}_{11}{+}32.00{x}_{21}{+}30.16{x}_{31}{+}32.00{x}_{41}{+}\dots {+}34.25{x}_{81}{+}36.88{x}_{82}{-} H1{=}0 \\ {}33.57{x}_{12}{+}36.14{x}_{13}{+}34.94{x}_{22}{+}37.62{x}_{23}{+}\dots {+}31.63{x}_{111}{+}32.32{x}_{121}{-} H2{=}0\\ {}38.50{x}_{14}{+}40.66{x}_{15}{+}40.08{x}_{24}{+}42.32{x}_{25}{+}\dots {+}32.47{x}_{151}{+}32.00{x}_{161}{-} H3{=}0 \\ {}39.88{x}_{94}{+}42.111{x}_{95}{+}40.08{x}_{104}{+}42.32{x}_{105}{+}{\dots} {+}34.94{x}_{162}{+}37.62{x}_{163}{-} H4{=}0 \end{array} $$

(6.4)

The coefficients of the decision variables v _kjt correspond to the volume harvested per hectare in period t when prescription j is assigned to stand k. For example, as we have just checked, the volume harvested in period 1 from stand 1 if it is assigned to its prescription 1 (v ₁₁₁ ) is equal to 30.7 × 10 m³/ha (Table 6.2).

• (d) The set of accounting equations to determine the area harvested in each period AH ₁ to AH ₄. Each equation (6.5 – analogous to Eq. 2.3 in Chap. 2) includes all decision variables that involve a harvest in the corresponding period.

  $$ \begin{array}{l}{x}_{11}+{x}_{21}+{x}_{31}+{x}_{41}+\dots +{x}_{81}+{x}_{82}- AH1=0\hfill \\ {}{x}_{12}+{x}_{13}+{x}_{22}+{x}_{23}+\dots +{x}_{111}+{x}_{121}- AH2=0\hfill \\ {}{x}_{14}+{x}_{15}+{x}_{24}+{x}_{25}+\dots +{x}_{151}+{x}_{161}- AH3=0\hfill \\ {}{x}_{94}+{x}_{95}+{x}_{104}+{x}_{105}+\dots +{x}_{162}+{x}_{163}- AH4=0\hfill \end{array} $$

  (6.5)

• (e) The set of volume control constraints (6.6 – Eq. 2.4 in Chap. 2). It expresses a policy aiming at non-declining volume flows and at a maximum 10 % increase of volume harvested in consecutive periods.

  $$ \begin{array}{l} H1- H2\le 0\hfill \\ {} H2- H3\le 0\hfill \\ {} H3- H4\le 0\hfill \\ {} H2-1.1 H1\le 0\hfill \\ {} H3-1.1 H2\le 0\hfill \\ {} H4-1.1 H3\le 0\hfill \end{array} $$

  (6.6)

• (f) The set of area control constraints (6.7 - – analogous to Eq. 2.4 in Chap. 2). It expresses a policy aiming at maximum 10 % fluctuations of area harvested in consecutive periods.

  $$ \begin{array}{l} AH2-0.9 AH1\ge 0\hfill \\ {} AH2-1.1 AH1\le 0\hfill \\ {} AH3-0.9 AH2\ge 0\hfill \\ {} AH3-1.1 AH2\le 0\hfill \\ {} AH4-0.9 AH3\ge 0\hfill \\ {} AH4-1.1 AH3\le 0\hfill \end{array} $$

  (6.7)

• (g) The set of non-negativity constraints (6.8 – Eq. 2.6 in Chap. 2).

  $$ {x}_{11},{x}_{12},{x}_{13}\dots, {x}_{164},{x}_{165}\ge 0 $$

  (6.8)

According to the solution by the LP model (Table 6.3), the optimal long-term management plan is associated with an objective function value Z equal to 2,041.3 × 10³ €. It encompasses a periodic harvest of 4,089 × 10 m³. The area harvested ranged from 116.2 to 119.1 ha in periods 4 and 3, respectively. The solution thus demonstrates that the LP model may address efficiently and effectively both volume and area control objectives.

Table 6.3 Solution summaries

The plan proposed by the LP model reflects the stand age distribution. Younger stands are harvested later (Table 6.4) in periods 3 (stand 13) or 4 (stands 14–16). Conversely, older stands are harvested earlier in periods 1 (stands 5–8) or 2 (stands 1–4) in order to avoid opportunity costs associated with the delay of harvesting mature timber. Classical approaches might meet the regulation objectives and yet at a cost that might be higher than needed. The LP plan is efficient as it meets the regulation objectives while minimizing the opportunity costs of doing so.

Table 6.4 Harvest schedule: hectares harvested in each period

Nevertheless the LP solution aims at providing further insight about the forest management planning problem. The distinction made by Geoffrion (1976) between the mathematical programming “ostensible purpose” – optimization of a particular problem, and its “true purpose” – generation of information to support decision making is illuminating. The value of the LP dual variables (shadow prices) conveys the impact of changing the independent term in a constraint in the value of the objective function (Chap. 2). Thus the LP solution may be used to check the impact of setting alternative area and volume control objectives.

The usefulness of this information may be illustrated by analyzing the value of the shadow prices associated to the area constraints (Eq. 6.3). They reflect the marginal value of each stand for the forest owner (Table 6.5). As expected the marginal value of younger stands (stands 13 –16) is lower as they are harvested later in the planning horizon. The highest marginal value of stand 6 is due both to its age and its productivity (Table 6.2). This information provides insight about the value structure of the current inventory as well as about the management planning problem. The forest owner may take advantage further of this information when making decisions on whether and how to expand the forest land base. The LP solution provides an estimate of the maximum amount he might pay when buying an additional hectare of each stand. Conversely, it conveys the minimum price he should consider when selling one hectare of each stand.

Table 6.5 Stand marginal value

The LP solution also provides information about the opportunity costs associated with the selection of alternative plans. The reduced costs of decision variables measure the impact of selecting a non-optimal prescription on the value of the objective function (Chap. 2). For example, the solution highlights the costs of anticipating or delaying the timing of harvests (Table 6.6). It further shows that the option of not harvesting when available (stands 13–16) is associated with the highest costs. These result both from the loss of revenue that results from the harvests in those stands and from the loss of revenue that results from the need of adjusting the timing of harvests in other stands in order to meet the area and volume control targets.

Table 6.6 Prescription reduced cost

However useful, LP is not able to convey the geographical location of forest activities. Yet this may be important even in a long-term planning framework. LP divisibility may lead to solutions where stands are split into non spatially referenced units to be managed differently. For example stand 10 was split into 2 units of 29.4 and 0.1 ha to be managed according to its prescriptions 2 and 4, respectively. Further, computational constraints lead frequently to the aggregation of stands into analysis areas thus compounding the impact of LP divisibility. Solutions to such highly aggregated models are very sensitive to changes in assumptions and aggregation schemes (Rose 1984). In this context, the information produced by the solution may be of little value to understand the management problem and to support effectively decision-making. Formulation F1 may then be changed within a Model I framework to further address concerns with locational specificity. The resulting MIP formulation of Problem 1 (F2) may be described as:

• (a) Objective function Z. In this abbreviated form it displays the decision variables x _kj, i.e. whether stand k is assigned to prescription j, for stands 1, 2, 3 and 16:

  $$ \begin{aligned} {\it MAX}\ Z =\; & 155.6{x}_{11}{+}143.7{x}_{12}{+}131.5{x}_{13}{+}119.3{x}_{14}{+}107.6{x}_{15}{+}155.7{x}_{21}\\ & {+}143.8{x}_{22}{+}131.5{x}_{23}{+}119.4{x}_{24}{+}107.7{x}_{25}{+}152.1{x}_{31}{+}140.5{x}_{32}\\ & {+}128.5{x}_{33} +116.7{x}_{34}+105.2{x}_{35}+\dots +85.9{x}_{161}+79.4{x}_{162}\\ & {+}72.6{x}_{163}+68.5{x}_{164} \raisetag{12pt} \end{aligned} $$

  (6.9)

  (Eq. 2.7 in Chap. 2)

  In this model, the decision variables are integer to ensure that stands are not split by the assignment of prescriptions. Thus the coefficients of the decision variables c _kj correspond to the total net present value associated with prescription j for stand k. Again they include the value of the ending inventory. For example the net present value resulting from the assignment of stand 1 to its prescription 1 (c ₁₁ ) is equal to 155.6 × 10³ €. This is computed by multiplying the net present value per ha that results from this assignment – 5.0 × 10³ €/ha – by the stand area – 31 ha (Table 6.1).

  The maximization is subject to

• (b) The set of area constraints (Eq. 2.8 in Chap. 2) (6.10)

  $$ \begin{array}{l}{x}_{11}+{x}_{12}+{x}_{13}+{x}_{14}+{x}_{15}=1\hfill \\ {}{x}_{21}+{x}_{22}+{x}_{23}+{x}_{24}+{x}_{25}=1\hfill \\ {}{x}_{31}+{x}_{32}+{x}_{33}+{x}_{34}+{x}_{35}=1\hfill \\ {}\dots \hfill \\ {}{x}_{161}+{x}_{162}+{x}_{163}+{x}_{164}=1\hfill \end{array} $$

  (6.10)

• (c) The set of accounting equations to determine the volume harvested in each period H ₁ to H ₄ (Eq. 2.9 in Chap. 2). Each Eq. (6.11) includes all decision variables that involve a harvest in the corresponding period.

  $$ \begin{array}{l}953.0{x}_{11}{+}953.5{x}_{21}{+}931.7{x}_{31}{+}\dots {+}1027.5{x}_{81}{+}1106.4{x}_{82}{-} H1{=}0\\ {}1040.5{x}_{12}{+}1120.4{x}_{13}{+}1041.2{x}_{22}{+}\dots {+}933.2{x}_{91}{+}956.8{x}_{121}{-} H2{=}0\\ {}1193.6{x}_{14}{+}1260.5{x}_{15}{+}1194.3{x}_{24}{+}\dots {+}941.6{x}_{151}{+}950.3{x}_{161}{-} H3{=}0\\ {}1156.5{x}_{94}{+}1221.2{x}_{95}{+}1182.2{x}_{104}{+}\dots {+}1037.6{x}_{162}{+}1117.2{x}_{163}{-} H4{=}0\end{array} $$

  (6.11)

  The coefficients of the decision variables v _kjt correspond to the volume harvested in stand k in period t when assigned to prescription j. For example, the volume harvested in period 1 from stand 1 if it is assigned to its prescription 1 (v ₁₁₁ ) is approximately equal to 953 × 10 m³. This was computed as the product of the stand area (31 ha) by the volume per hectare in period 1 that results from that assignment (307.4 m³/ha (Table 6.2)).

• (d) The set of accounting equations to determine the area harvested in each period AH ₁ to AH ₄ (analogous to Eq. 2.9 in Chap. 2). Each Eq. (6.12) includes all decision variables that involve a harvest in the corresponding period. Its coefficients correspond to the stand area.

  $$ \begin{array}{l}31{x}_{11}+29.8{x}_{21}+30{x}_{31}+\dots +30{x}_{81}+30{x}_{82}- AH1=0\hfill \\ {}31{x}_{12}+31{x}_{13}+29.8{x}_{22}+\dots +29.6{x}_{111}+30.5{x}_{121}- AH2=0\hfill \\ {}31{x}_{14}+31{x}_{15}+29.8{x}_{24}+\dots +29{x}_{151}+29.7{x}_{161}- AH3=0\hfill \\ {}29{x}_{94}+29{x}_{95}+29.5{x}_{104}+\dots +29.7{x}_{162}+29.7{x}_{163}- AH4=0\hfill \end{array} $$

  (6.12)

• (e) and (f) Volume and area control constraints may now be expressed just like in the case of the linear programming model (6.6 – Eq. 2.4 in Chap. 2 and 6.7 – analogous to Eq. 2.4 in Chap. 2).

• (g) The set of constraints stating that the decision variables may take only the values 1 (if the prescription is assigned to the stand) or 0 (if the prescription is not assigned to the stand) (6.13 – Eq. 2.8 in Chap. 2)

  $$ {x}_{11},{x}_{12},{x}_{13},\dots, {x}_{165}\ \mathrm{are}\ \mathrm{binary} $$

  (6.13)

According to the solution by the IP model (Table 6.3), the optimal objective function value Z decreased to 2,021.0 × 10³ €. Stands 2 and 10 are no longer split by different prescriptions (Table 6.4) and this thus cost 20.3 × 10³ €. The harvest timings shifted in the case of three other stands in order to meet the new requirements. The requirement of locational specificity impacted the volumes and areas harvested in each period. They still meet the volume and area control constraints and yet are more uneven as management flexibility decreased (Table 6.3). In the case of larger forests with more stands the requirement of locational specificity may not have an impact as substantial on the evenness of areas and volumes harvested in each period. Yet it may have a higher impact on the computational cost.

Management Planning in Action 6.1: Volume Control in Long Term Industrial Forest Management Planning at Celbi in Portugal

Celbi is currently a factory of Altri, a leading Portuguese eucalypt pulp producer, with a capacity of up to 600 × 10⁶ tonnes (http://en.altri.pt/aboutaltri/). Currently Altri manages about 84 × 10³ ha of forest in Portugal all certified by the Forest Stewardship Council (FSC) and PEFC. Its wood self-sufficiency rate stands around 30 % and all its mills are entirely self-sufficient on power that is produced through the burning of wood components not suitable for pulp production (http://en.altri.pt/aboutaltri/).

In 2000, a priority of former Celbi owners (Stora Enso) was the assessment of the sustainability of pulpwood supply to this mill from its eucalypt land base extending over about 39 × 10³ ha. This prompted the development of a linear programming (LP) model within a sustainability assessment project coordinated by the Forest Research Centre (http://www.isa.ulisboa.pt/cef/). The LP model included about 664 × 10³ decision variables corresponding to prescriptions associated with 3,361 stands in Celbi eucalypt land base. The planning horizon included 31 one-year periods extending up to 2030. The model aimed at maximizing net present value. It included area and volume control constraints similar to the ones presented in 6.2. It further included constraints on the maximum area to be converted each year.

The project was successful as the LP model provided the information needed by the firm – e.g. the pulpwood potential supply ranging from 475 to 535 × 10³ m³, according to scenarios of productivity growth after a conversion as well of expansion of the eucalypt land base – to develop its strategic plan (Borges and Falcão 2000).

2.2 Heuristics

The locational specificity requirement may also be addressed by heuristic approaches. A heuristic may be defined as a technique that seeks good solutions at a reasonable computational cost without being able to guarantee optimality or even feasibility (Reeves 1993). The computational complexity of some industrial forest strategic management planning problems sometimes suggests the use of heuristics as these techniques may be more flexible and capable of addressing more complicated objective functions and constraints than exact algorithms. Moreover, given the uncertainties that derive from the large-scale attributes of the general forest management problem, good solutions may be adequate (Borges et al. 2002). As Gunn and Rai (1987) pointed out, solutions that are near optimal and near feasible may be adequate and even preferable if they can be produced with a greatly reduced solution effort, given the uncertainty about biological, technical and economic data in most forest management problems.

The design of heuristic approaches may often take advantage of the specific form of the forest management scheduling problem. Based on this design, specialized optimization solution processes can sometimes be evolved to address very large and complex problems (Borges et al. 2002). For example, Hoganson and Rose (1984) developed a specialized LP decomposition approach that may be used to solve this management planning problem thus circumventing the need to use MIP to address locational specificity requirements. Just like LP, this heuristic approach conveys information about the marginal values of resources and the volume flow targets thus contributing to the effectiveness of management planning.

The reader is referred to Borges et al. (2002) for a detailed review of the use of heuristics in multiple objective forest management. In this chapter we will consider for illustration purposes a meta-heuristic – simulated annealing (SA) – that has been widely used to address forest management planning problems (e.g. Lockwood and Moore 1993; Dahlin and Sallnas 1993; Murray and Church 1995; Tarp and Helles 1997; Boston and Bettinger 1999; Van Deusen 1999; Falcão and Borges 2002). In this illustration, the simulated annealing approach involved the conversion of the MIP formulation (Eqs. 6.6, 6.7, 6.9, 6.10, 6.11, 6.12, and 6.13) into a new objective (or evaluation) function. The resulting SA formulation of Problem 1 (F3) may be represented in abbreviated form as:

$$ \begin{aligned} {\it MAX}\ Z =\; &155.6{x}_{11}+143.7{x}_{12}+131.5{x}_{13}+119.3{x}_{14}+107.6{x}_{15}+\dots\\ &+85.9{x}_{161}+79.4{x}_{162}+72.6{x}_{163}+68.5{x}_{164}-\theta \raisetag{12pt} \end{aligned} $$

(6.14)

Where θ stands for a global penalty function that decreases the value of Z if the constraints are violated. The literature reports several approaches to design a penalty function (e.g. Michalewicz 1996). In this chapter we will follow the approach proposed by Falcão and Borges (2001) so that the penalty function is more sensitive to large violations of the constraints and less responsive to small deviations. The separable penalty functions thus consisted of parabolas where deviations from the area constraints and the volume and area control objectives do contribute to decrease the value of Z. In all cases it was assumed that a 5 % deviation from feasibility was equivalent to a 1 % deviation from unconstrained NPV when estimating the parameter that characterizes the shape of the parabola for each constraint. Thus this parameter was computed as

$$ {\displaystyle {A}_{{\it const}{\hbox{\_}} j}}=\Delta NPV/{\left(\Delta {\displaystyle {D}_{{\it const}\hbox{\_} j}}\right)}^2 $$

(6.15)

Where ΔNPV stands for an unconstrained NPV reduction of 1 % and ΔD _{const _ j} stands for a 5 % deviation from feasibility in constraint j. A _{const _ j} is equal to zero if constraint j is met. In the case of our example problem, the penalty function will thus include three terms, one per Eqs. 6.6, 6.7 and 6.10. θ may thus be described in an abbreviated form as

$$ \begin{aligned}\theta &\,{=}\,{A}_{{\it const}\hbox{\_}6\hbox{\_}10}\!\left[\!{\left({x}_{11}{+}{x}_{12}{+}{x}_{13}{+}{x}_{14}{+}{x}_{15}{-}1\right)}^2{+}{\dots} {+}{\left({x}_{161}{+}{x}_{162}{+}{x}_{163}{+}{x}_{164}{-}1\right)}^2\!\right] \\ &+{A}_{{\it const}\hbox{\_}6\hbox{\_}6}\left[{\left({H}_1\hbox{--} {H}_2\right)}^2{+}\dots {+}{\left({H}_3\hbox{--} {H}_4\right)}^2{+}{\left({H}_2\hbox{--} 1.1{H}_1\right)}^2{+}\dots {+}{\left({H}_4\hbox{--} 1.1{H}_3\right)}^2\right]\\ &+{A}_{{\it const}\hbox{\_}6\hbox{\_}7}\left[{\left(0.9 A{H}_1\hbox{--} A{H}_2\right)}^2{+}\dots {+}{\left(0.9 A{H}_3\hbox{--} \mathrm{A}{H}_4\right)}^2{+}{\left( A{H}_2\hbox{--} 1.1\mathrm{A}{H}_1\right)}^2{+}\dots \right. \\ & \left. + {\left( A{H}_4\hbox{--} 1.1\mathrm{A}{H}_3\right)}^2\right] \raisetag{17pt} \end{aligned} $$

(6.16)

with x ₁₁, x ₁₂, x ₁₃, …, x ₁₆₅ as binary

In summary, the SA objective (or evaluation) function thus included as its first term the MIP objective function and as its second term a penalty function. The latter penalizes the violation of the area constraints (the first term in Eq. 6.16), of the volume control constraints (the second term in Eq. 6.16) and of the area control constraints (the third term in Eq. 6.16).

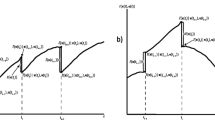
Afterwards, the SA approach involved an iterative process (Fig. 6.2) where solutions in each iteration were represented by a vector with 16 elements corresponding to the 16 stands. The value of each vector element consisted of a pointer to the prescription assigned to the corresponding stand. Solutions are thus integer.

Fig. 6.2

Flowchart of the simulated annealing heuristic. Z1 and Z2 solution values before and after a proposed move, T system “temperature”, rand random number between 0 and 1 (From Borges et al. 2002)

The solution process started by selecting randomly a solution vector and by computing its objective function value (Fig. 6.2). Each SA iteration consisted of changing randomly the assignment of a prescription in 5 stands (5-opt approach) and computing its objective function value Z2. In order to avoid premature convergence to a local optimum, an inferior solution i.e. a solution associated with a lower objective function value might be accepted.

The SA solution strategy was implemented as described by Borges et al. (2002). It involved the design of a solution acceptance function and the definition of a stopping criterion. The former determined whether an inferior solution might be accepted. The probability of accepting inferior solutions increased with the temperature and it decreased with the magnitude of the inferior move (Fig. 6.2):

$$ \exp \left[\left({\displaystyle {Z}_1}-{\displaystyle {Z}_2}\right)/ T\right]> rand $$

(6.17)

where exp stands for the exponential function, Z ₂ and Z ₁ stand for the value of the SA objective (fitness evaluation) function (Eq. 6.14) after and before the 5-opt move, respectively, T stands for the control parameter (temperature) which decreases with the number of iterations according to the cooling schedule and rand stands for a random number in the interval [0 1]. In this example, the initial temperature was equal to 100,000. The temperature was decreased in each iteration according to a cooling rate equal to 0.9999. The stopping criteria was the number of iterations (100,000).

Meta-heuristic solutions are sensitive to parameter and penalty values. Typically these are problem specific and require pre-testing so that values are selected that may lead to approximate the optimal solutions. In this illustration, the parameterization did lead to the optimal MIP solution (2021.1 × 10³ €) (Table 6.3). This is also a consequence of the problem small size.

2.3 Goal Programming and Pareto Frontier

Both LP and MIP have single criteria objective functions. Other objectives e.g. area and volume control were represented as constraints in the model. An alternative to this approach is to consider all criteria in the objective function. Goal programming is a technique that has been widely used for that purpose in strategic forest management planning. In the case of our example forest, the goal programming formulation of Problem 1 (F4) may be described as:

• (a) Objective function Z

  $$ \begin{aligned}[b] \mathrm{Min}\ \mathrm{Z}&=8.4746\ {\it PdevAH1}+8.4746\ {\it NdevAH1}+8.4746\ {\it PdevAH2} \\ {}& \quad +8.4746\ {\it NdevAH2}+ 8.4746\ {\it PdevAH3}+8.4746\ {\it NdevAH3} \\ {}& \quad +8.4746\ {\it PdevAH4}+8.4746\ {\it NdevAH4} +0.0244\ {\it NdevH1} \\ {}& \quad +0.0244\ {\it NdevH2}+0.0244\ {\it NdevH3}+0.0244\ {\it NdevH4} \\ {}& \quad +0.0049\ {\it NdevNPVt} \raisetag{12pt} \end{aligned} $$

  (6.18)

  Where the decision variables consist of the deviations from the levels of the criteria set by the decision-maker. The variables PdevAH1 to PdevAH4 and NdevAH1 to NdevAH4 represent, respectively, the positive and the negative deviations from the target set to the area harvested in each planning period to reflect the area control regulation objectives. The variables NdevH1 to NdevH4 correspond to the deviations from the harvest levels targeted in each period. It was assumed that there was no constraint to harvesting higher volumes in each period and thus positive deviations were not minimized. Finally, the third criteria corresponds to the discounted net revenue from the forest e.g. the criteria listed in the LP and the MIP objective functions. The coefficients of the decision variables correspond to the product of 1,000 by the inverse of the criteria target levels measured in hectares, cubic meters and Euros, in the case of the area harvested, the volume harvested and the discounted revenues, respectively. The GP model was set to minimize the percent deviations to overcome dimensional constraints to the treatment of all three criteria. The discounted revenues criteria was provided with a weight equal to 10 while the remaining two were weighted equally as 1. For example, in the case of NdevNPVt the coefficient is computed as 10*1,000*1/2,041,298 = 0.0049 while in the case of PdevAH1 the coefficient is computed as 1*1,000*1/118 = 8.4746.

• (b) The equation that computes the discounted net revenue from the forest

  $$ \begin{aligned} {}& \Big(155.6{x}_{11}+143.7{x}_{12}+131.5{x}_{13}+119.3{x}_{14}+107.6{x}_{15}+155.7{x}_{21} \\ {}& \quad +143.8{x}_{22}+131.5{x}_{23}+119.4{x}_{24}+ 107.7{x}_{25}+152.1{x}_{31}+140.5{x}_{32}\\ {}& \quad +128.5{x}_{33} +116.7{x}_{34}+105.2{x}_{35}+\dots 85.9{x}_{161}+79.4{x}_{162}+ 72.6{x}_{163}\\ {}& \quad +70.2{x}_{164}\Big) \times {10}^3- NPVt=0 \raisetag{12pt} \end{aligned} $$

  (6.19)

• (c) The Eq. 6.20 that set the target for the area harvested in each period (118 ha) to reflect the area control objectives, where this area is defined by Eq. 6.12

  $$ \begin{array}{l} AH1- PdevAH1+ NdevAH1=118\hfill \\ {} AH2- PdevAH2+ NdevAH2=118\hfill \\ {} AH3- PdevAH3+ NdevAH3=118\hfill \\ {} AH4- PdevAH4+ NdevAH4=118\hfill \end{array} $$

  (6.20)

• (d) The Eq. (6.21) that set the target for the volume harvested in each period (41 × 10³ m³) to reflect the volume control objectives, where this harvest level is defined by Eq. 6.11.

  $$ \begin{array}{l} H1- PdevH1+ NdevH1=4100\hfill \\ {} H2- PdevH2+ NdevH2=4100\hfill \\ {} H3- PdevH3+ NdevH3=4100\hfill \\ {} H4- PdevH4+ NdevH4=4100\hfill \end{array} $$

  (6.21)

• (e) The Eq. 6.22 that sets the target for the discounted net revenue from the forest (2,041,298 €).

  $$ {\it NPVt} - {\it PDevNPVt} + {\it NDevNPVt} =2,041.3 $$

  (6.22)

• (f) The set of constraints stating that the decision variables may take only the values 1 (if the prescription is assigned to the stand) or 0 (if the prescription is not assigned to the stand) (Eq. 6.13)

  $$ {x}_{11},{x}_{12},{x}_{13},\dots, {x}_{165}\ \mathrm{are}\ \mathrm{binary} $$

In this illustration, the target values were set to emulate the area and volume control objectives and took advantage of the insights provided by the solutions by the other techniques. For example, the target for the criteria NPV was set as the value of the optimal LP solution. Generally, the targets are set based on a priori knowledge about the criteria space e.g. about the productive potential of the industrial forest.

The solution by the GP model (Table 6.3) shows that the NPV criteria target was almost achieved (2,040,967.45 €) while still guaranteeing that no stand was assigned to more than one prescription (Table 6.4). Yet this was at the cost of deviations from other targets. The MIP solution did point out that in order to meet the volume and area control objectives, while ensuring locational specificity of management options, the maximum net returns from the forest were equal to 2,021,000 €. For example, in the GP model the harvest levels in periods 1 and 2 did not meet the 41 × 10³ m³ targets. Further, there was a decline in harvest levels in periods 3 and 4.

This solution highlighted that often decision-makers lack the a priori knowledge about the productive potential of the industrial forest that is needed to specify coherent targets. It showed that setting a higher target level for the NPV criteria led to the underachievement of criteria emulating the area and volume control objectives. In fact, the information regarding the long-term impact of forest management options on objectives and conditions of interest is hardly ever perfect. The efficiency and the effectiveness of a multiple criteria approach to industrial forest strategic management planning calls for the use of models and methods as learning devices. The quality of decisions may be enhanced by a learning process that may provide additional insights about the resource capability model and the trade-offs between objectives (Borges et al. 2014a).

Most multiple criteria approaches reported in the forestry literature typically require the decision-maker to either specify the desired level of achievement or specify the preferences for the various objectives (Martins and Borges 2007). As often there is little information about what is possible to achieve (e.g. volume flows), defining a priori the goals and preferences may not be realistic and lead to poor management decisions (Tóth et al. 2006). Shortcomings of mechanistic approaches to the specification of the levels of achievement of various objectives as well as of the decision-makers preferences have been pointed out by Tóth and McDill (2009) and Romero (2004). In order to overcome them, Tóth and McDill (2009) demonstrated the possibility of developing and displaying a Pareto frontier e.g. of finding the non-dominated points in the feasible set in the criteria space (FSCS) in the case of problems with up to three forest management planning objectives. Romero (2004) discussed the use of several achievement functions and corresponding assumptions regarding decision-makers preferences.

Providing information about the set of efficient solutions can help the decision-maker understand the trade-offs between competing objectives. The analysis of these trade-offs may provide further insight about the forest management planning problem and help set adequate levels of achievement for various objectives (Borges et al. 2014a). In this section, we will apply an interactive modelling approach to generate the Pareto frontier of our industrial forest strategic management planning problem (Problem 1). The approach builds from the LP formulation of Problem 1 to display the trade-offs between discounted returns (NPV) and timber volume harvested (Fig. 6.3). The reader is referred to Borges et al. (2014a) for a detailed description of the modelling approach.

Fig. 6.3

Decision map showing the Edgeworth-Pareto Hull for a two criteria planning problem – NPV and Timber – subject to volume and area control constraints, considering minimum achievement levels min NPV = 1,700 × 10³ € and min Timber = 162 × 10³ m³. Point A corresponds to the point in the Pareto frontier with NPV = 2,012.4 × 10³ € and Timber = 166.9 × 10³ m³

This trade-off information helps decision-makers set informed levels of achievement that reflect their preferences. It shows that harvesting over about 163 × 10³ m³ leads to a decrease of NPV. The LP solution did indeed highlight that it was not profitable to harvest more timber while meeting the volume and area control objectives. For illustration purposes lets assume that the decision-maker took advantage of this information to set as levels of achievement NPV = 2,012,415.5 € and Timber = 166,914.5 m³ (Point A in Fig. 6.3). The modeling approach may then be used to retrieve the corresponding LP solution in the feasible set in the decision space (Table 6.3). The solution highlights that the timber volume increase results from higher harvest levels in periods 3 and 4 at the cost of lower harvest values in earlier periods (Table 6.3). Harvesting later stands 9 and 14 (Table 6.4) leads to higher volumes yet this timber was financially mature earlier. As a consequence the value of NPV decreases.

2.4 Binary Search

Simulation is a technique that has also been widely used to address volume and area control objectives. In summary, binary search starts by setting the harvest level deemed as sustainable and by ordering the forest stands according to the priority for harvesting or harvest rule (Fig. 6.4).

Fig. 6.4

Flowchart of simulation approach

The simulation approach proceeds by going down the list of ordered stands and harvesting them until the harvest level is met. Afterwards it projects the inventory to the next planning period. In this step, simulation parameters such as the area burned or new forest areas to include may be used to update the inventory. The stands are again ordered according to the harvest rule and this process is iterated successively to check whether the target volume level is sustainable or not. If, for example it finds that the initial level was too high, the estimate is decreased while if the inventory becomes too high the estimate is increased.

For illustration purposes, lets assume that the target level is set at 40,865 m³ (the volume in the LP solution) and that stands are ordered according to the age. Results from the simulation approach show that the average age of the forest decreases over time from 43.7 years in the current inventory to 13.2 years in the inventory in period 7 when that harvest level may no longer be met. This suggests that the length of the planning horizon considered in Formulations 1–4 may have been too short. The harvest levels are not sustainable over longer periods. The simulation of other harvest levels help estimate the long term sustainable yield (Fig. 6.5).

Fig. 6.5

Average stand age in the example forest as a function of periodic harvest levels

Management Planning in Action 6.2: Assessing the Sustainability of National Pulpwood Supply: An Application in Portugal

Eucalypt (Eucalyptus globulus Labill) is the most important pulpwood producing species in Portugal. Eucalypt plantations extend over 647 × 10³ ha – about 20.6 % of the total forest area in Portugal with a total yield of about 5.75 × 10⁶ m3 per year. Nevertheless the land base owned or managed by vertically integrated pulp and paper companies provides at most 30 % of its pulpwood needs. In 2004 a priority of CELPA (http://www.celpa.pt), the Portuguese pulp and paper association, was the assessment of the sustainability of pulpwood supply from areas not owned or managed by the industry.

This prompted the development of a simulation approach similar to the one presented in 6.2 by the Large-Scale Informatics Systems Laboratory (http://lasige.di.fc.ul.pt/) and the Forest Research Centre (http://www.isa.ulisboa.pt/cef/). The eucalypt area not owned or managed by the industry was classified into analysis areas according to criteria such as age, coppice cycle, site index and location. Analysis areas were ranked for harvesting according to a weighted average of age, location and quadratic mean diameter. Simulation parameters included the probabilities of wildfire occurrence, of conversion i.e. of a clearcut and of abandonment. The possibility of expansion of the eucalypt area was also considered (Falcão 2006). This approach is being used by CELPA since 2004.

The mathematical programming and the simulated annealing approaches to address volume and area control in long term industrial forest management planning considered the objective of maximizing net present value. However, it is worthwhile to briefly note how the choice of objective function can influence the “personality” of the resultant model and the implications for how key constraints should be formulated. In a nutshell, the cost minimization model tends to be “lazy” and the profit maximization model tends to be “greedy.”

In the case of the cost minimization model, the production constraints such as volume constraints must be specified as minimum targets (i.e., greater-than-or-equal-to constraints) or the optimal solution will be to produce nothing. This can be the most appropriate model when the plantation is owned by a vertically-integrated company that requires the forest to produce a certain volume of wood each year to meet the production requirements of a mill. In such models, a key concern may be the feasibility of meeting other constraints – such as sustainability or environmental constraints – while meeting the needs of the mill. Another possibility is that the mill requirements can be met too easily, and the forest is underutilized, which should make it easy to meet sustainability and environmental constraints but may not be in the best interest of the company.

With profit-maximization models, it is generally best to let the model determine the profit-maximizing level of production over time, but to add constraints that prevent the outputs (or inputs) of some products from fluctuating too wildly from one period to the next as illustrated in this section. If the model projects more production than is required by the mill this excess can potentially be sold to other companies, and if the projected production is less than is required, the company can either buy wood on the open market, buy more forestland, or develop more intensive management prescriptions that will produce higher yields.

Unless specifically required to by model constraints, profit maximization models often will not meet sustainability and environmental constraints. In particular, with a finite planning horizon, a profit-maximizing model will tend to harvest anything it can before the end of the planning horizon. This was highlighted by the binary approach to solve Problem 1. This is usually not a desirable outcome, so some kind of ending constraints must usually be imposed on profit-maximizing harvest scheduling models. As with any other aspect of harvest scheduling models, there are many ways to ensure that the model leaves the forest in a desirable condition at the end of the planning horizon. Furthermore, more than one approach can be incorporated into a model. One approach is to require the model to achieve a specific age-class distribution – such as a regulated forest – at the end of the planning horizon. While this approach may be useful in some circumstances, there are two disadvantages of this approach. First, if the planning horizon is not long enough it may not be possible to achieve the desired age-class distribution within that time frame and the model will be infeasible. Second, even if it is feasible, these constraints will tend to drive much of what the model does, especially in the final periods, and it leaves the model with very little flexibility to achieve any other management objectives. Three more promising ways to ensure that the model will leave the forest in a desirable ending condition are (1) to include a value of the ending forest in the objective function coefficients as in our case study, (2) to require the average age of the forest as a whole at the end of the planning horizon to be greater than or equal to some target, or (3) to require the total forest inventory at the end of the planning horizon to be greater than or equal to some target, as illustrated in the next section.

3 Long-Term Industrial Forest Management Planning to Address Both Multiple Product and Stock Control Objectives (Problem 2)

The focus of strategic management planning is on the assessment of the long-term sustainability of the industrial forest resource base. The implementation of volume and area control policies targets the provision of even or non-declining product flows from the industrial forest over the planning horizon. The solution of Problem 1 by several techniques (Sect. 6.2) did demonstrate the success of those policies. Nevertheless it highlighted that those policies, in particular if framed by revenue maximization objectives, do not guarantee the long-term sustainability of the industrial forest. Thus, Problem 1 was modified to address concerns with that sustainability. Specifically, for illustration purposes, the policy model was extended to include a condition on the value of the inventory at the end of the planning horizon.

Climate change concerns have led society and forest managers to focus on the potential of forests as carbon sinks. Accordingly, since 2000, carbon has emerged as an important product of industrial plantations (Chap. 14). The scale and scope of the carbon market has since expanded. Therefore it is increasingly important to assess the sustainability of carbon stock targets in strategic industrial forest management planning. The policy model of Problem 1 was thus further expanded to include conditions on the fluctuations of the carbon stock in the industrial forest.

In this section we will illustrate how to build mathematical programming models and how to design heuristic approaches to address jointly revenue optimization, area and volume control objectives as well as stock control concerns. The introduction of the new policy scenario defines our strategic management planning Problem 2. We will further interpret the solution of the new problem and assess the impact of constraints on the value of the ending inventory and on the average carbon stock on the harvest schedule and on the timber supply. Finally, we will illustrate how to assess the potential of specific solution techniques to address Problem 2.

3.1 Linear and Integer Programming

In the case of our example forest, the LP formulation of Problem 1 (F1) may be extended to represent Problem 2 (Formulation 5) by including (a) an accounting equation to compute the volume of the ending inventory, (b) a set of accounting equations to determine the average carbon stock in each planning period, (c) a constraint on the value of the ending inventory and (d) a set of constraints on the average carbon stock over the planning horizon.

• (a) The accounting equation to compute the volume of the ending inventory. In this abbreviated form, it displays the decision variables x _kj, i.e. the area of stand k assigned to prescription j, for stands 1, 2 and 16:

  $$ \begin{aligned} {}& 18.2{x}_{11}+14.0{x}_{12}+9.7{x}_{13}+5.4{x}_{14}+2.1{x}_{15}+18.9{x}_{21}{+}14.6{x}_{22}{+}10.1{x}_{23}\\ {}& \quad +5.7{x}_{24}+2.1{x}_{25}+\dots +2.2{x}_{161}+0.2{x}_{162}+38.6{x}_{164}- VolEI=0\end{aligned} $$

  (6.23)

  Where VolEI represents the volume of standing timber in the whole forest at the end of the planning horizon. The coefficients of the decision variables VolEI _kj correspond to the volume per hectare in the ending inventory in stand k if it is managed according to prescription j. For example, if one hectare of stand 1 is managed according to prescription 1, the value of the ending inventory in that hectare will be VolEI ₁₁ = 18.2 × 10³ m³ (Table 6.2).

• (b) The set of accounting equations to determine the average carbon stock in each planning period (Eq. 6.24):

  $$ \begin{aligned} {}& 6.1{x}_{11}+9.0{x}_{12}+9.0{x}_{13}+9.0{x}_{14}+9.0{x}_{15}+6.4{x}_{21}+9.4{x}_{22}+9.4{x}_{23}\\ {}& \quad +9.4{x}_{24}+9.4{x}_{25}+\dots {+}4.9{x}_{161}{+}4.9{x}_{162}{+}4.9{x}_{163}{+}4.9{x}_{164}{-} {\it CStock1} \\ {}& 23.6{x}_{11}+20.1{x}_{12}+7.2{x}_{13}+10.6{x}_{14}+10.6{x}_{15}+2.5{x}_{21}{+}21.0{x}_{22}{+}7.6{x}_{23}\\ {}& \quad +11.0{x}_{24}{+}11.0{x}_{25}+\dots {+}7.4{x}_{161}{+}7.4{x}_{162}{+}7.4{x}_{163}{+}7.4{x}_{164}- {\it CStock2} \\ {}& 20.5{x}_{11}+9.2{x}_{12}+23.6{x}_{13}+22.9{x}_{14}+8.2{x}_{15}+21.4{x}_{21}+9.6{x}_{22}{+}2.5{x}_{23}\\ {}& \quad +23.8{x}_{24}+8.5{x}_{25}+\dots {+}6.4{x}_{161}{+}9.4{x}_{162}{+}9.4{x}_{163}{+}9.4{x}_{164}{-} {\it CStock3} \\ {}& 4.7{x}_{11}+3.4{x}_{12}+20.5{x}_{13}+9.2{x}_{14}+23.6{x}_{15}+4.9{x}_{21}+3.5{x}_{22}+21.4{x}_{23}\\ {}& \quad +9.6{x}_{24}{+}2.4{x}_{25}{+}\dots {+}24.5{x}_{161}{+}20.9{x}_{162}{+}7.5{x}_{163}{+}11.0{x}_{164}{-} {\it CStock4} \end{aligned} $$

  (6.24)

  Where CStockt represents the average carbon stock in our example forest in period t. The coefficients of the decision variables CS _kjt correspond to the average carbon stock in period t in an hectare of stand k when managed according to prescription j. For example, if one hectare of stand 1 is managed according to prescription 1, the value of the average carbon stock in period 1 in that hectare will be CS ₁₁₁ = 6.2 × 10 Mg C (Table 6.2).

• (c) The constraint on the value of the ending inventory (Eq. 6.25)

  $$ VolEI\ge 5,500 $$

  (6.25)

  It is thus assumed that sustainability concerns may be addressed by setting the volume of the ending inventory criteria as 55,000 m³.

• (d) The set of constraints on the average carbon stock over the planning horizon (Eq. 6.26).

  $$ \begin{array}{l}0.9 CStock1- CStock2\le 0\hfill \\ {}0.9 CStock2- CStock3\le 0\hfill \\ {}0.9 CStock3- CStock4\le 0\hfill \\ {} CStock2-1.1 CStock1\le 0\hfill \\ {} CStock3-1.1 CStock2\le 0\hfill \\ {} CStock4-1.1 CStock3\le 0\hfill \end{array} $$

  (6.26)

  No fluctuations over 10 % are thus allowed between the average carbon stocks in two consecutive periods.

According to the solution by the LP model (Table 6.3), the optimal long-term management plan is associated with an objective function value Z equal to 1,937.7 × 10³ €. It encompasses a periodic harvest of 4,020.2 × 10 m³. The area harvested ranged from 106.8 to 116.6 ha in periods 4 and 1, respectively. The average carbon stock decreased from 2,799.1 × 10 Mg C in period 1 to 2,040.6 × 10 Mg C in period 4. The solution thus demonstrates that the LP model may address too efficiently and effectively both volume and area control regulation objectives as well as concerns with stock control and the sustainability of the resource.

The LP solutions to Problems 1 and 2 also provide information about the opportunity cost associated with the new policy scenario. In fact, the NPV as measured by the objective function decreased by 5 % while the period harvest levels decreased by about 690 m³. The constraint on the volume at the ending inventory is active and harvest levels must be lowered in order to meet the 55,000 m³ target. The average carbon stock is always higher than in the solution to F1 yet it decreases substantially over time. This suggests that the current harvest levels may still not be sustainable and that the target for the volume of ending inventory may need to be adjusted. In fact, the simulation approach described in Sect. 6.2.4 did highlight that the 4,020.2 × 10 m³ harvest level is not sustainable in the long term.

The plan proposed by the LP model reflects again the stand age distribution. Younger stands are proposed to be harvested later than in the case of F1 in periods 3 or 4 or are proposed not be harvested in order to meet the ending inventory constraint (Table 6.4). Conversely, just like in the case of F1, older stands are harvested earlier in periods 1 (stands 5–8) or 2 (stands 1–4) in order to avoid opportunity costs associated with the delay of harvesting mature timber. Nevertheless, some additional stands were split into more than one prescription in order to meet the stock control constraints.

The value of the shadow prices associated to the area constraints (Eq. 6.3) shows that in general the marginal value of each stand for the forest owner is higher in the case of F5 (Table 6.5). As expected the marginal value of younger stands (Stands 13–16) increases the most as they are instrumental to meet the stock control objectives. An additional hectare of one of these stands contributes directly to the net present value through the revenues resulting from its harvest. It contributes further indirectly to the net present value by relaxing the need to shift the harvest of older stands to later periods. Stand 6 is still the stand with the highest marginal value due both to its age and its productivity (Table 6.2). Nevertheless its value decreased as its harvest forces costly shifts of harvest timings in other stands. The LP solution thus adjusted the estimates of the maximum amount the forest owner might pay when buying an additional hectare of each stand when stock control objectives are considered. It further provided updated information about the opportunity costs associated with the selection of alternative plans e.g. the costs of anticipating or delaying the timing of harvests in each stand (Table 6.6). In particular it highlights the opportunity costs associated with the anticipation of harvest in older stands. These result from the loss of revenue that results from the need of adjusting the timing of harvests in other stands in order to regulate the harvest schedule and to meet the stock control objectives.

The strategic targets may turn out to be infeasible because of tactical and operational considerations that were left out from Problem 2. Feasible strategic targets may be approximated by enforcing locational specificity constraints. This may be even more critical in the case of Problem 2 as more stands had to be split between prescriptions to comply with the new policy scenario. It may thus be interesting to modify F5 within a Model I framework to further address concerns with locational specificity. The resulting MIP formulation of Problem 2 (F6) is an extended version of the MIP Formulation of Problem 1 (F2) to include further (a) an accounting equation to compute the volume of the ending inventory, (b) a set of accounting equations to determine the average carbon stock in each planning period, (c) a constraint on the value of the ending inventory and (d) a set of constraints on the average carbon stock over the planning horizon:

• (a) The accounting equation to compute the volume of the ending inventory. In this abbreviated form, it displays the decision variables x _kj, i.e. whether stand k is assigned to prescription j, for stands 1, 2 and 16:

  $$ \begin{aligned} {}& 563.6{x}_{11}{+}434.1{x}_{12}{+}299.6{x}_{13}+168.3{x}_{14}{+}64.1{x}_{15}+563.8{x}_{21}{+}434.4{x}_{22}\\ {}& \quad +299.7{x}_{23} +168.4{x}_{24}+64.1{x}_{25}+\dots +63.9{x}_{161}+7{x}_{162}+1147.2{x}_{164}\\ {}& \quad - {\it Vol\ EI}{=}0 \raisetag{12pt} \end{aligned} $$

  (6.27)

  The coefficients of the decision variables VolEI _kj correspond now to the volume in the ending inventory in stand k if it is managed according to prescription j. For example, if stand 1 is managed according to prescription 1, the value of the ending inventory in that stand will be VolEI ₁₁ = 563.3 × 10³ m³. This was computed as the product of the stand area (31 ha) by the volume per hectare at the end of the planning horizon that results from this assignment (18.2 × 10³ m³ (Table 6.2)).

• (b) The set of accounting equations to determine the average carbon stock in each planning period (Eq. 6.28):

  $$ \begin{aligned} {}& 190.1{x}_{11}{+}279.5{x}_{12}{+}279.5{x}_{13}{+}279.5{x}_{14}{+}279.5{x}_{15}{+}190.2{x}_{21}{+}279.6{x}_{22}\\ & \quad +279.6{x}_{23}{+}279.6{x}_{24}{+}279.6{x}_{25}{+}\dots {+}145.9{x}_{161}{+}145.9{x}_{162}{+}145.9{x}_{163}\\ & \quad +145.9{x}_{164}- {\it CStock1} \\ {}& 73.2{x}_{11}+62.5{x}_{12}+225.1{x}_{13}+328{x}_{14}+328{x}_{15}+73.2{x}_{21}+624.8{x}_{22}\\ & \quad +225.2{x}_{23}{+}328.2{x}_{24}{+}328.2{x}_{25}{+}\dots {+}216.9{x}_{152}{+}216.9{x}_{153}{+}216.9{x}_{154}\\ & \quad +219{x}_{161}+219{x}_{162}+219{x}_{163}+219{x}_{164}- {\it CStock2}\\ {}& 637.5{x}_{11}+286.2{x}_{12}+732{x}_{13}+710.3{x}_{14}+253.6{x}_{15}{+}637.8{x}_{21}{+}286.4{x}_{22}\\ & \quad +73.2{x}_{23}+710.6{x}_{24}{+}253.8{x}_{25}{+}\dots {+}189.5{x}_{161}{+}278.7{x}_{162}{+}278.7{x}_{163}\\ & \quad +278.7{x}_{164}- {\it CStock3} \\ {}& 146.3{x}_{11}+105.2{x}_{12}+637.58{x}_{13}{+}286.3{x}_{14}{+}732{x}_{15}{+}146.4{x}_{21}{+}105.2{x}_{22}\\ & \quad +637.8{x}_{23}+286.4{x}_{24}{+}73.2{x}_{25}{+}\dots {+}729.9{x}_{161}{+}622.7{x}_{162}{+}224.4{x}_{163}\\ & \quad +327.1{x}_{164}- {\it CStock4} \raisetag{12pt} \end{aligned} $$

  (6.28)

  The coefficients of the decision variables CS _kjt correspond now to the average carbon stock in period t in stand k when managed according to prescription j. For example, if one hectare of stand 1 is managed according to prescription 1, the value of the average carbon stock in period 1 in that stand will be CS ₁₁₁ = 190.1 × 10 Mg C. This was computed as the product of the stand area (31 ha) by the average carbon per hectare in stand 1 that results from this (6.2 × 10 Mg C (Table 6.2)).

• (c) and (d) The constraints on the value of the ending inventory and on the average carbon stock may now be expressed just like in the case of the LP model F5 (Eqs. 6.25 and 6.26, respectively)

According to the solution by the IP model (Table 6.3), the optimal objective function value Z decreased to 1,867.1 × 10³ €. No stands are split between different prescriptions (Table 6.4) and this thus cost 106.6 × 10³ €. The requirement of locational specificity in Problem 2 is thus five times more expensive than in Problem 1. The model proposed to delay the harvest of most stands. It further proposed a no harvest prescription in the case of the younger stands (stands 13–16). The stock control objectives when combined with the requirement of locational specificity thus did impact substantially the volumes and areas harvested in each period, which are considerably lower. The average carbon stock is thus higher. Moreover, the lack of management flexibility lead to a harvest plan that left a volume at the ending of the planning horizon that is much higher than required (83,355 m³). Again, in the case of larger forests with more stands the requirement of locational specificity may not have an impact as substantial on the adjustment of harvest plans and on the criteria levels. Yet it may have an even higher impact on the computational cost.

3.2 Heuristics

The locational specificity requirement in Problem 2 may also be addressed by heuristic approaches such as simulated annealing (SA). In the case of our example forest, the SA approach involved the extension of the SA formulation for Problem 1 (F3) to address the new policy scenario. In summary, the SA formulation for Problem 2 (F7) takes the objective (evaluation) function of F3 (Eq. 6.14) and modifies its penalty function to include two further terms that penalize deviations from the target volume at the end of the planning horizon and from the average carbon stock constraints. In both cases, it was assumed that a 5 % deviation from feasibility was equivalent to a 1 % deviation from unconstrained NPV when estimating the parameter that characterizes the shape of the parabola for each of these two constraints. The penalty function may thus be represented in abbreviated form as:

$$ \begin{aligned} {}\theta&{\,=\,}{A}_{{\it const}\hbox{\_}6\hbox{\_}10}\!\left[\!{\left({x}_{11}{+}{x}_{12}{+}{x}_{13}{+}{x}_{14}{+}{x}_{15}{-}1\right)}^2{+}{\dots} {+}{\left({x}_{161}{+}{x}_{162}{+}{x}_{163}{+}{x}_{164}{-}1\!\right)}^2\!\right]\\ & +{A}_{{\it const}\hbox{\_}6\hbox{\_}6}\left[{\left({H}_1\hbox{--} {H}_2\right)}^2{+}{\dots} {+}{\left({H}_3\hbox{--} {H}_4\right)}^2{+}{\left({H}_2\hbox{--} 1.1{H}_1\right)}^2{+}\dots {+}{\left({H}_4\hbox{--} 1.1{H}_3\right)}^2\right] \\ {} & +{A}_{{\it const}\hbox{\_}6\hbox{\_}7}\left[{\left(.9 A{H}_1\hbox{--} A{H}_2\right)}^2+\dots +{\left(.9 A{H}_3\hbox{--} \mathrm{A}{H}_4\right)}^2+{\left( A{H}_2\hbox{--} 1.1\mathrm{A}{H}_1\right)}^2+\dots \right. \\ & +\left. {\left( A{H}_4\hbox{--} 1.1\mathrm{A}{H}_3\right)}^2\right] +{A}_{{\it const}\hbox{\_}6\hbox{\_}21}{\left( VolEI-5500\right)}^2\hfill \\ {} & +{A}_{{\it const}\hbox{\_}6\hbox{\_}22}\left[{\left(.9 CStoc{k}_1\hbox{--} CStoc{k}_2\right)}^2+\dots +{\left(.9 CStoc{k}_3\hbox{--} CStoc{k}_4\right)}^2 \right. \\ & +\left. {\left( CStoc{k}_2\hbox{--} 1.1 CStoc{k}_1\right)}^2+\dots +{\left( CStoc{k}_4\hbox{--} 1.1 CStoc{k}_3\right)}^2\right] \raisetag{12pt} \end{aligned} $$

(6.29)

Afterwards, the SA approach involved an iterative process identical to the process described in Sect. 6.2.2 (Fig. 6.2) where solutions in each iteration were represented by a vector with 16 elements corresponding to the 16 stands. Penalties and heuristic parameters were the same as in the case of Problem 1. In this illustration, the parameterization did lead again to the optimal MIP solution (1,867.1 × 10³ €) (Table 6.3). This is also a consequence of the problem small size.

Management Planning in Action 6.3: Impacts of Timber Management Scheduling on Multiple Product and Stock Control Objectives in Minnesota

Minnesota is located in the United States Upper Midwest and it extends over about 21 × 10⁶ ha. Its forest area extends over about one third of the territory. In 1989, a citizen petition was submitted to the Minnesota Environmental Quality Board (EQB) to seek action to address a potential increase of nearly 3.62 × 10⁶ m³ in annual timber harvesting activity associated with a proposed 2.2 × 10⁹ USD increase in the state’s primary wood processing plant capacity (Kilgore 1992). As a consequence, the state of Minnesota decided to develop a Generic Environmental Impact Statement (GEIS) of timber harvesting.

For that purpose, prescriptions were associated to 13,536 USDA Forest Service’s Forest Inventory and Analysis (FIA) plots, assumed to represent forest conditions in Minnesota. The most appropriate prescription for each stand/plot was selected by a scheduling model that matched demand for a product with the stand or forest area best able to supply that product and in consideration of mitigations and other constraints (Rose et al. 1993; Jaakko Consulting Inc 1994). The scheduling model was based on a Lagrangean relaxation of a typical forest management planning LP model such as the ones presented in 6.2 and 6.3 (Hoganson and Rose 1984). This model, developed at the University of Minnesota (http://www.forestry.umn.edu/), encompassed specialized techniques to search for the values of the dual variables of the LP model as well as the design of maps of wood procurement zones for each market to overcome the combinatorial nature of integrating harvest timing decisions and wood shipping decisions (Hoganson and Kapple 1991).

The GEIS involved over 60 scientists and it represented one of the most extensive studies of timber harvesting and forest resources conducted in the United States (http://iic.gis.umn.edu/download/geis/documnts.html). It was influential to (1) determine the extent of industrial timber harvesting and related timber management activities in Minnesota; (2) identify and assess the environmental and related impacts of industrial timber harvesting; and (3) recommend strategies to mitigate adverse impacts where such were found to be significant (Kilgore and Ek 2007).

3.3 Goal Programming and Pareto Frontier Methods

In the case of our example forest, the goal programming formulation of Problem 2 (F8) consists of a modification of its formulation for Problem 1 (F4). The objective function includes new terms in order to minimize the deviations from targets regarding the average carbon stock in each planning period and the volume at the end of the planning horizon. The formulation may be described as

• (a) Objective function Z

  $$ \begin{aligned} \mathrm{Min}\ Z& =8.4746\ PdevAH1+8.4746\ NdevAH1+8.4746\ PdevAH2 \\ & \quad +8.4746\ NdevAH2+ 8.4746\ PdevAH3+8.4746\ NdevAH3 \\ {}& \quad +8.4746\ PdevAH4 +8.4746\ NdevAH4+0.0244\ NdevH1 \\ {}& \quad + 0.0244\ NdevH2 +0.0244\ NdevH3 +0.0244\ NdevH4 \\ {}& \quad +0.0049\ NdevNPVt {+}0.04\ NdevCStock1 {+} 0.04\ NdevCStock2\\ {}& \quad +0.04\ NdevCStock3{+}0.04\ NdevCStock4 {+}0.04\ PdevCStock1 \\ {}& \quad +0.04\ PdevCStock2{+}0.04\ PdevCStock3{+}0.04\ PdevCStock4\\ {}& \quad +0.0182\ NdevVolEI \raisetag{12pt}\end{aligned} $$

  (6.30)

  Where the decision variables consist again of the deviations from the levels of the criteria set by the decision-maker. Two additional criteria were added, the average carbon stock CStock in period t and the volume of ending inventory VolEI. In the case of CStock the objective function penalizes both over and under achievements while in the case of VolEI it aims at minimizing the under achievement. The coefficients of the corresponding decision variables correspond to the product of 1,000 by the inverse of the criteria target levels measured in Mg and cubic meters, in the case of the average carbon stock and the volume of the ending inventory, respectively. Like before, the new GP model was set to minimize the percent deviations to overcome dimensional constraints to the treatment of all five criteria. The discounted revenues criteria was provided again with a weight equal to 10 while the remaining four were weighted equally as 1.

• (b) The Eq. 6.20 setting a new target (89 ha) for the area harvested in each period to reflect the area control objectives, where this area is defined by Eq. 6.12.

• (c) The Eq. 6.21 setting a new target for the volume harvested in each period (35 × 10³ m³) to reflect the volume control objectives, where this harvest level is defined by Eq. 6.11.

• (d) The Eq. 6.22 setting a new target for the discounted net revenue from the forest (1,870,000 €), where the discount net revenue is defined by Eq. 6.19

• (e) The Eq. 6.31 setting a target for the volume of ending inventory, where this volume is defined by Eq. 6.27:

  $$ VolEi+ PdevVolEi+ NdevVolEi=5,500 $$

  (6.31)

• (f) The Eq. 6.32 setting a target for the average carbon stock in each period (24 × 10³ Mg C) to reflect the stock control objectives, where this average is defined by Eq. 6.28.

  $$ \begin{array}{l} Cstock1- PdevCstock1+ NdevCstock1=2,400\hfill \\ {} Cstock2- PdevCstock2+ NdevCstock2=2,400\hfill \\ {} Cstock3- PdevCstock3+ NdevCstock3=2,400\hfill \\ {} Cstock4- PdevCstock4+ NdevCstock4=2,400\hfill \end{array} $$

  (6.32)

• (g) The set of constraints stating that the decision variables may take only the values 1 (if the prescription is assigned to the stand) or 0 (if the prescription is not assigned to the stand) (Eq. 6.13)

  $$ {x}_{11},{x}_{12},{x}_{13},\dots, {x}_{165}\ \mathrm{are}\ \mathrm{binary} $$

In this illustration, the target values were set by taking advantage of the insights provided by the solutions by the other techniques. For example, the target for the criteria NPV was set as the value of the optimal MIP solution. The solution by the GP model (Table 6.3) shows that the NPV criteria target was almost achieved (1,866,130 €) while still guaranteeing that no stand was assigned to more than one prescription (Table 6.4). Else the solution has a pattern similar to the MIP and SA solutions i.e. under achievement of harvest levels and over achievement of targets for both average carbon stock and volume in the ending inventory.

The Pareto frontier method may again be used to explore further the tradeoffs between the criteria and help set meaningful targets. The approach may build now from the LP formulation of Problem 2 (F5). Lets assume that the decision-maker wants to analyze the tradeoffs between four criteria e.g. NPV, VolEI, the average carbon stock over the whole planning horizon and the total volume harvested.

The Pareto frontier method may then be used to generate three-dimensional decision maps for which the values of the third, fourth,… criterion are fixed (e.g. Fig. 6.6 where the value of total timber harvested is fixed for each map and where the value of the average carbon stock is fixed for each set of decision maps). The maps are monotonic: a map contains all maps with better values of the third, fourth,…criterion (e.g. Fig. 6.6). When arranged in the form of horizontal series or even matrices, bi- or three-dimensional decision maps developed by this approach may provide information about the Pareto frontier in spaces up to five dimensions (Borges et al. 2014a).

Fig. 6.6

Decision maps displaying the Edgeworth-Pareto Hull of a four criteria planning problem considering minimum achievement levels for the four criteria (min NPV = 1,700 × 10³ €, min VolEI = 55 × 10³ m³, min CStock = 24.0 × 10³ Mg C and min Timber = 135 × 10³ m³). Each set of decision maps corresponds to a specific average carbon stock (CStock) (a) 24.0 × 10³ Mg C, (b) 26.0 × 10³ Mg C…, d) 30.0 × 10³ Mg C. Points A and B in (a) correspond to solutions selected by decision-makers from two decision maps associated with VolEI target levels of 55 and 75 × 10³ m³)

Based on the tradeoff information provided by the Pareto frontier approach, lets assume that the decision-maker sets 24,000 Mg C as the level of achievement for the average carbon stock criteria (set of decision maps (a) in Fig. 6.6) and that he wants to explore solutions associated with an average carbon stock CStock = 24.0 × 10³ Mg C (Figs. 6.6a) and alternative VolEI target levels (e.g. about 55 and 75 × 10³ m³ – points A and B in Fig. 6.6a, respectively).

The Pareto frontier approach may then be used to retrieve both solutions in the LP feasible set in the decision space (Table 6.3) and generate further insights about the management planning problem. As Borges et al. (2014a) pointed out, the usefulness of the Pareto frontier approach lies mostly in the preprocessing of the management planning problem to generate trade-off information so that the first specification of the levels of achievement by the decision-maker is more informed. Nevertheless, as this approach is based on the approximation of the Pareto frontier, the retrieval of a feasible solution requires the use of an achievement function to minimize the deviations between the solution selected in a decision map by the decision-maker and the feasible set in the criteria space, This is similar to the solution process by goal programming. Thus special attention should be also provided to the selection of an achievement function (Romero 2004).

Management Planning in Action 6.4: Long Term Cork Forest Management Scheduling to Address Multiple Product and Stock Control Objectives in Southern Portugal

In 2003, the Portuguese Regional Agriculture Office of Alentejo (DRAPAL) (http://www.drapal.min-agricultura.pt/) and the Extremadura Regional Government in Spain (http://www.gobex.es/consejerias/ceei_tecnologica.php) launched the project “Development of an information system for ecological-economic cork and holm oak ecosystem management”. This cross-border cooperation initiative (http://ec.europa.eu/regional_policy/archive/interreg3/abc/voleta_west_en.htm) encompassed a regional sustainability assessment of cork flows to the forest industry.

This prompted the development and application of a modeling approach similar to LP model 6.3 by the Forest Research Centre (CFS) (http://www.isa.ulisboa.pt/cef/). The cork and holm oak land base extending over 1 × 10⁶ ha in Alentejo was inventoried and firstly classified into 23,373 land units that were further aggregated into 84 analysis areas. The model included up to 8,400 prescriptions over a 5 ten-year periods planning horizon. Besides the area constraints, the LP model further included timber and cork non-declining flow constraints as well as carbon stock targets (Borges et al. 2009). The solution highlighted the constraining impact of the current inventory on potential cork supply in the first planning period and that both timber and cork non-declining flows policies may be sustained over the planning horizon (Borges et al. 2009).

More recently, in order to address DRAPAL concerns, the LP model was integrated by CFS and the Research Centre in Mathematics and Applications (http://www.cima.uevora.pt/) within a multi-criteria approach targeting timber, cork, carbon, net present value and value of ending inventory achievement levels (Borges et al. 2014a). This approach is similar to the Pareto frontier approach described in Sect. 6.3.3

4 Designing the Industrial Forest Landscape in Long Term Management Planning

Financial efficiency usually dictates the concentration of activities of harvesting and infrastructure (e.g. road network) development. Conversely, broader economic and environmental goals often suggest its dispersion in time and space. For example, area and volume control objectives reflect concerns with the sustainability of timber supply and constrain the concentration of the timing of harvests in industrial plantations (Sect. 6.2). Nevertheless, the implementation of forest plans also requires spatially feasible prescriptions that may address simultaneously environmental concerns with the sustainability of the industrial land base and financial concerns with the dispersion of forest operations. These often encompass the definition of adjacency constraints: a maximum size of openings or a range of feasible opening sizes and a minimum exclusion period – the minimum time that must elapse between harvests on neighboring stands.

The spatial context of harvest scheduling decisions is typically addressed at tactical and operational planning scales (Chaps. 2 and 7). Nevertheless the possibility of balancing strategic and tactical goals may be facilitated if long-term management planning does provide a strategic design of the industrial forest landscape that may help accommodate requirements of tactical management planning. This may be achieved by extending Problem 2 and its concerns with timber harvesting regulation and with stock control objectives to include adjacency constraints.

Typically, this combinatorial optimization problem (Problem 3) involves very large numbers of integer variables and constraints. The literature reported several approaches to build and solve a forest management planning problem with adjacency constraints. For example, Borges et al. (2002) discussed thoroughly the use of heuristic approaches to address it, while Constantino et al. (2008) presented a range of mathematical programming representations of the adjacency problem. In fact, as Borges et al. (2002) pointed out, currently available optimization packages combine often the use of both heuristic and mathematical programming techniques. For example, heuristic techniques may utilized directly in optimization packages to help in key aspects of the solution process like in (1) finding initial feasible solutions, (2) finding initial bounds on optimal solutions, (3) selecting branches to search in a standard branch and bound technique and (4) selecting the specific mathematical programming strategy to use for solving a specific mixed integer problem (Borges et al. 2002).

In order to illustrate how to accommodate concerns with the design of our industrial forest landscape example, the policy model of Problem 2 was further expanded to include adjacency constraints. In this section we will illustrate how to build mathematical programming models and how to design heuristic approaches to address jointly revenue optimization, area and volume control objectives, stock control concerns and adjacency constraints. For illustration purposes we will consider the Path approach to build the adjacency constraints (McDill et al. 2002). The introduction of the new policy scenario defines our strategic management planning Problem 3. We will further interpret the solution of the new problem and assess the impact of adjacency constraints on the value of the ending inventory, on the average carbon stock, on the harvest schedule and on the timber supply. Finally, we will illustrate how to assess the potential of specific solution techniques to address Problem 3.

4.1 Mixed Integer Programming

The adjacency problem requires information about the location of management options. Thus LP may no longer be used to address Problem 3. In the case of our example forest, assuming that the maximum size of openings is 60 ha and that a 1-period exclusion is considered, the MIP formulation of Problem 2 (F6) should be expanded to include the path adjacency constraints (6.33 – Eq. 2.13 in Chap. 2) to define the MIP formulation of Problem 3 (F9):

$$ \begin{aligned}[b]\allowdisplaybreaks {}&{x}_{11}+{x}_{21}\le 1\hfill \\ {}&{x}_{11}+{x}_{21}+{x}_{41}\le 2\hfill \\ {}&{x}_{11}+{x}_{21}+{x}_{52}+{x}_{53}\le 2\hfill \\ {}&{x}_{11}+{x}_{31}+{x}_{41}\le 2\hfill \\ {}&{x}_{11}+{x}_{41}+{x}_{51}+{x}_{52}\le 2\hfill \\ {}&{x}_{11}+{x}_{41}+{x}_{61}+{x}_{62}\le 2\hfill \\ {}&{x}_{11}+{x}_{21}+{x}_{71}+{x}_{72}\le 2\hfill \\ {}&{x}_{11}+{x}_{21}+{x}_{81}+{x}_{82}\le 2\hfill \\ {}&{x}_{21}+{x}_{31}+{x}_{41}\le 2\hfill \\ {}&{x}_{21}+{x}_{41}+{x}_{51}+{x}_{52}\le 2\hfill \\ {}&{x}_{21}+{x}_{51}+{x}_{52}+{x}_{81}+{x}_{82}\le 2\hfill \\ {}&{x}_{31}+{x}_{41}+{x}_{51}+{x}_{52}\le 2\hfill \\ {}&{x}_{31}+{x}_{41}+{x}_{61}+{x}_{62}\le 2\hfill \\ {}&{x}_{31}+{x}_{41}+{x}_{71}+{x}_{72}\le 2\hfill \end{aligned} $$

(6.33)

According to the solution by the MIP model (Table 6.3), the optimal objective function value Z decreased to 1,866.6 × 10³ €. No stands were split between different prescriptions (Table 6.4) and all adjacency constraints were met. The solution was very similar to the MIP solution of Problem 2. This demonstrates that the 60 ha opening size limit is very easy to meet.

4.2 Heuristics

The adjacency constraints in Problem 3 may also be addressed by simulated annealing (SA). In the case of our example forest, the SA approach involved the extension of the SA formulation for Problem 2 (F7) to address the new policy scenario. In summary, the SA formulation for Problem 3 (F10) takes the objective (evaluation) function of F7 (Eq. 6.29) and modifies its penalty function to include one further term that penalizes deviations from adjacency constraints. These deviations were more penalized than the deviations from the other constraints. All other penalties and heuristic parameters were the same as in the case of Problem 2. The penalty function may thus be represented in abbreviated form as:

$$ \begin{aligned} \theta & {\,=\,}{A}_{{\it const}\hbox{\_}6\hbox{\_}10}\!\left[\!{\left({x}_{11}{+}{x}_{12}{+}{x}_{13}{+}{x}_{14}{+}{x}_{15}{-}1\right)}^2{+}{\dots} {+}{\left({x}_{161}{+}{x}_{162}{+}{x}_{163}{+}{x}_{164}{-}1\right)}^2\!\right]\\ & +{A}_{const\hbox{\_}6\hbox{\_}6}\left[\!{\left({H}_1\hbox{--} {H}_2\right)}^2{+}\dots {+}{\left({H}_3\hbox{--} {H}_4\right)}^2{+}{\left({H}_2\hbox{--} 1.1{H}_1\right)}^2{+}\dots {+}{\left({H}_4\hbox{--} 1.1{H}_3\right)}^2\!\right]\\ {}& +{A}_{{\it const}\hbox{\_}6\hbox{\_}7}\left[{\left(.9 A{H}_1\hbox{--} A{H}_2\right)}^2+\dots +{\left(.9 A{H}_3\hbox{--} \mathrm{A}{H}_4\right)}^2+{\left( A{H}_2\hbox{--} 1.1\mathrm{A}{H}_1\right)}^2+\dots \right. \\ &+\left. {\left( A{H}_4\hbox{--} 1.1\mathrm{A}{H}_3\right)}^2\right] +{A}_{{const}\hbox{\_}{6\hbox{\_}{21}}}{\left( {\it VolEI}-5500\right)}^2 \\ & +{A}_{{\it const}\hbox{\_}{6\hbox{\_}{22}}}\left[{\left(.9 {\it CStock}_1\hbox{--} {\it CStock}_2\right)}^2+\dots +{\left(.9 {\it CStock}_3\hbox{--} {\it CStock}_4\right)}^2 \right. \\ &+\left. {\left( {\it CStock}_2\hbox{--} 1.1 {\it CStock}_1\right)}^2+\dots +{\left( {\it CStock}_4\hbox{--} 1.1 {\it CStock}_3\right)}^2\right]\hfill \\ {}& +{A}_{{\it const}\hbox{\_}{6\hbox{\_}{33}}}\left[{\left({x}_{11}+{x}_{21}-1\right)}^2+\dots +{\left({x}_{31}+{x}_{41}+{x}_{71}+{x}_{72}-2\right)}^2\right] \raisetag{17pt} \end{aligned} $$

(6.34)

Afterwards, the SA approach involved an iterative process identical to the process described in Sect. 6.2.2 (Fig. 6.2) where solutions in each iteration were represented by a vector with 16 elements corresponding to the 16 stands. In this illustration, the parameterization lead to a suboptimal solution (1,866.1 × 10³ €) (Table 6.3). Nevertheless the best solution found by this random search heuristic did meet all constraints thus highlighting again that the 60 ha opening size is easy to meet. Computational costs were low as a consequence of the problem size.

4.3 Goal Programming

In the case of our example forest, the goal programming Formulation of Problem 3 (F11) consists of a modification of F8 to include the adjacency constraints (Eq. 6.33). No target was changed. The solution (Tables 6.3 and 6.4) again highlights that the adjacency constraints had little impact on the proposed plan.

Research is currently being conducted so that the Pareto frontier approach considered in earlier sections may address multi-criteria problems such as Problem 3, where the spatial context of stand-level decisions must be acknowledged. The integration of the Pareto frontier approach with combinatorial resource capability and policy models (e.g. mixed integer programming models) will provide the functionality needed to analyze tradeoffs between criteria before setting their levels of achievement.

Management Planning in Action 6.5: Designing the Forest Landscape: Applications in Portugal and in Minnesota

In 1998, Celbi, currently a factory of a leading Portuguese eucalypt pulp producer (Altri) (see Management Planning in Action 6.1), decided to lay out the harvest of one of its properties extending over about 640 ha in Central Portugal to minimize the environmental impacts of eucalypt stands clearcutting. All 144 stands in this property (Vale do Mouro) were mature. Yet it was decided to schedule the harvest over five 1-year periods so that no adjacent stands might be harvested in the same period. Decision-makers further wanted to minimize the opportunity cost of harvest delay.

This prompted the application of a dynamic programming approach to solve a simplified version of the MIP model in Sect. 6.3 (no product flow or stock control objectives were considered) within a project coordinated by the Forest Research Centre (http://www.isa.ulisboa.pt/cef/). For a detailed description of the technique the reader is referred to Hoganson and Borges (1998) and Borges et al. (1999a). The industry found that the adjacency constraints led to a decrease of about 3 % of the net present value (Borges et al. 1999b).

This technique was extended to further analyze trade-offs between timber production and environmental objectives in the early 2000s in a forest area comprising Minnesota DNR managed lands in Itasca and Cass County (http://www.dnr.state.mn.us/index.html) and USDA Forest Service lands within the Chippewa National Forest (http://www.fs.usda.gov/chippewa/). Approximately 302,000 ha distributed over 92,000 stands were modeled (Hoganson et al. 2004). This project coordinated by the University of Minnesota (http://www.forestry.umn.edu/) estimated the impact of landscape design, namely of the supply of interior space, on industrial timber management scheduling (USDA Forest Service 2004).

5 Integrating Road Building Schedules in Long Term Industrial Forest Management Planning

Harvest scheduling and road building problems have traditionally been addressed in two sequentially linked steps. In the first step, the optimal harvest scheduling model identifies the areas that will be harvested during the planning horizon, without accounting for road building considerations. In the second step, the minimal road cost program that provides road accessibility for the optimal harvest schedule is determined. During the 1960s and 1970s tactical forest planning was essentially designed using this sequential approach (Guignard et al. 1998). According to Weintraub and Navon (1976), a sequential approach leads to two main problems: the wrong set of stands (nodes) may be made accessible, and the selection of the access period for each stand may be not optimal. Kirby et al. (1986) suggest that since the integrated formulation is less constrained than the sequential formulation, the cost of implementing a management plan using an integrated approach will be always smaller than or equal to the cost of a management plan based on the equivalent sequential procedure. Thus, for example, a slight increase in harvest cost due to a change in harvest location could result in a significant reduction in road building cost, an improvement that could not be recognized in a sequential procedure. Guignard et al. (1998) found that if the objective is to maximize the net present value of the timber minus road building and transportation costs, then the integrated approach can generate up to 60 % greater profits than the traditional sequential approach.

Weintraub and Navon (1976) present one of the first integrated models reported in the literature, where silvicultural and transportation activities are simultaneously considered. The authors suggest a MIP approach to find the maximum value for discounted revenues earned from the sale of timber, where road, timber management, and transportation costs are included in the analysis. Kirby et al. (1986) introduce the Integrated Resource Planning Model (IRPM), which is a Goal MIP problem formulated as an assignment problem where management decisions are associated with treatment units explicitly identified on the ground. Decision variables are defined for every unit and management alternative, in terms of the proportion of the unit area (0–1) assigned to every management alternative. Constraints impose minimum requirements on water run-off, recreation usage, wildlife usage, erosion, timber yield, visual degradation, employment and revenue. The road network is formulated as a multi-commodity, multi-period, fixed charge, capacitated network problem with mutually exclusive road capacities. Their results produce up to a 21 % reduction in cost compared to the traditional sequential model.

Guignard et al. (1998) suggest additional improvements to the original Kirby et al. (1986) model. Lifting and branch and bound priorities based on double contraction considerations are used to reduce the computational time required to solve the problem to optimality. Different road standards are considered in the model, including dirt, gravel and paved alternatives along with the associated building and transportation costs and capacity and seasonality restrictions. Following the original strengthened model proposed by Guignard et al. (1998), Andalaft et al. (2003) combine road capacity reduction with triggers and lifting constraints using Lagrangian relaxation. The proposed model is applied to a Chilean pine plantation problem with planning horizons between 2 and 5 years. Operational seasonality (winter and summer) and road standards (dirt, gravel and paved roads) are included in the model. Adjacency constraints are formulated differently than in traditional methods, where a minimum harvest area (as opposed to a maximum harvest area) is imposed to guarantee acceptable operational fixed costs.

5.1 Potential Road Network

Forest road networks used as input for the model are defined considering potential and actual road segments meeting the minimum technical road requirements and providing full accessibility to every management unit in the forest. In the conceptual network, landings are represented by nodes and road segments are represented by arcs. In the initial step, a minimum number of landings is identified. Usually, landing locations are identified based on the machinery available for logging operations. A road exit node represents the connection point between the forest road network and the road that connects the forest with the final destination for the timber. Note that, even though forests can have multiple road exits, the problem can be easily be transformed into a one exit node problem by creating a dummy node that connects all the potential and existing exit nodes.

Based on a topographic analysis of the forest, a set of potential road segments is created such that every node is connected to the exit node. The set of potential road segments is identified by R _ij , representing the arc that connects node i with node j. f ^t _ij represents the timber volume flow between node i and node j, and f ^t _ji represents the timber volume flow between node j and node i. This differentiation is used to model road networks where cycles are allowed. Even though flow directions are differentiated by the flow variables f ^t _ij and f ^t _ji , road decision variables are undirected variables, and consequently r _ij represents both arcs (i, j) and (i, j) simultaneously.

5.2 The Integrated Harvest Road Model

The general MIP formulation for the harvest scheduling problem (Chap. 2) can be adapted to incorporate road building decisions using an integrated approach. Different formulations can be used for this purpose, and the strength of the resulting models can be appreciably different. Tight or strong formulations are important in practice, as computation times required to obtain acceptable solutions are directly related to this characteristic. Thus the integrated harvest road model can be modeled as follows:

Sets

• T Set of periods in the planning horizon, such that T = {1, 2, …, n _T }.

• M Set of management units, such that M = {1, 2, …, n _M }.

• M ⁱ Set of management units associated with transportation node i. In other words, the set of management units from which timber will be hauled through node i.

• N Set of nodes in the road network.

• A Set of the current and potential road segments where (i, j) describes an arc between nodes i and j such that (i, j) ∈ A

• P ^m Set of road segments that belong to the path between the node associated with management unit m and the exit node in the road network.

Decision Variables

• x ^t _m Binary variable which assumes a value of 1 if management unit m is harvested in period t, and 0 otherwise. Notice that x ⁰ _m  = 1 represents that management unit m is not harvested at all during the planning horizon.

• r ^t _ij Binary variable which assumes a value of 1 if road segment (i, j) is built in period t, and 0 otherwise.

• f ^t _ij Total annual timber flow (mbf/year) from node i to node j in period t.

Constants

• a _m Area of management unit m (acres).

• v ^t _m Volume per acre (mbf/acre) obtained from unit m if it is harvested in period t.

• c ^t _m Net discounted revenue per acre ($) if management unit m is harvested in period t. Assuming a discount rate r (expressed as decimal fraction), it is calculated as c ^t _m  = c ^t * _m /(1 + r)^t, where c ^t * _m is the revenue per acre earned at period t if unit m is harvested in this period.

• q _ij Timber flow capacity per time unit (mbf/year) of road segment (i, j).

• R ^t _ij Net discounted building cost ($) if the road segment (i, j) is built in period t. This cost includes road and bridge building costs. Assuming a discount rate expressed as decimal fraction, it is calculated as R ^t _ij  = R ^t * _ij /(1 + rate)^t, where R ^t * _ij is the road building cost incurred at period t if road segment (i, j) is built in this period.

Objective Function

• $$ M ax\ Z={\displaystyle \sum_{m\in M}{\displaystyle \sum_{t\in T\cup \left\{0\right\}}{c}_m^t{a}_m^t{x}_m^t}}-{\displaystyle \sum_{\left( i, j\right)\in A}{\displaystyle \sum_{t\in T}{r}_{ij}^t{R}_{ij}^t}}, $$

  (6.35)

• Subject to,

• $$ \begin{array}{cc}\hfill {\displaystyle \sum_{m\in {M}^i}{v}_m^t{a}_m{x}_m^t}+{\displaystyle \sum_{\left( k, i\right)\in A}{f}_{ki}^t}-{\displaystyle \sum_{\left( i, l\right)\in A}{f}_{i l}^t=0,}\hfill & \hfill \kern0.84em i\in N\backslash \left\{ exit\right\}, t\in T,\hfill \end{array} $$

  (6.36)
• $$ \begin{array}{cc}\hfill {\displaystyle \sum_{m\in M}{v}_m^t{a}_m{x}_m^t}-{\displaystyle \sum_{\left( k, exit\right)\in A}{f}_{k, exit}^t=0,}\hfill & \hfill \kern1.2em t\in T,\hfill \end{array} $$

  (6.37)
• $$ \begin{array}{cc}\hfill {f}_{ij}^t+{f}_{ji}^t-{q}_{ij}{\displaystyle \sum_{t^{\prime }=1}^t{r}_{ij}^{t^{\prime }}\le 0,}\hfill & \hfill \kern1.92em \left( i, j\right)\in A, t\in T,\hfill \end{array} $$

  (6.38)
• $$ \begin{array}{cc}\hfill {f}_{ij}^t\ge 0,{r}_{ij}^t\in \left\{0,1\right\},\hfill & \hfill \kern2.88em \left( i, j\right)\in A, t\in T.\hfill \end{array} $$

  (6.39)

Equation 6.35 represents the modified objective function for the integrated approach, where it is maximized the total discounted net revenue obtained from the forest. Note that in this formulation, road building costs are discounted from the net revenue obtained from the volume harvested during the planning horizon and the ending forest value. Equation set 6.36 defines the volume flow balance equations for non-exit nodes, where it is guaranteed that all flows entering a non-exit node will exit in the same period (Fig. 6.7a). Thus, in a given period t, this set of equations forces the total inflow volume coming from the associated management units and the connected nodes (f ^t _ji , f ^t _ki  ) to equal the total volume that leaves node i (f ^t _ij , f ^t _ik  ). This equation set differs from the constraints suggested by Kirby et al. (1986) and Guignard et al. (1998), since in this case it is assumed that all volume produced in the forest will be transported to external exit nodes. Equation set 6.37 is defined as the volume flow balance equations for the exit node at the end of each period t. In particular, it is assumed that all the volume produced in the forest will be transported to the exit node (Fig. 6.7b), from which it will be shipped to the final market destination. Constraint set 6.38, named as road capacity constraint set, defines the maximum timber flow allowed through a particular road segment. The upper flow bound is defined by the flow capacity q _ij , which is based on the technical road characteristics. Notice that if f ^t _ij  ≥ 0 or f ^t _ji  ≥ 0, this equation can only be satisfied when ${\displaystyle \sum_{t^{\hbox{'}}=1}^t}{r}_{ij}^{t^{\prime}}\ge 1$. A set of logical constraints ensuring that a road segment can only be built once during the planning horizon $\left({\displaystyle \sum_{t\in T}}{r}_{ij}^t=1\right)$ could be included, but such a constraint is unnecessary in the formulation. Finally, constraint set 6.39 describes the nature of the continuous and binary road variables used in the integrated formulation approach.

Fig. 6.7

Timber flow representation in a road network

An advantage of this formulation lies in its flexibility to accommodate different road network structures, including road networks with and without cycles (spanning tree). However, as with the fixed charge network problem, if capacities are much larger than the actual flows, the LP relaxation of this model tends to produce weak bounds (Wolsey 1998). In this context, road capacity reduction has been proposed as a way to obtain tighter formulations (Weintraub et al. 2000). Even though, previous research has proposed reducing the capacity bounds as much as possible (Andalaft et al. 2003), it may be difficult to apply on road networks where cycles are allowed.

5.3 Unitary Flow model (UF)

The Unitary Flow model (UF) attempts to overcome the drawbacks observed with the traditional fixed charge network flow problem without losing the flexibility produced by accommodating different network structures. As mentioned, given that road capacities are usually much larger than the actual flows, capacity constraints mainly play a trigger function for binary variables associated with road-building decisions. Thus, in order to reduce the gap between road capacities and actual flows, unitary harvest volume can be assumed for road constraint modeling purposes. In this case, the potential volume that flows from a management unit to a given node (associated landing) can be assumed to always be unitary in the context of the road building constraints. Thus, an upper bound equal to the total number of management units in the forest can be used as the road capacity for any road segment in the network.

This formulation includes the objective function described in Eq. 6.35, constraints 6.39, and additional road constraints defined as follows:

$$ \begin{array}{cc}\hfill {\displaystyle \sum_{m\in {M}^i}{x}_m^t}+{\displaystyle \sum_{\left( k, i\right)\in A}{f}_{ki}^t}-{\displaystyle \sum_{\left( i, l\right)\in A}{f}_{i l}^t=0,}\hfill & \hfill \kern0.72em i\in N\backslash \left\{ exit\right\}, t\in T,\hfill \end{array} $$

(6.40)

$$ \begin{array}{cc}\hfill {\displaystyle \sum_{m\in M}{x}_m^t}+{\displaystyle \sum_{\left( k, exit\right)\in A}{f}_{k, exit}^t=0,}\hfill & \hfill \kern1.8em t\in T,\hfill \end{array} $$

(6.41)

$$ \begin{array}{cc}\hfill {f}_{ij}^t+{f}_{ji}^t-\left| M\right|{\displaystyle \sum_{t^{\prime }=1}^t{r}_{ij}^{t^{\prime }}\le 0,}\hfill & \hfill \kern2.28em \left( i, j\right)\in A, t\in T.\hfill \end{array} $$

(6.42)

Equation set 6.40, named as volume flow balance equation set for non-exit nodes, guarantees that no timber will be left at a non-exit node by requiring that all the traffic entering a particular node will exit in the same period. Inbound volumes from harvested management units are defined by ${\displaystyle {\sum}_{m\in {M}^i}{x}_m^t}$, assuming unitary harvest volume from management units. Equation set 6.41 guarantees that all volume harvested from the forest will exit through the exit node. Similar to equation set 6.40, it is assumed unitary volume from each management unit harvested. Constraint set 6.42 is defined to trigger the building of a particular road segment if there is a non-zero flow of timber on that road. For this set of constraints, the maximum flow for any road segment can be defined as the number of management units in the problem (|M|, cardinality of set M).

5.4 Integer Constraint One-by-Unit Model (IC-OU)

An alternative approach to the fixed charge network flow problem can be used when road networks follow a spanning tree structure. With a spanning tree structure, there is a unique path between every management unit and the exit node. This can be used to construct a set of trigger constraints to incorporate road building decisions into the model. In this case, when a management unit is harvested, all road variables associated with the path from that unit to the exit node must be built during or before the harvest period.

This formulation includes the objective function described in Eq. 6.35, constraints 6.39, and additional road constraints defined as follows:

$$ \begin{array}{cc}\hfill \left|{P}^m\right|{x}_m^t-{\displaystyle \sum_{t^{\prime }=1}^t{\displaystyle \sum_{\left( i, j\right)\in {P}^m}^t{r}_{ij}^{t^{\prime }}\le 0,}}\hfill & \hfill\;m\in M, t\in T,\hfill \end{array} $$

(6.43)

$$ \begin{array}{cc}\hfill {\displaystyle \sum_{t\in T}{r}_{ij}^{t^{\prime }}\le 1,}\hfill & \hfill \kern0.48em \left( i, j\right)\in A.\hfill \end{array} $$

(6.44)

Set of constraints 6.43 requires that if management unit m is harvested in period t, then the respective path P ^m to the exit node must be built, either previously or in period t (Fig. 6.8). Notice that |P ^m| represents the cardinality of set P, i.e., the number of road segments in the path. Thus, when x ^t _m equals 1, then ${\displaystyle {\sum}_{t^{\prime }=1}^t{\displaystyle {\sum}_{\left( i, j\right)\in {P}^m}{r}_{ij}^{t^{\prime }}\ge \left|{P}^m\right|}}$, otherwise the constraints will not be satisfied. In this context, we need the set of logical constraints defined by constraint set 6.44. Otherwise, a less expensive road segment in P ^m could be built more than once to satisfy constraint set 6.43.

Fig. 6.8

Graphical representation of a path from a management unit to its respective exit node. In this case, all the road segments in the path must to be built to harvest management unit m

5.5 Integer Constraint One-by-Road (IC-OR)

An alternative way to incorporate road building decisions using an approach similar to IC-OU is to subdivide constraint set 6.43 into |P ^m| new sets of constraints, one for each road segment in P ^m. This formulation includes the objective function described in 6.35, constraints 6.40 and 6.44, and additional road constraints defined as follows:

$$ \begin{array}{cc}\hfill {x}_m^t-{\displaystyle \sum_{t^{\prime }=1}^t{r}_{ij}^{t^{\prime }}\le 0},\hfill & \hfill \kern0.72em m\in M,\left( i, j\right)\in {P}^m, t\in T,\hfill \end{array} $$

(6.45)

5.6 Tightening Constraint (TC)

Even though road constraints can be fully incorporated using any of the previous four formulations, additional superfluous constraints can be added to obtain tighter formulations. By including these constraints, integer-infeasible solutions can be eliminated from consideration, improving LP relaxation bounds. In particular, two sets of constraints that have been proposed in previous research are considered: road-to-road and project-to-road constraints, which are formulated as follows:

$$ \begin{array}{cc}\hfill {r}_{ij}^t+{\displaystyle \sum_{\left( i, l\right)\in A}{\displaystyle \sum_{t^{\prime }=1}^t{r}_{ij}^{t^{\prime }}}}-{\displaystyle \sum_{\left( k, j\right)\in A}{\displaystyle \sum_{t^{\prime }=1}^t{r}_{ij}^{t^{\prime }}\le 0}},\hfill & \hfill \kern0.6em \left( i, j\right)\in A, t\in T,\hfill \end{array} $$

(6.46)

$$ \begin{array}{cc}\hfill {x}_m^t-{\displaystyle \sum_{\left( i, j\right)\in A}{\displaystyle \sum_{t^{\prime }=1}^t{r}_{ij}^{t^{\prime }}\le 0}},\hfill & \hfill \kern0.96em m\in M, t\in T,\hfill \end{array} $$

(6.47)

Constraint set 6.46, named as road-to-road set of constraints, prevents isolated road segments from being built. As illustrated in Fig. 6.9, road segment (i, j) only should be built if node i or node j are already connected with some other nodes in the network, in this case with nodes l ₁, l ₂, k ₁ or k ₂, otherwise an unconnected road segment would be built.

Fig. 6.9

Road-to-road constraint representation

Constraint set 6.47, named as road-to-project set of constraints, requires that if a management unit is harvested, its associated node must be connected. In Fig. 6.10, management unit m can be harvested only if node i is already connected to one of its neighboring nodes j, k, or l.

Fig. 6.10

Node accessibility representation, when the associated node to management unit m is potentially connected with the other three neighbor nodes

Management Planning in Action 6.6: Integrating Road Building Schedules in Long-Term Forest Management Planning in Pennsylvania

To illustrate the integrated formulation, we consider from the PA Bureau of Forestry, the landscape named as Whitaker Hollow and the problem of road building scheduling over a five 10 years temporal horizon. This landscape is made up of even-aged stands in two forest types, Northern and Allegheny Hardwoods. Based on the topographic characteristics of the Whitaker Hollow landscape, a total of 113 nodes are identified on the map (Fig. 6.11a). Then, a road network following a spanning tree structure (without cycles) was designed, generating 113 road segments with a total distance of 20.85 miles. Considering the topographic requirements, 5 bridges were identified on this road network (spanning tree). The model assumes that a bridge will only be built if the respective road segment requiring a bridge is considered in the road building program.

Fig. 6.11

(a) The potential spanning tree road network for the Whitaker Hollow landscape. (b) The potential road network allowing cycles for the Whitaker Hollow landscape

Similarly, a second road network allowing cycles was designed for the Whitaker Hollow landscape (Fig. 6.11b). In this case, 201 road segments were identified, almost twice the number in the spanning tree structure. Similarly, the potential road length increased from 20.85 to 41.18 miles when cycles were allowed. The network with cycles requires more variables and constraints in the model, however it provides a much larger set of potential solutions for the problem. Even if the initial road network allows cycles, given that transportation costs are not considered in the analysis, the road network built in the optimal solution will always follow a spanning tree structure. In fact, it can be shown that if a node is connected to more than one node on its way to the exit node, an improved solution can be obtained just by building the less expensive connected arc (road segment) that connects the arc with a path toward the exit node.

Figure 6.12a shows a map of the solution obtained using the traditional sequential approach for the Whitaker Hollow landscape. In this approach, the road building program is determined by finding the minimal cost road network satisfying the accessibility requirements imposed by the optimal harvest schedule, which had been determined irrespective of road building decisions. During the first half of the planning horizon (periods 1 and 2), harvest operations are mainly scheduled in the western part of the landscape, and during the last three periods (periods 3, 4 and 5), harvest operations are concentrated on the eastern part of the landscape. Similarly, Figure 8 shows a map of the optimal solution for the integrated model using a spanning tree road network structure. In this graphical representation, it is possible to verify that the sequential and integrated approach solutions harvest exactly the same management units and build the same road network.

Fig. 6.12

(a) Solution for the traditional sequential approach. Colors indicate the periods in which management units are scheduled to be harvested and road segments are scheduled to be built. (b) Solution for the integrated model with a spanning tree road network. Colors indicate the periods in which management units are scheduled to be harvested and road segments are scheduled to be built. (c) Solution for the integrated model including a road network with cycles. Colors indicate the periods in which management units are scheduled to be harvested and road segments are scheduled to be built

The main difference between the solutions is the sequencing of the harvest decisions and the road building activities. Figure 6.12c shows a map of the optimal solution for the integrated model using a road network structure with cycles. The same management units are scheduled for harvest as in the solutions obtained via the traditional sequential approach and the integrated approach incorporating a spanning tree road network. However, the sequence of the harvest operations is different. In particular, the different harvest timings allow the model to take advantage of the flexibility offered by a road network with cycles. In this case, different road segments were built. Even though the potential road network allows cycles, the final solution follows a spanning tree structure.

6 Summary

Long term considerations typically frame all decision processes in industrial forests management planning. The sustainability of the resource and the stability of product supply can hardly be addressed at another temporal scale as a consequence of the biological processes at the core of the forest production system. Thus strategic management scheduling is at the apex of the hierarchy of planning levels. It provides the input needed by tactical and operational management planning that will be addressed later in this book in Chaps. 7 and 8. For example, it generates information about the range of product supply values that may be targeted in the short term by tactical management planning while safeguarding the future. Nevertheless, the adequacy of those estimates increases with the amount of detail of long-term analysis. The effectiveness of strategic management planning does depend in part on how it addressed tactical and operational constraints.

Long-term management planning of industrial forests unfolds as summarized in Chap. 2. It requires data and information about the land base and the vegetation dynamics as well as about the management options and the costs and revenues resulting from their implementation. These data and information items were discussed in detail in earlier chapters. Data acquisition and management – e.g. inventory and land classification, prescription generation, growth and yield projections and market analysis – is a lengthy and costly process that takes a huge part of the time needed to develop a strategic management plan. It requires computerized tools that will be characterized later in Chap. 9.

In this chapter we have built from the state of the art reported by over 94 researchers from all over the world (Borges et al. 2014b) to characterize the dimensions – e.g. spatial scale, number of objectives, type of goods and services, spatial context – of strategic forest management planning of industrial plantations. We further provided a brief historical overview of how the relative importance of these dimensions evolved in recent decades. This led to the classification of long term problems into four main clusters. The first cluster was characterized by objectives (criteria) such as revenue maximization e.g. maximization of the value of the industrial forest, cost minimization and the regulation of the forest over the planning horizon. The second cluster included additional stock control objectives. The third cluster included further landscape design objectives. The forth cluster addressed strategic road building objectives within the framework proposed by the first cluster.

For illustration purposes, in the case of the first cluster we considered concerns with the regularity of the volume and the area harvested over the planning horizon. This is often a concern of managers of industrial plantations: how much to harvest so that there is no rupture in raw material supply. In the case of the second cluster we considered further both carbon sequestration objectives and concerns with the sustainability of the industrial forest by including a constraint on the inventory at the end of the planning horizon. In the case of the third cluster we included adjacency constraints. All these three clusters encompassed only harvesting decisions. The fourth cluster included further road building decisions. Other criteria might have been included in each cluster yet we think that we have considered the most representative for illustrating the processes of model building and for analysing the potential of operations research techniques to address strategic forest management scheduling as well as for interpreting its solutions.

The forestry literature reports several alternative modelling approaches to address strategic management planning problems within each cluster (e.g. Martins and Borges 2007; Diaz-Balteiro and Romero 2008). In this chapter we have classified them into mathematical programming and heuristic approaches. We have differentiated further between approaches that address explicitly one or else several objectives. Moreover we have referred to the potential of a posteriori preference modeling approaches. This was influential to highlight the potential of each broad class of techniques. For illustration purposes we have selected from each group, modeling approaches such linear programming, mixed integer programming, goal programming, simulation, simulated annealing and Pareto frontier methods. Again, other techniques are available that may be used to address strategic management planning. Nevertheless we think that the selection made does provide the information needed to help develop both model building and model solving to address the most representative problems.

This chapter builds from the formal presentation of management planning models in Chap. 2 to illustrate how each technique may be used to address each problem. For that purpose we have introduced an example forest with 16 stands. This academic example does provide the data and the information needed for a detailed numerical illustration of model building. It facilitates further the interpretation of results. A list of problems at the end of the chapter builds from the same example forest to support model building, model solving and interpretation of results by readers

7 Problems

• 1. Discuss the potential of mathematical programming to address strategic industrial forest management scheduling.

• 2. The prescriptions available to each of the 16 stands are summarized in Table 6.2. It was assumed that timber prices were constant and independent of the stand age. Often this is not the case. Consider the information in Table 6.7 and build a new prescription table to reflect the relation between stand age and timber price.

  Table 6.7 Timber prices

• 3. The solutions by linear programming (LP) to Problems 1 (LP Run #1) and 2 (LP Run #2), assuming constant prices, are reported in Tables 6.3, 6.4, 6.5, and 6.6. Use LP to optimize the objective function of Problems 1 and 2 subject only to the stand area constraints (Eq. 6.3) and assuming that prices are either constant or as reported in Table 6.7. Summarize the solutions of these runs (LP Run #3 and LP Run #4, respectively) in Tables similar to 6.3, 6.4, 6.5, and 6.6. Explain how you could determine the optimal schedule without even using linear programming. How could one derive the dual prices for each stand?

• 4. Use LP to solve Problems 1 and 2, assuming that prices are as reported in Table 6.7. Summarize the solutions of these runs (LP Run #5 and LP Run #6, respectively) in Tables similar to 6.3, 6.4, 6.5, and 6.6.

• 5. The binary search check demonstrated that the inclusion of the value of ending inventory value in the objective function coefficients (Problems 1 and 2) as well as the inclusion of a 55,000 m³ constraint on the volume of ending inventory (Problem 2) did not prevent the models from prescribing harvest levels that are not sustainable in the long term. Change Problem 2 to include a 75,000 m³ constraint on the volume of the ending inventory. Consider prices reported in Table 6.7 and use LP to solve this problem and summarize the solution of this run (LP Run #7) in Tables similar to 6.3, 6.4, 6.5, and 6.6.

• 6. Compare Run #1 to #7 in terms of the differences in volumes harvested in each planning period and volume of ending inventory. Based on the characteristics of each LP model, explain the differences, if any.

• 7. Use LP to solve Problem 2 (considering a 75,000 m³ constraint on the volume of the ending inventory), assuming that prices are as reported in Table 6.7, and modified so that no area, volume or carbon stock control constraints are considered. Summarize the solution of this run (LP Run #8) in Tables similar to 6.3, 6.4, 6.5, and 6.6.

• 8. Compare Run #4 and Run #8 in terms of the differences in the stands that are not harvested over the planning horizon. Based on the characteristics of the stands involved, explain the differences. i.e. why did each run select not to harvest the stands that it did?

• 9. Consider the reduced costs for stand # 1 in the case of Runs #4 and #8. Try to explain why the reduced costs changed as they did between these runs. Be as specific as you can. Why did they change more for some prescriptions than for others?

• 10. Determine how much the marginal value changed between Runs #4 and #5 for each stand. Explain these changes the best you can i.e. why are some changes larger than others? Why do some increase and others decrease?

• 11. Consider the changes in reduced costs for prescriptions for stands #1, #5, and #11 between Run #4 and #5. Explain the changes (direction and relative magnitude) the best you can in terms of the characteristics of the stands and the characteristics of the management planning problems.

• 12. Using Run #4 as the basis of comparison, the simple “with and without principle” of economics, and the value of the objective function found for Runs #4 through #8 determine on a per hectare basis:

  • (a) The cost of area and volume control constraints

  • (b) The combined cost of area and volume control constraints + the constraint on the carbon stock + the 55,000 m³ ending inventory constraint

  • (c) The cost of the 75,000 m³ ending inventory constraint

  • (d) The combined cost of area and volume control constraints + the constraint on the carbon stock + the 75,000 m³ ending inventory constraint

• 13. From your understanding of the original problem try to explain why you think the costs in question 12 are of the magnitude that they are. Do you think these costs are significant? Why?

• 14. If you were asked to estimate the cost of the constraint on the carbon stock in Problems 1 and 2 how would you proceed? Do you expect that cost to be significant? Why?

• 15. Assume that the industrial forest owner learns that timber demand in each period is equal to 10,000 m³. Modify the model for Run #4 to include the new constraints. Summarize the solution of this run (LP Run #9) in Tables similar to 6.3, 6.4, 6.5, and 6.6.

• 16. In the case of Run #9 very few stands are scheduled for harvest during the planning horizon. Based on stand characteristics, explain why the model picked to harvest the stands that it did.

• 17. Consider Runs #4 and #9. Explain the marginal values of the stands in the case of Run #9 in terms of values associated to Run #4. Be as specific as you can.

• 18. One might say that with forest management scheduling models “the marginal value of valuable stands likely decreases and the marginal value of marginal stands likely increases.” Do you agree with this statement? Explain why or why not.

• 19. Replicate Runs #4 to #9 with the requirement that no stands are fragmented:

  • (a) Do you need to use Mixed Integer Programming (MIP) or Simulated Annealing (SA) to get the integer solutions to Runs #3 and #4? Why?

  • (b) What is the cost of the locational specificity requirement in the case of Runs #4 to #9. Explain the differences based on the characteristics of the management planning problems.

• 20. Build and solve a goal programming (GP) model representing the problem that corresponds to Run #8. When would you rather use GP than pure LP to address an industrial forest management planning problem?

• 21. Discuss the potential of Pareto frontier approaches to address industrial forest management planning problems.

• 22. Develop your own heuristic to solve Problem 3, assuming that prices are as reported in Table 6.7 and a 75,000 m³ ending inventory constraint. Summarize the solution of this run in Tables similar to 6.3, 6.4, 6.5, and 6.6.

  • (a) Compare your solution to the Mixed Integer Programming (MIP) solution to this problem.

  • (b) What is the cost of the adjacency constraints? Do you think they are significant?

• 23. Discuss the potential of heuristics to address industrial forest management planning problems.