1 Introduction

Manufacturing of dairy food is a major industry in most developed and developing economies of the world. There is a wide range of dairy products corresponding to the large diversity of consumer tastes and consumption trends. Due to factors such as high variability of raw materials, intermediate and final products, fluctuating prices, or variable processing times, production planning in dairy industry is a generally challenging task (Lütke Entrup 2005). Optimizing resources and processes is the key to turning these challenges into a competitive advantage. To address the challenges of the new market as well as adopt business process to the changing conditions and regulations of this industry, more efforts should be focused on new methods aimed at optimizing a real case production scheduling problem arising in the dairy industry.

This research is motivated by a practical problem in which a production facility with limited capacity is producing perishable products that require delivery to a set of geographically dispersed distribution centres on or before their effective life times expire. The problem is formulated as a mixed integer linear programming (MILP) model, which is an extension of the formulation previously studied by Doganis and Sarimveis (2008a, 2008b). The model is extended to account for backlogging, overtime, and delivery to distribution centres. Shelf life dependent pricing component is also incorporated in the same way as in the model developed by Lütke Entrup et al. (2005). Several features of the model characteristics considered in the literature are combined within the proposed model. Moreover, the model is embedded in a hybrid MILP and simulation framework to explore the stochastic operation times.

In this paper operation times in the MILP model are considered as the dynamic factor and adjusted by the results from independently developed simulation model. Hybrid MILP and simulation models are aimed at combining the strength of MILP and the simulation model and reducing the impact of limiting characteristics of these models. Iterative use of MILP and simulation methodologies exploit the benefit of obtaining optimal solutions, while revealing the impact of operation time uncertainty on system performance (Kim and Kim 2001; Acar et al. 2010).

The main contributions of this paper can be summarized as follows: (i) Propose a MILP formulation for the production scheduling and distribution planning problem within the dairy industry, (ii) Develop a hybrid approach that combines the advantages of simulation model and MILP model, (iii) applying the model to a real world production scheduling and distribution planning problem arises in a leading company of the dairy industry in Turkey.

This paper is organized as follows. In the next section, brief survey of relevant literature is given. Section 3 gives a detailed description of the problem. Section 4 describes the hybrid approach consisting of MILP model formulation and simulation model. The case study is then presented to highlight the characteristics of the proposed model and methodology in Sect. 5. Finally in Sect. 6, some conclusions and future research directions are drawn.

2 Literature review

Based on the characteristics of the problem, we review the most relevant and recent literature on production scheduling in dairy industry and application of hybrid MILP and simulation modelling approach to the production and distribution planning problems.

2.1 Production scheduling in dairy industry

Despite its importance in practical settings, only few researchers have addressed the production scheduling problem in dairy industry. Pioneering works was done by Smith-Daniels and Ritzman (1988), Claassen and van Beek (1993), van Dam et al. (1993), Nakhla (1995). Smith-Daniels and Ritzman (1988) develop a general lot sizing model for process industries and apply their method to a situation representative of a food processing facility. Claassen and van Beek (1993) develop an approach to solve a planning and scheduling problem for the bottleneck packaging facilities of the cheese production division of a large dairy company. van Dam et al. (1993) have investigated and compared the origins of the increasing complexity of the scheduling problems of several companies in the process industry producing dairy products, pharmaceutical products, tobacco, paint, chocolate products, and foods. And they have analyzed the ways in which these companies deal with this increasing complexity in different situations. Nakhla (1995) emphasizes the need for flexibility for operations scheduling in the dairy industry, and proposes a rule-based approach for scheduling packaging lines in a dairy industry. Foulds and Wilson (1997) have proposed two heuristic algorithms for a variation of the generalized assignment problem arising in the New Zealand dairy industry. Then Basnet et al. (1999) have described an exact algorithm to solve scheduling and sequencing problem in the same industry. Recent years there are also papers that focus on side aspects of production scheduling, like environmental effects of production tasks and scheduling of workforce. Berlin et al. (2007) study a heuristic to arrange products to minimize the environmental impact of yoghurt products in their life cycle.

Until recently, the use of optimization based techniques for the production planning problem in the dairy industry has received little attention in the operations research literature. Lütke Entrup et al. (2005) present three different MILP formulations for scheduling fresh food industry. The shelf life of the products has been explicitly considered. To guarantee the compactness and computability of the models, a block planning approach developed by Gunther and Neuhaus (2004) is chosen. However the MILP models presented in the paper focus on flavoring and packaging stages. Thus operations involving the processing and storage of products are neglected.

Doganis and Sarimveis (2007) propose a model that aims the optimal production scheduling in a single yoghurt production line. The model takes into account all the standard constraints encountered in production scheduling (material balances, inventory limitations’, machinery capacity). It also considers special features that characterize yoghurt production which are limitations in production sequencing mainly due to different fat contents and flavors of various products and sequence dependent setup times and costs. However the model is limited to single production line. In another study Doganis and Sarimveis (2008a) present a methodology for optimum scheduling of yoghurt packaging lines that consist of multiple parallel machines. The methodology incorporates features that allow it to tackle industry specific problems, such as multiple intermediate due dates, job mixing and splitting, product specific machine speed, minimum, maximum lot size and sequence dependent changeover times and costs. However the model does not incorporate multi-stage production decisions, and ignores some industry-specific characteristics, such as shelf life. Doganis and Sarimveis (2008b) build on the work on modelling of the special constraints in food production systems by Doganis and Sarimveis (2007, 2008a) and extend them to include the factor of shelf life. The extended model considers shelf life restrictions and optimizes the balance between the cost inflicting factors and the profit-contributing aspects of minimizing time duration between production and delivery of products to the retailers. Marinelli et al. (2007) propose a solution approach for a capacitated lot sizing and scheduling problem with parallel machines and shared buffers, arising in a packaging company producing yoghurt. A two-stage heuristic methodology based on decomposition of the problem into lot sizing and scheduling problem has been developed. However it is assumed that the production rate is fixed by a single bottleneck stage, setup times and costs are sequence independent. In a very recent study, Gellert et al. (2011) investigate the planning for filling lines, within the successful framework for integrated sequencing and scheduling problems from the authors’ previous study, taking into account the new aspect of flexible scheduling environment regarding cleaning and sterilization. However, their problem only concerns the scheduling and sequencing for filling lines and ignores all potential limitations regarding rest of the processing system. Amorim et al. (2011) develop multi-objective mixed integer programming (MIP) models to deal with simultaneous lot sizing and scheduling of perishable products for different strategic scenarios: pure make to order and hybrid make to order, make to stock environments. A hybrid genetic algorithm is developed to solve both models, and it is tested in various problem instances based on the real-life dairy plant described by Kopanos et al. (2010). The main contribution of this paper lies on the multi-objective framework. They differentiate, in a multi-objective framework, between costs and freshness. Ahumada and Villalobos (2011) present an integrated tactical planning model for the packaging and distribution of fresh produce with the inclusion of perishability. The model handles the perishability of the crops through storage constraints, and used a loss function in the objective function. Alternative transportation modes are also taken into consideration. More recently, Amorim et al. (2012) present the study that addresses the integrated production and distribution planning of perishable products in a multi-objective framework. They formulate models for the case where perishable goods have a fixed and a loose shelf life.

Kopanos et al. (2010) study on the lot sizing and scheduling problem in a multi-product yoghurt production line of a real life plant. A mixed discrete/continuous time MILP model is proposed. The problem under question is mainly focused on the packaging stage, whereas timing and capacity constraints are imposed with respect to the pasteurization, homogenization and fermentation stage. Sequence dependent setup times and costs are explicitly taken into account and optimized by the proposed framework. However, the scheduling problem they consider only involves the packaging stage. Kopanos et al. (2011a), present a MILP framework for the resource constrained production planning problem in semi-continuous food process, similar to the dairy industry. Quantitative as well as qualitative optimization goals are included in the proposed model. Renewable resource limitations are appropriately taken into account. All of the above mentioned works are related to the single stage production systems in dairy industry. Kopanos et al. (2011b) present a novel MILP formulation and solution strategy to address the challenging production scheduling problems in multi-product multi-stage food industries. The main features of the proposed approach rely on the integrated production stages, and the inclusion of strong valid integer cuts favoring shorter computational times. In a paper by Kopanos et al. (2012a) the MILP model developed by Kopanos et al. (2011b) is further enhanced by introducing new sets of tightening constraints in order to improve computational efficiency in industrial size scheduling problems in food industries. Both papers consider production scheduling problem in a real world multi-stage food processing industry with the limited shelf life of intermediate mixes in the aging stage. In a very recent work, Kopanos et al. (2012b) present a novel MILP framework based on a hybrid discrete/continuous time representation for the simultaneous detailed production and distribution planning problem of multi-site, multi-product, semi-continuous food processing industry. The novelty of the proposed mathematical formulation lays on the integration of the different modelling approaches and the detailed production and distribution operations.

As demonstrated by the amount of recent contributions to the dairy industry research, this field has gained a remarkable momentum in the last decade. Although there is an increasingly interest in the subject of production scheduling in dairy industry, there is only a small number of papers that have focused on both production and distribution. To the best of our knowledge, we have found only one paper (Kopanos et al. 2012b) that deals with production scheduling and distribution planning in the dairy industry. The model proposed by Kopanos et al. (2012b) decides the assignment of transportation trucks to processing sites-distribution center in every period as well as transportation load for every truck. They impose material balance and logistics operations constraints. Three different transportation modes and min/max truck capacity are taken into consideration. Our paper differs from the model by Kopanos et al. (2012b) by handling the perishability issues in production scheduling and distribution planning model within the dairy industry.

2.2 Hybrid analytic and simulation approach in the supply chain planning problems

Mathematical approaches require too many simplifications to model realistic chain problems. Real world situations are characterized by a high degree of uncertainty. Inclusion of uncertainties often makes pure mathematical modelling intractable. Discrete event simulation is emerging as a decision support tool for the food industry due to powerful and realistic modelling and analysis characteristics (Yoo et al. 2010). On the other hand hybrid approaches proposed in the literature offer the advantages of simulation based methodologies together with the optimization capabilities of mathematical programming models for the effective decision making.

Major drawback in most past research on dairy industry is the assumption that the critical parameter such as the operation time is deterministic, whereas the uncertainty can be observed, such as machine breakdowns, late deliveries. Therefore it is necessary to handle the uncertainty. Discrete event simulation allows production scheduling to be modeled more realistically.

Shanthikumar and Sargent (1983) discuss comparative advantages and disadvantages of analytic versus simulation models giving a unifying definition for hybrid simulation, analytic approaches and modelling. Several researchers have developed iterative solution approaches for various types of problems that integrate optimization and simulation approaches. Byrne and Bakir (1999) study a hybrid algorithm combining mathematical programming and simulation models of a manufacturing system for the multi-period, multi-product production planning problem. Kim and Kim (2001) propose an iterative approach for finding the capacity-feasible production plan, applying the hybrid framework by Byrne and Bakir (1999). An extended formulation of linear programming (LP) model is proposed to consider the workload profile of the production quantity and the actual amount of the capacity to be allocated to the requirements for each machine. Lee and Kim (2002) develop an integrated multi-period, multi-product, multi-shop production and distribution model. They also take into consideration various kinds of uncertain factors so that the integrated supply chain system can reflect the dynamic characteristics of the real system. Operation time in the analytic model is considered as a dynamic factor. They propose a hybrid approach that combines both the analytic and the simulation model. In another paper Lee et al. (2002) study the same model. While the operation time is a stochastic factor in their previous work (Lee and Kim 2002), machine capacity and distribution capacity are considered as stochastic factors in this paper. Hsieh (2002) reviews hybrid approaches and their applications and proposes a new hybrid modelling class, and illustrates a cost function for selecting analytic or simulation modelling approaches through a problem solving process. Gnoni et al. (2003) consider the production planning problem of a multi-site manufacturing system subject to capacity constraints in case of an uncertain, multi-product and multi-period demand. A hybrid model, resulting from the integration of a MILP model and a simulation model, is developed to solve a lot sizing and scheduling problem. Byrne and Hossain (2005) describe an extended LP model for the hybrid approach proposed by Byrne and Bakir (1999) incorporating JIT concepts.

Safaei et al. (2010) propose a hybrid mathematical-simulation model to solve the multi-product, multi-period, multi-site production distribution planning problem. Almeder et al. (2009) present a new approach that combines the advantages of complex simulation models and abstract optimization models. They include simulation and optimization in an iterative process in order to gain the advantages of optimization (exact solution) and simulation (nonlinearities, complex structure, stochasticity). Acar et al. (2010) develop a decision support framework for a global specialty chemical manufacturer that operates under demand, supply, and transportation lead-time uncertainties. Their modelling approach combined optimization and simulation methodologies to obtain optimal supply chain plans via mathematical modelling, while incorporating uncertainties in the execution of these plans via simulation. In a recent paper Nikolopoulou and Ierapetritou (2012) propose a hybrid simulation and optimization approach for the integrated planning and scheduling problem. The simulation based optimization strategy uses an agent based system to model the supply chain network.

Among the recent studies no study deals with the integration of different modelling methodologies, such as integration of analytical and simulation models, in order to join advantages offered by each of them in facing complex scheduling problems arising in the dairy industry. The discussion of previous scheduling literature on the dairy industry establishes the need for a hybrid model in dairy industry that efficiently recognizes uncertainty. This study proposes a hybrid approach for the production scheduling and distribution planning problem in the dairy industry.

3 Problem definition

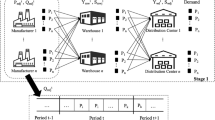
In this paper we address the production scheduling and distribution planning problem in a yoghurt production line of the multi-product dairy plants. The dairy industry can be considered as a part of the process industry. In general the plant must closely coordinate three primary processes: (1) the transformation of raw materials into intermediate products, and (2) the filling and packaging operations of final products, and (3) the delivery of end products to the distribution centres. Yoghurt production process starts with collection of milk and continues with pasteurization, standardization, homogenization, culture addition, packaging, fermentation, cold storage and distribution processes respectively. Yoghurt product types differ from each other according to fat rate of milk and cup sizes. While cup size is determined in packaging operation, fat rate is arranged with standardization operation. The packaging process is considered in the scheduling problem. The other operations in the process are assumed as infinite. Production scheduling is also interrelated with a part of transportation problem. The demand collected from customers is determined the quantity that the production scheduling model should produce. The complexity of the problem is further compounded by the delivery. In addition, sequence dependent setup times are considered in the system. There are strong limitations for the product sequence.

The problem that is investigated in this paper has the following structures:

  1. 1.

    The supply network consists of several plants which deliver the final products to the various distribution centres.

  2. 2.

    Each plant comprises several not necessarily identical packaging production lines. Each packaging line produces a given range of products. Multiple assignments of products to the production lines are allowed.

  3. 3.

    For each product, inventory balances are updated on a daily basis according to the production output from the various lines at the plants, the outbound transportation quantities send to the distribution centres.

  4. 4.

    The demand for each product in each day is collected from the distribution centres respectively. The scheduling horizon is supposed as 5 days. The time horizon of short term planning for yoghurt manufacturing is usually one week (Nakhla 1995).

  5. 5.

    The changeover time and cost are involved for only possible transitions between products. In the dairy industry, there is often a natural sequence in which the various products are to be produced in order to minimize total changeover time such as, from the lower taste to the stronger or from the brighter color to the darker (Gunther and Neuhaus 2004).

  6. 6.

    The time for quality control process is considered in the model. It is not allowed that the products are not delivered before they complete the required time for the quality control process. A quarantine time is defined as a precondition for the achievement of the desired sensory qualities (Lütke Entrup et al. 2005).

  7. 7.

    The freshness that has a significant part in competition is taken into account for profitability. The objective function aims at maximizing the contribution margin taking into account a shelf life-dependent pricing component as stated in the model developed by Lütke Entrup et al. (2005).

  8. 8.

    Operation cost for two products that can be produce at the same packaging line differs from each other. Therefore, the operation cost is computed for each product and line.

  9. 9.

    The available working hours for the lines are defined according to the shifts. An overtime production of the third shift is allowed in every working day under environment of heavy demand. If necessary, the production day can be proceeded with Sunday shifts and the third shifts in weekdays which are defined as overtime. Only on Mondays, two of shifts are reserved as cleaning time for the production unit. The cleaning time is not flexible that it cannot be shortened and delayed, because the yoghurt is fresh and sterilized production.

  10. 10.

    The production speed of each product is considered as dynamic within the lines. It is an important factor for production scheduling.

  11. 11.

    Backlogging is considered in MILP model. The unmet demand in the previous periods is transferred to the next periods. In addition, it causes a cost for every additional day.

Key decision variables are:

  1. (i)

    the produced quantity for each product, on each line, and in each period,

  2. (ii)

    the optimal assignment of products to each production line, and in each production period,

  3. (iii)

    the optimal quantity of each product transported from each line to each distribution center in each demand period,

  4. (iv)

    the sequencing among products on each production line in each period,

  5. (v)

    the starting and completion time of each product on each line,

  6. (vi)

    The inventory level of each product at the end of the day,

  7. (vii)

    The unmet demand for each product over the planning horizon.

4 Solution approach

The analytic model tends to provide exact and static information, while simulation model provides approximate and dynamic information about the system of interest or problem entity (Hsieh 2002). The products are assigned to the related lines on MILP model. In real world system, operation times cannot be considered as fixed values. For that reason, simulation is used to take into consider the down times and obtain more realistic solution. In achieving real solution, simulation and MILP model are evaluated together for the production scheduling problem in the yoghurt production process.

4.1 Model formulation

In this section, the proposed MILP formulation is presented for the production scheduling and distribution planning problem described above. Our presented model is inspired from the model provided by Doganis and Sarimveis (2008a, 2008b). The model is extended to account for unmet demand, overtime, shelf life dependent benefit pricing component, and the delivery of products to the distribution centres. The penalty for the unmet demand and transportation costs are also included in the objective function. On the other hand shelf life-dependent pricing component has been included in the objective function in a similar way as in the model developed by Lütke Entrup et al. (2005). The mathematical model determines the optimal scheduling program to maximize the benefit by considering the shelf life dependent pricing component and costs.

i :

days

d :

demand days

j,k,t :

products

l :

lines

a :

distribution centres

benefit j :

maximum benefit for meeting the maximum shelf life of product j, (TL/unit)

cr j :

critical rate for shelf life of product j required by customers, (% of maximum shelf life)

sl j :

shelf life of product j, (day)

\(c_{jl}^{\mathit{Prod}}\) :

production cost of one unit of product j on line l, (TL/unit)

\(c_{j}^{\mathit{Inv}}\) :

inventory cost for one unit of product j for a day, (TL/unit)

\(c_{j}^{\mathit{Unmet}}\) :

cost of unmet demand for product j, (TL/unit)

\(c_{jk}^{\mathit{Setup}}\) :

changeover cost from product j to product k, (TL)

\(c_{l}^{\mathit{overtime}}\) :

cost for overtime of line l per unit of time, (TL/hour)

\(c_{al}^{\mathit{transportation}}\) :

cost for transportation from plant including line l to distribution center a, (TL/unit)

d jad :

demand from distribution center a for product j on demand day d, (unit)

qq j :

quarantine time, which is the required time for quality control operation for product j, (day)

ls jl :

machine speed for product j on line l, (unit/hour)

s jk :

changeover time from product j to product k, (hour)

maxtime li :

maximum available time of line l on day i, (hour)

rtime li :

regular in use shift of line l on day i, (hour)

MinL j :

minimum lot size of product j

MaxL j :

maximum lot size of product j

M :

Extremely big number

p :

Extremely small number

x ijld :

quantity of product j produced on line l on day i for demand day d, (unit)

y jlad :

quantity of product j transported from line l to distribution center a and on demand day d, (unit)

input j :

total production of product j during the whole scheduling period, (unit)

output j :

total demand of product j during the whole scheduling period, (unit)

ud jad :

unmet demand of product j on demand day d for distribution center a, (unit)

inv ijl :

inventory level of product j on line l at the end of day i, (unit)

overtime il :

overtime on line l on day i, (hour)

PT ijl :

utilization of line l for product j on day i, (hour)

ST ijl :

starting time for processing of product j on line l on day i, (hour)

FT ijl :

finishing time for processing of product j on line l on day i, (hour)

lasttime il :

finishing time of the last product on line l on day i

b ijl :

1, if product j is produced on line l, on day i.

z ijkl :

1, if product k is produced exactly after product j on line l on day i.

Objective function

$$ \begin{aligned}[b] &\sum_{i = 1}^{I} \sum_{j = 1}^{J} \sum_{l = 1}^{L} \sum_{d = 1}^{D} \mathit{benefit}_{j} \cdot \frac{(1 - \mathit{cr}_{j})\cdot sl_{j} - (d - i)}{(1 - \mathit{cr}_{j})\cdot sl_{j}}\cdot x_{ijld} \\ &\quad {} - \sum_{i = 1}^{I} \sum_{j = 1}^{J} \sum_{l = 1}^{L} \sum_{d = 1}^{D} c_{jl}^{\mathit{prod}}\cdot x_{ijld} - \sum_{i = 1}^{I} \sum_{j = 1}^{J} \sum_{l = 1}^{L} c_{j}^{inv}\cdot \mathit{inv}_{ijl} \\ &\quad {}- \sum_{j = 1}^{J} \sum_{d = 1}^{D} \sum_{a = 1}^{A} c_{j}^{\mathit{unmet}}\cdot \mathit{ud}_{jda} - \sum_{i = 1}^{I} \sum_{j = 1}^{J} \sum_{k = 1}^{J} \sum_{l = 1}^{L} c_{jk}^{\mathit{setup}}\cdot z_{ijkl} \\ &\quad {} - \sum_{i = 1}^{I} \sum_{l = 1}^{L} c_{l}^{\mathit{overtime}}\cdot \mathit{overtime}(i,l) - \sum_{j = 1}^{J} \sum_{l = 1}^{L} \sum_{a = 1}^{A} \sum_{d = 1}^{D} c_{al}^{\mathit{transport}}\cdot y_{jlad} \end{aligned} $$
(1)

The objective function (1) aims to maximize the benefit by considering the shelf life of products and costs such as production, setup, storage, overtime, unmet demand and transportation. It is supposed that the manufacturer yields a financial benefit if the products have a longer residual shelf life when being delivered (Lütke Entrup et al. 2005). The shelf life-dependent benefit increases linearly because the benefits for customer increase with every additional day of residual shelf life. For instance, suppose that product j has a total shelf life of 30 days, the customers require 66 % of shelf life as a minimum residual shelf life (cr j =0.66). If product is delivered on 3th day of its shelf life, the benefit will be benefit j ⋅0.70, however if product is delivered on 6th day of its shelf life, the benefit will be benefit j ⋅0.41 for the product.

(2)
(3)
(4)
(5)
(6)

Lower and upper bounds on the product lot sizes are imposed by the Constraints (2)–(3). The variables input j and output j in Constraints (4), (5) and (6) are designed to satisfy demand of day d fully or partially for product j. Constraint (4) refers to sum of production quantity and unmet demand of product j. Products that will cover demand at demand day d have to be produced within a specific time window concerning shelf life and quarantine time. The parameter qq j refers to the quarantine time. A quarantine time is precondition for achievement of the desired sensory qualities. The products can only be delivered after quarantine time has passed (i+qq j ≤d). Moreover, the shelf life lost (d−i) may not exceed a threshold defined by customer requirements on shelf life (d−i)≤(1−cr j )⋅sl j ) (Lütke Entrup et al. 2005). Constraint (5) corresponds to the sum of demand from all distribution centres during the whole scheduling period for product j and unmet demand of distribution centres. Constraint (6) guaranties that sum of production and unmet demand for product j during the last period should be equal to the sum of demand that comes from all distribution centres during the whole scheduling period.

$$ x_{ijld} =0 \quad \forall i \geq\ \forall j,\ \forall l $$
(7)

According to Constraint (7), production quantity must equal to zero out of the time windows defined. That is, demand of demand day d cannot be produced in the same day (d=i) or after the demand day (i>d). Production is impossible when production day is greater than the demand day.

$$ \sum_{a = 1}^{A} y_{jlad} = \sum_{i = 1}^{I} x_{ijld}\quad \forall j,\ \forall l,\ \forall d $$
(8)

Constraint (8) provides the quantity of product j produced on line l for the demand of day d to be the same with the quantity of product j transferred to the various distribution centres for demand of day d.

(9)
(10)

According to constraints (9) and (10), sum of unmet demand of distribution center a for product j on demand day d and the quantity of product j that transferred from various production lines to distribution center a should be equal to sum of the demand of distribution center a for product j on demand day d and unmet demand for product j from the previous period.

(11)
(12)

Constraints (11)–(12) are the inventory balance equations. Constraint (11) shows the inventory level only for the first day. The inventory of product j on line l at the end of first day is equal to the quantity of product j produced on line l during the first day to meet the demands of different demand days minus the quantity of product j shipped from line l to the various distribution centres during the first day. Constraint (12) refers to the inventory level at the end of day i on line l. On the remaining days inventory of product j on line l is equal to the quantity of product j produced on line l on day i to meet the demands of different demand days plus the inventory of the previous day and minus the quantity of product j shipped from line l to the various distribution centres during period i.

(13)
(14)
(15)
(16)

Constraints (13)–(16) are timing constraints that define the starting and finishing time for each product on each line and day. The processing time of a product is calculated by dividing the production quantity by the line speed for the product as declared by Constraint (13). The starting time of the first product is set to zero in each day as shown in Constraint (14). The finishing time of product j on line l and day i is defined in Constraint (15), and is determined by adding, processing time and changeover time needed for the transition to the next product to be produced to the starting timeNote that, when a product is not produced, processing time, and all associated binary variables equal to zero. The finishing time is exactly same with the starting time. The starting time of product j on line l on day i should be greater than the finishing time of the previous product as emphasized in Constraint (16).

(17)
(18)
(19)

The total processing time in a day is equal to the finishing time of the last product. It is considered in Constraint (17), lasttime il refers to the finishing time of the last product on line l on day i. The total machine time is bounded with the maximum time available a machine can work in Constraint (18). rtime il corresponds to regular shift of line l on day i. Last time passing over the regular shift means over time for line l on day i. Overtime needed on line l on day i is computed in Constraint (19).

(20)
(21)
(22)
(23)
(24)
(25)
(26)

Binary variable in Constraint (20) is equal to 1 if and only if product j is produced on line l on day i for demand of day d. Constraint (21) ensures that only specific sequence of product is allowed on line l. The relationship between b ijl and b ikl is illustrated in Constraints (22) and (23). z ijkl is equal to 1, if product j and k are produced in a row. Constraint (24) shows that the number of produced items, minus the number of setups must be less than or equal to 1. In all cases where the line produces at least one product during a day, this constraint holds. In the unlikely case where the line is not utilized at all during a day, Constraint (24) still holds, as both the number of produced items and the number of setups are equal to 0. Although Constraint (24) does not add new information to the model, it increases the speed of model to obtain the solution. Constraints (25)–(26) link the binary variables.

(27)

Nonnegativity and integrity constraints are defined in (27).

4.2 Simulation model

In real-world system, operation times cannot be accepted as a static factor. Because of the dynamic nature of the real system, the exact solution obtained from the mathematical model cannot be applied practically. Simulation models include nonlinearities, complex structure and stochastic structure which are main features of the real system.

The simulation model is established to represent the MILP model. It includes machine failures as different from the mathematical model. The conceptual model of the system is shown in Fig. 1. Production starts with the products on a line considering the production day row. The priority of products is important, since it is not allowed the product with high sequence number to produce firstly in the MILP model. For that reason, the simulation model always starts with the first product. After the desired quantity of the first product is completed, the model controls the conditions and starts the production of second product. When all program given according to MILP results for day i is completed, the model starts the production of the following day. During the program, the failures become active. Thus, the operation times required for the production schedule given by MILP model can be measured. In order to obtain mean operation times, five independent replications are performed in the simulation model.

Fig. 1
figure 1

Conceptual model

Full size image

4.3 Hybrid solution approach

The production systems generally include dynamic nature in real systems. The simulation model provides to insert real operation times to the mathematical model. The production schedule that is achieved from the mathematical model is taken as an input for the simulation model. The simulation model result gives us total production time for each product. The total time of a product spent in a machine is used to compute the real operation time for that product on a particular machine. The solution of simulation model is reflected as the operation time in the mathematical model. Therefore, the operation time in the mathematical model is adjusted by the results of the simulation model and the mathematical model regenerates new production scheduling program by the adjusted operation time (Safaei et al. 2010). The interaction between simulation and optimization is displayed in Fig. 2. Within this framework it is possible to test the optimal deterministic solution of the MILP model in a stochastic environment and to analyze whether this solution is also feasible in the context of a more complex and more realistic simulation model.

Fig. 2
figure 2

Interaction between simulation model and MILP model

Full size image

The iteration ends if the difference rate between preceding simulation operation time (POT) and current simulation operation time (COT) is close enough to be acceptable. When the difference is close enough, the mathematical model is regarded as reflecting the realistic situation through the simulation model. Therefore, the scheduling program taken from mathematical model at that iteration reflects the stochastic situations and regarded as realistically optimal.

The procedure consists of 7 steps (Safaei et al. 2010):

  1. Step 1

    Solve the mathematical model and obtain the production plan.

  2. Step 2

    Run the simulation model based on the current production plan.

  3. Step 3

    Obtain current operation times for products on each machine via simulation model (COT).

  4. Step 4

    If the difference rate between preceding operation time (POT) and current operation time (COT) is within the rate of 0.025, then go to step 6, otherwise go to step 5.

  5. Step 5

    Solve the mathematical model using operation times for products on each line as machine speed.

  6. Step 6

    Mathematical solution: Optimal production plan.

  7. Step 7

    Stop.

A flow diagram in Fig. 3 illustrates the solution procedure.

Fig. 3
figure 3

Flow diagram of hybrid method

Full size image

5 Case study and computational results

A scheduling problem in yoghurt production lines of multi-product dairy plants is analyzed in this research. The dairy firm is a milk-processing company that runs two factories located in different cities. Ten different product types are produced in factories that include nine production lines to satisfy demands of customers. The product types differ from each other based on cup size and yoghurt type. Five types of products are common that they can be produced in both factories. While two of them can be produced only in Factory 1, three of them can be produced in Factory 2 because of the location of the production lines. The assignment of the nine production lines to the factories is shown in Table 1. Lines 1, 2, 3 and 7 are located in Factory 1 and Lines 4, 5, 6, 8 and 9 are located in Factory 2. For that reason some products can only be produced in one factory. Table 2 refers to assignment of products to the lines and factories. In the Table 1, P1 refers to product type 1 and L1 refers to production line 1. While some products can be produced in more than one machine, some machines can produce more than one product. Table 3 shows the machine speeds for each product type, and production line. Some products which can be produced more than one production line have the same machine speed for the different production lines.

Table 1 Plant-production line matrix
Full size table
Table 2 Machine–product matrix
Full size table
Table 3 Machine speeds for product types
Full size table

In multi-product machines, changeover times should be considered because in a machine, more than one product can be produced and setup times are sequence dependent. In the dairy industry, there is often a natural sequence in which the various products are to be produced in order to minimize total changeover time such as, from the lower taste to the stronger or from the brighter color to the darker (Nakhla 1995; Gunther and Neuhaus 2004). In dairy industry, it is common that products have to spend at least a minimum time. This can be caused by obligatory quality checks (Lütke Entrup 2005). Therefore, all products should complete their quality control process after the production. For all yoghurt products, the quality control process is completed in 2 days. It means that, the customer should order the demands at least two days before or the demands should be produced at least 2 days before the order day. The demands for all products come from 7 different distribution centres. In this case, production horizon is determined as 5 days which starts on Monday. The demands of Wednesday are defined as the beginning of demand period because of the two-day-long quality process. It consists of 5 days that starts with Wednesday and ends with Sunday. Because the yoghurt is a perishable product, stock level should be kept in an acceptable level. It is important to determine the production quantity in every period of time properly. The stock level should minimize the unmet demand with maximum freshness. Shelf life takes a significant part in the objective function because customers tend to buy the product with a longer remaining shelf life. The financial benefit of a product increases, if the product has a longer shelf life when being delivered. The shelf life dependent benefit increases linearly between the minimum customer requirement on shelf life and the maximum possible shelf life (Lütke Entrup et al. 2005).

Regular, overtime and maximum working hours can be seen from Table 4. Table 5 provides the main data regarding maximum benefit for meeting the maximum shelf life of product, critical rate, quarantine time, unmet demand cost, and inventory cost for each product type. Transportation cost from production lines to distribution centres is stated in Table 6. Production cost is defined for each product and production line, and overtime cost is defined for each production line. These data are shown in Tables 7 and 8, respectively. Product demands for the case study are given in Table 9.

Table 4 Scheduling horizon for yoghurt production
Full size table
Table 5 Data defined by product type
Full size table
Table 6 Transportation cost from lines to distribution centers
Full size table
Table 7 Production cost
Full size table
Table 8 Overtime cost for each line
Full size table
Table 9 Demand data
Full size table

In real systems, the theoretical capacities for machines cannot be used completely because of failures. Production disturbances on packaging lines are studied based on machine failures. Machine breakdowns are one of the sources of capacity disruptions. In this system, there are two types of breakdowns as short and long failures. When a breakdown comes out during production, the production of a product is prevented because of the failure. Table 10 shows the probability density of failure and repair times for the production lines. Short failures emerge more often than long failures. But, the repair times for short failure types are shorter and they do not prevent production as much as the long failures.

Table 10 Probability density of failure and repair times
Full size table

The results of initial condition for operation times and mean of results are listed in Table 11. In Table 11, pt11 refers the operation time of a unit of Product 1 on Line 1. Similarly, pt45 refers the operation time of Product 4 on Line 5. Mean operation times obtained from simulation model are used as speed of machines in the MILP model. The resulting operation time for each product and production line through the iterations are given in Table 12. Operation times are fluctuating. However the widths of fluctuation decrease as iteration is increased. It can be seen from Table 12 of results that dramatic changes have occurred in operation times immediately after the initial iteration.

Table 11 The results of simulation model for each replication in initial conditions
Full size table
Table 12 Simulation results for each iteration
Full size table

In Table 13, the computation of critical rate is shown for the hybrid method. The operation times correspond to the results of simulation model for iterations 1–4. For instance, the operation time of Product 5 on Line 3 is 0.013 for the initial solution, 0.014 for iterations 1, 2, 3, and 4. The critical rate indicates the rate between iterations. Critical rate is calculated by dividing absolute value of (preceding operation time-current operation time) by the current operation time.

Table 13 Computation of critical rate for hybrid method
Full size table

The mathematical formulation was solved using CPLEX 12.4. The simulation model was implemented in Arena version 10.0. They were solved on a laptop with Intel Core i7 Q720, 1.73 GHz and 8 GB memory. The computational results are summarized in Table 14. The variability of objective function in each iteration can be seen in Fig. 4. The changes in machine speed have also resulted in substantial increase in total system costs over the original analytic optimum. The solution identified by the hybrid procedure after the initial iteration involves reduced machine speed. Hence this solution incurs high costs, which results in a reduction in the profit, due the capacity disruption. Despite of decreasing in objective value, the last iteration gives us more realistic and practical solution for the problem.

Fig. 4
figure 4

The changes of objective function

Full size image
Table 14 Computational results for the case study
Full size table

As well as objective value, the trend of decision variables that affects the objective value is represented in the following tables for the iterations. The variations in unmet demand for the products are shown in Fig. 5 and Table 15. While the unmet demand of Product 1 decreases in the last iteration, increasing for Product 10 is observed in the last iteration.

Fig. 5
figure 5

The unmet demand of products based on iterations

Full size image
Table 15 The quantity of unmet demand for products in each day
Full size table

In Figs. 6 and 7, the trend of inventory is represented. Figure 6 shows the variation in the inventory level for production lines in each iteration. We observe that storage constraints result in a reduction of inventories by initiating failure in operation time. As can be seen in Fig. 6, there is no great change between the iterations, since simulation models leads to similar operation times after the initial iteration. Dramatic changes have occurred after the initial iteration. Figure 7 shows the total inventory levels between iterations and the initial solution.

Fig. 6
figure 6

Inventory levels for lines

Full size image
Fig. 7
figure 7

Total inventory levels in each iteration

Full size image

Figure 8 shows the total and particularly overtime variability for the lines between iterations. Only lines 1, 2, 7, 8 and 9 need overtime for the production program. As it is seen in Fig. 8, overtime value increases at iteration 1. However, there is no difference between iterations after the initial solution, as convergence is achieved. While there is no need to overtime for Line 1 and Line 8 in the initial solution, overtime starts at iteration 1 for Line 1 and Line 8. The failures considered in the hybrid model causes the decreasing of the machine speed. That’s why the lines need overtime for meeting the demands.

Fig. 8
figure 8

Overtime for iterations in each line

Full size image

The production quantities for the products in each iteration are shown in Fig. 9. In general, after the first iteration, there is a little change in production quantities for each day. The system is balanced with the second iteration. Finally; the optimal production scheduling program obtained through the hybrid method is tabulated as Gantt chart in Table 16.

Fig. 9
figure 9

Production quantity for products in each iteration

Full size image
Table 16 Gantt chart for optimal production scheduling program
Full size table

Through the computational experiments, we can conclude the following results:

  • The overall benefit decreases in comparison with the initial solution. However, the results obtained by considering stochastic factors reflect the real system features.

  • The overtime values are redesigned for the lines, thus the workforce can be planned in a more realistic way.

  • The inventory level of the lines starts decreasing at iteration 1. That means the inventory holding cost decreases compared to the initial condition.

  • Unmet demand is not affected from failures, since the capacity is distributed optimally by the MILP model.

6 Conclusion

This paper addresses the short term production scheduling and distribution planning problem within the dairy industry. The problem is modeled as a MILP. An efficient hybrid solution methodology based on a MILP formulation and a simulation approach is presented to obtain optimal production schedules, and distribution plan via mathematical modelling while incorporating uncertainties in the execution of these plans via simulation. To evaluate the model and the solution method, a case study is introduced.

The objective function aims to maximize the benefit by considering the shelf life dependent pricing component and various cost components. The shelf life constraints are designed in MILP model to improve product freshness. The shelf-life dependent pricing components are determined based on the real data. In addition, sequence dependent setup time, demand due dates, different machine speed for products, overtime planning, unmet demand, and delivery to the distribution centres are included in the MILP model formulation.

As a result, MILP model provides a scheduling program by optimizing the resources. In order to apply scheduling program in practice, the stochastic factors that are ignored in the MILP model are added to the problem by the simulation model. While the attributes of food processing are accepted as fixed values in most of the previous studies, operation time is inserted as a stochastic parameter for the realistic solution. It is adjusted according to the simulation model results. For determining operation time, probability density of machine failures and repair times are considered as short and long durations in the simulation model. Hybrid approach combines the advantages of MILP model and simulation model. Therefore, it is clear that this approach is more realistic even compared with traditional planning approaches. The key limitation of the overall solution approach lies in the large computational times that are mainly due to large number of integer variables. As a future research direction, we are investigating methods to reduce the time spent in MILP and simulation models. There are several extensions and variations to be investigated as future research. On practical side, the current model may be expanded to incorporate multi-stage production scheduling. The other stochastic factors can be added to the model besides operation time for more realistic solution.