1 Introduction

Markov repairable system with state aggregated is a hot topic in the literature, because there have been the number of papers devoted to this class of models recently. The research in this direction has used aggregated stochastic processes which developed greatly in Ion channel modeling, for example, Colquhoun and Hawkes (1982) introduced an aggregated Markov process to model the performance of Ion-Channel. Recently, some scholars have borrowed the techniques in Ion channel modeling on repairable systems. For example, Cui et al. (2012a) studied a single-unit repairable system with state aggregations. Cui et al. (2007) developed an aggregated Markov repairable system with history-dependent up and down states, in which some states are changeable. Wang and Cui (2011) extended the model into the semi-Markov repairable system with history-dependent up and down states which is more realistic than previous one. Wang et al. (2011) studied a Markov repairable system with stochastic regimes switching and got the distribution of up time of the system. Time interval omission problem is very important in the fields of in Ion-Channel theory and reliability. Ball et al. (1991) considered an aggregated semi-Markov process incorporating time interval omission in terms of Ion-Channel modeling theory. In the field of reliability, Zheng et al. (2006) first developed a new model which is based on a single-unit Markov repairable system. In that model, if a short repair time does not affect the system operating or throughput, the system could be thought of as operating during this repair time, and availability was discussed for the model in detail by the authors in that paper. Bao and Cui (2010) further extended the work of Zheng et al. (2006) to series Markov repairable system with neglected or delayed failures. However, there are only two states, i.e., one up state and one down state, in the state space for the model in Zheng et al. (2006), so that some practical situation still cannot be covered, for example, there are several hundred states in a electricity transmission system, so we develop an aggregated Markov system with time interval omission in the paper, whose finite state space is grouped into two sets, the set of working states and the set of failed states.

Availability (Li et al. 2006) and interval reliability (in Cui et al. 2012b, it is called interval availability) are two important reliability measures in the field of reliability. Availability is the probability that system is ‘up’ at time t (Barlow and Proschan 1965). The interval reliability is the probability that system is ‘up’ throughout the time interval [a,b]. Csenki (1994, 1995) discussed the interval reliability of systems modeled by finite semi-Markov processes. Csenki (2007) further studied the joint interval reliability for a Markov repairable system. There are also many indexes to be used in describing the various properties of the repairable systems, for example, in Hawkes et al. (2011), several reliability indexes for repairable systems were given. Although it exists many indexes for a repairable system such as distribution of up or down duration, visit number to up or down sets in a cycle, and their mean and so forth, the availability is a main considered index in many repairable systems such as in Cui et al. (2007) and Bao and Cui (2010), and so on. However, Zheng et al. (2006) discussed only one reliability index, i.e., the availability for the model, there are still many reliability indexes that need to be discussed for the repairable system with time interval omission. So we first develop an aggregated Markov system with time interval omission that is an extension of Zheng et al. (2006), then we discussed some new reliability indexes, i.e., availability, interval reliability, and interval unreliability for the model in the paper. In Cui et al. (2012b), model II in the paper is exactly the same with our model in the paper, and the consideration reliability indexes also are the same as these in our present paper, but we present a new method based on Laplace transforms to give the formulae on the interval reliability in the present paper, and the interval unreliability was not included in Cui et al. (2012b) paper, because of sum not being one for interval reliability and unreliability. We first consider the interval reliability for the aggregated Markov system with time interval omission in the given time interval [0,t], then we further consider the interval reliability in the general time interval [a,b] by using Markov property. The interval unreliability is also considered in the present paper.

The rest of the paper is organized as follows. In Sect. 2, the model is developed and some assumptions are also given. Several reliability indexes are obtained for the model in Sect. 3. Some special cases are also discussed in this section. A numerical example is presented to illustrate the results of the paper in Sect. 4. Finally, conclusions are given in Sect. 5.

2 Assumptions and modeling

Given a repairable system, denoted as a homogenous irreducible continuous-time Markov stochastic process {X(t),t≥0}, with transition rate matrix Q and finite state space S={1,2,…,n}. The state space, S, can be grouped into two sets, W and F (i.e. S=W∪F,(W∩F=ϕ)), where W is the set of working (or ‘up’) states and F is the set of failed (or ‘down’) states. Thus the repairable system will alternate between W and F indefinitely. The initial probability vector is Φ 0=(π W ,π F ) and the transition rate matrix Q can be divided into four parts in terms of the partition of state space, i.e.,

$$\mathbf{Q} = \left ( \begin{array}{c@{\quad }c} \mathbf{Q}_{WW} & \mathbf{Q}_{WF} \\\noalign{\vspace*{3pt}} \mathbf{Q}_{FW} & \mathbf{Q}_{FF} \end{array} \right ). $$

Some basic notation and results which are used in the present paper are now summarized. In terms of Colquhoun and Hawkes (1982), the transition probability matrix of {X(t),t≥0}, denoted as P(t), can be defined as follows:

$$\mathbf{P}(t) \buildrel{\Delta} \over{ =} \bigl( p_{ij}(t) \bigr)_{\vert S \vert \times \vert S \vert } = \exp (\mathbf{Q}t),\quad i,j \in S, $$

where p ij (t)=P{X(t)=j|X(0)=i},i,j∈S and P(t) denotes probabilities, given initial probability vector, that the repairable system be in each state of S at instance time t. Colquhoun and Hawkes (1982) defined another matrix as follows:

$$\mathbf{P}_{WW}(t) \buildrel{\Delta} \over{ =} \bigl( P\bigl\{ X(t) = j, X(u) \in W,u \le t|X(0) = i\bigr\} \bigr) = \exp (\mathbf{Q}_{WW}t), \quad i,j \in W, $$

where P WW (t) denotes probabilities, given initial probability vector, that the repairable system stays in the working states W throughout a given time interval [0,t].

The density matrix of the duration of a sojourn in W is given by

$$\mathbf{G}_{WF}(t) = \exp (\mathbf{Q}_{WW}t) \mathbf{Q}_{WF}. $$

Taking Laplace transform, it follows that

$$\mathbf{G}_{WF}^{ *} (s) = \int_{0}^{\infty} e^{ - st}\mathbf{G}_{WF}(t)dt = (s\mathbf{I} - \mathbf{Q}_{WW})^{ - 1}\mathbf{Q}_{WF}. $$

The matrix, \(\mathbf{G}_{WF}^{ *} (0)\), will be denoted simply as G WF , for brevity, i.e.,

$$\mathbf{G}_{WF} = \mathbf{G}_{WF}^{ *} (0) = - \mathbf{Q}_{WW}^{ - 1}\mathbf{Q}_{WF}. $$

The density matrix of the duration of sojourns in F is given by

$$\mathbf{G}_{FW}(t) = \exp (\mathbf{Q}_{FF}t) \mathbf{Q}_{FW}. $$

Thus

$$\everymath{\displaystyle} \begin{array}{rcl} \boldsymbol{\varPsi} _{\tau} ^{ *} (s) &=& \int_{0}^{\tau} e^{ - st}\mathbf{G}_{FW}(t)dt = \int_{0}^{\tau} e^{ - st}\exp (\mathbf{Q}_{FF}t)\mathbf{Q}_{FW}dt \\\noalign{\vspace*{6pt}} &=& (s\mathbf{I} - \mathbf{Q}_{FF})^{ - 1} \bigl(\mathbf{I} - \exp \bigl( - (s\mathbf{I} - \mathbf{Q}_{FF}) \bigr)\tau \bigr)\mathbf{Q}_{FW}, \end{array} $$

denotes the Laplace transform of duration of sojourns in F, and the duration of the sojourns is less than a given nonnegative critical value τ.

The probability that the repairable system stays in the failed states F being less than τ is as follows

$$\int_{0}^{\tau} \mathbf{G}_{FW}(t)dt = \mathbf{Q}_{FF}^{ - 1}\bigl[\exp (\mathbf{Q}_{FF}\tau ) - \mathbf{I}\bigr]\mathbf{Q}_{FW}. $$

In the following, a new model is defined on the basic assumptions for the original Markov repairable system.

  1. (1)

    The new system has two possible states: one working state and one failure state, i.e., state 1 and state 0, respectively.

  2. (2)

    The new system is in the working state 1 when the original Markov repairable system is in the working states W.

  3. (3)

    If the original Markov repairable system enters a failed state, and stays in failed states F less than a given nonnegative critical value τ, i.e., it takes no longer τ to repair the system to enter a working state, then the new system is still in the working state 1 during this repair time.

  4. (4)

    If the original Markov repairable system enters the failed states F, and stays in failed states more than a given nonnegative critical value τ, i.e., it takes more than τ to repair the system to enter a working state, then the new system is considered to remain in the failure state 0 during this repair time until the repair is finished.

Notice that if a repair time at each state is less thanτ, but the sum of these repair times are greater than τ, then the multiple failure states are classified as failure state 0 in the new model. Our model doesn’t consider the delayed failures.

The evolution of the new system follows a new continuous-time stochastic process \(\{ \tilde{X}(t),t \ge 0\}\), which is defined as follows

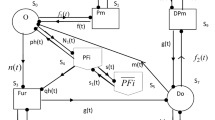
$$\tilde{X}(t) = \left \{ \begin{array}{l@{\quad }l} 1,& \mbox{if the new system in the working state at time}\ t, \\\noalign{\vspace*{3pt}} 0, & \mbox{if the new system in the failure state at time}\ t. \end{array} \right . $$

Some possible sample paths of the original Markov repairable system and the new model for Cases I and II are presented in Figs. 1 and 2.

Fig. 1
figure 1

A possible sample path of the original Markov repairable system and the new model for Case I

Full size image
Fig. 2
figure 2

A possible sample path of the original Markov repairable system and the new model for Case II

Full size image

3 Reliability indexes

3.1 Availability

The availability of the original Markov repairable system of {X(t),t≥0} can be got easily

$$A_{X}(t) \buildrel{ \Delta} \over {=} P \bigl\{ X(t) \in W\bigr\} = (\boldsymbol{\pi} _{W},\boldsymbol{\pi} _{F})\exp (\mathbf{Q}t)\left ( \begin{array}{l} \mathbf{1}_{W} \\\mathbf{0}_{F} \end{array} \right ), $$

where 1 W and 0 F is a unit column vector and a zero column vector with appropriate dimensions, respectively, see Csenki (2007).

Definition 1

The availability of the new model of \(\{ \tilde{X}(t),t \ge 0\}\) is defined as follows

$$A_{\tilde{X}}(t) \buildrel{\Delta} \over{ =} P \bigl\{ \tilde{X}(t) = 1\bigr\}. $$

Theorem 1

For the new model of \(\{ \tilde{X}(t),t \ge 0\}\) as described in Sect. 2, the availability is

$$\everymath{\displaystyle} \begin{array} {rcl} A_{\tilde{X}}(t) &=& A_{X}(t) \\\noalign{\vspace*{3pt}} &&{}+ \int_{0}^{\min (t,\tau )} \bigl\{ (\boldsymbol{\pi} _{W},\boldsymbol{\pi} _{F})\exp \bigl(\mathbf{Q}(t - s)\bigr)\left ( \begin{array} {l} \mathbf{I}_{\vert W \vert \ \times \vert W \vert } \\\mathbf{0}_{\vert F \vert \boldsymbol{\times} \vert W \vert } \end{array} \right )\\\noalign{\vspace*{3pt}} &&{}\times \mathbf{Q}_{WF}\bigl[\exp (\mathbf{Q}_{FF}s) - \exp (\mathbf{Q}_{FF}\tau )\bigr] \mathbf{1}_{F}\bigr\} ds, \end{array} $$

where I is a unit matrix with appropriate size, 0 is a zero matrix with appropriate size.

Proof

From the assumptions of the new model, we have

$$\everymath{\displaystyle} \begin{array} {rcl} A_{\tilde{X}}(t) &\buildrel{ \Delta} \over{ =}& P\bigl\{ \tilde{X}(t) = 1\bigr\} = P\bigl\{ \tilde{X}(t) = 1,X(t) \in W\bigr\} + P\bigl\{ \tilde{X}(t) = 1,X(t) \in F\bigr\} \\&=& P\bigl\{ X(t) \in W\bigr\} + P\bigl\{ \tilde{X}(t) = 1,X(t) \in F\bigr\}\\\noalign{\vspace*{3pt}} &=& A_{X}(t) \\\noalign{\vspace*{3pt}} &&{}+ \int_{0}^{\min (t,\tau )} \bigl\{ (\boldsymbol{\pi} _{W},\boldsymbol{\pi} _{F})\exp \bigl(\mathbf{Q}(t - s)\bigr) \left ( \begin{array} {l} \mathbf{I}_{\vert W \vert \times \vert W \vert } \\\mathbf{0}_{\vert F \vert \times \vert W \vert } \end{array} \right )\\\noalign{\vspace*{3pt}} &&{}\times \mathbf{Q}_{WF} \bigl[\exp (\mathbf{Q}_{FF}s) - \exp ( \mathbf{Q}_{FF}\tau ) \bigr]\mathbf{1}_{F}\bigr\} ds, \end{array} $$

since (π W ,π F )exp(Q(t−s)) is a probability vector that the original Markov repairable system of {X(t),t≥0} sojourns in each state of S at instance time t−s, and the function of matrix is to keep the repairable system starts from the working states of W, and [exp(Q FF s)−exp(Q FF τ)]1 F is probabilities that the duration of the Markov repairable system of {X(t),t≥0} remains within in the failed states is greater than s, but less than τ, so that the repair time interval can be omitted. The column vector 1 F is to sum up all possible probabilities satisfied the requirements. The proof is completed. □

3.2 Interval reliability

In general, the given nonnegative critical value τ is very small, so, we only consider the case t>τ in the following section.

The interval reliability of the original Markov repairable system of {X(t),t≥0}, given a time interval [0,t], can be got easily

$$A_{X}[0,t] \buildrel{\Delta} \over{ =} P\bigl\{ X(u) \in W,\quad \mbox{for all}\ u \in [0,t]\bigr\} = \boldsymbol{\pi} _{W}\exp ( \mathbf{Q}_{WW}t)\mathbf{1}_{W}, $$

see Csenki (2007).

The interval reliability of the original Markov repairable system of {X(t),t≥0}, given a time interval [a,b], can be got easily

see Csenki (2007).

Definition 2

The interval reliability of the new model of \(\{ \tilde{X}(t),t \ge 0\}\), given a time interval [0,t], is defined as follows:

$$A_{\tilde{X}}[0,t] \buildrel{\Delta} \over{ =} P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t]\bigr\}. $$

In the following, we shall discuss the interval reliability of the new model of \(\{ \tilde{X}(t),t \ge 0\}\).

Based on the total probability formula, we can get

$$\everymath{\displaystyle} \begin{array} {rcl} A_{\tilde{X}}[0,t] &\buildrel{ \Delta} \over{ =}& P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t]\bigr\} \\\noalign{\vspace*{3pt}} &=& P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t], X(0) \in W\bigr\} + P\bigl\{ \tilde{X}(u) = 1, \\\noalign{\vspace*{3pt}} &&\hphantom{P\bigl\{ \tilde{X}(u) = 1,}\,\ \mbox{for all}\ u \in [0,t], X(0) \in F\bigr\} \\\noalign{\vspace*{3pt}} &=& P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t] | X(0) \in W \bigr\} P\bigl\{ X(0) \in W\bigr\} \\\noalign{\vspace*{3pt}} &&{}+ P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t] | X(0) \in F \bigr\} P\bigl\{ X(0) \in F\bigr\} \\\noalign{\vspace*{3pt}} &=& \boldsymbol{\pi} _{W}\mathbf{1}_{W}P \bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t] | X(0) \in W \bigr\} \\\noalign{\vspace*{3pt}} &&{}+ \boldsymbol{\pi} _{F} \mathbf{1}_{F}P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t] | X(0) \in F \bigr\}. \end{array} $$

We first consider \(P\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t] | X(0) \in W \}\). Figure 1 is a possible sample path for the original Markov repairable system of {X(t),t≥0}, and the new model of \(\{ \tilde{X}(t),t \ge 0\}\) for this case, we call it Case I. Case I can be decomposed into Situations 1 and 2 in the following.

$$\everymath{\displaystyle} \begin{array} {rcl} P\bigl\{ \tilde{X}(u) &=& 1,\ \mbox{for all}\ u \in [0,t] | X(0) \in W \bigr\} \\\noalign{\vspace*{3pt}} &=& \sum_{j = 0}^{\infty} P \bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],N(t) = j | X(0) \in W \bigr \}, \end{array} $$

where N(t) denotes the complete up-down cycle number of the original Markov repairable system of {X(t),t≥0} by time t. Further, the two situations X(t)∈W and X(t)∈F will be considered, respectively. In fact, totally, we need to consider 4 situations for getting \(A_{\tilde{X}}[0,t]\), i.e.

  1. Situation 1:

    X(t)∈W,N(t)=0,1,…,conditional on X(0)∈W,

  2. Situation 2:

    X(t)∈F,N(t)=0,1,…,conditional on X(0)∈W,

  3. Situation 3:

    X(t)∈W,M(t)=0,1,…,conditional on X(0)∈F,

  4. Situation 4:

    X(t)∈F,M(t)=0,1,…,conditional on X(0)∈F.

Notice that M(t) denotes the complete down-up cycle number of the original Markov repairable system of {X(t),t≥0} by time t.

In the following, we will consider 4 situations listed above, respectively.

Situation 1

\(\sum_{j = 0}^{\infty} P\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],N(t) = j, X(t) \in W | X(0) \in W \}\).

Let T j and D j be sums of the first jth working and repair durations within j complete up-down cycles, respectively. Let T 0=D 0=0, and

$$\everymath{\displaystyle} \begin{array}{l} f_{\mathbf{W}(i_{1})\mathbf{W}(i_{2}) - (j,j)}(u) \buildrel{ \Delta} \over{ =} \lim_{du \to 0}P\bigl\{ T_{j} + D_{j} \in (u,u + du), \\\noalign{\vspace*{3pt}} X(T_{j} + D_{j}) = i_{2}|X(0) = i_{1}\bigr\} /du,\quad i_{1},i_{2} \in W. \end{array} $$

Based on the results of Colquhoun and Hawkes (1982), thus we have

$$\mathbf{f}_{WW - (j,j)}^{*}(s) = \bigl[\mathbf{G}_{WF}^{*}(s) \boldsymbol{\varPsi} _{\tau} ^{ *} (s)\bigr]^{j} = \bigl( f_{_{W(i_{1})W(i_{2}) - (j,j)}}^{*}(s) \bigr)_{|W| \times |W|}, $$

where \(f_{_{W(i_{1})W(i_{2}) - (j,j)}}^{*}(s) = \int_{0}^{\infty} e^{ - su}f_{W(i_{1})W(i_{2}) - (j,j)}(u)du\).

Note that in order to guarantee \(f_{W(i_{1})W(i_{2}) - (j,j)}(u)\) to be a proper probability density function, we have

$$f_{W(i_{1})W(i_{2}) - (j,j)}(u) = \frac{\ell ^{ - 1}[f_{_{W(i_{1})W(i_{2}) - (j,j)}}^{*}(s)](u)}{f_{_{W(i_{1})W(i_{2}) - (j,j)}}^{*}(0)},$$

and

$$\mathbf{f}_{WW - (j,j)}(u) = \bigl( f_{W(i_{1})W(i_{2}) - (j,j)}(u) \bigr)_{|W| \times |W|}. $$
$$\everymath{\displaystyle} \begin{array} {rcl} H_{1 - W - W}(t) &=& \sum _{j = 0}^{\infty} P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],N(t) = j, X(t) \in W | X(0) \in W \bigr\} \\\noalign{\vspace*{3pt}} &=& P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],N(t) = 0, X(t) \in W | X(0) \in W \bigr\} \\\noalign{\vspace*{3pt}} &&{} + \sum_{j = 1}^{\infty} P \bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],N(t) = j, X(t) \in W | X(0) \in W \bigr\} \\\noalign{\vspace*{3pt}} &=& \frac{\boldsymbol{\pi} _{W}}{\boldsymbol{\pi} _{W}\mathbf{1}_{W}}\exp (\mathbf{Q}_{WW}t) \mathbf{1}_{W}\\\noalign{\vspace*{6pt}} &&{} + \sum_{j = 1}^{\infty} P \bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],N(t) = j, X(t) \in W | X(0) \in W \bigr\}. \end{array} $$

We now consider the summation

$$\sum_{j = 1}^{\infty} P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],N(t) = j, X(t) \in W | X(0) \in W \bigr\}. $$

In fact, we can get

$$\everymath{\displaystyle} \begin{array} {l} \sum_{j = 1}^{\infty} P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],N(t) = j, X(t) \in W | X(0) \in W \bigr\} \\\noalign{\vspace*{3pt}} \quad {}= \sum_{j = 1}^{\infty} P\bigl\{ T_{j} + D_{j} < t \le T_{j + 1} + D_{j} | X(0) \in W \bigr\}\\\noalign{\vspace*{6pt}} \quad {} = \frac{\boldsymbol{\pi} _{W}}{\boldsymbol{\pi} _{W}\mathbf{1}_{W}}\sum _{j = 1}^{\infty} \int_{0}^{t} \mathbf{f}_{WW - (j,j)}(u)\exp \bigl(\mathbf{Q}_{WW}(t - u)\bigr) du \mathbf{1}_{W}. \end{array} $$

Note that each duration of repair in the complete working-repair cycles must be less than the given nonnegative critical value τ, so that the repair interval can be omitted and the original Markov repairable system of {X(t),t≥0} can be thought of as the working during this repair interval.

Thus, it is obvious that

The Laplace transform of H 1−W−W (t) is

$$H_{1 - W - W}^{ *} (s) = \frac{\boldsymbol{\pi} _{W}}{\boldsymbol{\pi} _{W}\mathbf{1}_{W}} \bigl( \mathbf{I} - \mathbf{G}_{WF}^{*}(s)\boldsymbol{\varPsi} _{\tau} ^{ *} (s) \bigr)^{ - 1} ( s\mathbf{I} - \mathbf{Q}_{WW} )^{ - 1}\mathbf{1}_{W}. $$

Situation 2

\(\sum_{j = 0}^{\infty} P\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],N(t) = j, X(t) \in F | X(0) \in W \}\).

When j=0, we have

$$\everymath{\displaystyle} \begin{array} {l} P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all} \\u \in [0,t],N(t) = 0, X(t) \in F | X(0) \in W \bigr\} \\\noalign{\vspace*{6pt}} \quad {}= \frac{\boldsymbol{\pi} _{W}}{\boldsymbol{\pi} _{W}\mathbf{1}_{W}}\int_{0}^{t} \mathbf{G}_{WF}(t) \mathbf{R}_{\tau} (t - u) du \mathbf{1}_{F}, \end{array} $$

where

$$\mathbf{R}_{\tau} (v) = \left\{\begin{array}{l@{\quad }l} \exp (\mathbf{Q}_{FF}v) - \exp (\mathbf{Q}_{FF}\tau ), & \mbox{when}\ v < \tau; \\\noalign{\vspace*{3pt}} \mathbf{0}, & \mbox{otherwise}.\end{array}\right. $$

In the following, we consider the summation

$$\sum_{j = 1}^{\infty} P \bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],N(t) = j, X(t) \in F| X(0) \in W \bigr\}. $$

In fact, we get

$$\everymath{\displaystyle} \begin{array} {l} \sum_{j = 1}^{\infty} P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],N(t) = j, X(t) \in F | X(0) \in W \bigr\} \\\noalign{\vspace*{6pt}} \quad {}= \sum_{j = 1}^{\infty} P\bigl\{ t - \tau < T_{j + 1} + D_{j} < t \le T_{j + 1} + D_{j + 1} | X(0) \in W \bigr\} \\\noalign{\vspace*{6pt}} \quad {}= \frac{\boldsymbol{\pi} _{W}}{\boldsymbol{\pi} _{W}\mathbf{1}_{W}}\sum _{j = 1}^{\infty} \int_{0}^{t} \mathbf{f}_{WF - (j + 1,j)}(u)\mathbf{R}_{\tau} (t - u) du \mathbf{1}_{F}. \end{array} $$

So, we have

$$H_{2 - W - F}(t) = \frac{\boldsymbol{\pi} _{W}}{\boldsymbol{\pi} _{W}\mathbf{1}_{W}}\sum_{j = 0}^{\infty} \int_{0}^{t} \mathbf{f}_{WF - (j + 1,j)}(u)\mathbf{R}_{\tau} (t - u) du\mathbf{1}_{F}. $$

So, the Laplace transform of H 2−W−F (t) is

$$\everymath{\displaystyle} \begin{array} {rcl} H_{2 - W - F}^{ *} (s) &=& \frac{\boldsymbol{\pi} _{W}}{\boldsymbol{\pi} _{W}\mathbf{1}_{W}}\bigl[\mathbf{I} - \mathbf{G}_{WF}^{*}(s) \boldsymbol{\varPsi} _{\tau} ^{ *} (s)\bigr]^{ - 1} \mathbf{G}_{WF}^{*}(s) \\\noalign{\vspace*{6pt}} &&{}\times \biggl\{ ( s\mathbf{I} - Q_{FF} )^{ - 1}\bigl(\mathbf{I} - \exp \bigl( - (s\mathbf{I} - \mathbf{Q}_{FF}) \bigr)\tau \bigr) - \frac{1}{s}\bigl(1 - e^{ - s\tau} \bigr)\exp (\mathbf{Q}_{FF}\tau ) \biggr\} \mathbf{1}_{F}, \end{array} $$

where \(\mathbf{f}_{WF - (j + 1,j)}^{*}(s) = [\mathbf{G}_{WF}^{*}(s)\boldsymbol{\varPsi} _{\tau} ^{ *} (s)]^{j}\mathbf{G}_{WF}^{*}(s) = ( f_{_{W(i_{1})F(i_{2}) - (j,j)}}^{*}(s) )_{|W| \times |F|}\),

For \(P\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t] | X(0) \in F \}\), Fig. 2. is a possible sample path for the original Markov repairable system of {X(t),t≥0}, and the new model of {Y(t),t≥0} for this case, we call it Case II. Case II can be decomposed into Situations 3 and 4.

Situation 3

\(\sum_{j = 0}^{\infty} P\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],M(t) = j, X(t) \in W | X(0) \in F \}\).

When j=0, we have

$$\everymath{\displaystyle} \begin{array} {l} P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],M(t) = 0, X(t) \in W | X(0) \in F \bigr\} \\\noalign{\vspace*{6pt}} \quad {}= \frac{\boldsymbol{\pi} _{F}}{\boldsymbol{\pi} _{F}\mathbf{1}_{F}}\int_{0}^{\tau} \mathbf{G}_{FW}(u)\exp \bigl(\mathbf{Q}_{WW}(t - u)\bigr)du \mathbf{1}_{W}. \end{array} $$

In the following, we consider the summation

$$\sum_{j = 1}^{\infty} P \bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],M(t) = j, X(t) \in W | X(0) \in F \bigr\}. $$

In fact, we get

$$\everymath{\displaystyle} \begin{array} {l} \sum_{j = 1}^{\infty} P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],M(t) = j, X(t) \in W | X(0) \in F \bigr\} \\\noalign{\vspace*{6pt}} \quad {}= \sum_{j = 1}^{\infty} P\bigl\{ D_{j + 1} + T_{j} < t \le D_{j + 1} + T_{j + 1} | X(0) \in F \bigr\} \\\noalign{\vspace*{6pt}} \quad {}= \frac{\boldsymbol{\pi} _{F}}{\boldsymbol{\pi} _{F}\mathbf{1}_{F}}\sum _{j = 1}^{\infty} \int_{0}^{t} f_{F(i_{1})W(i_{2}) - (j + 1,j)}(u)\exp \bigl(\mathbf{Q}_{WW}(t - u)\bigr)du \mathbf{1}_{W}. \end{array} $$

So, we have

$$\everymath{\displaystyle} \begin{array} {rcl} H_{3 - F - W}(t) &=& \frac{\boldsymbol{\pi} _{F}}{\boldsymbol{\pi} _{F}\mathbf{1}_{F}}\int_{0}^{\tau} \mathbf{G}_{FW}(u) \exp \bigl(\mathbf{Q}_{WW}(t - u)\bigr)du \mathbf{1}_{W} \\\noalign{\vspace*{6pt}} &&{} + \frac{\boldsymbol{\pi} _{F}}{\boldsymbol{\pi} _{F}\mathbf{1}_{F}}\sum _{j = 1}^{\infty} \int_{0}^{t} \mathbf{f}_{FW - (j + 1,j)}(u)\exp \bigl(\mathbf{Q}_{WW}(t - u)\bigr)du \mathbf{1}_{W}. \end{array} $$

So, the Laplace transform of H 3−F−W (t) is

$$H_{3 - F - W}^{ *} (s) = \frac{\boldsymbol{\pi} _{F}}{\boldsymbol{\pi} _{F}\mathbf{1}_{F}} ( \mathbf{I} - \boldsymbol{\varPsi} _{\tau} ^{ *} (s)\mathbf{G}_{WF}^{*}(s) )^{ - 1}\boldsymbol{\varPsi} _{\tau} ^{ *} (s) ( s\mathbf{I} - \mathbf{Q}_{WW} )^{ - 1}\mathbf{1}_{W}, $$

where \(\mathbf{f}_{FW - (j + 1,j)}^{*}(s) = [\boldsymbol{\varPsi} _{\tau} ^{ *} (s)\mathbf{G}_{WF}^{*}(s)]^{j}\boldsymbol{\varPsi} _{\tau} ^{ *} (s) = ( f_{_{F(i_{1})W(i_{2}) - (j + 1,j)}}^{*}(s) )_{|F| \times |W|}\),

Note that the first duration of repair interval must be less than the given nonnegative critical value τ in this situation, so that although the system starts from a down state, the first repair interval can be omitted.

Situation 4

\(\sum_{j = 0}^{\infty} P\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],M(t) = j, X(t) \in F | X(0) \in F \}\).

When j=0, we have

$$P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],M(t) = 0, X(t) \in F | X(0) \in F \bigr\} = P\bigl\{ t < D_{1} < \tau | X(0) \in F\bigr\}. $$

Because we only consider the case t>τ, so we have

$$P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],M(t) = 0, X(t) \in F | X(0) \in F \bigr\} = 0. $$

In the following, we consider the summation

$$\sum_{j = 1}^{\infty} P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],M(t) = j, X(t) \in F | X(0) \in F \bigr\}. $$

In fact, we get

$$\everymath{\displaystyle} \begin{array} {l} \sum_{j = 1}^{\infty} P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [0,t],M(t) = j, X(t) \in F | X(0) \in F \bigr\} \\\noalign{\vspace*{6pt}} \quad {}= \sum_{j = 1}^{\infty} P\bigl\{ t - \tau < D_{j} + T_{j} < t \le D_{j + 1} + T_{j} | X(0) \in F \bigr\}\\\noalign{\vspace*{6pt}} \quad {} = \frac{\boldsymbol{\pi} _{F}}{\boldsymbol{\pi} _{F}\mathbf{1}_{F}}\sum _{j = 1}^{\infty} \int_{0}^{t} \mathbf{f}_{FF - (j,j)}(u)\mathbf{R}_{\tau} (t - u) du \mathbf{1}_{F}. \end{array} $$

So, we have

$$H_{4 - F - F}(t) = \frac{\boldsymbol{\pi} _{F}}{\boldsymbol{\pi} _{F}\mathbf{1}_{F}}\sum_{j = 1}^{\infty} \int_{0}^{t} \mathbf{f}_{FF - (j,j)}(u) \mathbf{R}_{\tau} (t - u) du\mathbf{1}_{F}. $$

The Laplace transform ofH 4−F−F (t) is

$$\everymath{\displaystyle} \begin{array} {rcl} H_{4 - F - F}^{ *} (s) &=& \frac{\boldsymbol{\pi} _{W}}{\boldsymbol{\pi} _{W}\mathbf{1}_{W}}\bigl[\mathbf{I} - \boldsymbol{\varPsi} _{\tau} ^{ *} (s)\mathbf{G}_{WF}^{*}(s)\bigr]^{ - 1} \boldsymbol{\varPsi} _{\tau} ^{ *} (s)\mathbf{G}_{WF}^{*}(s) \\\noalign{\vspace*{6pt}} &&{}\times \biggl\{ ( s\mathbf{I} - Q_{FF} )^{ - 1}\bigl(\mathbf{I} - \exp \bigl( - (s\mathbf{I} - \mathbf{Q}_{FF}) \bigr)\tau \bigr) - \frac{1}{s}\bigl(1 - e^{ - s\tau} \bigr)\exp (\mathbf{Q}_{FF}\tau ) \biggr\} \mathbf{1}_{F}, \end{array} $$

where \(\mathbf{f}_{FF - (j,j)}^{*}(s) = [\boldsymbol{\varPsi} _{\tau} ^{ *} (s)\mathbf{G}_{WF}^{*}(s)]^{j} = ( f_{_{F(i_{1})F(i_{2}) - (j,j)}}^{*}(s) )_{|F| \times |F|}\),

Integrating the above results, we have

$$\everymath{\displaystyle} \begin{array} {rcl} A_{\tilde{X}}^{ *} [0,t](s) &=& \int_{0}^{\infty} e^{ - st}A_{\tilde{X}}[0,t]dt \\\noalign{\vspace*{6pt}} &=& \boldsymbol{\pi} _{W} \mathbf{1}_{W}H_{1 - W - W}^{ *} (s) + \boldsymbol{\pi} _{W}\mathbf{1}_{W}H_{2 - W - F}^{ *} (s) + \boldsymbol{\pi} _{F}\mathbf{1}_{F}H_{3 - F - W}^{ *} (s)\\\noalign{\vspace*{6pt}} &&{} + \boldsymbol{\pi} _{F}\mathbf{1}_{F}H_{4 - F - F}^{ *} (s). \end{array} $$

Taking inverse Laplace transform, we can easily get the formula of \(A_{\tilde{X}}[0,t]\).

Theorem 2

For the new model of \(\{ \tilde{X}(t),t \ge 0\}\) as described in Sect. 2, the interval reliability \(A_{\tilde{X}}[0,t]\) is

$$A_{\tilde{X}}[0,t] = \ell ^{ - 1}\bigl(A_{\tilde{X}}^{ *} [0,t](s)\bigr) (t), $$

where the symbol ℓ −1 denotes the inverse Laplace transform.

Definition 3

The interval reliability of the new model of \(\{ \tilde{X}(t),t \ge 0\}\), given a time interval [a,b],0≤a≤b, is defined as follows

$$A_{\tilde{X}}[a,b] \buildrel{\Delta} \over{ =} P\bigl\{ \tilde{X}(u) = 1,\ \mbox{for all}\ u \in [a,b]\bigr\}. $$

Theorem 3

For the new model of \(\{ \tilde{X}(t),t \ge 0\}\) as described in Sect. 2, the interval reliability \(A_{\tilde{X}}[a,b]\) is

$$A_{\tilde{X}}[a,b] = A_{\tilde{X}}[0,b - a] | _{\boldsymbol{\varPhi} _{0} = \mathbf{P}(a)} , $$

where P(a)=(π W ,π F )exp(Q a) is the probability vector of the original Markov repairable system of {X(t),t≥0} stays in each state of S at instance time a.

Proof

Because of the time homogeneity and Theorem 2, the poof can be got easily. □

3.3 Interval unreliability

Definition 4

The interval unreliability of the new model of \(\{ \tilde{X}(t),t \ge 0\}\) is defined as follows

$$\bar{A}_{\tilde{X}}[a,b] \buildrel{\Delta} \over{ =} P\bigl\{ \tilde{X}(u) = 0,\ \mbox{for all}\ u \in [a,b]\bigr\}. $$

Theorem 4

For the new model of \(\{ \tilde{X}(t),t \ge 0\}\) as described in Sect. 2, the interval unreliability is

$$\everymath{\displaystyle} \begin{array} {rcl} \bar{A}_{\tilde{X}}[a,b] &=& \boldsymbol{\pi} _{F}\exp \bigl(\mathbf{Q}_{FF}\max \{ b,\tau \} \bigr)\mathbf{1}_{F} \\\noalign{\vspace*{6pt}} &&{}+ \int_{0}^{a} \bigl\{ (\boldsymbol{\pi} _{W},\boldsymbol{\pi} _{F})\exp \bigl( \mathbf{Q}(a - s)\bigr)\left ( \begin{array} {l} \mathbf{I}_{\vert W \vert \times \vert W \vert } \\\mathbf{0}_{\vert F \vert \times \vert W \vert } \end{array} \right ) \\\noalign{\vspace*{6pt}} &&{}\times \mathbf{Q}_{WF}\bigl[\exp \bigl( \mathbf{Q}_{FF}\max \{ b - a + s,\tau \} \bigr)\bigr] \mathbf{1}_{F}\bigr\} ds. \end{array} $$

Proof

From the assumptions of the model, we can get easily

$$\bar{A}_{\tilde{X}}[a,b] \buildrel{\Delta} \over{ =} P\bigl\{ \tilde{X}(u) = 0,\ \mbox{for all}\ u \in [a,b]\bigr\} = P\bigl\{ \tilde{X}(u) = 0, X(u) \in F,\ \mbox{for all}\ u \in [a,b]\bigr\}. $$

The first term π F exp(Q FF max{b,τ})1 F is the probability that the original Markov repairable system stays in failed states before instance time b.

Since exp(Q FF max{b−a+s,τ}) is the probability that the duration of the original Markov repairable system of {X(t),t≥0} stays in the failed states is greater than both b−a+s and τ, so that the repair time interval cannot be omitted. The proof is completed. □

3.4 Special cases

In order to understand easily the previous results, we can consider some special cases as follows.

When |S|=2, i.e., |W|=|F|=1, , (π W ,π F )=(α,1−α). In fact, this is a single unit Markov repairable system. We can get

$$\everymath{\displaystyle} \begin{array} {rcl} \bar{A}_{\tilde{X}}[a,b] &=& (1 - \alpha )\exp \bigl( - \mu \max \{ b,\tau \} \bigr) \\\noalign{\vspace*{6pt}} &&{} + \int_{0}^{a} \frac{1}{\lambda + \mu} \bigl[\alpha (\lambda + \mu )e^{ - (\lambda + \mu )(a - s)}\\\noalign{\vspace*{6pt}} &&{} - \mu e^{ - (\lambda + \mu )(a - s)} + \mu \bigr]\lambda \bigl[\exp \bigl( - \mu \max \{ b - a + s, \tau \} \bigr)\bigr]ds. \end{array} $$

Taking inverse Laplace transform by using Maple software, we can get the formula of \(A_{\tilde{X}}[0,t]\), but the formula is so verbose that we do not list it here.

Specially, when α=1, \(A_{X}(t) = \frac{\mu}{\lambda + \mu} + \frac{\lambda}{\lambda + \mu} e^{ - (\lambda + \mu )t}\), and when α=1, \(A_{\tilde{X}}(t) = A_{X}(t) + \int_{0}^{\min (t,\tau )} \frac{1}{\lambda + \mu} [\mu + \lambda e^{ - (\lambda + \mu )(t - s)}]\lambda (e^{ - \mu s} - e^{ - \mu \tau} )ds\), this result degenerates into the result in the Zheng et al. (2006), i.e., the result in Zheng et al. (2006) is a special case of our result in the paper.

When α=1, \(\bar{A}_{\tilde{X}}[a,b] = \int_{0}^{a} \frac{1}{\lambda + \mu} [\mu + \lambda e^{ - (\lambda + \mu )(a - s)}]\lambda [\exp ( - \mu \max \{ b - a + s,\tau \} )]ds\).

4 Numerical examples

In the following section, some numerical examples will be showed to illustrate the results obtained above.

Let |S|=4, i.e., |W|=|F|=2,

τ=0.5. For convenience, we consider t>τ. Based on the results in Sect. 3, we can get \(A_{\tilde{X}}[0,t]\) by using inverse Laplace transform.

We can get the following numerical results.

  1. (i)

    When the value of t is given, the interval reliability A X [0,t] and \(A_{\tilde{X}}[0,t]\) can be obtained, respectively. We take t=1.5 and t=2, respectively, then we get

    The curves of interval reliability for the new model, and original Markov repairable system are shown in Fig. 3.

    Fig. 3
    figure 3

    The curves of interval reliability for the new model, and original Markov repairable system

    Full size image
  2. (ii)

    When the values of a,b are given, the interval reliability A X [a,b] and \(A_{\tilde{X}}[a,b]\) can be obtained respectively. We take a=2,b=3.25 and a=2,b=3.65, respectively, then we get

    $$\everymath{\displaystyle} \begin{array} {l} A_{X}[2,3.25] \approx 0.0716, \qquad A_{\tilde{X}}[2,3.25] \approx 0.4702, \\\noalign{\vspace*{6pt}} A_{X}[2,3.65] \approx 0.0480,\qquad A_{\tilde{X}}[2,3.65] \approx 0.4006. \end{array} $$

    It is obvious that

    It is also clear that the curve of \(A_{\tilde{X}}[0,t]\) is upper on the curve of A X [0,t] at any instance time t, i.e., the interval reliability for the new system is higher than the ones for the original Markov repairable system, because the repair interval may be omitted in the new model. In fact, the property is also applicable for the availability.

Of course, for any given 0≤a<b 1<b 2, we get

$$A_{X}[a,b_{1}] \ge A_{X}[a,b_{2}],\qquad A_{\tilde{X}}[a,b_{1}] \ge A_{\tilde{X}}[a,b_{2}], $$

Its proofs is easily finished based on the previous theorems, they are omitted here. And it is obvious that \(A_{X}[2,3.25] > A_{X}[2,3.65], A_{\tilde{X}}[2,3.25] > A_{\tilde{X}}[2,3.65]\), which illustrate the property that \(A_{X}[a,b_{1}] \ge A_{X}[a,b_{2}],A_{\tilde{X}}[a,b_{1}] \ge A_{\tilde{X}}[a,b_{2}]\).

5 Conclusions

In the paper, a new model based on the original Markov repairable system whose state space is partitioned into working state set and failed state set, is developed. While the model is the same as model II in Cui et al. (2012b), the analysis methods are different. The interval reliability formulae in Cui et al. (2012b) included a double integral and Laplace transform, which may cause some computation problems. Our method only employs Laplace transforms to express the results, which are more compact. Our method is more efficient for numerical calculation. Several reliability indexes for the new model, i.e., availability, interval reliability, and interval unreliability have been presented. In particular, Laplace transform method is used to formulate the interval reliability. Finally, some special cases and numerical examples are also discussed to illustrate the results obtained in the paper. The future work may be included by considering the multi-point availability and multi-interval reliability for the new model, and by extending the original Markov repairable systems into the semi-Markov cases.