Two-stage stochastic lot-sizing problem under cost uncertainty

Abstract

For production planning problems, cost parameters can be uncertain due to marketing activities and interest rate fluctuation. In this paper, we consider a single-item two-stage stochastic lot-sizing problem under cost parameter uncertainty. Assuming cost parameters will increase or decrease after time period p each with certain probability, we minimize the total expected cost for a finite horizon problem. We develop an extended linear programming formulation in a higher dimensional space that can provide integral solutions by showing that its constraint matrix is totally unimodular. We also project this extended formulation to a lower dimensional space and obtain a corresponding extended formulation in the lower dimensional space. Final computational experiments demonstrate that the extended formulation is more efficient and performs more stable than the two-stage stochastic mixed-integer programming formulation.

1 Introduction

The traditional single-item uncapacitated lot-sizing problem (see, e.g., Wagner and Whitin 1958 and Nemhauser and Wolsey 1999) is to determine a production plan for a product to satisfy demands in a finite time horizon (e.g., T time periods) while minimizing total costs that include setup, production, and inventory holding costs. In certain practice, demands can maintain to be deterministic and cost parameters are uncertain. For instance, for several cases shown in Heikkilä (2002), manufactures obtain deterministic demand information when a good relationship is maintained with customers. In addition, long life circle products and customized products provide deterministic demand information as well. For instance, in the chemical industry, a company produces mainly functional products, which are defined as ones that have long product life cycles and deterministic demands (see, e.g., Lee and Chen 2005). In the furniture industry, a portion of a company’s products are built after the company gets orders from customers. Under these situations, the demand can be easily forecasted accurately. However, the cost parameter forecast may need to be adjusted monthly or quarterly. The cost parameter uncertainty can come from different ways. In the business environment, when manufacturers purchase materials and resources from upper-stream suppliers, the purchasing cost varies with the upper-stream marketing activities such as promotions (see, e.g., Narasimhan 1988 and Simester 1997). Because promotions are marketing tools of the upper-stream suppliers, they are uncertain and directly reflected as the production cost for the lower-stream manufacturers. When a promotion happens, the production cost for the lower-stream manufacturers will change accordingly. In addition, the interest rate and currency exchange rate fluctuations also increase or decrease the production costs of manufacturers, especially in the global business environment (see, e.g., Campa and Goldberg 2005).

Motivated by the above problem settings, in this paper we concentrate on studying production planning problems under cost parameter uncertainty, and in particular, analyzing the mathematical insights of a special case, e.g., a single-item problem. We study the single-item lot-sizing problem in which cost parameters after a given time period (e.g., time period p) will be uncertain and follow a discrete probability distribution with finite support. We formulate the problem as a two-stage multi-period stochastic integer program, which is an extension of the single-item deterministic uncapacitated lot-sizing problem. There has been extensive research on the deterministic lot-sizing problems. A survey of results and solution approaches are described in Pochet and Wolsey (2006). In the following literature review part, we focus on convex hull description and extended formulation studies on single-item lot-sizing problems for both deterministic and stochastic cases.

For the single-item deterministic uncapacitated lot-sizing problem, the convex hull description has been derived in Barany et al. (1984). In Pochet and Wolsey (1988), the first polyhedral study is performed for this problem with backlogging, and the convex hull description for this problem with backlogging is described in Küçükyavuz and Pochet (2007). In addition, Wagelmans et al. (1992) introduced the Wagner-Whitin costs, i.e., $\alpha_{i}+h'_{i} \geq\alpha_{i+1}$, $b'_{i}+\alpha_{i+1} \geq\alpha_{i}$ with 1≤i≤T−1, where α _i , $h'_{i}$ and $b'_{i}$ are unit production, inventory, and backlogging costs for time period i, and implemented an ${{\mathcal{O}}}(T)$ time dynamic programming algorithm to solve the problem. Accordingly, Pochet and Wolsey (1994) developed an extended formulation for the single-item Wagner-Whitin cost case with ${{\mathcal{O}}}(T^{2})$ constraints when backlogging is not considered, and with ${{\mathcal{O}}}(2^{T})$ constraints plus an ${{\mathcal{O}}}(T^{2}\log T)$ time separation algorithm when backlogging is considered.

For the single-item stochastic uncapacitated lot-sizing problem (SULS), most recent research works focus on developing efficient algorithms. The first polynomial time algorithm was studied in Guan and Miller (2008). Huang and Ahmed (2009) considered the case without setup cost and developed primal and dual algorithms for a multi-stage stochastic linear programming formulation for the problem. The computational complexity of the proposed algorithm is shown within $\mathcal{O}(N^{2})$, where N is the number of nodes in the scenario tree. Huang and Küçükyavuz (2008) considered the variation of the problem with the consideration of random lead times, and developed a dynamic programming algorithm that runs in $\mathcal{O}(N^{3})$ time. Recently, Jiang and Guan (2011) improves Huang and Küçükyavuz (2008)’s algorithm to be $\mathcal{O}(N^{2})$ time. The reformulation for the problem was originally introduced in Ahmed et al. (2003). Later on, in Guan et al. (2006a), the extended (strong) formulation approach was proved to be equivalent to adding the (ℓ,S) inequalities in the original formulation, in terms of providing LP lower bounds. However, both approaches could not provide integral solutions for SULS. Thus, efficient cutting planes (see, e.g., Guan et al. 2006b; Summa and Wolsey 2008) have been studied for its deterministic equivalent scenario tree based reformulation. An extended formulation that provides integral solutions for SULS up to now is only for two-period cases, which was developed in Guan et al. (2006a). Other related research works are referred to Feiringa and Sastri (1990), Ahmed and Garcia (2003), Terkaj and Tolio (2006), and Zanjania et al. (2010).

In this paper, we study the extended formulation of two-stage stochastic lot-sizing problem with backlogging and uncertain cost parameters. Compared with SULS without backlogging, SULS with backlogging is more complicated with more flexibility to satisfy demands. First, we develop an extended formulation in a higher dimensional space that can provide integral solutions by showing that its constraint matrix is totally unimodular. Second, we project this extended formulation to a lower dimensional space and obtain a corresponding extended formulation in the lower dimensional space. In other words, we provide an alternative linear formulation with more decision variables for the two-stage stochastic lot-sizing problem that can provide integral solutions. For the computational performance, we first report the value of the stochastic solution of our proposed two-stage multi-period stochastic integer program. Then, instead of solving a stochastic mixed-integer programming problem, the SULS with backlogging problem is directly solved as a linear program, which improves the computational efficiency and performs stably for different sizes of test instances.

This paper contributes to expanding the study of extended formulations for the deterministic lot-sizing problem to the two-stage stochastic programming setting. It provides one of the first studies on extended formulations for the stochastic lot-sizing problems. In addition, the SULS with backlogging is a subproblem of multi-item stochastic lot-sizing problems. The extended formulation of SULS with backlogging could help simplify the subproblem for multi-item stochastic lot-sizing problems and analyze their polyhedral structures. The extended formulation can also be embedded into the decomposition framework (e.g., the Lagrange relaxation decomposition) to speed up solving large scale production planning under uncertainty problems.

The remaining part of this paper is organized as follows: In Sect. 2, we define the Wagner-Whitin cost condition for the two-stage stochastic lot-sizing problem. We also discover the optimality condition and use it to generate an extended formulation in a higher dimensional space. We prove that the constraint matrix for the extended formulation is totally unimodular. In Sect. 3, we project the extended formulation back to a lower dimensional space such that we can find valid inequalities that can describe the convex hull of the problem in the lower dimensional space. In Sect. 4, we report the computational results and demonstrate the efficiency of the proposed extended formulation. Finally, in Sect. 5, we conclude our research.

2 Mathematical formulation

In this section, we first provide the list of notation in the following table. The detailed explanation will be provided when we introduce them.

As described in the introduction part, we assume the cost parameters for period 1 to a given period (defined as period p) are deterministic. After the given period (i.e., period p), cost parameters are uncertain and follow a discrete probability distribution with finite support. The corresponding two-stage multi-period stochastic lot-sizing problem can be formulated as follows (cf. Birge and Louveaux 1997):

where

Note here as indicated in Table 1, t(i) represents the time period of node i and $s_{i-1}^{2}(w) = s_{p}$ if t(i−1)=t(p). Decision variables (z _i ,x _i ,s _i ,ℓ _i ) and $(z^{2}_{i}(w), x^{2}_{i}(w), s^{2}_{i}(w), \ell_{i}^{2}(w))$ represent the setup decision, production level, inventory level, and backlogging level on the first and second stages, respectively. The corresponding cost parameters are $(\beta', \alpha, h', b'_{i})$ and $(\beta'(w), \alpha(w), h'(w), b'_{i}(w))$. Parameter d _i represents the demand in time period i, which is deterministic.

Table 1 Notation for two-stage SULS with backlogging

After exploring possible realizations of the second-stage random variables $( \beta'_{i}, \alpha_{i}, h'_{i}, b'_{i})$, we can generate a two-stage stochastic scenario tree for the problem as shown in Fig. 1. Nodes 1,…,p are the first-stage nodes and nodes q ₁,…,ℓ _W are the second-stage nodes, where the branching node p connects the first and the second stages and is unique on the scenario tree. Assuming there are W possible scenarios, as listed in Table 1, we let $\mathcal{P}_{w}$, 1≤w≤W, represent the branch where scenario w happens and accordingly let ρ _w , 1≤w≤W, represent the probability that scenario w will happen. Since there is no demand uncertainty, we have d _i =d _t(i)≥0 for the second-stage nodes as well. We let $\mathcal{V}$ represent the set of nodes in the scenario tree, $\mathcal{V}(i)$ represent the set of nodes which are descendants of node i, ${\mathcal{P}} (i, j)$ represent the set of nodes on the path from node i to node j, and ${\mathcal{P}}^{i}_{t} (w)$ represent the set of nodes on the path from node i to node j, which is on ${\mathcal{P}}_{w}$ and t(j)=t. For brevity, we let ${\mathcal{P}}(j)$ represent the set of nodes on the path from the root node to node j. We let $\mathcal{C}(i)$ represent the set of children of node i and $\mathcal{L}$ represent the set of leaf nodes. Finally, we let W(i) represent the set of scenarios that will occur after node i. For instance, if i≤p, then W(i)={1,…,W}; otherwise, if t(i)≥t(p)+1, then W(i) contains a single element w such that $i\in{\mathcal{P}}_{w}$. The deterministic equivalent formulation of the two-stage stochastic lot-sizing under cost uncertainty problem, referred to as two-stage stochastic lot-sizing with backlogging (SULSB), can be described as follows:

where (x _i ,s _i ,ℓ _i ,z _i ) presents the decision variables for node i and, as indicated in Table 1, a(i) is the parent node of node i. Without loss of generality, we assume s ₀=0, ℓ ₀=0, and tighten $M_{i}=\sum_{t=t(i)}^{T}d_{t}$.

Fig. 1

The scenario tree for the two-stage SULSB

Now, we study the optimal solution forms of inventory and backlogging levels for the two-stage SULSB with Wagner-Whitin costs (defined as SULSB-WW) and generate a reformulation which can describe the integral polyhedron of the problem in a higher dimensional space.

First, we define Wagner-Whitin costs for two-stage SULSB. We substitute x _i =d _i +s _i −ℓ _i −s _a(i)+ℓ _a(i) to eliminate decision variable x _i in the original formulation. Then, we get a reformulation of the problem in the (s,ℓ,z) space as follows:

where

and $\beta_{i} = \beta'_{i}$ if 1≤t(i)≤t(p) and $\beta_{i} =\rho_{w}\beta'_{i}$ otherwise. We let $\alpha_{\mathcal{C}(i)}=0$ if $i\in\mathcal{L}$.

Definition 1

A two-stage SULSB is said to have Wagner-Whitin costs if for all $i\in{\mathcal{V}}$,

$$ h_{i}\geq0, \qquad b_{i}\geq0, \quad \mbox{and} \quad \beta_{i} \geq\sum_{j\in \mathcal{C}(i)}\beta_{j}. $$

(1)

For the deterministic version, the optimal solution forms of inventory and backlogging levels are studied by Pochet and Wolsey (1994). For two-stage SULSB, we consider the optimal solution forms of inventory level s _i and backlogging level ℓ _i for each $i\in{\mathcal{V}}$. In the optimal solution for SULSB-WW, the demand for each node i will be satisfied (1) by setting up the production at node i, (2) by inventory left from its parent node, or (3) by backlogging from its children. Before we describe the proposition, we show a three-period example to demonstrate the optimal solution form as shown in Fig. 2. In this example, if the unit inventory cost at node 1 and the setup costs at nodes 2 and 5 are very high, then it may happen in the optimal solution that productions are set up at nodes 1, 3, and 4. Demand at node 1 is satisfied by the production of itself. Demand at node 2 is satisfied by backlogging from node 4. Node 3 covers demands in nodes 3 and 5. Thus the second-stage nodes 2 and 3 are backlogged and set up respectively. Meanwhile, the first-stage node 1 does not cover any demand in the second stage.

Fig. 2

The scenario tree for a three-period SULSB

To describe the property of the optimal solution and generate the extended formulation, besides listing the notation in Table 1, we provide the detailed explanation as follows:

f _i ::

binary decision variable to indicate if node i is stocked (if yes, f _i =1; otherwise, f _i =0)

g _i ::

binary decision variable to indicate if node i is backlogged (if yes, g _i =1; otherwise, g _i =0)

$m^{i}_{t}$::

binary decision variable to indicate if the inventory left from node i covers the demand at time period t, t≥t(i)+1 (if yes, $m^{i}_{t}=1$; otherwise $m^{i}_{t}=0$)

$n^{i}_{t}$::

binary decision variable to indicate if the backlogging at node i covers the demand at time period t, t≤t(i) (if yes, $n^{i}_{t}=1$; otherwise $n^{i}_{t}=0$)

ψ(i)::

the time period of the earliest descendant of node i which is set up or backlogged, i.e., $\psi(i)=\min\{t(j): z_{j}=1 \ \mbox{or} \ g_{j}=1,\ j \in\mathcal{V}(i)\setminus\{i\}\}$

η(i,t)::

the ancestor node of node i at time t, i.e., $\eta(i,t)=\{k\in{\mathcal{P}}(i): t(k)=t\}$

ξ(i,t,w)::

a descendant of node i at time period t and at the branch corresponding to scenario w.

In addition, as shown in Fig. 3, we define $\varPsi(i)=\{r \in\mathcal{V}(i),\ t(i)< t(r)<\psi(i)\}$, ${\varLambda}(i)=\bigcup_{r \in\mathcal{L} \cap\mathcal {V}(i)}\arg\min\{t(k): k\in{\mathcal{P}}(i, r) \setminus\{i\} \mbox{ and }z_{k}=1\}$, and $\varPhi(i)= \bigcup_{j\in\varLambda (i)}{\mathcal{P}} (i,j)\setminus\{i,j\}$.

Fig. 3

The subtree of node i

Proposition 1

For two-stage SULSB-WW, there exists an optimal inventory level of the form:

$$ s_{i}=\sum_{t=t(i)+1}^{\psi(i)-1}d_{t}, \quad i\in\mathcal{V}, $$

(2)

and an optimal backlogging level of the form:

$$ \ell_{j}=\max_{1\leq\tau\leq t(j)}\sum_{t=\tau}^{t(j)}d_{t} \biggl[g_{\eta(j,t)}-\sum_{r\in\mathcal{P}(\eta(j,t),j)}z_{r} \biggr]^{+}, \quad j\in\varPhi(i). $$

(3)

In addition, the optimal solutions of two-stage SULSB-WW satisfy the following conditions:

(4)

(5)

(6)

Proof

Let $\varLambda=\{ i\in\mathcal{V}: z_{i}=1\}$. First, for each i∈Λ, we prove that (2) and (3) hold by showing (2) and

$$ \ell_{j}=\sum_{t=\psi(i)}^{t(j)}d_{t} \quad\mbox{for each }j\in\varPhi(i)\setminus \varPsi(i) $$

(7)

hold first. Then, we show (3) holds based on (7).

Proof of (2) and (7). We prove (2) and (7) by contradiction under three cases:

Case 1::

(2) does not hold and (7) holds. In this case, the optimal inventory level $s^{*}_{i}$ is either larger or less than $\sum_{t=t(i)+1}^{\psi(i)-1}d_{t}$.

Case 1.1.:

If $s_{i}^{*}<\sum_{t=t(i)+1}^{\psi(i)-1}d_{t}$, then there exists at least one node j∈Ψ(i) for which t(j)=ψ(i)−1 and whose demand is not satisfied. Thus, $s_{i}^{*}$ is not a feasible solution, which is a contradiction.

Case 1.2.:

If $s_{i}^{*}>\sum_{t=t(i)+1}^{\psi(i)-1}d_{t}$, then let $\hat{s_{i}}=\sum_{t=t(i)+1}^{\psi(i)-1}d_{t}-\varepsilon$, where $0<\varepsilon\leq s_{i}^{*}-\sum_{t=t(i)+1}^{\psi(i)-1}d_{t}$. It can be observed that $(\hat{s}, \ell^{*})$ is also a feasible solution and leads to an equal total cost or a smaller total cost, which is a contradiction. For the former case, we can increase ε such that (2) holds.

Case 2::

(2) holds and (7) does not hold. We can give the similar proof as in Case 1 to find a contradiction.

Case 3::

Neither (2) nor (7) holds. In order to satisfy the demand in each node in Φ(i), we can construct two feasible solutions for two-stage SULSB-WW.

Let $s^{1}_{i}=s_{i}^{*}+\varepsilon$, where ε is a small positive number, and each node j in Λ(i) produces ε less. Then $\ell^{1}_{j}=\ell_{j}^{*}-\varepsilon$, j∈Φ(i)∖Ψ(i). The corresponding objective value is

$$ F^{1}=\sum_{i\in\mathcal{V}} (h_{i}s_{i}+b_{i} \ell_{i}+\beta_{i}y_{i} )+\sum _{j\in\varPsi(i)}h_{j}\varepsilon-\sum _{j\in\varPhi(i)\setminus\varPsi(i)}b_{j}\varepsilon. $$

Let $s^{2}_{i}=s_{i}^{*}-\varepsilon$, and each node j in Λ(i) produces ε more. Then $\ell^{2}_{j}=\ell_{j}^{*}+\varepsilon$, j∈Φ(i)∖Ψ(i). The corresponding objective value is

$$ F^{2}=\sum_{i\in\mathcal{V}} (h_{i}s_{i}+b_{i} \ell_{i}+\beta_i y_i )-\sum _{j\in\varPsi(i)}h_{j}\varepsilon+\sum _{j\in\varPhi(i)\setminus\varPsi(i)}b_{j}\varepsilon. $$

If ∑ _j∈Ψ(i) h _j <∑ _{j∈Φ(i)∖Ψ(i)} b _j , then F ¹<F ^∗; if ∑ _j∈Ψ(i) h _j >∑ _{j∈Φ(i)∖Ψ(i)} b _j , then F ²<F ^∗. This contradicts the assumption that F ^∗ is the optimal objective value. Note here, if ∑ _j∈Ψ(i) h _j =∑ _{j∈Φ(i)∖Ψ(i)} b _j , we can increase (or decrease) s ^∗ and decrease (or increase) ℓ ^∗ to match the optimal form. Therefore, (7) holds.

Proof of (3): According to (7), s _i covers demands for nodes in Ψ(i). In order to minimize the objective function, nodes in Ψ(i) do not obtain backlogging. Thus, g _j =0, j∈Ψ(i). Therefore, $\ell_{j}=\max_{\{\tau: 1\leq\tau\leq t(j)\}}\sum_{t=\tau}^{t(j)}d_{t} [g_{\eta(j,t)}-\sum_{r\in \mathcal{P}(\eta(j,t),j)}z_{r} ]^{+}=\sum_{t=\psi(i)}^{t(j)}d_{t}$. Therefore, (2) and (3) hold.

Second, we prove that conditions (4), (5), and (6) hold.

According to the definition of f _i and g _i , $i\in \mathcal{V}$, it is obvious that conditions (5) and (6) hold.

Now we prove that condition (4) holds by two cases:

Case 1.:

If j∈Ψ(i), then the demand in node j is satisfied by inventory and f _j =1. In order to keep the smallest production cost, f _j +g _j +z _j =1.

Case 2.:

If j∈[Φ(i)∖Ψ(i)]∪Λ(i), then f _j =0 and we need to prove g _j +z _j =1. In order to satisfy the demand, g _j +z _j ≥1.

Case 2.1.:

If j∈Λ(i), z _j =1. If g _j =1, then we can let node j produce more to cover the backlogging amount and reduce the objective value, which is a contradiction. Therefore, g _j =0 and f _j +g _j +z _j =1.

Case 2.2.:

If j∈Φ(i)∖Ψ(i), g _j =1. According to (3), the demand of node j can be covered by backlogging from its children. In order to minimize the objective function, z _j =0.

Therefore, based on Cases 1 and 2, f _j +g _j +z _j =1, j∈Φ(i).

 □

Under (4), at most one of g _η(i,k) and z _η(i,k) equals 1. Then g _η(i,k)−z _η(i,k)=1 if g _η(i,k)=1; g _η(i,k)−z _η(i,k)≤0 if g _η(i,k)=0. Thus,

(8)

From (4), we also have

$$ f_{i}+g_{i}+z_{i}=f_{{a(i)}}+g_{{a(i)}}+z_{{a(i)}}=1. $$

(9)

Thus, one of constraints (5) and (6) is redundant. That is, if constraint (5) holds, then (6) must hold based on (9). Now, we introduce three types of inequalities corresponding to the optimal inventory level for node i on the scenario tree.

• 1. Path I inequality. This type of inequality is for the second-stage nodes. For a given node i on the second stage, w is determined and

  $$ m^{i}_{t} \geq f_{\xi(i,t,w)} - \sum _{j\in\mathcal{P}^{i}_{t}(w)\setminus \{i, \xi(i,t,w)\}}z_j,\quad t(i)\geq t(p)+1,\ t\geq t(i)+1. $$

  (10)

  That is, node i covers demands along its branch until next backlogging or production.

• 2. Path II inequality. This type of inequality is for the first-stage nodes (except node p). For a given node i on the first stage, node i+1 is its child node and

  

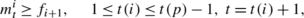  (11)
  

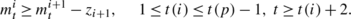  (12)

  Inequality (11) indicates that if the demand of child node i+1 is satisfied by inventory, then the inventory left from node i covers the demand of node i+1. Inequality (12) indicates that if node i+1 is not set up and the inventory left from node i+1 covers the demand up to time t, t≥t(i)+2, then the inventory left from node i also covers the demand up to time t.

• 3. Connection inequality. This type of inequality is for the branching node p,

  

  (13)
  

  (14)

  Inequalities (13) and (14) are similar to (11) and (12). The inventory left from node p will cover demands from period t(p)+1 to t−1 unless there is a set up or a backlogging, before or at time period t along each scenario path.

With the information of $m^{i}_{t}$, the inventory level left from each node i in the scenario tree is as follows:

$$ s_{i}=\sum_{t=t(i)+1}^{T}d_{t}m^{i}_{t}, \quad i\in\mathcal{V.} $$

(15)

Because for a given node i, its ancestor at time period t, η(i,t), is unique, the following two inequalities hold for each node $i\in{\mathcal{V}}$ based on (8):

(16)

(17)

Constraints (4), (5), (10)–(17) guarantee the feasibility of the reformulation for two-stage SULSB-WW since the demand for each time period is covered. Now, we show these constraints provide an extended formulation for two-stage SULSB-WW, which accordingly provides an integral solution for the problem.

Proposition 2

Constraints (4), (5), and (10) to (17) provide an extended formulation for two-stage SULSB-WW.

Proof

Because constraints (15) and (17) can be directly transferred to the objective function, we prove this proposition by showing the constraint matrix described by constraints (4), (5), (10)–(14), and (16) is totally unimodular. The detailed proof is shown in Appendix. □

3 Projection to a lower dimensional space

Now, we study the integral polyhedron in the (f,g,z,s,ℓ) space to generate an extended formulation for the two-stage SULSB-WW problem. First, we define

(18)

(19)

We prove that Q _M is an integral polyhedron for the two-stage SULSB-WW problem in the (f,g,z,s,ℓ) space, by showing that it is a projection of Q _H into the (f,g,z,s,ℓ) space, where Q _H records the polyhedron of the two-stage SULSB-WW problem in the (f,g,z,m,n,s,ℓ) space, i.e.,

$$\begin{aligned} Q_H = \bigl\{&(f,g,z,m,n,s,\ell): (f,g,z,m,n,s,\ell) \mbox{ satisfies} \\ & \mbox{(4), ( 5), (10) to (17)}, \nonumber \\ & 0 \leq f_i, g_i, z_i, m^{i}_{t}, n^{i}_{t'} \leq1,\ s_i, \ell_i \geq0, \ t(i)+1 \leq t \leq T,\ 1 \leq t' \leq t(i),\ i\in{\mathcal{V}}\bigr \}. \end{aligned} $$

Proposition 3

Proj _{(f,g,z,s,ℓ)} Q _H =Q _M .

Proof

We prove this proposition by showing the following two claims:

Claim 1. All inequalities in Q _M are valid for Q _H .

Claim 2. For an arbitrary extreme point (f,g,z,s,ℓ)∈Q _M , there exists a (f,g,z,m,n,s,ℓ)∈Q _H .

Proof of Claim 1. We prove Claim 1 by showing that

(20)

(21)

are valid for Q _H , because if (20) and (21) hold, then

Based on (16), (17) and the nonnegativity of $n^{i}_{t}$, we have

Thus, (21) holds.

Now, we prove (20) by two conditions. (1) t(i)≥t(p)+1; (2) t(i)≤t(p).

For condition (1), t(i)≥t(p)+1, based on (10), (15), and the nonnegativity of $m^{i}_{t}$, we have

where w _t is the single element in W(i) for each t(p)+1≤t≤T. Thus, (20) holds.

For condition (2), t(i)≤t(p), we have

where (22) is based on (11), (12), and the nonnegativity of $m^{i}_{t}$, and (23) is based on (13), (14), and the nonnegativity of $m^{i}_{t}$.

If t(i)=t(p), as shown in (23), based on (10)

where the second equation holds due to $\xi(q_{w_{t}}, t,w_{t}) = \xi(p,t,w_{t})$, ${\mathcal{P}}^{q_{w_{t}}}_{t}(w_{t})\subseteq{\mathcal{P}}^{p}_{t}(w_{t})$ and ${\mathcal{P}}^{q_{w_{t}}}_{t}(w_{t})\setminus\xi(q_{w_{t}}, t,w_{t}) ={\mathcal{P}}^{p}_{t}(w_{t})\setminus\{p, \xi(q_{w_{t}}, t,w_{t})\}$, because w _t is the single element in W(p) for each t(p)+1≤t≤T. Thus, (20) holds.

Now, we only need to show that, if t(i)<t(p),

$$ \bigl[m^{i+1}_{t}-z_{i+1}\bigr]^{+} \geq \biggl[f_{\xi(i,t,w_t)}-\sum_{j\in {\mathcal{P}}^{i}_{t}(w_t)\setminus\{i, \xi(i,t,w_t)\}}z_j \biggr]^{+}. $$

(24)

By observation, if t≤t(p), (24) holds based on (11) and (12). Hence, we discuss t=t(p)+1 and t>t(p)+1.

(a) If t=t(p)+1, then

$$ \bigl[m^{i+1}_{t} - z_{i+1}\bigr]^{+} \geq\Biggl[m^{p}_{t}-\sum_{j=i+1}^{p}z_j \Biggr]^{+} \geq\Biggl[f_{q_{w_t}} - \sum _{j=i+1}^{p}z_j\Biggr]^{+}= \biggl[f_{q_{w_t}} - \sum_{j\in{\mathcal{P}}^{i}_{t}(w_t)\setminus\{ i,q_{w_t}\}}z_j \biggr]^{+}, $$

where the first inequality follows (12) and the second inequality follows (13).

(b) If t>t(p)+1, then

where the first inequality follows (12), the second one follows (14), and the third one follows (10). Thus, (20) holds.

Therefore, Claim 1 holds.

Now, we prove Claim 2 holds.

For any give extreme point (f,g,z,s,ℓ)∈Q _M , we construct m and n such that (f,g,z,m,n,s,ℓ)∈Q _H . That is, (f,g,z,m,n,s,ℓ) satisfies the conditions (4), (5), (10) to (17). Now, for a given extreme point $({\widehat{f}},{\widehat{g}},{\widehat{z}},{\widehat{s}},{\widehat{\ell}})\in Q_{M}$, let

(25)

(26)

Since $({\widehat{f}},{\widehat{g}},{\widehat{z}},{\widehat{s}},{\widehat{\ell}})$ is an extreme point in Q _M , we first observe that $({\widehat{f}},{\widehat{g}},{\widehat{z}},{\widehat{s}},{\widehat{\ell}})$ satisfies equation (15) based on (25) and (18). Similarly, $({\widehat{f}},{\widehat{g}},{\widehat{z}},{\widehat{s}},{\widehat{\ell}})$ satisfies equation (17) based on (26) and (19). It is also obvious that $({\widehat{f}},{\widehat{g}},{\widehat{z}},{\widehat{m}},{\widehat{n}},{\widehat{s}},{\widehat{\ell}})$ satisfies (4) and (5). Based on (25), inequalities (10), (11), and (13) hold. Based on (26) and the nonnegativity of ${\widehat{n}}^{i}_{t}$, inequality (16) holds.

Now, we only need to show that (12) and (14) hold.

For (12), let w ^∗ be the scenario where ${\widehat{m}}^{i+1}_{t}$ achieves the maximum value. Then, we observe that ${\widehat{m}}^{i}_{t}$ achieves the maximum value in the same scenario w ^∗. We prove (12) holds when ${\widehat{z}}_{i+1}=1$ and ${\widehat{z}} _{i+1}=0$. If ${\widehat{z}}_{i+1}=1$, then ${\widehat{m}}^{i}_{t}=0$ based on (25). Then, ${\widehat{m}}^{i}_{t}=0 \geq{\widehat{m}}^{i+1}_{t}-1 = {\widehat{m}} ^{i+1}_{t}-{\widehat{z}}_{i+1}$. If ${\widehat{z}}_{i+1}=0$, then

Thus, (12) holds.

For (14), according to (25),

Now, for each particular w _t ∈W(p),

where the second equation follows $\mathcal{P}^{p}_{t}(w_{t})\setminus\{p, q_{w_{t}}\}= \mathcal{P}^{q_{w_{t}}}_{t}(w_{t})\setminus \{q_{w_{t}}\}$ and the third equation follows $\widehat{m}^{q_{w_{t}}}_{t}=f_{\xi(q_{w_{t}}, t,w_{t})}-\sum_{j\in \mathcal{P}^{q_{w_{t}}}_{t}(w_{t})\setminus \{q_{w_{t}}, \xi(p,t,w_{t})\}}\widehat{z}_{j}$ for a given w _t ∈W(p). Then, (14) holds. Thus, $({\widehat{f}},{\widehat{g}},{\widehat{z}},{\widehat{m}},{\widehat{n}},{\widehat{s}}, {\widehat{\ell}})\in Q_{H}$ and Claim 2 holds.

Therefore, the conclusion holds. □

4 Computational experiments

In this section, we report the computational results to mainly demonstrate the computational efficiency and stability of the extended formulation for SULS with backlogging. All algorithms are implemented in C++ and carried out on a Linux workstation with two AMD Opteron Quad-Core 2.2 GHz processors and 32 GB RAM. We use CPLEX 12.4 Callable Library to implement our extended formulation and the two-stage mixed-integer programming formulation. To fairly compare the performance of these two formulations, we restrict the CPLEX Callable Library to run on a single thread.

The computational experiments are designed for two purposes, examining the value of stochastic solution of SULSB (VSS_SULSB) and demonstrating the efficiency and stability of the extended formulation of SULSB. A number of SULSB instances are generated corresponding to different scenario tree structures and different ratios of the setup cost to the unit production cost. We consider the underlying two-stage scenario tree is balanced with T time periods and W branches. We consider 27 different tree structures for both purposes. To test the extended formulation, we consider T∈{50,100,150}, W∈{10,20,30}, and p∈{0.2T,0.4T,0.6T}. To examine VSS_SULSB, we consider a larger number of scenarios with W∈{100,200,300}, the same time horizon T∈{50,100,150}, and the branching time period p∈{0.4T,0.5T,0.6T}. We consider the setup cost to production cost ratios to be 25 and 50, respectively. Therefore, there are 54 combinations in total for each case.

For each combination, we generate 5 random instances as follows. For each node i in the scenario tree, the unit production cost α _i is uniformly distributed in the interval [10,30] with average production cost $\bar{\alpha}=20$ and the setup cost $\beta'_{i}$ is uniformly distributed in the interval $[0.8(\beta'/\alpha)\bar {\alpha},1.2(\beta'/\alpha)\bar{\alpha} ]$. We let the demand d _i , the unit inventory cost $h'_{i}$, and the unit backlogging cost $b'_{i}$ uniformly distribute in the intervals [50,100], [2,7], and [2,5], respectively. Finally, all W branches are assigned equal probabilities, i.e., ρ _w =1/W. For each combination, we run 5 instances and report the average value.

We first test the mixed-integer programming formulation of SULSB and its corresponding expected (mean) value problem, where the expected value problem (EV_SULSB) is obtained by substituting all random variables in SULSB by their expected values. Then, the value of using the expected value solution, e.g., EEV_SULSB, can be obtained by solving SULSB in which the first-stage variables are replaced by the corresponding solution of EV_SULSB. In Tables 2, 3, 4, we report the percentage value of the stochastic solution of SULSB, i.e., VSS_SULSB/EEV_SULSB to demonstrate the needs to solve SULSB, where VSS_SULSB=EEV_SULSB−Obj_SULSB with Obj_SULSB representing the optimal objective value of SULSB. As described in Birge and Louveaux (1997), VSS measures how good (bad) a decision based on the EV problem solution compared with the decision based on stochastic programming. We let “Ratio 1” and “Ratio 2” indicate the cases in which the ratios between the setup cost and the unit production cost β′/α are 25 and 50, respectively.

Table 2 The percentage value of the stochastic solution for SULSB: T=50

Table 3 The percentage value of the stochastic solution for SULSB: T=100

Table 4 The percentage value of the stochastic solution for SULSB: T=150

The results in Tables 2 to 4 indicate that under the same setting in terms of time horizon, scenario number, and β′/α ratio, the percentage VSS_SULSB increases when the branching node time period, p, decreases. In average, the values of percentage VSS_SULSB are 2.5 %, 1.5 %, and 1.2 % corresponding to branching node time periods 0.2T, 0.4T, and 0.6T, respectively. Thus, the computational results demonstrate that the cost of ignoring uncertainties is higher when cost uncertainties happen at an earlier time period in the planning horizon.

Second, we test both the mixed-integer programming and extended linear programming formulations for SULSB, and evaluate the performance of these two formulations by comparing their running times to obtain an optimal solution. The running times (in seconds) of these two formulations are reported in Tables 5, 6, 7. We let “MIP”, “ELP” and “GAP” denote the mixed-integer programming formulation, the extended linear programming formulation, and the computational time difference between the mixed-integer programming formulation and the extended linear programming formulation, i.e., GAP=(Time_MIP−Time_ELP)/Time_ELP. We also let “Ratio 1” and “Ratio 2” indicate the cases in which the ratios between the setup cost and the unit production cost β′/α are 25 and 50, respectively.

Table 5 Computational time (in seconds) comparison between stochastic programming formulation and extended formulation of SULSB: T=50

Table 6 Computational time (in seconds) comparison between stochastic programming formulation and extended formulation of SULSB: T=100

Table 7 Computational time (in seconds) comparison between stochastic programming formulation and extended formulation of SULSB: T=150

Tables 5 to 7 demonstrate that all these two formulations obtain an optimal solution within 30 seconds for all tested instances. In average, the time spent for the mixed-integer programming approach is 2.77 times of that of the extended formulation approach. Meanwhile, the performance of the extended formulation is stable for both “Ratio 1” and “Ratio 2” cases. But the mixed-integer programming approach takes more times to run “Ratio 2” than “Ratio 1” instances in average.

The above computational results show that the extended formulation approach has a better chance to be more efficient and stable, as compared to the mixed-integer programming formulation approach.

5 Conclusion

In this research, we studied the two-stage stochastic lot-sizing problem under cost uncertainty and developed an extended linear programming formulation for the problem that can provide an integral optimal solution. In future research, a part of our results can be applied to a more general multi-stage stochastic programming setting. For instance, under the multi-stage setting, Proposition 1 still holds. The relationship between nodes in the stochastic scenario tree is similar to the relationship described in constraints (10) to (14). It is possible that similar reformulation can provide an extended formulation for the multi-stage stochastic lot-sizing problem under cost uncertainty in a higher dimensional space. In addition, we will target to solve large scale production planning problems under cost uncertainty, in which the extended formulation for each single-item problem can be embedded into a decomposition framework (e.g., the Lagrange relaxation decomposition). We will evaluate how this approach helps solve large scale practical production planning under uncertainty problems.

Appendix:  Proof of Proposition 2

To show that the constraint matrix described by constraints (4), (5), (10)–(14), and (16) is totally unimodular, we order variables f _i , g _i , and z _i with loop i ranging from 1 to $|\mathcal{V}|$. Variable $m^{i}_{t}$ is ordered with an outer loop i ranging from 1 to $|\mathcal{V}|$, and an inner loop t ranging from t(i)+1 to T. Variable $n^{i}_{t}$ is ordered with an outer loop i ranging from 1 to $|\mathcal{V}|$, and an inner loop t ranging from 1 to t(i). Table 8 shows the constraint matrix corresponding to Fig. 2.

Table 8 The matrix of constraints (4), (5), (10) to (14), and (16) for the example in Fig. 2

As the submatrix corresponding to variable $n^{i}_{t}$ is an identity matrix for $i\in\mathcal{V}$ and t≤t(i), we do not need to consider $n^{i}_{t}$ in our construction. As the submatrix corresponding to variable $m^{i}_{t}$ is an identity matrix for t(i)≥t(p)+2, $i\in\mathcal{V}$, and t≥t(i)+1, we only need to consider $m^{i}_{t}$, 1≤t(i)≤t(p)+1, t≥t(i)+1 in our construction. In the following, we only study the constraint submatrix for the variables we need to consider, denoted as matrix A.

We show that for any column subset J of matrix A, there exist partitions J ₁ and J ₂ of J such that

$$ \biggl|\sum_{j\in J_1} a_{ij} - \sum_{j\in J_2} a_{ij}\biggr| \leq1 $$

(27)

for all i. We partition variables f, g, z, m in J starting from branching node p and then, extend it in both directions to nodes after p and before p.

First, we define M(i) as the closest ancestor of node i such that z _M(i)∈J and m(i) as the closest descendant of node i such that z _m(i)∈J.

In the following Steps 1 to 5, we allocate the decision variables m and z to J ₁ and J ₂:

Step 1.:

Allocate $m^{p}_{t}$ to J ₁, z _p to J ₁, and $z_{q_{w}}$ to J ₂, where t≥t(p)+1, $q_{w} \in\mathcal{C}(p)$.

Step 2.:

Allocate $m^{q_{w}}_{t}$, t≥t(p)+2 to the same set as $z_{q_{w}}$ (if $z_{q_{w}} \in J$), or to the same set as $m^{p}_{t}$ (if $z_{q_{w}} \notin J$ and $m^{p}_{t}\in J$), or to J ₁ (if $z_{q_{w}}\notin J$ and $m^{p}_{t}\notin J$).

Step 3.:

Allocate z _i , t(i)≥t(p)+2, to the opposite set of z _M(i), if M(i) exists and t(M(i))≥t(p). Otherwise, allocate z _i to the opposite set of $m^{p}_{t}$ if $m^{p}_{t}\in J$. If $m^{p}_{t} \notin J$, then allocate z _i to J ₂.

Step 4.:

Allocate z _i , 1≤i≤p−1, to the opposite set of z _m(i), if m(i) exists and t(m(i))≤t(p). Otherwise, allocate z _i to J ₁.

Step 5.:

Allocate $m^{i}_{t}$, 1≤i≤p−1, to the opposite set of z _m(i), if m(i) exists and t(m(i))≤t(p). Otherwise, allocate $m^{i}_{t}$ to J ₁.

In the following Steps 6 and 7, we allocate the decision variables f and g to J ₁ and J ₂:

Step 6.:

Allocate f _i to the same set of z _M(i) if M(i) exits; allocate f _i to the opposite set of z _i if M(i) does not exist and z _i ∈J; allocate f _i to the opposite set of z _m(i) if m(i) exists, M(i) does not exist, and z _i ∉J; allocate f _i to J ₁ if m(i) and M(i) do not exist and z _i ∉J.

Step 7.:

Allocate g _i to the same set of z _m(i) if m(i) exists; allocate g _i to the opposite set of z _i if m(i) does not exist and z _i ∈J; allocate g _i to the opposite set of z _M(i) if m(i) does not exist, M(i) exists, and z _i ∉J; allocate g _i to J ₂ if m(i) and M(i) do not exist and z _i ∉J.

Following the above partition steps, we observe the following two properties:

Claim 1

If z _i ∈J and M(i) exists, z _i goes to the opposite set of z _M(i) for all $i\in{\mathcal{V}}\setminus\{1\}$.

Proof of Claim 1

If 1≤t(M(i))≤t(i)≤t(p), because the closest descendant of M(i) is i and t(i)≤t(p), m(M(i))=i, z _M(i) goes to the opposite set of z _i based on Step 4.

If 1≤t(M(i))<t(p)<t(i)≤T, z _M(i) goes to J ₁ based on Step 4 and z _i goes to J ₂ based on Step 3 (if t(i)≥t(p)+2) or based on Step 1 (if t(i)=t(p)+1).

If t(p)=t(M(i))<t(i)≤T, z _M(i) goes to J ₁ based on Step 1 (i.e., M(i)=p), z _i goes to J ₂ based on Step 1 (if i=q _w ) or Step 3 (if t(i)≥t(p)+2). Thus, z _i goes to the opposite set of z _M(i).

If t(p)+1≤t(M(i))<t(i)≤T, z _i goes to the opposite set of z _M(i) based on Step 3.

Therefore, Claim 1 holds. □

Claim 2

If $j(w_{k_{1}})$ and $j(w_{k_{2}})$ are the first second-stage nodes corresponding to scenarios $w_{k_{1}}$ and $w_{k_{2}}$ such that $z_{j(w_{k_{1}})}, z_{j(w_{k_{2}})} \in J$, then $z_{j(w_{k_{1}})}$ and $z_{j(w_{k_{2}})}$ go to the same set.

Proof of Claim 2

For any first second-stage node j(w), if j(w)=q _w , then z _j(w) goes to J ₂ based on Step 1, otherwise j(w) goes to J ₂ based on Step 3 due to the fact that j(w) is the first second-stage node in J and on the branch corresponding to w and t(p)≤t(j(w))≤T. Thus, the claim holds. □

Now, we verify that (27) holds for constraints (4), (5), (10)–(14), and (16) under the above partition. First, corresponding to each row, if J contains at most one decision variable in A, then it is obvious that (27) holds. In the following, we consider the case in which J contains at least two decision variables in each row of A.

• 1. For constraint (4), we discuss the following four cases:

  • 1.1 {f _i ,g _i }⊆J and z _i ∉J

    • 1.1.1 If both M(i) and m(i) exist, f _i goes to the same set of z _M(i) based on Step 6; g _i goes to the same set of z _m(i) based on Step 7. Because M(m(i))=M(i) (due to z _i ∉J), z _m(i) goes to the opposite set of z _M(i) based on Claim 1. Thus, f _i goes to the opposite set of g _i . Then, (27) holds.

    • 1.1.2 If M(i) exists and m(i) does not exist, f _i goes to the same set of z _M(i) based on Step 6; g _i goes to the opposite set of z _M(i) based on Step 7. Thus, f _i goes to the opposite set of g _i .

    • 1.1.3 If m(i) exists and M(i) does not exist, g _i goes to the same set of z _m(i) based on Step 7; f _i goes to the opposite set of z _m(i) based on Step 6. Thus, f _i goes to the opposite set of g _i .

    • 1.1.4 If neither m(i) nor M(i) exists, f _i and g _i go to J ₁ and J ₂ respectively based on Steps 6 and 7.

  • 1.2 {g _i ,z _i }⊆J and f _i ∉J

    • 1.2.1 If m(i) exists, then g _i goes to the same set of z _m(i) based on Step 7. Because M(m(i))=i, z _m(i) goes to the opposite set of z _i based on Claim 1. Thus, g _i goes to the opposite set of z _i . Then, (27) holds.

    • 1.2.2 If m(i) does not exist, g _i goes to the opposite set of z _i based on Step 7. Thus, (27) holds.

  • 1.3 {f _i ,z _i }∈J and g _i ∉J

    • 1.3.1 If M(i) exists, f _i goes to the same set of z _M(i) based on Step 6; z _i goes to the opposite set of z _M(i) based on Claim 1. Then, f _i goes to the opposite set of z _i . Thus, (27) holds.

    • 1.3.2 If M(i) does not exist, f _i goes to the opposite set of z _i based on Step 6. Thus, (27) holds.

  • 1.4 {f _i ,g _i ,z _i }∈J. This conclusion directly follows 1.3, because f _i goes to the opposite set of z _i . Then, (27) holds no matter where g _i goes.

• 2. For constraint (5), we discuss the following four cases:

  • 2.1 If {g _i ,z _i }∈J and g _a(i)∉J this condition is the same as 1.2. Thus, (27) holds.

  • 2.2 If {g _a(i),z _i }∈J and g _i ∉J, g _a(i) goes to the same set as z _i due to z _i =z _m(a(i)) based on Step 7. Thus, (27) holds.

  • 2.3 If {g _i ,g _a(i)}∈J and z _i ∉J, we first have m(i)=m(a(i)). If (a) m(i)=m(a(i)) exists, then g _i and g _a(i) go to the same set as z _m(i) based on Step 7. If (b) m(i)=m(a(i)) does not exist and z _a(i)∈J, then g _a(i) goes to the opposite set of z _a(i) based on Step 7. Also, because z _a(i)∈J, we have z _M(i)=z _a(i). Then, g _i goes to the opposite set of z _a(i) based on Step 7. Thus, g _i and g _a(i) go to the same set. If (c) m(i)=m(a(i)) does not exist, z _a(i)∉J and M(a(i)) exists, then z _M(i)=z _M(a(i)). Because z _i ∉J, g _i and g _a(i) go to the opposite set of z _M(i)=z _M(a(i)) based on Step 7. Thus, g _i and g _a(i) go to the same set. If (d) m(i)=m(a(i)), M(a(i)) does not exist, z _a(i)∉J, then both g _i and g _a(i) go to J ₂ based on Step 7.

  • 2.4 If {g _i ,g _a(i),z _i }∈J, this conclusion directly follows 2.2, because g _a(i) and z _i go to the same set. Then, (27) holds no matter where g _i goes.

• 3. For constraint (10), we consider two cases:

  • 3.1 t(i)≥t(p)+2. For this case, we do not need to consider $m^{i}_{t}$ based on the identity matrix argument at the beginning of the proof. Then, based on Step 6, f _ξ(i,t,w) goes to the same set of z _M(ξ(i,t,w)), where z _M(ξ(i,t,w))∈J and the corresponding M(ξ(i,t,w)) is the largest-index such node in path ${\mathcal{P}}^{i}_{t}(w)$ with ${\mathcal{P}}^{i}_{t}(w)$ representing the set of nodes on the path from node i to a node at time period t and on the branch corresponding to scenario w. Note that there must exist at least one such M(ξ(i,t,w)) based on the assumption that we have at least two elements in J for each constraint. Based on Step 4, z _j alternatively goes to J ₁ and J ₂ based on Step 4, where t(p)+2≤t(j)≤t. Thus, (27) holds.

  • 3.2 t(i)=t(p)+1. For this case, i=q _w , for some 1≤w≤W. We discuss the following two cases:

    • 3.2.1 If $m^{q_{w}}_{t}\notin J$, this argument is the same as 3.1. Thus, (27) holds.

    • 3.2.2 If $m^{q_{w}}_{t}\in J$, under this condition, we discuss $f_{\xi(q_{w},t,w)}\notin J$ and $f_{\xi(q_{w},t,w)}\in J$ respectively.

      • 3.2.2.1 $f_{\xi(q_{w},t,w)}\notin J$. Under this case, if $z_{q_{w}}\in J$, $m^{q_{w}}_{t}$ and $z_{m(q_{w})}$ go to the same set and the opposite set of $z_{q_{w}}$ based on Steps 2 and 3 respectively; if $z_{q_{w}}\notin J$, $m^{q_{w}}_{t}$ goes to the same set as $m^{p}_{t}$ (i.e., J ₁) if $m^{p}_{t}\in J$ or J ₁ if $m^{p}_{t}\notin J$ based on Step 2 and similarly $z_{m(q_{w})}$ goes to J ₂ based on Step 3. Thus, $m^{q_{w}}_{t}$ and $z_{m(q_{w})}$ go to the opposite sets. Besides these, z _j ∈J alternatively goes to J ₁ and J ₂ where t(p)+2≤t(j)≤t based on Step 3. Thus, (27) holds.

      • 3.2.2.2 $f_{\xi(q_{w},t,w)}\in J$. Under this case, we discuss two cases depending on if there exists a node $j\in{\mathcal{P}}^{i}_{t}(w)\setminus\{i, \xi(i, t, w)\}$ such that z _j ∈J.

        3.2.2.2.1  If no such node j exists, then $\{f_{\xi(q_{w},t,w)}, m^{q_{w}}_{t}\}\in J$, based on our assumption that at least two elements in each constraint in matrix A. If $z_{q_{w}}\in J$, M(ξ(q _w ,t,w))=q _w due to z _j ∉J for each $j \in{\mathcal{P}}^{i}_{t}(w)\setminus\{i, \xi(i, t, w)\}$. Based on Steps 6 and 2, $f_{\xi(q_{w},t,w)}$ and $m^{q_{w}}_{t}$ go to the same set of $z_{q_{w}}$. If $z_{q_{w}}\notin J$, based on Step 2, $m^{q_{w}}_{t}$ goes to J ₁. In the following, we prove that $f_{\xi (q_{w}, t,w)}$ goes to J ₁ in this case. Based on Step 6, $f_{\xi(q_{w}, t, w)}$ goes to (a) the same set of $z_{M(\xi(q_{w}, t, w))}$ if M(ξ(q _w ,t,w)) exists, (b) the opposite set of $z_{\xi(q_{w}, t, w)}$ if M(ξ(q _w ,t,w)) does not exist and $z_{\xi(q_{w}, t,w)}\in J$, (c) the opposite set of $z_{m(\xi(q_{w}, t,w))}$ if m(ξ(q _w ,t,w)) exists, M(ξ(q _w ,t,w)) does not exist, and $z_{\xi(q_{w}, t,w)} \notin J$, or (d) J ₁ if M(ξ(q _w ,t,w)) and m(ξ(q _w ,t,w)) do not exist, and $z_{\xi (q_{w}, t,w)} \notin J$. For (a), M(ξ(q _w ,t,w)) exists and $z_{q_{w}} \notin J$. Based on Step 4, $z_{M(\xi(q_{w}, t, w))}$ goes to J ₁, because 1≤t(M(ξ(q _w ,t,w)))≤t(p). For (b), $z_{\xi (q_{w}, t, w)}\in J$, $z_{q_{w}}\notin J$, and M(ξ(q _w ,t,w)) does not exist. Then, $z_{\xi(q_{w}, t, w)}$ goes to J ₂ based on Step 3 and accordingly $f_{\xi(q_{w}, t, w)}$ goes to J ₁. For (c), $z_{m(\xi(q_{w},t,w))}\in J$, and $z_{\xi(q_{w}, t, w)}, z_{M(\xi(q_{w}, t, w))}, z_{q_{w}}\notin J$. Then, $z_{m(\xi(q_{w},t,w))}$ goes to J ₂ based on Step 3. Thus, accordingly $f_{\xi(q_{w}, t, w)}$ goes to J ₁. Then, $f_{\xi(q_{w}, t, w)}$ and $m^{q_{w}}_{t}$ go to the same set.

        3.2.2.2.2  If there exists such a node j, then $f_{\xi(q_{w},t,w)}$ goes to the same set of $z_{M(\xi(q_{w}, t, w))}$ based on Step 6. If $z_{q_{w}}\in J$, $m^{q_{w}}_{t}$ goes to the same set of $z_{q_{w}}$ based on Step 2, and $z_{m(q_{w})}$ goes to the opposite set of $z_{q_{w}}$ based on Step 3. If $z_{q_{w}}\notin J$, $m^{q_{w}}_{t}$ goes to J ₁ based on Step 2 and $z_{m(q_{w})}$ goes to J ₂ based on Step 3. Thus, for both $z_{q_{w}}\in J$ and $z_{q_{w}}\notin J$, $m^{q_{w}}_{t}$ goes to the opposite set of $z_{m(q_{w})}$. Besides these, z _j alternatively goes to J ₁ and J ₂, $j\in {\mathcal{P}}^{i}_{t}(w)\setminus\{i,\xi(i,t,w)\}$. Thus, (27) holds.

• 4. For constraint (11), we only need to consider the case in which $\{m^{i}_{t}, f_{i+1}\}\in J$.

  • 4.1 If M(i+1) exists, f _i+1 goes to the same set as z _M(i+1) based on Step 6. If m(i) exists and t(m(i))≤t(p), $m^{i}_{t}$ goes to the opposite set of z _m(i) based on Step 5. Because m(i)=m(M(i+1)), z _M(i+1) and z _m(i) go to the opposite set based on Step 4. Thus, f _i+1 and $m^{i}_{t}$ go to the same set. If m(i) does not exist, or m(i) exists and t(m(i))>t(p), then m(M(i+1)),t(m(M(i+1)))≤t(p), does not exist. Thus, z _M(i+1) and $m^{i}_{t}$ go to J ₁ based on Steps 4 and 5. Thus, $m^{i}_{t}$ and f _i+1 go to the same set. Therefore, (27) holds.

  • 4.2 If M(i+1) does not exist and z _i+1∈J, then m(i)=i+1. Thus, $m^{i}_{t}$ and f _i+1 go to the opposite set of z _i+1 based on Steps 5 and 6. Thus, (27) holds.

  • 4.3 If M(i+1) does not exist, z _i+1∉J, and m(i+1) exists, then, m(i)=m(i+1). If 1≤t(m(i+1))≤t(p), $m^{i}_{t}$ and f _i+1 go to the opposite set of z _m(i+1) based on Steps 5 and 6; otherwise, if t(m(i+1))>t(p), $m^{i}_{t}$ goes to J ₁ and f _i+1 goes to the opposite set of z _m(i+1). Since z _m(i+1) goes to J ₂ based on Step 1 (if t(m(i+1))=t(p)+1) or Step 3 (under this case, M(m(i+1)) does not exist), f _i+1 and $m^{i}_{t}$ go to the same set. Then, (27) holds.

  • 4.4 If neither M(i+1) nor m(i+1) exists and z _i+1∉J, then $m^{i}_{t}$ and f _i+1 go to J ₁ based on Steps 5 and 6. Then, (27) holds.

• 5. For constraint (12), we discuss the following four cases:

  • 5.1 $\{m^{i}_{t},z_{i+1} \}\subseteq J$, and $m^{i+1}_{t}\notin J$. Based on Step 5, $m^{i}_{t}$ goes to the opposite set of z _i+1 since z _i+1 is the closest descendant of node i. Thus, (27) holds.

  • 5.2 $\{m^{i+1}_{t},z_{i+1} \}\subseteq J$, and $m^{i}_{t} \notin J$. Under this case, $m^{i+1}_{t}$ and z _i+1 will go to the same set, because both z _i+1 and $m^{i+1}_{t}$ are in the opposite set of z _m(i+1), if m(i+1) exists and t(m(i+1))≤t(p) or in J ₁ otherwise, based on Steps 4 and 5.

  • 5.3 $\{m^{i}_{t},m^{i+1}_{t} \}\subseteq J$, and z _i+1∉J. Because z _i+1∉J, $m^{i}_{t}$ and $m^{i+1}_{t}$ are in the same set based on Step 5.

  • 5.4 $\{m^{i}_{t},m^{i+1}_{t},z_{i+1} \}\subseteq J$. The conclusion follows from Step 5. Variable $m^{i}_{t}$ goes to the opposite set of z _i+1, since z _i+1 is the closest descendant of node i. Then, (27) holds no matter where $m^{i+1}_{t}$ goes.

• 6. For constraint (13), we only need to consider the case in which $\{f_{q_{w}}, m^{p}_{t}\} \subseteq J$. Based on Step 1, $m^{p}_{t}$ goes to J ₁. In the following, we show that $f_{q_{w}}$ goes to J ₁.

  • 6.1 If M(q _w ) exists, then $z_{M(q_{w})}$ goes to J ₁ based on Step 1 if M(q _w )=p, or Step 4 if t(m(M(q _w )))≤t(p)−1. Thus, based on Step 6, $f_{q_{w}}$ goes to the same set of $z_{M(q_{w})}$, which is J ₁.

  • 6.2 If $z_{q_{w}}\in J$, M(q _w ) does not exist, then $z_{q_{w}}$ goes to J ₂ based on Step 1. Based on Step 6, $f_{q_{w}}$ goes to the opposite set of $z_{q_{w}}$, which is J ₁.

  • 6.3 If m(q _w ) exists, $z_{q_{w}} \notin J$ and M(q _w ) does not exist, then t(m(q _w ))≥t(p)+2 and $z_{m(q_{w})}$ goes to the opposite set of $m^{p}_{t}$ based on Step 3. Based on Step 6, we have $f_{q_{w}}$ goes to the opposite set of $z_{m(q_{w})}$. Thus, $f_{q_{w}}$ and $m^{p}_{t}$ go to the same set, which is J ₁.

  • 6.4 If m(q _w ) and M(q _w ) do not exist and $z_{q_{w}}\notin J$, then $f_{q_{w}}$ goes to J ₁ based on Step 6.

• 7. For constraint (14), we need to consider the following four cases:

  • 7.1 $\{m^{p}_{t},z_{q_{w}} \}\subseteq J$ and $m^{q_{w}}_{t}\notin J$. Based on Step 1, $m^{p}_{t}$ and $z_{q_{w}}$ go to J ₁ and J ₂, respectively. Thus, (27) holds.

  • 7.2 $\{m^{q_{w}}_{t}, z_{q_{w}} \}\subseteq J$ and $m^{p}_{t}\notin J$. $m^{q_{w}}_{t}$ and $z_{q_{w}}$ go to the same set based on Step 2.

  • 7.3 $\{m^{p}_{t},m^{q_{w}}_{t} \}\subseteq J$ and $z_{q_{w}}\notin J$. Under this case, $m^{p}_{t}$ and $m^{q_{w}}_{t}$ go to the same set based on Step 2.

  • 7.4 $\{m^{p}_{t},m^{q_{w}}_{t}, z_{q_{w}}\}\subseteq J$. Under this case, $m^{p}_{t}$ and $z_{q_{w}}$ go to J ₁ and J ₂, respectively based on Step 1. Then, (27) holds no matter where $m^{q_{w}}_{t}$ goes.

• 8. For constraint (16), we do not need to consider $n^{i}_{t}$ based on the identity matrix argument at the beginning of the proof. Based on Step 7, g _η(i,t) goes to the same set of z _m(η(i,t)). Note here, there must exist m(η(i,t)) based on the assumption that we have at least two elements in J. If t(m(η(i,t)))≤t(p) or t(η(i,t))≥t(p)+1, then η(i,t) and m(η(i,t)) are one-to-one corresponding. Otherwise, all z _m(η(i,t)) in different scenarios go to the same set based on Claim 2 because t(m(η(i,t)))≥t(p)+1. Besides these, z _j alternatively goes to J ₁ and J ₂ based on Claim 1. Thus, (27) holds.

Therefore, the desired property (27) holds for constraints (4), (5), (10)–(14), and (16), and the corresponding constraint matrix is totally unimodular.