1 Introduction and background

Mining is a complex, expensive, but potentially lucrative business. Before the first ounces of metal are recovered for revenue, hundreds of millions of dollars and years of effort may be required for permitting, financing, site construction, and training. As in all natural resource exploration industries, these investments do not guarantee a profit. Tight margins and volatile mineral markets necessitate efficient ore removal schemes to maximize the mine’s expected return on investment, thereby increasing the likelihood of being profitable.

A common method to extract hard-rock minerals from the ground is surface, or open pit, mining. A block model contains three-dimensional rectangular blocks (e.g., 50′×50′×100′) representing the material to be removed. By removing material directly from the surface, open pit mines benefit from tremendous efficiencies of scale through the use of massive equipment (e.g., 360-ton trucks that haul material from the pit). These efficiencies are realized in enormous mining operations that may span decades and include tens of thousands to millions of blocks. This paper focuses on solving the open pit block sequencing (OPBS) problem, which is that portion of the production scheduling problem specifying which blocks to extract, and when, to maximize the value of the extracted ore. The difficulty in solving the OPBS problem depends on both the number of blocks, and on the amount of detail included in the problem specification (e.g., the number of different resources required to extract the blocks, whether or not extracted material may be stockpiled, whether or not the attributes of extracted material must satisfy specific proportions).

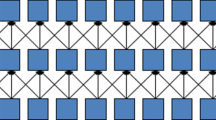
Precedence constraints enforce geospatial limitations to ensure that pit walls do not fall in on themselves (e.g., pit wall slopes may not be inclined more than 45 degrees as measured from the horizontal). One example of such a constraint precludes removing a lower level block b prior to removing the blocks above and adjacent to each face of b (see Fig. 1). We refer to those predecessor blocks b′ in the level directly above b as b’s direct predecessor set, and the predecessor blocks b″ in all levels above b as b’s complete predecessor set, or b’s predecessor pit. Analogously, if we choose not to mine block b, a set of blocks has its extraction held up by block b. We refer to this set as block b’s complete hold set, and it includes all other blocks which contain block b in their predecessor sets.

Fig. 1
figure 1

Blocks 2–6 must be mined prior to mining block 1

Full size image

Resource capacities limit the amount of material extracted from the pit and processed at the mill. The maximum production capacity is a function of the available equipment (e.g., shovels and trucks) and the equipment’s ability to access the pit (e.g., road capacities into and out of the pit). The maximum processing capacity is a function of the mill’s throughput, where mineral content is separated from waste. The scale and nature of production and processing operations is such that stopping and re-starting is not always practical, and hence, minimum resource requirements may also exist. For example, to prevent firing and re-hiring a highly trained workforce, a mine planner may enforce a minimum production rate in each period. Some processing operations are self-sustaining, and many mines enter into long-term delivery contracts, both of which imply a minimum processing rate each period. From a tractability standpoint, the inclusion of these minimum requirements is challenging, as they preclude myopic approaches which may be valid when only maximum capacities exist.

The mine planner must develop a schedule specifying if and when to remove each block from the pit, subject to precedence constraints between blocks, and resource constraints that dictate minimum and maximum extraction and processing rates. The major challenge is to select from among numerous feasible sequences one that maximizes the net present value of the extracted ore. Identifying that sequence requires integer programming, because blocks may not be partially mined.

2 Literature review

Lerchs and Grossmann (1965) present an efficient method of solving the open pit mine design problem, with subsequent papers providing insights, algorithmic enhancements, and/or extensions to robust planning, e.g., Underwood and Tolwinski (1998), Hochbaum and Chen (2000), and Altner and Ergun (2011). Solving this ultimate pit limit (UPL) problem identifies the most economical subset of blocks to extract from within the entire proposed open pit mine. However, by ignoring resource requirements and the dimension of time, solving the UPL problem cannot provide a production schedule.

The sheer size of real-world open pit mine scheduling problems limits the feasibility of solving the monolith with naive integer programming formulations. Therefore, various decomposition and aggregation approaches are common in the literature. Johnson (1968) provides the first published attempt at formulating and solving the open pit production scheduling monolith, determining extraction times and destinations for individual blocks while enforcing resource constraints. Dagdelen (1985) improves upon this attempt with Lagrangian relaxation, decomposing the constraint set into two groups: (i) constraints which form a network (sequencing constraints) and (ii) constraints associated with production and processing capacities (side constraints). He then dualizes the side constraints to take advantage of the underlying network structure of the sequencing constraints.

Caccetta and Hill (2003) provide an exact approach to solving the open pit production scheduling problem, explicitly defining variables that represent whether a block is extracted by time period t, a variable substitution approach first proposed in Johnson (1968), which is now standard in open pit production scheduling formulations. Ramazan (2007), Boland et al. (2009), and Gleixner (2008) use block aggregation approaches; while successful, effective disaggregation remains a challenge. Bley et al. (2010) strengthen the integer formulation of the open pit mine production scheduling problem by adding valid cutting planes for both single- and multiple-block sets. They do so considering each attribute of a block, the mine’s corresponding capacity to handle that attribute, and the combined precedence set of multiple blocks. Askari-Nasab et al. (2010) present two formulations based on a “mining-cut” construct, which suggests a block aggregation scheme. Their formulations seek to accurately model pit slopes while increasing tractability relative to unaggregated models.

Kawahata (2006) extends the work of Dagdelen and Johnson (1986) by using aggregation, pre-determined sequences, and Lagrangian relaxation to reduce the solution time for large-scale open pit mine production scheduling problems, subject to maximum production and processing capacities. His results show reductions in solution time, although he does not consider all constraints in the sub-problem as strict.

Chicoisne et al. (2012) and Moreno et al. (2010) quickly solve the linear programming (LP) relaxation of the OPBS problem for extremely large sets of blocks. Their TopoSort algorithm induces a topological sorting of the nodes in the problem’s underlying network structure, and then uses rounding heuristics to derive integer feasible solutions. Similarly, Bienstock and Zuckerberg (2010) present an algorithm to quickly generate solutions to the LP relaxation of the open pit production scheduling problem including constraints on the maximum amount of resources, for millions of blocks. Both of these are seminal approaches to solving the LP relaxation of the OPBS problem constrained by maximum resource capacities. The work does not consider minimum resource requirements.

Gaupp (2008) considers both (strict) minimum resource requirements and maximum resource capacities in his treatment of the OPBS problem. Specifically, he uses variable reduction, cutting planes, and Lagrangian relaxation to reduce solution times from those resulting from direct solution of the monolith. Cullenbine et al. (2011) combine Lagrangian relaxation within a sliding time window heuristic (STWH) to find solutions for the same variant of the OPBS problem. Their approach yields good results for problems containing tens of thousands of blocks and 15 time periods. However, the procedure is a heuristic, and the authors note that it is possible that no feasible solution could result from the application of said heuristic. See Newman et al. (2010) for a detailed literature review covering both open pit and underground mine planning.

Our work continues these efforts towards enhancing an exact approach to solve the OPBS problem with strict minimum resource requirements and maximum resource capacities. We incorporate a solution resulting from the ultimate pit limit problem and a sliding time window heuristic in an algorithm to generate an initial feasible solution for the OPBS problem. Then, we use information from our algorithm to tailor a Lagrangian relaxation procedure to a given problem instance. Our contributions lie in the following: (i) we solve as large instances as have been solved to date containing the detail of both strict minimum resource requirements and maximum resource capacities; (ii) rather than a heuristic, we provide an exact, tailored approach for this OPBS problem variant; and (iii) we provide a procedure to determine initial feasible solutions, which could be used not only in conjunction with our exact approach, but also with heuristic approaches such as that proposed in Cullenbine et al. (2011). The second and third contributions may be generalized to integer programming applications beyond those found in open pit mining, or even in production scheduling in general.

3 Mathematical model

We make the following assumptions in our model: (i) blocks require a single time period to mine and must be mined in their entirety; (ii) blocks contain a pre-specified, deterministic amount of ore and waste; (iii) the ratio of valuable mineral to waste dictates a priori whether the block, if extracted, is sent to the mill for processing or to the dump as waste; (iv) the mine holds no stockpiles. The first assumption can easily be relaxed by either redefining time period length or including an appropriate lag parameter in the precedence constraints. The second, third, and fourth assumptions are stronger; they are appropriate for long-term models in which the goal is to determine whether or not a deposit is generally economically viable. Operational schedules would contain the detail of a variable cutoff grade, i.e., the model would determine whether or not a block is sent to the mill or to a waste dump, and might also contain several types of stockpiles. It is our intention here to present an approach for solving large, long-term models with less detail, though arguably, sufficiently detailed short-term models also provide a viable avenue for future research.

The mathematical formulations of the ultimate pit limit (UPIT) and the constrained pit limit (CPIT) problems follow. The solution to (UPIT) identifies the most economical subset of blocks to extract from within the entire proposed pit, ignoring resource constraints and the dimension of time. The solution to (CPIT) identifies an extraction sequence specifying which blocks to extract and when, while respecting resource constraints. We name these problems to be consistent with Espinoza et al. (to appear). Our abbreviation convention identifies formulated problems with italicized capital letters surrounded by parentheses (e.g., (UPIT)), algorithms with italicized capital letters without parentheses (e.g., STWH), and acronyms with unitalicized capital letters (e.g., OPBS).

3.1 Mathematical formulation of the Ultimate Pit Limit Problem (UPIT)

The network-based (UPIT) formulation strives to maximize the (undiscounted) value of the extracted blocks while satisfying precedence constraints. The solution to (UPIT) then is the highest-valued subset of blocks within the entire pit satisfying block precedences.

Indices and sets:

  • b∈B: set of all blocks b

  • b′∈B b : set of blocks b′ which must be extracted directly before block b, i.e., b’s direct predecessors

Data:

  • v b : net value generated by extracting block b ($)

Decision variables:

  • \(y_{b}: \begin{cases} 1 & \text{if block $b$ is extracted}\\ 0 & \text{otherwise} \end{cases} \)

Objective function:

$$ (\mathit{UPIT}) \quad\max\sum_{b\in B} v_{b} y_{b} $$
(1)

Constraints:

(2)
(3)

The objective function (1) seeks to maximize the undiscounted value of all extracted blocks. Constraints (2) prevent block b from being mined unless all of its predecessors are mined. Constraints (3) restrict the decision variables to assume a value between 0 and 1.

(UPIT) includes no time index, which precludes the consideration of discounting; thus, v b is the net value of removing block b, as opposed to the net present value (NPV) of removing block b. The precedence constraints (2) collectively form a totally unimodular A matrix, so that decision variables are guaranteed to assume integer values in an optimal solution. As such, constraints (3) only restrict y b to continuous values between 0 and 1, avoiding the integrality requirement and longer solve time associated with an integer formulation.

3.2 Mathematical formulation of the Constrained Pit Limit Problem (CPIT)

We formulate the OPBS problem as a precedence-constrained binary knapsack, with decision variables indicating whether or not to remove a block by a given time period. The solution provides an NPV-maximizing block extraction sequence which satisfies geospatial precedences and resource constraints. Additional notation and the (CPIT) formulation are presented below.

Indices and sets:

  • t∈T: set of time periods t

  • r∈R: set of operational resources r (1 = production, 2 = processing)

Data:

  • v bt : net present value generated by extracting block b in time period t ($)

  • a rb : amount of operational resource r used to process block b (tons)

  • \(\underline{e}_{r}/\overline{e}_{r}\): per period minimum required usage/maximum usage capacity for operational resource r (tons)

Decision variables:

  • \(w_{bt}: \begin{cases} 1 & \mbox{if block $b$ is extracted \textit{by} time $t$}\\ 0 & \mbox{otherwise} \end{cases} \)

Objective function:

$$ (\mathit{CPIT})\quad\max\sum_{b\in B}\sum _{t \in T}v_{bt} (w_{bt}-w_{b,t-1} ) $$
(4)

Constraints:

(5)
(6)
(7)
(8)

The objective function (4) seeks to maximize the NPV of all extracted blocks. Constraints (5) ensure that block b is not extracted by time period t unless every block b′ in b’s direct predecessor set (B b ) is also extracted by time period t. Constraints (6) enforce minimum resource requirements and maximum resource capacities in each period. Constraints (7) enforce the by behavior of the variables w bt , where a block b extracted by period t−1 must also be extracted by period t. Constraints (8) restrict all decision variables to be binary.

Relative to (UPIT), (CPIT) adds the dimension of time, and imposes operational resource and integrality restrictions. (CPIT)’s resource constraints (6) destroy the underlying network structure of the precedence constraints (5), thereby requiring integrality restrictions (8) on the variables.

4 Solution methodologies

(CPIT), which can be thought of as a precedence-constrained knapsack problem, is strongly NP-hard (see Johnson and Niemi 1983). Solving (to near-optimality) instances of (CPIT) containing about 10,000 blocks and 10 time periods with a naive integer formulation can require hours; in some cases, the model can run for days without finding an integer solution. When (CPIT) includes non-zero minimum resource requirements, the competing demands of satisfying the minimum processing requirement without exceeding the maximum production capacity can be a significant challenge to tractability. Our Maximum Value Feasible Pit (MVFP) algorithm identifies if this challenge exists for a given problem instance, and consequently how best to tailor the solution strategy. We suggest three approaches to reduce solution time: (i) we eliminate variables which must assume a value of 0 in the optimal solution; (ii) we use the MVFP algorithm to generate, and then provide to (CPIT), an initial integer feasible solution (IIFS), and finally; (iii) we use a Tailored Lagrangian Relaxation (TLR) in which we dualize various resource constraints (6) according to insights garnered from the MVFP algorithm.

4.1 Pre-processing for variable elimination

We reduce problem size through pre-processing to eliminate variables whose values must equal 0 in any feasible solution. Precedence requirements enable us to eliminate variables a priori, as block b is not accessible until blocks overlying b are removed. Furthermore, this removal occurs at rates restricted by both maximum production and maximum processing capacities. This now standard notion of early starts (ES) identifies variables w bt , corresponding to time periods t, such that t<ES b , by which block b may not be extracted due to maximum resource capacities. ES are used in both open pit models, e.g., Gaupp (2008), Amaya et al. (2009), and Chicoisne et al. (2012), and also in underground mine planning, e.g., Martinez and Newman (2011).

Our inclusion of minimum resource requirements gives rise to the concept of enhanced early starts (EES), introduced in Lambert et al. (to appear), which enable further variable reductions beyond ES. Just as maximum resource capacities for either production or processing may limit the ability to extract certain blocks by certain time periods, the minimum processing requirement alone forces the extraction of a minimum number of ore blocks in each period. This then may implicitly preclude the extraction of certain blocks by certain time periods. For example, consider block b whose complete predecessor set contains no ore blocks, and contains blocks with a combined total tonnage equal to a single period’s production capacity. While the production capacity exists to extract b in the first period, doing so would violate any non-zero minimum processing requirement. In this case, the variable w b1 must assume the value of 0 in any feasible solution, and may therefore be eliminated from the model. More generally, EES identify additional variables w bt , corresponding to time periods t, such that t<EES b and EES b >ES b , by which block b may not be extracted due to minimum resource requirements. All computations in this paper are performed after variable elimination based on EES.

The analogous concept of late starts (LS b ) introduced in Gaupp (2008) suggests fixing variable values to 1 for those block-time period combinations in which block b must have already been extracted. Late starts rely on the fact that block b must be extracted prior to extracting any blocks b′ within b’s hold set. Extracting all blocks other than b and those in b’s hold set at a rate satisfying the minimum resource requirement implies there is a latest period t′ by which b must be extracted. That period t′ is block b’s late start, LS b . We find that late start times do not fix a sufficient number of variables in our problem instances to significantly impact performance, and we therefore do not include them.

4.2 Finding an Initial Integer Feasible Solution (IIFS)

(CPIT) is a maximization problem, and therefore, providing the optimizer with an initial lower bound enables early fathoming of dominated branches during the branch-and-bound algorithm. Providing this bound’s associated solution (variable values) enables aggressive use of the optimizer’s local search heuristics, as the solution establishes a neighborhood within which the heuristic may explore (IBM 2010). The IIFS must satisfy all constraints, and therefore, the difficulty in generating an IIFS depends on the problem instance.

For problem specifications in which resources are only constrained by maximum capacities (i.e., there are no minimum requirements), greedy algorithms can quickly identify an initial solution. For example, one method would be to sort all blocks, descending by profit, and then proceed through the list, scheduling blocks and their predecessors for extraction as long as sufficient resources exist. Chicoisne et al. (2012) and Moreno et al. (2010) extend this concept by exploiting the underlying network structure of (CPIT) to find solutions to the LP relaxation, and then derive integer solutions with a rounding heuristic. Both approaches work well on OPBS problem instances constrained by maximum resource capacities.

Imposing minimum resource requirements in addition to maximum capacities may make finding an IIFS more challenging. To illustrate, consider as an example the case of deriving an IIFS for a time horizon of τ with a minimum processing requirement of \(\underline{e}_{2}\) in each period. Suppose a solution exists for periods {1..t}, t<τ, but none of the un-extracted blocks accessible in period t+1 are ore blocks. In this case, the existence of a feasible solution depends on whether or not the ore blocks already scheduled for extraction in periods {1..t} may be re-sequenced in such a way as to provide sufficient ore in period t+1, while not violating the minimum requirements in periods {1..t}. Even if such a sequence is found, there is no guarantee that this same dilemma will not occur in period t+2.

4.2.1 Sliding Time Window Heuristic (STWH)

A Sliding Time Window Heuristic (STWH), as described in Pochet and Wolsey (2006) and Cullenbine et al. (2011), may be more likely to determine an integer feasible solution than a simple greedy approach, for problems which include minimum resource requirements. With the STWH, a sub-problem is formed by partitioning the set of time periods in the horizon (T) into windows (T≡T Fix∪T Int∪T Rlx), within which variables are fixed to integer values (T Fix), or their integrality is either relaxed (T Rlx) or enforced (T Int). Solving this sub-problem produces a partial solution which is integer feasible for variables in T Int. Then, a subsequent sub-problem is formed by changing the partition of T (i.e., sliding the window) to enforce integrality in an adjacent set of time periods, and the procedure is repeated. Finally, linking the partial, integer feasible solutions from each sub-problem creates a complete solution. While this approach does not guarantee an integer feasible solution for a monolith with minimum resource requirements, the integer feasible solutions for each window may assist in this endeavor. In Table 5 of Lambert et al. (to appear), we show that a STWH finds an IIFS, within a time limit, for 10 of the 12 data sets presented in the results section of this paper, and that providing this IIFS to (CPIT) reduces overall solution time. In the other 2 of 12 data sets, the STWH reaches a time limit prior to finding an IIFS.

Additional notation for the STWH

Indices and sets:

  • ϕ∈Φ: set of time windows ϕ

  • \(\underline{t}_{\phi}\), \(\overline{t}_{\phi}\): first, and last, periods in window ϕ during which integrality is enforced

  • \(T_{\phi}^{\mathit{Fix}}\): set of periods t, in time window ϕ, in which values are fixed for variables \(\bar{w}_{bt}\)

    \(T_{\phi}^{\mathit{Fix}}\equiv\{1.. \underline{t}_{\phi}-1\}\); For ϕ=1, \(\underline{t}_{1}=1 \Rightarrow T_{\phi}^{\mathit {Fix}}\equiv \emptyset\)

  • \(T_{\phi}^{\mathit{Int}}\): set of periods t, in time window ϕ, in which integrality is enforced on variable w bt

    \(T_{\phi}^{\mathit{Int}} \equiv\{\underline{t}_{\phi} .. \overline {t}_{\phi}\} \)

  • \(T_{\phi}^{\mathit{Rlx}}\): set of periods t, in time window ϕ, in which integrality is relaxed for variables \(\tilde{w}_{bt}\)

    \(T_{\phi}^{\mathit{Rlx}} \equiv\{ \overline{t}_{\phi}+1 .. \tau\}\)

  • \(T \equiv T_{\phi}^{\mathit{Fix}} \cup T_{\phi}^{\mathit {Int}} \cup T_{\phi }^{\mathit{Rlx}}\), ∀ϕ∈Φ

figure a

Both solution time and quality are impacted by the trade-off between the number of windows, |Φ|, and the number of time periods in each window within which to enforce integrality, \(|T_{\phi}^{\mathit{Int}}|\). For example, two possible implementations of the above STWH for a ten-time period problem might be (i) ten windows with integrality enforced in a single period for each window, or (ii) five windows with integrality enforced in two consecutive periods for each window. The STWH algorithm presented above incorporates a mutually exclusive, collectively exhaustive distribution of the subsets across the windows (i.e., \(T = \bigcup_{\varPhi} T_{\phi}^{\mathit{Int}}\)), although this is not required. Another implementation of the STWH could contain overlap between the subsets \(T_{\phi}^{\mathit{Int}}\) and \(T_{\phi+1}^{\mathit{Int}}\). For example, in window ϕ, we might enforce integrality in two periods (\(T_{\phi}^{\mathit{Int}} = \{1,2\}\)), and then in window ϕ+1, fix variables from the first period to their integer values while again enforcing integrality in the second period (\(T_{\phi+1}^{\mathit{Fix}} = \{1\}\) and \(T_{\phi+1}^{\mathit {Int}} = \{ 2,3\}\)). The fastest solution times for our data sets result from the mutually exclusive, collectively exhaustive subsets shown above, with |Φ|=5, \(|T_{\phi}^{\mathit{Int}}|=2\) for τ=10, and |Φ|=5, \(|T_{\phi}^{\mathit{Int}}|=3\) for τ=15.

4.2.2 Maximum Value Feasible Pit (MVFP) algorithm

A new approach to generating an IIFS for (CPIT) is an algorithm we term the Maximum Value Feasible Pit (MVFP) algorithm. For a given time horizon of length τ, we use a three-phased approach to determine a maximum-value subset of blocks, M, and then search within M for an integer-feasible block extraction sequence (IFBES) which satisfies (CPIT) constraints (5)–(8). The blocks of M must form a sub-pit in which precedence constraints are satisfied. Also, the blocks in M collectively possess the maximum undiscounted value of extracted blocks possible (e.g., see Eq. (1)) for any set containing |M| blocks, because we find M using (UPIT). If a feasible sequence exists within M, then the variable values corresponding to that sequence may be used as an initial solution when solving (CPIT) for all the blocks in B. For the case in which M does not contain a feasible sequence, the MVFP can be re-run with modified resource requirements to produce a larger set, M′. Although the MVFP does not guarantee an integer feasible sequence, for each of the data sets we test, the MVFP produces such a sequence.

For example, consider a pit of 1,000 equally weighted blocks, where, in each period, the schedule requires extracting ten to fifteen blocks, five to seven of which are ore. Over a ten-period time horizon, any feasible sequence must include 100–150 blocks, of which 50–70 are ore. It should be faster to find an IFBES from within a sub-pit of 150 blocks than from within the full pit of 1,000 blocks. Therefore, in this example, the MVFP algorithm attempts to (i) find the smallest, highest valued sub-pit containing 50–70 ore blocks, (ii) expand that sub-pit if it contains fewer than 100 total blocks, and (iii) find an IFBES, if one exists. While a sub-pit with more than 150 total blocks and 70 ore blocks may contain an IFBES (e.g., the trivial example is the original pit), our goal with the MVFP algorithm is to reduce the decision space over which to search for a feasible sequence.

The three phases of the MVFP algorithm to generate an IIFS are:

Phase I::

Repeatedly solve (UPIT), with varying ore price, to find a subset of blocks containing sufficient ore to satisfy the total processing requirement for time horizon τ.

Phase II::

If M does not require sufficient production resources to satisfy minimum production requirements over the entire time horizon, solve an integer program to expand the set of blocks contained in M.

Phase III::

Either solve (CPIT) or implement a STWH to find an integer-feasible extraction sequence within the modified subset of blocks.

Phase I leverages (UPIT)’s relatively fast solution time to quickly find a small sub-pit containing sufficient ore to meet the total processing requirement for time horizon τ. Phase II is only executed if the aggregate material of all blocks in the Phase I sub-pit does not satisfy the production requirements for τ, in which case we use an integer program to expand the sub-pit. Finally, in Phase III, we either use a STWH or solve (CPIT) for the sub-pit to find an IFBES satisfying both processing and production requirements for each period in τ (i.e., 1,2,3,…,τ).

Phase I—Find a reduced set of blocks containing sufficient ore to meet processing constraints

A challenge to finding an IIFS for the entire pit is knowing where within the entire pit to search. The MVFP approach first quickly identifies a subset of blocks likely to contain an IFBES, thereby reducing the search space. We commence with a time horizon τ, which, in conjunction with the minimum and maximum per period processing limits (\(\underline{e}_{2}, \overline{e}_{2}\)), determines the processing limits for the entire horizon (\(\tau* \underline{e}_{2} \equiv\underline{e}_{2}^{\tau}\) and \(\tau* \overline{e}_{2} \equiv\overline{e}_{2}^{\tau}\)). Our Iterative Ultimate Pit Limit (IUPL) algorithm repeatedly solves (UPIT), varying the ore price to generate pits containing different quantities of ore (i.e., \(e_{2}^{i}\) for iteration i), until we find a pit containing a total ore weight (\(e_{2}^{f}\) in the final iteration) within the aggregate processing limits (\(\underline{e}_{2}^{\tau} \leq e_{2}^{f} \leq\overline{e}_{2}^{\tau}\)). The IUPL is not guaranteed to find such a sub-pit, as there exist situations in which no ore price used in solving (UPIT) will produce a pit containing \(\underline{e}_{2}^{\tau} \leq e_{2}^{f} \leq\overline{e}_{2}^{\tau}\). (This is the well known mine planning problem of “gaps.”) If this occurs, Phase I returns the smallest pit found by IUPL such that \(\overline{e}_{2}^{\tau} < e_{2}^{f}\).

Additional notation for phase I—IUPL algorithm

Indices and sets:

  • i∈{1..I}: iteration i from 1 to maximum number of iterations I

  • b i∈U i: set of blocks in the (UPIT) solution, for iteration i, where U f is the final set

Data:

  • p i : per unit price of ore in iteration i, where p 0 is an initial price ($/ounce)

  • θ i : positive price adjustment factor for iteration i, where θ 0 is an initial price adjustment factor ($)

  • g b : average grade of block b (ounces, tons, percentage)

  • c b : cost of extracting block b ($)

  • v bi : net value of extracting block b in iteration i ($)

    \(v_{bi}: \begin{cases} p_{i} * g_{b} - c_{b} & \mbox{if } g_{b} > \text{cutoff grade}\\ - c_{b} & \mbox{otherwise} \end{cases} \)

  • \(e_{r}^{i} \): total tonnage of r in the (UPIT) solution for iteration i, where \(e_{r}^{f}\) is the tonnage for the final iteration (tons)

  • \(\underline{e}_{r}^{\tau}\), \(\overline{e}_{r}^{\tau} \): minimum and maximum acceptable tonnage, respectively, in a (UPIT) solution for a time horizon of τ periods (tons)

  • I: maximum number of iterations

Variables:

  • \(y^{*}_{b}\): value of y b for block b in the solution of (UPIT)

figure b

Phase II—Find additional blocks outside of U f to satisfy minimum production

Modifying the ore price in the Phase I IUPL algorithm produces sub-pits of varying size, and with the exception of the “gap” problem described above, allows us to find a sub-pit satisfying the processing constraints. However, the resulting sub-pit may violate production requirements, either by containing excessive \((\overline{e}_{1}^{\tau} < e_{1}^{f})\), or by possessing insufficient \((e_{1}^{f} < \underline{e}_{1}^{\tau})\), material. A sub-pit U f containing material in excess of the maximum production capacity (\(\overline{e}_{1}^{\tau} < e_{1}^{f}\)) may be larger than necessary to find a feasible sequence. A sub-pit U f containing insufficient material to satisfy the minimum processing requirement, however, cannot possibly contain a feasible sequence. Therefore, if the sub-pit U f resulting from Phase I does not contain at least \(\underline{e}_{1}^{\tau}\) tons of material, then we solve the Pit Expansion integer program (PE IP) in Phase II, finding additional blocks to supplement U f.

Additional notation for phase II—Pit Expansion integer program (PE IP)

Indices and sets:

  • \(b \in\overline{U}^{f}\): subset of blocks b in B and not in U f (i.e., b∈B∧b∉U f)

  • b∈U +: subset of blocks b in the (PE IP) solution

Data:

  • \(\tilde{e}_{1}\): residual production required to meet \(\overline {e}_{1}^{\tau}\), (\(\tilde{e}_{1}=\overline{e}_{1}^{\tau} - e^{f}_{1}\)), where \(e^{f}_{1}\) results from the IUPL algorithm

  • \(\tilde{e}_{2}\): residual processing capacity available, (\(\tilde{e}_{2}=\overline{e}_{2}^{\tau} - e^{f}_{2}\)), where \(e^{f}_{2}\) results from the IUPL algorithm

Objective function:

$$ \bigl(\mathit{PE}^{\mathit{IP}}\bigr) \quad\max\sum_{b \in \overline{U}^{f}}v_{b} y_{b} $$
(9)

Constraints:

(10)
(11)
(12)
(13)
(14)

The objective function (9) seeks to maximize the value of blocks extracted from \(\overline{U}^{f}\). Constraints (10) enforce extraction of all blocks from the Phase I sub-pit U f. Constraints (11) ensure block b in \(\overline{U}^{f}\) is not extracted unless every block b′ in b’s direct predecessor set (B b ) is extracted. Constraints (12) ensure sufficient material is extracted to exceed \(\tilde{e}_{1}\), while constraints (13) ensure additional processing does not exceed \(\tilde{e}_{2}\). (PE IP) selects mostly waste blocks for the sake of feasibility, and so the objective of maximizing present value minimizes the number of costly waste blocks extracted. Finally, constraints (14) restrict all decision variables to be binary.

Combining the blocks from the Phase II solution (U +) with those from Phase I (U f) yields the set of blocks M in which to search for a feasible sequence. For the situation in which Phase II is not performed, then M←U f.

Phase III—Find an integer feasible block extraction sequence within M

Given the reduced set of blocks, M, we consider two approaches for finding an integer feasible extraction sequence. The naive approach is to simply solve (CPIT) for the blocks contained within the subset M, which we refer to as a sub-pit sequencing integer program (SPS IP). Solving (SPSIP) produces an integer feasible block extraction sequence, if one exists. Because |M|≪|B|, solving (SPS IP) should require less time than solving (CPIT) for all blocks in B. Alternatively, we may implement the previously described STWH over the blocks in M, which we refer to as the sub-pit sequencing sliding time window heuristic (SPS STWH).

Using the solution from Phase III as an IIFS when solving (CPIT) for the entire pit

We let \(\mathbb{W}\) be the set of variable values in the solution from Phase III. If the corresponding solution forms a feasible sequence to (CPIT) in M, it is guaranteed to form an IIFS to (CPIT) in B, because M⊂B. If the solution does not form a feasible sequence to (CPIT) in M, the set of variable values \(\mathbb{W}\) may still be of value to the optimizer when solving (CPIT) in B. This is because the optimizer heuristics may be able to derive an integer feasible solution by “repairing” the infeasible solution formed by the variable values in \(\mathbb{W}\) (IBM 2010).

4.3 Tailored Lagrangian Relaxation (TLR)

In the open pit block sequencing problem (CPIT), resource constraints (6) destroy the underlying network structure formed by the precedence constraints (5). Dualizing one or more of these resource constraints and solving the problem via Lagrangian relaxation may reduce solution times. (For a detailed treatment of Lagrangian relaxation, see Fisher 1981.) Dualizing all resource constraints and solving the resulting Lagrangian subproblem provides an objective function value no lower, i.e., an upper bound on the original problem no tighter, than that achieved by solving the original problem’s linear programming relaxation (Ahuja et al. 1993). Therefore, we selectively dualize resource constraints to achieve faster performance through tightening the upper bound on (CPIT)’s optimal objective function value, and finding solutions likely to be feasible in (CPIT). The common approach to formulating a Lagrangian relaxation problem is to dualize those constraints which are likely to be “difficult” to satisfy. Our method takes the opposite approach; it strictly enforces those same “difficult” constraints with the rationale that if a constraint is likely to be difficult to satisfy, then we should not permit the optimization model to consider its violation.

Gaupp (2008) obtains the fastest solution times for his data sets by dualizing the maximum processing constraints. However, this may not be the best dualization scheme for all data sets, as ore is distributed differently in every deposit, suggesting different constraints may be “difficult” to satisfy depending on the problem instance. The challenge is to identify these likely troublesome resource constraints, and to derive an associated dualization scheme prior to solving the problem. We present a methodology to identify an appropriate dualization scheme based on the particular data set, without having to first test all possible combinations.

Our approach relies on information garnered during the execution of the MVFP algorithm. Specifically, we use three guidelines based upon MVFP performance: (i) whether or not the Phase I sub-pit contains sufficient ore to satisfy processing constraints, (ii) whether or not Phase II is executed, and (iii) if Phase II is not executed, whether or not the Phase I sub-pit contains material in excess of the maximum production capacity.

If the IUPL algorithm in Phase I is not able to find a pit containing sufficient ore to satisfy processing constraints, then a “gap” problem exists. In this case, the Phase I sub-pit contains the fewest blocks possible while still exceeding processing requirements (i.e., \(\overline{e}_{2}^{\tau} < e_{2}^{f}\)), and we can make no conjecture as to which constraints may be difficult to satisfy when solving (CPIT). This occurs in only one of our data sets, and additional testing is required to identify the best dualization strategy.

If Phase II is executed, then the Phase I sub-pit contains sufficient ore to satisfy processing, but contains insufficient material to satisfy minimum production (i.e., \(\underline{e}_{2}^{\tau} \leq e_{2}^{f} \leq\overline{e}_{2}^{\tau}\) and \(e_{1}^{f} < \underline{e}_{1}^{\tau}\)). (UPIT) maximizes value and extracting waste blocks is costly; hence, (UPIT) minimizes the number of waste blocks required to extract underlying ore blocks. If (UPIT) is able to find a sub-pit of sufficient ore and minimal waste, this implies that it should not be difficult to find a solution to (CPIT) which satisfies minimum processing. This, in turn, suggests a Lagrangian formulation strategy of dualizing both minimum resource constraints, as minimum processing should be easy to satisfy, and the Lagrange multiplier may prevent a minimum production violation. In the event that the Lagrangian sub-problem solution violates minimum production, then solving a smaller integer program (analogous to Phase II of MVFP) to add more blocks to the solution may make the current iteration’s solution feasible, while increasing the Lagrange multiplier value may prevent violations in future iterations.

If the Phase I sub-pit contains sufficient ore to satisfy processing constraints and sufficient material to satisfy production constraints (\(\underline {e}_{2}^{\tau} \leq e_{2}^{f} \leq\overline{e}_{2}^{\tau}\) and \(\underline {e}_{1}^{\tau} \leq e_{1}^{f} \leq\overline{e}_{1}^{\tau}\)), this implies that ore is distributed throughout the deposit such that it should not be difficult to find a solution to (CPIT) which satisfies all production and processing constraints. This then suggests adopting a strategy of dualizing both minimum resource constraints, for the same reasons as outlined in the case directly above.

If, however, the Phase I sub-pit contains sufficient ore to satisfy processing constraints and the total material exceeds the maximum production constraint (\(\overline{e}_{1}^{\tau} \leq e_{1}^{f}\)), this implies that the distribution of ore in the deposit is relatively sparse. In this case, it may be difficult to find a solution to (CPIT) containing sufficient ore to satisfy minimum processing without exceeding maximum production. However, satisfying the opposite bounds of maximum processing and minimum production in (CPIT) should not be difficult, suggesting a strategy of dualizing these two constraints, while maintaining minimum processing and maximum production as explicit constraints.

4.3.1 Tailored Lagrangian Relaxation (TLR) formulation

We tailor a Lagrangian relaxation formulation to allow for specified resource constraints to be dualized while others are explicitly maintained.

Additional notation for the Tailored Lagrangian Relaxation (TLR) formulation

  • \(\underline{\lambda}_{rt} / \overline{\lambda}_{rt}\) = Lagrange multiplier for minimum requirement/maximum capacity constraint on resource r in period t

  • \(\underline{D} / \overline{D}\) = set of resources r for which minimum requirement/maximum capacity constraint is dualized

  • \(\underline{N} / \overline{N}\) = set of resources r for which minimum requirement/maximum capacity constraint is not dualized and maintained as an explicit constraint

  • \(\underline{D} \cup \underline{N} \equiv R\) and \(\overline{D} \cup \overline{N} \equiv R\)

Objective function:

(15)

Constraints:

(16)
(17)
(18)
(19)
(20)
(21)
(22)

Constraints (16), (19), and (20) enforce precedences, the relationship between by variables for block b, and integrality in (TLR), similar to (5), (7), and (8), respectively, in (CPIT). Constraints (17) and (18) in (TLR) explicitly enforce minimum requirements and maximum capacities, for resources in \(\underline{N}\) and \(\overline{N}\), respectively, replacing constraints (6) in (CPIT). Constraints (21) and (22) require the Lagrangian multipliers to be non-negative. When we provide (TLR) an IIFS, we use that generated by the MVFP algorithm because the IUPL portion of the MVFP algorithm provides the dualization strategy with which to tailor the Lagrangian procedure.

To implement the Lagrangian relaxation algorithm, we do the following: (i) solve the linear programming relaxation of the monolith (CPIT LP) to establish an initial upper bound and to initialize the Lagrange multiplier values \((\underline{\lambda}_{rt}, \overline{\lambda}_{rt})\) to the dual variable values from (CPIT LP); (ii) solve (TLR); (iii) if the best bound of (TLR) is better (lower) than the incumbent, then update the upper bound; (iv) if the (TLR) solution is infeasible for (CPIT) due to a violation of \(\underline{e}_{1}\), solve an integer program to add blocks to the solution; (v) if the resulting solution is feasible in (CPIT) and better (higher) than the incumbent, then update the lower bound; (vi) update the Lagrange multipliers using the subgradient method, and resolve the Lagrangian. Iterate in this fashion until an optimality gap (the difference between the lower and upper bounds) is less than 2 %.

5 Results

To test our methodologies, we solve instances of the OPBS problem for twelve block models derived from two data sets. The first data set is a 10,819 block model which we refer to as 10k. To generate additional instances, we perturb the mineral content of each block in 10k by ±5 %, yielding seven models we refer to as 10kA, 10kB, …, 10kG. Collectively, we refer to these eight model instances as the 10k data sets.

The second data set comes from the Whittle software test data set known as “Marvin,” and contains 53,668 blocks, composed of 17 levels, with each level containing up to 3,660 blocks (61 × 60). From this “Marvin” data set we extract four smaller models, two each containing five levels (18,300 blocks), and seven levels (25,620 blocks), designated 18kA, 18kB, 25kA, and 25kB, respectively. Collectively, we refer to these four models as the Mrv data sets.

Lambert et al. (to appear) utilize a time horizon of τ=10 for both the 10k and Mrv data sets to demonstrate the effect of EES, the STWH, and an IIFS. Here, we utilize a time horizon of τ=15 for the 10k, and τ=10 for the Mrv, data sets, respectively, to demonstrate the effect of the MVFP algorithm and (TLR) formulation. Some practitioners question the viability of techniques demonstrated on block models of this magnitude, citing the existence of realistic instances with millions of blocks. We note that there also exist realistic instances with tens or hundreds of thousands of blocks, occurring for cases in which blocks are aggregated (e.g., in a flat mine) and/or block content is similar for geographically close blocks (Brickey 2012). Table 1 displays summary characteristics of all twelve data sets, with the number of variables and constraints included in the problem instance solved, after variable reductions from EES.

Table 1 Data sets and their characteristics
Full size table

While EES reduce a greater percentage of variables for the 10k data set than for the larger Marvin data sets, this is not simply attributable to the number of blocks (i.e., it is incorrect to assume that the effectiveness of EES decreases with an increase in the number of blocks). Instead, the effectiveness of EES is dependent on the production and processing requirements (\(\underline{e}_{r}, \overline{e}_{r}\)) and the shape and characteristics of the deposit. For example, EES are likely to produce greater variable reductions for deposits which are relatively deep and/or contain a heterogeneous distribution of ore, as opposed to deposits which are flat and/or contain a homogeneous distribution of ore. Additional discussions regarding the EES impact are presented in Lambert et al. (to appear).

We perform all data pre-processing in Java, and formulate all optimization models (including the MVFP algorithm) in AMPL, version 11.11 (AMPL 2009). From AMPL, we pass formulations to the CPLEX solver, version 12.2.0 (IBM 2009). We use a Sun X4150 with 2 × 2.83 GHz processors and 16 GB RAM.

Our test results are shown in Table 2. The first two columns list each data set and its associated time horizon τ. Columns three through six display the time required, in seconds, for the MVFP algorithm to generate an IIFS, for each phase, and overall. For Phase II, the (SPS STWH) dominates the (SPS IP) for all data sets, in the time required for both MVFP Phase II and for solving the follow-on (CPIT IIFS), and hence, we only report the (SPS STWH) results. Columns seven through ten display the times required to solve (CPIT IIFS) and (TLR IIFS), to within 2 % of optimality, and the reductions attributable to (TLR).

Table 2 Empirical results for each data set and time horizon. Columns three through six list solution time (s) for the individual MVFP phases and their sum. Columns seven through nine display solution time (s) for (CPIT), (CPIT IIFS), and (TLR IIFS), solved to within 2 % of optimality. The final column is the percentage reduction in solution time attributable to the (TLR)
Full size table

5.1 Generating an IIFS with the MVFP algorithm

The MVFP algorithm phases require different proportions of time for the 10k and Mrv data sets. For all the 10k data sets, the MVFP algorithm requires approximately 1,600 seconds to find a sub-pit in Phase I with the IUPL, and bypasses the Phase II pit expansion because production exceeds \(\overline{e}^{\tau}_{1}\). Phase III requires approximately twice as long as Phase I to find an IFBES using the (SPS STWH). Overall, the MVFP requires roughly 5,000 seconds, on average, to produce an IIFS for a τ=15, for each of the 10k data sets.

The Mrv data sets are as much as three times the size of the 10k, as measured by the number of variables and constraints. Considering all four Mrv data sets, the MVFP algorithm requires, on average, 2,080 seconds to find a sub-pit in Phase I with the IUPL. The 18kA, 18kB, and 25kA data sets require 591 seconds, on average, to expand the sub-pit in Phase II. Again considering all four Mrv data sets, finding an initial sequence requires, on average, 102 seconds using the (SPS STWH) in Phase III. Overall, the MVFP requires roughly 2,773 seconds, on average, to produce an IIFS for a τ=10, for each of the Mrv data sets. The 25kB data set experiences the “gap” problem, in which the IUPL algorithm alternates between producing a pit with no blocks, and producing a pit with resource requirements exceeding both \(\overline {e}^{\tau}_{1}\) and \(\overline{e}^{\tau}_{2}\). Therefore, although Phase II pit expansion is not required, we cannot make any conjectures about which specific constraints are difficult to satisfy in this case. For 25kB, we dualize \(\underline{e}_{2}\) and \(\underline{e}_{1}\) in the (TLR), but further testing with data sets including “gaps” is required before we can recommend any particular dualization strategy for this case.

5.2 Using the IIFS with (CPIT) and (TLR)

CPLEX is unable to find an integer solution to (CPIT) within a ten hour (36,000 second) time limit for all but two of our twelve data sets. For the Mrv data sets 18kA and 18kB, CPLEX is able find a solution to within 2 % of optimality in under the ten hour time limit. Providing (CPIT) with the IIFS from the MVFP algorithm enables CPLEX to find solutions within 2 % of optimality for all but the two largest data sets, 25kA and 25kB, in which case (CPIT IIFS) is still able to establish an optimality gap. Solution times are then significantly reduced by providing (TLR) with the IIFS. For the 10k data sets, (TLR) reduces solution times by 59 %, on average, from those of (CPIT IIFS). For the 18kA and 18kB data sets, (TLR) reduces solution times by 22 %, on average, from those of (CPIT IIFS).

6 Conclusions

Mining engineers and operations researchers have sought to effectively model and “solve” the OPBS problem for over 40 years. One of the major challenges lies in the size of real-world instances and the resulting number of block-sequence combinations which must be evaluated in an exact approach. The pioneering work of Johnson (1968) and Dagdelen (1985) establishes what was, and continues to be, a basis for holistically solving the OPBS problem with mixed-integer approaches.

Effectively modeling large-scale, difficult optimization problems, such as those encountered in the mining industry, requires leveraging “knowledge of the problem” to effectively tailor the techniques and formulations (Klotz and Newman to appear). The challenges lie in identifying both an initial solution, and problem information useful in tailoring the formulation, prior to solving the problem. We demonstrate an algorithm to generate an IIFS and the benefit of using that solution when solving the OPBS problem. When formulating a Lagrangian relaxation model for an instance of the OPBS problem, knowing which of the resource constraints to dualize, and which to maintain as explicit, is not a trivial task. Insights from our MVFP algorithm provide guidance in this regard, and lead to formulations which yield substantial reductions in solution time over that from solving either the original problem outright (monolith), or the original problem with an IIFS.

These approaches for (i) identifying an IIFS, and (ii) utilizing insights to tailor a formulation specific to the problem instance, should help expedite solutions for instances of any size. These techniques are scalable and can be applied to instances with either more blocks and/or more time periods than those we present here, as long as the underlying model of interest has the same format as (CPIT), or is a relaxation of (CPIT). As hardware and software capabilities increase, so should the size of instances which will benefit from the direct application of our methodologies. For these larger instances, the method presented to determine an initial feasible solution may yield a feasible solution for the monolith. However, even if it does not, some sophisticated commercial solvers, e.g., CPLEX, can still “repair” an infeasible solution, i.e., render the solution feasible with its heuristics for use in the branch-and-bound algorithm.

Future research might extend the techniques we present here to directly determine initial feasible solutions for more complicated open pit block sequencing models. Although it is possible that future research might identify procedures more efficient than our (TLR) approach for solving instances of (CPIT), or even more detailed versions of open pit production scheduling problems, our ideas may lend themselves to other applications with similar problem structure for which a (nonstandard implementation of) Lagrangian relaxation is suitable. Conversely, it may be possible to use an extension of our approach for more detailed versions of open pit production scheduling problems.