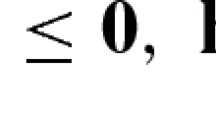1 Introduction

In this paper, we focus on bilevel programming problems where the upper-level deals with discrete decisions and the lower-level is a mixed complementarity problem (MCP). It is a variant of the traditional mathematical program with equilibrium constraints (MPEC) where the leader is only allowed to make discrete decisions. We call the whole formulation DC-MPEC (Gabriel et al. 2010).

Gabriel et al. (2010) propose a heuristic to solve the DC-MPEC problem based on Benders decomposition. They rephrase the problem as a mixed integer linear problem (MILP) and decompose the problem by placing all constraints and objective elements containing lower-level variables in the Benders subproblem. The master problem domain is a priori heuristically partitioned into subdomains of x with the aim of finding subdomains where the lower level objective is convex. Afterwards each subdomain is solved by Benders decomposition method. It is shown that the heuristic can give a sub-optimal solution unless all subdomains are convex.

In our new approach we develop an idea mentioned in Gabriel et al. (2010) with a dynamic branching procedure that partitions the subdomains as the algorithm proceeds. We branch until the subdomains which have candidates for the global solution are convex and thereby guarantee to find the optimal solution. As opposed to the branching on single variables as employed in many branch-and-bound approaches, we use intersection of Benders cuts to partition the upper-level decision domain. The branching procedure is supported by lower bounding based on Lagrangean relaxation, which makes it possible to cut off parts of the master problem domain and thereby increase the efficiency of the algorithm compared to the static version. Using LR to accelerate the branch-and-bound procedure was introduced in both Geoffrion (1974) for MILPs and Falk (1969) for non-convex programs.

Several papers contribute on how to improve the convergence properties of Benders decomposition, for a nice review see Saharidis and Ierapetritou (2010). One common approach is to add cuts to the relaxed master problem, as for instance Saharidis et al. (2011) do. Similarly we utilize the solution value from the Lagrangean relaxation as a bound in the Benders decomposition somewhat inspired by cross decomposition (van Roy 1983,1986). To the best of our knowledge this is a new way of utilizing Lagrangean relaxation results in bilevel programming: using it both in the lower bounding in the branch-and-bound procedure and to accelerate the Benders decomposition used to find the upper bound.

We also show how the addition of strong duality constraints, enabled by the Benders decomposition, increases the robustness of the transformation from DC-MPEC to MILP. When the lower-level is a two-stage stochastic MCP, we show how the lower bounding method can be adapted using scenario decomposition (Carøe and Schultz 1999) to achieve further decomposition, and test this on a natural gas application.

Our computational results show that using the dynamic partitioning algorithm supported by the strong duality constraints considerably reduces the partitioning work needed compared to the static version of the algorithm.

Even the continuous linear bilevel programming problem has been shown to be NP-hard (Hansen et al. 1992) and the discrete nature of upper-level variables and their related constraints would make the DC-MPEC problem even more intractable. A substantial amount of contributions exists for the different problem classes within bilevel programming, and we will point out the ones closest related to our DC-MPEC problem. For a broader overview see for instance Dempe (2002) or Colson et al. (2007) on bilevel programming and Luo et al. (1996), Outrata et al. (1998) or Fukushima and Lin (2004) on MPEC.

Gabriel and Leuthold (2010) formulate a Stackelberg game within the electric power market as a DC-MPEC and provide exact solutions with standard branch-and-bound after reformulating to a MILP. On the contrary most solution procedures for DC-MPEC are heuristics. Meng et al. (2009) and Meng and Wang (2011) use genetic algorithms supplemented with suitable procedures for solving lower level parametric VIs for facility location and service network design applications, respectively. Another DC-MPEC application is presented by Wang and Lo (2008) who transforms their problem into a mixed integer nonlinear program solved with an application specific heuristic.

Mesbah et al. (2011) use generalized Benders decomposition to solve a bilevel problem on transportation network design. Their upper level has binary variables and a non-linear objective function. Lower level consists of three parts, two optimization problems and an equilibrium problem. Lagrangean relaxation is used to solve the optimization lower-level problems.

Saharidis and Ierapetritou (2009) propose Benders decomposition for problems closely related to our DC-MPEC, but with lower level limited to LP. They decompose the problem into a master problem containing all integer variables and pure integer constraints and a bilevel subproblem. The subproblem is transformed into a single level problem by KKT conditions and provides a feasibility cut or optimality cut for the master problem in each iteration. The integrality conditions are handled by adding integer exclusion cuts to the master problem. This work differs from ours in different ways of decomposing the problem and different ways of treating the integrality requirements.

Wen and Yang (1990) also solve DC-MPEC with the lower level limited to LP. They do not use the common reformulation to MILP based on KKT conditions, but develop valid bounds adapted to the bilevel structure and apply these in branch-and-bound. A similar strategy is used by Moore and Bard (1990) for bilevel problem with integrality constraints in both upper and lower level, and they also point out why standard bounding and fathoming rules for branch-and-bound in integer programming do not apply for their problem.

The rest of this paper is organized as follows: First we present the basic ideas of the algorithm, with lower bounding, upper bounding and dynamic partitioning. Then follows a pseudocode overview of the total algorithm and proofs for the validity of bounds and overall convergence. The section ends with a description on how to adapt the lower bounding method to stochastic programs. Next follows numerical results on general problems with randomly generated data and on a natural gas supply chain problem before we conclude.

2 Dynamic algorithm

The overall discretely-constrained mathematical program with equilibrium constraints (DC-MPEC) is given as follows:

(1)

where \(x \in Z^{n_{x}}\) and \(y \in R^{n_{y}}\) are integer upper-level variables and continuous lower-level variables, respectively. The constraints Qx≤q contain the bounds on the x’s and other linear constraints with only x variables; Ax+By≥a are the joint linear constraints of x and y. The solution set of the lower-level MCP is given by

(2)

where \(z \in R^{n_{z}}\), z≥0 and \(w \in R^{n_{w}}\). z and w are lower-level variables that typically correspond to dual variables of a underlying optimization problem. It is assumed that the dimension of each data element (i.e. c, d, Q, q, A, B, a, E, e, M, N, k, D, F, g) agrees with its associated variables. E is a symmetric and positive semi-definite matrix of the convex quadratic function \(\frac {1}{2}y^{\mathrm{T}} Ey+e^{\mathrm{T}}y\) so that the KKT conditions are necessary and sufficient optimality conditions. Note that the lower-level problem also covers linear problems (LP) and quadratic convex problems (QP) since the KKT optimality conditions of these problem classes are MCP problems. We assume that a solution to Problem (1) exists.

As previously shown by amongst others (Fortuny-Amat and McCarl 1981) an MPEC can be rephrased to an MILP through replacing the lower-level complementarity conditions by disjunctive constraints, binary variables and a large constant C. This reformulation implies an optimistic view on the lower-level in the sense that if multiple equilibria exist in lower-level the most favorable according to the upper-level objective is chosen. We denote the problem resulting from this reformulation (MILP).

We decompose (MILP) with Benders decomposition into a master problem:

(3)

and a subproblem:

(4)

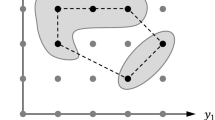
Only x variables are placed in the master problem and the other variables are in the subproblem. Because of the disjunctive variables \(\bar{b}\) and \(\tilde{b}\) the function α(x) is piecewise linear but not in general convex in x (Gabriel et al. 2010). The non-convexity means Benders decomposition method is not guaranteed to converge to an optimal solution for (MILP) (Benders 1962). The main idea of the dynamic partitioning algorithm is to partition the domain of \(X=\{x \in Z^{n_{x}} | Qx \leq q\}\) into subdomains where α(x) is convex, as illustrated in Fig. 1. The partitioning is controlled by upper and lower bounds that will converge as the non-convexities are removed in exchange for an increasing number of subdomains. \(\breve{Q}x \leq\breve{q}\) is a set of linear partitioning constraints defining a subdomain. An overview of the problems used in this paper and their relations is given in Fig. 2.

Fig. 1
figure 1

Illustration of how partitioning transforms a domain with a non-convex function into two subdomains with convex functions

Full size image
Fig. 2
figure 2

Problem and subproblem overview

Full size image

2.1 Lower bounding

Traditionally the LP relaxation is used for bounding in branch-and-bound, but the MILP reformulation with binary variables and large constants gives weak LP bounds. Instead we apply the Lagrangean relaxation algorithm (LR) as lower bound of (MILP) relaxing Qx≤q with μ as the Lagrangean multiplier. The mathematical formulation of the Lagrangean subproblem (MILP(μ)) is given as Problem (5) and its dual problem is defined as z LD=max μ {ϕ(μ)|μ≥0}. (MILP(μ)) is a relaxation of (MILP) as proved in Geoffrion (1974).

(5)

(MILP(μ)) is a mixed integer linear program that usually will be solved repeatedly to make the Lagrangean process converge. This means (MILP(μ)) needs to be significantly simpler than (MILP) to solve to make the lower bounding worthwhile. Generally that means there should be a substantial number of constraints Qx≤q or these constraints should have a complicating structure (see Conejo et al. 2006) as in the example of stochastic programming in Sect. 3.2.

In our implementation of LR, the Lagrangean multipliers (μ) are updated by a cutting plane method (Conejo et al. 2006). The Lagrangean iterations are stopped whenever the gap between the cutting plane problem (relaxed Lagrangean dual problem) and the Lagrangean subproblem (MILP(μ)) are sufficiently small. Also a limit on the number of iterations is implemented to avoid any cycling. A duality gap can occur because the Lagrangean subproblem has integral variables, as shown in Geoffrion (1974). This represents a non-convexity domain for α(x) that will cause further partitioning.

2.2 Upper bounding

We apply Benders decomposition method (BD) as described in Conejo et al. (2006) to measure the upper bound (UB) of (MILP). The function α(x) in master problem (3) is relaxed, and through the solution procedure rebuilt by iteratively solving the relaxed master problem (MP) and subproblem (SP) below.

(6)
(7)

In each Benders iteration, k, the solution of (SP) for a given x (k) gives a new Benders cut α≥α(x (k))+λ T(x−x (k)) that is added to (MP) to approximate α(x). Let z down(x (v))=c T x (v)+α(x (v)) and z up(x (v))=c T x (v)+d T y (v). Figure 3 illustrates a non-convex α(x) function and a master problem approximation based on a single Benders cut (broken line).

  • If α(x) is convex for a given subdomain, Benders cuts create a lower envelope of α(x). In each iteration v, (MP) and (SP) provide lower and upper bound on z B-MILP, respectively, z down(x (v))≤z B-MILP≤z up(x (v)) and these bounds iteratively converge (Conejo et al. 2006).

  • If α(x) is non-convex for a given subdomain, the Benders cuts may overestimate α(x) and eliminate a true optimum in the subdomain. This implies that either z down(x (v)) and z up(x (v)) converge to a value greater than the true optimum or z down(x (v))>z up(x (v)) which stops the iterations. These situations are illustrated in Fig. 3 for x=2 and x=5, respectively.

Fig. 3
figure 3

Illustration of non-convex α(x) and a single Benders cut (broken line)

Full size image
Algorithm 1
figure 4

Main

Full size image
Subroutine 1
figure 5

ComputeBounds(N,D(N))

Full size image
Subroutine 2
figure 6

SolveAndBound(N,D(N),Incumbent)

Full size image
Subroutine 3
figure 7

DecomposeDomain(N,D(N))

Full size image

In either case z up(x (v)) gives a valid upper bound, which is justified by the proof in the Appendix. Because of assumption (A2) that follows in Sect. 2.5, we do not consider feasibility cuts.

2.2.1 Accelerating the Benders decomposition by including the lower bound

We could utilize the solution from (MILP(μ)) to warm-start the Benders iterations seeking to reduce the number of Benders iterations. The solution of x from (MILP(μ)) are set as the initial solution of (MP) and the objective value of (MILP(μ)) forms a lower bound for (MP), expressed by the optimality cut c T x+α≥LB. The optimality cut removes solutions inferior to the incumbent in the current iteration of the Benders decomposition, thereby reducing the search space and potentially producing faster convergence of the algorithm. Table 1 compares the number of iterations and computation time of BD for two cases: without and with the warm-start (ws). Ten test problems were solved. All data were generated from the intervals [0,100] with uniform distributions. The upper-level decision variables were all binary; the lower-level problems are built by deriving the KKT conditions of LP problems. Matlab (ver. 7.0) and Xpress-MP (ver. 2006) were used to implement both BD and LR algorithms. LB and UB converged to the same value for all instances. As can be seen from the last two columns, the warm-start greatly reduced the number of iterations as well as the computation time.

Table 1 Numerical results: Speeding up UB measure by warm-starting with LB solution. The left part gives the dimensions of (MP) and (SP), where \(\dim(b) = \dim(\bar{b})+\dim(\tilde{b})\). C is the value of the disjunctive constant. The right part gives the number of iterations and solution time in seconds for computing UB without and with warm-start (ws)
Full size table

2.2.2 Strong duality constraint

The complementarity constraints in the lower-level problem were linearized with disjunctive binaries and big constant C in Gabriel et al. (2010), Gabriel and Leuthold (2010), Labbé et al. (1998), Hu et al. (2008), Mitsos (2010), Saharidis and Ierapetritou (2009) and DeNegre and Ralphs (2009), where their common question was the value of C for which the feasible region formed by complementarity constraints is not altered. Hu et al. (2008) proposed a solution method which does not require knowing the big constants, but the method is limited to linear programs with linear complementarity constraints (LPCC). Gabriel et al. (2010) show that C can be chosen by a sensitivity analysis or when the matrix M has a specific property the constants can be chosen analytically.

For lower-level problems with E=0 (defined in Problem (2)), which for instance correspond to the KKT conditions of an LP, we impose the strong duality constraint (e T−w T D)y=z T(k−Nx) to (B-MILP). The constraint was induced from the two complementarity constraints y T(e−M T z−D T w)=0 and z T(My+Nx−k)=0. A similar strong duality constraint cannot be imposed when E≠0 since that would give a non-linear constraint. This constraint is also not applicable if the lower-level problem does not contain the pair of complementarity constraints, which may be the situation if the problem has equilibriums that are not derived from an underlying optimization problem.

Tables 2 and 3 contain results from testing the use of the strong duality constraint. We compare the valid range of C in (B-MILP) with strong duality constraint and (MILP) without this constraint. The valid range is the range where the optimal objective value of the original bilevel problem is reproduced. GAMS (ver. 23.0) and Xpress-MP (ver. 2006) were used to compute the solutions by enumeration. The bar graphs in the tables represent the effective range of C for each test problem. The strong duality constraint played a major role in making (B-MILP) almost insensitive to the choice of C.

Table 2 The working range for C increases when strong duality constraints are added. For each instance the objective value, shape of the α(x)-function and working range within [1E4, 1E10] for (B-MILP) with strong duality constraints and (MILP) is given. The integer upper-level variable is limited to [−10,10], all model parameters are in [0,10] and dim(x)=1, dim(y)=10, dim(z)=5, \(\dim(\bar{b})+\dim(\tilde{b})=15\)
Full size table
Table 3 The working range for C increases when strong duality constraints are added. For each instance the objective value, shape of the α(x)-function and working range within [1E4, 1E10] for (B-MILP) with strong duality constraints and (MILP) is given. The integer upper-level variables are limited to [−10,10], all model parameters are in [0,100] and dim(x)=2, dim(y)=400, dim(z)=200, \(\dim(\bar{b})+\dim(\tilde{b})=600\)
Full size table

The single-level approach in Gabriel and Leuthold (2010) and Audet et al. (2007), which corresponds to (MILP) may not use the strong duality constraint since it would make the problem non-linear and non-convex because x variables in the constraint cannot be fixed. Hence the working range of C for the single level approach would be narrow compared to the decomposed problem.

2.3 Branch-and-bound

Each node in the branch-and-bound tree represents a subdomain for the upper-level variables x. The literature shows several ways to do branching of the subdomains, for instance in Bard and Moore (1990), Hansen et al. (1992) and Gabriel et al. (2010). We have chosen to follow Gabriel et al. (2010). Two sample points s i (for i=1,2) are picked and Benders cuts, \(\alpha(x) \geq\alpha(s_{i} ) + \lambda_{i}^{\mathrm{T}}(x-s_{i} )\), are calculated for each point. λ i is the dual variable vector to the linear constraint x=s i of (SP). Two planes are obtained by changing the inequality symbols of the Benders cuts to equality, that is, \(\alpha(x) = \alpha (s_{i} ) + \lambda_{i}^{\mathrm{T}}(x-s_{i} )\), and where these planes intersect, \(\alpha(s_{1} ) + \lambda_{1}^{\mathrm{T}}(x-s_{1} ) = \alpha(s_{2} ) + \lambda_{2}^{\mathrm{T}}(x-s_{2} )\), the domain is partitioned. Since α(x) can be non-convex, the two Benders cuts might not partition the domain into two non-empty subdomains. In that case new sample points are chosen a limited number of times, and if proper branching is still not achieved an arbitrary partition of the subdomain into two non-empty subdomains is chosen.

We use the following branching and fathoming rules:

  • Branch if |(UB−LB)/LB|>TOL and LB<Incumbent

  • Pruning by optimality if |(UB−LB)/LB|≤TOL

  • Pruning by bound if LB≥Incumbent

Here Incumbent is the value of the best solution found so far and TOL is a user-specific tolerance.

2.4 Pseudocode for the algorithm

Algorithm 1 is a pseudocode that describes the overall algorithm. The main workload is the branch-and-bound process, where N refers to the index of current node, L is the list of active nodes in the partitioning tree and D(N) refers to the subdomain defined by node N. Three subroutines are used for solving the subproblems, making bounding decisions and branching and these are described in Subroutines 1–3. SelectNextNode(L) is a subroutine that selects next node from L. In our tests SelectNextNode(L) has applied the depth-first principle.

2.5 Convergence of the dynamic algorithm

To prove that the algorithm in Sect. 2.4 converges, we make the following assumptions:

Assumption 1

(A1)

The feasible region of (MP), \(X = \{x \in Z^{n_{x}} | Qx \leq q \}\), is a bounded, non-empty set.

Assumption 2

(A2)

The feasible region of (SP) for a given x, Ω SP(x)≠∅ when x∈X.

Theorem 1

Suppose that assumptions (A1) and (A2) hold and we are able to solve all sub problems within tolerance TOL. Then, the above dynamic DC-MPEC algorithm converges to a global optimum of problem (MILP), within the accuracy TOL, in a finite number of iterations.

Proof

This theorem is proved in two steps. First, we prove that we cannot prune the subdomain containing the optimal solution. Next, we prove that the algorithm in a finite number of iterations will be able to partition in such a way that the optimal solution is in a subdomain with convex α(x).

  1. 1.

    We prune by bound when the solution of the Lagrangean subproblem z MILP(μ)≤Incumbent. Geoffrion (1974) proves in Theorem 1(a) that the Lagrangean subproblem is a valid lower bound for (MILP) which means no optimal solution can be lost by pruning.

  2. 2.

    Since we have a limit on the number of Lagrange iterations, the computation of lower bound from (MILP(μ)) ends in a finite number of iterations. The computation of the upper bound z B-MILP using Benders decomposition also terminates in a finite number of steps according to Benders (1962). By assumption (A1) there are a finite number of points in the domain X and each branching is forced to leave at least one point in each subdomain, which means branch-and-bound can reach subdomains containing single points within a finite number of partitions. By definition α(x) is convex in subdomains containing a single point.

From the following three observations, we know that the algorithm will find the global optimal solution: (i) the subdomain containing the global optimal solution cannot be pruned by 1; (ii) we can find the subdomain containing the global optimal solution where α(x) is convex by 2; and (iii) according to Benders (1962), Benders decomposition algorithm provides the global solution for a convex α(x). □

2.6 Scenario decomposition

In the setting where the lower-level is a two-stage stochastic complementarity program the structure of the problem can be utilized when solving the Lagrangean subproblem (MILP(μ)) using scenario decomposition (Carøe and Schultz 1999).

The uncertainty is described by a set of scenarios j with the probability p j , j=1,…,J, where \(\sum_{j=1}^{J} p_{j} = 1\). For a problem with a two-stage stochastic program in the lower-level, Problem (1) can be written as:

(8)

where \(x_{j} \in Z^{n_{x}}\), \(\check{y}_{j} \in R^{n_{\check{y}}}\) and \(\hat {y}_{j} \in R^{n_{\hat{y}}}\) for j=1,…,J and

(9)

Here \(\check{y}_{j}\) and \(\check{z}_{j}\) are the first-stage decisions and \(\hat{y}_{j}\), \(\hat{z}_{j}\) and \(\hat{w}_{j}\) are the second-stage decisions of the lower-level for scenario j. The two last equation sets of S(x 1,…,x J ) are non-anticipativity constraints (Rockafellar and Wets 1976) included to make sure the first-stage decisions are equal in all scenarios.

We transform the complementarity conditions of Problem (9) into disjunctive constraints as described earlier, transforming the problem into a MILP. The underlying stochastic program gives the resulting MILP matrix a structure of nearly separable blocks for each scenario. To achieve separability in the scenarios the non-anticipativity constraints are dualized using Lagrangean relaxation. Since one set of optimality conditions contain a sum over all scenarios also these constraints need to be dualized to achieve separability. Note that also the upper-level variables and some disjunctive binary variables act as first-stage variables in this setting.

Scenario decomposition corresponds to Lagrangean relaxation of an integer program. As stated in Theorem 1 in Geoffrion (1974) this gives a lower bound on the original problem which makes it valid for our lower bounding purpose, but does not guarantee a tight bound.

3 Results

The dynamic algorithm has been tested both on randomly generated test data for the general model formulation and on three cases for an application of the DC-MPEC problem from the Norwegian natural gas supply chain. For all tests the tolerance was set to TOL=10−5.

3.1 Results on randomly generated data

In this section, we present our computational results with the dynamic DC-MPEC algorithm based on randomly generated data. Each lower-level problem is created by deriving the KKT conditions from a LP or convex QP problem. 59 LP-based problems are generated by random data from the interval [−500,500] with a uniform distribution. Similarly, data for 40 QP-based problems are sampled from a uniform distribution [−100,100]. The test problems are grouped according to the dimension of the variable vectors and underlying problem type, as summarized in Table 4. Sensitivity analysis has been conducted to find the working range for the disjunctive constant C, and the values reported in Table 4 is within this range and corresponds to the results reported in the following tables. Data for Groups 1 to 4 is provided in the online appendix for Gabriel et al. (2010), while the rest is new test problems. All tests were conducted on a computer with 2.34 GHz processor and 23.55 GB memory. The algorithm was implemented with MATLAB (ver. 7.0) and GAMS (ver. 23.6) interfacing where GAMS used Xpress-MP for its MILP solver. Test runs using more than 10 hours were stopped, giving rise to “n/a” in the result tables.

Table 4 Random generated test problem groups. MP and SP give the dimension of the variable vectors. The value of the disjunctive constant used for the tests are given by C. Whether the lower level problem is derived from a LP or QP is indicated by the problem type
Full size table

Table 5 lists the number of subdomains and the number of sampling and branching attempts for the alternative algorithms. Results are given for the original static algorithm (“Stat”) as in Gabriel et al. (2010) and the dynamic algorithm with and without warm-starting the Benders algorithm with the solution from Lagrangean relaxation (“Dyn ws” and “Dyn”, respectively). For the dynamic algorithm the number of subdomains corresponds to leaf nodes in the branch-and-bound tree, while in the static algorithm subdomains are identified by comparing (\(\lambda^{\mathrm{T}}, \bar{b} ^{\mathrm {T}}, \tilde{b} ^{\mathrm{T}}\)) as described in Gabriel et al. (2010). We observe that the dynamic algorithm reduces the number of subdomains and samplings compared to the static algorithm. In Table 6 the solution times for the same test problems and algorithms are given. “Bounding time” covers the Lagrangean and Benders algorithms (Subroutines 1–2), “Sampling time” sampling and branching the x-domain (Subroutine 3), and “Total time” is the sum of the two. The dynamic algorithm shows a significant reduction in solution time compared to the static algorithm, mainly caused by a major reduction in “Sampling time”. This corresponds well to the reduction in number of subdomains and sampling, and shows that the gain from fewer subdomains because of dynamic branching is larger than the added work on computing bounds. We observe that including the warm-start of the Benders algorithm makes the dynamic algorithm able to solve the problem in the root node for all test problems, also those with non-convex α(x), which indicates that Lagrangean relaxation gives a very strong lower bound for the problem. We have not been able to prove that this result is guaranteed for the problem class in general. The tables also show that the dynamic algorithm with warm-start solves all test problems, while the dynamic algorithm without warm-start leaves two problems unsolved and the static leaves five unsolved due to long solution times.

Table 5 Number of subdomains and samplings for random generated test problem solved by static algorithm and dynamic algorithm without and with warm-start (ws). # subdomains refers to the finest partitioning of the x-domain, which corresponds to the leaf nodes of the branch-and-bound tree for the dynamic algorithm. For the static algorithm the subdomains are identified through sampling and comparing (\(\lambda^{\mathrm{T}}, \bar{b} ^{\mathrm{T}}, \tilde{b} ^{\mathrm {T}}\)) as described in Gabriel et al. (2010). The true number of subdomains are identified by enumeration, where a subdomain is defined as a set of integer x points where (\(\lambda^{\mathrm{T}}, \bar{b} ^{\mathrm{T}}, \tilde {b} ^{\mathrm{T}}\)) is the same. Mean and median values cover all test problems that were solved by all three algorithms
Full size table
Table 6 Solution times for random generated test problem solved by static algorithm and dynamic algorithm without and with warm-start (ws). The convexity of α(x) is checked through plotting, and is therefore only available for 2-dimensional problems. Bounding time covers Benders and Lagrangean algorithm, Sampling time is time for sampling and branching while Total time is the sum Bounding and Sampling. Mean and median values covers all test problems that were solved by all three algorithms. All times in seconds
Full size table

3.2 Application to a natural gas supply chain

3.2.1 Background

The presented algorithm is tested on a stochastic two-stage problem from the Norwegian natural gas supply chain. For this problem we use the scenario decomposition described earlier. Because of high investment costs thorough planning is required for field and infrastructure developments in the natural gas industry. This planning typically has a bilevel structure where the investment level should be coordinated within the network, taking into account the competitive behavior of multiple producers in the operational level. Further, the investments are binary decisions taken under both long-term and operational uncertainty.

3.2.2 Model description

The model presented here is a MPEC that can be written on this form:

(10)

where \(x \in Z^{n_{x}}\), \(y \in R^{n_{y}}\), and

(11)

The upper-level takes the perspective of a central planner making binary decisions on which fields and pipelines to invest in and when to invest. These decisions are represented by x. The investments have investment costs, c, and there can be dependencies between the possible investments given by Qx≤q. The central planner maximizes the long term profits generated in the supply chain taking into account the short term operations, y.

For the lower-level problem we use a multi-period version of the model by Midthun (2007) with some extension to facilitate a connection to the upper-level decisions. Midthun (2007) describes a stochastic mixed complementarity problem where several producers make production decisions, trade in a transportation market, deliver natural gas in long term contracts and sell natural gas spot. The producers maximize their profit consisting of natural gas sales income, transportation costs and production cost. The natural gas spot market has exogenously given stochastic prices and delivery obligations in contracts are stochastic. The independent system operator (ISO) routes the gas and makes transportation capacity available in the transportation market according to the physical capacities of the network. The market for transportation capacity is modeled endogenously in two stages. In the primary market large prequalified producers book capacity at a fixed price before the uncertainty is resolved. In the secondary market the ISO offers spare capacity, the large producers trade and the optimality conditions of a competitive fringe give a demand curve that clears the market. One producer do not know the other producers’ primary booking in the second stage, an assumption that makes it possible to formulate the whole operational level as a Generalized Nash equilibrium. Figure 4 gives an overview over this model.

Fig. 4
figure 8

Overview over natural gas value chain model

Full size image

Midthun (2007) shows that a competitive transportation market where decisions partly is taken under uncertainty gives some losses compared to a centralized coordination maximizing the social surplus of the supply chain. These losses are caused by excess transportation booking that carries forward to excess production and sale. The investment decisions by a centralized upper level planner in our model will typically search for network structures that counteract these losses by providing a flexible network design.

3.2.3 Numerical results

Three small instances of this problem are solved by the dynamic DC-MPEC algorithm. Two datasets (Datasets 1 and 2) are entirely synthetic, while the last (Dataset 3) have production capacities from an extract of the existing fields. Each dataset have several instances with different number of scenarios.

For the natural gas application, the main coordination of the dynamic DC-MPEC algorithm is implemented in Matlab. Scenario decomposition was used for lower bounding, implemented with Mosel/Xpress to solve subproblems. To speed up the upper bounding the mixed complementarity problem from the lower-level was solved by GAMS/PATH and provided an initial solution for the binary variables of the Benders subproblem solved with GAMS/Xpress. As benchmark the whole bilevel problem is formulated as a single MILP and solved with Mosel/Xpress.

Table 7 presents the datasets and results from the tests. The disjunctive constant C was 105 for Dataset 1 and 106 for Dataset 2 and 3. Dataset 1 and 2 were tested on a HP dl160 G3 with 2×3.0 GHz Intel E5472 Xeon processors and 16 GB RAM and Dataset 3 was tested on a Pentium 4 with 3.6 GHz processor and 3.0 GB RAM.

Table 7 Numerical results for natural gas application. Three datasets are tested, each for several different numbers of scenarios. MP and SP give the dimension of the variable vectors. For the dynamic algorithm with warm-start the upper and lower bound and solution time in seconds is reported. For the benchmark, Xpress solving (MILP) is the objective value and solution time in seconds reported
Full size table

The benchmark was faster in the small instances, but our algorithm was able to solve substantially larger instances for Datasets 1 and 3. It is not surprising to find the benchmark faster on small instances, since our research code combining several software has a significant overhead in data transfer. We observe that in all tests where the real optimal value was known from the benchmark the dynamic DC-MPEC algorithm provided an optimal solution, as expected based on the theory.

We have experienced challenges related to numerical stability in the testing of our algorithm. In several occasions the solver provided a solution to a MILP problem, but when asking the solver to fix the binary variables according to the solution and resolve, the solver claimed the resulting LP to be infeasible. To overcome this situation the tests on Datasets 2 and 3 were run without the presolve function activated in the Xpress solver (www.gams.com/dd/docs/solvers/xpress.pdf) for upper bounding, and on Dataset 3 we also had to use different values for MIP tolerance on different instances. Naturally, deactivating presolve gives a disadvantage to the dynamic DC-MPEC algorithm when it comes to solution time.

4 Conclusions

We have presented a dynamic DC-MPEC algorithm to solve discretely constrained mathematical programs with equilibrium constraints (DC-MPEC) which is a class of bilevel program with integer program in the upper-level and mixed complementary problem in the lower-level. We develop a new branch-and-bound method for DC-MPEC problems applying Benders decomposition and Lagrangean relaxation methods. We provide convergence theory for the new method showing that it will find the global optimum and implement the new dynamic DC-MPEC algorithm on a set of test problems for both convex and non-convex domains. The numerical results show that the dynamic DC-MPEC algorithm outperforms the static counterpart presented by Gabriel et al. (2010) due to reduced sampling and branching efforts. The dynamic algorithm is further improved by warm-starting the Benders algorithm with the solution found by Lagrangean relaxation. We enhance the new method with the scenario decomposition method (Carøe and Schultz 1999) for two-stage stochastic DC-MPEC problems with discrete probability space. Then we compare the stochastic DC-MPEC algorithm with the single level approach by Fortuny-Amat and McCarl (1981) for a application for the Norwegian natural gas value chain. These numerical results present the effectiveness of our branch-and-bound algorithm and demonstrate the potential of the algorithm for a decision support tool for upper-level planners whose decisions are discrete.