1 Introduction

Unit commitment is one of the key optimization problems in power system operations and control. The objective of the unit commitment problem is to minimize the production cost of the generators to supply the load. This optimization problem is a mixed integer linear programming (MILP) problem since the problem formulation includes integer variables indicating the on/off statuses of generation units and other constraints such as capacity limits, minimum on/off hours and ramping constraints. As there could be hundreds of generation units and transmission lines in some systems, the unit commitment problem can become a computationally very challenging problem due to the large number of integer variables and constraints. Many techniques or constraints are used to model the reliability issues, such as transmission constraints (Fu et al. 2005, 2006), “n−1” criteria (O’Neill et al. 2010), stochastic demands (Wang et al. 2008), etc. Various optimization techniques including Lagrangian relaxation and branch-and-bound based MILP methods have been used to solve the problem (Hobbs et al. 2001; Shahidehpour et al. 2002). Benders decomposition and other decomposition techniques have been also used to reduce the computational requirement by separating the master unit commitment problem from the reliability checking subproblems (Fu et al. 2005; Fu et al. 2006). Benders cuts can be generated from the reliability checking or contingency simulation subproblems and added to the master unit commitment problem if any violation exists (Conejo et al. 2006; Fu et al. 2006), when the subproblems are linear programs.

In the past several years, more advanced power system operations methods have been proposed to address the variability and uncertainty brought by uncertain demand and increasing penetration of renewable energy sources. Stochastic unit commitment has emerged as one of the most promising tools (Barth et al. 2006; Ruiz et al. 2009; Tuohy et al. 2009; Wang et al. 2009). The idea of stochastic unit commitment is to capture the uncertainty and variability of the underlying factors by simulating a number of scenarios. Each scenario defines a possible realization of the uncertain sources. By simulating the scenarios, the uncertainty can be represented to a large extent. However, because of the large number of scenarios, the computational requirement also increases dramatically. More advanced optimization techniques need to be applied in these cases. In Wang et al. (2008), the unit commitment problem with uncertain wind power was modeled as a two-stage problem where the master problem determines the unit commitment and the second stage simulates the possible wind power output scenarios. By Benders decomposition, the problem can be solved in an efficient manner because of the small size of the master and subproblems.

However, the above models only considered unit commitment in the master problem. The modeling of quick-start units in the second stages is missing. In practice, there are generally two types of generators, i.e., quick-start generators such as gas turbines and combined-cycle units and non-quick-start generators such as coal-fired power plants and nuclear units. Those quick-start units can be committed on/off very quickly and have great ramping capabilities while it usually takes a long time for the non-quick-start generators to be committed. Thus, quick-start generators are often used as remedies to meet the stochastic demand in real time. Because binary variables are needed to model the commitment statuses of the quick-start units in the second stage of the stochastic problem, the problem becomes a stochastic mixed integer program (SMIP) with discrete decision variables in both the first and the second stages. This problem is very difficult to solve directly by the state-of-the-art commercial optimization software when a large number of scenarios in the second stage are used.

Benders decomposition has achieved a lot successful implementations in the unit commitment related problems, especially the two-stage stochastic problems without discrete variables in the second stage. In many cases, the convergence of Bender Decomposition algorithm is not ideal. To this end, a lot of research has been conducted to accelerate the convergence of Benders decomposition. Of the many approaches, some focus on reducing the computational expense on individual restricted master problem or subproblem. In McDaniel and Devine (1977), the algorithm first solves the relaxed version of the mixed integer master problem, by using the solution of which the subproblem still can generate a valid Benders cut, and heuristic rules determines when the integrality constraints are enforced. In Cote and Laughton (1984), the mixed integer master problem is not solved to optimality, and the first integer feasible solution is used to generate Benders cut, and again heuristic rules are used to determine when the master problem needs to be solved optimally. In Rei et al. (2009), local branching is used to speed up the convergence. In Zakeri et al. (2000), feasible solutions of the dual programs to the subproblems are used to construct Benders cuts, which saves computation time on solving the subproblems optimally. However, the other approaches are focusing on Benders cuts generation to improve either cut-generation efficiency or effectiveness of the Benders cuts. In Magnanti and Wong (1981), the Pareto-optimal cuts, which are not dominated by any other cut, is used to improve convergence. In Saharidis and Ierapetritou (2010), the maximum feasible sub-system cut generation strategy is used. In Saharidis et al. (2010), the covering cut bundle generation strategy for multiple constraint generation is proposed. Acceleration strategies have experienced shorter computational times in applications to stochastic two-stage unit commitment problems without discrete second-stage decision variables (Wu and Shahidehpour 2010). For those stochastic unit commitment problems with discrete second stage, algorithms from stochastic mixed integer programming are needed to address the nonconvexity of the second stage.

Stochastic mixed integer programming (SMIP) has been drawing a lot of attention recently. When integer variables exist only in the first stage, the problem is relatively easier to solve, since generally L-shaped method (Van Slyke and Wets 1969) or Benders decomposition (Benders 1962) would work. This is because the value function for the second stage is convex with respect to the first stage variables. However, the second stage value function becomes non-convex when there are integer decision variables in the second stage as discussed in Blair and Jeroslow (1982). This makes Benders decomposition (Benders 1962) or generalized Benders decomposition (Geoffrion 1972) not readily applicable because of the duality gap of integer programs. Within the last two decades, a lot of research has been done to solve SIMP problems with integer variables in the second stage. In Laporte and Louveaux (1993), a decomposition-based branch-and-cut method is proposed, where both feasibility and optimality cuts are applied, for SMIP with pure binary variables in the first stage. In Carøe and Tind (1998), a generalized L-shape method is proposed based on the generalized Benders decomposition (Geoffrion 1972), where both Gomory cuts and branch-and-bound algorithm are applied. In Sherali and Fraticelli (2002) and Sherali and Zhu (2006), modified Benders decomposition methods are developed by sequentially convexifying the discrete subproblem using reformulation-linearization technique (Sherali and Adams 1994). In Sen and Higle (2005), Ntaimo and Sen (2008) and Ntaimo (2010), decomposition methods are proposed for SMIP with random recourse and discrete second stage based on disjunctive programming (Balas 1979). Recently, a finite branch-and-cut solution algorithm is developed for SMIP with pure integer decision variables in the second stage, and a cutting plane framework for multi-stage stochastic integer program is studied in Guan et al. (2009).

In previous research, significant progress has been made on stochastic programming approaches to solve the unit commitment problem with the objective of minimizing total expected cost. A multistage stochastic programming formulation was developed early in Takriti et al. (1996). Meanwhile, an augmented Lagrangian decomposition framework was studied in Carpentier et al. (1996). The relevant Lagrangian decomposition literature also includes Dentcheva and Römisch (1997) and Gollmer et al. (2000). Recently, the stochastic programming approach for unit commitment to generate supply curves in electricity pool markets was studied in Philpott and Schultz (2006), and the stochastic programming approach for unit commitment to serve as a decision aid for scheduling and hedging in the wholesale power market was studied in Sen et al. (2006). In this paper, we study the two-stage stochastic programming formulation for the unit commitment problem, and propose a method which also exploits Benders cuts for the second stage subproblems, and these cuts are reusable given any first stage solution. Also our method generates multiple cuts while solving the subproblem of only one scenario, by taking advantage of the special structure of the unit commitment problem.

The remaining part of this paper is organized as follows. Section 2 gives the extensive formulation of the two-stage stochastic unit commitment problem, and uses the piecewise linear function to approximate the quadratic fuel cost function. In order to avoid solving the whole extensive formulation directly, Sect. 3 shows how the Benders decomposition is adjusted and applied to this problem by taking advantage of the problem structure. Section 4 presents the decomposition algorithm. Numerical experiments are shown in Sect. 5. Finally, Sect. 6 concludes the paper.

2 Problem formulation

This paper considers a two-stage unit commitment scheduling problem while taking into account real-time demand uncertainties. In the first-stage scheduling, the model makes commitment decisions for all units, including both non-quick-start and quick-start generators, since power plants may need to know the generation scheduling of all power units one day ahead. However, in the second-stage scheduling, only quick-start units can be rescheduled, because the startup time is much shorter than the length of one time period. The model in this paper is more general since it assumes that the rescheduling may induce some extra costs due to the discrepancies between the original scheduling and the real-time scheduling of quick-start generators. This is because the system operators receive different bidding prices in the day-ahead market and the real-time market. Also, the power dispatch on any unit, whose status is “on” at that time period in the original schedule, can be adjusted in real time.

The first stage consists of constraints (3)–(7) and objective function (1). And the second stage consists of constraints (8)–(24) and objective function (2), where F(p) is a quadratic function of p with a positive second order derivative. The most obvious difference between the first-stage and second-stage constraints is whether the constraints are associated with the scenarios. The extensive formulation is shown as follows,

(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24)

In order to facilitate the description of the model, sets and indices used in this paper are listed in Table 1, parameters in Table 2, and decision variables in Table 3. Decision variable α it denotes the commitment status of unit i at time period t, with “0” meaning “off” and “1” meaning “on”. γ it is the start-up action indicator, of which “1” means there is a start-up action and “0” else, and δ it is the shut-down action indicator, respectively. Constraints (3) and (4) are respectively the minimum up and down time requirement constraints of the first stage scheduling. Constraints (5) and (6) define the start-up and shut-down action indicators respectively. The cost of first stage is shown in (1), which consists of only the start-up and shut-down costs since power dispatches are decided in the second stage or real time.

Table 1 SCUC sets and indices
Full size table
Table 2 SCUC parameters
Full size table
Table 3 SCUC decision variables
Full size table

The objective function of the second stage is defined by (2) which is the expected total cost of dispatch and rescheduling. Decision variable \(\beta_{jt}^{\xi}\) is the rescheduled commitment status variable of quick-start unit j at time t in scenario ξ. \(\gamma_{jt}^{\xi}\) and \(\delta_{jt}^{\xi}\) are the start-up and shut-down action indicator variables respectively. Because the day-ahead schedule of quick-start units might not be the least-cost solution for the real-time situation, they might need to be rescheduled in real time. Let \(y_{jt}^{\xi}\) denote the start-up rescheduling indicator. This indicator has three possible choices: “1” means that there is a start-up action for unit j at time t under scenario ξ but not in the day-ahead schedule; “0” means that real-time schedule of scenario ξ is the same as day-ahead one for unit j at time t; “−1” means that there is a start-up action for unit j at time t in the day-ahead schedule but not in the schedule of scenario ξ. The same definition applies for \(z^{\xi}_{jt}\), shut-down rescheduling indicator. In the second stage, demands are satisfied in constraint (8), and constraints (9) and (10) are the spinning reserve and non-spinning or supplemental reserve constraints respectively. The right hand sides can be considered as the difference between the customer demands subtracted by the renewable resource availability. For example, in a scenario with abundant wind and/or solar energy, the total demand for thermally generated power will be low. Constraints (11) and (12) are the start-up and shut-down action rescheduling indicator constraints. Constraints (13) and (14) define the start-up and shut-down action indicators of the quick-start generators respectively. Constraints (15) and (16) define the range of values that the dispatches and take spinning reserves of non-quick-start generators can take. Constraints (17) and (18) do the same for the quick-star generators. Constraint (19) requires the maximum ramp-up and ramp-down limits. Constraint (20) gives the maximum spinning reverses that generators can provide. Constraint (21) defines the non-spinning or supplemental reserves, which are actually the generating capacity of the uncommitted quick-start generators. The first and second stages are connected by the non-quick-start units’ commitment decisions and the start-up and shut-down action indicators of the quick-start units.

In the extensive formulation [ESCUC], both γ it and δ it can be simply treated as nonnegative continuous variables since the positive costs related to them in the objective function and constraints (5) and (6) will ensure that they can take only either 0 or 1. For convenience, let p ξ be a vector composed of all \(p_{it}^{\xi}\), i=1,…,N c , t=1,…,T. So do s ξ, q ξ, α, β ξ, γ, γ ξ, δ, δ ξ, y ξ and z ξ through the rest of this paper.

2.1 Piecewise linear approximation of the fuel cost function

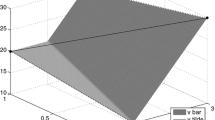
As is noted in the second stage objective function (2), the fuel cost is a function of the power dispatches on generators, usually a quadratic function with a positive second order derivative. This quadratic mixed 0-1 integer programming problem is difficult to solve when a lot of generators are considered. However, a piecewise linear approximation of the quadratic function can make the original problem [ESCUC] a mixed integer linear programming (MILP) problem. The solution to the MILP is very close to the real optimal solution (Hobbs et al. 2001). Because the cost function itself is convex, the piecewise linear approximation function is still convex. Hence we can use the following function, (25), and constraints, (26)–(28), to replace the original function F(p) in the objective function, as is shown in Fig. 1.

$$ F(p) = \sum_{k=1}^KC_k \lambda_k.$$
(25)

And we need to add the following constraints,

(26)
(27)
(28)
Fig. 1
figure 1

Piecewise linear approximation of the fuel cost function

Full size image

However, as is seen from Fig. 1, the cost function usually does not start from the origin, (0,0), and p=λ k =0, k=1,…,K, if this unit is not committed. To handle this situation, we need to include the commitment status variable α in the above constraints. In stead of “1”, the right hand side of (27) is replaced by the commitment status variable α, which is shown as follows,

$$ \sum_{k=1}^K\lambda_k=\alpha.$$
(29)

Because α is the commitment status, and λ k s are nonnegative variables, the cost F(p) is zero when the commitment status is “off”, i.e., α=0. And the new equation, (29), is the same as the old one, (27), when the commitment status is “on”, i.e., α=1. Constraints (26), (28) and (29) will also ensure that P min α≤p≤P max α, since usually we have that Δ1=P min and Δ K =P max. Hence, in the extensive formulation [ESCUC], constraints (15) and (17) can be dropped if the above linear approximation techniques are used to replace the quadratic fuel cost function.

3 Problem decomposition

Even after the piecewise linear approximation, the remaining problem is still a very difficult problem since the second stage may contain a lot of scenarios, which include an even larger number of integer variables. For this nontrivial problem, the best way to solve it is to decompose it to multiple smaller problems and assemble the solution information from the smaller problems, and then to tell whether an optimal solution to the original extensive problem was obtained or how far the current solution is away from it. This section discusses how the original problem is decomposed based on Benders decomposition, which finally leads to the solution algorithm in Sect. 4.

3.1 Generating valid Benders cuts from discrete subproblems

In order to take advantage of the dual solution of the second stage problem, Benders Decomposition or Generalized Benders Decomposition requires the second stage problem to be a linear program or a convex program. In the model of this paper, the second stage is neither a linear program nor a convex program. In order to tackle this difficulty and still be able to apply Benders Decomposition, one way is to convexify the second stage mixed integer programs to get valid and effective Benders cuts for the first stage, i.e., the restricted master problem. The approach proposed by Sherali and Fraticelli (2002) is inspiring. They analyze the following two stage mixed integer program,

$$\begin{array}{@{}l@{\quad }l@{\quad }l@{}}[\mathbf{P}]{:} & \mathrm{min} &c^T x+d^Ty, \\\noalign{\vspace*{3pt}}&\mathrm{s.t.} & Ax+Dy\ge b,\\\noalign{\vspace*{3pt}}&& x\in X,\qquad x\in\{0,1\}^n,\qquad y\in Y,\end{array}$$

where y is a vector including integer variables, and X is a nonempty polytope. If we can find the convex hull of the following region

$$\{Ax+Dy\ge b, y\in Y\} $$
(30)

for any given x, then Benders’ decomposition can be applied because the linear relaxation of the subproblem (convex hull formulation) will have the same optimal solution as the discrete subproblem, and then the subproblem can simply be treated as a linear programming problem. To achieve this goal, Reformulation-Linearization-Technique or Lift-and-Project cuts are iteratively added to the subproblem in Sherali and Fraticelli (2002). These are called global cuts, which means that they are valid for the original problem [P] but focus on cutting the region of (30), which has the following format,

$$\alpha_k^Ty+\psi_k^Tx\ge \beta_k, \quad k=1,\dots, K, $$
(31)

where k denotes the kth cut. There are also other cuts (Balas et al. 1993; Sen and Sherali 2006, etc.) that possess the same properties which (31) has. With these cuts added, the relaxed subproblem will be as follows,

$$\begin{array}{@{}l@{\quad }l@{}}\mathrm{min}& d^Ty\\\noalign{\vspace*{3pt}}\mathrm{s.t.}& Dy\ge b-Ax,\\\noalign{\vspace*{3pt}}&\Gamma y \ge\gamma,\\\noalign{\vspace*{3pt}}&\alpha_k^Ty\ge\beta_k-\psi_k^T\hat{x}, \quad k=1,\dots, K,\end{array}$$

where Γy≥γ is the linear relaxation of the set Y. Then we just need to solve the above linear problem to produce Benders cuts for the first stage. For convenience, the subproblem is assumed to be feasible given any first stage solution, \(\hat{x}\), since we can always add an artificial variable and assign a big penalty to it to make the problem feasible. Suppose the optimal dual solutions are ϕ 1, ϕ 2, and ϕ 3 corresponding to the above three constraints respectively. Then a valid Benders’ cut can be obtained as follows,

$$z \ge(b-Ax)^T\phi_1+\gamma^T\phi_2+\sum_{k=1}^K \bigl(\beta_k-\psi_k^Tx\bigr)\phi_{3_k}.$$

Even when the convex hull of the subproblem is not completely obtained, the Benders cuts are still valid to the first stage problem. This is because the relaxed subproblem always provides a lower bound to the subproblem, which means it also provides a valid lower bound for z.

3.2 Embedded Benders decomposition for the stochastic security constrained unit commitment

The extensive formulation is too difficult to solve because of the huge number of scenarios, which means even more binary variables. So we would like to decompose the problem into two stages, where the restricted master problem and subproblems individually have much fewer variables and constraints. In this paper, we adopt a similar method proposed by Zheng and Pardalos (2010). The first stage is the restricted master problem, which determines the optimal first-stage schedule of all generating units without considering the second-stage stochastic demands explicitly, while including the feedback cuts (e.g., Benders cuts) from the second stage. The Restricted Master Problem (RMP) is shown as follows,

(32)
(33)
(34)
(35)

where γ it and δ it are relaxed to nonnegative continuous variables in (34), because they are associated with positive costs in the objective function and are determined by binary variables α it and α i(t−1) in constraints (5) and (6). χ ξ is an auxiliary variable for the recourse function of scenario ξ, and \(\hat{\text{x}}_{it}^{\xi,n}\), \(\hat {\text{d}}_{jt}^{\xi,n}\), \(\hat{\text{e}}_{jt}^{\xi,n}\) and bξ,n are the coefficients of cut n, which will be explained in details later on.

When the first stage decision variables are fixed, the second stage is decomposed into |Ξ| separate subproblems, each of which solves a unit commitment problem of a specific scenario. The only difference between two subproblems are the demands as shown in the following formulation. This eases the burden from too many scenarios, but information based on the solutions of subproblems of individual scenarios needs to be collected and sent to [RMP] in the form of feedback cuts. Later in this paper, details of assembling valid and effective Benders cuts are provided. For each scenario ξ∈Ξ, the subproblem, with fixed values of first stage decision variables, is shown as follows,

(36)
(37)
(38)
(39)
(40)

where the fuel cost function is replaced by its linear approximation (36) and auxiliary constraints (37), (38) and (39).

Given the first-stage schedule \(\hat{\alpha}\), \(\hat{\gamma}\) and \(\hat{\delta}\), the second-stage unit commitment problem [SPξ] might be infeasible because we cannot change the commit status of the non-quick-start units promptly in real time, and the quick-start units solely do not have enough total capacity to satisfy the high demand. In order to avoid dealing with infeasible subproblems, we can relax the subproblem to make it always feasible by introducing a dummy quick-start generator, indexed by d, with a big enough capacity but much higher costs. The higher cost will ensure the relaxed problem has the same optimal solution as the original problem if the original is feasible. The new problem is then referred to as the modified subproblem, [MSPξ]. The only difference between [SPξ] and [MSPξ] is the set of quick-start units. In [MSPξ], this set is N g ∪d, and we assume \(\hat{\gamma}_{dt}=\hat{\delta}_{dt}=0\), t=1,…,T.

Because the modified subproblem is still a mixed integer program, we need to further modify it in order to find a legitimate dual optimal solution to construct a valid and effective cutting plane for the [RMP]. Our strategy is to keep convexifying the subproblem while returning cuts to the [RMP] along the iterations. When the second-stage commitment status of all quick-start units are determined as \(\hat{\beta}^{\xi}\), along with the first-stage commitment status of all non-quick-start units, \(\hat{\alpha}\), the subproblem associated with scenario ξ reduce to a linear program, [LPξ], shown as follows,

(41)
(42)
(43)
(44)
(45)
(46)
(47)
(48)
(49)
(50)

where the variables on the right of the left-pointing arrows are the corresponding dual variables. Solving the above [LPξ] can generate a new cut, which is shown in (51), for the restricted master program of [MSPξ].

(51)

where \(\hat{l}^{\text{I},\xi}\), \(\hat{l}^{\text{II},\xi}\), \(\hat{h}^{\text {I},\xi}\), \(\hat{h}^{\text{II},\xi}\), \(\hat{h}^{\text{III},\xi}\), \(\hat{u}^{\xi}\), \(\hat{v}^{\xi}\), \(\hat{w}^{\xi\mp}\), \(\hat{r}^{\text{I},\xi }\), \(\hat{r}_{jt}^{\text{II},\xi}\) are the optimal dual solution corresponding to constraints (41)–(50) respectively. For convenience, we rewrite (51) in vector format as follows,

$$b^\xi\beta^\xi+\pi^\xi\geq f^\xi+a^\xi \hat{\alpha}.$$

By including these new cuts (51) and relaxing the integer restrictions, the relaxation of the [MSPξ], which is referred to as the relaxed linear program [RLPξ], can be constructed as follows,

(52)
(53)
(54)
(55)
(56)
(57)
(58)
(59)
(60)
(61)

where \(\mathcal{K}^{\xi}\) is the set containing all these cuts (51) for scenario ξ, \(y^{\xi}_{jt}\) and \(z^{\xi}_{jt}\) are replaced by \(\dot{y}^{\xi}_{jt}-1\) and \(\dot{z}^{\xi}_{jt}-1\), in order to have only nonnegative variables after relaxation. Then constraints (59) and (60) result from the linear relaxation of constraints (40). However, these two constraints can be dropped without affecting the optimal solution of [RLPξ], because \(\dot{y}^{\xi}_{jt}\) and \(\dot{z}^{\xi}_{jt}\) are both associated with positive coefficients in (52), of which the constant term results from the variable replacement.

Proposition 1

The cut, (51), obtained by solving [LP ξ] is a valid cut for [RLP ξ] given any first stage solution, \(\hat{\alpha}\), \(\hat{\gamma}\) and \(\hat{\delta}\).

Proof

In [LPξ], both first-stage decisions and second-stage discrete decisions are fixed. Based on its optimal dual solution, a Benders cut can be constructed, for the remaining problem obtained by removing constraints and the objective function of [LPξ] from the original extensive formulation, as follows,

$$b^\xi\beta^\xi+\pi^\xi-a^\xi\alpha \geq f^\xi,$$

where first-stage decision variable α is free to be chosen as long as it satisfies the above cut. Also, first-stage decision variables, γ and δ, do not appear in this cut. Hence, this cut is valid for [RLPξ] given any first-stage solution. □

These cuts are often referred to as global cuts. By “global”, it means that the cut is valid for [RLPξ] given any first-stage solution, i.e., the solution from the first stage (restricted master problem), \(\hat{\alpha}\), \(\hat{\gamma}\) and \(\hat{\delta}\). Since the above [RLPξ] is a linear program, whose feasible region is an approximation of the convex hull of [MSPξ]s feasible region, we can derive a valid Benders cut for [RMP], shown in (62), by solving [RLPξ]’s dual problem optimally.

(62)

where \(\hat{\eta}_{k}^{\xi}\) is the optimal dual solution corresponding to the kth global cuts in [RLPξ], and \(\hat{\theta}^{\xi}\), \(\hat{\sigma}^{\xi}\) and \(\hat{\rho}^{\xi}\) are the optimal dual solutions corresponding to constraints (53), (54) and (58) respectively.

Proposition 2

The cut (62) based on the dual solution of [RLP ξ] is a valid cut for [RMP].

Proof

Let \(\mathsf{Z}_{MSP}^{\xi}(\alpha, \gamma, \delta)\) and \(\mathsf{Z}_{RLP}^{\xi}(\alpha, \gamma, \delta)\) be the optimal objective value of [MSPξ] and [RLPξ] given any first-stage decision (α,γ,δ). Because (51) is a global cut for [RLPξ] and (62) is a Benders cut for [RMP],

Because [RLPξ] is the relaxation of the minimization problem [MSPξ],

$$\mathsf{Z}_{MSP}^\xi(\alpha, \gamma, \delta)\geq\mathsf{Z}_{RLP}^\xi (\alpha, \gamma, \delta),$$

for any first stage decision. Hence, (62) is a valid cut for [RMP]. □

It is interesting to note that all [LPξ]s share the same dual space (dual feasible region) since the costs in the objective functions and left-hand-side coefficients are the same. Hence the dual solution obtained by solving a specific [LPξ] could be used to construct the global cuts for other scenarios. A generalization to all scenarios leads to the following corollary.

Corollary 1

The global cut of scenario ξ, (51), with right hand side being changed to \(f^{\zeta}-a^{\xi}\hat{\alpha}\), is also valid for [RLP ζ] given any first stage solution, for all ζ∈Ξ.

In constraint (57), the set of cuts, \(\mathcal{K}^{\xi}\), is designated to only one single scenario, ξ. However, we can generalize this set for all scenarios, which means that only one cut set \(\mathcal{K}\) is needed for all subproblems of different scenarios.

For all scenarios, this constraint, (51), is almost the same except \(f^{\zeta}_{k}\), which is calculated as follows,

where the (k) in the subscripts denotes the kth optimal dual solution in \(\mathcal{K}^{\xi}\), and

$$f_k^{c,\xi}=\sum_{t=1}^T\biggl[\sum_{i\in\{N_c\cup N_g\cup d\}} \bigl( - D_i \hat{w}_{k,it}^{\xi-} + U_i \hat{w}_{k,it}^{\xi+}+ S^{\max }_i \hat{r}^{\text{I}, \xi}_{k,it} \bigr) +\sum_{j\in\{N_g\cup d\}} P^{\max}_j \hat{r}^{\text{II}, \xi}_{k,it} \biggr],$$

which is independent of scenario ζ. So \(f^{\zeta}_{k}\) can be considered as an affine function of \(\mathit{PD}_{t}^{\zeta}\), \(\mathit{RS}_{t}^{\zeta}\) and \(\mathit{RO}_{t}^{\zeta}\), in which \(f_{k}^{c,\xi}\) is the constant part. Then all [RLPξ]s can share the same global cut set except for the right hand sides. Instead of multiple global cut sets for all the scenarios, we only need to maintain a single global cut set as follows,

$$b_k\beta^\zeta+\pi^\zeta\geq f_k^\zeta+a_k\hat{\alpha},\quad k\in \mathcal{K}, $$
(63)

where the only differences between the scenarios are the names of variables and right hand sides.

After we replace (57) in [RLPξ] by (63), the left-hand-side coefficients of [RLPξ] are not dependent of the scenarios any more because b k is the same for all scenarios. This also means that all [RLPξ]s have the same dual feasible region because they are all linear programs. So an optimal dual solution to one scenario is also a feasible dual solution to another scenario. Hence the dual optimal solutions, \(\hat{\theta}^{\xi}\), \(\hat{\sigma}^{\xi}\), \(\hat{\psi}^{\xi}\), \(\hat{\phi}^{\xi}\), \(\hat{\eta}^{\xi}\), and \(\hat{\rho}^{\xi}\) to [RLPξ] can help construct valid Benders cuts from all other scenarios, but with different \(f_{k}^{\zeta}\)’s, which leads to the following proposition.

Proposition 3

For all ζ∈Ξ, the inequality

(64)

is a valid Benders cut for [RMP] given any first stage solution, where \(\hat{\theta}^{\xi}\), \(\hat{\sigma}^{\xi}\), \(\hat{\eta}^{\xi}\), and \(\hat{\rho}^{\xi}\) are the dual optimal solutions to [RLP ξ].

With these disaggregated cuts being added into the [RMP], we need to include |Ξ| recourse variables, χ ξ, ξ∈Ξ. In the case of a big number of scenarios, this could increase the computational burden of solving the restricted master problem. However, all cuts generated by the same dual solution of [RLPξ] can be aggregated to one single cut by adding them together while multiplying each of them by the probability of its corresponding scenario. The aggregated cut is shown as follows,

(65)

where ∑ ξ∈Ξ Prob ξ χ ξ is replaced by χ, and \(\overline{\mathit{RS}}\), \(\overline{\mathit{RO}}\), and \(\overline{\mathit{PD}}\) are the expectations of the random spinning reserve, operating reserve and demand. \(\bar{h}_{t}^{\text{I},\xi}\), \(\bar{h}_{t}^{\text{II},\xi }\) and \(\bar{h}_{t}^{\text{III},\xi}\) are aggregated optimal dual solutions as follows,

If we choose to add the aggregated cuts into the relaxed master problem, RMP, the term, ∑ ξ∈Ξ χ ξ, in its objective function can be then simply replaced by χ. According to the number of scenarios, we could choose different strategies to add valid Benders cuts. As discussed in Birge and Louveaux (1997), the disaggregated scheme is preferred in the case of a small number of scenarios, and the aggregated scheme is in favor instead when |Ξ| is large. We prefer the aggregated scheme because the aggregated cuts contain more information from all scenarios and are very easy to generate due to the sharing of same dual space.

4 Solution algorithm

If there is no Benders’ cut being added in the [RMP], without including recourse variable χ in the objective function, its optimal solution is \((\hat{\alpha}, \hat{\beta}, \hat{\gamma}, \hat{\delta})=0\). It is because all the variables are nonnegative and the costs of startup and shutdown are positive. Hence 0 is the best objective value that the [RMP] without any cut can achieve. Then we can use this as the initial solution for the algorithm based on Benders decomposition. At each iteration, after we solve the [RMP], its optimal objective value is used as a lower bound of [ESCUC]. An upper bound can be obtained as follows,

$$\mathsf{Z}_{UB} = \mathsf{Z}_{RMP} - \hat{\chi}+ \sum _{\xi\in\Xi}\mathit{Prob}^\xi \mathsf{Z}_{MSP}^{\xi},$$
(66)

where \(\mathsf{Z}_{MSP}^{\xi}\), Z RMP and \(\hat{\chi}\) are the optimal objective values of [MSPξ] and [RMP], and the solution of χ respectively. This actually represents the cost of a feasible solution to the relaxed [ESCUC] with a dummy costly generator being added.

The lower bound based on the solution of [RMP] could improve very slowly in practice when the UB and LB are very close to each other. One of the methods to avoid slow convergence or even stalling is to apply the integer L-shaped cut since it is an optimality cut improving the lower bound if there exists a solution with a higher objective value. An integer L-shaped “optimality” cut is as follows,

$$z\geq\bigl(Q(\hat{x}) - L\bigr) \biggl(\sum_{j\in\mathbb{T}(\hat{x})}x_j - \sum_{j\in\mathbb{F}(\hat{x})}x_j - \bigl|\mathbb{T}(\hat{x})\bigr|+1 \biggr) + L$$

where \(Q(\hat{x})\) is the recourse function of \(\hat{x}\), the first stage solution, and L is a lower bound for the second stage problem, and \(\mathbb{T}(\hat{x})=\{j|\hat{x}_{j} = 1\}\) and \(\mathbb{F}(\hat{x})=\{j|\hat{x}_{j} = 0\}\), if x is the first stage decision variable and \(\hat{x}\) is the current solution. This follows from the fact that the right hand side will be equal to \(Q(\hat{x})\) if \(x=\hat{x}\), and less than L otherwise since \((\sum_{j\in\mathbb{T}(\hat{x})} x_{j} -\sum_{j\in \mathbb{F}(\hat{x})}x_{j} - |\mathbb{T}(\hat{x})|+1 )\leq0\) if \(x\neq \hat{x}\). We refer interested readers to Laporte and Louveaux (1993) for the detailed proof of its validity and convergence. Without having to define the two sets, \(\mathbb{T}(\hat{x})\) and \(\mathbb{F}(\hat{x})\), after rearranging terms the cut can be expressed by the following equivalent inequality,

$$\bigl(Q(\hat{x}) - L\bigr) \sum_j (1-2\hat{x}_j)x_j +z\geq Q(\hat{x}) - \bigl(Q(\hat{x}) - L\bigr)\sum_j \hat{x}_j.$$

The first stage problem, [RMP], is a pure integer program with only 0-1 variables, and then we can apply the integer L-shaped “optimality” cut in [RMP], which is shown as follows,

(67)

where the recourse Q(⋅) is a function of only α, the commitment status of both coal and gas power generators, since the best optimal objective value of the second stage is uniquely defined once they are determined. If all non-quick-start generators remain “on” at all time periods, the total cost from the quick-start generators is the least; this is because they have start-up costs and higher fuel costs, and then are only used as needed. So the second-stage optimal objective cost under this condition can be used as an lower bound of the second stage, L. The embedded Benders decomposition algorithm is shown as follows,

Step 0.:

Set UB=∞, LB=0, \(\mathcal{K}=\emptyset\), \((\hat{\alpha}, \hat{\gamma}, \hat{\delta}) =0\), Z UB =0, Z RMP =0, and \(\hat{\chi}=0\);

Step 1.:

Solve [MSPξ] given \((\hat{\alpha}, \hat{\gamma},\hat{\delta})\), ξ∈Ξ, and suppose that optimal solution and objective value are (\(\hat{\beta}^{\xi}\), \(\hat{p}^{\xi}\), \(\hat{q}^{\xi}\), \(\hat{\lambda}^{\xi}\), \(\hat{y}^{\xi}\), \(\hat{z}^{\xi}\), \(\hat{\gamma}^{\xi}\), \(\hat{\delta}^{\xi}\)), and \(\mathsf{Z}_{MSP}^{\xi}\), ξ∈Ξ;

Update Z UB ;

UB←min(UB,Z UB );

Step 2.:

Solve [LPξ] given \(\hat{\alpha}\) and \(\hat{\beta}^{\xi}\), and dual optimal solutions are (\(\hat{l}^{\text{I}}\), \(\hat{l}^{\text{II}}\), \(\hat{h}^{\text{I}}\), \(\hat{h}^{\text{II}}\), \(\hat{h}^{\text{III}}\), \(\hat{u}\), \(\hat{v}\), \(\hat{r}^{\text{I}}\), \(\hat{r}^{\text{II}}\));

Add this new dual solution to the set, \(\mathcal{K}\);

Repeat this for all ξ∈Ξ;

Step 3.:

Solve [RLPξ] given \((\hat{\alpha}, \hat{\gamma}, \hat{\delta})\), and suppose the optimal dual solution is (\(\hat{\theta}\), \(\hat{\sigma}\), \(\hat{\eta}\), \(\hat{\rho}\));

Add a new aggregated cut, as in (65), into [RMP];

Repeat this for all ξ∈Ξ;

Step 4.:

Add an integer L-shaped “optimality” cut, as in (67), into [RMP];

Step 5.:

Solve [RMP], and suppose that optimal solution and objective value are (\(\hat{\alpha}, \hat{\gamma}, \hat{\delta},\hat{\chi}\)) and Z RMP respectively;

LB←max(LB,Z RMP );

Step 6.:

If UB−LB≤ϵ, stop; Otherwise, go to Step 1,

where ϵ is a small value for the gap tolerance. As is shown above, we repeatedly solve [LPξ] and [RLPξ] for all scenarios in steps 2 and 3 respectively. However, in order to improve computational efficiency we do not need to repeat for all scenarios since all [LPξ]s and [RLPξ]s which are corresponding to the same first stage decision. One way is to sample from all the scenarios and only solve a limited number of [LPξ]s and [RLPξ]s.

In this algorithm, we maintain two sets of cuts: one for convexifying the mixed integer subproblems, and one for constructing the future benefit functions. For convenience, the first set of cuts are referred to as inner convexification (IC) cuts, and the second set of cuts are referred to as outer feedback (OF) cuts. In the above algorithm both types of cuts are actually Benders cuts, and IC cuts are embedded in the subproblems to provide valid OF cuts. When the algorithm actually terminates, we may need to check the solution in order to determine if the original extensive formulation is feasible or not. Any variable related to the dummy costly generator should be equal to zero. Otherwise, extensive formulation is infeasible because even all of the available generators are turned on, some of requirement constraints (8), (9) or (10) cannot be satisfied without resorting to the costly dummy generator, which means the demands are actually greater than the total generation capacity of all units. In most cases the dummy generator is not in use in the optimal solution, because most of the original problems are feasible, which means that we have enough generating capacity to meet the demands.

5 Numerical experiments

In this section, we present numerical results of our algorithm on serval problems with different sizes and settings. We code our algorithm in Microsoft Visual C++ while calling CPLEX 11 (Concert Technology) to solve the decomposed problems. All programs are run in Microsoft Windows XP Professional 2002 operating system on a Dell Desktop with Intel Pentium 4 CPU 3.40 GHz and 2 GB RAM.

A simple example of security constrained unit commitment problem with four generators, of which G3 and G4 are quick-start generators, is discussed below. The generator data are shown in Table 4. For convenience, we solve a problem with two time periods and three scenarios, with data shown in Table 5. By applying our algorithm, after 5 iterations with 10 cuts added in the first stage, the algorithm reaches the optimality and returns the same optimal solution as the extensive model directly solved by CPLEX, which takes 23 iterations and adds 8 cuts . The results are shown in Table 6. Computational times (in seconds) of more examples are shown in Tables 7, 8 and 9, in which the column of EXTS records the computational times of solving the extensive formulation directly by CPLEX MIP solver, and columns of RMP, MSP, LP, RLP and TTL record the total computational times of solving [RMP], [MSP], [LP], [RLP] and the algorithm proposed in this paper. For all the problem instances in these tables, the decomposition algorithm reaches the same optimal solutions as those obtained by solving the extensive formulation directly by CPLEX MIP solver. As can be seen in Table 7, computing times almost increase linearly with respect to the number of scenarios, which means the method proposed in this paper is well suited to problems with a large number of scenarios. Also, the method spends a big portion of time to solve [MSP] and [LP]. Hence it is possible to further reduce computing time if we do not calculate new IC and OF cuts for each scenario in Step 1 through Step 3 because looping through all scenarios takes a lot of time, especially when we have a huge number of scenarios. Computational experiments with more time periods and generation units are shown in Tables 8 and 9, where all problems are solved optimally by both methods, and ∗ denotes the cases in which the corresponding algorithm either is running out of memory (more often) or cannot close the optimality gap within 1 hour. The decomposition algorithm did not experience the shortage of memory space since the sizes of the problems it solves are usually much smaller than the extensive formulation.

Table 4 Generators data
Full size table
Table 5 Load forecast of a simple example
Full size table
Table 6 Solution of the 4-unit SCUC with 3 scenarios
Full size table
Table 7 Computational results of SCUC
Full size table
Table 8 Computational results of SCUC (K=11)
Full size table
Table 9 Computational results of SCUC (K=11)
Full size table

6 Conclusion

This paper discusses a very important problem of power systems, the two-stage stochastic unit commitment problem. In addition to considering the traditional unit commitment constraints, spinning reserves and ramping constraints, the model includes two-stage scheduling to address the fact that both quick-start and non-quick-start units are present in thermal plants, and quick-start units are used to meet the uncertain demands in the second stage or real time. This means that this stochastic model includes integer decision variables in both the first and second stages. The presence of integer decision variables in the second stage makes this problem very difficult to solve, especially when there are a large number of scenarios. This paper, then, uses a method based on Benders decomposition and integer L-shaped method to solve the two-stage problem. Numerical results show that this algorithm is efficient when experiencing a large number of scenarios. Future research could focus on how to make the algorithm converge faster by more advanced implementation and stronger Benders cuts, e.g., Pareto optimal cuts, high density cuts, etc.