1 Introduction

A comparator is a circuit able to compare different signals and switch its outputs indicating which is larger, and is mandatory in analog-to-digital converters (ADCs). Some of the performance metrics of the comparator affect directly the overall ADC performance, such as power consumption and maximum speed. Still, in the context of ADCs, the stochastic phenomena involved on the comparison process (i.e. offset voltage and noise) may lead to errors on the converters. In some architectures, the comparator offset leads to an offset on the ADC transfer curve, while in others, it may appear as non-linearity [1]. Fortunately, diverse offset calibration schemes have been devised in order to bring the comparator offset to levels that satisfy ADC specifications. On the other hand, the noise generated by the comparator circuit during the comparison is generally more critical, since it appears added to the quantization noise at the ADC output. Some ADC designs on the literature report that a significant drop on the effective resolution was caused by comparator noise [2]. Recently, a technique that employs averaging was proposed in [3] in order to reduce the impact of comparator noise on the ADC signal-to-noise ratio (SNR), at the cost of increased energy consumption and reduced speed.

Nevertheless, comparator noise is an important parameter and its estimation is non-trivial, since most of the comparator architectures employed in modern designs rely on a positive feedback loop, in order to speed-up the operation and avoid meta-stability. In this context, the operation of such a circuit is highly non-linear and does not have a constant steady-state operating point. Even though time-domain analysis together with transient noise is possible, it poses a significant computational cost and is extremely time-consuming. In that approach, many comparison cycles must be simulated in order to achieve sufficient accuracy.

There has been some effort to provide better estimation techniques for the comparators noise. In [4], the authors analyze the noise on comparators relying on the use of stochastic differential equations, and are able to provide valuable design guidelines. In [5], the authors provide a linear time-varying (LTV) analysis framework for the same purpose, which is based on the input sensitivity-function (ISF). Also, the latter approach enabled simulation-based verification of comparator noise relying on the use of techniques commonly applied for RF circuits with a periodic steady-state (PSS) operating point [6]. This allows the quick and accurate verification of input referred noise employing an RF circuit simulator bundle, such as SpectreRF, or HSPICE-RF.

Still, optimizing the comparator performance poses a very complex task if multiple performance metrics are considered, due to the large amount of trade-offs involved between specifications. If this is summed up to tight requirements, progressive reduction of minimum design features and complex transistor models, it leads to a tough burden even for experienced designers. On the other hand, considering the increasingly availability of computational resources, it becomes advantageous the use of computer optimization tools to carry out this task.

In this paper, we present a methodology to optimize comparator circuits regarding power, delay and noise. This is done employing a multi-objective evolutionary algorithm together with a simplified method to evaluate the comparator metrics on RF circuit simulators, based on [5]. The accuracy of the method is verified comparing the results with the conventional approach based on transient noise simulation.

This paper is organized as follows. Section 2 provides the theoretical background on the comparator noise estimation method developed. Following, Sect. 3 describes the simulation-based noise measurement procedure, Sect. 4 reports the optimization framework based on evolutionary algorithms and Sect. 5 provides a design example for a comparator architectures widely used in literature. Finally, Sect. 6 presents and discusses the optimization results and Sect. 7 concludes this paper.

2 Review on comparator noise calculation

The input sensitivity function (ISF) \(\varGamma (\tau )\) was initially devised for oscillators in [7], and was later generalized for other classes of periodic circuits in [8]. It expresses the time-varying impulse response for impulses arriving at the time \(\tau\), evaluated at a predefined observation time instant \(t_\mathrm {obs}\). Thus, the output voltage of a LTV system observed at \(t_\mathrm {obs}\) may be written as in (1), demonstrating that the output is a weighted average of the input signal \(v_i\) using \(\varGamma (\tau )\) as the weighting factor.

$$\begin{aligned} v_o (t_\mathrm {obs}) = \int \limits _{-\infty }^{\infty } v_i(\tau )\cdot \varGamma (\tau ) \,\, \mathrm {d} \tau \end{aligned}$$
(1)

Similarly, we are able to develop ISF’s for all the noise contributors on a given circuit and find the total output noise at \(t_\mathrm {obs}\). Thus, assuming only white noise sources, the output noise \(\sigma _{n,o}(t_\mathrm {obs})\) of a system may be expressed as a function of all the \(N\) noise sources as in:

$$\begin{aligned} \sigma _{n,o}(t_\mathrm {obs}) = \sqrt{\sum _{i=0}^{N} \sigma _i^2 \int \limits _{-\infty }^{\infty } \varGamma _i^2(\tau ) \,\, \mathrm {d} \tau } \end{aligned}$$
(2)

Since we are generally interested in the noise power referred to the input of the system, \(\sigma _{n,o}\) has to be divided by its near-DC gain \(G\):

$$\begin{aligned} \sigma _{n,i}(t_\mathrm {obs})=\frac{\sigma _{n,o}(t_\mathrm {obs})}{G} \end{aligned}$$
(3)

The near-DC gain of the system is expressed as (4) and is equal to the area of the ISF.

$$\begin{aligned} G=\frac{v_{o}(t_\mathrm {obs})}{v_{i}(t_\mathrm {obs})} = \int \limits _{-\infty }^{\infty } \varGamma (\tau ) \,\, \mathrm {d} \tau \end{aligned}$$
(4)

In the context of RF circuit simulation, \(\sigma _{n,o}\) and \(G\) may be found through the use of PNOISE and PAC analyses, respectively, once that \(t_\mathrm {obs}\) has been properly chosen. This allows us to find \(\sigma _{n,i}\) using (3). A much more detailed explanation may be found in [5] and [8].

3 Comparator noise measurement

We depict the procedure for simulating the comparator noise in Fig. 1 and 2, where we show the comparator test bench, the expected simulation waveforms and an example of simulation commands for SpectreRF. The requirement to simulate the comparator with PSS/PNOISE analyses is the test setup to be periodic, with the clock signal period equal to the simulation beat period \(T_b\). The input differential voltage source must have a small DC amplitude to avoid meta-stability (we have employed 0.5 mV with success). This same voltage source must also have a non-zero PAC magnitude (we use 1 V), allowing us to calculate the PAC gain later. Then, the measurement procedure follows the steps below:

  1. (1)

    Initially, the periodic steady-state operating point of the circuit must be found through a PSS analysis;

  2. (2)

    Based on the PSS response, the observation time \(t_\mathrm {obs}\) has to be chosen (the procedure is described next);

  3. (3)

    Then, we run a PNOISE and a PAC at the specified \(t_\mathrm {obs}\);

  4. (4)

    The near-DC gain at \(t_\mathrm {obs}\) is found from the PAC response;

  5. (5)

    The output noise power is found applying the result from the PNOISE analysis in (5), where PSD is the noise power spectral density and \(T_b\) is the PSS beat period. We integrate from 0 to \(\frac{1}{2T_b}\) because SpectreRF outputs the single-sided PSD.

    $$\begin{aligned} \sigma _{n,o}(t_\mathrm {obs}) = \sqrt{ \int \limits _{0}^{1/2T_b} \mathrm {PSD} (f,t_\mathrm {obs}) \, \mathrm {d}{f} } \end{aligned}$$
    (5)
  6. (6)

    Thus, \(\sigma _{n,i}\) is found by plugging (5) into (3).

Fig. 1
figure 1

Test setup for the comparator noise measurement using PSS/PNOISE, with example SpectreRF commands

Full size image
Fig. 2
figure 2

Illustrative waveforms

Full size image

An important step of this method to measure comparator input noise is the proper choice of \(t_\mathrm {obs}\). In [5], the authors develop the choice criteria and demonstrate that this choice is not unique, as a range of time points satisfy the requirements. They also present two methods with this purpose: choose \(t_\mathrm {obs}\) where the small-signal gain \(G(t_\mathrm {obs})\) has the maximum value; and choose the time point where the incremental gain \(G^*(t_\mathrm {obs})\) computed from two large-signal responses deviates more than 10 % from \(G(t)\). However, both the proposed methods rely on post-processing, and need the simulator to evaluate PAC and PNOISE at a range of time points for later choice of \(t_\mathrm {obs}\), significantly increasing the simulation time. Therefore, these methods are not ideal for an optimization framework, where the computational time spent on each iteration must be reduced and a one-step approach is preferred.

In this work, we have employed a different and very straightforward approach for choosing \(t_\mathrm {obs}\). SpectreRF allows the evaluation of strobed PAC and PNOISE responses. In other words, we directly calculate the gain and noise when a given trigger signal crosses a specified threshold level. For PNOISE, this is only accessible by the phase modulation jitter (pmjitter) mode that, even though is devised for jitter calculation, also reports the output noise voltage. The trigger signal, in our case, is the differential output signal of the comparator. This is better understood with the example SpectreRF commands shown in Fig. 2. We have set the strobing threshold voltage as \(V_\mathrm {DD}/2\), and we show later in Sect. 6 that this choice provides accurate and reliable results.

4 Multi-objective optimization framework

The optimization framework employed in this work uses a kernel based on the NSGA-II [9] multi-objective genetic algorithm (GA). The GAs are a class of algorithms based on the principles of population dynamics, and allow the use of black-box models (no gradients necessary) in the evaluation function. This characteristic makes these algorithms good candidates for Spice-simulation-in-a-loop circuit sizing. Our custom Python-language implementation allows objectives with the forms of “minimize” and “maximize”, and constraints with the forms of “smaller than X”, “larger than X” and “between X and Y”. We have used a polynomial mutation operator with \(\eta _m=20\) and probability of chromosome mutation of 5 %, and a simulated binary crossover operator with \(\eta _c=20\). A more detailed description of these parameters is found in [9].

5 Design example

Fig. 3
figure 3

Topology of dynamic comparator used for optimization

Full size image

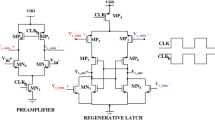
Using the procedure for noise measurement and the multi-objective optimization framework previously described, we have sized the comparator topology shown in Fig. 3. This is a dynamic comparator architecture commonly found in literature, which uses positive feedback to speed-up the operation and avoid meta-stability. The mutation probability of the genetic algorithm was set to 10 % and the crossover probability to 90 %. We constrained the sizing to 156 generations of 64 individuals, resulting in roughly 10,000 evaluations. We have employed a 130 nm CMOS process with 1.2 V supply voltage, and constrained the device widths to \(0.16{-}5\,\upmu \hbox {m}\) and lengths to \(0.12{-}1\,\upmu \hbox {m}\), with discrete steps of 10 nm. The outputs of the comparator under optimization drive 10fF capacitors, that represent a realistic load of a couple of logic gates and some routing. The rise and fall times of the clock signal were kept at 100 ps. The optimization takes into account input referred noise, power (given in terms of the spent energy in a complete cycle of comparison and reset) and delays for comparison and for reset. The objectives and constraints are summarized in Table 1.

Table 1 Comparator goals and constraints
Full size table

6 Results and discussion

We have run the optimization 20 times, with all the parameters set as described in the previous section, in an Intel i7-3770K with 8 GB RAM Linux machine. The average time necessary for a single run is around 27 mins (employing 8 cores), with a standard deviation of around 12 seconds. Thus, the computational time spend for each evaluation is roughly 1.3 seconds. The pareto fronts for all the runs are shown in Fig. 4, with the \(y\)-axis demonstrating the energy spent in a comparison (including reset) and the \(x\)-axis showing the achieved input referred noise. The selection mechanism of the constrained-version of the NSGA-II algorithm guarantees that solutions which do not satisfy the constraints do not appear in the Pareto front. Therefore, all the solutions shown in Fig. 4 have comparison and reset delays smaller than 1 ns, and thus we omit these metrics in the plot to improve readability. Moreover, a small set of randomly picked solutions found by the optimizer is shown in Table 2.

It is noteworthy that for all the solutions, even those that favor a smaller power consumption at the expense of a larger input referred noise, the transistors of the input pair present relatively large sizes. This matches the intuition that the input-pair is the critical part of the circuit when noise is concerned. The input transistors present a large aspect ratio, which consequentially increases the transconductance and decreases thermal noise. The optimizer found solutions with short but non-minimal lengths for the input-pair transistors, which may be related to the dependence of white noise gamma factor \(\gamma\) to the channel length [10].

Moreover, the results in Table 2 reveal aspect ratios for the tail transistor \(W_{\mathrm {tail}}\) that are very small when compared to the aspect ratios of the other transistors, but are still sufficiently large to enable the comparison to be completed during the specified time window. Interestingly, this matches with the design guidelines presented in [4], that show that the input-referred noise is inversely proportional to \(\rho\), given in (6) and to \(\phi\), given in (7).

$$\begin{aligned} \rho&= \frac{\beta _{\mathrm {in}}}{\beta _{\mathrm {tail}}}=\frac{W_{\mathrm {in}}/L_{\mathrm {in}}}{W_{\mathrm {tail}}/L_{\mathrm {tail}}} \end{aligned}$$
(6)
$$\begin{aligned} \phi&= \frac{\beta _{\mathrm {ln}}}{\beta _{\mathrm {tail}}}=\frac{W_{\mathrm {ln}}/L_{\mathrm {ln}}}{W_{\mathrm {tail}}/L_{\mathrm {tail}}} \end{aligned}$$
(7)

In order to prove that the framework have reached solutions close to optimal, we would need to know the optimal Pareto front. However, if we consider the comparator model as a black-box (and perhaps discontinuous), this is only possible if we employ brute-force evaluation of all the design space. This becomes impractical for this problem because the number of parameter combinations is around \(1.4\times 10^{23}\). On the other hand, we can see that the Pareto fronts found in each run are located in the same region in Fig. 4, indicating consistency among the runs.

In order to verify the accuracy of the input referred noise simulation method, we compare the results achieved by the PSS/PNOISE method with the noise achieved with transient noise simulations.

For this reference model, we simulate the same comparator (same transistors dimensions) varying the input differential voltage, while all the other parameters are preserved unchanged. For each value of input voltage, the outputs of 5000 comparisons within a transient simulation with noise frequency constrained to 50 GHz are stored. Then, the simulated probability of “1”s at the comparator output is plotted as function of the input voltage. Finally, assuming that the noise is a white Gaussian process, these values may be fitted to the normal cumulative distribution function (CDF), shown in (8).

$$\begin{aligned} \mathrm {CDF}(x) = \frac{1}{2}\left[ 1 + \mathrm {erf} \left( \frac{x-\mu }{ \sigma \sqrt{2}} \right) \right] \end{aligned}$$
(8)

The procedure is depicted in Fig. 5. The outcome of the curve fitting is the mean value \(\mu\) (deterministic offset) and the standard deviation \(\sigma\) (input referred noise) of the comparator. The procedure for each one of the solutions needs approximately 4 hours in the same machine, which corresponds to roughly 11,000 times more than the PSS/PNOISE method.

We have carried this procedure for the solutions shown in Table 2. The comparison between the results achieved with PSS/PNOISE and the transient noise methods is shown in the bars plot of Fig. 6. The maximum difference in the noise measurements is 9.8 %, and the standard deviation of the differences is 3.47 %.

Fig. 4
figure 4

Pareto fronts achieved in 20 runs of comparator optimization

Full size image
Fig. 5
figure 5

Simulated probability of “1” with different differential input voltages, and curve fitting to the normal CDF

Full size image
Fig. 6
figure 6

Results achieved with PSS/PNOISE and transient noise methods

Full size image
Table 2 Example comparators sized by the optimizer (\(W\)’s and \(L\)’s given in \(\upmu \mathrm {m}\))
Full size table

7 Conclusions

In this paper we have presented a computational framework for sizing and optimization of clocked voltage comparators. The system minimizes input referred noise and power, with the comparator subject to constraints of maximum delays. Regarding the noise calculation, we have employed a simplified method based on simulation techniques that are generally employed for RF simulations, namely PSS and PNOISE analyses. The achieved solutions conform with the reference noise model that is based on transient noise simulation. The proposed framework outputs a set of 64 different comparators in the Pareto front that trade-off power and input referred noise, taking about 27 mins in a conventional workstation. The characteristics of the proposed optimization framework allow to drastically reduce the effort on the design cycle of a comparator circuit.