Robust Bayes estimation using the density power divergence

Abstract

The ordinary Bayes estimator based on the posterior density can have potential problems with outliers. Using the density power divergence measure, we develop an estimation method in this paper based on the so-called “$R^{(\alpha )}$-posterior density”; this construction uses the concept of priors in Bayesian context and generates highly robust estimators with good efficiency under the true model. We develop the asymptotic properties of the proposed estimator and illustrate its performance numerically.

1 Introduction

Among different statistical paradigms, the Bayesian approach is logical in many ways and it is often easy to communicate with others in this language while solving real-life statistical problems. However, the ordinary Bayes estimator, which is based on the usual posterior density, can have potential problems with outliers. Recently Hooker and Vidyashankar (2014), hereafter HV, proposed a methodology for robust inference in the Bayesian context using disparities (Lindsay 1994) yielding efficient and robust estimators. It is a remarkable proposal and has many nice properties. However, there are also some practical difficulties which may limit its applicability. The proposal involves the use of a nonparametric kernel density estimator, and hence the associated issues and difficulties such as bandwidth selection, run-time requirement, boundary problem for densities with bounded support and convergence problems for high dimensional data have to be dealt with. In addition, disparities are not additive in the data and hence the posteriors in this case cannot be simply augmented when new observations are available, but the whole posterior has to be computed afresh (unlike likelihood-based posteriors). Clearly other robust estimators can still be useful in this context.

In this paper we will develop an alternative robust Bayes estimator based on the density power divergence (DPD) measure proposed by Basu et al. (1998), hereafter BHHJ. The benefits of the proposal will be discussed and defined in the subsequent sections. We expect that the proposed estimator will be free from the issues considered in the previous paragraph.

The rest of the paper is organized as follows. In Sect. 2 we describe the “$R^{(\alpha )}$-Posterior density” and related estimators. Section 3 provides the asymptotic properties of the estimator. We describe the robustness properties of the proposed estimator under contamination of data and the prior in Sects. 4 and 5, respectively. In Sect. 6 we present some numerical illustration to demonstrate the performance of the estimators and to substantiate the theory developed. Concluding remarks are given in Sect. 7.

2 The robustified posterior density

Suppose $X_1, \ldots , X_n$ are independently and identically distributed (i.i.d.) observations from the true density $g$, which is modeled by the parametric class of densities $\{ f_\theta : \theta \in \varTheta \}$. BHHJ defined the density power divergence (DPD) measure as

$$\begin{aligned} \mathrm{d}_\alpha (g,f_\theta ) = \int f_\theta ^{1+\alpha } - \frac{1+\alpha }{\alpha } \int f_\theta ^\alpha g + \frac{1}{\alpha } \int g^{1+\alpha }, \quad \text{ if } \ \alpha > 0, \end{aligned}$$

and

$$\begin{aligned} \mathrm{d}_0(g,f_\theta ) = \lim _{\alpha \rightarrow 0} \mathrm{d}_\alpha (g,f_\theta ) = \int g \log (g/f_\theta ). \end{aligned}$$

The measure is a function of a single tuning parameter $\alpha$. Since the last term of the divergence is independent of $\theta$, the minimum DPD estimator with $\alpha > 0$ is obtained as the minimizer of $\int f_\theta ^{1+\alpha } - \frac{1+\alpha }{\alpha } \int f_\theta ^\alpha g$ or, equivalently, as the maximizer of $\frac{1+\alpha }{\alpha } \int f_\theta ^\alpha g - \int f_\theta ^{1+\alpha }$. Then the minimum DPD estimator with $\alpha > 0$ is obtained as the maximizer of

$$\begin{aligned} Q_n^{(\alpha )}(\theta )&= \frac{n}{1+\alpha } {\left[ \frac{1+\alpha }{\alpha } \int f_\theta ^\alpha \mathrm{d}G_n - \int f_\theta ^{1+\alpha } \right] } \nonumber \\&= {\left( \frac{1}{\alpha } \right) } \sum _{i=1}^n f_\theta ^\alpha (X_i) - \frac{n}{1+\alpha } \int f_\theta ^{1+\alpha } = \sum _{i=1}^n q_\theta (X_i), \quad \text{ say }, \end{aligned}$$

(1)

where $q_\theta (y) = (\frac{1}{\alpha }) f_\theta ^\alpha (y) - \frac{1}{1+\alpha } \int f_\theta ^{1+\alpha }$ and $G_n$ is the empirical distribution based on the data. However, for $\alpha = 0$, the corresponding objective function to be maximized will be $Q_n^{(0)}(\theta ) = n \int \log (f_\theta ) \mathrm{d}G_n = \sum _{i=1}^n \log (f_\theta (X_i))$ which is the usual log-likelihood function that is maximized by the efficient but non-robust maximum likelihood estimator (MLE). We will refer to $Q_n^{(\alpha )}(\theta )$ as the $\alpha$-likelihood. There is a trade-off between robustness and efficiency with a larger $\alpha$ being associated with greater robustness but reduced efficiency. We propose to replace the log-likelihood with $Q_n^{(\alpha )}$ and study the robustness properties of the associated posterior and the corresponding estimators in the Bayesian context.

In case of Bayesian estimation, the inference is based on the posterior density which is defined by the Bayes formula as $\pi (\theta |X) = \frac{\pi (X|\theta )\pi (\theta )}{\int \pi (X|\theta )\pi (\theta ) \mathrm{d}\theta }$ where $\pi (\theta )$ is the prior density of $\theta$ and $\pi (X|\theta ) = \prod _{i=1}^n f_\theta (X_i) = \exp (\mathrm {Log~ Likelihood})$. Our exercise produces the quantity

$$\begin{aligned} \pi _R^{(\alpha )}(\theta |X) = \frac{\exp (Q_n^{(\alpha )}(\theta ))\pi (\theta )}{\int \exp (Q_n^{(\alpha )}(\theta )) \pi (\theta ) \mathrm{d}\theta }, \end{aligned}$$

(2)

which we will refer to as the $\alpha$-robustified posterior density or simply as the $R^{(\alpha )}$-posterior. Note that the $R^{(\alpha )}$-posterior is a proper probability density for any $\alpha \ge 0$ and $R^{(0)}$-posterior is just the ordinary posterior. As in the usual Bayesian estimation, all the inference about $\theta$ can be done based on this $R^{(\alpha )}$-posterior. Thus, for the loss function $L( \cdot , \cdot )$, the corresponding $\alpha$-robustified Bayes estimator, or the $R^{(\alpha )}$-Bayes estimator, is obtained as

$$\begin{aligned} \hat{\theta }_n^{(\alpha )L} = \arg \min _t \int L(\theta , t) \pi _R^{(\alpha )}(\theta |X) \mathrm{d}\theta . \end{aligned}$$

(3)

Clearly $R^{(0)}$-Bayes estimators are again the usual Bayes estimators. For the squared error loss, the corresponding $R^{(\alpha )}$-Bayes estimator is the Expected $R^{(\alpha )}$-Posterior Estimator (ERPE) given by

$$\begin{aligned} \hat{\theta }_n^{(\alpha )e} = \int \theta \pi _R^{(\alpha )}(\theta |X) \mathrm{d}\theta . \end{aligned}$$

(4)

For notational simplicity we will, generally, omit the superscript $\alpha$.

Clearly, inference about $\theta$ based on the $R^{(\alpha )}$-posterior density does not require any nonparametric kernel density estimation. Further, since the quantity $Q_n^{(\alpha )}(\theta )$ can be expressed as a sum of $n$ i.i.d. terms, we can express the $R^{(\alpha )}$-posterior density alternatively as $\pi _R(\theta |X) \propto [ \prod _{i=1}^n \exp (q_\theta (X_i))] \pi (\theta )$. Thus, if some new data $X_{n+1}, \ldots , X_m$ are obtained, the corresponding $R^{(\alpha )}$-posterior for the combined data $X_1, \ldots , X_m$ can be obtained using the $R^{(\alpha )}$-posterior for the first $n$ observations $\pi _R(\theta |X_1, \ldots , X_n)$ as the prior for $\theta$ (like the usual likelihood-based posterior) which gives

$$\begin{aligned} \pi _R(\theta |X_1, \ldots , X_m) \propto \left[ \prod _{i= n+1}^m \exp (q_\theta (X_i)) \right] \pi _R(\theta | X_1, \ldots , X_n). \end{aligned}$$

The $R^{{(\alpha )}}$-posterior is not the true posterior in the usual probabilistic sense. However, the main spirit of the Bayesian paradigm is to update prior information on the basis of observed data. This objective is fulfilled in this case, and our use of the name $R^{(\alpha )}$-posterior and $R^{(\alpha )}$-Bayes estimator is consistent with this spirit. In the following, wherever the context makes it clear, we will drop the superscript $\alpha$ from the notation $Q_n^{(\alpha )}$.

Also note that the $R^{(\alpha )}$-posterior defined above is in fact a pseudo-posterior. There has been substantial interest in recent times in developing several pseudo-posteriors for solving different problems. For example, the Gibbs posterior (Zhang 1999) $\hat{\Pi }$ is defined as

$$\begin{aligned} \hat{\Pi }(\theta ) = \frac{\exp (-\lambda R_n(\theta ))\pi (\theta )}{\int \exp (-\lambda R_n(\theta ))\pi (\theta )\mathrm{d}\theta }, \end{aligned}$$

where $\pi (\theta )$ is the prior for $\theta$, $\lambda$ is a scalar parameter and $R_n(\theta )$ is an empirical risk function that may or may not be additive. The Gibbs posterior is seen to perform better with respect to the risk incurred under model misspecification, since it uses the nonparametric estimate of the risk function directly; see Jiang and Tanner (2008, 2010). There has been a lot of research on the properties and applications of the Gibbs posterior; see Li et al. (2014); Jiang and Tanner (2013), among others, for details. Another important approach for constructing pseudo-posteriors is the PAC-Bayesian approach (Catoni 2007) that was highly successful in the supervised classification scenario. The recent developments in this area include Alquier and Lounici (2011), Rigollet and Tsybakov (2011), etc. Many of these approaches have found application in fields such as data mining, econometrics and many others. The robust $R^{(\alpha )}$-posterior approach presented in this paper is closely related to these approaches in terms of its basic structure; however, the effect and the purpose of the $R^{(\alpha )}$-posterior is quite different from that of the others. Our approach has a strong connection with the Bayesian philosophy, but the PAC approach only has a weak connection with the latter. The Gibbs posterior and $R^{(\alpha )}$-posterior have an interesting relationship similar to the relation between the nonparametric and robust statistics; the first one minimizes parametric model assumptions while the second one provides protection against model misspecifications, often manifested by large outliers. In this paper we describe the $R^{(\alpha )}$-posterior and its advantages mainly with respect to the robustness point of view under the spirit of Bayesian paradigm; it will be seen to successfully ignore the potential outliers with respect to the assumed model family and give much more importance to any subjective prior belief compared to the usual Bayes approach.

3 Asymptotic efficiency

Consider the set up of Sect. 2. Let $\hat{\theta }$ be the minimum density power divergence estimator (MDPDE) of $\theta$ based on $X_1, \ldots , X_n$ corresponding to the tuning parameter $\alpha$, which we will generally suppress in the following; also let $\theta ^g$ be the best fitting parameter which minimizes the DPD measure between $g$ and the model densities over $\theta \in \varTheta$. Let $\nabla$ and $\nabla ^2$ denote the first and second derivative with respect to $\theta$, and let $\nabla _{jkl}$ represent the indicated partial derivative. Consider the matrix $J_\alpha (\theta )$ defined by

$$\begin{aligned} J_\alpha (\theta )&= - E_g[ \nabla ^2 q_\theta ^{(\alpha )}(X)] \nonumber \\&= \frac{1}{1+\alpha } E_g\left[ \nabla ^2 \left\{ \int f_\theta ^{1+\alpha } - \left( \frac{1+\alpha }{\alpha }\right) f_\theta ^\alpha (X) \right\} \right] , \end{aligned}$$

(5)

which can be (strongly) consistently estimated by $\hat{J}_\alpha (\hat{\theta }_n) = - \frac{1}{n}\nabla ^2 Q_n(\hat{\theta }_n)$. We make the following assumptions for proving the asymptotic normality of the posterior.

• (E1) Suppose Assumptions (D1)–(D5) of Basu et al. (2011) hold. These imply that the MDPDE $\hat{\theta }_n$ of $\theta ^g$ is consistent.

• (E2) For any $\delta > 0$, with probability one,

  $$\begin{aligned} \sup _{||\theta - \theta ^g|| > \delta } ~ \frac{1}{n} (Q_n(\theta ) - Q_n(\theta ^g)) < - \epsilon , \end{aligned}$$

  for some $\epsilon > 0$ and for all sufficiently large $n$.

• (E3) There exists a function $M_{jkl}(x)$ such that

  $$\begin{aligned} |\nabla _{jkl}q_\theta (x)| \le M_{jkl}(x) \quad \forall \theta \in \omega , \end{aligned}$$

  where $E_g[M_{jkl}(X)] = m_{jkl} < \infty$    for all $j, k$ and $l$.

Note that the above assumptions are not very hard to examine for most standard parametric models. The conditions (E1) and (E3) are in fact common in the context of minimum density power divergence estimation and are shown to hold for several parametric models in Basu et al. (2011). The condition (E2) is specific to the case of the DPD-based posterior; however, it is in fact a routine generalization of the similar condition needed for the asymptotic normality of the usual posterior (see Ghosh and Ramamoorthi 2003). Using similar arguments as in the case of the usual likelihood-based posterior one can easily show that the DPD-based condition (E2) holds for most common parametric families. We will present a brief argument to show that it holds for the normal model $f_\theta \equiv N(\theta , \sigma ^2)$ with known $\sigma$ and $\alpha >0$. Let $\theta ^g$ be the true parameter value. In this particular case, $Q_n(\theta ) = \frac{1}{\alpha (\sqrt{2\pi }\sigma )^\alpha } \sum _{i=1}^n \mathrm{e}^{-\frac{\alpha (\theta -X_i)^2}{2\sigma ^2}} - n \zeta _\alpha ,$ where $\zeta _\alpha = (\sqrt{2\pi }\sigma )^{-\alpha } (1+\alpha )^{-\frac{3}{2}}$. Thus,

$$\begin{aligned} \frac{1}{n} (Q_n(\theta ) - Q_n(\theta ^g))&= \frac{1}{\alpha (\sqrt{2\pi }\sigma )^\alpha } \frac{1}{n} \sum _{i=1}^n \left[ \mathrm{e}^{-\frac{\alpha \left( \theta -X_i\right) ^2}{2\sigma ^2}} - \mathrm{e}^{-\frac{\alpha (\theta ^g-X_i)^2}{2\sigma ^2}}\right] \\&\le - \frac{1}{\alpha \left( \sqrt{2\pi }\sigma \right) ^\alpha } \frac{1}{n} \sum _{i=1}^n \left[ \frac{\alpha (\theta -X_i)^2}{2\sigma ^2}-\frac{\alpha (\theta ^g-X_i)^2}{2\sigma ^2}\right] \mathrm{e}^{-K}, \end{aligned}$$

for a small positive constant $K$. Here we have used the mean value theorem on the function $\mathrm{e}^{-z}$. However,

$$\begin{aligned}&- \frac{1}{\alpha (\sqrt{2\pi }\sigma )^\alpha } \frac{1}{n} \sum _{i=1}^n \left[ \frac{\alpha (\theta -X_i)^2}{2\sigma ^2}-\frac{\alpha (\theta ^g-X_i)^2}{2\sigma ^2}\right] \mathrm{e}^{-K}\\&\quad = - \frac{\mathrm{e}^{-K}}{2\sigma ^2 (\sqrt{2\pi }\sigma )^\alpha } \left( 2\bar{X} - \theta - \theta ^g\right) (\theta ^g - \theta ) \\&\quad \rightarrow - \frac{\mathrm{e}^{-K}}{2\sigma ^2 (\sqrt{2\pi }\sigma )^\alpha } (\theta ^g - \theta )^2 < 0, \end{aligned}$$

almost surely as $n \rightarrow \infty$, under the model distribution $N(\theta ^g, \sigma ^2)$, by strong law of large numbers. So, for all sufficiently large $n$, we have, with probability one under $N(\theta ^g, \sigma ^2)$,

$$\begin{aligned} \frac{1}{n} (Q_n(\theta ) - Q_n(\theta ^g)) < - \frac{\mathrm{e}^{-K}}{4\sigma ^2 (\sqrt{2\pi }\sigma )^\alpha } (\theta ^g - \theta )^2. \end{aligned}$$

Then it follows that, given any $\delta >0$, the condition (E2) holds with $\epsilon = \frac{\mathrm{e}^{-K}\delta ^2}{8\sigma ^2 (\sqrt{2\pi }\sigma )^\alpha }$. Now, we will present the main theorem of this section providing the asymptotic normality of the robust $R^{(\alpha )}$-posterior under above conditions.

Theorem 1

Suppose Assumptions (E1)–(E3) hold and let $\pi (\theta )$ be any prior which is positive and continuous at $\theta ^g$. Then, with probability tending to one,

$$\begin{aligned} \lim _{n\rightarrow \infty } ~ \int \left| \pi _n^{*R}(t) - \left( \frac{|J_\alpha (\theta ^g)|}{2\pi }\right) ^{p/2} \mathrm{e}^{-\frac{1}{2} t' J_\alpha (\theta ^g)t}\right| = 0, \end{aligned}$$

(6)

where $\pi _n^{*R}(t)$ is the $R^{(\alpha )}$-posterior density of $t = \sqrt{n} (\theta - \hat{\theta }_n)$ given the data $X_1, \ldots , X_n$. Also, the above holds with $J_\alpha (\theta ^g)$ replaced by $\hat{J}_\alpha (\hat{\theta }_n)$.

Note that the above theorem about asymptotic normality of $R^{(\alpha )}$-posterior is quite similar to the Bernstein–von Mises (BVM) theorem on the usual posterior (see Ghosh et al. 2006; Ghosh and Ramamoorthi 2003) except that here we are considering convergence with probability tending to one (convergence in probability). Thus the proof of the above theorem is in line with that of BVM results with some required modifications. In order that the flow of the paper is not arrested, we will present the proof of this theorem in the appendix. Our next theorem gives the asymptotic properties of the ERPE.

Theorem 2

In addition to the conditions of the previous theorem assume that the prior $\pi (\theta )$ has finite expectation. Then the Expected $R^{(\alpha )}$-Posterior Estimator (ERPE) $\hat{\theta }_n^e$ satisfies

• (a) $\displaystyle \sqrt{n}(\hat{\theta }_n^e - \hat{\theta }_n) \displaystyle \mathop {\rightarrow }^{P} 0 \ \text{ as } \ n \rightarrow \infty$.

• (b) If, further, $\displaystyle \sqrt{n}(\hat{\theta }_n - \theta ^g) \mathop {\rightarrow }^{D} N(0, \Sigma (\theta ^g))$ for some positive definite $\Sigma (\theta ^g)$, then $\displaystyle \sqrt{n}( \hat{\theta }_n^e - \theta ^g) \mathop {\rightarrow }^{D} N(0, \Sigma (\theta ^g))$.

It was proved in Basu et al. (2011) that under the conditions (D1)–(D5), we have $\displaystyle \sqrt{n}( \hat{\theta }_n - \theta ^g) \mathop {\rightarrow }^D N(0,J^{-1}K J^{-1} )$, where $J$ and $K$ are as defined in Equations (9.14) and (9.15) of Basu et al. (2011), respectively. Thus, by the above theorem, the ERPE $\hat{\theta }_n^e$ also has the same asymptotic distribution.

Remark 1

Instead of assuming the simple consistency of the MDPDE $\hat{\theta }_n$ of $\theta ^g$ in Assumption (E1), if we assume the condition(s) under which this MDPDE is strongly consistent, then we can prove, along similar lines, all the convergence results of this section as almost sure convergence.

4 Robustness properties: contamination in data

The major advantage of inference based on the density power divergence is that the generated robustness properties entail very little loss in statistical efficiency for small values of $\alpha$. In the Bayesian context we use the data as well as the prior as our input. So, the robustness of the estimators obtained can be with respect to the data input or with respect to the choice of prior or both. In the present section, we will consider the contamination in the first input, namely the data input, and explore the robustness properties of the corresponding estimators using the Influence Function (Hampel 1974) of the estimators.

Let the sample data $X_1, \ldots , X_n$ be generated from the true distribution $G$ which we will model by the family $\{ F_\theta : \theta \in \varTheta \}$. Let $g$ and $f_\theta$ be the corresponding densities and $\pi (\theta )$ be the prior on the unknown parameter $\theta$. In the spirit of $Q_n^{(\alpha )}(\theta )$ let us define

$$\begin{aligned} n Q^{(\alpha )}(\theta ; G,F_\theta ) = n \left[ \frac{1}{\alpha } \int f_\theta ^\alpha (x) \mathrm{d}G(x) - \frac{1}{1+\alpha } \int f_\theta ^{1+\alpha }(x) \mathrm{d}x \right] . \end{aligned}$$

We will consider the $R^{(\alpha )}$-posterior density as a functional of the true data generating distribution $G$, besides considering it as a function of only the unknown parameter $\theta$ as

$$\begin{aligned} \pi _\alpha (\theta ; G) = \frac{ \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta )}{\int \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta }. \end{aligned}$$

(7)

For a fixed sample size $n$, the $R^{(\alpha )}$-Bayes functional with respect to the loss function $L(\cdot ,\cdot )$ is given by

$$\begin{aligned} T_n^{(\alpha )L} (G) = \arg \min _t \ \frac{\int L(\theta , t) \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta }{\int \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta }. \end{aligned}$$

(8)

In particular, under the squared error loss function, the Expected $R^{(\alpha )}$-Posterior (ERP) functional is defined as

$$\begin{aligned} T_n^{(\alpha )e} (G) = \frac{\int \theta \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta }{\int \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta }. \end{aligned}$$

(9)

Note that unlike most classical statistical functionals under the i.i.d. setup, here the functional explicitly depends on the sample size $n$. Thus, in this context our influence function will also depend on the sample size explicitly giving the effect of the contamination under a fixed sample size. This is akin to influence function for the robust Bayes estimators using disparities proposed by HV. However, in some special cases, we can derive the asymptotic result independently of $n$ by considering the influence function at the fixed sample size and taking its asymptotic expansion as $n$ tends to infinity.

Now we consider the contaminated model $H_\epsilon = (1-\epsilon ) G + \epsilon \Lambda _y$ where $\epsilon$ is the contamination proportion and $\Lambda _y$ is the contaminating distribution degenerate at $y$. Then the influence function of the $R^{(\alpha )}$-Bayes functional $T_n^{(\alpha )L} (\cdot )$ for the fixed sample size $n$ at the distribution $G$ is defined as

$$\begin{aligned} IF_n(y,T_n^{(\alpha )L},G) = \frac{\partial }{\partial \epsilon } T_n^{(\alpha )L} (H_\epsilon ) |_{\epsilon =0}. \end{aligned}$$

4.1 Influence function of expected $R^{(\alpha )}$-posterior estimator

Let us first consider the simplest $R^{(\alpha )}$-Bayes estimator under the squared error loss function, namely the Expected $R^{(\alpha )}$-Posterior Estimator (ERPE). Routine differentiation shows that the influence function of the ERPE at the fixed sample size is given by

$$\begin{aligned} IF_n(y,T_n^{(\alpha )e},G) = n ~ \text{ Cov }_{P_R} (\theta , k_\alpha (\theta ; y ,g)), \end{aligned}$$

(10)

where $\text{ Cov }_{P_R}$ is the covariance under the $R^{(\alpha )}$-posterior distribution (the subscript “$P_R$” is used to denote the $R^{(\alpha )}$-posterior) and

$$\begin{aligned} k_\alpha (\theta ; y ,g) = \frac{\partial }{\partial \epsilon } Q^{(\alpha )}(\theta ; H_\epsilon , F_\theta )|_{\epsilon =0} = \frac{1}{\alpha } \left[ f_\theta ^\alpha (y) - \int f_\theta ^\alpha g \right] , \end{aligned}$$

(11)

whenever $\alpha >0$. However, for $\alpha =0$, we have $k_0(\theta ; y ,g) = \log f_\theta (y) - \int g \log f_\theta$ and hence the influence function of the Expected $R^{(0)}$-Posterior (ERP) estimator i.e. the usual posterior mean at the fixed sample size $n$ can also be derived from above Eq. (10) substituting $\alpha =0$.

However, in this case we can also derive an asymptotic version of the influence functions that gives us clearer picture about the differences in the robustness of the proposed ERPE with respect to the choice of $\alpha$ with the usual posterior mean at $\alpha =0$. Let us denote $\bar{\theta } = E_{P_R}[\theta ]$, where the expectation is with respect to the $R^{(\alpha )}$-posterior distribution; using the Taylor series expansion of $k_\alpha (\theta ; y ,g)$ around $\bar{\theta }$, we get the following theorem about the asymptotic expansion of the influence function of the ERPE.

Theorem 3

Assume that Assumptions (E1)–(E3) hold and the matrix $J_\alpha (\theta )$ defined in Eq. (5) is positive definite. Further assume that the true data generating density $g$ is such that there exists a best fitting parameter $\theta ^g$ minimizing the expected squared error loss under the $R^{(\alpha )}$-posterior distribution. Then the influence function of the Expected $R^{(\alpha )}$-Posterior (ERP) estimator $T_n^{(\alpha )e}$ at the fixed sample size $n$ has the following asymptotic expansion as $n \rightarrow \infty$:

$$\begin{aligned} IF_n(y,T_n^{(\alpha )e},G) = J_\alpha ^{-1}(\theta ^g)\left[ f_{\theta ^g}^\alpha (y) u_{\theta ^g}(y) - \int f_{\theta ^g}^\alpha g u_{\theta ^g}\right] + o_P(n^{-1/2}). \end{aligned}$$

(12)

It is interesting to note that the first expression in the RHS of the Eq. (12) is independent of the choice of the prior $\pi (\theta )$ and is exactly equal to the influence function of the minimum density power divergence estimator. This fact is quite expected as we have seen that the ERPE and the MDPDE are asymptotically equivalent and hence the influence of contamination in data should also be similar for both the estimators for large sample sizes. Further the influence function for large sample sizes is seen to be independent of the prior, which is again expected as the large volume of the data makes the effect of the prior insignificant.

It also turns out that for most of the common models the large sample influence function of the ERPE given by the RHS of the Eq. (12) is bounded for all $\alpha >0$ and unbounded for $\alpha =0$. This leads us to infer that for large samples the ERPE is robust for all $\alpha > 0$ whereas the usual posterior mean corresponding to $\alpha =0$ is not so.

4.2 Influence function of the general $R^{(\alpha )}$-Bayes estimator

Now we will derive the influence function of the general $R^{(\alpha )}$-Bayes estimator with respect to the general loss functions $L(\cdot ,\cdot )$. We will first assume the differentiability of the loss function with respect to its second argument. Note that the $R^{(\alpha )}$-Bayes functional $T_n^{(\alpha )L} (G)$ with respect to the loss function $L(\cdot ,\cdot )$ defined in Eq. (8) is nothing but the minimizer of some function of $t$. Upon differentiating with respect to $t$, the $R^{(\alpha )}$-Bayes estimator can also be obtained as the solution of the estimation equation

$$\begin{aligned} \frac{\partial }{\partial t} \left[ \frac{\int L(\theta , t) \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta }{\int \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta } \right] = 0. \end{aligned}$$

Thus, we must have

$$\begin{aligned} \frac{\partial }{\partial t} \left[ \frac{\int L(\theta , t) \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta }{\int \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta }\right] \Bigg |_{t=T_n^{(\alpha )L} (G)} = 0, \end{aligned}$$

or,

$$\begin{aligned} \int L'(\theta , T_n^{(\alpha )L} (G)) \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta = 0, \end{aligned}$$

(13)

where we denote

$$\begin{aligned} L'(\theta , T_n^{(\alpha )L} (G))= \frac{\partial L(\theta , t)}{\partial t}\Bigg |_{t=T_n^{(\alpha )L} (G)}. \end{aligned}$$

Now to derive the influence function of the $R^{(\alpha )}$-Bayes estimator we replace $G$ by the contaminated density $H_\epsilon$ in the estimating Eq. (13), differentiate with respect to $\epsilon$, and evaluate at $\epsilon =0$. Thus, we get the influence function of the $R^{(\alpha )}$-Bayes estimator at the fixed sample size $n$ given by

$$\begin{aligned} IF_n(y,T_n^{(\alpha )L},G)&= - n \frac{\int L'(\theta , T_n^{(\alpha )L}(G)) k_\alpha (\theta ; y ,g) \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta }{\int L''(\theta , T_n^{(\alpha )L}(G)) \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta } \nonumber \\&= - n ~ \frac{E_{P_R} \left[ L'(\theta , T_n^{(\alpha )L}(G)) k_\alpha (\theta ; y ,g)\right] }{E_{P_R} \left[ L''(\theta , T_n^{(\alpha )L}(G))\right] }, \end{aligned}$$

(14)

where the expectation in the last line is under the $R^{(\alpha )}$-posterior distribution. In particular at $\alpha =0$, we will get the fixed sample influence function of the usual Bayes estimator under the general loss function.

Note that the above expression of the influence function of the general $R^{(\alpha )}$-Bayes estimator is valid only for the loss functions which are twice differentiable with respect to their second argument. In particular, for squared error loss, we will recover the influence function of the ERPE derived in Eq. (10) from Eq. (14). But this does not include two other famous non-differentiable loss functions, namely the absolute error loss function and the zero-one loss function. However, we can separately derive the influence function for the corresponding $R^{(\alpha )}$-Bayes estimators.

The $R^{(\alpha )}$-Bayes estimator corresponding to the absolute error loss function $L(\theta ,t) = |\theta - t|$, denoted by $T_n^{(\alpha )a}(G)$, say, is nothing but the median of the $R^{(\alpha )}$-posterior distribution. Hence, it is defined by the estimating equation

$$\begin{aligned} \int _{-\infty }^{T_n^{(\alpha )a}(G)} \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta = \int _{T_n^{(\alpha )a}(G)}^{+\infty } \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta . \end{aligned}$$

(15)

Thus, substituting the contaminated distribution $H_\epsilon$ in place of the true distribution $G$ in the above estimating equation and differentiating it with respect to $\epsilon$ at $\epsilon =0$, we get the influence function of the $R^{(\alpha )}$-Bayes estimator corresponding to the absolute error loss function which turns out to be

$$\begin{aligned} { IF}_n(y,T_n^{(\alpha )a},G)\!=\! - n \frac{\int \mathrm{sgn}(\theta - T_n^{(\alpha )a}(G)) k_\alpha (\theta ; y ,g) \mathrm{e}^{n Q^{(\alpha )}(\theta ; G,F_\theta )} \pi (\theta ) \mathrm{d}\theta }{2 \mathrm{e}^{n Q^{(\alpha )}(T_n^{(\alpha )a}(G); G,F_\theta )} \pi (T_n^{(\alpha )a}(G))}, \qquad \end{aligned}$$

(16)

where sgn(.) is the signum function.

Further, the $R^{(\alpha )}$-Bayes estimators corresponding to the zero-one loss function denoted, say, by $T_n^{(\alpha )m}(G)$, is the mode of the $R^{(\alpha )}$-posterior distribution. We can also derive its fixed sample influence function similarly.

4.3 Influence on the overall $R^{(\alpha )}$-posterior distribution

In the Bayesian literature it is common to report the whole posterior distribution instead of only the summary measures. Thus, it will be of interest to investigate the influence of the contaminated data on the overall posterior distribution as a whole. However, since there is no standard literature about the influence function of a overall density function, we will here try to quantify these influences by a couple of new (albeit similar) approaches.

Consider the change $\pi _\alpha (\theta ; H_\epsilon ) - \pi _\alpha (\theta ; G)$ in the $R^{(\alpha )}$-posterior density at the contaminated distribution $H_\epsilon$ at the true distribution $G$ and consider the measure of local change as the limit $\lim _{\epsilon \downarrow 0} \frac{\pi _\alpha (\theta ; H_\epsilon ) - \pi _\alpha (\theta ; G)}{\epsilon },$ which exists under very weaker assumption on the models. Routine calculation shows that the above limit equals

$$\begin{aligned}&\lim _{\epsilon \downarrow 0} \frac{\pi _\alpha (\theta ; H_\epsilon ) - \pi _\alpha (\theta ; G)}{\epsilon } = \frac{\partial }{\partial \epsilon } \pi _\alpha (\theta ; H_\epsilon ) \big |_{\epsilon =0} \nonumber \\&\quad = \pi _\alpha (\theta ; G) n [ k_\alpha (\theta ; y ,g) - E_{P_R}\{k_\alpha (\theta ; y ,g)\}], \end{aligned}$$

(17)

where the last expectation is taken under the true $R^{(\alpha )}$-posterior distribution $\pi _\alpha (\theta ; G)$. Note that this limit gives us a similar kind of interpretation as the influence function of a general statistical functional at the fixed sample size. Specially, whenever the function

$$\begin{aligned} \mathcal {I}_\alpha (\theta ;y;G) = n\,\,\, [ k_\alpha (\theta ; y ,g) - E_{P_R}\{k_\alpha (\theta ; y ,g)\}] \end{aligned}$$

(18)

in the RHS of Eq. (17) remains bounded, the limiting change in the $R^{(\alpha )}$-posterior density due to contamination in the data remains in the bounded neighborhood of the true posterior density and hence gives robust inference about the true posterior. On the other hand, whenever the function $\mathcal {I}_\alpha (\theta ;y;G)$ becomes unbounded, the corresponding change in the $R^{(\alpha )}$-posterior density also becomes infinite indicating that the inference based on the posterior density at the contaminated model will then be highly unstable. Also the expectation of the function $\mathcal {I}_\alpha (\theta ;y;G)$ under the true $R^{(\alpha )}$-posterior density is zero. Under the true model, therefore, there should not be any expected change in the posterior density due to limiting contamination. We will thus denote this function $\mathcal {I}_\alpha (\theta ;y;G)$ as the pseudo-influence function of the $R^{(\alpha )}$-posterior density at the finite sample size $n$.

Based on the measure $\mathcal {I}_\alpha (\theta ;y;G)$ we can now also define local and global measures of sensitivity of the $R^{(\alpha )}$-posterior density with respect to the contamination in data, respectively, by $\gamma _\alpha (y) = \sup _\theta \mathcal {I}_\alpha (\theta ;y;G),$ for all contamination point $y$ and $\gamma _\alpha ^* = \sup _y \gamma _\alpha (y) = \sup _y \sup _\theta \mathcal {I}_\alpha (\theta ;y;G).$ They have standard robustness implications for the $R^{(\alpha )}$-posterior.

To further justify the use of the pseudo-influence function, we consider some statistical divergences between the $R^{(\alpha )}$ posterior densities at the contaminated and true distribution as in the case of Bayesian robustness with perturbation priors (eg. Gustafson and Wasserman 1995; Gelfand and Dey 1991). In particular we consider the $\phi$-divergences which have been used in the context of Bayesian robustness by Dey and Birmiwal (1994). The $\phi$ divergence between densities $\nu _1$ and $\nu _2$ is defined by $\rho (\nu _1, \nu _2) = \int \phi (\displaystyle \frac{\nu _1}{\nu _2})\nu _2$, where $\phi$ is a smooth convex function with bounded first and second derivatives near 1 with $\phi (1) = 0$. Accordingly, we will consider the divergence $\rho (\pi _\alpha (\theta ; H_\epsilon ), \pi _\alpha (\theta , G))$. Since $\lim _{\epsilon \downarrow 0}\rho (\pi _\alpha (\theta ; H_\epsilon ), \pi _\alpha (\theta , G)) = 0$, we will magnify the divergence by $\epsilon$. The form of the $\phi$-divergence and standard differentiation then yields the following result.

$$\begin{aligned} \lim _{\epsilon \downarrow 0} \frac{\rho (\pi _\alpha (\theta ; H_\epsilon ), \pi _\alpha (\theta ; G))}{\epsilon }&= \frac{\partial }{\partial \epsilon } \rho (\pi _\alpha (\theta ; H_\epsilon ), \pi _\alpha (\theta ; G)) |_{\epsilon =0} \nonumber \\&= \phi '(1) E_{P_R}[\mathcal {I}_\alpha (\theta ;y;G)] = 0. \end{aligned}$$

(19)

However, if we magnify the divergence by $\epsilon ^2$, then we get a non-zero limit as follows:

$$\begin{aligned} \lim _{\epsilon \downarrow 0} ~ \frac{\rho (\pi _\alpha (\theta ; H_\epsilon ), \pi _\alpha (\theta ; G))}{\epsilon ^2}&= \frac{\partial ^2}{\partial ^2\epsilon }\rho (\pi _\alpha (\theta ; H_\epsilon ), \pi _\alpha (\theta ; G))|_{\epsilon =0} \nonumber \\&= \phi ''(1) E_{P_R}[\mathcal {I}_\alpha (\theta ;y;G)]^2 \nonumber \\&= \phi ''(1) Var_{P_R}[\mathcal {I}_\alpha (\theta ;y;G)] \nonumber \\&= \phi ''(1) n^2 ~ Var_{P_R}[k_\alpha (\theta ; y ,g)]. \end{aligned}$$

(20)

This non-zero limit also gives us a possible measure of the local sensitivity of the $R^{(\alpha )}$-posterior density under the contamination at the data and we will denote this by $s_\alpha (y)$, i.e.,

$$\begin{aligned} s_\alpha (y) = \lim _{\epsilon \downarrow 0} \frac{\rho (\pi _\alpha (\theta ; H_\epsilon ), \pi _\alpha (\theta ; G))}{\epsilon ^2} = \phi ''(1) Var_{P_R}[\mathcal {I}_\alpha (\theta ;y;G)]. \end{aligned}$$

(21)

Based on this, a global measure of sensitivity can be defined as $s_\alpha ^* = \sup _y s_\alpha (y)$. This measure again gives us the indication about the extend of robustness for the proposed $R^{(\alpha )}$-posterior with lower values implying greater robustness.

All the results proved in this section are particularly useful in real practice to check the robustness of the proposed method with respect to the potential outliers in the data. The boundedness of the influence function ensures that the proposed estimators will be able to ignore the outlying observations from the sample and generate more meaningful insights. The maximum values of the influence function or the global sensitivity measure can provide guidance for choosing the appropriate tuning parameter $\alpha$ for the assumed model and prior density. We will present a detailed illustration of these practical advantages of the proposed estimators in Sect. 6 in respect of the normal model.

5 Bayesian robustness: perturbation in the prior

Another important and desirable property for any estimation procedure in the Bayesian context is the Bayesian robustness with respect to contamination in prior distributions. In this section we will consider this aspect of the proposed $R^{(\alpha )}$-posterior. However, here we will only consider the local measures of sensitivities with small perturbations in the prior, an approach which has become very popular in recent days in the usual Bayesian context (see Ghosh et al. 2006). We will first introduce some additional notation.

Following Gustafson and Wasserman (1995), let $\pi$ be a prior density and $\pi ^x$ be corresponding posterior density given the data $x$ defined as

$$\begin{aligned} \pi ^x(\theta ) = \frac{f_\theta (x)\pi (\theta )}{\int f_\theta (x)\pi (\theta ) \mathrm{d}\theta }. \end{aligned}$$

Consider the set $\mathcal {P}$ of all probability densities over the parameter space $\varTheta$ and a distance $d : \mathcal {P} \times \mathcal {P} \rightarrow {\mathbb {R}}$ to quantify the changes between original and contaminated densities. Further let $\nu _\epsilon$ denote a perturbation of the prior $\pi$ in the direction of another density $\nu$. Then Gustafson and Wasserman (1995) defined the local sensitivity of $\mathcal {P}$ in the direction of $\nu$ as

$$\begin{aligned} s(\pi ,\nu ; x) = \lim _{\epsilon \downarrow 0 } \frac{\mathrm{d}(\pi ^x, \nu _\epsilon ^x)}{\mathrm{d}(\pi , \nu _\epsilon )}. \end{aligned}$$

In the present context of $R^{(\alpha )}$-posterior, we similarly define the $R^{(\alpha )}$-posterior density corresponding to prior $\pi$ given data $x$ by

$$\begin{aligned} \pi _\alpha ^x(\theta ) = \frac{\exp (q^{(\alpha )}_\theta (x)) \pi (\theta )}{\int \exp (q^{(\alpha )}_\theta (x)) \pi (\theta ) \mathrm{d}\theta }, \end{aligned}$$

(22)

where $q^{(\alpha )}_\theta (x)$ is as defined in Sect. 2. Then we define the local sensitivity of $\mathcal {P}$ for the $R^{(\alpha )}$-posterior in the direction of $\nu$ by

$$\begin{aligned} s_\alpha (\pi ,\nu ;x) = \lim _{\epsilon \downarrow 0 } \frac{\mathrm{d}(\pi _\alpha ^x, (\nu _\epsilon )_\alpha ^x)}{\mathrm{d}(\pi , \nu _\epsilon )}. \end{aligned}$$

Here for simplicity, we will consider the $\phi$-divergence defined earlier as the distance $d(\cdot ,\cdot )$ in the above definition. Also, as in usual practice, we consider two different types of perturbations $\nu _\epsilon$—one is the linear perturbation defined by $\nu _\epsilon = (1-\epsilon )\pi + \epsilon \nu$; and the second is the geometric perturbation defined by $\nu _\epsilon = c(\epsilon ) \pi ^{1-\epsilon }\nu ^\epsilon$ (see Gelfand and Dey (1991)).

Note that for any divergence, we know that $\mathrm{d}(\pi _\alpha ^x, (\nu _\epsilon )_\alpha ^x)$ and $\mathrm{d}(\pi , \nu _\epsilon )$ both converge to zero as $\epsilon \downarrow 0$. Also, as in the previous section, we can show that for the $\phi$-divergence $\rho (\cdot ,\cdot )$, $\lim _{\epsilon \downarrow 0} \frac{\partial }{\partial \epsilon } \rho (\pi _\alpha ^x, (\nu _\epsilon )_\alpha ^x) = 0$ and $\lim _{\epsilon \downarrow 0} \frac{\partial }{\partial \epsilon } \rho (\pi , \nu _\epsilon ) = 0$, i.e. the measure is zero in either case. Thus, for the $\phi$-divergences we indeed have

$$\begin{aligned} s_\alpha (\pi ,\nu ;x) = \lim _{\epsilon \downarrow 0 } \frac{\rho (\pi _\alpha ^x, (\nu _\epsilon )_\alpha ^x)}{\rho (\pi , \nu _\epsilon )} = \lim _{\epsilon \downarrow 0 }\frac{\frac{\partial ^2}{\partial ^2\epsilon } \rho (\pi _\alpha ^x, (\nu _\epsilon )_\alpha ^x)}{\frac{\partial ^2}{\partial ^2\epsilon } \rho (\pi , \nu _\epsilon )}. \end{aligned}$$

Hence, calculating above limit, we can get the form of the local sensitivity $s_\alpha (\pi ,\nu ;x)$ for different types of perturbations which are presented in the following theorems. The proof of these theorems follow along the lines of Theorems 3.1 and 3.2 of Dey and Birmiwal (1994).

Theorem 4

Consider linear perturbations of the prior and suppose $\int \frac{\nu ^2(\theta )}{\pi (\theta )} \mathrm{d}\theta < \infty$. Then

$$\begin{aligned} s_\alpha (\pi ,\nu ;x) = V_{\pi _\alpha ^x}\left( \frac{\nu (\theta )}{\pi (\theta )}\right) \Bigg /V_{\pi }\left( \frac{\nu (\theta )}{\pi (\theta )}\right) , \end{aligned}$$

(23)

where $V_\pi$ denotes variance with respect to the density $\pi$.

Theorem 5

Consider geometric perturbations of the prior and suppose that $\int (\log \frac{\nu (\theta )}{\pi (\theta )})^2 \pi (\theta ) \mathrm{d}\theta < \infty$ and $\int (\log \frac{\nu (\theta )}{\pi (\theta )})^2 (\frac{\nu (\theta )}{\pi (\theta )})^\epsilon \pi (\theta ) \mathrm{d}\theta < \infty$ for some $\epsilon > 0$. Then

$$\begin{aligned} s_\alpha (\pi ,\nu ;x) = V_{\pi _\alpha ^x}\left( \log \frac{\nu (\theta )}{\pi (\theta )}\right) \Bigg / V_{\pi }\left( \log \frac{\nu (\theta )}{\pi (\theta )}\right) . \end{aligned}$$

(24)

It is interesting to note that the results obtained in this section regarding the Bayesian robustness of the proposed $R^{(\alpha )}$-posterior and related inferences are similar to the corresponding results on the usual posterior in the Bayes paradigm (see Ghosh et al. 2006 and references therein for the corresponding details). These results basically describe the stability of the posterior-based inference under prior misspecification and are widely used in prior elicitation by the Bayesian statisticians. The theorem proved here will help one to use the proposed $R^{(\alpha )}$-posterior-based estimators with the above philosophy and to check its robustness with respect to the departures from true prior belief. As we have noted, the proposed methodology, besides providing robustness with respect to potential outliers in the observed data, also gives more emphasis on the prior belief over the usual posterior. The results derived in this section are helpful for the proper elicitation of the prior in case of the new pseudo-posterior-based approach. In the recent future, we hope to explore the different methods of prior elicitation and their criticisms with respect to the newly proposed $R^{(\alpha )}$-posterior based on all these results. Some numerical illustration regarding the effect of priors on the $R^{(\alpha )}$-Bayes estimators are presented in the next Section.

6 Simulation study: normal mean with known variance

We now illustrate the performance of the proposed $R^{(\alpha )}$-posterior densities and the Expected $R^{(\alpha )}$-Posterior (ERP) estimator. We consider the most common normal model with unknown mean and known variance. Let us assume that the data $X_1, \ldots , X_n$ come from the true normal density $g \equiv N(\theta _0,\sigma ^2)$ where the mean parameter $\theta _0$ is unknown but $\sigma ^2$ is known. We model this by the family $\mathcal {F}=\{f_\theta \equiv N(\theta ,\sigma ^2) : \theta \in \varTheta =\mathbb {R}\}$. Further, we consider the uniform prior for $\theta$ over the whole real line; $\pi (\theta ) = 1$ for all $\theta \in \mathbb {R}$.

From the form of the normal density, it is easy to see that

$$\begin{aligned} Q_n(\theta ) = \frac{1}{\alpha (\sqrt{2\pi }\sigma )^\alpha } \sum _{i=1}^n \mathrm{e}^{-\frac{\alpha (\theta -X_i)^2}{2\sigma ^2}} - n \zeta _\alpha , \end{aligned}$$

where $\zeta _\alpha = (\sqrt{2\pi }\sigma )^{-\alpha } (1+\alpha )^{-\frac{3}{2}}$. Thus, for any $\alpha >0$, the $R^{(\alpha )}$-posterior density is given by

$$\begin{aligned} \displaystyle \pi _R^\alpha (\theta |\underline{X}) \propto \exp \left[ \frac{1}{\alpha (\sqrt{2\pi }\sigma )^\alpha } \sum _{i=1}^n \mathrm{e}^{\displaystyle -\frac{\alpha (\theta -X_i)^2}{2\sigma ^2}}\right] . \end{aligned}$$

(25)

However, for $\alpha =0$, the $R^{(\alpha )}$-posterior is the ordinary posterior, which has the $N(\bar{X}, \frac{\sigma ^2}{n})$ distribution. Under a symmetric loss function the ordinary Bayes estimator is $\bar{X}$, which is highly sensitive to outliers. Indeed, one large outlier can make ordinary Bayes estimator arbitrarily large, and hence this estimator has zero asymptotic breakdown point. Yet we will see that for $\alpha >0$, the $R^{(\alpha )}$-Bayes estimator $\hat{\theta }_n^{(\alpha )}$ corresponding to the squared error loss function, which is the mean of the $R^{(\alpha )}$-posterior, is highly robust against outliers.

For any $\alpha \ge 0$, it follows from Theorem 1 that the $R^{(\alpha )}$-posterior density of $\sqrt{n} (\theta - \hat{\theta }_n^{(\alpha )})$ converges in the $L_1$-norm to a normal with mean $0$ and variance $J_\alpha ^{-1}$, where $J_\alpha = (\sqrt{2\pi })^{-\alpha } \sigma ^{-(\alpha +2)} (1+\alpha )^{-\frac{3}{2}}.$ Further, it follows from Theorem 2 that the asymptotic distribution of $\sqrt{n} (\hat{\theta }_n^{(\alpha )} - \theta _0)$ is the same as that of the MDPDE of the normal mean. From BHHJ it follows that this latter asymptotic distribution is $N(0, (1+\frac{\alpha ^2}{1+2\alpha })^{3/2}\sigma ^2)$ for all $\alpha \ge 0$. Thus,

$$\begin{aligned} \sqrt{n} (\hat{\theta }_n^{(\alpha )} - \theta _0) \rightarrow N\left( 0,\left( 1+\frac{\alpha ^2}{1+2\alpha }\right) ^{3/2}\sigma ^2\right) . \end{aligned}$$

Hence, the asymptotic relative efficiency of the Expected $R^{(\alpha )}$-Posterior estimator (ERPE) $\hat{\theta }_n^{(\alpha )}$ relative to the ordinary Bayes estimator $\hat{\theta }_n^{(0)} = \bar{X}$ is given by $(1+\frac{\alpha ^2}{1+2\alpha })^{ - \frac{3}{2}}$. For small positive $\alpha$, this ARE is very high, being 98.76 and 94.06 % at $\alpha =0.1$ and $0.25$, respectively. Thus, the loss in efficiency due to the use of the $R^{(\alpha )}$-posterior is asymptotically negligible for small values of $\alpha >0$.

For small sample sizes we can compare the efficiency of the ERPE $\hat{\theta }_n^{(\alpha )}$ with the usual Bayes estimator $\hat{\theta }_n^{(0)}$ through simulation. For any $\alpha >0$ the ERPE has no simplified expression and needs to be calculated numerically. For any given sample, we can estimate the ERPE by an importance sampling Monte Carlo algorithm using a $N(\bar{X},s_n^2)$ proposal distribution where $\bar{X}$ and $s_n^2$ denotes the sample mean and variance, respectively. We have simulated samples of various sizes from the $N(5,1)$ distribution, and using importance sampling with 20,000 steps, we estimate the empirical bias and mean squared error (MSE) of the ERPE based on 1,000 replications. Table 1 presents the empirical bias and MSE for several cases. Clearly the MSE of the ERPE for fixed $\alpha$ decreases with the sample size $n$, and for any fixed $n$ the MSE increases with $\alpha$. This is expected as the ERPE corresponding to the ordinary posterior at $\alpha =0$ is most efficient among all ERPEs under the true model (without contamination). The estimators for small positive $\alpha$ are highly efficient; the shift in the value of the MSE is minimal for small values of $\alpha$. We have also computed a popular summary measure used in the Bayesian paradigm, namely the credible interval for the normal mean based on equal tail probabilities (Table 1). Note that for the MDPDE with any fixed $\alpha \ge 0$, its length decreases with the sample size as expected. However, for any fixed sample size, the credible interval under pure data becomes slightly wider as $\alpha$ increases although this difference is not very significant for smaller positive values of $\alpha$.

Table 1 The empirical bias, MSE and credible interval (CI) of the ERPE for different sample sizes $n$ and tuning parameter $\alpha$ (without contamination)

Now we examine the robustness properties of the ERPE. The ordinary Bayes estimator (which is the sample mean) is highly non-robust in the presence of outliers. We will study the nature of the influence functions of the ERPEs at the model as developed in Sect. 4. Following the notation of Sect. 4, we can compute $Q^{(\alpha )}(\theta ,F_{\theta _0}, F_\theta )$ and $k_\alpha (\theta ,y, f_{\theta _0})$ for all $\alpha \ge 0$. Then the $R^{(\alpha )}$-posterior functional with $\alpha >0$ at $F_{\theta _0}$ is given by

$$\begin{aligned} \pi _\alpha (\theta ;F_{\theta _0}) \propto \exp \left[ \frac{n}{\alpha (\sqrt{2\pi }\sigma )^\alpha \sqrt{1+\alpha }} \mathrm{e}^{-\displaystyle \frac{\alpha (\theta -\theta _0)^2}{2(1+\alpha )\sigma ^2}}\right] . \end{aligned}$$

(26)

However, the $R^{(0)}$-posterior functional (or the usual posterior functional) at the model is a normal density with mean $\theta _0$ and variance $\sigma ^2/n$. Thus, the fixed sample influence function of the ordinary Bayes estimator (the usual posterior mean) corresponding to $\alpha = 0$ simplifies to $\mathrm{IF}_n(y,T_n^{(0)},F_{\theta _0}) = y - \theta _0$. This influence function, independent of the sample size, is clearly unbounded implying the non-robust nature of the usual Bayes estimator. However, the fixed sample influence function of the ERPE corresponding to $\alpha >0$ is given by

$$\begin{aligned} \mathrm{IF}_n(y,T_n^{(\alpha )},F_{\theta _0}) \!=\! \frac{n}{\alpha (\sqrt{2\pi }\sigma )^\alpha } Cov_{\pi _\alpha } \left( \!\theta , \mathrm{e}^{\displaystyle -\frac{\alpha (y-\theta )^2}{2\sigma ^2}} \!-\! \frac{1}{\sqrt{1+\alpha }} \mathrm{e}^{-\displaystyle \frac{\alpha (\theta -\theta _0)^2}{2(1+\alpha )\sigma ^2}} \!\right) \!, \end{aligned}$$

where the covariance is taken under the $R^{(\alpha )}$-posterior functional density.

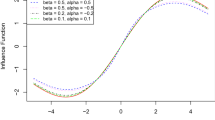
Figure 1 shows the plots of this fixed sample influence functions of the ERPE for different $\alpha >0$ and sample sizes $n=20$ and $n=50$. Clearly, for any fixed sample size this influence function is bounded.

Fig. 1

Plots of the fixed sample influence function of the ERPE for several $\alpha$ for different sample sizes $n$

Next, we study the influence on the whole $R^{(\alpha )}$-posterior density as given in Sect. 4.3. We empirically compute the pseudo-influence surface for various sample size $n$ and $\alpha > 0$ (Fig. 2). Here we assume, without loss of generality, that $\phi ''(1) = 1$. Clearly, all the fixed sample pseudo-influence functions for $\alpha >0$ are bounded implying the robustness of the $R^{(\alpha )}$-posterior density with $\alpha > 0$. However, the pseudo-influence function of the usual posterior at $\alpha = 0$ is $\mathcal{I}(\theta ; y, F_{\theta _0}) = \frac{n}{\sigma ^2} (y - \theta _0)(\theta - \theta _0)$, that is unbounded. Thus, $\gamma _0^* = \infty$ and the usual posterior is non-robust in the presence of outliers. The values of the maximum $\gamma _\alpha ^*$ of pseudo-influence function, shown in Fig. 3, are bounded for all sample sizes $n$ and $\alpha >0$ and decreases with $\alpha$. Hence, the robustness of the $R^{(\alpha )}$-posterior density increases with $\alpha$.

Fig. 2

Plots of the fixed sample pseudo-influence function of the $R^{(\alpha )}$-posterior density for several $\alpha$ and sample sizes $n$

Fig. 3

Plots of $\gamma _\alpha ^*$ and $s_\alpha ^*$ over $\alpha$ for different sample sizes $n$ (solid line $n=50$, dotted line $n=30$, dashed line $n=20$)

We have also computed the second measure of robustness, namely $s_\alpha (y)$ for different $\alpha >0$ numerically and its maximum $s_\alpha ^*$ that are shown in Fig. 3. Interestingly, the $s_\alpha ^*$ values seem to be independent of the sample size $n$ in this example although they again give the similar inference about the robustness of the $R^{(\alpha )}$-posterior density for $\alpha >0$. For the usual posterior corresponding to $\alpha =0$, we have $s_\alpha (y) = \frac{n}{\sigma ^2} (y-\theta _0)^2$ which is unbounded; thus, $s_0^* = \infty$, indicating the lack of robustness of the usual posterior density.

Now we consider the bias, MSE and the credible interval of the ERPE under contamination. The true data generating density is now $N(5,1)$ and we contaminate $100\epsilon \%$ of the data by the value $x = 8$ (i.e., we replace $100~\epsilon \%$ of the sample observations by the constant value 8), which may be considered an extreme point. The empirical summary estimates are given in Tables 2 and 3. The MSE and the bias are computed against the target value of $5$. Clearly larger values of $\alpha$ lead to more accurate inference compared to $\alpha =0$. In terms of the credible interval, note that as the contamination proportion increases its length decreases but the true value of the parameter (which is $5$) is pushed to the border and eventually lies outside the credible interval for small values of $\alpha$ including $0$; thus, the Bayes inference based on the credible interval produced by the usual posterior $(\alpha = 0)$ cannot give us the true result under contamination. However, once again the credible intervals produced by the robust posteriors with larger $\alpha \ge 0.5$ give much more accurate and stable inference in the presence of contamination.

Table 2 The empirical bias, MSE and credible interval (CI) of the ERPE for sample sizes $n=20$ with contamination at the point $x=8$ ($\epsilon$ denotes the contamination proportion)

Table 3 The empirical bias, MSE and credible interval (CI) of the ERPE for sample sizes $n=50$ with contamination at the point $x=8$ ($\epsilon$ denotes the contamination proportion)

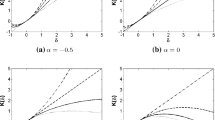
Finally we provide an exploration of the behavior of the ERPE under variations in the nature of contamination, prior parameters, and sample size. In Fig. 4a we provide a plot of $n$ times the mean square error (MSE) of the ERPE. In this experiment the model is the $N(\theta , 1)$ family, and the data are generated from the $N(5, 1)$ distribution; the mean parameter $\theta$ is the parameter of interest, and the assumed prior for $\theta$ is the $N(\mu = 5, \tau = 1)$ distribution. The processes which correspond to larger values of $\alpha$ place greater confidence on the prior mean, and for small values of the sample size $n$ the MSE of the ERPE of $\theta$ is a decreasing function of $\alpha$. For very small sample sizes the MSE corresponding to the ERPE$_{\alpha = 0.8}$ is significantly smaller than the MSE of ERPE$_{\alpha = 0}$. However, as the sample size increases the data component becomes more dominant and eventually there is a reversal in the order of the MSEs over $\alpha$ as may be expected. These reversals take place between sample sizes of 25 and 35. This loyalty towards the prior mean leads to a poorer MSE for the ERPEs corresponding to large values of $\alpha$ when the prior mean is actually misstated. This is observed in Fig. 4b, where the prior mean is chosen to be 6, while the other conditions are identical to those in the current experiment.

Fig. 4

Plots of $n~\times$ MSE of the ERPE over sample sizes $n$ for several values of $\alpha$ with prior parameters $(\mu ; \tau = 1)$ a $\mu =5$ b $\mu =6$

Next we study the effect of simultaneously misstating the prior mean and having a contamination component on the ERPE of $\theta$. All the remaining figures in this section refer to a prior mean of $\mu = 6$. In Figs. 5 and 8 we present the MSEs for sample sizes 20 and 50, respectively, where the effect of letting the prior standard deviation $\tau$ increase indefinitely may be observed. These two figures represent the no contamination case. The observations here are consistent with the findings of Table 1. In Figs. 6 and 7 we present, respectively, the bias and the MSEs of the ERPEs for sample size 20 and different values of $\alpha$ when the prior standard deviation is allowed to increase indefinitely, making the prior a very weak one in the limit. In Fig. 6 there is a contamination at $y = 0$, while in Fig. 7 the contamination is at $y = 10$. In either case the bias and the MSE become insignificant for large values of $\alpha$. In Figs. 9 and 10 similar observations are made when the above experiment is repeated with a sample size of 50. In these cases the contamination component dominates the departure from the true conditions, and reduces the misspecified prior to an issue of minor importance. In each of these cases the estimators corresponding to large values of $\alpha$ lead to better stability.

Fig. 5

Plots of Bias and MSE of the ERPE over prior SD $\tau$ for several $\alpha$ with sample size $n = 20$, prior mean $\mu = 6$ and no contamination in data

Fig. 6

Plots of Bias and MSE of the ERPE over prior SD $\tau$ for several $\alpha$ with sample size $n = 20$, prior mean $\mu = 6$ and 10 % contamination at $y = 0$

Fig. 7

Plots of Bias and MSE of the ERPE over prior SD $\tau$ for several $\alpha$ with sample size $n = 20$, prior mean $\mu = 6$ and 10 % contamination at $y = 10$

Fig. 8

Plots of Bias and MSE of the ERPE over prior SD $\tau$ for several $\alpha$ with sample size $n = 50$, prior mean $\mu = 6$ and no contamination in data

Fig. 9

Plots of Bias and MSE of the ERPE over prior SD $\tau$ for several $\alpha$ with sample size $n = 20$, prior mean $\mu = 6$ and 10 % contamination at $y = 0$

Fig. 10

Plots of Bias and MSE of the ERPE over prior SD $\tau$ for several $\alpha$ with sample size $n = 50$, prior mean $\mu = 6$ and 10 % contamination at $y = 10$

From the above simulation study, it appears that the robustness of the proposed estimator (ERPE) with respect to the presence of outliers increases as $\alpha$ increases; also the degree of stability of the estimators for any types of departure from true conditions increases with $\alpha$. All these suggest the choice of large values of $\alpha$ for application in practical scenarios. However, a large value of $\alpha$ would increase the MSE of the estimator under the true model conditions and so we need to trade-off between these two considerations. It is interesting to note that (Fig. 3) the degree of stability of the estimators increases drastically as $\alpha$ increases from zero to around $0.5$ but the change becomes very slow beyond $\alpha =0.5$. On the other hand, Table 1 shows that the loss in efficiency under pure data is also not very significant at $\alpha =0.5$. Thus, our empirical suggestion is to use $\alpha =0.5$ for analyzing any practical scenario. However, further work on the choice of $\alpha$ based on theoretical arguments or an extensive simulation study might still be worthwhile.

7 Concluding remarks

In this paper we have constructed a new “robust” estimator in the spirit of the Bayesian philosophy. The ordinary Bayes estimator based on the posterior density can have potential problems with “outliers”. We have demonstrated that the estimators with large values of $\alpha$ provide better stability in the estimators compared to those based on small values of $\theta$. All the properties of the estimators have been rigorously described, and several angles of this estimation procedure are described in detail, which substantiates the theory developed.

In this paper we have focused on the Bayesian philosophy, but in general comparisons of our estimators with frequentist ones could be of some interest. We hope to carry out such comparisons in future.

8 Appendix: Proof of Theorem 1

Note that, using the form of $\pi _R(\theta |X_1,\ldots , X_n)$ as in (2), we have

$$\begin{aligned} \pi _n^{*R}(t)&= \frac{\exp \left( Q_n\left( \hat{\theta }_n + \frac{t}{\sqrt{n}}\right) \right) \pi \left( \hat{\theta }_n + \frac{t}{\sqrt{n}}\right) }{\int \exp \left( Q_n\left( \hat{\theta }_n + \frac{t}{\sqrt{n}}\right) \right) \pi \left( \hat{\theta }_n + \frac{t}{\sqrt{n}}\right) \mathrm{d}t} \nonumber \\&= c_n^{-1} \exp \left[ Q_n\left( \hat{\theta }_n + \frac{t}{\sqrt{n} }\right) - Q_n(\hat{\theta }_n)\right] \pi \left( \hat{\theta }_n + \frac{t}{\sqrt{n}}\right) \quad \text{(say) }. \end{aligned}$$

(27)

Define $g_n(t) = \pi (\hat{\theta }_n + \frac{t}{\sqrt{n}}) \exp [Q_n(\hat{\theta }_n + \frac{t}{\sqrt{n} }) - Q_n(\hat{\theta }_n)] - \pi (\theta ^g) \mathrm{e}^{-\frac{1}{2} t' J_\alpha (\theta ^g) t}.$ Then, to prove the first part of the theorem it is enough to show that, with probability tending to one,

$$\begin{aligned} \int |g_n(t)|\mathrm{d}t \rightarrow 0 \quad \text{ as } \ n \rightarrow \infty . \end{aligned}$$

(28)

For this purpose we consider $S_1 = \{ t : ||t|| > \delta _0 \sqrt{n} \} \ \text{ and } \ S_2 = \{ t : ||t|| \le \delta _0 \sqrt{n} \}.$ We will separately show that, with probability tending to one, $\int _{S_i} |g_n(t)|dt \rightarrow 0,$ as $n \rightarrow \infty$ for $i = 1, 2$. Note that, by definition of $\hat{\theta }_n$,

$$\begin{aligned} \nabla Q_n(\hat{\theta }_n) = 0, \end{aligned}$$

and by the weak law of large numbers (WLLN)

$$\begin{aligned} -\frac{1}{n} \nabla ^2 Q_n(\theta ^g)&= - \frac{1}{n} \sum _{i=1}^n \nabla ^2 q_{\theta ^g}(X_i) \mathop {\rightarrow }^P J_\alpha (\theta ^g).\\ \text{ Now, } Q_n\left( \hat{\theta }_n + \frac{t}{\sqrt{n}}\right) - Q_n(\hat{\theta }_n)&= \frac{1}{2n} t' [\nabla ^2 Q_n(\hat{\theta }_n)] t + \frac{1}{6n \sqrt{n}}\sum _{i,j,k} t_i t_j t_k \nabla _{ijk} Q_n(\theta _n') \\&= -\frac{1}{2} t' [ \hat{J}_\alpha (\hat{\theta }_n)] t + R_n(t) \quad \text{(say) }. \end{aligned}$$

However, using the condition (E3), it is routinely observed that (see proof of the BVM theorem in Ghosh and Ramamoorthi 2003) $\hat{J}_\alpha (\hat{\theta }_n) \mathop {\rightarrow }^P J_\alpha (\theta ^g),$ and for any fixed $t$ $|R_n(t)| \rightarrow 0 \ \text{ as } ~~n \rightarrow \infty .$ Thus, for any fixed $t$, we have

$$\begin{aligned} \pi \left( \hat{\theta }_n + \frac{t}{\sqrt{n}}\right) \exp \left[ Q_n\left( \hat{\theta }_n + \frac{t}{\sqrt{n} }\right) - Q_n(\hat{\theta }_n)\right] \rightarrow \pi (\theta ^g) \mathrm{e}^{-\frac{1}{2} t' J_\alpha (\theta ^g) t}, \end{aligned}$$

which implies that $g_n(t) \rightarrow 0$, because $\pi (\theta )$ is continuous at $\theta ^g$.

For $t \in S_2$, using assumption (E3), we can choose $\delta _0$ sufficiently small such that $|R_n(t)| < \frac{1}{4} t' [\hat{J}_\alpha (\hat{\theta }_n)]t,$ for all sufficiently large $n$. So, for $t \in S_2$,

$$\begin{aligned}&Q_n\left( \hat{\theta }_n + \frac{t}{\sqrt{n}}\right) - Q_n(\hat{\theta }_n) < -\frac{1}{2} t' [\hat{J}_\alpha (\hat{\theta }_n)]t + \frac{1}{4} t' [\hat{J}_\alpha (\hat{\theta }_n)]t = -\frac{1}{4} t' [\hat{J}_\alpha (\hat{\theta }_n)]t ,\\&\quad \rightarrow \exp \left[ Q_n\left( \hat{\theta }_n + \frac{t}{\sqrt{n}}\right) - Q_n(\hat{\theta }_n) \right] < \mathrm{e}^{-\frac{1}{4} t' [\hat{J}_\alpha (\hat{\theta }_n)]t} < \mathrm{e}^{-\frac{1}{8} t' [J_\alpha (\theta ^g)]t}. \end{aligned}$$

Hence, for $t \in S_2$,

$$\begin{aligned} |g_n(t)| \le 2\pi (\theta ^g) \mathrm{e}^{-\frac{1}{8} t' [J_\alpha (\theta ^g)]t} + \pi (\theta ^g) \mathrm{e}^{-\frac{1}{2} t' [J_\alpha (\theta ^g)]t}, \end{aligned}$$

which is integrable. Thus, by the dominated convergence theorem

$$\begin{aligned} \int _{S_2} |g_n(t)|\mathrm{d}t \rightarrow 0 \ \text{ as } \ n \rightarrow \infty . \end{aligned}$$

Next we consider the integral over $S_1$. Note that for $t \in S_1$,

$$\begin{aligned}&\frac{1}{n} \left[ Q_n\left( \hat{\theta }_n + \frac{t}{\sqrt{n}}\right) - Q_n(\hat{\theta }_n) \right] \nonumber \\&\quad = \frac{1}{n} \left[ Q_n\left( \hat{\theta }_n + \frac{t}{\sqrt{n}}\right) - Q_n(\theta ^g) \right] + \frac{1}{n} [ Q_n(\theta ^g) - Q_n(\hat{\theta }_n)] \nonumber \\&\quad \le \sup _{||\theta - \theta ^g||>\frac{\delta _0}{2}} ~ \frac{1}{n} [ Q_n(\theta ) - Q_n(\theta ^g)] \nonumber \\&\qquad + \frac{1}{2 n} (\hat{\theta }_n -\theta ^g)'[\nabla ^2 Q_n(\hat{\theta }_n)] (\hat{\theta }_n -\theta ^g)\nonumber \\&\qquad + \frac{1}{6 n} \sum _{i,j,k} (\hat{\theta }_{ni} -\theta _i^g)(\hat{\theta }_{nj} -\theta _j^g)(\hat{\theta }_{nk} -\theta _k^g) \nabla _{ijk} Q_n(\theta _n^*), \end{aligned}$$

(29)

where $\theta _n^*$ lies between $\hat{\theta }_n$ and $\theta ^g$. The first term in the last inequality comes from the fact that $\hat{\theta }_n$ is consistent for $\theta ^g$ and $\frac{||t||}{\sqrt{n}} > \delta _0$ as $t \in S_1$. Now using Assumption (E3), it is easy to see that the second and the third term in (29) above goes to zero almost surely as $n \rightarrow \infty$. Further, using Assumption (E2), the first term in (29) above is less than $- \epsilon$ with probability one for all sufficiently large $n$ and for some $\epsilon > 0$. Hence we have, with probability one, $\frac{1}{n} [ Q_n(\hat{\theta }_n + \frac{t}{\sqrt{n}}) - Q_n(\hat{\theta }_n)] < -\frac{\epsilon }{2},$ for all sufficiently large $n$. Therefore, we get

$$\begin{aligned} \int _{S_1} |g_n(t)|\mathrm{d}t&\le \int _{S_1} \pi (\hat{\theta }_n)\mathrm{e}^{-\frac{n\epsilon }{2}} \mathrm{d}t + \int _{S_1} \pi (\theta ^g)\mathrm{e}^{-\frac{1}{8} t' [J_\alpha (\theta ^g)]t} \mathrm{d}t \\&\le \mathrm{e}^{-\frac{n\epsilon }{2}} \sqrt{n} \int \pi (\theta ) \mathrm{d}\theta + \int _{S_1} \pi (\theta ^g)\mathrm{e}^{-\frac{1}{8} t' [J_\alpha (\theta ^g)]t} \mathrm{d}t. \end{aligned}$$

But the second term in the above equation, being the normal tail probability, goes to zero as $n \rightarrow \infty$. Also clearly the first term in above goes to zero as $n \rightarrow \infty$ provided the prior is proper. Hence, with probability tending to one, $\int _{S_1} |g_n(t)|\mathrm{d}t \rightarrow 0, ~\text{ as } ~ n \rightarrow \infty .$ This completes the proof of the first part of the theorem.

The second part of the theorem follows from the first part and the in probability convergence of $\hat{J}_\alpha ^*(\hat{\theta }_n)$ to $J_\alpha (\theta )$. $\square$