Similarity-based multi-criteria decision making technique of pythagorean fuzzy sets

Abstract

Pythagorean fuzzy set (PFS) is a more flexible and effective way than intuitionistic fuzzy set (IFS) to seize indeterminacy. In this context, the main aim is to develop a number of new diverse types of PFS similarity measures which not only satisfy the well-known axioms, but also conquer the division-by-zero problem successfully. Moreover, the developed measures are based on two concepts of t-norm and s-norm together with the distance measure between PFSs. In order for further clarifying the role of proposed PFS similarity measures, we assess here two aspects of comparison: the microscopy aspect and the macroscopy aspect. The latter aspect allows us to know how the results are actually obtained on the basis of structural form of similarity measures, and the former aspect enables us to judge about the results of similarity measures without considering how they have been concluded. We then investigate a number of desirable properties of proposed PFS similarity measures, and show their effectiveness compared to the existing ones by encountering both of existing and newly constructed measures in some case studies concerning pattern recognition and medical diagnosis.

1 Introduction

Intuitionistic fuzzy set (IFS) as the generalization of Zadeh’s fuzzy set (Zadeh 1965) was first initiated by Atanassov (Atanassov 1999) in which the sum of its membership and non-membership degrees, denoted respectively by $\mu$ and $\nu$, satisfy the inequality $\mu + \nu \le 1$. This concept was intentionally proposed for being more flexible and practical in dealing with fuzziness and uncertainty than traditional fuzzy sets.

Later on, Yager (Yager 2013) indicated that the theory of IFS is not well suitable to deal with vagueness and hesitancy. For instance, if the preference towards an object is to be expressed by 0.3 for the membership degree $\mu$ and 0.8 for the non-membership degree $\nu$ then we find that $\mu + \nu 1$ while $\mu^{2} + \nu^{2} \le 1$ To handle such a case, Yager (Yager 2013) introduced the concept of Pythagorean fuzzy set (PFS) which expands the feasible region from the area under the curve $\mu + \nu \le 1$ to that under the curve $\mu^{2} + \nu^{2} \le 1$ Yager (Yager 2013) and others (Nguyen et al. 2019; Peng 2018; Peng and Garg 2019; Peng et al. 2017) have pointed out that this concept is more general than the concept of IFS.

In recent years, a lot of scholars have conducted research on PFS similarity measures (Farhadinia and Herrera-Viedma 2018; Farhadinia 2017, 2016). Wei and Wei (Wei and Wei 2018) proposed a class of 10 cosine-based PFS similarity measures based on the degrees of membership, non-membership and hesitation of PFSs to enhance the ability of dealing with the two optimization problems associated with the pattern recognition and medical diagnosis processes. Zhang (Zhang 2016) firstly defined a type of similarity measure for Pythagorean fuzzy numbers (PFNs) and then investigated its desirable properties. In the sequel, Zhang proposed a multiple criteria group decision making method on the basis of PFS similarity measure to solve the selection problem of photovoltaic cells. Zeng et al. (Zeng et al. 2018) presented two kinds of PFS similarity measures, one type is initiated based on distance measure which takes into account the five parameters, namely membership degree, non-membership degree, hesitation degree, strength of commitment, and direction of commitment. The other type is constructed with respect to the two aspects of similarity and dissimilarity measures of PFNs. The proposed similarity measure was then used to analyse the experts’ evaluation in a multiple criteria Pythagorean fuzzy group decision-making method. Peng et al. (Peng et al. 2017) constructed the axiomatic definitions of PFS information measures including similarity measure together with giving the transformation rule of those information measures. Then, in order to support the findings and moreover to demonstrate the effectiveness of similarity measures, Peng et al. applied them to pattern recognition, clustering analysis, and medical diagnosis. Nguyen et al. (Nguyen et al. 2019) presented a set of PFS similarity measures in whose construction the exponential functions of membership and non-membership degrees play the main role. Then, they studied the desirable combinations and the features of PFS similarity measures in an extended context. To investigate the efficiency of PFS similarity measures, Nguyen et al. presented a number of counter-intuitive examples. Those examples were served to show that Nguyen et al.’s measures do not fail under some certain cases. Peng and Garg (Peng and Garg 2019) presented a number of PFS similarity measures by considering three parameters including the $L_{p}$ norm, the levels of uncertainties and also the slope of relations. Furthermore, they discussed in detail the effect of the three aforementioned parameters on the ordering and classification of patterns. Eventually, Peng and Garg investigated thoroughly a number of applications of existing similarity measures to particular scenarios, including case studies of ore identification, bacterial detection, medical diagnosis, and jewellery identification. Peng (Peng 2018) proposed a PFS similarity measure by relying on the parameters $L_{p}$ norm and levels of vagueness whose relation to the PFS similarity measure was discussed in detail.

However, by reviewing the existing literature on PFS similarity measures, it will be clear that they have some drawbacks that encourage us to develop a more efficient class of PFS similarity measures. The drawbacks of the existing similarity measures are (1) some of them are not able to avoid the meaningless case (i.e., dividing by zero) (Peng et al. 2017; Wei and Wei 2018; Ye 2011), (2) a number of them cannot prevent counter-intuitive examples (Boran and Akay 2014; Chen 1997; Chen and Chang 2015; Hung and Yang 2004; Hong and Kim 1999; Li and Cheng 2002; Li and Xu 2001a; Li et al. 2007; Liang and Shi 2003; Mitchell 2003; Peng et al. 2017; Wei and Wei 2018; Ye 2011; Zhang 2016), and (3) they may lead to illogical results (Nguyen et al. 2019; Peng 2018; Peng and Garg 2019; Peng et al. 2017).

To eliminate the drawbacks of the above-mentioned PFS similarity measures, we describe here a class of fruitful PFS similarity measures whose most important terms are distance measure between PFSs together with two concepts of t-norm and s-norm. More specifically, the PFS distance measure is described by using of distance degree between the end and middle points of two PFS membership intervals. Then, we will carry out the comparison process between the proposed PFS similarity measures and the existing ones into two stages: the microscopy process and the macroscopy process. The latter process allows us to know how the results are actually obtained on the basis of structural form of similarity measures, and the former process enables us to judge about the results of similarity measures without considering how they have been concluded.

By the way, the present paper is organized as the followings: We review berifly the concepts of fuzzy set, IFS and PFS in Sect. 2. Then, we state all the required preliminaries which are required in constructing the novel class of PFS similarity measures. In Sect. 3, we will develop the class of PFS similarity measures whose structures are defined by a distance measure between PFSs and two concepts of t-norm and s-norm. Section 4 is devoted to the investigation of proposed and existing PFS similarity measures from microscopic and macroscopic processes. In Sect. 5, the applications of proposed PFS similarity measures in pattern recognition and medical diagnosis procedures are illustrated.

2 Preliminaries

The theory of fuzzy sets presented by Zadeh (Zadeh 1965) serves as an effective tool for understanding realistically the behaviour of humanistic systems in which emotions, perceptions, and human judgement play an important role.

Definition 2.1

(See (Zadeh 1965)) Any fuzzy set on the universal set $X = \left\{ {x_{1} ,x_{2} ,...,x_{n} } \right\}$ is in the form of $\alpha_{F} = \left\{ {\langle x,\mu_{{\alpha_{F} }} \left( x \right)\rangle :x \in X} \right\}$ in which $\mu_{{\alpha_{F} }} :X \to \left[ {0,1} \right]$ for all $x \in X$. Moreover, the value $\mu_{{\alpha_{F} }} \left( x \right)$ is named as the degree of membership of $x$ in $\alpha_{F}$.

With the more and more vague and imprecise information in the real-world problems, different extensions of fuzzy set have been developed by some researchers, among which, we present IFS and PFS as the followings:

Definition 2.2

(See (Atanassov 1999)) Any intuitionistic fuzzy set on the universal set $X = \left\{ {x_{1} ,x_{2} ,...,x_{n} } \right\}$ is in the form of $\alpha_{I} = \left\{ {\langle x,\mu_{{\alpha_{I} }} \left( x \right),\nu_{{\alpha_{I} }} \left( x \right)\rangle :x \in X} \right\}$ in which $\mu_{{\alpha_{I} }} :X \to \left[ {0,1} \right]$ and $\nu_{{\alpha_{I} }} :X \to \left[ {0,1} \right]$ are such that $0 \le \mu_{{\alpha_{I} }} \left( x \right) + \nu_{{\alpha_{I} }} \left( x \right) \le 1$ for all $x \in X$. Moreover, the values $\mu_{{\alpha_{I} }} \left( x \right)$ and $\nu_{{\alpha_{I} }} \left( x \right)$ are named as the degree of membership and non-membership of $x$ in $\alpha_{I}$, respectively.

For notational convenience, Xu (Li and Xu 2001a) called $\alpha_{I} = \langle \mu_{{\alpha_{I} }} \left( x \right),\nu_{{\alpha_{I} }} \left( x \right)\rangle$ an intuitionistic fuzzy value, and denoted it briefly by $\alpha_{I} = \langle \mu_{{\alpha_{I} }} ,\nu_{{\alpha_{I} }} \rangle$.

Definition 2.3

(See (Yager 2013)) Any Pythagorean fuzzy set (PFS) on the universal set $X = \left\{ {x_{1} ,x_{2} ,...,x_{n} } \right\}$ is in the form of $\alpha_{P} = \left\{ {\langle x,\mu_{{\alpha_{P} }} \left( x \right),\nu_{{\alpha_{P} }} \left( x \right)\rangle :x \in X} \right\}$ in which $\mu_{{\alpha_{P} }} :X \to \left[ {0,1} \right]$ and $\nu_{{\alpha_{P} }} :X \to \left[ {0,1} \right]$ are such that $0 \le \mu_{{\alpha_{P} }}^{2} \left( x \right) + \nu_{{\alpha_{P} }}^{2} \left( x \right) \le 1$ for all $x \in X$. Moreover, the values $\mu_{{\alpha_{P} }} \left( x \right)$ and $\nu_{{\alpha_{P} }} \left( x \right)$ are named as the degree of membership and non-membership of $x$ in $\alpha_{P}$, respectively.

As well as to the contraction of Xu (Li and Xu 2001a) above, Yager (Yager 2014) called $\alpha_{P} = \langle \mu_{{\alpha_{P} }} \left( x \right),\nu_{{\alpha_{P} }} \left( x \right)\rangle$ a Pythagorean fuzzy value (PFV), and denoted it briefly by $\alpha_{P} = \langle \mu_{{\alpha_{P} }} ,\nu_{{\alpha_{P} }} \rangle$.

Furthermore, we denote the degree of indeterminacy of $\alpha_{P} = \langle \mu_{{\alpha_{P} }} ,\nu_{{\alpha_{P} }} \rangle$ by $\pi_{{\alpha_{P} }} = \sqrt {1 - \mu_{{\alpha_{P} }}^{2} - \nu_{{\alpha_{P} }}^{2} }$.

Hereafter and for notational convenience, we simply denote $\alpha_{P} = \langle \mu_{{\alpha_{P} }} ,\nu_{{\alpha_{P} }} \rangle$ by $\alpha = \langle \mu_{\alpha } ,\nu_{\alpha } \rangle$.

Definition 2.4

(See (Yager 2014, 2013)) If $\alpha = \langle \mu_{\alpha } ,\nu_{\alpha } \rangle$ and $\beta = \langle \mu_{\beta } ,\nu_{\beta } \rangle$ are two PFVs, then some of operations on PFVs are defined as the followings:

$$\begin{gathered} \bar{\alpha } = \langle \mu _{{\bar{\alpha }}} ,\nu _{{\bar{\alpha }}} \rangle = \langle \nu _{\alpha } ,\mu _{\alpha } \rangle ; \hfill \\ \alpha \subset \beta\, if\;and\;only\;if\mu _{\alpha } \le \mu _{\beta } and\nu _{\alpha } \ge \nu _{\beta } ; \hfill \\ \alpha = \beta\, if\;and\;only\;if\mu _{\alpha } = \mu _{\beta } and\nu _{\alpha } = \nu _{\beta } ; \hfill \\ 1 = \langle \mu _{1} ,\nu _{1} \rangle = \langle 1,0\rangle ;0 = \langle \mu _{0} ,\nu _{0} \rangle = \langle 0,1\rangle ; \hfill \\ \alpha \cap \beta = \langle \min \left\{ {\mu _{\alpha } ,\mu _{\beta } } \right\},\max \left\{ {\nu _{\alpha } ,\nu _{\beta } } \right\}\rangle ; \hfill \\ \alpha \cup \beta = \langle \max \left\{ {\mu _{\alpha } ,\mu _{\beta } } \right\},\min \left\{ {\nu _{\alpha } ,\nu _{\beta } } \right\}\rangle . \hfill \\ \end{gathered}$$

Before dealing with the main issue of this contribution which is nothing else than the introduction of similarity measure for PFSs, it is appropriate to present some preliminaries as follows.

The fundamental role in the definition of new PFS similarity measure is played by a strictly monotone decreasing function $F:\left[ {0,1\left] \to \right[0,1} \right]$ which can be chosen as:

$$ \begin{aligned} F_{1} \left( \eta \right) & = 1 - \eta ; \\ F_{2} \left( \eta \right) & = 1 - \eta ^{2} ; \\ F_{3} \left( \eta \right) & = \frac{1}{{1 + \eta }}; \\ F_{4} \left( \eta \right) & = \frac{{1 - \eta }}{{1 + \eta }}; \\ F_{5} \left( \eta \right) & = e^{{ - \eta }} ; \\ F_{6} \left( \eta \right) & = 1 - \eta e^{{\eta - 1}} . \\ \end{aligned}$$

Keeping the above concepts in mind, we define the following mappings of both membership and non-membership degrees of two PFVs $\alpha = \langle \mu_{\alpha } ,\nu_{\alpha } \rangle$ and $\beta = \langle \mu_{\beta } ,\nu_{\beta } \rangle$:

$$ F_{1\mu } \left( {\alpha ,\beta } \right): = F_{1} \left( {\eta = \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|} \right) = 1 - \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|; $$

(1)

$$ F_{2\mu } \left( {\alpha ,\beta } \right): = F_{2} \left( {\eta = \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|} \right) = 1 - (\left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|)^{2} ; $$

(2)

$$ F_{3\mu } \left( {\alpha ,\beta } \right): = F_{3} \left( {\eta = \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|} \right) = \frac{1}{{1 + \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|}}; $$

(3)

$$ F_{4\mu } \left( {\alpha ,\beta } \right): = F_{4} \left( {\eta = \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|} \right) = \frac{{1 - \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|}}{{1 + \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|}}; $$

(4)

$$ F_{5\mu } \left( {\alpha ,\beta } \right): = F_{5} \left( {\eta = \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|} \right) = e^{{ - \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|}} ; $$

(5)

$$ F_{6\mu } \left( {\alpha ,\beta } \right): = F_{6} \left( {\eta = \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|} \right) = 1 - \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|e^{{\left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right| - 1}} , $$

(6)

and moreover,

$$ F_{1\nu } \left( {\alpha ,\beta } \right): = F_{1} \left( {\eta = \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|} \right) = 1 - \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|; $$

(7)

$$ F_{2\nu } \left( {\alpha ,\beta } \right): = F_{2} \left( {\eta = \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|} \right) = 1 - (\left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|)^{2} ; $$

(8)

$$ F_{3\nu } \left( {\alpha ,\beta } \right): = F_{3} \left( {\eta = \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|} \right) = \frac{1}{{1 + \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|}}; $$

(9)

$$ F_{4\nu } \left( {\alpha ,\beta } \right): = F_{4} \left( {\eta = \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|} \right) = \frac{{1 - \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|}}{{1 + \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|}}; $$

(10)

$$ F_{5\nu } \left( {\alpha ,\beta } \right): = F_{5} \left( {\eta = \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|} \right) = e^{{ - \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|}} ; $$

(11)

$$ F_{6\nu } \left( {\alpha ,\beta } \right): = F_{6} \left( {\eta = \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|} \right) = 1 - \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|e^{{\left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right| - 1}} . $$

(12)

Here, it needs to be examined the properties of mappings $F_{i\mu }$ and $F_{i\nu }$ for $i = 1,2,...,6$.

Theorem 2.5

Suppose that $\alpha = \langle \mu_{\alpha } ,\nu_{\alpha } \rangle$ , $\beta = \langle \mu_{\beta } ,\nu_{\beta } \rangle$ , and $\gamma = \langle \mu_{\gamma } ,\nu_{\gamma } \rangle$ are three PFVs. Then, the mappings $F_{i\mu }$ and $F_{i\nu }$ (for $i = 1,2,...,6$ ) given respectively by formulas ( 1 ) – ( 6 ) and ( 7 ) – ( 12 ) satisfy the following properties:

(S0) $0 \le F_{i\mu } \left( {\alpha ,\beta } \right),{ }F_{i\nu } \left( {\alpha ,\beta } \right) \le 1$

(S1) $F_{i\mu } \left( {\alpha ,\beta } \right) = F_{i\mu } \left( {\beta ,\alpha } \right)$ and $F_{i\nu } \left( {\alpha ,\beta } \right) = F_{i\nu } \left( {\beta ,\alpha } \right)$

(S2) $F_{i\mu } \left( {\alpha ,\beta } \right) = F_{i\nu } \left( {\alpha ,\beta } \right) = 1$ if and only if $\alpha = \beta$

(S3) If $\alpha \subseteq \beta \subseteq \gamma$ then

$$ \begin{gathered} F_{i\mu } \left( {\alpha ,\gamma } \right) \le F_{i\mu } \left( {\alpha ,\beta } \right){ }\,and\,{ }F_{i\mu } \left( {\alpha ,\gamma } \right) \le F_{i\mu } \left( {\beta ,\gamma } \right); \hfill \\ F_{i\nu } \left( {\alpha ,\gamma } \right) \le F_{i\nu } \left( {\alpha ,\beta } \right){ }\,and\,{ }F_{i\nu } \left( {\alpha ,\gamma } \right) \le F_{i\nu } \left( {\beta ,\gamma } \right). \hfill \\ \end{gathered} $$

Proof

Taking any PFVs $\alpha = \langle \mu_{\alpha } ,\nu_{\alpha } \rangle$ $\beta = \langle \mu_{\beta } ,\nu_{\beta } \rangle$ and $\gamma = \langle \mu_{\gamma } ,\nu_{\gamma } \rangle$ into account, we then conclude that:

Proof of (S0): As follows from definition of strictly monotone decreasing mappings $F_{i\mu } :\left[ {0,1\left] \to \right[0,1} \right]$ and $F_{i\nu } :\left[ {0,1\left] \to \right[0,1} \right]$, we immediately conclude that the property (S0) is satisfied.

Proof of (S1): With respect to the formulas (1)–(6) and (7)–(12), we easily find that $F_{i\mu }$ and $F_{i\nu }$ are symmetric.

Proof of (S2): From the formulas (1)–(6) and (7)–(12), it can be obviously seen that $F_{i\mu } \left( {\alpha ,\beta } \right) = F_{i\nu } \left( {\alpha ,\beta } \right) = 1$ if and only if $\left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right| = 0$ and $\left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right| = 0$ if and only if $\alpha = \beta$.

Proof of (S3): In the case where $\langle \mu_{\alpha } ,\nu_{\alpha } \rangle \subseteq \langle \mu_{\beta } ,\nu_{\beta } \rangle \subseteq \langle \mu_{\gamma } ,\nu_{\gamma } \rangle$, we get $0 \le \mu_{\alpha } \le \mu_{\beta } \le \mu_{\gamma } \le 1$ together with $1 \ge \nu_{\alpha } \ge \nu_{\beta } \ge \nu_{\gamma } \ge 0$. Therefore, it is deduced that

$$ \left| {\mu_{\alpha }^{2} - \mu_{\gamma }^{2} \left| \ge \right|\mu_{\alpha }^{2} - \mu_{\beta }^{2} \left| {{ }and{ }} \right|\mu_{\alpha }^{2} - \mu_{\gamma }^{2} \left| \ge \right|\mu_{\beta }^{2} - \mu_{\gamma }^{2} } \right|; $$

(13)

$$ \left| {\nu_{\alpha }^{2} - \nu_{\gamma }^{2} \left| \ge \right|\nu_{\alpha }^{2} - \nu_{\beta }^{2} \left| {{ }and{ }} \right|\nu_{\alpha }^{2} - \nu_{\gamma }^{2} \left| \ge \right|\nu_{\beta }^{2} - \nu_{\gamma }^{2} } \right|. $$

(14)

Since the mappings $F_{i\mu }$ and $F_{i\nu }$ are strictly monotone decreasing with respect to their arguments, thus, from the latter Eqs. (13) and (14), we conclude that

$$ \begin{gathered} F_{i\mu } \left( {\alpha ,\gamma } \right) \le F_{i\mu } \left( {\alpha ,\beta } \right){ }\,and\,{ }F_{i\mu } \left( {\alpha ,\gamma } \right) \le F_{i\mu } \left( {\beta ,\gamma } \right); \hfill \\ F_{i\nu } \left( {\alpha ,\gamma } \right) \le F_{i\nu } \left( {\alpha ,\beta } \right){ }\,and\,{ }F_{i\nu } \left( {\alpha ,\gamma } \right) \le F_{i\nu } \left( {\beta ,\gamma } \right). \hfill \\ \end{gathered} $$

Let us now expand the set of properties beyond those mentioned in Theorem 2.5 by considering the following axiom:

Lemma 2.6

If a PFV $\alpha = \langle \mu_{\alpha } ,\nu_{\alpha } \rangle$ is to be a crisp value, that is, $\alpha = 1 = \langle 1,0\rangle$ or $\alpha = 0 = \langle 0,1\rangle$ , then the following results for ( $i = 1,2,4,6$ ) can be observed:

$$ \begin{gathered} F_{i\mu } \left( {\alpha ,\overline{\alpha }} \right) = 0, \hfill \\ F_{i\nu } \left( {\alpha ,\overline{\alpha }} \right) = 0, \hfill \\ \end{gathered} $$

where the complement PFV $\overline{\alpha }$ is defined by $\overline{\alpha } = \langle \mu_{{\overline{\alpha }}} ,\nu_{{\overline{\alpha }}} \rangle = \langle \nu_{\alpha } ,\mu_{\alpha } \rangle$.

Proof

The proof is more straightforward and direct by using formulas (1)–(6) and (7)–(12).

The above lemma allows the set of properties of mappings $F_{i\mu }$ and $F_{i\nu }$ (for $i = 1,2,...,6$) to be enlarged more than that in Theorem 2.5 by encountering the following axiom:

(S4) $F_{i\mu } \left( {\alpha ,\overline{\alpha }} \right) = F_{i\nu } \left( {\alpha ,\overline{\alpha }} \right) = 0$ (for $i = 1,2,4,6$) if and only if $\alpha$ is a crisp set.

As will be seen in the next section, the new proposed PFS similarity measures are constructed by the help of t-norms and s-norms, too. Therefore, in the following, we review the well-known definition of t-norms and s-norms (see e.g., (Farhadinia 2015)): the continuous t-norm $\tau :\left[ {0,1\left] \times \right[0,1\left] \to \right[0,1} \right]$ fulfils.

• ($\tau 1$) Boundary condition: $\tau \left( {x,1} \right) = x$;

• ($\tau 2$) Monotonicity: If $y \le z$ then $\tau \left( {x,y} \right) \le \tau \left( {x,z} \right)$;

• ($\tau 3$) Commutativity: $\tau \left( {x,y} \right) = \tau \left( {y,x} \right)$;

• ($\tau 4$) Associativity: $\tau \left( {x,\tau \left( {y,z} \right)} \right) = \tau \left( {\tau \left( {x,y} \right),z} \right)$ and the continuous s-norm $\sigma :\left[ {0,1\left] \times \right[0,1\left] \to \right[0,1} \right]$ satisfies;

• ($\sigma 1$) Boundary condition: $\sigma \left( {x,0} \right) = x$;

• ($\sigma 2$) Monotonicity: If $y \le z$ then $\sigma \left( {x,y} \right) \le \sigma \left( {x,z} \right)$;

• ($\sigma 3$) Commutativity: $\sigma \left( {x,y} \right) = \sigma \left( {y,x} \right)$;

• ($\sigma 4$) Associativity: $\sigma \left( {x,\sigma \left( {y,z} \right)} \right) = \sigma \left( {\sigma \left( {x,y} \right),z} \right)$.

By taking the above-mentioned axioms into account, we are now able to present a number of frequently used t-norms and s-norms (Farhadinia 2015):

Algebraic t-norm and s-norm:

$$ \tau_{1} \left( {x,y} \right) = xy, $$

(15)

$$ \sigma_{1} \left( {x,y} \right) = x + y - xy; $$

(16)

Einstein t-norm and s-norm:

$$ \tau_{2} \left( {x,y} \right) = \frac{xy}{{1 + \left( {1 - x} \right)\left( {1 - y} \right)}}, $$

(17)

$$ \sigma_{2} \left( {x,y} \right) = \frac{x + y}{{1 + xy}}; $$

(18)

Hamacher t-norm and s-norm:

$$ \tau_{3} \left( {x,y} \right) = \frac{xy}{{ + \left( {1 - } \right)\left( {x + y - xy} \right)}}, $$

(19)

$$\sigma _{3} \left( {x,y} \right) = \frac{{x + y - xy - \left( {1 - } \right)xy}}{{1 - \left( {1 - } \right)xy}},{\text{ }} \in {\text{ > }}0;$$

(20)

Frank t-norm and s-norm:

$$ \tau _{4}^{ \in } \left( {x,y} \right) = log_{ \in } {\text{ }}\left( {1 + \frac{{\left( { \in ^{x} - 1 \in ^{y} - 1} \right)}}{{ \in - 1}}} \right),{\text{ }}$$

(21)

$$\sigma _{4} \left( {x,y} \right) = 1 - log_{ \in } \left( {1 + \frac{{\left( { \in ^{{1 - x}} - 1 \in ^{{1 - y}} - 1} \right)}}{{ \in - 1}}} \right), \in > 1$$

(22)

3 Similarity measure for PFSs

Now, with the preliminaries given in Sect. 2 and the next definition of distance measure, we are going to establish a class of similarity measures between PFVs.

In the sequel, we will demonstrate that the concept of similarity measure for PFVs can be easily extended to that for PFSs.

In this part of the section, we describe how a a distance measure between two PFVs $\alpha = \langle \mu_{\alpha } ,\nu_{\alpha } \rangle$ and $\beta = \langle \mu_{\beta } ,\nu_{\beta } \rangle$ can be constructed by using the end and middle points of intervals $\left[ {\mu_{\alpha }^{2} ,1 - \nu_{\alpha }^{2} } \right]$ and $\left[ {\mu_{\beta }^{2} ,1 - \nu_{\beta }^{2} } \right]$. Before doing so, we would regard the end and middle points of intervals $\left[ {\mu_{\alpha }^{2} ,1 - \nu_{\alpha }^{2} } \right]$ and $\left[ {\mu_{\beta }^{2} ,1 - \nu_{\beta }^{2} } \right]$ as

$$ L_{k} \left( \alpha \right): = L_{k} \left( {\langle \mu_{\alpha } ,\nu_{\alpha } \rangle } \right) = \left( {1 - \frac{k}{2}} \right)\mu_{\alpha }^{2} + \frac{k}{2}\left( {1 - \nu_{\alpha }^{2} } \right), $$

(23)

$$ L_{k} \left( \beta \right): = L_{k} \left( {\langle \mu_{\beta } ,\nu_{\beta } \rangle } \right) = \left( {1 - \frac{k}{2}} \right)\mu_{\beta }^{2} + \frac{k}{2}\left( {1 - \nu_{\beta }^{2} } \right), k = 0,1,2. $$

(24)

In view of these observations, we may construct the distance measure

$$\begin{aligned} d_{L} \left( {\alpha ,\beta } \right): & = d_{L} \left( {\langle \mu _{\alpha } ,\nu _{\alpha } \rangle ,\langle \mu _{\beta } ,\nu _{\beta } \rangle } \right) = \sqrt {\frac{1}{3}\mathop \sum \limits_{{k = 0}}^{2} {\text{}}[L_{k} \left( \alpha \right) - L_{k} \left( \beta \right)]^{2} } \\ & = \sqrt {\frac{1}{3}(\left[ {\mu _{\alpha }^{2} - \mu _{\beta }^{2} ]^{2} + \frac{1}{4}} \right[\left( {\mu _{\alpha }^{2} - \mu _{\beta }^{2} } \right) - \left( {\nu _{\alpha }^{2} - \nu _{\beta }^{2} } \right)]^{2} + \left[ {\nu _{\alpha }^{2} - \nu _{\beta }^{2} ]^{2} } \right)} \\ \end{aligned}$$

(25)

Lemma 3.1

The mapping $d_{L}$ defined in the form of (25) is a meter, that is, for any PFVs $\alpha = \langle \mu_{\alpha } ,\nu_{\alpha } \rangle$ , $\beta = \langle \mu_{\beta } ,\nu_{\beta } \rangle$ and $\gamma = \langle \mu_{\gamma } ,\nu_{\gamma } \rangle$ , it holds that.

$$ \left( {{\text{D}}0} \right)\;0 \le d_{L} \left( {\alpha ,\beta } \right) \le 1 $$

$$ \left( {{\text{D1}}} \right)\;d_{L} \left( {\alpha ,\beta } \right) = d_{L} \left( {\beta ,\alpha } \right) $$

(D2) $d_{L} \left( {\alpha ,\beta } \right) = 0$ if and only if $\alpha = \beta$

$$ \left( {{\text{D3}}} \right)\;d_{L} \left( {\alpha ,\gamma } \right) \le d_{L} \left( {\alpha ,\beta } \right) + d_{L} \left( {\beta ,\gamma } \right) $$

Proof

The proof of axioms (D0), (D1) and (D3) are clear.

We only prove the axiom (D2). For this case and from definition of mapping $d_{L}$ given by (25), we conclude that

$$\begin{gathered} d_{L} \left( {\alpha ,\beta } \right) = 0, \hfill \\ if{\mkern 1mu} {\mkern 1mu} and{\mkern 1mu} {\mkern 1mu} only{\mkern 1mu} {\mkern 1mu} if{\mkern 1mu} [L_{k} \left( \alpha \right) - L_{k} \left( \beta \right)]^{2} = 0,k = 0,1,2, \hfill \\ {\mkern 1mu} if{\mkern 1mu} {\mkern 1mu} and{\mkern 1mu} {\mkern 1mu} only{\mkern 1mu} .if\left[ {\mu _{\alpha }^{2} - \mu _{\beta }^{2} ]^{2} = 0,} \right[\left( {\mu _{\alpha }^{2} - \mu _{\beta }^{2} } \right) - \left( {\nu _{\alpha }^{2} - \nu _{\beta }^{2} } \right)]^{2} = 0,[\nu _{\alpha }^{2} - \nu _{\beta }^{2} ]^{2} = 0, \hfill \\ \end{gathered}$$

which all of these equalities imply that $\mu_{\alpha }^{2} = \mu_{\beta }^{2}$ and $\nu_{\alpha }^{2} = \nu_{\beta }^{2}$, and consequently, $\alpha = \langle \mu_{\alpha } ,\nu_{\alpha } \rangle = \langle \mu_{\beta } ,\nu_{\beta } \rangle = \beta$.

Coping with all the above requirements, we are now in a position to introduce a new and novel class of similarity measures for PFVs which is described below.

Theorem 3.2

Suppose that $\alpha = \langle \mu_{\alpha } ,\nu_{\alpha } \rangle$ , $\beta = \langle \mu_{\beta } ,\nu_{\beta } \rangle$ and $\gamma = \langle \mu_{\gamma } ,\nu_{\gamma } \rangle$ are to be PFVs. Considering the definition of $F_{i\mu }$ , $F_{i\nu }$ (for $i = 1,2,...,6$ ) and $d_{L}$ given respectively by ( 1 )–( 6 ), ( 7 )–( 12 ) and (25), we define.

$$ S_{\tau } \left( {\alpha ,\beta } \right) = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + \tau \left( {F_{i\mu } \left( {\alpha ,\beta } \right),F_{i\nu } \left( {\alpha ,\beta } \right)} \right)} \right]; $$

(26)

$$ S_{\sigma } \left( {\alpha ,\beta } \right) = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + \sigma \left( {F_{i\mu } \left( {\alpha ,\beta } \right),F_{i\nu } \left( {\alpha ,\beta } \right)} \right)} \right], $$

(27)

which satisfy

$$ \begin{gathered} \left( {S_{*} 0} \right)\;0 \le S_{*} \left( {\alpha ,\beta } \right) \le 1; \hfill \\ \left( {S_{*} 1} \right)\;S_{*} \left( {\alpha ,\beta } \right) = S_{*} \left( {\beta ,\alpha } \right); \hfill \\ \left( {S_{*} 2} \right)\;S_{*} \left( {\alpha ,\beta } \right) = 1\;{\text{if and only if}}\;\alpha = \beta ; \hfill \\ \left( {S_{*} 3} \right)\;{\text{If}}\;\alpha \subseteq \beta \subseteq \gamma \;{\text{then}}\,S_{*} \left( {\alpha ,\gamma } \right) \le S_{*} \left( {\alpha ,\beta } \right)\,and\,S_{*} \left( {\alpha ,\gamma } \right) \le S_{*} \left( {\beta ,\gamma } \right); \hfill \\ \left( {S_{*} 4} \right)\;{\text{For any}}\;i = 1,2,4,6\;{\text{we get}}\;S_{*} \left( {\alpha ,\bar{\alpha }} \right) = 0\;{\text{if}}\;\alpha 1mu{\text{is a crisp set}}. \hfill \\ \end{gathered}$$

Here, the notation '*' indicates the index $\tau$ or $\sigma$.

Proof

Proof of ($S_{*} 0$): From definition of t-norm $\tau :\left[ {0,1\left] \times \right[0,1\left] \to \right[0,1} \right]$ and s-norm $\sigma :\left[ {0,1\left] \times \right[0,1\left] \to \right[0,1} \right]$ together with the property (D0) in Lemma 3.1 which may be re-stated by $1 \ge 1 - d_{L} \left( {\alpha ,\beta } \right) \ge 0$ we find that $0 \le S_{*} \left( {\alpha ,\beta } \right) \le 1$ for ${*} = \tau$ or $\sigma$.

Proof of ($S_{*} 1$): The implication of axiom ($S_{*} 1$) under the symmetrical property of $F_{i\mu }$, $F_{i\nu }$ and $d_{L}$ will easily follow.

Proof of ($S_{*} 2$): Assume that $S_{*} \left( {\alpha ,\beta } \right) = 1$ holds true for the index $\tau$ or $\sigma$. Then, by employing the Eqs. (26) and (27), we find that

$$ \begin{gathered} S_{\tau } \left( {\alpha ,\beta } \right) = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + \tau \left( {F_{i\mu } \left( {\alpha ,\beta } \right),F_{i\nu } \left( {\alpha ,\beta } \right)} \right)} \right] = 1; \hfill \\ S_{\sigma } \left( {\alpha ,\beta } \right) = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + \sigma \left( {F_{i\mu } \left( {\alpha ,\beta } \right),F_{i\nu } \left( {\alpha ,\beta } \right)} \right)} \right] = 1, \hfill \\ \end{gathered} $$

if and only if

$$ \begin{gathered} 1 - d_{L} \left( {\alpha ,\beta } \right) = 1, and \tau \left( {F_{i\mu } \left( {\alpha ,\beta } \right),F_{i\nu } \left( {\alpha ,\beta } \right)} \right) = 1; \hfill \\ 1 - d_{L} \left( {\alpha ,\beta } \right) = 1, and \sigma \left( {F_{i\mu } \left( {\alpha ,\beta } \right),F_{i\nu } \left( {\alpha ,\beta } \right)} \right) = 1. \hfill \\ \end{gathered} $$

Now, from definition of $d_{L}$, $\tau$, $\sigma$, $F_{i\mu }$ and $F_{i\nu }$, we can conclude that the latter relations hold true if and only if $\alpha = \beta$.

Proof of ($S_{*} 3$): If $\alpha \subseteq \beta \subseteq \gamma$, that is, $\langle \mu_{\alpha } ,\nu_{\alpha } \rangle \subseteq \langle \mu_{\beta } ,\nu_{\beta } \rangle \subseteq \langle \mu_{\gamma } ,\nu_{\gamma } \rangle$, then it holds that $0 \le \mu_{\alpha } \le \mu_{\beta } \le \mu_{\gamma } \le 1$ together with $1 \ge \nu_{\alpha } \ge \nu_{\beta } \ge \nu_{\gamma } \ge 0$. Thus, we conclude that

$$ \begin{gathered} \left| {\mu_{\alpha }^{2} - \mu_{\gamma }^{2} \left| \ge \right|\mu_{\alpha }^{2} - \mu_{\beta }^{2} \left| {{ }\,and\,{ }} \right|\mu_{\alpha }^{2} - \mu_{\gamma }^{2} \left| \ge \right|\mu_{\beta }^{2} - \mu_{\gamma }^{2} } \right|; \hfill \\ \left| {\nu_{\alpha }^{2} - \nu_{\gamma }^{2} \left| \ge \right|\nu_{\alpha }^{2} - \nu_{\beta }^{2} \left| {{ }\,and\,{ }} \right|\nu_{\alpha }^{2} - \nu_{\gamma }^{2} \left| \ge \right|\nu_{\beta }^{2} - \nu_{\gamma }^{2} } \right|. \hfill \\ \end{gathered} $$

Since $F_{i\mu }$ and $F_{i\nu }$ are strictly monotone decreasing mappings, hence, the latter equations result in

$$ \begin{gathered} F_{i\mu } \left( {\alpha ,\gamma } \right) \le F_{i\mu } \left( {\alpha ,\beta } \right){ }\,and\,{ }F_{i\mu } \left( {\alpha ,\gamma } \right) \le F_{i\mu } \left( {\beta ,\gamma } \right); \hfill \\ F_{i\nu } \left( {\alpha ,\gamma } \right) \le F_{i\nu } \left( {\alpha ,\beta } \right){ }\,and\,{ }F_{i\nu } \left( {\alpha ,\gamma } \right) \le F_{i\nu } \left( {\beta ,\gamma } \right). \hfill \\ \end{gathered} $$

Using the monotonicity property of both t-norm $\tau$ and s-norm $\sigma$ along with the latter relations, we get

$$ \tau \left( {F_{i\mu } \left( {\alpha ,\gamma } \right) \le F_{i\nu } \left( {\alpha ,\gamma } \right)} \right) \le \tau \left( {F_{i\mu } \left( {\alpha ,\beta } \right) \le F_{i\nu } \left( {\alpha ,\beta } \right)} \right), $$

(28)

$$ \tau \left( {F_{i\mu } \left( {\alpha ,\gamma } \right) \le F_{i\nu } \left( {\alpha ,\gamma } \right)} \right) \le \tau \left( {F_{i\mu } \left( {\beta ,\gamma } \right) \le F_{i\nu } \left( {\beta ,\gamma } \right)} \right); $$

(29)

$$ \sigma \left( {F_{i\mu } \left( {\alpha ,\gamma } \right) \le F_{i\nu } \left( {\alpha ,\gamma } \right)} \right) \le \sigma \left( {F_{i\mu } \left( {\alpha ,\beta } \right) \le F_{i\nu } \left( {\alpha ,\beta } \right)} \right), $$

(30)

$$ \sigma \left( {F_{i\mu } \left( {\alpha ,\gamma } \right) \le F_{i\nu } \left( {\alpha ,\gamma } \right)} \right) \le \sigma \left( {F_{i\mu } \left( {\beta ,\gamma } \right) \le F_{i\nu } \left( {\beta ,\gamma } \right)} \right). $$

(31)

On the other hand, $0 \le \mu_{\alpha } \le \mu_{\beta } \le \mu_{\gamma } \le 1$ and $1 \ge \nu_{\alpha } \ge \nu_{\beta } \ge \nu_{\gamma } \ge 0$ give rise to

$$ d_{L} \left( {\alpha ,\gamma } \right) \ge d_{L} \left( {\alpha ,\beta } \right){ }\,and\,{ }d_{L} \left( {\alpha ,\gamma } \right) \ge d_{L} \left( {\beta ,\gamma } \right) $$

which imply that

$$ 1 - d_{L} \left( {\alpha ,\gamma } \right) \le 1 - d_{L} \left( {\alpha ,\beta } \right){ }\,and\,{ }1 - d_{L} \left( {\alpha ,\gamma } \right) \le 1 - d_{L} \left( {\beta ,\gamma } \right). $$

(32)

Putting together the relations (28)–(32), we easily conclude that

$$ \begin{gathered} S_{\tau } \left( {\alpha ,\gamma } \right) \le S_{\tau } \left( {\alpha ,\beta } \right){ }\,and\,{ }S_{\tau } \left( {\alpha ,\gamma } \right) \le S_{\tau } \left( {\beta ,\gamma } \right); \hfill \\ S_{\sigma } \left( {\alpha ,\gamma } \right) \le S_{\sigma } \left( {\alpha ,\beta } \right){ }\,and\,{ }S_{\sigma } \left( {\alpha ,\gamma } \right) \le S_{\sigma } \left( {\beta ,\gamma } \right). \hfill \\ \end{gathered} $$

Proof of ($S_{*} 4$): For any $i = 1,2,4,6$, we suppose that $\alpha = \langle \mu_{\alpha } ,\nu_{\alpha } \rangle$ is a crisp set, that is, $\alpha = \langle 1,0\rangle$ or $\alpha = \langle 0,1\rangle$. Then, $d_{L} \left( {\alpha ,\overline{\alpha }} \right) = 1$. On the other hand, from Lemma 2.6, we result in

$$ \begin{gathered} F_{i\mu } \left( {\alpha ,\overline{\alpha }} \right) = 0, \hfill \\ F_{i\nu } \left( {\alpha ,\overline{\alpha }} \right) = 0, \hfill \\ \end{gathered} $$

which imply that $\tau \left( {0,0} \right) = 0$ and $\sigma \left( {0,0} \right) = 0$. Hence, we conclude that $S_{\tau } \left( {\alpha ,\overline{\alpha }} \right) = 0$ and $S_{\sigma } \left( {\alpha ,\overline{\alpha }} \right) = 0$.

We now indicate how we are going to extend the class of proposed similarity measures for PFVs to those by taking the above-mentioned t-norms and s-norms into account:

• Algebraic norm-based similarity measures:

  $$ S_{{\tau_{1} }} \left( {\alpha ,\beta } \right) = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + \tau_{1} \left( {F_{i\mu } \left( {\alpha ,\beta } \right),F_{i\nu } \left( {\alpha ,\beta } \right)} \right)} \right] = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + F_{i\mu } \left( {\alpha ,\beta } \right)F_{i\nu } \left( {\alpha ,\beta } \right)} \right]; $$

  (33)
  $$ \begin{aligned} S_{{\sigma_{1} }} \left( {\alpha ,\beta } \right) & = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + \sigma_{1} \left( {F_{i\mu } \left( {\alpha ,\beta } \right),F_{i\nu } \left( {\alpha ,\beta } \right)} \right)} \right] \\ & = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + F_{i\mu } \left( {\alpha ,\beta } \right) + F_{i\nu } \left( {\alpha ,\beta } \right) - F_{i\mu } \left( {\alpha ,\beta } \right)F_{i\nu } \left( {\alpha ,\beta } \right)} \right]; \\ \end{aligned} $$

  (34)

• Einstein norm-based similarity measures:

  $$ S_{{\tau_{2} }} \left( {\alpha ,\beta } \right) = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + \tau_{2} \left( {F_{i\mu } \left( {\alpha ,\beta } \right),F_{i\nu } \left( {\alpha ,\beta } \right)} \right)\left] { = \frac{1}{2}} \right[1 - d_{L} \left( {\alpha ,\beta } \right) + \frac{{F_{i\mu } \left( {\alpha ,\beta } \right)F_{i\nu } \left( {\alpha ,\beta } \right)}}{{1 + \left( {1 - F_{i\mu } \left( {\alpha ,\beta } \right)} \right)\left( {1 - F_{i\nu } \left( {\alpha ,\beta } \right)} \right)}}} \right]; $$

  (35)
  $$ S_{{\sigma_{2} }} \left( {\alpha ,\beta } \right) = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + \sigma_{2} \left( {F_{i\mu } \left( {\alpha ,\beta } \right),F_{i\nu } \left( {\alpha ,\beta } \right)} \right)\left] { = \frac{1}{2}} \right[1 - d_{L} \left( {\alpha ,\beta } \right) + \frac{{F_{i\mu } \left( {\alpha ,\beta } \right) + F_{i\nu } \left( {\alpha ,\beta } \right)}}{{1 + F_{i\mu } \left( {\alpha ,\beta } \right)F_{i\nu } \left( {\alpha ,\beta } \right)}}} \right]; $$

  (36)

• Hamacher norm-based similarity measures:

  $$ \begin{aligned} S_{{\tau_{3} }} \left( {\alpha ,\beta } \right) & = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + \tau_{3} \left( {F_{i\mu } \left( {\alpha ,\beta } \right),F_{i\nu } \left( {\alpha ,\beta } \right)} \right)} \right] \\ & = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + \frac{{F_{i\mu } \left( {\alpha ,\beta } \right)F_{i\nu } \left( {\alpha ,\beta } \right)}}{{ + \left( {1 - } \right)\left( {F_{i\mu } \left( {\alpha ,\beta } \right) + F_{i\nu } \left( {\alpha ,\beta } \right) - F_{i\mu } \left( {\alpha ,\beta } \right)F_{i\nu } \left( {\alpha ,\beta } \right)} \right)}}} \right]; \\ \end{aligned} $$

  (37)
  $$ \begin{gathered} S_{{\sigma_{3} }} \left( {\alpha ,\beta } \right) = \frac{1}{2} \hfill \\ \left[ \begin{gathered} 1 - d_{L} \left( {\alpha ,\beta } \right) + \sigma_{3} \left( {F_{i\mu } \left( {\alpha ,\beta } \right),F_{i\nu } \left( {\alpha ,\beta } \right)} \right)\left] { = \frac{1}{2}} \right[1 - d_{L} \left( {\alpha ,\beta } \right) + \hfill \\ \frac{{F_{i\mu } \left( {\alpha ,\beta } \right) + F_{i\nu } \left( {\alpha ,\beta } \right) - F_{i\mu } \left( {\alpha ,\beta } \right)F_{i\nu } \left( {\alpha ,\beta } \right) - \left( {1 - } \right)F_{i\mu } \left( {\alpha ,\beta } \right)F_{i\nu } \left( {\alpha ,\beta } \right)}}{{1 - \left( {1 - } \right)F_{i\mu } \left( {\alpha ,\beta } \right)F_{i\nu } \left( {\alpha ,\beta } \right)}} \hfill \\ \end{gathered} \right], \in > 0; \hfill \\ \end{gathered} $$

  (38)

• Frank norm-based similarity measures:

  $$ \begin{aligned} S_{{\tau_{4} }} \left( {\alpha ,\beta } \right) & = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + \tau_{4} \left( {F_{i\mu } \left( {\alpha ,\beta } \right),F_{i\nu } \left( {\alpha ,\beta } \right)} \right)} \right] \\ & = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + log \left( {1 + \frac{{\left( {^{{F_{i\mu } \left( {\alpha ,\beta } \right)}} - 1} \right)\left( {^{{F_{i\nu } \left( {\alpha ,\beta } \right)}} - 1} \right)}}{ - 1}} \right)} \right]; \\ \end{aligned} $$

  (39)
  $$ \begin{aligned} S_{{\sigma _{4}^{ \in } }} \left( {\alpha ,\beta } \right) & = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + \sigma _{4}^{ \in } \left( {F_{{i\mu }} \left( {\alpha ,\beta } \right),F_{{i\nu }} \left( {\alpha ,\beta } \right)} \right)} \right] \\ & = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + 1 - log_{ \in } \left( {1 + \frac{{\left( { \in ^{{1 - F_{{i\mu }} \left( {\alpha ,\beta } \right)}} - 1} \right)\left( { \in ^{{1 - F_{{iv}} \left( {\alpha ,\beta } \right)}} - 1} \right)}}{{ \in - 1}}} \right)} \right], \in > 0 \\ \end{aligned}$$

  (40)

The above formulas will be more specific, if we replace $F_{i\mu }$ and $F_{i\nu }$ with those given by (1–6) and (7–12). For instance, by taking $d_{L} \left( {\alpha ,\beta } \right)$ as given by (25) and Algebraic norm-based similarity measures, we are able to construct the following similarity measures for PFVs:

$$ \begin{aligned} S_{{\tau_{1} }} \left( {\alpha ,\beta } \right) & = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + F_{1\mu } \left( {\alpha ,\beta } \right)F_{1\nu } \left( {\alpha ,\beta } \right)} \right] \\ & = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + \left( {1 - \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|} \right)\left( {1 - \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|} \right)} \right]; \\ S_{{\sigma_{1} }} \left( {\alpha ,\beta } \right) & = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + F_{1\mu } \left( {\alpha ,\beta } \right) + F_{1\nu } \left( {\alpha ,\beta } \right) - F_{1\mu } \left( {\alpha ,\beta } \right)F_{1\nu } \left( {\alpha ,\beta } \right)} \right] \\ & = \frac{1}{2}\left[ {1 - d_{L} \left( {\alpha ,\beta } \right) + \left( {1 - \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|} \right) + \left( {1 - \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|} \right) - \left( {1 - \left| {\mu_{\alpha }^{2} - \mu_{\beta }^{2} } \right|} \right)\left( {1 - \left| {\nu_{\alpha }^{2} - \nu_{\beta }^{2} } \right|} \right)} \right]. \\ \end{aligned} $$

We are now in a position to extend the proposed similarity measures for PFVs to those for PFSs as follows:

$$ S_{*} \left( {\alpha ,\beta } \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} S_{*} \left( {\alpha \left( {x_{i} } \right),\beta \left( {x_{i} } \right)} \right), $$

(41)

where ${*}$ may be by $\tau$ or $\sigma$.

4 Investigating PFS similarity measures from microscopic and macroscopic viewpoints

In this section, we compare thoroughly the performance of proposed similarity measures for PFSs with that of existing similarity measures from the microscopy and macroscopy viewpoints. Here, we employ the common data sets which were already considered in Nguyen et al. (2019); Peng 2018; Peng and Garg 2019; Peng et al. 2017).

Before that and in order to provide the information required for conducting the comparison, we describe here those similarity measures studied priorly (see (Nguyen et al. 2019; Peng 2018; Peng and Garg 2019; Peng et al. 2017)).

Given two PFSs $\alpha = \langle \mu_{\alpha } ,\nu_{\alpha } \rangle$ $\beta = \langle \mu_{\beta } ,\nu_{\beta } \rangle$ on $X = \left\{ {x_{1} ,x_{2} ,...,x_{n} } \right\}$ the considered PFS similarity measures might be briefly described as:

• Li et al.’s measure (Li et al. 2007)

  $$ S_{L} \left( {\alpha ,\beta } \right) = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {S_{\mu }^{2} \left( {x_{i} } \right) + S_{\nu }^{2} \left( {x_{i} } \right)} \right)}}{2n}, $$

  (42)

  where $S_{\mu } \left( {x_{i} } \right) = \mu_{\alpha } \left( {x_{i} } \right) - \mu_{\beta } \left( {x_{i} } \right)$ and $S_{\nu } \left( {x_{i} } \right) = \nu_{\alpha } \left( {x_{i} } \right) - \nu_{\beta } \left( {x_{i} } \right)$.

• Chen’s measure (Chen 1997)

  $$ S_{C} \left( {\alpha ,\beta } \right) = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left| {S_{\alpha } \left( {x_{i} } \right) - S_{\beta } \left( {x_{i} } \right)} \right|}}{2n}, $$

  (43)

  where $S_{\alpha } \left( {x_{i} } \right) = \mu_{\alpha } \left( {x_{i} } \right) - \nu_{\alpha } \left( {x_{i} } \right)$ and $S_{\beta } \left( {x_{i} } \right) = \mu_{\beta } \left( {x_{i} } \right) - \nu_{\beta } \left( {x_{i} } \right)$

• Chen and Chang’s measure (Chen and Chang 2015)

  $$ S_{CC} \left( {\alpha ,\beta } \right) = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left[ {\left| {\mu_{\alpha } \left( {x_{i} } \right) - \mu_{\beta } \left( {x_{i} } \right)} \right| + \left( {\mathop \smallint \nolimits_{0}^{1} \left| {\mu_{{\alpha_{{x_{i} }} }} \left( u \right) - \mu_{{\beta_{{x_{i} }} }} \left( u \right)} \right|du} \right)} \right] \times \left( {\frac{{\pi_{\alpha } \left( {x_{i} } \right) - \pi_{\beta } \left( {x_{i} } \right)}}{2}} \right)}}{n}, $$

  (44)

  where

  $$ \mu_{{\alpha_{{x_{i} }} }} \left( u \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & { if\,{ } u = \mu_{\alpha } \left( {x_{i} } \right) = 1 - \nu_{\alpha } \left( {x_{i} } \right); } \hfill \\ {\frac{{1 - \nu_{\alpha } \left( {x_{i} } \right) - u}}{{1 - \mu_{\alpha } \left( {x_{i} } \right) - \nu_{\alpha } \left( {x_{i} } \right)}},} \hfill & { if\, { }u \in \left[ {\mu_{\alpha } \left( {x_{i} } \right),1 - \nu_{\alpha } \left( {x_{i} } \right)} \right]; } \hfill \\ {0,} \hfill & { Otherwise; } \hfill \\ \end{array} } \right. $$

  (45)

• Hung and Yang’s measures (Hung and Yang 2004)

  $$ S_{HY1} \left( {\alpha ,\beta } \right) = 1 - d_{H} \left( {\alpha ,\beta } \right), $$

  (46)
  $$ S_{HY2} \left( {\alpha ,\beta } \right) = \frac{{e^{{ - d_{H} \left( {\alpha ,\beta } \right)}} - e^{ - 1} }}{{1 - e^{ - 1} }}, $$

  (47)
  $$ S_{HY3} \left( {\alpha ,\beta } \right) = \frac{{1 - d_{H} \left( {\alpha ,\beta } \right)}}{{1 + d_{H} \left( {\alpha ,\beta } \right)}}, $$

  (48)

  where $d_{H} \left( {\alpha ,\beta } \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} {\text{max}}\left\{ {\left| {\mu_{\alpha } \left( {x_{i} } \right) - \mu_{\beta } \left( {x_{i} } \right)\left| , \right|\nu_{\alpha } \left( {x_{i} } \right) - \nu_{\beta } \left( {x_{i} } \right)} \right|} \right\}$.

• Hong and Kim’s measure (Hong and Kim 1999)

  $$ S_{HK} \left( {\alpha ,\beta } \right) = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\left| {\mu_{\alpha } \left( {x_{i} } \right) - \mu_{\beta } \left( {x_{i} } \right)\left| + \right|\nu_{\alpha } \left( {x_{i} } \right) - \nu_{\beta } \left( {x_{i} } \right)} \right|} \right)}}{2n}. $$

  (49)

• Li and Cheng’s measure (Li and Cheng 2002)

  $$ S_{LC} \left( {\alpha ,\beta } \right) = 1 - \sqrt[p]{{\frac{{\mathop \sum \nolimits_{i = 1}^{n} |\psi_{\alpha } \left( {x_{i} } \right) - \psi_{\beta } \left( {x_{i} } \right)|^{p} }}{n}}}, $$

  (50)

  where $\psi_{\alpha } \left( {x_{i} } \right) = \frac{{\mu_{\alpha } \left( {x_{i} } \right) + 1 - \nu_{\alpha } \left( {x_{i} } \right)}}{2}$ and $\psi_{\beta } \left( {x_{i} } \right) = \frac{{\mu_{\beta } \left( {x_{i} } \right) + 1 - \nu_{\beta } \left( {x_{i} } \right)}}{2}$.

• Li and Xu’s measure (Li and Xu 2001a)

  $$ S_{LX} \left( {\alpha ,\beta } \right) = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\left| {\left( {\mu_{\alpha } \left( {x_{i} } \right) - \nu_{\alpha } \left( {x_{i} } \right)} \right) - \left( {\mu_{\beta } \left( {x_{i} } \right) - \nu_{\beta } \left( {x_{i} } \right)} \right)\left| + \right|\left( {\mu_{\alpha } \left( {x_{i} } \right) - \mu_{\beta } \left( {x_{i} } \right)} \right)\left| + \right|\left( {\nu_{\alpha } \left( {x_{i} } \right) - \nu_{\beta } \left( {x_{i} } \right)} \right)} \right|} \right)}}{4n}. $$

• Liang and Shi’s measures (Liang and Shi 2003)

  $$ S_{LS1} \left( {\alpha ,\beta } \right) = 1 - \sqrt[p]{{\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\phi_{\mu } \left( {x_{i} } \right) + \phi_{\nu } \left( {x_{i} } \right)} \right)}}{n}}}, $$

  (51)

  where $\phi_{\mu } \left( {x_{i} } \right) = \frac{{\left| {\mu_{\alpha } \left( {x_{i} } \right) - \mu_{\beta } \left( {x_{i} } \right)} \right|}}{2}$ $\phi_{\nu } \left( {x_{i} } \right) = \frac{{\left| {\left( {1 - \nu_{\alpha } \left( {x_{i} } \right)} \right) - \left( {1 - \nu_{\beta } \left( {x_{i} } \right)} \right)} \right|}}{2}$ and $1 \le p < \infty$

  $$ S_{LS2} \left( {\alpha ,\beta } \right) = 1 - \sqrt[p]{{\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\varphi_{s1} \left( {x_{i} } \right) + \varphi_{s2} \left( {x_{i} } \right)} \right)}}{n}}}, $$

  (52)

  where

  $$ \begin{gathered} \varphi_{s1} \left( {x_{i} } \right) = \frac{{\left| {m_{\alpha 1} \left( {x_{i} } \right) - m_{\beta 1} \left( {x_{i} } \right)} \right|}}{2}, \hfill \\ \varphi_{s2} \left( {x_{i} } \right) = \frac{{\left| {m_{\alpha 2} \left( {x_{i} } \right) - m_{\beta 2} \left( {x_{i} } \right)} \right|}}{2}, \hfill \\ m_{\alpha 1} \left( {x_{i} } \right) = \frac{{\left( {\mu_{\alpha } \left( {x_{i} } \right) + m_{\alpha } \left( {x_{i} } \right)} \right)}}{2}, \hfill \\ m_{\beta 1} \left( {x_{i} } \right) = \frac{{\left( {\mu_{\beta } \left( {x_{i} } \right) + m_{\beta } \left( {x_{i} } \right)} \right)}}{2}, \hfill \\ m_{\alpha 2} \left( {x_{i} } \right) = \frac{{\left( {1 - \nu_{\alpha } \left( {x_{i} } \right) + m_{\alpha } \left( {x_{i} } \right)} \right)}}{2}, \hfill \\ m_{\beta 2} \left( {x_{i} } \right) = \frac{{\left( {1 - \nu_{\beta } \left( {x_{i} } \right) + m_{\beta } \left( {x_{i} } \right)} \right)}}{2}, \hfill \\ m_{\alpha } \left( {x_{i} } \right) = \frac{{\left( {1 - \nu_{\alpha } \left( {x_{i} } \right) + \mu_{\alpha } \left( {x_{i} } \right)} \right)}}{2}, \hfill \\ m_{\beta } \left( {x_{i} } \right) = \frac{{\left( {1 - \nu_{\beta } \left( {x_{i} } \right) + \mu_{\beta } \left( {x_{i} } \right)} \right)}}{2}, \hfill \\ 1 \le p < \infty \hfill \\ \end{gathered} $$
  $$ S_{LS3} \left( {\alpha ,\beta } \right) = 1 - \sqrt[p]{{\frac{{\mathop \sum \nolimits_{i = 1}^{n} (\eta_{1} \left( i \right) + \eta_{2} \left( i \right) + \eta_{3} \left( i \right))^{p} }}{3n}}}, $$

  (53)

  where

  $$ \begin{gathered} \eta_{1} \left( i \right) = \phi_{\mu } \left( {x_{i} } \right) + \phi_{\nu } \left( {x_{i} } \right), \hfill \\ {\text{or}}\;\eta_{1} \left( i \right) = \varphi_{s1} \left( {x_{i} } \right) + \varphi_{s2} \left( {x_{i} } \right), \hfill \\ \eta_{2} \left( i \right) = \left| {\psi_{\alpha } \left( {x_{i} } \right) - \psi_{\beta } \left( {x_{i} } \right)} \right|, \hfill \\ \eta_{3} \left( i \right) = {\text{max}}\left\{ {l_{\alpha } \left( i \right),l_{\beta } \left( i \right)} \right\} - {\text{min}}\left\{ {l_{\alpha } \left( i \right),l_{\beta } \left( i \right)} \right\} \hfill \\ \end{gathered} $$

  where

  $$ \begin{gathered} l_{\alpha } \left( i \right) = \frac{{\left( {1 - \nu_{\alpha } \left( {x_{i} } \right) - \mu_{\alpha } \left( {x_{i} } \right)} \right)}}{2}, \hfill \\ l_{\beta } \left( i \right) = \frac{{\left( {1 - \nu_{\beta } \left( {x_{i} } \right) - \mu_{\beta } \left( {x_{i} } \right)} \right)}}{2}, \hfill \\ 1 \le p < \infty \hfill \\ \end{gathered} $$

• Mitchell’s measure (Mitchell 2003)

  $$ S_{M} \left( {\alpha ,\beta } \right) = \frac{1}{2}\left( {\rho_{\mu } \left( {\alpha ,\beta } \right) + \rho_{\nu } \left( {\alpha ,\beta } \right)} \right), $$

  (54)

  where $\rho_{\mu } \left( {\alpha ,\beta } \right) = 1 - \sqrt[p]{{\frac{{\mathop \sum \nolimits_{i = 1}^{n} |\mu_{\alpha } \left( {x_{i} } \right) - \mu_{\beta } \left( {x_{i} } \right)|^{p} }}{n}}}$ and $\rho_{\nu } \left( {\alpha ,\beta } \right) = 1 - \sqrt[p]{{\frac{{\mathop \sum \nolimits_{i = 1}^{n} |\nu_{\alpha } \left( {x_{i} } \right) - \nu_{\beta } \left( {x_{i} } \right)|^{p} }}{n}}},{ }1 \le p < \infty$.

• Ye’s measure (Ye 2011)

  $$ S_{Y} \left( {\alpha ,\beta } \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \frac{{\mu_{\alpha } \left( {x_{i} } \right)\mu_{\beta } \left( {x_{i} } \right) + \nu_{\alpha } \left( {x_{i} } \right)\nu_{\beta } \left( {x_{i} } \right)}}{{\sqrt {\mu_{\alpha }^{2} \left( {x_{i} } \right) + \nu_{\alpha }^{2} \left( {x_{i} } \right)} \sqrt {\mu_{\beta }^{2} \left( {x_{i} } \right) + \nu_{\beta }^{2} \left( {x_{i} } \right)} }}. $$

  (55)

• Wei and Wei’s measure (Wei and Wei 2018)

  $$ S_{WW} \left( {\alpha ,\beta } \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \frac{{\mu_{\alpha }^{2} \left( {x_{i} } \right)\mu_{\beta }^{2} \left( {x_{i} } \right) + \nu_{\alpha }^{2} \left( {x_{i} } \right)\nu_{\beta }^{2} \left( {x_{i} } \right)}}{{\sqrt {\mu_{\alpha }^{4} \left( {x_{i} } \right) + \nu_{\alpha }^{4} \left( {x_{i} } \right)} \sqrt {\mu_{\beta }^{4} \left( {x_{i} } \right) + \nu_{\beta }^{4} \left( {x_{i} } \right)} }} $$

  (56)

• Zhang’s measure (Zhang 2016)

  $${S}_{Z}(\alpha ,\beta )=\frac{1}{n}\sum_{i=1}^{n}(|{\mu }_{\alpha }^{2}({x}_{i})-{\nu }_{\beta }^{2}({x}_{i})|+|{\nu }_{\alpha }^{2}({x}_{i})-{\nu }_{\beta }^{2}({x}_{i})|+|{\pi }_{\alpha }^{2}({x}_{i})-{\pi }_{\beta }^{2}({x}_{i})|) /(|{\mu }_{\alpha }^{2}({x}_{i})-{\mu }_{\beta }^{2}({x}_{i})|+|{\nu }_{\alpha }^{2}({x}_{i})-{\nu }_{\beta }^{2}({x}_{i})|+|{\pi }_{\alpha }^{2}({x}_{i})-{\pi }_{\beta }^{2}({x}_{i})|+|{\mu }_{\alpha }^{2}({x}_{i})-{\nu }_{\beta }^{2}({x}_{i})|+|{\mu }_{\beta }^{2}({x}_{i})-{\nu }_{\alpha }^{2}({x}_{i})|+|{\pi }_{\alpha }^{2}({x}_{i})-{\pi }_{\beta }^{2}({x}_{i})|).$$

  (57)

• Peng et al.’s measures (Peng et al. 2017)

  $$ S_{P1} \left( {\alpha ,\beta } \right) = 1 - \frac{1}{2n}\mathop \sum \limits_{i = 1}^{n} \left| {\left( {\mu_{\beta }^{2} \left( {x_{i} } \right) - \nu_{\alpha }^{2} \left( {x_{i} } \right)} \right) - \left( {\mu_{\beta }^{2} \left( {x_{i} } \right) - \nu_{\beta }^{2} \left( {x_{i} } \right)} \right)} \right|, $$

  (58)
  $$ S_{P2} \left( {\alpha ,\beta } \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \frac{{\left( {\mu_{\alpha }^{2} \left( {x_{i} } \right) \wedge \mu_{\beta }^{2} \left( {x_{i} } \right)} \right) + \left( {\nu_{\alpha }^{2} \left( {x_{i} } \right) \wedge \nu_{\beta }^{2} \left( {x_{i} } \right)} \right)}}{{\left( {\mu_{\alpha }^{2} \left( {x_{i} } \right) \vee \mu_{\beta }^{2} \left( {x_{i} } \right)} \right) + \left( {\nu_{\alpha }^{2} \left( {x_{i} } \right) \vee \nu_{\beta }^{2} \left( {x_{i} } \right)} \right)}}, $$

  (59)
  $$ S_{P3} \left( {\alpha ,\beta } \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \frac{{\left( {\mu_{\alpha }^{2} \left( {x_{i} } \right) \wedge \mu_{\beta }^{2} \left( {x_{i} } \right)} \right) + \left( {1 - \nu_{\alpha }^{2} \left( {x_{i} } \right) \wedge 1 - \nu_{\beta }^{2} \left( {x_{i} } \right)} \right)}}{{\left( {\mu_{\alpha }^{2} \left( {x_{i} } \right) \vee \mu_{\beta }^{2} \left( {x_{i} } \right)} \right) + \left( {1 - \nu_{\alpha }^{2} \left( {x_{i} } \right) \vee 1 - \nu_{\beta }^{2} \left( {x_{i} } \right)} \right)}}. $$

  (60)

  where $\wedge$ and $\vee$ indicate the operators $\mathrm{min}$ and $\mathrm{max}$, respectively.

• Boran and Akay’s measure (Boran and Akay 2014)

  $$ \begin{gathered} S_{BA} \left( {\alpha ,\beta } \right) \hfill \\ = 1 - \sqrt[p]{{\frac{{\mathop \sum \nolimits_{i = 1}^{n} (\left| {k\left( {\mu_{\alpha } \left( {x_{i} } \right) - \mu_{\beta } \left( {x_{i} } \right)} \right) - \left( {\nu_{\alpha } \left( {x_{i} } \right) - \nu_{\beta } \left( {x_{i} } \right)} \right)|^{p} + } \right|\left( {\mu_{\alpha } \left( {x_{i} } \right) - \mu_{\beta } \left( {x_{i} } \right)} \right) - k\left( {\nu_{\alpha } \left( {x_{i} } \right) - \nu_{\beta } \left( {x_{i} } \right)} \right)|^{p} }}{{2n(k + 1)^{p} }}}}, \hfill \\ { }1 \le p < \infty . \hfill \\ \end{gathered} $$

  (61)

• Nguyen et al.’s measures (Nguyen et al. 2019)

  $$ S_{N0} \left( {\alpha ,\beta } \right) = \mathop \sum \limits_{i = 1}^{n} e^{{ - \left| {\mu_{\alpha }^{2} \left( {x_{i} } \right) - \mu_{\beta }^{2} \left( {x_{i} } \right)} \right|}} \times e^{{ - \left| {\nu_{\alpha }^{2} \left( {x_{i} } \right) - \nu_{\beta }^{2} \left( {x_{i} } \right)} \right|}} , $$

  (62)
  $$ S_{N1} \left( {\alpha ,\beta } \right) = \mathop \sum \limits_{i = 1}^{n} \frac{{e^{{ - \left| {\mu_{\alpha }^{2} \left( {x_{i} } \right) - \mu_{\beta }^{2} \left( {x_{i} } \right)} \right|}} + e^{{ - \left| {\nu_{\alpha }^{2} \left( {x_{i} } \right) - \nu_{\beta }^{2} \left( {x_{i} } \right)} \right|}} }}{2}. $$

  (63)

• Peng and Garg’s measures (Peng and Garg 2019)

  $$ \begin{aligned} S_{PG1} \left( {\alpha ,\beta } \right) & = 1 - \sqrt[p]{{\frac{1}{{2n\lambda_{k}^{p} }}\mathop \sum \limits_{i = 1}^{n} |\left( {\lambda_{k} - 1} \right)\left( {\mu_{\alpha }^{2} \left( {x_{i} } \right) - \mu_{\beta }^{2} \left( {x_{i} } \right)} \right) - \left( {\nu_{\alpha }^{2} \left( {x_{i} } \right) - \nu_{\beta }^{2} \left( {x_{i} } \right)} \right)|^{p} }} \\ & \quad \overline{{ + |\left( {\lambda_{k} - k} \right)\left( {\nu_{\alpha }^{2} \left( {x_{i} } \right) - \nu_{\beta }^{2} \left( {x_{i} } \right)} \right) - k\left( {\mu_{\alpha }^{2} \left( {x_{i} } \right) - \mu_{\beta }^{2} \left( {x_{i} } \right)} \right)|^{p} }} ; \\ \end{aligned} $$

  (64)
  $$ \begin{gathered} S_{PG2} \left( {\alpha ,\beta } \right) = 1 - \sqrt[p]{{\frac{1}{{n\lambda_{k}^{p} }}\mathop \sum \limits_{i = 1}^{n} {\text{max}}\{ |\left( {\lambda_{k} - 1} \right)\left( {\mu_{\alpha }^{2} \left( {x_{i} } \right) - \mu_{\beta }^{2} \left( {x_{i} } \right)} \right) - \left( {\nu_{\alpha }^{2} \left( {x_{i} } \right) - \nu_{\beta }^{2} \left( {x_{i} } \right)} \right)|^{p} }} \hfill \\ \overline{{,|\left( {\lambda_{k} - k} \right)\left( {\nu_{\alpha }^{2} \left( {x_{i} } \right) - \nu_{\beta }^{2} \left( {x_{i} } \right)} \right) - k\left( {\mu_{\alpha }^{2} \left( {x_{i} } \right) - \mu_{\beta }^{2} \left( {x_{i} } \right)} \right)|^{p} \} }} ,\, \lambda_{k} \ge k + 1,{ }k \ge 0,1 \le p < \infty \hfill \\ \end{gathered} $$

  (65)

• Peng et al.’s measure (Peng et al. 2017)

  $$ S_{PYY} \left( {\alpha ,\beta } \right) = 1 - \frac{1}{2n}\mathop \sum \limits_{i = 1}^{n} \left( {\left| {\mu_{\alpha }^{2} \left( {x_{i} } \right) - \mu_{\beta }^{2} \left( {x_{i} } \right)\left| + \right|\nu_{\alpha }^{2} \left( {x_{i} } \right) - \nu_{\beta }^{2} \left( {x_{i} } \right)\left| + \right|\pi_{\alpha }^{2} \left( {x_{i} } \right) - \pi_{\beta }^{2} \left( {x_{i} } \right)} \right|} \right); $$

  (66)

• Peng’s measures (Peng 2018)

  $$ \begin{aligned} S_{P} \left( {\alpha ,\beta } \right) & = 1 - \sqrt[p]{{\frac{1}{{2n(\lambda + 1)^{p} }}\mathop \sum \limits_{i = 1}^{n} |\left( {\lambda + 1 - a} \right)\left( {\mu_{\alpha }^{2} \left( {x_{i} } \right) - \mu_{\beta }^{2} \left( {x_{i} } \right)} \right) - a\left( {\nu_{\alpha }^{2} \left( {x_{i} } \right) - \nu_{\beta }^{2} \left( {x_{i} } \right)} \right)|^{p} }} \\ \overline{\begin{aligned} & \quad + |\left( {\lambda + 1 - b} \right)\left( {\nu_{\alpha }^{2} \left( {x_{i} } \right) - \nu_{\beta }^{2} \left( {x_{i} } \right)} \right) \\ & \quad - b\left( {\mu_{\alpha }^{2} \left( {x_{i} } \right) - \mu_{\beta }^{2} \left( {x_{i} } \right)} \right)|^{p} \\ \end{aligned} } ; \\ 0\left\langle {a,b,a + b \le \lambda + 1,{ }\lambda } \right\rangle 0,1 \le p < \infty . \\ \end{aligned} $$

  (67)

  In the next portion, we are going to present evaluations on the proposed PFS similarity measures compared to the above-mentioned similarity measures from two stages: the microscopy process and the macroscopy process. The latter process allows us to know how the results are actually obtained on the basis of structural form of similarity measures, and the former process enables us to judge about the results of similarity measures without considering how they have been concluded.

4.1 Microscopic process of comparison

In order for having a more precise comparison, we re-consider in Table 1 the six sets of PFVs which are evaluated using the similarity measures $S_{L}$ (Chen 1997; Chen and Chang 2015; Hung and Yang 2004; Hung and Yang 2004; Hung and Yang 2004; Hong and Kim 1999; Li and Cheng 2002; Li and Xu 2001a; Li et al. 2007; Liang and Shi 2003; Liang and Shi 2003; Liang and Shi 2003; Mitchell 2003; Peng et al. 2017; Peng et al. 2017; Peng et al. 2017; Wei and Wei 2018; Ye 2011; Zhang 2016), and $S_{BA}$ (Boran and Akay 2014).

Table 1 The comparison of existing and proposed similarity measures

By referring to the axioms given in Theorem 3.2, we observe that the above-mentioned similarity measures still have some problems:

• A violation of axiom $\left( {S_{*} 2} \right)$ can be derived from Set 1 in which $S_{C} \left( {\alpha ,\beta } \right) = S_{LC} \left( {\alpha ,\beta } \right) = S_{Y} \left( {\alpha ,\beta } \right) = S_{WW} \left( {\alpha ,\beta } \right) = S_{{P_{1} }} \left( {\alpha ,\beta } \right) = 1$ meanwhile, $\alpha = \left\{ {\langle x,0.3,0.3\rangle } \right\}$ and $\beta = \left\{ {\langle x,0.4,0.4\rangle } \right\}$ are not the same.

• It is seen from Set 2 that $S_{Z} \left( {\alpha ,\beta } \right) = 0$ and from Set 3 that $S_{HY1} \left( {\alpha ,\beta } \right) = S_{HY2} \left( {\alpha ,\beta } \right) = S_{HY3} \left( {\alpha ,\beta } \right) = S_{{P_{2} }} \left( {\alpha ,\beta } \right) = 0$ while $\beta \overline{\alpha }$These results indicate a violation of axiom $\left( {S_{*} 4} \right)$

• An inspection of the values listed in Table 1 indicates that the bold data show difficulty in differentiating the differences between PFVs. For instance, the value of $0.9$ which corresponds to $S_{L}$in Sets 1, 2 and 5; the value of $1$ that corresponds to $S_{C}$in Sets 1, 4 and 5; and so on.

In Table 1 and subsequent tables, we will assume that $p = 1$ in $S_{M}$ $S_{LS1}$ $S_{LS2}$ $S_{LS3}$ and $\lambda = 2$ in $S_{BA}$. The bold data indicates unreasonable results, and the notation $N/A$ indicates that the corresponding similarity measure suffers from the problem of division by zero.

In view of the discussions presented in Subsection 4.1, we still observe that most of existing similarity measures have some drawbacks in Tables 2 and 3 (highlighted by the bold font).

4.2 Macroscopic process of comparison

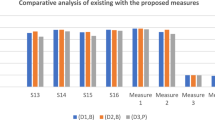
In order to compare the behaviour of existing and proposed similarity measures, we depict the graphs of existing similarity measures $S_{L}$ to $S_{BA}$ given in the first block of Table 1 together with their aggregated measure in circle-dotted line in Fig. 1. Furthermore, we plot the graphs of proposed similarity measures $S_{{\tau_{1} }}$ to $S_{{\tau_{4} }}$ given in the third block of Table 1 together with their aggregated measure (in magenta circle-dotted line) and the aggregated measure of existing similarity measures $S_{L}$ to $S_{BA}$ (in black circle-dotted line) in Figs. 2, 3, 4, 5, 6 It needs to be mentioned that the aggregated measures of all six sets of PFVs in Figs. 1 and 2 are respectively the arithmetic mean of existing similarity measures $S_{L}$ to $S_{BA}$ and proposed similarity measures $S_{{\tau_{1} }}$ to $S_{{\tau_{4} }}$.

Fig. 1

The graphs of existing similarity measures $S_{L}$ to $S_{BA}$ given in Table 1 together with their aggregated measure in circle-dotted line

Fig. 2

The graphs of proposed similarity measures $S_{{\tau_{1} }}$ to $S_{{\tau_{4} }}$ given in Table 1 together with their aggregated measure (in magenta circle-dotted line) and the aggregated measure of existing similarity measures $S_{L}$ to $S_{BA}$ (in black circle-dotted line)

Fig. 3

The graphs of existing similarity measures $S_{L}$ to $S_{BA}$ given in Table 2 together with their aggregated measure in circle-dotted line

Fig. 4

The graphs of proposed similarity measures $S_{{\tau_{1} }}$ to $S_{{\tau_{4} }}$ given in Table 2 together with their aggregated measure (in magenta circle-dotted line) and the aggregated measure of existing similarity measures $S_{L}$ to $S_{BA}$ (in black circle-dotted line)

Table 2 The comparison of existing and proposed similarity measures

Fig. 5

The graphs of existing similarity measures $S_{L}$ to $S_{BA}$. given in Table 3 together with their aggregated measure in circle-dotted line

Table 3 The comparison of existing and proposed similarity measures

Fig. 6

The graphs of proposed similarity measures $S_{{\tau_{1} }}$ to $S_{{\tau_{4} }}$ given in Table 3 together with the aggregated measure (in magenta circle-dotted line) and the aggregated measure of existing similarity measures $S_{L}$ to $S_{BA}$ (in black circle-dotted line)

From Fig. 2, we observe that the aggregated measures of existing similarity measures $S_{L}$ to $S_{BA}$ and proposed similarity measures $S_{{\tau_{1} }}$ to $S_{{\tau_{4} }}$ according to the given six sets of PFVs have more or less similar behaviour from macroscopic viewpoint. This is while, the graphs of existing similarity measures $S_{L}$ to $S_{BA}$ (given in Table 1) depicted in Fig. 1 are much more scattered than that of proposed similarity measures $S_{{\tau_{1} }}$ to $S_{{\tau_{4} }}$ (given in Table 1).

In order to have a complete picture of behaviour of existing similarity measures $S_{L}$ to $S_{BA}$ and proposed similarity measures $S_{{\tau_{1} }}$ to $S_{{\tau_{4} }}$ in other cases, such a way of plotting have been provided for the next cases in the subsequent figures.

Figure 7 shows the graphs of proposed similarity measures ${S}_{{\tau }_{1}}$ to ${S}_{{\tau }_{4}^{\epsilon }}$ for ${F}_{4}$ given in the fourth block of Table 1 together with their aggregated measure (in magenta circle-dotted line) and the aggregated measure of ${S}_{N0}$ to ${S}_{P}$ given in the second block of Table 1 (in black circle-dotted line).

Fig. 7

The graphs of proposed similarity measures $S_{{\tau_{1} }}$ to $S_{{\tau_{4} }}$ for $F_{4}$ given in Table 1 together with their aggregated measure (in magenta circle-dotted line) and the aggregated measure of $S_{N0}$ to $S_{P}$ (in black circle-dotted line)

Furthermore, Fig. 8 shows the graphs of proposed similarity measures ${S}_{{\tau }_{1}}$ to ${S}_{{\tau }_{4}^{\epsilon }}$ for ${F}_{6}$ given in the fifth block of Table 1 together with their aggregated measure (in magenta circle-dotted line) and the aggregated measure of ${S}_{N0}$ to ${S}_{P}$ given in the second block of Table 1 (in black circle-dotted line).

Fig. 8

The graphs of proposed similarity measures $S_{{\tau_{1} }}$ to $S_{{\tau_{4} }}$ for $F_{6}$ given in Table 1 together with their aggregated measure (in magenta circle-dotted line) and the aggregated measure of $S_{N0}$ to $S_{P}$ (in black circle-dotted line)

The same process of comparison is also followed by the use of data from Tables 2, 3 in Figs. 9, 10, 11 and 12.

Fig. 9

The graphs of proposed similarity measures $S_{{\tau_{1} }}$ to $S_{{\tau_{4} }}$ for $F_{4}$ given in Table 2 together with their aggregated measure (in magenta circle-dotted line) and the aggregated measure of $S_{N0}$ to $S_{P}$ (in black circle-dotted line)

Fig. 10

The graphs of proposed similarity measures $S_{{\tau_{1} }}$ to $S_{{\tau_{4} }}$ for $F_{6}$ given in Table 2 together with their aggregated measure (in magenta circle-dotted line) and the aggregated measure of $S_{N0}$ to $S_{P}$ (in black circle-dotted line)

Fig. 11

The graphs of proposed similarity measures $S_{{\tau_{1} }}$ to $S_{{\tau_{4} }}$ for $F_{4}$ given in Table 3 together with their aggregated measure (in magenta circle-dotted line) and the aggregated measure of $S_{N0}$ to $S_{P}$ (in black circle-dotted line)

Fig. 12

The graphs of proposed similarity measures $S_{{\tau_{1} }}$ to $S_{{\tau_{4} }}$ for $F_{6}$ given in Table 3 together with their aggregated measure (in magenta circle-dotted line) and the aggregated measure of $S_{N0}$ to $S_{P}$ (in black circle-dotted line)

What seems to be worthwhile from all figures is that the graph of aggregated measure of existing similarity measures behaves similarly as the graph of aggregated measure of proposed similarity measures.

5 Decision making under Pythagorean fuzzy environment

In the following section, we are interested in studying the behaviour of the proposed PFS similarity measures, when they are applied to pattern recognition and medical diagnosis.

5.1 Pattern recognition problem under Pythagorean fuzzy environment

In this part of the contribution, we are going to testify the pattern recognition problems which were considered in Peng et al. (2017) priorly.

Example 5.1

Suppose that there exist three known patterns $\pi_{k}$ $(k = 1,2,3)$ with the characteristics in terms of PFSs over the feature space $X = \left\{ {x_{1} ,x_{2} ,x_{3} } \right\}$ as:

$$ \begin{gathered} \pi_{1} = \left\{ {\langle x_{1} ,0.3,0.3\rangle ,\langle x_{2} ,0.4,0.4\rangle ,\langle x_{3} ,0.4,0.4\rangle ,\langle x_{4} ,0.4,0.4\rangle } \right\}, \hfill \\ \pi_{2} = \left\{ {\langle x_{1} ,0.5,0.5\rangle ,\langle x_{2} ,0.1,0.1\rangle ,\langle x_{3} ,0.5,0.5\rangle ,\langle x_{4} ,0.1,0.1\rangle } \right\}, \hfill \\ \pi_{3} = \left\{ {\langle x_{1} ,0.5,0.4\rangle ,\langle x_{2} ,0.4,0.5\rangle ,\langle x_{3} ,0.3,0.3\rangle ,\langle x_{4} ,0.2,0.2\rangle } \right\}. \hfill \\ \end{gathered} $$

We consider the unknown pattern

$$ {\Pi } = \left\{ {\langle x_{1} ,0.4,0.4\rangle ,\langle x_{2} ,0.5,0.5\rangle ,\langle x_{3} ,0.2,0.2\rangle ,\langle x_{4} ,0.3,0.3\rangle } \right\} $$

which should be recognized.

The goal here is to classify the pattern ${\Pi }$ in one of classes $\pi_{k}$ for $k = 1,2,3$. If we employ the existing and proposed similarity measures for computing the similarity degree of ${\Pi }$ from $\pi_{k}$ for $k = 1,2,3$ then the results can be obtained as those in Table 4. From Table 4, it is clear the largest degree of similarities is that between ${\Pi }$ and $\pi_{3}$, and therefore, the pattern ${\Pi }$ is recognized by $\pi_{3}$ which is actually in accordance with the principle of maximum degree of PFS similarity measures.

Table 4 Similarity measures between the unknown pattern $\Pi$ and the known patterns ${\pi }_{k}$ ($k=\mathrm{1,2},3$) in Example 5.1

From the data presented in Table 4 we find that the proposed similarity measures and the existing similarity measures, except $S_{C}$, $S_{LC}$, $S_{Y}$ and $S_{BA}$, are able to recognize the pattern ${\Pi }$ by $\pi_{3}$.

Example 5.2

Let the three known patterns $\pi_{k}$ ( $k = 1,2,3$ ) with the characteristics in terms of PFSs over the feature space $X = \left\{ {x_{1} ,x_{2} ,x_{3} } \right\}$ be as follows:

$$ \begin{gathered} \pi_{1} = \left\{ {\langle x_{1} ,0.1,0.1\rangle ,\langle x_{2} ,0.5,0.1\rangle ,\langle x_{3} ,0.1,0.9\rangle } \right\}, \hfill \\ \pi_{2} = \left\{ {\langle x_{1} ,0.5,0.5\rangle ,\langle x_{2} ,0.7,0.3\rangle ,\langle x_{3} ,0.0,0.8\rangle } \right\}, \hfill \\ \pi_{3} = \left\{ {\langle x_{1} ,0.7,0.2\rangle ,\langle x_{2} ,0.1,0.8\rangle ,\langle x_{3} ,0.4,0.4\rangle } \right\}. \hfill \\ \end{gathered} $$

Moreover, the unknown pattern is considered as

$$ {\Pi } = \left\{ {\langle x_{1} ,0.4,0.4\rangle ,\langle x_{2} ,0.6,0.2\rangle ,\langle x_{3} ,0.0,0.8\rangle } \right\}. $$

Here, we are going to classify the pattern $\Pi$ in one of classes ${\pi }_{k}$ for $k=\mathrm{1,2},3$. In the case that we employ the existing and proposed similarity measures for computing the similarity degree of $\Pi$ from ${\pi }_{k}$ for $k=\mathrm{1,2},3$, then the results are achieved as those in Table 5. As follows from Table 5, the largest degree of similarities is that between $\Pi$ and ${\pi }_{2}$, and thus, the pattern $\Pi$ is recognized by ${\pi }_{2}$.

Table 5 Similarity measures between the unknown pattern $\Pi$ and the known patterns ${\pi }_{k}$ ($k=\mathrm{1,2},3$) in Example 5.2

From data presented in Table 5, we deduce that the proposed similarity measures and the existing similarity measures, except $S_{C}$ and $S_{LC}$, are able to recognize the pattern ${\Pi }$ by $\pi_{2}$.

Example 5.3

Consider the three known patterns ${\pi }_{k}$ ( $k=\mathrm{1,2},3$ ) with the characteristics in terms of PFSs over the feature space $X=\{{x}_{1},{x}_{2},{x}_{3}\}$ as:

$$ \begin{gathered} \pi_{1} = \left\{ {\langle x_{1} ,0.3,0.3\rangle ,\langle x_{2} ,0.6,0.1\rangle ,\langle x_{3} ,0.2,0.6\rangle ,\langle x_{4} ,0.7,0.3\rangle } \right\}, \hfill \\ \pi_{2} = \left\{ {\langle x_{1} ,0.5,0.3\rangle ,\langle x_{2} ,0.8,0.1\rangle ,\langle x_{3} ,0.2,0.6\rangle ,\langle x_{4} ,0.7,0.3\rangle } \right\}, \hfill \\ \pi_{3} = \left\{ {\langle x_{1} ,0.5,0.3\rangle ,\langle x_{2} ,0.6,0.1\rangle ,\langle x_{3} ,0.2,0.6\rangle ,\langle x_{4} ,0.7,0.3\rangle } \right\}. \hfill \\ \end{gathered} $$

Moreover, the unknown pattern is considered as

$$ {\Pi } = \left\{ {\langle x_{1} ,0.4,0.3\rangle ,\langle x_{2} ,0.7,0.1\rangle ,\langle x_{3} ,0.3,0.6\rangle ,\langle x_{4} ,0.7,0.3\rangle } \right\}. $$

In the case of classifying the pattern $\Pi$ in one of classes ${\pi }_{k}$ for $k=\mathrm{1,2},3$, the results are obtained as those given in Table 6. From Table 6, we conclude that the largest degree of similarities is that between $\Pi$ and ${\pi }_{2}$, and thus, the pattern of $\Pi$ is recognized by ${\pi }_{2}$.

Table 6 Similarity measures between the unknown pattern $\Pi$ and the known patterns ${\pi }_{k}$ ($k=\mathrm{1,2},3$) in Example 5.3

From data presented in Table 6, we deduce that the proposed similarity measures and only the existing similarity measure ${S}_{P1}$ are able to recognize the pattern $\Pi$ with ${\pi }_{1}$.

Example 5.4

Suppose that there are three known patterns ${\pi }_{k}$ $(k=\mathrm{1,2},3)$ with the characteristics in terms of PFSs over the feature space $X=\{{x}_{1},{x}_{2},{x}_{3}\}$ as follows:

$$ \begin{gathered} \pi_{1} = \left\{ {\langle x_{1} ,0.2,0.8\rangle ,\langle x_{2} ,0.4,0.6\rangle ,\langle x_{3} ,0.5,0.5\rangle ,\langle x_{4} ,0.4,0.6\rangle } \right\}, \hfill \\ \pi_{2} = \left\{ {\langle x_{1} ,0.5,0.4\rangle ,\langle x_{2} ,0.3,0.7\rangle ,\langle x_{3} ,0.5,0.5\rangle ,\langle x_{4} ,0.4,0.6\rangle } \right\}, \hfill \\ \pi_{3} = \left\{ {\langle x_{1} ,0.5,0.5\rangle ,\langle x_{2} ,0.4,0.6\rangle ,\langle x_{3} ,0.4,0.6\rangle ,\langle x_{4} ,0.4,0.6\rangle } \right\}. \hfill \\ \end{gathered} $$

Moreover, the unknown pattern is considered as

$$ {\Pi } = \left\{ {\langle x_{1} ,0.4,0.6\rangle ,\langle x_{2} ,0.4,0.6\rangle ,\langle x_{3} ,0.5,0.5\rangle ,\langle x_{4} ,0.4,0.6\rangle } \right\}. $$

Now, we are going to classify the pattern $\Pi$ in one of classes ${\pi }_{k}$ for $k=\mathrm{1,2},3$. If we employ the existing and proposed similarity measures for computing the similarity degree of $\Pi$ from ${\pi }_{k}$ for $k=\mathrm{1,2},3$, then the results are gotten as those in Table 7.

Table 7 Similarity measures between the unknown pattern $\Pi$ and the known patterns ${\pi }_{k}$ ($k=\mathrm{1,2},3$) in Example 5.4

Before discussing the findings in Table 7, let us take a brief look at the structure of unknown pattern $\Pi$ and known patterns ${\pi }_{k}$ ($k=\mathrm{1,2},3$) in Example 5.4. It is interesting to note that the only difference between the unknown pattern $\Pi$ and the known pattern ${\pi }_{1}$ is related to the feature ${x}_{1}$. As a result, the degree of similarity between $\Pi$ and ${\pi }_{1}$ may be considered as the largest degree. This is while, the output of the existing similarity measure ${S}_{PYY}$ (Peng et al. 2017) is the known pattern ${\pi }_{3}$, and not ${\pi }_{1}$. However, the proposed similarity measures consider both the degree of similarity between $\Pi$ and ${\pi }_{1}$, and that between $\Pi$ and ${\pi }_{3}$ as the largest degrees. This finding verifies that the proposed ones are more flexible compared to the existing ones.

5.2 Medical diagnosis problem under Pythagorean fuzzy environment

In order to state the advantage of explored PFS similarity measures, we illustrate their application to the medical diagnosis progress, and compare the obtained results with those of existing similarity measures for PFSs.

Example 5.5

Szmidt et al. 2004) Suppose that a doctor is going to make a suitable diagnosis $\{ Viral fever,Malaria,Typhoid,$ $Stomach problem,Chest problem\}$ for a group of patients $\left\{ {Al,Bob,Joe,Ted} \right\}$ in accordance with the values of symptoms $\left\{ {Temperature,Headache,cough,Stomach pain,Chest pain} \right\}$. The characteristic symptoms for the latter-mentioned diagnoses are given in Table 8, and the corresponding symptoms for each patient are presented in Table 9. Based on PFS forms of elements of Tables 8, 9, the target is to find a proper diagnosis for each patient.

Table 8 Symptom characteristics for the diagnoses in Example 5.5

Table 9 Symptom characteristics for the patients in Example 5.5

By computing the proposed PFS similarity measures between the symptoms characteristic of each diagnose and that of each patient, we are able to obtain the diagnostic results which are shown in Tables 10, 11, 12, 13 below.

Table 10 Similarity values between each considered patient and the set of possible diagnoses by the use of ${S}_{{\tau }_{1}}$ based on ${\tau }_{1}({F}_{1\mu },{F}_{1\nu })$

Table 11 Similarity values between each considered patient and the set of possible diagnoses by the use of ${S}_{{\sigma }_{1}}$ based on ${\sigma }_{1}({F}_{1\mu },{F}_{1\nu })$

Table 12 Similarity values between each considered patient and the set of possible diagnoses by the use of ${S}_{{\tau }_{2}}$ based on ${\tau }_{2}({F}_{1\mu },{F}_{1\nu })$

Table 13 Similarity values between each considered patient and the set of possible diagnoses by the use of ${S}_{{\sigma }_{2}}$ based on ${\sigma }_{2}({F}_{1\mu },{F}_{1\nu })$

From Tables 10, 11, 12, 13, we observe that Al, Bob, Joe and Ted suffer respectively from Malaria, Stomach problem, Typhoid, and Viral fever.

To save more space, we ignore to mention the other results of $S_{{\tau_{3} }}$ based on $\tau_{3} \left( {F_{1\mu } ,F_{1\nu } } \right)$ $\left[ { \in = \frac{1}{2}} \right]$;$S_{{\tau_{3} }}$ based on $\tau_{3} \left( {F_{1\mu } ,F_{1\nu } } \right)$ $S_{{\tau_{4} }}$ based on $\tau_{4} \left( {F_{1\mu } ,F_{1\nu } } \right)$ $\left[ { \in = 2} \right]$ and $S_{{\tau_{4} }}$ based on $\tau_{4} \left( {F_{1\mu } ,F_{1\nu } } \right)$

However, in order for having a deeply analysis, we recall here the results of previous works (De et al. 2001; Own 2009; Peng and Liu 2019; Szmidt et al. 2004, 2001; Vlachos and Sergiadis 2007) and (Wei et al. 2011). Table 14 shows the results of the current study and latter-mentioned works.

Table 14 All considered similarity values between each patient and the set of possible diagnoses in Example 5.5

What is apparent from Table 14 is that different similarity measures do not generally correspond to the same result. We observe from the two first block of Table 14 that Al suffers from Viral fever in 14 out of the 28 existing similarity measures, while Al does from Malaria in 15 out of the 28 existing measures. Bob suffers from a Stomach problem because all the existing similarity measures provide the same result. Joe suffers from Typhoid in 26 out of the 28 existing similarity measures, while, the other existing measures indicate that Joe suffers from Malaria and Stomach problem. Eventually, Ted suffers from Viral fever in 22 out of the 28 existing similarity measures, while, the other existing measures indicate that Ted suffers from Malaria in 6 out of the 28 existing measures.

Peng et al. (Peng et al. 2017) and Peng and Liu (Peng and Liu 2019) confessed that they knew nothing of which patient suffers from which diagnoses in some cases. For instance, they are hesitant to make their decisions whether Al suffers from Viral fever or from Malaria because these two symptoms are involved with each other.

In this study, we implement an attractive technique to deal with such an aforementioned limitation. This technique is known as majority criterion and it is applied to situation in where a single candidate is preferred to others by a majority of voters. Indeed, the majority criterion is a single-winner voting system which expresses that "if one candidate is ranked first by a majority of voters, then that candidate must win" (Boland 1989).

To provide the preliminary information needed for using majority criterion technique, we now suppose that the vector $\langle i_{1} ,i_{2} ,i_{3} ,i_{4} ,i_{5} \rangle$ (for $i_{k} \in \left\{ {0,1} \right\}$) returns the numerical value of five-tuple $\langle { }Viralfever,Malaria,Typhoid,$ $Stomach{ }problem,Chest{ }problem\rangle$ corresponding to each patient with respect to each similarity measure.

Under this setting, each array of Table 14 can be correspondingly re-stated by the use of a vector with binary entries being given in Table 15. For instance, the first array of Table 14 can be interpreted by the vector $\langle \mathrm{1,0},\mathrm{0,0},0\rangle$ in Table 15 which means that the patient AL returns the diagnose "Viral fever" corresponding to the use of similarity measure of ${S}_{L}$.

Table 15 Implementing the majority criterion technique to all arrays of two top blacks of Table 15

Applying this technique to the arrays of two top blacks of Table 14 gives rise to the vectors of two top blacks of Table 15 below.

If we simply add up the entries of each column of Table 15, then the summation row of Table 15 will be achieved.

Keeping the issue of majority criterion technique into consideration, which says that the candidate wins if s/he is ranked first by a majority of voters, we are able to conclude from each summation array that which one is the corresponding output array.

From the output row of Table 15, we easily find that:

$\langle 0,1\left( {15} \right),0,0,0\rangle$ discloses of the diagnosis Malaria to the patient Al;

$\langle 0,0,0,1\left( {28} \right),0\rangle$ discloses of the diagnosis Stomach problem to the patient Bob;

$\langle 0,0,1\left( {27} \right),0,0\rangle$ discloses of the diagnosis Typhoid to the patient Joe;

$\langle 1\left( {22} \right),0,0,0,0\rangle$ discloses of the diagnosis Viral fever to the patient Ted.

Interestingly, the aforementioned outcomes are almost identical with those of proposed similarity measures (except for $S_{{\tau_{3} }}$ based on $\tau_{3} \left( {F_{1\mu } ,F_{1\nu } } \right)$ for Ted) which are given in the last eight rows of Table 14.

Such results indicate that the proposed PFS similarity measures are more effective than the existing similarity measures in making an appropriate decision.

6 Conclusions and future works

The basic contributions in this study may be highlighted and summarized as the followings:

• We developed a novel class of PFS similarity measures which are characterized by using the concepts of t-norm and s-norm together with an interesting PFS distance measure.

• In this study, two comparison aspects were taken into account: (1) the microscopy aspect which allows us to know how the results are actually obtained on the basis of structural form of similarity measures and (2) the macroscopy aspect which enables us to judge about the results of similarity measures without considering how they have been concluded.

• The effectiveness of proposed PFS similarity measures were shown in some case studies concerning pattern recognition and medical diagnosis.

The next step of such a contribution can be devoted to the study of similarity measures into other aspects, such as group decision making, data mining and information retrieval. Furthermore, since this work presents just an applicative study concerning the PFS similarity measures, we should try to consider the development of some software to better implement the introduced similarity measures in the real-life setting.