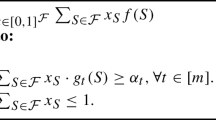Candidate selections with proportional fairness constraints

Abstract

Selecting a subset of candidates with various attributes under fairness constraints has been attracting considerable attention from the AI community, with applications ranging from school admissions to committee selections. The fairness constraints are usually captured by absolute upper bounds and/or lower bounds on the number of selected candidates in specific attributes. In many scenarios, however, the total number of selected candidates is not predetermined. It is, therefore, more natural to express these fairness constraints in terms of proportions of the final selection size. In this paper, we study the proportional candidate selection problem, where the goal is to select a subset of candidates with maximum cardinality while meeting certain proportional fairness constraints. We first analyze the computational complexity of the problem and show strong inapproximability results. Next, we investigate the algorithmic aspects of the problem in two directions. First, by treating the proportional fairness constraints as soft constraints, we devise two polynomial-time algorithms that could return (near) optimal solutions with bounded violations on each fairness constraint. Second, we design an exact algorithm with a fast running time in practice. Simulations based on both synthetic and publicly available data confirm the effectiveness and efficiency of our proposed algorithms.

1 Introduction

The problem of selecting a collection of alternatives from a larger pool has a wide range of applications in the AI realm, ranging from qualified school admissions [1, 2, 15, 18, 19, 24, 25] to representative program committee selections [3, 9, 12, 16, 17, 26, 31]. To ensure sufficient representation of minorities, a number of recent research turn their attention to the issue of fairness. In the literature, the fairness constraints are usually defined based on attributes (or types) of candidates [9, 12]. Consider forming a program committee for an AI conference, for example. In order to ensure fairness among different sub-areas, one may want to diversify the selection and make sure that at least a certain number of senior members are selected in each sub-area.

Formally speaking, consider a set of n candidates and a set of m characterization attributes such as expertise, gender, or region. Each candidate is associated with some attributes. Then the fairness constraints on the selected candidate set S require that given non-negative integers $l_j$ and $u_j$, S should contain at least $l_j$ and/or at most $u_j$ candidates for each attribute $j \in [m]$.

However, in many scenarios, the fairness constraints expressed using absolute values are inadequate. Take school enrollment as an example [14]. In 1989, each school in the city of White Plains (New York) was required to have the same proportions of Blacks, Hispanics, and “Others” (which includes Whites and Asians). The plan allowed for a discrepancy among schools of only 5 percent. Translating this requirement to fairness upper bound constraints with absolute numbers, it (roughly) means that a school of capacity 1,000 can have at most about 350 students from each racial category. However, this translation relies on a critical assumption that the school will always be fully allocated, which is often not the case in real life. For example, the enrollment has dropped from 426,215 in 2000 to about 350,535 in 2013 observed by Chicago Public Schools, resulting in almost 50 percent of the schools being half-empty. If the school of capacity 1,000 ends up only enrolling 500 students, the absolute-valued fairness constraints may lead to a worst-case of 0 students enrolled in a specific category! This situation may render the fairness requirement null and void and lead to a clearly undesirable situation.

Consider another motivated example where an online streaming platform would like to buy a set of movies from a database. Each movie can be described by multiple attributes, e.g., genre, country, length, and so on. Due to the limited slots in the platform, the online streaming platform may have an upper bound on the size of selected movies. The platform may also impose some fairness (or diversity) requirements on different attributes, e.g., at least 40 percent of selected movies are drama. Then the platform wants to select a maximum set of movies according to the diversity criteria.

In this paper, we investigate this issue by looking at the proportional candidate selection problem, where the goal is to select a subset of candidates while satisfying certain proportional fairness constraints. Specifically, the proportional fairness constraints require that, for every attribute $j \in [m]$, the selected candidate set S has at least $\alpha _j$ fraction and at most $\beta _j$ fraction of candidates that possess this attribute. Note that the proportional constraints can be trivially satisfied by selecting an empty set. Instead, we are interested in finding a feasible set of maximum size under an overall capacity constraint.

1.1 Our contributions

We present both hardness and algorithmic results for the proportional candidate selection problem in this paper. In Sect. 3, we first consider the computational complexity of the problem. Our first result is a hardness result on finding even a non-empty feasible solution.

Theorem 1

(NP-hardness of feasibility) It is NP-hard to check whether there is a nonempty feasible solution of the proportional candidate selection problem.

Consequently, this leads to the following strong inapproximability result of the optimization problem.

Corollary 1

(Inapproximability) The proportional candidate selection problem is NP-hard to approximate within any ratio $\gamma \ge 1$.

Given the intractability of the proportional candidate selection problem, it naturally leads to two algorithmic questions:

• Can we devise a polynomial time algorithm if we treat the fairness constraints soft (e.g., each proportional fairness constraint can be violated by a small additive/multiplicative factor)?

• Can we design time-efficient algorithm that runs fast in practice even though the worst-case running time remains exponential?

In this paper we answer both questions in the affirmative, and our proposed algorithms are verified through various experiments in Sect. 5.

Algorithms with Soft Constraints. We first give a randomized rounding algorithm in Sect. 4.1:

Theorem 2

(Informal) Under mild conditions, for some $0< \epsilon < 1$, with positive probability our randomized algorithm produces a solution with size at least $1-\epsilon$ fraction of the optimum size while each constraint (including the capacity constraint) is violated by at most a multiplicative ratio of $(1+\epsilon )/(1-\epsilon )$.

The algorithm utilizes randomized rounding of the linear programming relaxation, and the approximation is guaranteed by the concentration property using Chernoff bounds.

Then, in Sect. 4.2 we give another polynomial time algorithm that returns a solution with bounded additive violations on all fairness constraints. More specifically, we have the following:

Theorem 3

(Informal) Our deterministic algorithm produces a solution with size at least the optimum solution while the capacity constraint is not violated and each fairness constraint is violated by at most an additive error of $2 \varDelta + 1$, where $\varDelta$ is the maximum number of attributes that a candidate can have.

The algorithm makes use of the iterative method (see [27]) developed for solving many combinatorial optimization problems.

Exact Solution. In the second direction, we focus on exact algorithms to the proportional candidate selection problem in Sect. 4.3. A commonly used method in practice is to formulate the NP-hard problem as an Integer Linear Programming (ILP) and directly apply an ILP solver to solve it. While in our algorithm, we first enumerate the possible value of the optimum solution, and solve a “constant” version of the problem for each of our guess. Intuitively, this straightforward decomposition can reduce the number of nonzero coefficients in the ILP, which leads to faster implementation in practice. Moreover, we propose an iterative framework that guesses the optimum solution in a more efficient way, leading to fewer iterations of solving the “constant” versions.

1.2 Related works

Fairness in Computational Social Choice. There is a growing literature in computational social choice on fairness issues. In particular, some previous works considered the assignment and matching mechanisms subject to either lower- or upper-bound constraints on different types of objects [1, 2, 4, 7, 8, 13, 15, 18, 19, 24, 25, 28, 30]. Most of these works made use of absolute values in their lower- and/or upper-bound covariants, which have distinct difference with our model where proportional fairness constraints are imposed. The only exception is the work by [28] where their model only deals with the special case that each candidate only has one attribute. Our model is more general in the sense that we allow each candidate to possess multiple attributes.

As a further related topic, fair division in computational social choice deals with fair allocations of resources to interested participants. The literatures in this field can be categorized by the types of resources to be allocated: divisible resources (e.g., [29]), indivisible resources (e.g., [10]), and their combination (e.g., [6]).

Variable Winners in Multiwinner Voting Problem. Another related line of research on fairness (or diversity) constraints is on the multiwinner voting problem [3, 9, 12, 26]. In the standard setting of the multiwinner voting problem, the winning sets are required to have exactly a fixed number of k candidates. Thus it is natural to use absolute values, instead of proportions, to capture the fairness constraints. Some researchers also noticed that the number of winners could be variable in some real-world scenarios [17, 22, 31]. However, none of these works addressed the proportional fairness constraints.

There are three research works [9, 12, 26] that are most closely related to our work in this area. First, Lang and Skowron [26] considered the problem of multi-attribute proportional representation where the goal is to look for a set of fixed size that fits as much as possible the desired distribution on all attributes according to some criteria, e.g., minimizing the sum of differences between the proportion of the committee and the desired distribution. Although they discussed the proportionality issues, in their setting, the size of selected set is predefined instead of a variable number, which means those lower and upper quotas for attributes can be viewed as absolute numbers. Another major difference is that our objective is to maximize the size of selected candidates based on proportional fairness constraints while their focus is on minimizing the distribution difference, which makes our setting orthogonal to theirs. Bredereck et al. [9] and Celis et al. [12] focused on the problem of selecting a committee with maximum score (e.g., a submodular function over the committee) subject to fairness/diversity constraints on the attributes of the candidates, where the fairness/diversity requirements are modeled using absolute values. On the other hand, our model study the case when the size of committee is variable and the fairness conditions are proportional to the size of committee. In Sect. 6.1 we provide a detailed technical comparison between previous works [9, 12, 26] and ours.

2 Preliminaries

Consider a set C of n candidates and a set P of m properties (or attributes) where each candidate i possesses a set of properties $P_i \subseteq P$. Moreover, let $\varDelta$ be the maximum number of properties that a candidate can possess, i.e., $\varDelta = \max _{i \in C} |P_i|$. We use “attributes” and “properties” interchangeably in this paper.

We first define the proportional fairness constraints. Denote $\varvec{\alpha } = \{\alpha _1, \ldots , \alpha _m\}$ and $\varvec{\beta } = \{\beta _1, \ldots , \beta _m\}$ where $0 \le \alpha _j \le \beta _j \le 1$ for all $j\in [m]$.

Definition 1

Given candidate set C and $\varvec{\alpha }, \varvec{\beta }$, a subset $C' \subseteq C$ of candidates is said to satisfy the proportional fairness constraints with $\varvec{\alpha }$ and $\varvec{\beta }$ if for each property $j \in P$, the number of candidates in $C'$ that have property j is at least $\alpha _j |C'|$ and at most $\beta _j |C'|$, i.e.,

$$\begin{aligned} \alpha _j |C'| \le |\{i \in C' \mid j \in P_i\}| \le \beta _j |C'|. \end{aligned}$$

Now we are ready to define our main problem.

Definition 2

Given a set of candidates C, a set of properties P, fairness parameters $\varvec{\alpha }, \varvec{\beta }$ and the cardinality threshold k, the Proportional Candidate Selection Problem aims to find a subset of candidates $C'$ of maximum size, such that $|C'| \le k$ and $C'$ satisfies all proportional fairness constraints. We denote $|C'| \le k$ as the cardinality constraint.

Integer Linear Programming formulation. Let $p_{ij} = 1$ if candidate i has attribute j and $p_{ij} = 0$ otherwise. The proportional candidate selection problem can be easily formulated as the following ILP:

$$\begin{aligned}&\text {max. }&\sum _{i \in C} x_i&\end{aligned}$$

(1)

$$\begin{aligned}&\text {s. t. }&\alpha _j \sum _{i \in C} x_i \le \sum _{i \in C} p_{ij} x_i \le \beta _j \sum _{i \in C} x_i&\quad \forall j \in P, \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{i \in C} x_i \le k&\end{aligned}$$

(3)

$$\begin{aligned}&&x_i \in \{0, 1\}&\forall i \in C. \end{aligned}$$

(4)

Here $x_i$ is a binary variable that represents whether or not candidate i is selected in the solution. The natural linear relaxation of ILP (1-4), which is denoted by LP (1-4), is to replace $x_i = \{0, 1\}$ with $x_i \in [0,1]$ for each element $i \in C$ in Constraint (4). We also denote $\mathsf {OPT}_{1-4}$ and $\mathsf {LP}_{1-4}$ as optimum values of ILP (1-4) and LP (1-4), respectively. It is clear that $\mathsf {LP}_{1-4} \ge \mathsf {OPT}_{1-4}$. Similar notations can be defined analogously for other ILPs.

Case Study on University Enrollment Data We provide a case study about student enrollment at UC Berkeley. This case study will be used to facilitate a better understanding of our techniques and will be tested against various algorithms in the experimental study (Sect. 5.2).

Background: Many universities consider fairness (or diversity) as a priority issue in their enrollment process. For example, as stated by UC Berkeley’s Strategic Plan for Equity, Inclusion, and Diversity, ¹ a goal is to “create a critical mass of talented students [...] that will fully represent California’s excellence and diversity.” At present, UC Berkeley does not represent the diversity of the state. Part of the work of the Division of Equity and Inclusion is to help redress this lack of representation at UC Berkeley.

Data Collection: We collect data based on the international student enrollment report (2018) from UC Berkeley ². Each student is characterized by four categories: Gender, Major, Region, and Type. See Table 1 for the data statistics and fairness parameter setting (the details are deferred to Sect. 5.2). Note that in this case study, the number of attributes $m = 17$ and the maximum number of attributes that a candidate can possess $\varDelta = 4$.

Table 1 Dataset characterization and parameter setting

3 Hardness results

We investigate the computational complexity of the proportional candidate selection problem and show hardness results in this section.

Given the NP-hardness of the general candidate selection problem with absolute-valued constraints [9, 12], it is not surprising that the proportional candidate selection problem is also NP-hard. In the following we show an even stronger claim: We prove that it is NP-hard even to decide whether there exists a nonempty feasible solution.

Theorem 1

It is NP-hard to check whether there is a nonempty feasible solution of the proportional candidate selection problem.

Our proof idea is as follows. We will construct a problem instance, in which all the feasible solutions are restricted to have value either 0 or a specific nonzero number (say, $k'$). Then we will show that, even knowing the value of $k'$, it is NP-hard to decide whether there exists a feasible solution with value $k'$ for this instance.

We are ready to prove Theorem 1:

Proof

(Proof of Theorem 1) We reduce the NP-hard problem of Exact Cover by 3-Sets (X3C) [21] to our proportional candidate selection problem. Given a set F of $3k_1$ elements and a collection T of $k_2$ triples (i.e., three-element subsets of F), the X3C problem asks whether there exists a sub-collection $T'$ of T with size $k_1$ such that every element in F appears in exactly one triple in $T'$.

Given an X3C instance, we construct our proportional candidate selection problem instance as follows. For each element and each triple in the X3C problem, we have a corresponding property (for an element) j in P and a corresponding candidate (for a triple) i that has exactly 3 properties in C. We additionally have a special candidate $i^*$ and a special property $j^*$ where $i^*$ only has a single property $j^*$ and $j^*$ is only possessed by a single candidate $i^*$. Thus we have $|P| = 3k_1 + 1$ and $|C| = k_2 + 1$. Let $\alpha _j = \beta _j = 1 / (k_1 + 1)$ for all $j \in P$. This implies that we require each property is contained in exactly $1 / (k_1 + 1)$ fraction of the size of selected candidates (i.e., the inequalities in Constraint (2) become equalities for all properties).

Given the construction, we show that every nonempty solution to the proportional candidate selection problem must

• 1. Contain the candidate $i^*$ with property $j^*$; and

• 2. Have value of $k_1+1$.

The reason is as follows. Let $C'$ be a feasible solution of size $k' > 0$. The correctness of part (1) can be easily seen as candidate $i^*$ is the only candidate with property $j^*$ and $\alpha _{j^*} = 1/ (k_1 +1) > 0$.

Next we prove part (2) using the counting argument. We focus on the properties in $P \setminus \{j^*\}$. Since each candidate except $i^*$ has exactly 3 properties by construction and $i^* \in C'$ by part (1), all candidates in $C' \setminus \{i^*\}$ will have $3 (|C'|-1) = 3(k'-1)$ properties (counting multiplicity) in total. On the other hand, since $\alpha _j = \beta _j =1 / (k_1 + 1)$ for all $j \in P$, every property in $P \setminus \{j^*\}$ must be possessed by exactly $k' / (k_1 + 1)$ candidates in $C' \setminus \{i^*\}$. Therefore the total number of properties (counting multiplicity) possessed by all candidates in $C' \setminus \{i^*\}$ is $(|P|-1) \cdot k' /(k_1 + 1) = 3k_1 \cdot k' /(k_1 + 1)$. Thus we have $3(k' - 1) = 3k_1 \cdot k' /(k_1 + 1)$, which implies that $k' = k_1 + 1$.

Since each property in this feasible solution is possessed by exactly $k' / (k_1 + 1) = 1$ candidate in $C'$. A nonempty solution $C'$ to the proportional candidate selection problem thus implies an exact cover $C' \setminus \{ i^* \}$ of X3C.

On the other hand, given an exact cover $T'$ for an instance of X3C, it is easy to see that $T' \cup \{ i^* \}$ is a feasible solution to the corresponding instance of the proportional candidate selection problem. This concludes the reduction and the proof of this theorem. $\square$

Furthermore, we have the following inapproximability result for proportional candidate selection problem, which can be directly derived from Theorem 1.

Corollary 1

(Inapproximability) The proportional candidate selection problem is NP-hard to approximate within any ratio $\gamma \ge 1$.

Proof

Suppose that we have a $\gamma$-approximate algorithm $\mathcal {A}$ for some $\gamma \ge 1$. It is easy to see that we can utilize $\mathcal {A}$ to distinguish whether there exists a nonempty feasible solution for any instance: Report ‘yes’ if $\mathcal {A}$ returns a nonempty solution and ‘no’ otherwise. This contradicts Theorem 1 and completes our proof. $\square$

FPT-Algorithm with respect to m. We remark that the number of properties m is a variable in the hardness proof of Theorem 1. When m is fixed, the proportional candidate selection problem admits a fixed-parameter tractable (FPT) algorithm with respect to m. Specifically, given a problem instance, we can guess the optimum value from n to 0, and with each guess transform the problem into another problem with constant fairness constraints, i.e., lower- and upper-bound covariants that correspond to fairness constraints are absolute numbers. For this “constant” version of the problem, Bredereck et al. [9] (Theorem 10 in their work) showed an FPT-algorithm with respect to m via solving a mixed ILP with $2^m$ integer variables. However, the algorithm has m as the exponent in its time complexity. With m as large as 6 in our experiments in Sect. 5, the algorithm cannot terminate in reasonable time for most instances. Thus we do not find such an FPT-algorithm applicable in real-world scenarios and view it more of theoretical interest.

4 Algorithms

In this section we present our algorithmic results. We devise two polynomial time approximation algorithms in Sects. 4.1 and 4.2, at the expense of having bounded multiplicative and additive violations on proportional fairness constraints respectively. Then Sect. 4.3 gives an algorithm based on the “guess-and-verify” strategy to solve the problem exactly.

4.1 Randomized algorithm

Our randomized algorithm RandRounding follows the classic methodology of randomized rounding. In particular, the algorithm consists of two major steps. In the first step, RandRounding solves LP (1-4) and obtains an optimal fractional solution $x^*$ with optimum value $\mathsf {LP}_{1-4}$. The second step applies standard randomized rounding to round $x^*$ to an integral solution $\hat{x}$, i.e., for each i, we set $\hat{x}_i =1$ with probability $x^*_i$; 0 with probability $1 - x^*_i$. Let the size of $\hat{x}$ be $\mathsf {ALG}$. For convenience, we use $\mathsf {LP}$ and $\mathsf {OPT}$ to denote $\mathsf {LP}_{1-4}$ and $\mathsf {OPT}_{1-4}$ in this subsection, respectively.

In the following we show that the rounded integral solution $\hat{x}$ is close to the actual optimal solution with high probability. We restate the result of Theorem 2 in a formal way:

Theorem 4

For any $\sqrt{\frac{3 \ln (2m+3)}{\min _j{\alpha _j} \mathsf {OPT}}}< \epsilon < 1$, with probability of $1-(2m+3)\exp \left( \frac{- {\epsilon }^2 \min _j \alpha _j \mathsf {LP}}{3}\right) > 0$, the output of Algorithm RandRounding satisfies

• 1. $\mathsf {ALG}\ge (1-\epsilon ) \mathsf {OPT}$,

• 2. the cardinality constraint $|C'| \le k$ is violated by a multiplicative ratio of no more than $(1+\epsilon )$, and

• 3. each proportional fairness constraint is violated by a multiplicative ratio of no more than $(1+\epsilon )/(1-\epsilon )$, i.e., $\alpha _j \frac{1-\epsilon }{1+\epsilon } \mathsf {ALG}\le \sum _i p_{ij} \hat{x}_i\le \beta _j \frac{1+\epsilon }{1-\epsilon } \mathsf {ALG}$ for all $j \in P$.

Before we prove Theorem 4, we interpret this theorem using our case study (Sect. 2) as an example. In this case study, when we choose $\epsilon > 0.23$, the success probability of Theorem 4 is positive since $m = 17$ and $\min _j{\alpha _j} \mathsf {OPT}\approx 200$ (See Table 2 for the success probabilities with different values of $\epsilon$). In addition, we can boost this success probability by repeating the rounding step multiple times and returning the one with the best solution. For example, by repeating $O(\log (m)/\epsilon ^2)$ times, we can obtain a constant success probability. In our experiments (Sect. 5), the rounding process of Algorithm RandRounding is performed only once and this shows the algorithm has strong performance comparing to the theoretical bounds established in Theorem 4.

Table 2 The success probabilities in Theorem 4 for different values of $\epsilon$ based on the parameters in the case study

Proof

(Proof of Theorem 4) Because $\mathbb {E}[\mathsf {ALG}] = \mathsf {LP}$, by Chernoff bounds, we have

$$\begin{aligned} \Pr [\mathsf {ALG}< (1-\epsilon ) \mathsf {LP}]&\le \exp \left( \frac{ - \epsilon ^2 \mathsf {LP}}{3}\right) , \end{aligned}$$

(5)

and

$$\begin{aligned} \Pr [\mathsf {ALG}> (1+\epsilon ) \mathsf {LP}]&\le \exp \left( \frac{ - \epsilon ^2 \mathsf {LP}}{3}\right) . \end{aligned}$$

(6)

Next we check the constraint violation of ILP (1-4) due to the randomized rounding process. We first look at the cardinality constraint $|C'| \le k$. Again by Chernoff bounds, we have

$$\begin{aligned} \Pr [\mathsf {ALG}> (1+\epsilon ) k]&\le \exp \left( \frac{ - \epsilon ^2 k}{3}\right) \nonumber \\&\le \exp \left( \frac{ - \epsilon ^2 \mathsf {LP}}{3}\right) . \end{aligned}$$

(7)

Next we look at the proportional fairness constraints. Let $E_j$ be the event that $\sum _{i \in C \mid j \in P_i} \hat{x}_i \ge (1+\epsilon )\beta _j \mathsf {LP}$. We apply Chernoff bounds again to show that, for each constraint $j \in P$,

$$\begin{aligned} \Pr [E_j]&\le \exp \left( \frac{- {\epsilon }^2 \beta _j \mathsf {LP}}{3}\right) . \end{aligned}$$

Since we have m fairness constraints in total, by a union bound (a.k.a., Boole’s inequality), we obtain the probability bound:

$$\begin{aligned} \Pr [\exists j, E_j] \le m\exp \left( \frac{- {\epsilon }^2 \min _j \beta _j \mathsf {LP}}{3}\right) . \end{aligned}$$

(8)

Similarly, let $F_j$ be the event that $\sum _{i \in C \mid j \in P_i} \hat{x}_i \le (1-\epsilon )\alpha _j \mathsf {LP}$, and we have:

$$\begin{aligned} \Pr [\exists j, F_j] \le m\exp \left( \frac{- {\epsilon }^2 \min _j \alpha _j \mathsf {LP}}{3}\right) . \end{aligned}$$

(9)

Combining Inequalities (5-9), we know that any of the bad events $\mathsf {ALG}< (1-\epsilon ) \mathsf {LP}$,$\mathsf {ALG}> (1+\epsilon ) \mathsf {LP}$, $\mathsf {ALG}> (1+\epsilon ) k$, and $E_j$ and $F_j$ for all j will happen with probability at most $(2m+3)\exp \left( \frac{- {\epsilon }^2 \min _j \alpha _j \mathsf {LP}}{3}\right)$. In other words, given the assumption that $\sqrt{3 \ln (2m+3)/\min _j{\alpha _j} \mathsf {LP}}< \epsilon < 1$, we have the probability of $1-(2m+3)\exp \left( \frac{- {\epsilon }^2 \min _j \alpha _j \mathsf {LP}}{3}\right)$ is less than 1. Also we have $\mathsf {LP}\ge \mathsf {OPT}$. This completes the proof of this theorem. $\square$

We note that in real-world applications, the violation factor $\epsilon$ is usually rather small, since there are usually very few number of properties to consider, i.e. m is usually a very small number, and the number of candidates (and potentially the value of $\mathsf {OPT}$) is often relatively large.

Small violations on the cardinality constraints.

Note that RandRounding considers soft constraints and may select more candidates than the cardinality constraint. This is a feasible assumption in many applications, e.g., the school admission, which could tolerate a small violation on the total number of selected candidates. When the application requires hard cardinality constraint, we can randomly remove a few candidates from the selected set to meet the requirement. Because the violation is guaranteed to be small, these removals will not affect other constraints significantly. In particular, from Theorem 4, we know the number of removed candidates is at most $\epsilon k$ if we violate the hard cardinality constraint. For the upper-bound fairness constraint, in the worst case, the removed candidates do not hold the corresponding property while the total number of selected decreases. This means the violation for the upper-bound fairness would be enlarge. On the other hand, for the lower-bound counterpart, the worst case means the removed candidates all have the corresponding property. By simple calculations, we can get that $(\alpha _j \frac{1-\epsilon }{1+\epsilon }-\epsilon ) \mathsf {ALG}' \le \sum _i p_{ij} \hat{x}_i'\le (\beta _j \frac{1+\epsilon }{1-\epsilon } + \epsilon ) \mathsf {ALG}'$ for all $j \in P$ where $\hat{x}'$ is the solution and $\mathsf {ALG}'$ ($=k$) is the corresponding value of the solution after we randomly remove some candidates if we violate the hard cardinality constraint.

4.2 Iterative algorithm

We now present another algorithm, denoted by Iterative , with soft constraints which returns a solution with bounded additive violations on each fairness constraint.

We restate the result of Theorem 3 in a formal way:

Theorem 5

Algorithm Iterative returns a solution with value $\mathsf {ALG}$ for the proportional candidate selection problem such that

• 1. $\mathsf {ALG}\ge \mathsf {OPT}_{1-4}$, and

• 2. each proportional fairness constraint is violated by an additive factor of no more than $2\varDelta + 1$.

Recall that $\varDelta$ is defined as the maximum number of properties that a candidate can possess. In real-world application, $\varDelta$ would be small. For example, we have $\varDelta = 4$ in our case study in Sect. 2.

The general idea of our approach is as follows. We first transform ILP (1-4) to another ILP formulation and show that a “good” solution to the new formulation is also a “good” one to ILP (1-4). Then we solve the new ILP formulation using the iterative method [23, 27].

4.2.1 Step 1: Transformation

Let $x^*$ be a solution that corresponds to $\mathsf {LP}_{1-4}$. We also let $f_j = \lfloor \alpha _j \sum _{i \in C}{x_i^*} \rfloor$ and $g_j = \lceil \beta _j \sum _{i \in C}{x_i^*} \rceil$ for each $j \in P$, and let $f_0 = \lfloor \sum _{i \in C}{x_i^*}\rfloor$ and $g_0 = \lceil \sum _{i \in C}{x_i^*}\rceil$.

$$\begin{aligned}&\text {max. }&\sum _{i \in C} x_i&\end{aligned}$$

(10)

$$\begin{aligned}&\text {s. t. }&f_j \le \sum _{i \in C} p_{ij} x_i \le g_j&\quad \forall j \in P, \end{aligned}$$

(11)

$$\begin{aligned}&f_0 \le \sum _{i \in C} x_i \le g_0&\end{aligned}$$

(12)

$$\begin{aligned}&&x_i \in \{0, 1\}&\quad \forall i \in C. \end{aligned}$$

(13)

Note that in this transformed ILP, we replace the cardinality constraint, i.e., Constraint (3), in ILP (1-4) with Constraint (12) which will be useful for our analysis later.

We next show a relation between ILP (1-4) and ILP (10-13).

Lemma 1

Suppose we have an algorithm $\mathcal {A}$ that returns an integral solution y for ILP (10-13) such that:

• P1. $\sum _{i \in C} y_i \ge \mathsf {LP}_{10-13}$,

• P2. $f_0 \le \sum _{i \in C} y_i \le g_0$, and

• P3. there is an additive violation of at most s on the fairness constraints (Constraint (11)), i.e.,

  $$\begin{aligned} f_j - s \le \sum _{i \in C} p_{ij} y_i \le g_j + s~~~\forall j \in P. \end{aligned}$$

Then the integral solution y produced by $\mathcal {A}$ is a solution to ILP (1-4) satisfying:

• Q1. $\sum _{i \in C} y_i \ge \mathsf {OPT}_{1-4}$,

• Q2. $\lfloor \sum _{i \in C}{x_i^*} \rfloor \le \sum _{i \in C} y_i \le \lceil \sum _{i \in C}{x_i^*}\rceil \le k$, and

• Q3. there is an additive violation of at most $s+2$ on the fairness constraints (Constraint (2)), i.e.,

  $$\begin{aligned} \alpha _j \sum _{i \in C} y_i - s - 2 \le \sum _{i \in C} p_{ij} y_i \le \beta _j \sum _{i \in C} y_i + s + 2~~\forall j \in P. \end{aligned}$$

Proof

The property Q1 is straightforward since it is obvious to see that $x^*$ (an optimal solution to $\mathsf {LP}_{1-4}$) is a feasible solution for $\mathsf {LP}_{10-13}$. Moreover, the property Q2 is a direct consequence of the property P2 of Algorithm $\mathcal {A}$ and the fact that $g_0 = \lceil \sum _{i \in C}{x_i^*}\rceil \le k$ (since $x^*$ is a fractional solution satisfying $\sum _{i \in C}{x_i^*} \le k$).

We focus on proving Q3. Fix a property $j \in P$. By Algorithm $\mathcal {A}$, we have

$$\begin{aligned} \sum _{i \in C} p_{ij} y_i&\le \lceil \beta _j \sum _{i \in C}{x_i^*} \rceil + s \\&\le \beta _j \sum _{i \in C}{x_i^*} + s + 1\\&\le \beta _j \left(\lfloor \sum _{i \in C}{x_i^*} \rfloor + 1\right) + s + 1 \\&\le \beta _j \lfloor \sum _{i \in C}{x_i^*}\rfloor + s + 2 \\&\le \beta _j \sum _{i \in C} y_i + s + 2, \end{aligned}$$

where the fourth inequality follows as $\beta _j \le 1$ and the last inequality is due to the fact that $f_0 = \lfloor \sum _{i \in C}{x_i^*}\rfloor$ and the property P2 of Algorithm $\mathcal {A}$. Similarly, we also have $\sum _{i \in C} p_{ij} y_i \ge \alpha _j \sum _{i \in C} y_i - s - 2$, which completes the proof of Lemma 1. $\square$

4.2.2 Step 2: Iterative method

Guided by the relation explored in Lemma 1, we now focus on solving ILP (10-13). Before showing the algorithm, we first give a characterization of extreme point solutions of LP (10-13). We next present an important lemma which is the core of the iterative method [27]:

Lemma 2

(Rank Lemma [27]) Let $\mathcal {P} = \{x \mid Ax \ge b, x \ge 0\}$ and let x be an extreme point solution of $\mathcal {P}$ such that $x_i > 0$ for each i. Then any maximal number of linearly independent tight constraints of the form $A_ix = b_i$ for some row i of A equals the number of variables.

Let $j^{\forall }$ be a special property such that all candidates have this property $j^{\forall }$, where the corresponding constraint is shown as Constraint (12). The following lemma is then a direct application of the Rank Lemma (Lemma 2) which gives the characterization of extreme point solutions of LP (10-13):

Lemma 3

For any extreme point solution x to LP (10-13) with $0< x_i < 1$ for each $i \in C$, there exists $W \subseteq P \cup \{j^{\forall }\}$ such that

• 1. each constraint that corresponds to W is tight, i.e.,

• if $j \in W \cap P$, $\sum _{i \in C} p_{ij} x_i$ equals either $f_j$ or $g_j$;

• otherwise, i.e., $j=j^{\forall }$, $\sum _{i \in C} x_i$ equals either $f_0$ or $g_0$.

• 2. The constraints corresponding to W are linearly independent³.

• 3. $|W| = |C|$.

Now we are ready to present Iterative (Algorithm 1) where the corresponding result is shown in Lemma 4.

Lemma 4

Algorithm Iterative returns a solution y for ILP (10-13) such that:

• $\sum _{i \in C} y_i \ge \mathsf {LP}_{10-13}$,

• $\lfloor \sum _{i \in C}{x_i^*} \rfloor \le \sum _{i \in C} y_i \le \lceil \sum _{i \in C}{x_i^*} \rceil$, and

• there is an additive violation of at most $2\varDelta - 1$ on the fairness constraints (Constraint (11)), i.e., $\forall j \in p,$

  $$\begin{aligned} \lfloor \alpha _j \sum _{i \in C}{x_i^*} \rfloor - 2\varDelta + 1 \le \sum _{i \in C} p_{ij} y_i \le \lceil \beta _j \sum _{i \in C}{x_i^*} \rceil + 2\varDelta - 1. \end{aligned}$$

Proof

Algorithm Iterative processes in iterations where we get a (strictly) smaller LP after each iteration. In the following we will show that in each iteration, either we can set some variables to 0 or 1 in the original LP, or at least one constraint can be removed.

First we show that this theorem holds if Iterative terminates successfully. First, observe that we update the linear program in Steps 4-5 according to whether $x_i = 0$ or 1 such that the residual linear programming solution (current LP solution restricted to those $x_i$’s with value in the range of (0, 1)) remains a feasible solution for the modified linear program in the next iteration. This implies that the size of the current solution y plus the size of the LP solution, i.e., $\sum _{i \in C} y_i + x_i$ is always feasible with respect to $f_0$ and $g_0$ in the original LP during the algorithm. Also, in Step 6 when we remove a fairness constraint, the current LP solution remains a feasible solution. Therefore the size of the current solution y, i.e., $\sum _{i \in C} y_i$ plus the size of the LP solution does not decrease in any iteration, so at the final step the size of y is at least the cost of the first LP solution, which is at least $\mathsf {LP}_{10-13}$. Moreover, since we only remove a fairness constraint of a property when it is possessed by at most $2\varDelta - 1$ candidates, the fairness constraints are violated by at most $2\varDelta - 1$.

Thus it remains to show that Algorithm 1 always terminates successfully. That is, it can always either find a candidate i with $x_i = 0$ in Step 4 or $x_i = 1$ in Step 5, or finds a property j such that there are at most $2\varDelta - 1$ candidates with property j in the current candidate set, i.e., $|\{i \in C \mid j \in P_i\}| \le 2\varDelta - 1$, in Step 6.

Suppose by contradiction that none of the above conditions holds. Then we have $0< x_i <1$ for each $i \in C$ and $|\{i \in C \mid j \in P_i\}| \ge 2\varDelta$ for each $j \in P$. We show the contradiction via a counting argument. We assign $2\varDelta$ tokens to each candidate $i \in C$ for a total of $2 \varDelta |C|$ tokens. For each candidate i, we redistribute one token to each property $j \in P_i$, and $\varDelta$ tokens to property $j^{\forall }$. This can be done because each candidate has at most $\varDelta$ properties. Next, we will show that the constraints in W can collect $2 \varDelta |W|$ tokens in total while there are still some tokens left. This would imply $|C| > |W|$ which contradicts to Lemma 3.

For each constraint $j \in W \cap P$, it collects at least $2 \varDelta$ tokens since $|\{i \in C \mid j \in P_i\}| \ge 2\varDelta$. On the other hand, property $j^{\forall }$ collects $\varDelta |C|$ tokens. We then consider two cases:

Case (1). $W \subseteq P$. In this case, we know that W collects at least $2\varDelta |W|$ tokens and property $j^{\forall }$ collects $\varDelta |C|$ tokens. Since we have at most $2\varDelta |C|$ tokens in total, this contradicts Part 3 of Lemma 3.

Case (2). $|W \cap P| = |W| - 1$. We know that $W \cap P$ collects at least $2 \varDelta |W \cap P| = 2 \varDelta (|W|-1)$ tokens and property $j^{\forall }$ collects $\varDelta |C|$ tokens.

• If $|C| > 2$, this contradicts to Part 3 of Lemma 3.

• If $|C| < 2$, we note that $|C| \not = 0$ since the current LP (10-13) is not empty as in line 2. Hence $|C| = 1$. By assumption we have $0< x_i < 1$ for each $i \in C$, and $f_0, g_0$ are integers, this contradicts Part 1 of Lemma 3 where $\sum _{i \in C}{x_i}$ should be equal to either $f_0$ or $g_0$.

• If $|C| = 2$, this means that each candidate in C has exactly $\varDelta$ properties. This is because otherwise we know that (1) the total number of tokens assigned to property $j \in P_i$ for all $i\in C$ is strictly less than $\varDelta |C| = 2\varDelta$ and (2) $W \cap P$ collects at least $2 \varDelta |W \cap P| = 2 \varDelta (|W|-1)$ tokens. These two facts directly imply that $|W| < 2 = |C|$ and we already have the contradiction to Part 3 of Lemma 3.

  Then it is easy to see that for each $i \in C$, we have $\sum _{j \in W \cap P} p_{ij} = \varDelta$ which implies that $\sum _{i \in C} \sum _{j \in W \cap P} p_{ij} = \varDelta \cdot |C|$. This directly shows linear dependence⁴ to Constraint (12) as the corresponding vector $\sum _{i \in C} 1 = |C|$. Hence, we have the desired contradiction to Part 2 of Lemma 3.

This completes the proof of this theorem. $\square$

By Lemma 4 and Lemma 1, we complete the proof of Theorem 5.

4.2.3 Iterative Algorithm with Only Upper-Bound Fairness Constraints

In this subsection, we consider the case when there are only upper-bound fairness constraints, i.e., $\alpha _j = 0$ for all $j \in P$. First we note that Theorem 5 can be applied to solve this special case with additive violation of $2\varDelta + 1$ for each proportional fairness constraint. In the following, we propose another iterative algorithm (with different algorithmic handling and analysis) to solve this special with a better (i.e., smaller) additive violation of $\varDelta + 1$ for each proportional fairness constraint. After the proof of our main result in this subsection, we also discuss whether one can utilize the new iterative algorithm to solve the general case (with both lower and upper-bounds fairness constraints) with the improved performance.

The result is shown as follows.

Theorem 6

There exists an algorithm that returns a solution with value $\mathsf {ALG}$ for the proportional candidate selection problem with only upper-bound fairness constraints ($\alpha _j = 0$ for all $j \in P$) such that

• 1. $\mathsf {ALG}\ge \mathsf {OPT}_{1-4}$, and

• 2. each proportional fairness constraint is violated by an additive factor of no more than $\varDelta + 1$.

Again, recall that $\varDelta$ is defined as the maximum number of properties that a candidate can possess. The value of $\varDelta$ is normally small, e.g., $\varDelta = 4$ in our case study in Sect. 2.

The proof of the above theorem shares the same idea as in Theorem 5, except for we modify the iterative method (Algorithm 1) and its corresponding analysis. The result for Step 2 (in parallel to Lemma 4) is the following.

Lemma 5

There exists an algorithm that returns a solution y for ILP (10-13) with $\alpha _j = 0$ for all $j \in P$ such that:

• $\sum _{i \in C} y_i \ge \mathsf {LP}_{10-13}$,

• $\lfloor \sum _{i \in C}{x_i^*} \rfloor \le \sum _{i \in C} y_i \le \lceil \sum _{i \in C}{x_i^*} \rceil$, and

• there is an additive violation with $\varDelta - 1$ on fairness constraints (Constraint (11)), i.e.,

  $$\begin{aligned} \sum _{i \in C} p_{ij} y_i \le \lceil \beta _j \sum _{i \in C}{x_i^*} \rceil + \varDelta - 1 ~~~\forall j \in P. \end{aligned}$$

Theorem 6 is directly implied by Lemma 5 and Lemma 1. Next we show the proof of Lemma 5.

Proof

(Proof of Lemma 5) The algorithm is identical to Algorithm 1, except that we replace the Step 6 of Algorithm 1 with:

“For each property j, delete j from P if the current number of candidates that have property j is at most $g_j + \varDelta - 1$, i.e., $|\{i \in C \mid j \in P_i\}| \le g_j + \varDelta - 1$. Update LP (10-13).”

Following the proof of Theorem 5, we know that the theorem holds if the algorithm terminates successfully. Then it remains to show that the algorithm always terminates. In other words, we want to show that it can always find a candidate i with $x_i = 0$ in Step 4, or a candidate i with $x_i = 1$ in Step 5, or a property j such that with there are at most $g_j + \varDelta - 1$ candidates that has property j in the current candidate set, i.e. $|\{i \in C \mid j \in P_i\}| \le g_j + \varDelta - 1$, in Step 6. The remaining proof is similar to that of Theorem 5 with some modifications. We present it as following for completeness.

Assume by contradiction that none of the conditions holds. Then we have $0< x_i <1$ for each $i \in C$ and $|\{i \in C \mid j \in P_i\}| \ge g_j + \varDelta$ for each $j \in P$. We show the contradiction via a counting argument. We assign $\varDelta$ tokens to each candidate $i \in C$ for a total of $\varDelta \cdot |C|$ tokens. For each candidate i, we redistribute $1-x_i$ token to each property that i has, i.e., $j \in P_i$, and $\varDelta \cdot x_i$ token to property $j^{\forall }$. This is valid as each candidate has at most $\varDelta$ properties. Next, we will show that each constraint in W can collect $\varDelta$ tokens, and there are still some tokens left. This would imply $|C| > |W|$ which contradicts to Lemma 3.

For each constraint $j \in W \cap P$, it collects

$$\begin{aligned} \sum _{i \in C \mid j \in P_i} 1- x_i&= |\{i \in C \mid j \in P_i\}| - \sum _{i \in C \mid j \in P_i} x_i\\&= |\{i \in C \mid j \in P_i\}| - g_j \\&\ge \varDelta , \end{aligned}$$

where the second equality follows as the constraint that corresponds to j is tight, and the last inequality is due to the condition that $|\{i \in C \mid j \in P_i\}| \ge g_j + \varDelta$ for each $j \in P$. On the other hand, it is easy to see that property $j^{\forall }$ collects $\varDelta \cdot \sum _{i \in C}{x_i}$ tokens.

We will consider two cases in the following.

Case (1). $W \subseteq P$. In this case, we know that W collects at least $\varDelta |W|$ tokens and property $j^{\forall }$ collects $\varDelta \cdot \sum _{i \in C}{x_i}$ tokens. As we assume $x_i > 0$ for all i in this extreme point solution, we know that $\sum _{i \in C}{x_i} > 0$. Moreover, we have at most $\varDelta |C|$ tokens to be distributed in total, this contradicts Part 3 of Lemma 3.

Case (2). $|W \cap P| = |W| - 1$. We know that $W \cap P$ collects at least $\varDelta \cdot |W \cap P| = \varDelta \cdot (|W|-1)$ tokens and property $j^{\forall }$ collects $\varDelta \cdot \sum _{i \in C}{x_i}$ tokens. By assumption we have $0< x_i < 1$ for each $i \in C$ and $\sum _{i \in C}{x_i}$ should be equal to either $f_0$ or $g_0$ (according to Part 1 of Lemma 3). As $f_0, g_0$ are integers, we know $\sum _{i \in C}{x_i} \ge 1$ which implies that property $j^{\forall }$ collects $\varDelta \cdot \sum _{i \in C}{x_i} \ge \varDelta$ tokens. This means that each candidate in C has exactly $\varDelta$ properties since otherwise we already have the contradiction to Part 3 of Lemma 3. Then it is easy to see that for each i, we have $\sum _{j \in W \cap P} p_{ij} = \varDelta \cdot 1$ which shows linear dependence to Constraint (12).⁵ Hence, we have the desired contradiction to Part 2 of Lemma 3.

This completes the proof of this theorem. $\square$

Discussion on Solving General Instances. We first observe that an instance with both lower-bound and upper-bound proportional fairness constraints can be translated to an equivalent instance with only upper-bound constraints. (The detailed transformation can be found in Sect. 4.3.) Intuitively, a constraint that “at least 40 percent of selected candidates are female” can be translated to “at most 60 percent of students are non-female”, where non-female is a new property introduced.

A general instance $\mathcal {I}$ can then be translated to an equivalent instance $\mathcal {I'}$ with only upper-bound proportional fairness constraints. However, we observe that in $\mathcal {I'}$, the maximum number of properties that a candidate can possess, i.e., $\varDelta '$, is now equal to m, which is the number of properties in $\mathcal {I}$, since each candidate either possesses property A or property non-A in $\mathcal {I'}$. Thus applying Theorem 6 on instance $\mathcal {I'}$ will give a solution with additive violation of $\varDelta ' + 1 = m+1$ which is better than directly using Theorem 5 on instance $\mathcal {I}$ only if $\varDelta > m/2$. We also note that the value of $\varDelta$ is normally small compared with m, e.g., $\varDelta = 4$ and $m = 17$ in our case study in Sect. 2.

4.3 Exact solution

Besides algorithms with soft constraints, we also investigate exponential-time exact algorithms that run fast in practice.

We first consider an equivalent ILP formulation (see ILP (14-18)) with only upper-bound fairness constraints. The transformation is shown as follows. For each property j, we introduce a corresponding property $j'$ that is possessed by those candidates that do not have j (i.e., $j' \in P_i$ if and only if $j \not \in P_i$ for each $i \in C$). We collect these new property $j'$’s as $P'$ and set $\beta _{j'} = 1 - \alpha _j$. For example, a requirement that “at least 40 percent of selected candidates are female” can be translated to “at most 60 percent of students are non-female”, where non-female is a new attribute introduced. It is easy to check that ILP (14-18) with only upper-bound constraints is equivalent to the original one (ILP (1-4)).

$$\begin{aligned}&\text {max. }&\sum _{i \in C} x_i&\end{aligned}$$

(14)

$$\begin{aligned}&\text {s. t. }&\sum _{i \in C} p_{ij} x_i \le \beta _j \sum _{i \in C} x_i&\forall j \in P, \end{aligned}$$

(15)

$$\begin{aligned}&\sum _{i \in C} \overline{p}_{ij} x_i \le (1 - \alpha _j) \sum _{i \in C} x_i&\quad \forall j \in \overline{P}, \end{aligned}$$

(16)

$$\begin{aligned}&\sum _{i \in C} x_i \le k&\end{aligned}$$

(17)

$$\begin{aligned}&&x_i \in \{0, 1\}&\quad \forall i \in C. \end{aligned}$$

(18)

Here $\overline{p}_{ij} = 1$ if candidate i does not have attribute j, i.e., $p_{ij} = 0$, and $\overline{p}_{ij} = 0$ otherwise.

For our exact algorithm, we make use of a “guess-and-verify” strategy, in which the following ILP is solved for different values of guess s:

$$\begin{aligned}&\text {max. }&\sum _{i \in C} x_i&\end{aligned}$$

(19)

$$\begin{aligned}&\text {s. t. }&\sum _{i \in C} p_{ij}x_i \le \beta _j \cdot s&\quad \forall j \in P, \end{aligned}$$

(20)

$$\begin{aligned}&\sum _{i \in C} \overline{p}_{ij} x_i \le (1 - \alpha _j)\cdot s&\forall j \in \overline{P}, \end{aligned}$$

(21)

$$\begin{aligned}&\sum _{i \in C} x_i \le k&\end{aligned}$$

(22)

$$\begin{aligned}&&x_i \in \{0, 1\}&\quad \forall i \in C. \end{aligned}$$

(23)

For convenience, we use $\mathsf {LP}$ and $\mathsf {OPT}$ to denote $\mathsf {LP}_{1-4}$ and $\mathsf {OPT}_{1-4}$ below, respectively. The algorithm goes in iterations (lines 3-9) as follows. For the p-th iteration, we first guess an upper bound $s_p$ on $\mathsf {OPT}$. To guarantee $s_1$ is an initial upper bound, we set $s_1 \leftarrow \lfloor \mathsf {LP}\rfloor$ in line 1 since we know $\lfloor \mathsf {LP}\rfloor \ge \mathsf {OPT}$. Then we issue an ILP (19-23) with $s=s_p$ to obtain the optimum solution $y_p$ (line 4). We next consider the value of $y_p$. If $y_p \ge s_p$ in lines 5-6, we immediately return $x_p$ as the optimum solution $\mathsf {ALG}$. Otherwise, i.e., $0 \le y_p < s_p$, in lines 7-9 we derive another guess $s_{p+1} \leftarrow y_p$ for the $(p+1)$-st iteration. Note that the case of $y_p \ge s_p$ in line 5 coincides with case one of $y_p = s_p$, i.e., the case of $y_p > s_p$ will not happen.

We note that one cannot simply adopt a binary search approach for finding $\mathsf {OPT}$, because the solution space is not monotone. That is, a feasible solution with value s does not imply there exists feasible solution with value $s' < s$.

We now claim the while loop of Algorithm 2 is processed in finite number of iterations:

Lemma 6

The while loop (lines 3-9 of Algorithm 2) will terminate in O(n) iterations.

Proof

Suppose that the while loop terminates after the t-th iteration, i.e., $\mathsf {ALG}= y_t$. In other words, t is the first iteration that satisfies $y_t \ge s_t$ in lines 5-6. For all $1< p < t$, we will prove that $s_{p-1} > s_p$.

Consider a fixed iteration p such that $1< p < t$. Assume, to the contrary, that $s_{p-1} \le s_p$. We have $s_p = y_{p-1}$ by line 8 of Algorithm GuessAndVerify . Thus $s_{p-1} \le y_{p-1}$, which means that the algorithm should terminate in the $(p-1)$-st iteration due to lines 5-6, a contradiction. Thus we know the sequence of $\{s_i\}$ is strictly decreasing.

We also know that there exists a trivial solution with value 0 of ILP (14-18). Suppose the q-th guess is $s_q =0$, then we have $y_q = s_q = 0$ which implies $s_t \ge 0$. This also means that Algorithm 2 can always return a feasible solution. Moreover, we have $s_1 = k$, where $k = O(n)$, as shown in line 1. Thus we complete our proof. $\square$

We next prove the correctness of Algorithm GuessAndVerify .

Lemma 7

Algorithm GuessAndVerify solves the proportional candidate selection problem correctly.

Proof

Let $s_t$ be the first guess such that $s_t = y_t$. In other words, Algorithm 2 returns $y_t$ as the optimum solution $\mathsf {ALG}$ in line 6. We will show $y_t= \mathsf {OPT}$ in the following.

Suppose that $y_t > \mathsf {OPT}$. Since $s_t = y_t$, we know that $y_t$ corresponds to a feasible solution for the problem which contradicts the optimality of $\mathsf {OPT}$.

Suppose that $y_t < \mathsf {OPT}$. Note that this case cannot happen with $\mathsf {OPT}= 0$ since $y_t \ge 0$. From the proof of Lemma 6, we have $s_1> s_2> \cdots> s_{t-1} > s_t \ge 0$. Thus there must exist a guess $s_{j}$ such that $s_{j} \ge \mathsf {OPT}> s_{j+1} \ge s_t$ where $1 \le j \le t-1$. We observe that a larger guess implies a larger optimum value for ILP (19-23), i.e., $s_a \ge s_b$ implies $y_a \ge y_b$. Since $s_j \ge \mathsf {OPT}$, we have $y_j \ge y'_{opt}$ where $y'_{opt}$ is the optimum value of ILP (19-23) with guess $\mathsf {OPT}$. Then we conclude that $y'_{opt} \ge \mathsf {OPT}$ since, otherwise, it would violate the fact that $\mathsf {OPT}$ is a feasible (and optimum) solution to the proportional candidate selection problem. Moreover, according to our algorithm, we have $s_{j+1} = y_{j}$. Thus, $s_{j+1} = y_{j} \ge y_{opt}' \ge \mathsf {OPT}$ which contradicts the assumption that $\mathsf {OPT}> s_{j+1}$. The lemma follows. $\square$

We remark that this framework is capable of solving the proportional candidate selection problem as long as we have an exact solution, either in polynomial or exponential time, to solve ILP (19-23) at hand.

5 Experiments

In this section we conduct empirical evaluations of our proposed algorithms. Our experiments are partitioned into two parts based on the data generation settings: the first one aims to test the sensitivities of our algorithms under different parameter settings through the randomly generated data, and the other evaluates the performance of our algorithms via a case study based on the real-world data.

Experiment setups. We compare RandRounding (Sect. 4.1), Iterative (Sect. 4.2), and GuessAndVerify (Sect. 4.3) with the baseline method ILP-Generic, i.e., the ILP (1-4) is solved by a standard ILP solver directly. All experiments ran on a computer with Intel Xeon E5-2630v4 @2.2 GHz CPU and 64 GB RAM. Programs were coded in Python 3.7, and all the ILPs and LPs were solved by the Gurobi Optimizer (version 8.1.0). For all the tests, we perform 100 repeated runs per experiment and show the averages.

5.1 Sensitivity analysis over synthetic data

First we evaluate the above four algorithms using the synthetic data. Here we use the running time to assess the performance of our four algorithms and use the violation to evaluate the performance of our two approximation algorithms. What’s more, we use the percentage of the output size to show how the parameters will affect our instance. To be clear, the output size is not related to the usability of our algorithms, but related to the effect of the parameters on the instances. In this experiment, for each attribute j, we first randomly generate a probability $p_j$ and assign each candidate with this attribute with probability $p_j$ independently.

Then for the proportional constraints, for each attribute j we randomly generate a pair of parameters $\alpha _j$ and $\beta _j$ such that their gap $\gamma = \beta _j - \alpha _j$ is fixed and $\sum _{j} \frac{\beta _j + \alpha _j}{2} = 1$. We let the value of $\gamma$ vary from 0 to 0.2 instead of varying from 0 to 1. This is because according to our method to generate $\alpha _j$ and $\beta _j$, the central value, i.e., $\frac{\beta _j + \alpha _j}{2}$, will most likely be less than 0.2. Large value of $\gamma$ will make the proportional fairness constraints meaningless.

The cardinality threshold is set as the total number of candidates. That is, we do not consider the cardinality constraint in these experiments. This is because: (1) it simplifies the experiments as we already have several dimensions of the parameters to consider; (2) according to our previous study, determining a suitable value of cardinality threshold k is dataset-specific: when k is too small, the number of selected candidates always reaches k; when k is too large, imposing the cardinality constraint does not affect the current result.

We test our algorithms on a number of different problem instances generated by varying the number of candidates (i.e., $\{2,000,4,000,\ldots ,10,000\}$), the number of attributes (i.e., $\{3,4,\ldots ,7\}$), as well as the gap $\gamma$ between $\alpha _j$ and $\beta _j$ for each attribute j (i.e., $\{0.04,0.08,\ldots ,0.2\}$). In this analysis, we focus on looking at the running time, the output size ($\%$) and the number of violations where the output size ($\%$) is mainly used to describe the effect of different parameters. As for the relation between the size of candidates and the running time, our numerical test for the sensitivity analysis shows the same trend as our real data experiment (in Sect. 5.2), which is omitted in the experiments for the synthetic data.

5.1.1 Experiment results

Fig. 1

Running time with different number of attributes

Fig. 2

Output size (%) with different number of attributes

Figures 1 and 2 respectively show the running times and output sizes in percentage (i.e., the output size over the problem size) of different algorithms when the number of attributes varies from 3 to 7. Note that we consider all the problem instances with the number of candidates from 2,000 to 10,000, and we show the relation between the running time (averaged over all these instances with different problem sizes) and the number of attributes. The same strategy applies to the following experiments in this subsection. One can see clear trends that when the number of attributes increases, the running time increases while the output size decreases. This is because the problem becomes harder to solve if we have more attributes to deal with.

Fig. 3

Running time with different gap $\gamma$

Fig. 4

Output size (%) with different gap $\gamma$

Figures 3 and 4 show how the running time and output size in percentage (i.e., the output size over the problem size) of the algorithm change with regard to the gap $\gamma$. One can first see in Fig. 3 that the running times of Iterative , GuessAndVerify and RandRounding are insensitive to $\gamma$, while the running time of ILP-Genericdecreases as $\gamma$ increases. From Fig. 4 we see that when $\gamma$ increases, the fairness constraints become easier to satisfy, which is reflected by the larger output size of all algorithms.

Fig. 5

Output size (%) with different $\ell _1$ distances

Fig. 6

Running time with different $\ell _1$ distances

We also plot the running time and the output size of our algorithms with regard to the $\ell _1$-distance between $p_j$ and center of $[\alpha _j, \beta _j]$, as shown in Figs. 6 and 5 respectively. One can see in Fig. 5 that when this distance grows larger, all algorithms select a significantly smaller fraction of the candidates into the solution set. An interesting observation from Fig. 6 is that the problem becomes hard for ILP-Genericwhen the range of $\ell _1$ distance is in the center, say around $[0.4-0.6]$. A possible explanation of this phenomenon is that when the range of $\ell _1$ distance is small (resp., large), many (resp., few) candidates can be selected in the solution which makes the problem easier for ILP-Generic. On the other hand, the performances of other algorithms remain stable with respect to different $\ell _1$ distances.

Note that in Figs. 2 and 5, the (average) output size of ILP-Genericis smaller than that of GuessAndVerify . It is because in the synthetic dataset, there exist “hard” instances for which ILP-Genericdoes not return any (non-trivial) feasible solution within the cut-off time (set as 30 seconds in our experiments). In such situation, we simply use 0 (which is a trivial feasible solution) as the size of the selected set, which clearly makes the average output size smaller. On the other hand, our GuessAndVerify can finish all instances within the cut-off time of 30 seconds.

Fig. 7

Violation with different number of attributes

Fig. 8

Violation with different gap $\gamma$

Finally, because RandRounding and Iterative are approximation algorithms, their outputs may have violations over the fairness constraints. We also summarize the average violation size of each constraint of both algorithms in Figs. 7 and 8. One can see that with synthetic data, RandRounding actually has a smaller average violation than Iterative . But more importantly, both algorithms are able to find solutions with very small violations compared to the problem size. For example, with as many as 10,000 candidates, the largest violation of a single constraint for both algorithms is only 5.

Fig. 9

Output size ($\%$) with different number of attributes in a large instance

Fig. 10

Running time with different number of attributes in a large instance

Fig. 11

Violation with different number of attributes in a large instance

We also test our proposed algorithms (except for ILP-Generic) on a large instance in which the number of candidates is 30,000. We fix the gap $\gamma$ as 0.04 and vary the number of attributes. From Fig. 9, we can see that the output sizes (in percentage) of our three algorithms are almost identical. We can also observe that the output size decreases as the number of attributes increases, which presents a similar trend as in Fig. 2. Another observation of Fig. 9 is that there exist bumps in the curve. One possible explanation of this issue is due to the randomness of the generation of the problem instances which results in some instances have larger output size even these instances have larger number of attributes. Moreover, when the number of attributes is 14, the output size drops to a very small value, e.g., less than $3\%$, which is the reason that we set the maximum number of attributes as 13 in this group of experiments. Fig. 10 shows the running times of different algorithms. In particular, RandRounding runs the fastest among all the cases while GuessAndVerify performs better than Iterative when the number of attributes is at most 8. A possible reason is that when the number of attributes increases, the problem becomes harder to solve and GuessAndVerify requires more time to solve ILPs (as in Algorithm 2). Finally, we also look at the violations between Iterative and RandRounding in Fig. 11. Clearly, RandRounding can always have smaller number of violations than Iterative .

5.1.2 Extensions to weighted and correlated cases

In this part, we consider the extensions to weighted and correlated cases. In particular, in the weighted case, each candidate is associated with a weight and we want to maximize the sum of weights of selected candidates subject to the proportional fairness constraints. For the correlated case, we study the situation in which the generated attributes are correlated rather than independent.

Specifically, in the weighted case, we randomly assign a weight from 1 to 100 to each candidate while in the correlated case, we randomly assign a probability to each possible combination of attributes such that the sum of probabilities is equal to 1. For example, if we have 5 attributes and there are 2 choices (e.g., yes or no) for each attribute, we have $2^5 = 32$ different combinations of attributes. We focus on the performance of our proposed approximation algorithms since (1) GuessAndVerify cannot be effectively adapted to the weighted case, and (2) the exact algorithms for the correlated case perform similar to the previous results. Moreover, the only change to the algorithms for the weighted case is the objective function and the rest of algorithms remain the same. The gap is fixed as 0.04 in the following experiments.

Fig. 12

Running time with different number of attributes in the weighted case

Fig. 13

Running time with different number of candidates in the weighted case

Figures 12 and 13 show the running time with different number of attributes when the number of candidates is 10,000 and with different numbers of candidates when the number of attributes is 5 for the weighted case, respectively. It is clear that RandRounding runs faster than Iterative . Moreover, the averaged numbers of violations (for each constraint) is about 0.47 and 1.4 for RandRounding and Iterative (when we vary the number of attributes) and 0.44 and 1.11 for RandRounding and Iterative (when we vary the number of candidates). However, Iterative can always output a solution with better (i.e., around $1\%$ larger) objective value than the solution of ILP-Genericwhile RandRounding achieves almost the same objective value as ILP-Generic.

Fig. 14

Running time with different number of attributes in the correlated case

Fig. 15

Running time with different number of candidates in the correlated case

For the correlated case, the experimental results show the identical phenomenon as in the case when the generation of the attributes is independent. For example, Figs. 14 and 15 verify that RandRounding is more efficient than Iterative across different parameter settings. Similar findings also apply to the output size and the number of violations as we show in Sect. 5.1.1. This may indicate that our proposed algorithms are stable whether the attributes are correlated or not.

5.2 Case study on university enrollment data

This case study follows the description of the student enrollment at UC Berkeley in Sect. 2. In our experiment, for each student, we randomly assign him/her an attribute in each category using the attribute distribution of that category. For proportional fairness constraints, we set each fairness parameter $\alpha _j$, $\beta _j$ that is similar to the percentage of this attribute in the corresponding category. We also omit the fairness constraints for attributes that have small percentages in the dataset and relax the lower-bounds in fairness constraints for some attribute that has large proportion in its category. The cardinality threshold in this experiment is simply set as the total number of candidates. See Table 1 (in Sect. 2) for the data statistics and fairness parameter setting.

5.2.1 Experiment results

Figure 16 shows the running times of different algorithms with number of students ranging from 6,000 to 20,000. One can see that all other three algorithms outperform the benchmark ILP-Genericalgorithm by a clear margin. Both being exact algorithms, and with 20,000 students, GuessAndVerify is 3-times faster than the generic ILP-Genericalgorithm. At the expense of violating some fairness constraints, both RandRounding and Iterative run very fast in practice.

Moreover, the average number of LPs sovled by Iterative (as described in Algorithm 2 of Sect. 4.2) ranges from 13 to 15, which is very small compared to the number of candidates. From the figure, one can also observe an inconsistency of the running times for ILP-Genericwith different problem sizes. The reason to this phenomenon is that the running time of “hard” problem instances, i.e., the one that make ILP-Genericrun out of time (we set 300s for the ILP solver as the cut-off time), dominate the average running time of ILP-Generic. For each problem size, ILP-Generictimeouts for at least 29 and at most 46 (out of 100) instances. For a visual explanation, Fig. 17 gives a detailed running time analysis for ILP-Generic. The two curves in this figure are very similar, which indicates a clear dependence between the running time of ILP-Genericand the number of time-out instances in our experiment. On the other hand, the other three algorithms can finish every problem instance within the cut-off time of 300s.

For the output size ($\%$), all the algorithms can return a solution with around $80\%$ students selected from all the candidates. The maximum difference for the ratios of the output size of different algorithms is about $0.6\%$ in terms of the total number of candidates. This shows that both RandRounding and Iterative can return a solution with almost optimum size, and the output size ($\%$) is insensitive to the number of candidates in this setting. We also look at the maximum violations of RandRounding and Iterative of each fairness constraint. With 20,000 students, the maximum violations of Iterative and RandRounding are 5 and 3 respectively, both of which are rather small compared to the theoretical bounds we derived in the paper.

Fig. 16

Running time with different problem size

Fig. 17

Running time and number of time-out instances with different problem size for ILP-Generic. The blue line with square mark represents the running time with different problem sizes. The red line with circle mark represents the number of time-out instances (out of 100 instances) with different problem sizes

6 Discussions and conclusions

6.1 Discussions

In Sect. 1.2, we showed the relation to the most closely related works [9, 12, 26]. In general, these three works considered the problem which (1) needs to output a committee with fixed size and (2) requires fairness/diversity constraints using absolute numbers. In particular, Bredereck et al. [9] showed that there exist a polynomial-time algorithm when the attributes form special structure and a fixed-parameter tractable (FPT) algorithm when the number of attributes m is small. Celis et al. [12] gave a randomized polynomial-time algorithm that computes a committee with bounded violations on lower- and upper-bound fairness constraints. In contrast, our model studies the problem with a variable number of committee satisfying the proportional fairness constraints. As discussed in Sect. 4.3, our problem can be transformed into a series of problems where the fairness constraints are based on absolute values. This implies that we can apply previous algorithms (e.g., algorithms proposed in [9, 12, 26]) to solve our problem: We try out all the possible values of the solution, e.g., $k' \in \{1, \ldots , |C|\}$, and return the maximum value that admits a feasible solution. The technical comparisons between the methods from ([9, 12, 26])) and ours are as follows.

• Bredereck et al. [9] focused on algorithms dealing with attributes of special structure. The only exception is a fixed-parameter tractable (FPT) algorithm when the number of attributes m is small. Based on this FPT algorithm and the adaptation described above, in Sect. 3 we showed a FPT algorithm with respect to m for our problem, and discussed the applicability of this adapted algorithm in real-world scenario. In short, this algorithm requires solving a mixed ILP with $2^m$ integer variables, and has a much larger running time both in theory and in our experiments.

• Celis et al. [12] gave a randomized polynomial-time algorithm that computes a committee with bounded violations on (constant) lower- and upper-bound fairness constraints. Their algorithm makes use of the continuous greedy algorithm [11] which requires a time complexity of $\widetilde{O}(n^8)$.⁶ In addition, the adaptation needs to call the algorithm for the fairness constraints with absolute numbers once for each $k' \in \{1, \ldots , n\}$. Thus, the overall time complexity of the adapted algorithm is $\widetilde{O}(n^9)$. On the other hand, RandRounding is required to solve LP only once and Iterative performs at most n LPs, where the current best LP solver (due to [20]) runs in (roughly) $O^*(n^w)$ with the fast exponent of matrix multiplication $w \approx 2.37$.⁷ It is then easy to see that both RandRounding and Iterative have better time complexities than the adaptation using the algorithm in [12]. We also note that in our case study (Sect. 5.2), the average number of LPs solved by Iterative is at most 15 when the number of candidates n is from 6,000 to 20,000. This implies that Iterative solves a much smaller number of LPs than the worst case of n LPs.

• Lang and Skowron [26] provided a randomized polynomial-time local search algorithm (denoted by the LS algorithm) that outputs a committee with a bounded total variance between the fairness constraints and the real fraction of each attribute. The LS algorithm is equipped with a parameter $\ell$ indicating the number of elements that will be changed in each round of local search. If $\ell = 1$, the adapted LS algorithm (the above described adaptation with the LS algorithm) runs in $\sum _{k = 1}^n O(n m^2k^2) = O(n^4m^2)$ where $O(n m^2k^2)$ is the time complexity for the LS algorithm (when $\ell = 1$) with committee size k. Similarly, for $\ell = 2$, the time complexity of the adapted LS algorithm is $\sum _{k = 1}^n O(n^2 m^2k^3) = O(n^6m^2)$ where $O(n^2 m^2k^3)$ is the time complexity for the LS algorithm (when $\ell = 2$) with committee size k. As demonstrated above, our proposed algorithms RandRounding and Iterative have much smaller time complexities than the adapted LS algorithms. Furthermore, the LS algorithms, with $\ell = 1$ and $\ell = 2$, provide an output with an average (among all categories) error of 1 and $\frac{\ln (k/2)}{2\ln (k/2)-1}(1+\frac{6}{k})$ (which is around $\frac{1}{2}$), respectively. In other words, when $\ell = 1$, the additive violation for each attribute could be as large as n/2 (e.g., for a category with two attributes, the target distribution is (1/2, 1/2) and the output distribution is (0, 1)). On the other hand, both RandRounding and Iterative have better performances in terms of violations (See Theorems 4 and 5 for comparison).

Based on these discussions, we see that simple adaptations of the existing algorithms might not be practical for real-world applications. On the other hand, our proposed randomized and iterative algorithms can solve these problems in much shorter time.

6.2 Conclusions

In this paper, we study the proportional candidate selection problem in which the fairness constraints are captured by the proportions in terms of the final selection size. We provide both hardness and algorithmic results for this problem. We also conduct experiments over synthetic and real-world data to evaluate the performances of our proposed algorithms.

A natural generalization of this problem considers the weighted case where each candidate has a weight and one wants to maximize the total weights of selected candidates. We remark that both RandRounding and Iterative can be easily modified to address this variation (as discussed and tests in the experiments) while we leave the design of efficient exact algorithms for the weighted case as an future work. Another interesting future direction is to consider the incentives of the candidates to reveal their true attributes in order to increase their chances to be selected. In addition, a standard scenario of our problem setting is the enrollment for a single school. In future research, it would be interesting to look at assignment problems with proportional fairness constraints for multiple schools.