1 Introduction

Often you own a potentially valuable object, such as an antique, a jewel, a used car or a land-plot, but do not know its exact value and cannot calculate it yourself. There are various scenarios in which you may need to know the exact object value. For example: (a) You intend to sell the object and want to know how much to ask when negotiating with potential buyers. (b) You want to know how much to invest in an insurance policy covering that object. (c) The object is a part of an inheritance you manage in behalf of your co-heirs, and you want to prove to them that you manage it appropriately. (d) The object is a land-plot that might contain oil, and you want to know whether to invest in developing it. (e) You are a firm and required by law to include the value of assets you own in your periodic report. (f) You are a government auctioning a public asset, and want to publish an accurate value-estimate in order to attract more firms to participate in the auction. Moreover, you may be required by law (or by political pressure from your voters) to obtain and disclose its true value, to avoid accusations of corruption.

A common solution in these situations is to buy the desired information from an agent with an expertise in evaluating similar objects [4, 6, 30]. Examples of such agents are: antique-shop owners, jewelers, car-dealers, or oil-firms that own nearby land-plots and thus can drill and estimate the prospects of finding oil in your plot. The problem is that, in many cases, the information is not verifiable: the information buyer (henceforth “the principal”) cannot tell if the information received is correct. This results in a strong incentive for the agent to provide an arbitrary value whenever the extraction of the true value is costly or requires some effort, knowing the principal will not be able to tell the difference. For example, if an antique agent gives you a low appraisal for an antique object, and you sell it for that low value, you will never know that you were scammed.

Even if the true value can be verified later on (e.g, due to unsuccessful drilling for oil), this might be too late—the damage due to using the wrong value might be irreversible and the agent might be too far away to be punished. Our goal is thus to—

—develop mechanisms that obtain the true value of an object by incentivizing an agent to compute and report it, even when it is costly for the agent, and even when the information is unverifiable by the principal.

The literature on information elicitation usually makes one of two assumptions: either the information is verifiable by the principal, or there are two or more information agents such that reports can be compared with peer reports [14]. We study a more challenging setting in which the information is unverifiable, and yet there is only a single agent who can provide it. At first glance this seems impossible: how can the agent be incentivized to report truthfully if there is no other source of information for comparison? We overcome this impossibility by allowing, with some small probability, the transfer of the object to the agent for some fee, as an alternative means of compensation (instead of directly paying the agent for the information). This is applicable as long as the agent gains value from owning the object, i.e., it is both capable of evaluating the object and benefiting from owning it. This is quite common in real life. For example, both the antique-shop owner and the car-dealer, who play the role of the agent in the motivating settings above, can provide a true valuation for the car/antique based on their expertise, and can also benefit from owning it (e.g. for resale). Similarly, the oil-firm who owns nearby sea-plots has access to relevant information enabling it to calculate the true value of the plot in question, and will also benefit from owning that plot.

We use this principle of “selling” (transferring for a fee) the object to the agent with a small probability for designing a mechanism for eliciting the required information (Sect. 3). Our analysis proves that the mechanism is truthful whenever the information computation cost is sufficiently small relative to the object’s expected value; the exact threshold depends on the prior distribution of the value. For example, when the object value is distributed uniformly, the mechanism is truthful whenever the computation cost is less than 1/4 of the expected object value, which is quite a realistic assumption.

While our mechanism allows the principal to learn the true information, this information does not come for free: the principal “pays” for it by the risk of selling the object to the agent for a price lower than its true value. Our next goal, then, is to minimize the principal’s loss subject to the requirement of true information elicitation. We show that our mechanism parameters can be tuned such that the principal’s expected loss is only slightly more than its computation cost (Sect. 4). This is an optimal guarantee, since the principal could not get the information for less than its computation cost even if she had the required expertise herself.

We then show how the mechanism can be augmented to handle some extensions of the basic model. These include the case where the object is divisible (Sect. 5), when the principal and the agent have different valuations for the object (Sect. 6), and when the cost the agent incurs when computing the information is unknown to the principal (Sect. 7).

In addition to the mechanism provided in Sect. 3, we present two alternative mechanisms that differ in their privacy considerations, in the sequence of roles of the principal and the agent (in the resulting Stackelberg game), and in the nature of the decisions made by the different players (Sect. 8). Interestingly, despite their differences, all three mechanisms are equivalent in terms of the guarantees they provide. This leads us to conjecture that these guarantees are the best possible.

Finally, we deal with the case where the delivery of information is costly (Sect. 9). Here, we show that in a multi-object setting, whenever it suffices for the principal to know merely which of the objects has a value greater than some threshold (as in the case of seeking the value of opportunities she can either exploit or give up on), substantial savings can be obtained by using alternative queries. Previous related work is surveyed in Sect. 10. Discussion and suggested extensions for future work are given in Sect. 11.

2 The model

There is a principal who needs to know the true value of o, an object she owns. The monetary value of this object for the principal is denoted by v. While the principal does not know v, she has a prior probability distribution on v, denoted by f(v), defined over the interval \([v^{\min },v^{\max }],\) with \(v^{\min }<v^{\max }.\)Footnote 1

The principal can interact with a single agent. Initially, the agent too does not know v and knows only the prior distribution f(v). However, the agent has a unique ability to compute v, by incurring some cost \(c\ge 0.\) Initially we assume that the cost c is common knowledge; in Sect. 7 we relax this assumption.

The principal’s goal is to incentivize the agent to compute and reveal the true v. However, the principal cannot verify v and has no other sources of information besides the agent, so the incentives cannot depend directly on whether v is correct.

Similar to the common value setting studied extensively in auction theory [27], our model assumes that the value of the object to both the principal and the agent is the same. A realistic example of this setting is when both the principal and the agent are oil firms: the principal owns an oil field but does not know its value, while the agent owns nearby fields and can gain information about the oil field from its nearby drills. In Sect. 6 we relax this assumption and allow the two values to be different.

The mechanism-design space available to the principal includes transferring the object to the agent, as well as offering and/or requesting a payment to/from the agent. The principal has the power to commit to the mechanism rules, i.e, the principal is assumed to be truthful. The challenge is to design a mechanism that will incentivize truthfulness on the side of the agent too.

The agent is assumed to be risk-neutral and have quasi-linear utilities. I.e, the utility of the agent from getting the object for a certain price is the object’s value minus the price paid. If the agent calculates v, then the cost c is subtracted from his utility too. As for the the principal, as mentioned above her primary goal is to elicit the exact value v from the agent. Subject to this, she wants to minimize her expected loss, defined as the object value v (if transferred to the agent) minus the payments received (or plus the payment given).

3 Truthful value-elicitation mechanism

The mechanism most commonly used in practice for eliciting information is to pay the agent the cost c (plus some profit margin) in money. However, when information is not verifiable, monetary payment alone cannot incentivize the agent to actually incur the cost of calculation and report the true value.

Instead, in our mechanism, the principal “pays” to the agent by transferring the object to the agent with some small probability. The mechanism guarantees the agent’s truthfulness, meaning that, under the right conditions (detailed below), a rational agent will choose to incur all costs related to computing the correct value, and report it truthfully. The mechanism is presented as Mechanism 1. It is parameterized by a small positive constant \(\epsilon ,\) and a probability distribution represented by its cumulative distribution function G.

Mechanism 1 Parameters: \(\epsilon >0\): a constant, \(G(\cdot )\): a cdf.

1. The principal secretly selects r at random, distributed in the following way:

         \(\bullet\) With probability \(\epsilon ,\) this r is distributed uniformly in \([v^{\min },v^{\max }]\);

         \(\bullet\) With probability \(1-\epsilon ,\) this r is distributed like G(r).

2. The agent provides a value b.

3. The principal reveals r and then:

         \(\bullet\) If \(b\ge r,\) the principal transfers the object to the agent, and the agent pays r to the principal.

         \(\bullet\) If \(b<r,\) no transfers nor payments are made.

Note that the payment r may be negative, in which case the the agent is actually receiving a payment from the principal. This can happen for example when the object has a negative value (e.g., a company who turns out to be in debt and the agent ends up gaining ownership over it, in exchange for a payment received from the principal).

From the agent’s perspective the strategic situation is equivalent to participating in a second-price sealed-bids auction—the value r can be seen as the best bid among those placed by all other bidders. If the agent wins, he gains an object of value v while paying r. Since bidding in second price auctions is known to be truthful [39], this holds in our case too, and thus it is a dominant strategy for the agent to provide \(b=v.\) The challenge is to show that it is optimal for the agent to actually calculate v. This crucially depends on the selection of the cdf G(r). Below we prove a necessary and sufficient condition for the existence of an appropriate G(r) that guarantees calculation. We assume throughout the analysis that \(\epsilon\) is positive but infinitesimally small (i.e, \(\epsilon \rightarrow 0\)). Below, \(E[\cdot ]\) denotes the expected value of the expression inside the brackets. The notation \(E_v[\cdot ]\) emphasizes that the expectation is with regards to the prior distribution of v.

Theorem 1

There exists a function G(r) with which Mechanism 1is truthful, if-and-only-if \(c<E_v[\max (0, v - E[v])].\) One cdf with which the mechanism is truthful in this case is:

$$G^{\ast}(r) = \mathbb {1}_{r>E[v]}$$
(1)

(\(\mathbb {1}_{r>E[v]}\) is an indicator that equals 1 when \(r>E[v]\) and 0 otherwise).

Before proving the theorem, we illustrate its practical applicability with some examples.

Example 1

Assume that v is uniform in [0, 2M] (so \(v^{\min }=0\) and \(M=\frac{v^{\max }}{2}\)). Then \(E_v[\max (0,v-E[v])]=M/4\) so Mechanism 1 is applicable iff \(c < M / 4\)—the object’s appraisal cost should be less than one quarter of the object’s expected value.

With the function \(G^*\) in (1), Mechanism 1 selects r in the following way: with probability \(\epsilon ,\) r is selected uniformly at random from [0, 2M]; with probability \(1-\epsilon ,\) \(r = E[v] = M.\)

Example 2

Assume that v is uniform in \([- 2 M, 0],\) i.e., the object’s value is negative. Then still \(E[\max (0,v-E[v])]=M/4,\) so Mechanism 1 is applicable iff \(c < M / 4.\) Here, the incentive of the agent for participating in the mechanism is the possibility of receiving a payment that will be larger than the object’s negative value.

Example 3

Assume that v has a symmetric triangular distribution in [0, 2M] with mean M, i.e, its pdf is \(f(v) = \mathbb {1}_{0\le v\le M} \cdot {v\over M^2} + \mathbb {1}_{M\le v\le 2 M} \cdot {2 M-v\over M^2}.\) Here, Mechanism 1 is applicable iff \(c < M / 6.\)

The conditions above are realistic, since usually the cost of appraising an object is at least one or two orders of magnitude less than the object’s expected value. For example, used cars usually cost (often tens of) thousands of dollars and the cost of a pre-purchase car inspection generally ranges from $100 to $200.Footnote 2 Similarly, a used engagement ring typically costs thousands of dollars, while hourly rates of a diamond ring appraisals range from $50 to $150.Footnote 3

To further examine the applicability of Theorem 1, we consider the application of selling a used car, based on real data from “Kelley Blue Book” (kbb.com). Here, the principal is an individual and the agent is a mechanic. The principal is interested in having the agent check and report the true condition (from which the worth is derived) of a specific car she is interested in selling. For the mapping from condition to worth we use KBB, which specifies four values, each corresponding to a different car condition, as detailed in Table 1.

Table 1 Probability distribution of car conditions based on kbb.com website. The underlying probability function is car-model independent and determined by KBB
Full size table

Based on Theorem 1, there exists a function G(r) with which Mechanism 1 is truthful, if-and-only-if \(c<E_v[\max (0, v - E[v])].\) Figure 1 depicts (at the seventh column of the table) the maximum car inspection cost at which the latter condition holds for ten different (randomly selected) car models, of various years and mileage. Columns 2-6 provide the car’s worth based on the four possible conditions and the expected worth, taking into account the underlying probability function, respectively. The last column provides the percentage of the maximum c value out of E[v].

Fig. 1
figure 1

The worth of ten different (randomly selected) car models (of random years and mileage) based on the four possible conditions and their probabilities as appear on the ”Kelley Blue Book” website (columns 2-6); the maximum car inspection cost at which the condition on Theorem 1 holds (column 7); the percentage of the maximum c value out of E[v] (column 8)

Full size image

Note that the probability distribution in Fig. 1 is very different than the uniform distribution used in Example 1, and accordingly the threshold values (as fractions of E[v]) are much smaller. However, the values are still always above $100 and often above $200, which are realistic car inspection costs.

We move on to proving Theorem 1.

Proof of Theorem 1

The agent has two main strategies. We call them, following Faltings and Radanovic [14], “cooperative” and “heuristic”:

  • In the cooperative strategy, the agent computes v and uses the result to determine b as a function of v.

  • In the heuristic strategy, the agent does not compute v, and determines b based only on the prior f(v).

The agent will use the cooperative strategy iff its expected utility is larger than the expected utility of the heuristic strategy by more than c. Therefore in the following paragraphs we calculate the expected utility of the agent in each strategy, showing that under the condition given in the theorem there always exists a cdf G for which the above holds and otherwise the condition cannot hold. For the formal analysis we denote by \(\widehat{G}\) the integral of G: \(\widehat{G}(v) := \int _{r=0}^v G(r)dr.\)

By the cooperative strategy, the agent gets the object iff \(r \le b(v),\) and then his utility is \(v-r.\) Therefore his expected utility isFootnote 4:

$$\int _{r=0}^{b(v)} [(1-\epsilon )G'(r) + {\epsilon \over v^{\max }-v^{\min }}] (v-r)dr$$

The integrand is positive iff \(r<v.\) Therefore the expression is maximized when \(b(v)=v,\) and hence it is a strictly dominant strategy for the agent to provide \(b=v.\) In this case, his utility is \((1-\epsilon )\int _{r=0}^{v}G'(r)(v-r)dr + {\epsilon \over v^{\max }-v^{\min }}\int _{r=0}^{v}(v-r)dr .\) We assume that \(\epsilon \rightarrow 0,\)Footnote 5 so that the gain is approximately \(\int _{r=0}^{v}G'(r)(v-r)dr.\) By integrating by parts, one can see that this expression equals \(\widehat{G}(v).\) Hence, before knowing v, the expected utility of the agent from the cooperative strategy, denoted \(U_{\text{coop}}(G),\) is:

$$U_{\text{coop}}(G) = E[\widehat{G}(v)]$$

where E denotes expectation taken over the prior f(v).

By the heuristic strategy, the agent’s expected utility as a function of b is:

$$\begin{aligned} &E\left[ \int _{r=0}^{b} \left[ (1-\epsilon )G'(r) + {\epsilon \over v^{\max }-v^{\min }}\right] (v-r)dr\right] \\ &\quad = \int _{r=0}^{b} \left[ (1-\epsilon )G'(r) + {\epsilon \over v^{\max }-v^{\min }}\right] (E[v] -r)dr. \end{aligned}$$

The integrand is positive iff \(r< E[v],\) so it is a strictly dominant strategy for the agent to provide \(b=E[v].\) In this case, his gain when \(\epsilon \rightarrow 0,\) denoted \(U_{\text{heur}}(G),\) is:

$$U_{\text{heur}}(G) = \widehat{G}(E[v])$$

The net utility of the agent from being cooperative rather than heuristic is the difference:

$$U_{\text{net}}(G) := U_{\text{coop}}(G) - U_{\text{heur}}(G) = E[\widehat{G}(v)] - \widehat{G}(E[v])$$
(2)

The mechanism is truthful iff \(U_{\text{net}}(G) > c,\) i.e, the net utility of the agent from being cooperative is larger than the cost of being cooperative. Therefore, it remains to show that there is a cdf G satisfying \(c < U_{\text{net}}(G),\) iff \(c < E_v[\max (0, v-E[v])].\) This is equivalent to showing that \(E_v[\max (0, v-E[v])]\) is the maximum possible value of \(U_{\text{net}}(G),\) over all cdfs G. This is a non-trivial maximization problem since we have to maximize over a set of functions. We first present an intuitive solution and then a formal solution.

Intuitively, to maximize \(E[\widehat{G}(v)] - \widehat{G}(E[v])\) we have to make \(\widehat{G}(E[v])\) as small as possible, and subject to that, make \(\widehat{G}\) as large as possible. The smallest possible value of \(\widehat{G}\) is 0, so we let \(\widehat{G}(E[v])=0.\) Therefore we must have \(G(r)=0\) for all \(r\le E[v].\) Now, to make \(\widehat{G}\) as large as possible, we must let it increase at the largest possible speed from E[v] onwards; therefore we must make its derivative G as large as possible, so we let \(G(r)=1\) for all \(r>E[v]\) (1 is the largest possible value of a cdf). All in all, the optimal G is the step function: \(G^*(r) = \mathbb {1}_{r>E[v]},\) which gives \(U_{\text{net}}(G^*) = E[\max (0,v-E[v])]\) as claimed.

To prove this formally, we use mathematical tools that have been previously used in the analysis of revenue-maximizing mechanisms [22, 29]. In particular, we use Bauer’s maximization principle:

In a convex and compact set, every linear function has a maximum value, and it is attained in an extreme point of the set—a point that is not the midpoint of any interval contained in the set.

Denote by \({\mathcal {G}}\) the set of all cumulative distribution functions with support contained in \([v^{\min },v^{\max }].\) \({\mathcal {G}}\) is a convex set, since any convex combination of cdfs is also a cdf. Moreover, it is compact with respect to the sup-norm topology, as shown by Manelli and Vincent [29]. The objective function \(U_{\text{net}}(\cdot )\) is linear, so in particular it is convex. Therefore, to find its maximum value it is sufficient to consider the extreme points of the set \({\mathcal {G}}.\) We claim that the only extreme points of \({\mathcal {G}}\) are 0-1 step functions—functions G for which \(G(r)\in \{0,1\}\) for all r. Indeed, suppose that G is not a step function, so there is some \(r_0\) for which \(0< G(r_0) < 1.\) Then the following two functions are different elements of \({\mathcal {G}}\) (see Fig. 2):

$$\begin{aligned} G_1(r)&= \min (1, 2 G(r))\\ G_2(r)&= \max (0, 2 G(r) - 1) \end{aligned}$$

G is the midpoint of the segment \(G_1\)–\(G_2,\) so G is not an extreme point of \({\mathcal {G}}.\)

Fig. 2
figure 2

The cdf denoted by G is not an extreme point of the set \({\mathcal {G}},\) since it is the midpoint of two different elements of \({\mathcal {G}},\) namely the cdfs \(G_1\) and \(G_2\)

Full size image

Therefore, it is sufficient to maximize \(U_{\text{net}}\) on cdfs of the following form, for some parameter \(t\in [v^{\min },v^{\max }]\):

$$G_t(r) = \mathbb {1}_{r>t}$$

Integrating \(G_t(r)\) yields \(\widehat{G}_t(v) = \max (0, v-t),\) so by (2):

$$\begin{aligned} U_{\text{net}}(G_t)&= E[\max (0, v - t)] - \max (0, E[v] - t)\\&= \int _{v=t}^{v^{\max }} (v - t) f(v) dv + \min (0, t - E[v]) \end{aligned}$$

To find the t that maximizes \(U_{\text{net}}(G_t),\) we take its derivative with respect to t:

  • The derivative of the leftmost term is \(-\int _{v=t}^{v^{\max }}f(v) dv = -\Pr [v\ge t],\) which is always between 0 and \(-1.\)

  • The derivative of the rightmost term is 1 when \(t < E[v]\) and 0 when \(t > E[v].\)

Therefore, \(U_{\text{net}}(G_t)\) is increasing when \(t < E[v]\) and decreasing when \(t > E[v].\) Therefore its maximum is attained for \(t = E[v]\) and it is \(E[\max (0,v-E[v])]\) as claimed. \(\square\)

4 Minimizing the principal’s loss

The function \(G^*\) from Theorem 1 allows the principal to elicit true information for a large range of costs. However, the information does not come for free: the principal “pays” for the information by the risk of giving away the object for less than its value.Footnote 6 As stated earlier, obtaining the information is mandatory. Hence, the principal naturally seeks to minimize the loss resulting from giving away the object. In other words, from the set of all cdfs with which Mechanism 1 is truthful, the principal would like to choose a single cdf G (possibly different than \(G^*\)) which minimizes her loss.

The principal loses utility whenever the agent gets the object, i.e., whenever \(v>r.\) In this case, the principal’s net loss is \(v-r.\) Therefore, the expected loss of the principal (when \(\epsilon \rightarrow 0\)), denoted \(L_{\text{net}}(G),\) is:

$$L_{\text{net}}(G) := E_v\left[ \int _{r=0}^{v} G'(r)(v-r)dr \right]$$

A simple calculation shows that this expression equals \(E_v[\widehat{G}(v)],\) which is exactly \(U_{\text{coop}}(G)\)—the utility of the agent from playing the cooperative strategy. This is not surprising as the agent and the principal are playing a zero-sum game.

To induce cooperative behavior, \(U_{\text{coop}}(G)\) must equal \(c',\) for some \(c' > c.\) Therefore the principal’s loss must be \(c'\) too. Fortunately, the principal can attain this loss even for \(c'\) arbitrarily close to c. We define:

$$\begin{aligned} p_{c'}&:= {c'\over E_v[\max (0, v - E[v])]} \\ G_{c'}(r)&:= p_{c'}\cdot \mathbb {1}_{r>E[v]} + (1-p_{c'})\cdot \mathbb {1}_{r=v^{\max }} \end{aligned}$$
(3)

With this \(G_{c'},\) Mechanism 1 selects r as follows. With probability \(p_{c'},\) r is selected using the function \(G^*\) from (1), which guarantees the agent a utility of \(E_v[\max (0, v - E[v])].\) With probability \(1-p_{c'},\) the principal chooses r so large that the agent never gets the object. Therefore the expected utility of the agent is \(p_{c'}\cdot E_v[\max (0, v - E[v])] = {c'}.\) Consequently the loss of the principal is \({c'}\) too. When \({c'}\rightarrow c,\) the principal’s loss approaches the theoretic lower bound—she obtains the information for only slightly more than its computation cost.

The probability that the principal has to give away the object is quite low in realistic settings. For example, consider the case mentioned in Example 1 where v is uniform in [0, 2M]. Suppose the object is a car. Typical values are \(c=\$200\) and \(M=\$40,000.\) Here \(p_c = c/(M/4) = 0.02.\) So the information is computed and delivered truthfully with probability 1, whereas with probability 98% the principal keeps the car (and incurs no loss), and with probability 2% the principal sells the car for its expected value of $40,000 (and loses the difference \(v-\$40,000\)).

An interesting special case is \(c=0,\) i.e., the agent already knows v. In this case, the principal does not need to know the prior distribution f(v) and can simply use

$$G_0(r) := \delta + (1-\delta )\cdot \mathbb {1}_{r=v^{\max }}$$
(4)

If \(\delta >0,\) the agent’s net utility is positive so the mechanism is truthful; when \(\delta \rightarrow 0,\) the principal’s loss approaches 0.

5 Divisible objects

So far we assumed the object is indivisible, so it is either transferred entirely to the agent or not at all. In general the object may be divisible. For example, it may be possible to transfer only a part of an oil field, or only transfer shares in the field’s future profits. In this case, instead of using the function \(G_{c'}(r)\) of (3), we can run Mechanism 1 using the function \(G^*(r),\) but if the object needs to be transferred in step 3—only a fraction \(p_{c'}\) of it is actually transferred. The analysis of this mechanism is the same—cooperation is still a dominant strategy for the agent whenever \(c<c',\) and the principal’s loss is still \(c'.\) The advantage is that a risk-averse agent may prefer to get a fraction \(p_{c'}\) of the object with certainty, than to get the entire object with probability \(p_{c'}.\) Moreover, a risk-averse principal may prefer to keep a fraction \(1-p_{c'}\) of the object with certainty, than to risk losing the entire object with probability \(p_{c'}.\)

6 Different values

So far we assumed that the object’s value is the same for the principal and the agent. In general the values might be different. For example, suppose the principal is the owner of a used car and the agent is a car dealer. While the dealer certainly has a positive value for owning the car, it may be lower (in case the dealer already has several cars of the same model) or higher (in case the dealer can fix and make improvements in the car at a reduced cost) than its value for the car owner.

Let \(v_p\) be the object’s value for the principal and \(v_a\) its value for the agent. The agent’s utility is calculated as before, using \(v_a\) instead of v:

$$\begin{aligned} U_{\text{coop}}(G)&= E[\widehat{G}(v_a)] \quad U_{\text{heur}}(G) = \widehat{G}(E[v_a]) \\ U_{\text{net}}(G)&= E[\widehat{G}(v_a)] - \widehat{G}(E[v_a])\end{aligned}$$
(5)

Therefore, if the condition of Theorem 1 holds on \(v_a,\) i.e.:

$$c < E[\max (0, v_a-E[v_a])$$

then, using the cdf \(G^*(r) := \mathbb {1}_{r>E[v_a]},\) Mechanism 1 is still “truthful” in that it induces the agent to reveal the true \(v_a.\) Obviously the mechanism does not reveal the true \(v_p,\) and indeed no one else can directly tell the principal what her value of the object should be. However, in the common case in which \(v_a\) and \(v_p\) are correlated, the principal can use the knowledge of \(v_a\) to gain some knowledge about \(v_p.\)

In contrast to the common-value setting, however, the game here is no longer zero-sum—the principal’s loss does not equal the agent’s utility, so it may be larger or smaller than c. The principal’s expected loss is now:

$$\begin{aligned} L_{\text{net}}(G)&:= E\left[ \int _{r=0}^{v_a} G'(r)(v_p-r)dr \right] \\&= E[\widehat{G}(v_a) + (v_p-v_a)\cdot G(v_a)] \\&= U_{\text{coop}}(G) + E[(v_p-v_a)\cdot G(v_a)] \end{aligned}$$
(6)

So, when \(v_p > v_a\) the principal’s loss is larger than the agent’s utility, and when \(v_p < v_a\) it is smaller.

Suppose we want the agent’s net utility to be at least \(c',\) for some \(c'>c.\) Then, the principal’s minimization problem is:

$$\begin{aligned} \text{minimize}&\qquad E[\widehat{G}(v_a)] + E[ (v_p-v_a)\cdot G(v_a)] \\ \text{subject to}&\qquad G\in {\mathcal {G}}\text{ and } E[\widehat{G}(v_a)] - \widehat{G}(E[v_a]) \ge c' \end{aligned}$$
(7)

This is still a problem of minimizing a linear objective function over a convex set of functions, so the minimum is still attained in the extreme points of the set. However, finding the extreme points and minimizing G over that points is much harder. So far, the best we could do with this problem is simplify it in the special case in which \(v_p\ge v_a\) with probability 1. This is a realistic case: an oil field is usually worth more to its owner than to a geologist, and a car is usually worth more to its owner than to an appraiser. We prove below that the principal’s minimization problem can be simplified to:

$$\begin{aligned} \text{minimize}&\qquad E[ (v_p-v_a)\cdot G(v_a)] \\ \text{such that}&\qquad G\in {\mathcal {G}}\text{ and } E[\widehat{G}(v_a)] = c' \text{ and } \widehat{G}(E[v_a]) = 0 \end{aligned}$$
(8)

Lemma 1

If \(v_p \ge v_a\) with probability 1, then the minimization problems (7) and (8) have the same solutions.

Proof

First, note that in (8), the minimization goal can be written equivalently as \(E[\widehat{G}(v_a)] + E [ (v_p-v_a)\cdot G(v_a) ],\) since in that problem the leftmost term is the constant \(c'.\) So the minimization goals in both problems are identical. The problems differ only in the constraints: the constraints of (8) are stricter. Therefore it is sufficient to prove that, for every cdf satisfying the constraints of (7), there exists a cdf satisfying the stricter constraints of (8), which attains a weakly-smaller loss. The construction proceeds in two steps.

Step 1 Let \(G_0\) be a cdf satisfying the constraints of (7). Define a new cdf \(G_1\) as follows:

$$G_1(r) := {\left\{ \begin{array}{ll} 0 &{}\quad r \le E[v_a] \\ G_0(r) &{}\quad r > E[v_a] \end{array}\right.}$$

Since \(G_1(r)\le G_0(r)\) for all r, and \(v_p - v_a \ge 0\) always, this \(G_1\) has a weakly smaller loss than \(G_0.\)

The integral of \(G_1\) satisfies:

$$\widehat{G}_1(v) = \int _{r=0}^v G_1(r) dr = {\left\{ \begin{array}{ll} 0 &{}\quad v \le E[v_a]\\ \widehat{G}_0(v)-\widehat{G}_0(E[v_a]) &{}\quad v > E[v_a] \end{array}\right. }$$

Hence, \(G_1\) satisfies stricter constraints than \(G_0\):

  • \(\widehat{G}_1(E[v_a])=0\) is clearly satisfied;

  • \(E[\widehat{G}_1(v_a)]\ge c'\) is satisfied since, for all v, \(\widehat{G}_1(v) \ge \widehat{G}_0(v) - \widehat{G}_0(E[v_a]).\) Therefore, \(E[\widehat{G}_1(v)] \ge E[\widehat{G}_0(v)] - \widehat{G}_0(E[v_a]).\)

    The latter expression is at least \(c',\) by the assumption that \(G_0\) satisfies the constraints of (7).

Step 2 Let \(y := c' / E[\widehat{G}_1(v_a)]\) and note that \(y\le 1.\) Define:

$$G_2(r) := y\cdot G_1(r)$$

Since \(y\le 1,\) \(G_2\) has a weakly smaller loss than \(G_1.\) Moreover, \(G_2\) satisfies the constraints of (8) since:

$$\begin{aligned} \widehat{G}_2(E[v_a])&= y\cdot \widehat{G}_1(E[v_a]) = 0\\ E[\widehat{G}_2(v_a)]&= y\cdot E[\widehat{G}_1(v_a)] = c'.\\ \end{aligned}$$

\(\square\)

We could not find a general solution to (8); we leave it for future work.Footnote 7

Open problem 1

Solve the minimization problem (8).

7 Unknown cost of computation

So far, we assumed that the principal knows the costs incurred by the agent when computing the true value of the object. This assumption is realistic in many cases. For example, when the object is a car, the mechanic can reveal its condition by running a set of standard checks that consume a known amount of time, so their cost can be reasonably estimated. However, in some cases the cost might be known only to the agent. In this section we assume that the principal only knows a prior distribution on c, given by pdf h and cdf H, with support \([c^{\min },c^{\max }].\) For simplicity we consider here the common value setting, \(v_p = v_a = v.\) We assume that the object’s value v and the cost c of computing that value are independent random variables.

If the principal must get the information at all costs (e.g., due to regulatory requirements), then she can simply run Mechanism 1 with the cdf \(G_{c'}\) of (3), taking \(c' = c^{\max }.\) This ensures that the agent calculates and reports the true information whenever \(c^{\max }< E[\max (0, v-E[v])],\) and the principal’s loss is \(\approx c^{\max }.\)

However, in some cases the principal might think that \(c^{\max }\) is too much to pay for the information. In this case, it may be useful for the principal to determine a utility of obtaining the information. We denote the principal’s utility from knowing the information by u, and assume that it is measured in the same monetary units as the function \(L_{\text{net}}\) of Sect. 4. In other words, the principal’s loss is:

  • \(L_{\text{net}}(G)\) when she elicits the true value using Mechanism 1 with cdf G;

  • u when she does not elicit the true value.

If \(u<c^{\max },\) it is definitely not optimal for the principal to use Mechanism 1 with the cdf \(G_{c'}\) taking \(c'=c^{\max }.\) What should the principal do in this case?

To gain insight on this situation, we compare it to bilateral trading. In standard bilateral trading, a single consumer wants to buy a physical product from a single producer; in our setting, the principal is the consumer, the agent is the producer, and the “product” is information. This is like bilateral trading, with the additional difficulty that the consumer cannot verify the “product” received.

The case when the production cost c is unknown in bilateral trading was studied by Baron and Myerson [9]. They define the virtual cost function of the producer by:

$$z(c) := c + {H(c)\over h(c)} \quad (c\in [c^{\min },c^{\max }])$$

(it is analogous to the virtual valuation function used in Myerson’s optimal auction theory). By Myerson’s theorem, the expected loss of the consumer in any truthful mechanism equals the expected virtual cost of the producer in that mechanism, \(E_c[z(c)].\) The “loss” of the consumer from not buying the product is her utility from having this product, which we denote by u. Therefore, to minimize her expected loss, the consumer should buy the product if-and-only-if \(z(c) < u.\)

Under standard regularity assumptions on h, the virtual cost function z(c) is increasing with c. In that case, the optimal mechanism for the consumer is to make a take-it-or-leave-it offer to buy the product for a price of:

$$R_{z,u} = {\left\{ \begin{array}{ll} 0 &{}\quad \text{if } u< z(c^{\min }) \\ z^{-1}(u) &{}\quad \text{if } z(c^{\min })\le u\le z(c^{\max }) \\ c^{\max }&{}\quad \text{if } z(c^{\max }) < u \end{array}\right. }$$
(9)

With this mechanism, the producer agrees to sell the product iff \(c<R_{z,u},\) which occurs iff \(z(c)<u.\)

We now return to our original setting, in which the “product” is the information about an object’s value. We emphasize that there are two values: the value for both agents of the object itself, which we denoted by v, and the value for the principal of knowing v, which we denote here by u.

Similarly to the setting of Baron and Myerson [9], the principal has to ensure that the agent sells the information iff \(z(c)<u,\) which happens iff \(c<R_{z,u}.\) Analogously to equations (3), we define:

$$\begin{aligned} p_{z,u}&= {R_{z,u}\over E_v[\max (0, v - E[v])]}\\ G_{z,u}(r)&= p_{z,u}\cdot \mathbb {1}_{r>E[v]} + (1-p_{z,u})\cdot \mathbb {1}_{r=v^{\max }} \end{aligned}$$

The principal can then execute Mechanism 1 using \(G_{z,u}\) as the cdf. As explained after equation (3), this gives the agent an expected net utility of \(R_{z,u},\) so the agent will agree to participate in the mechanism iff \(c < R_{z,u}.\) This decision rule of the agent is in fact the one that maximizes the expected utility of the principal.

Example 4

Suppose the cost c is distributed uniformly in \([0,c^{\max }].\) Then, the virtual cost function is \(z(c) = 2 c,\) so \(z^{-1}(u)=u/2\) and \(R_{z,u} = \min (c^{\max },u/2).\)

Consider first a physical product. If \(u>2 c^{\max },\) then the consumer offers \(c^{\max },\) the producer always sells, and the consumer’s loss is \(c^{\max }.\) If \(u<2 c^{\max },\) then the consumer offers u/2 and the producer sells only if the cost is less than u/2. This happens with probability \({u\over 2 c^{\max }},\) so the consumer’s expected loss is \({u\over 2 c^{\max }}\cdot {u\over 2} + (1-{u\over 2 c^{\max }})\cdot u = u\cdot (1-{u\over 4c^{\max }}),\) which is less than \(c^{\max }.\)

Now suppose that the “product” is information about an object’s value. Suppose that, a priori, the object’s value is distributed uniformly in [0, 2M]. As calculated in Example 1, in this case \(E[\max (0, v-E[v])] = M/4.\) We make the realistic assumption that \(c^{\max }< M/4\) (the maximum possible cost for appraising an object is less than a quarter of the expected value of the object). Therefore the following expression defines a valid probability:

$$p_{z,u} = { \min (c^{\max }, u/2) \over M/4}$$

The principal should run Mechanism 1 with the cdf \(G_{z,u}(r) = p_{z,u}\cdot \mathbb {1}_{r>E[v]} + (1-p_{z,u})\cdot \mathbb {1}_{r=v^{\max }}.\) The expected net utility of the agent from participating is \(U_{\text{net}}(G_{z,u}) = \min (c^{\max }, u/2).\)

If \(u>2 c^{\max },\) then \(U_{\text{net}}(G_{z,u}) = c^{\max },\) so the agent always participates, and the principal always obtains the information for an expected loss of \(c^{\max }.\)

If \(u<2 c^{\max },\) then \(U_{\text{net}}(G_{z,u}) = u/2\) and it might be higher or lower than the actual cost c. If \(c<u/2\) then the agent participates and the principal obtains the information for an expected loss of u/2; if \(c>u/2\) then the agent refuses to participate and the principal does not obtain the information, so her loss is u. All in all, the principal’s expected loss is \({u\over 2 c^{\max }}\cdot {u\over 2} + (1-{u\over 2 c^{\max }})\cdot u = u\cdot (1-{u\over 4c^{\max }}),\) which is less than \(c^{\max }.\)

8 Alternative mechanisms

In addition to Mechanism 1, we developed two alternative mechanisms for solving the same problem—eliciting a true value from a single information agent.

In Mechanism 2, the price of the object is not determined by the principal but rather calculated as a function of the agent’s reported value, similarly to a first-price auction.

Mechanism 2 Parameters: \(\epsilon >0\): a constant, G(r): a cdf.

1. The agent provides \(b \in [v^{\min },v^{\max }].\)

2. With probability G(b), the agent receives the object and pays:

\(\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad b - {\widehat{G}(b)/ G(b)}\)

where \(\widehat{G}\) is the integral of G: \(\widehat{G}(b) := \int _{r=v^{\min }}^b G(r) dr.\)

In Mechanism 3, the principal publicly posts a price and the agent decides whether to buy the object at this price or not.

Mechanism 3 Parameters: \(t>0\)—a constant, \(p\in [0,1]\)—a probability.

1. The principal publicly posts the price t.

2. The principal asks the agent whether or not he wants to pay t for the object.

3. If the agent says “yes”, then with probability p he receives the object and pays t. Otherwise the principal keeps the object to herself.

4. If in step 3 the principal keeps the object, then she runs Mechanism 1 with the function \(G_0\) of Eq. (4).

The three mechanisms are apparently different in various aspects such as the role of the different players in the underlying Stackelberg game (leader vs. follower), and whether or not there is a requirement for secrecy (Mechanism 1 requires to keep r secret while Mechanism 2 need no secrecy). Interestingly, they are equivalent in the conditions they impose on the cost c and the principal’s loss. We present a proof below.

Note that we consider the general case of different valuations of the agent and the principal (as in Sect. 6)—the agent’s value is \(v_a\) and the principal’s value is \(v_p.\)

In Mechanism 2, the agent’s expected utility for reporting b is:

$$G(b) \cdot (v_a - b + \widehat{G}(b)/G(b))$$

A higher b means a higher probability G(b) of receiving the object but also a higher purchase price. The agent calculates the optimal b by solving an optimization problem. The derivative w.r.t. b is:

$$\begin{aligned}&G' \cdot (v_a - b + \widehat{G}/G)+ G\cdot (-1 + (G^2-\widehat{G}G')/(G^2))\\&\quad = G'\cdot (v_a-b) \end{aligned}$$

Since G is an increasing function, \(G'\) is positive, so this expression is positive when \(b<v_a\) and negative when \(b>v_a,\) so the expected utility of the agent is maximized when \(b = v_a.\) Then his expected utility is:

$$U_{\text{coop}}(G) = E[G(v_a)\cdot (v_a - v_a + \widehat{G}(v_a)/G(v_a))] = E[\widehat{G}(v_a)]$$

Similarly, when the agent does not compute \(v_a,\) his utility is maximized when \(b = E[v_a],\) which gives him a utility of:

$$U_{\text{heur}}(G) = \widehat{G}(E[v_a])$$

These utilities are exactly as in Mechanism 1 and Equation (5).

Therefore, Theorem 1 is valid as-is for Mechanism 2, and the mechanism is applicable iff \(c < E[\max (0, v_a-E[v_a])],\) using the same cdf \(G^*\) of (1).

Moreover, the principal’s loss \(L_{\text{net}}\) is exactly as in equation (6). Therefore the principal has to solve the problem (8) for minimizing her loss, and the minimal loss is the same. In particular, in the common value setting \(v_a=v_p,\) the principal’s loss can be made arbitrarily close to the computation cost c.

In Mechanism 3, in step 2, the agent has to decide whether or not to receive the object for a payment of t. Calculating \(v_a\) may help him decide:

  • If the agent calculates \(v_a,\) it is optimal for him to say “yes” iff \(v_a > t,\) so his utility is \(E[p\cdot \max (0, v_a-t)].\)

  • Otherwise, it is optimal for the agent to say “yes” iff \(E[v_a]>t,\) so his expected utility is \(p\cdot \max (0,E[v_a]-t).\)

In case the agent decides to calculate \(v_a,\) in step 4 the situation is similar to the \(c=0\) case mentioned at the end of Sect. 4—the agent already knows the information so the cost for calculating it now is 0. Therefore, at step 4 the principal elicits the true information for almost zero additional loss. Define the following functions (depending on the mechanism parameters p, t):

$$\begin{aligned} G(r)&:= p\cdot \mathbb {1}_{r>t}\\ \widehat{G}(v)&:= \int _{r=0}^v G(r) dr = p\cdot \max (0, v-t) \end{aligned}$$

With these definitions, the agent’s utilities when computing / not computing \(v_a\) are exactly as in equation (5), and the principal’s loss in step 2 is the same as in equation (6). So Theorem 1 is valid, and the mechanism is truthful iff \(c < E[\max (0, v_a - E[v_a])],\) by taking \(t=E[v_a]\) and \(p>{c\over E[\max (0, v_a - E[v_a])]}.\)

Additionally, Mechanism 1 itself can be extended by adding a probability of sale—before actually selling the object to the agent for r, the principal tosses a biased coin with probability p of success (where p is a fixed parameter), and makes the sale only in case of success. This extension is actually already supported by the current mechanism: for any cdf G and parameter p, we can create a new cdf \(G_p\) by putting a probability mass of \(1-p\) on values larger than \(v^{\max }\) and a probability mass of p on the original G. This attains exactly the same effect as a sale with probability p, since with probability \(1-p,\) the value r will be so high that the object will never be sold. Hence, Theorem 1 applies to this extension too, so even with this generalization, the mechanism works iff \(c < E[\max (0,v-E[v])].\)

The fact that several different mechanisms lead to the same applicability conditions and loss expressions lead us to conjecture that these results are valid universally.

Conjecture 1

(a) There exists a mechanism for truthfully eliciting a single agent’s value \(v_a,\) if-and-only-if:

$$c < E[\max (0, v_a-E[v_a])].$$

(b) In any mechanism for truthfully eliciting \(v_a\) from a single agent, the principal’s loss is at least:

$$c + \min _{G\in {\mathcal {G}}_c} E[(v_p-v_a)\cdot G(v_a)],$$

where the minimization is over all cumulative distribution functions satisfying \(E[\widehat{G}(v_a)] = c\) and \(\widehat{G}(E[v_a]) = 0.\)

Remark 1

While our main goal in showing three inherently different mechanisms is primarily theoretic (supporting the conjecture), there are some practical advantages for preferring the use of some of them in specific cases. For example, an advantage of Mechanism 2 is that it does not require a mediator. Mechanism 1 requires a mediator to keep the reservation value r secret and reveal it only after the agent’s report (and this recurs in Mechanism 3 as it requires the principal to run also Mechanism 1 entirely). A dishonest mediator might collude with the agent and reveal the reservation value to him before the report, allowing him to report \(r+\epsilon\) and win the object without giving any information. The mediator might also collude with the principal and reveal a false reservation value \(b-\epsilon\) after hearing the report b. In Mechanism 2 no such problems arise.

Additionally, Mechanism 1 requires the agent to believe that the principal really draws r from the advertised distribution (or alternatively, use a third-party for doing the lottery). In Mechanism 2 the lottery is much simpler: a probability \(p=G(b)\) is calculated in a transparent manner, and the object is sold with probability p. Such lottery can be carried out transparently in front of the agent, so no trust is required.

On the other hand, Mechanism 1 has the advantage that the optimal strategy of providing \(b=v\) is more intuitive. In Mechanism 2, once the agent knows v, he needs to solve a complex optimization problem in order to calculate the optimal b and realize that it equals v. In contrast, in Mechanism 1, once the agent knows v, it is easy to realize that it is optimal to report \(b=v\): by reporting \(b>v\) he might buy the object at a price higher than its value, and by reporting \(b<v\) he might miss buying the object at a price lower than its value.

9 Cost of information delivery

So far we assumed that the information production is costly, but once the information is available—its delivery is free. In general, the information delivery too might be costly. For example, the agent might have to write a detailed report about how v was calculated, and have the report signed by the firm’s accountants. Throughout this section, we denote the cost of delivery by \(c_d\) and assume that it is common knowledge. We also assume that the agent incurs the same cost \(c_d\) whether the delivered information is true or false.

In settings where information delivery is costly, the principal can still naively guarantee the calculation of the value and its true delivery by promising the agent a payment of \(c_d\) for participating in Mechanism 1. This makes the strategic situation of the agent identical to the situation analyzed in Sect. 3. Mechanism 1 is still truthful whenever \(c<E_v[\max (0,v-E[v])].\) The principal’s loss is the sum of the production and delivery costs, which is the smallest loss possible since the agent’s expenses must be covered.

However, the naive method may not always be the most beneficial for the principal. In particular, if the principal needs to know the exact object value only when it is above a certain threshold T, as otherwise knowing the exact value is useless, it may be more beneficial to use a mechanism where the value is delivered only if it is above T.Footnote 8

This can be attained by using Mechanism 4, which is essentially Mechanism 3 adapted to include the delivery cost.

Mechanism 4 Parameters: \(T>0\)—a constant, \(p\in [0,1]\)—a probability.

The agent is asked to choose between the following two options.

Option A:

1. With probability p, the agent pays T to the principal and the principal transfers the object to the agent.

2. Otherwise (with probability \(1-p\)), the agent does not pay nor get the object. The agent reveals the value v to the principal and receives \(c_d\) as reimbursement of the delivery cost.

Option B: nothing happens: the agent does not reveal v nor pays nor receives the object.

If the agent calculates v, then it is optimal for him to choose option A iff \(v>T\): option A gives him an expected utility of \(p\cdot (v-T),\) while with option B his utility is 0. In this case, revealing the true value requires no additional cost for the agent, so we can assume he indeed reveals the true v in step 2 (alternatively, Mechanism 1 can be used with the function \(G_0\) to elicit the true v). The expected utility of the agent after calculating v is \(p \cdot E[\max (0,v-T)].\)

If the agent does not calculate v, then it is best for him to choose option A (and deliver some random value in step 2) iff \(E[v]>T.\) Hence his expected utility is \(p \cdot \max (0,E[v]-T).\) Therefore, the agent calculates v iff \(p \cdot (E[\max (v-T,0)] - \max (E[v]-T,0)) > c.\) Setting \(p=c / (E[\max (0, v-T)] - \max (0, E[v]-T)),\) Mechanism 3 is valid as long as \(c < E[\max (0, v-T)] - \max (0, E[v]-T),\) as otherwise the probability p becomes greater than 1.

As a practical use-case for Mechanism 3, suppose the object under consideration is in fact an opportunity which the principal can either exploit or give up on. Exploiting the opportunity requires the principal to incur an exploitation cost, which we denote by \(c_e.\) For example, the principal holds an option to buy a jewel or a stock at price \(c_e.\) Or, the principal holds an oil field that requires an investment of \(c_e\) in order to become operational. We assume that, in order to exploit the opportunity, the principal also needs a report regarding its exact value, which costs \(c_d\) to deliver. Therefore, it is optimal for the principal to use Mechanism 3 with a threshold of \(T = c_d + c_e,\) since then she will pay the delivery cost only when she intends to exploit the opportunity.

Indeed, if \(T < c_d+c_e,\) then whenever \(T< v < c_d+c_e,\) the agent will choose option A and the principal will have (with probability \((1-p)\)) to pay him \(c_d,\) but then the principal’s net gain from exploiting the opportunity will be \(v - c_d - c_e < 0.\) On the other hand, if \(T > c_d+c_e,\) then whenever \(T> v > c_d+c_e,\) the agent will choose option B and the principal will be unable to exploit the opportunity, although exploiting it in this case could yield her a net gain of \(v - c_d - c_e > 0.\)

Proposition 1

Given an opportunity with an exploitation cost \(c_e,\) i.e., the principal only needs to know whether the value v is above or below \(c_e\) in order to decide whether to exploit it, the strategy maximizing the principal’s expected utility is to use Mechanism 4 if and only if

$$E[\max (0, v-T)]-\max (0, E[v]-T) > c$$

where \(T=c_e+c_d\) is the threshold.

Proof

Consider using a threshold \(T>c_e+c_d.\) Here, any opportunity with value \(v\in (c_e+c_d, T)\) will no longer be returned to the principal, yet the principal will benefit from receiving such information as even after reimbursing the agent \(c_d\) the value of the opportunity is greater than its exploitation cost. Similarly, if using a threshold \(T<c_e+c_d,\) then any opportunity with value \(T<v<c_e+c_d\) delivered to the principal will be either exploited (if \(v>c_e\)) or discarded (otherwise), resulting either in a loss \(c_d\) or \(v-c_e-c_d<0,\) respectively. Hence \(T=c_e+c_d.\)

The condition \(E[\max (0, v-T)]-\max (0, E[v]-T)>c\) that should hold in order to request the valuation in the first place simply captures the expected gain from having the information (left hand side) compared to the expected loss due to the transfer of the item (which is exactly c, as explained above). \(\square\)

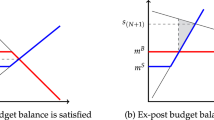
The above is illustrated in Fig. 3. The two graphs in the figure demonstrate the principal’s expected profit as a function of the threshold used. In the left graph, the value of the opportunity is distributed according to a normal distribution with \(\mu =2\) and \(\theta =1,\) and in the right graph, the value is distributed according to a uniform distribution between 0 to 2. The calculation of the principal’s expected profit with each corresponding threshold (on the horizontal axis) was carried out by drawing random opportunity values from the relevant distribution (uniform/normal). If the value chosen was above the threshold, the principal receives this information from the agent and therefore will have to pay both c and \(c_d.\) Additionally, if the drawn value is above its exploitation value (\(c_e\)) then the principal will be interested in exploiting this opportunity thus will have to pay also the cost of exploiting it, \(c_e,\) in addition to \(c_d\) and \(c_e.\) If however, the value drawn is lower than the threshold, the principal will not be interested in knowing the true value and will only need to pay for the extraction of the value by the agent. This was repeated one million times for each threshold, and the data points in the graphs are the average values over all runs for each threshold.Footnote 9 In both graphs it is quite clear that no matter what the value of c is, the maximal value for the principal’s profit is being received at \(T=c_e+c_d,\) as in Proposition 1.

Fig. 3
figure 3

An illustration of the principal’s expected profit as a function of the threshold used for both the case where the value of the opportunity is distributed according to a normal distribution (left graph) and according to a uniform distribution (right graph)

Full size image

10 Related work

Mechanisms by which an uninformed agent tries to elicit information from an informed agent are as old as King Solomon’s judgment (I Kings:3). About two centuries ago, the German poet Goethe invented a mechanism for eliciting the value of his new book from his publisher [30], but without considering the computation cost.

Various new mechanisms for truthful information elicitation have been studied in recent years, including mechanisms based on proper scoring rules [7, 26], the Bayesian truth serum [10, 35, 41], and its variants [32, 44], the peer truth serum [36], the ESP game, credit-based mechanisms [20], and similar output agreement mechanisms [40]. See also [28] for a recent unifying framework for several different kinds of mechanisms. Faltings and Radanovic [14] provide a comprehensive survey of such mechanisms in the computer science literature. They classify them into two categories:

The principle underlying all truthful mechanisms is to reward reports according to consistency with a reference. (1) In the case of verifiable information, this reference is taken from the ground truth as it will eventually be available. (2) In the case of unverifiable information, it will be constructed from peer reports provided by other agents.

The present paper provides a third category: the information is unverifiable, and yet there is a single agent to elicit it from.Footnote 10

Interactions between an informed agent and an uninformed principal have also been studied extensively in economics. A typical setting is that the agent is a seller holding an object and the principal is a buyer wanting that object (contrary to our setting, where the principal is the object owner). In some settings, the agent is a manager of a firm and the principal is a potential investor. Common to all cases is that the agent holds information that may affect the utility of the principal, and the question is if and how the agent can be induced to disclose this information.

The seminal work of Akerlof [1] shows that, when information is not verifiable and is not guaranteed to be correct (as in our setting), the incentive of the agent to provide false information might lead to complete market failure. In contrast, if the information is ex-post verifiable (i.e, the agent can hide information but cannot present false information), then market forces may be sufficient to push the agent to voluntarily disclose his information [17,18,19]. Mechanisms for information elicitation have been developed for settings where the information is verifiable [21], partially verifiable [15, 16] or verifiable at a cost [11, 13, 31, 43].

An additional line of research assumes that the information is unverifiable, however, if it is purchased, it is always correct. Moreover, their goal is to maximize the agent’s revenue rather than minimize the principal’s loss [2, 3, 5, 8, 37].

Our work is also related to contract theory [12], in which a principal tries to incentivize an agent to choose an action that is favorable to the principal. There, while the principal cannot observe the agent’s action, she can observe the (probabilistic) outcome of his action. In contrast, in our setting the principal has no way of knowing whether or not the agent calculated the true information.

Our work is motivated by government auctions for oil and gas fields. A lease for mining oil/gas is put to a first-price sealed-bid auction. One of the participating firms owns a nearby plot and can, by drilling in its own plot, compute relevant information about the potential value of the auctioned plot. Hendricks et al. [25] show that, in equilibrium, the informed firm underbids and gains information rent, while the uninformed firms have zero expected value. Porter [34] provides empirical evidence supporting this conclusion from almost 40 years of auctions by the US government. It indicates that information asymmetry causes the government to lose about 30% of the potential revenue. As a solution, Hendricks et al. [24] suggest to exclude the agent from the auction and induce him to reveal the information by promising him a fixed percentage of the auction revenues. However, they note that in practice it may be impossible to exclude a firm from a government auction. The present paper provides a different solution: the government (the principal) can use our Mechanism 1 to elicit the information from the informed firm (the agent). Then it can release the information to the other firms and by this remove the information asymmetry.

The decision rule in our Theorem 1 is similar to the ones used in optimal stopping problems, e.g., the one derived by Weitzman [42] for Pandora’s Box problem. While the latter considers a single player and has no strategic aspect, our model considers a strategic setting. Still the essence of the decision is somewhat similar as it considers the marginal expected profit from knowing the true value (as opposed to acting based on the best value found so far in Pandora’s problem, or the expected value in our case).

Mechanism 1 uses the reservation-price concept, which can be found in literature on auctions where agents have to incur a cost for learning their own value. For example, Hausch and Li [23] discuss an auction for a single item with a common value. Each bidder incurs a cost for participating in the auction, and additional cost for estimating the value of the item. Persico [33] discusses an extended model where the bidders can pay to make their estimate of the value more informative.

11 Discussion and future work

Information-providers are now ubiquitous, enabling people and agents to acquire information of various sorts. As self-interested agents, information providers typically seek to maximize their revenue. This is where the failure of direct payment becomes apparent, especially when the information provided is non-verifiable. The importance of the mechanisms provided and analyzed in the paper is therefore in their guarantee for truthfulness in the information elicitation process.

An important challenge for future work is to study the theoretic limitations of the setting studied in this paper—a single information-agent and unverifiable information. In particular, we conjecture that any truthful mechanism for this setting must sell the object with a positive probability, although we do not know how to prove this formally. Solving the minimization problem in Sect. 6 and settling the conjecture in Sect. 8 are interesting challenges too. Some other directions for future work are:

Unknown distribution of value Mechanism 1 requires to calculate \(E_v[\max (0, v-E[v])],\) which requires knowledge of the prior distribution of v. When the distribution is not known, truthfulness can be guaranteed only when \(c=0,\) since in this case G can be chosen independently of the distribution (see end of Sect. 4). It is interesting whether true information can be elicited by a prior-free mechanism also for \(c>0.\)

Risk-averse agents The current model assumes that the agent is risk-neutral, so that his utility from a random mechanism is the expectation of the value. It is interesting to check what happens in the common case in which the agent is risk-averse.

Suppose there is an increasing function \(u:{\mathbb {R}}\rightarrow {\mathbb {R}}\) that maps the value of the agent to his utility. So \(u(0)=0\) (no value means no utility) and \(u'(x)>0\) for all x (more value always means more utility). When the agent is risk-neutral (as we assumed so far), \(u'\) is constant; when the agent is risk-averse, \(u'\) is decreasing. Then, when the agent is cooperative and computes v, he gets the object iff \(r \le b(v),\) and then his utility is \(u(v-r).\) Therefore his expected utility is:

$$\int _{r=0}^{b(v)} [(1-\epsilon )G'(r) + {\epsilon \over v^{\max }-v^{\min }}] u(v-r)dr$$

Since \(u(v-r)\) is positive iff \(v-r\) is positive, the integrand is positive iff \(r<v.\) Therefore the expression is maximized when \(b(v)=v,\) and hence it is still a strictly dominant strategy for the agent to bid \(b=v.\) This is encouraging, since it means that at least the second part of Mechanism 1 (revealing the value after it is computed) remains truthful regardless of the agent’s risk attitude. However, computing the agent’s utility in the cooperative vs. the heuristic strategy is much harder. Similarly, Mechanisms 2 and 3 may behave differently when the agent is risk-averse.

Different effort levels In our setting, the agent has only two options: either calculate the accurate value, or not calculate it at all. When \(c>E_{v}[max(0, v-E[v])],\) it is optimal for the agent to not calculate the value at all. Then, it is optimal for the agent to bid E[v]. It is never optimal for the agent to bid an inaccurate value.

In more realistic settings, the agent may have three or more options. For example, it is possible that the agent can, by incurring a cost \(c_0 < c,\) get an inaccurate estimate of v (e.g., the agent learns some value \(v_0\) such that the true value is distributed uniformly in \([v_0-d,v_0+d],\) where d is the inaccuracy parameter). Then, the analysis of the agent’s behavior becomes more complex since there are more paths in which the agent may decide to calculate the true value: he may decide to incur the cost c already from the start, or incur only the cost \(c_0,\) and after observing the results—decide whether to incur an additional cost of c. The principal’s goal is to learn the true value at the end—regardless of how many intermediate calculations are done by the agent. It is interesting to characterize the mechanisms that let the principal attain this goal.