Abstract
We show that Cheeger deformations regularize G-invariant metrics in a very strong sense.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the presence of a group of isometries G, Cheeger developed a method for perturbing the metric on a non-negatively curved manifold M [1]. We will show, in the curvature free setting, that this method regularizes the metric in a very strong sense. Before stating our result we recall the definition of a Cheeger deformation.
Let G be a compact group of isometries of \((M,g_{M}).\) Let \(g_{{\mathrm {bi}}}\) be a bi-invariant metric on G, and consider the one-parameter family \(l^{2}g_{{\mathrm {bi}}}+g_{M}\) of metrics on \(G\times M\). G acts on \((G\times M,l^{2}g_{\mathrm {bi}}+g_{M})\) via
which we will call the Cheeger Action.
Modding out by the Cheeger Action we obtain a one-parameter family \(g_{l}\) of metrics on \(M\cong ( G\times M)/G.\) As \(l\rightarrow \infty , (M,g_{l}) \) converges to \(g_{M}\) [6].
The quotient map for the Cheeger Action is
For any point x in the union of the principal orbits, \(M^{\text {reg}},\) we define

where \(T_{x}G(x)\) is the tangent space to the orbit through x, and \(TG(x)^{\perp }\) is its orthogonal complement.
Theorem A
Let \((M,g_{M})\) be a complete, Riemannian G-manifold with G a compact Lie group. For any non-negative integer p and any G-invariant, pre-compact open subset \(\mathcal {U} \subset M^{{\mathrm {reg}}},\) as \(l\rightarrow 0\) the one-parameter family  converges in the \(C^{p}\)-topology to a G-invariant metric \(\tilde{g}\) so that the Riemannian submersion \(( \mathcal {U},\tilde{g}) \longrightarrow \mathcal {U} /G \) has totally geodesic, normal homogeneous fibers.
converges in the \(C^{p}\)-topology to a G-invariant metric \(\tilde{g}\) so that the Riemannian submersion \(( \mathcal {U},\tilde{g}) \longrightarrow \mathcal {U} /G \) has totally geodesic, normal homogeneous fibers.
The normal homogeneous metrics on the fibers have the following description:
Theorem B
For any \(x\in \mathcal {U}\) with isotropy \(G_{x},\) let \(\Phi _{x}:G/G_{x}\longrightarrow G(x) \) be the G-equivariant diffeomorphism, \(\Phi _{x}(gG_{x}) =gx.\) Let \(g_{{\mathrm {nh}},x}\) be the normal homogeneous metric on \(G/G_{x}\) induced by the submersion \((G,g_{{\mathrm {bi}}}) \longrightarrow G/G_{x}.\) Then \(\Phi _{x}:( G/G_{x},\,g_{{\mathrm {nh}},x}) \longrightarrow ( \mathcal {U},\,\tilde{g}) \) is a Riemannian embedding whose image is totally geodesic.
Remark 1
While the embedding \(\Phi _{x}:( G/G_{x},\,g_{{\mathrm {nh}},x}) \longrightarrow ( \mathcal {U},\,\tilde{g})\) preserves the Riemannian metric and has totally geodesic image, it need not be an isometry in the metric space sense, that is, the intrinsic and extrinsic metrics on the orbits need not coincide. Consider a “Berger” sphere obtained by expanding the constant curvature 1 metric in the Hopf directions, and leaving the metric on the horizontal distribution unchanged. It follows that the Hopf semi-circles between pairs of antipodal points have length \(>\) \(\pi .\) Since every geodesic which is horizontal for the Hopf fibration connects antipodal points, the extrinsic distance between any pair of antipodal points is \(\le \) \(\pi \), and so the intrinsic and extrinsic metrics on the Hopf fibers are different.
Remark 2
The class, \(\mathcal {P},\) of principal G-manifolds with totally geodesic, normal homogeneous orbits is invariant under Cheeger deformation. Theorems A and B say that all principal G-manifolds are attracted to \(\mathcal {P}\) by Cheeger deformations.
As Cheeger deformations and G-manifolds have been extensively studied, others may be aware of Theorems A and B. The closest result that we found in the literature, due to Schwachhöfer and Tapp, is Proposition 1.1 in [8], which deals with the case of Cheeger deforming a homogeneous space, \(M=G/H\), via G.
We believe there are many potential applications of Theorems A and B. For example, some of the curvature estimates in [7] can be obtained by combining Theorems A and with the Gray–O’Neill fundamental equations of a submersion [2, 5].
The paper is organized as follows. In Sect. 2, we establish our notations and conventions, and in Sect. 3, we prove Theorems A and B.
2 Notations and conventions
Throughout we assume that the compact Lie group, G, with bi-invariant metric \(g_{{\mathrm {bi}}}\), acts isometrically on the complete Riemannian manifold \(( M,g_{M}).\) The orbit through \(x\in M\) is called G(x) and the isotropy subgroup at x is \(G_{x}.\) We denote the Lie algebra of G by \(\mathfrak {g},\) and the Lie algebra of \(G_{x}\) by \(\mathfrak {g}_{x}.\) We call \(\mathfrak {m}_{x}\) the orthogonal complement, with respect to \(g_{{\mathrm {bi}}},\) of \(\mathfrak {g}_{x}\) in \(\mathfrak {g}.\) For the distribution on \(M^{\text {reg}}\) given by the tangent spaces to the orbits of G, we write \(T({\mathrm {orbits}}).\)
For an abstract G-manifold, N, let
be the bundle map that takes \((k,x) \in \mathfrak {g}\times N\) to the value at x of the Killing field generated by k, and let \( K_{N,x}=\left. K_{N}\right| _{\mathfrak {g}\times \left\{ x\right\} }.\) Note that the map \(K_{N}\) depends not only on N, but on the particular G-action on N. We adopt the convention that when \(N=G,\) the G-action is by right multiplication. The corresponding bundle map \(K_{G}:\mathfrak {g} \times G\longrightarrow TG\) is then the trivialization of TG given by the left invariant fields.
For \(x\in M^{\text {reg}},\) define \(\tilde{\Phi }_{x}:G\longrightarrow G\left( x\right) \) by \(\tilde{\Phi }_{x}( g) =gx.\) Let \(\pi :G\longrightarrow G/G_{x}\) be the quotient map, and let \(\Phi _{x}:G/G_{x}\longrightarrow G(x) \) be the G-equivariant diffeomorphism given by \(\Phi _{x}(gG_{x}) =gx.\) Since \(\Phi _{x}\circ \pi =\tilde{\Phi }_{x},\) \(D\pi _{e}=K_{G/G_{x},\,eG_{x}}\) and \((D\tilde{\Phi }_{x}) _{e}=K_{M,x},\) the chain rule gives
Since \(\left. K_{G/G_{x},\,eG_{x}}\right| _{\mathfrak {m}_{x}}\) is invertible,
Note that the differential of the quotient map
for the Cheeger Action, \(g(p,m)=(pg^{-1},\) gm) is
Recall from Chapter 2 of Hirsch [3] that two smooth maps \(\Phi ,\Psi :M\longrightarrow N\) are close in the weak \(C^{p}\)-topology if all of their values and partials up to order p are close with respect to fixed atlases for M and N. If the atlases are both finite, this leads to a notion of \(C^{p}\)-distance, which depends on the atlases, but will serve our purposes.
For bundle maps and tensors we will need a \(C^{p}\)-norm, which we now define. Recall that a Euclidean metric on a vector bundle E restricts to an inner product on each fiber of E and these inner products vary smoothly. Given vector bundles \(E_{1}\) and \(E_{2}\) with Euclidean metrics and a bundle map
we define the \(C^{p}\)-norm of \(\varphi , \left| \varphi \right| _{C^{p}},\) as follows: Let \(E_{1}^{1}\) be the unit sphere bundle of \(E_{1}.\) Define \(\left| \varphi \right| _{C^{p}}\) to be the \(C^{p}\)-distance from  to the zero bundle map. The \(C^{p}\)-norm of a tensor is its \(C^{p}\)-distance to the zero section. We note that the \(C^{p}\)-norm of a bundle map or tensor depends on the given Euclidean metrics. With the exception of TM, all of the vector bundles we consider will come with a clear choice of metric. For bundle maps \(\varphi \) that go to or from TM and for tensors \(\omega \) on M, we adopt the convention that \(\left| \varphi \right| _{C^{p}}\) and \(\left| \omega \right| _{C^{p}}\) are defined in terms of our initial G-invariant metric \(g_{M}.\)
to the zero bundle map. The \(C^{p}\)-norm of a tensor is its \(C^{p}\)-distance to the zero section. We note that the \(C^{p}\)-norm of a bundle map or tensor depends on the given Euclidean metrics. With the exception of TM, all of the vector bundles we consider will come with a clear choice of metric. For bundle maps \(\varphi \) that go to or from TM and for tensors \(\omega \) on M, we adopt the convention that \(\left| \varphi \right| _{C^{p}}\) and \(\left| \omega \right| _{C^{p}}\) are defined in terms of our initial G-invariant metric \(g_{M}.\)
3 Regular structure theorem
The vertical space for q at \((g,x)\in G\times M\) is
We recall from [1, 6, 7] that there is a linear reparametrization of the tangent space, called the Cheeger reparametrization. It is denoted by
and defined as
where \(\hat{v}_{l}\in TG\times TM\) is the horizontal vector for
that projects to v under the projection \(\pi _{2}:G\times M\longrightarrow M.\)
Although \(\hat{v}_{l}\) is completely determined by v, \(g_{{\mathrm {bi}}}, g_{M},\) and the G-action, the explicit formula is rather unpleasant [4, 9]. Fortunately, we will not need it, as we will use abstract, asymptotic arguments.
Every G-orbit in \(G\times M\) has a unique point of the form (e, m). To fix notation, we assume throughout that we are at such a point. When \(l=1\) and \(v\in T_{x}M,\) we denote the first factor of \(\hat{v}_{1}\) by \(\kappa _{x}( v).\) Then
For any l, we then have
For simplicity, we will write \(\hat{v}\) for \(\hat{v}_{l}.\)
Proposition 3.1
For \(x\in M^{{\mathrm {reg}}}\) we have the following:
-
1.
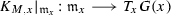 is an isomorphism that varies smoothly with x.
is an isomorphism that varies smoothly with x. -
2.
The map \(\kappa _{x}:T_{x}M\longrightarrow \mathfrak {g}_{x},\) given by \(v\mapsto \kappa _{x}(v),\) takes values in \(\mathfrak {m}_{x}\) and restricts to a linear isomorphism, \(T_{x}G( x) \longrightarrow \mathfrak {m}_{x},\) that varies smoothly with \(x\in M^{{\mathrm {reg}}}.\)
Proof
Part 1 follows from the definition of \(K_{M,x}.\)
Suppose \((u,v) \in T_{( e,x) }( G\times M) \) with \(u\notin \mathfrak {m}_{x}.\) Then there is a \(k\in \mathfrak {g}_{x}\) with \(g_{{\mathrm {bi}}}\left( k,u\right) \ne 0.\) It follows that
So ( u, v) is not horizontal. It follows that \(\kappa _{x}\) takes values in \(\mathfrak {m}_{x}.\)
\(\kappa _{x}\) is linear, since \( \mathrm{Ch}_{l}:T_{x}M\longrightarrow T_{x}M\) is linear and \(\kappa _{x}\) is projection to G composed with  .
.
For \(v\in TG( x),\) if \(( 0,v) \in T( G\times M) \) is horizontal, then \(v=0,\) and it follows that \(\kappa _{x}\) is injective. Since \(\dim ( \mathfrak {m}_{x}) =\dim ( G( x) ) ,\) \(\kappa _{x}:T_{x}G( x) \longrightarrow \mathfrak {m}_{x}\) is, in fact, an isomorphism, proving Part 2. \(\square \)
Before proceeding we define the following vector bundle over \(M^{\text {reg}}:\)
K and \(\kappa \) are then bundle maps
Proposition 3.2
Given any compact subset \(\mathcal {K}\subset M^{{\mathrm {reg}}}\) and any \(p\ge 0\) there is a constant \(C>0\) so that
Proof
This follows from compactness of the corresponding unit sphere bundles and the fact that K, \(\kappa ,\) \(K^{-1},\) and \(\kappa ^{-1}\) are \(C^{\infty }.\) \(\square \)
The next result shows that along the orbits \(\tilde{g}_{l}\) is approximately  and the error in this approximation has the form \(l^{2}\mathcal {\tilde{E}}\) for some bounded, symmetric ( 0, 2)-tensor \( \mathcal {\tilde{E}}.\)
and the error in this approximation has the form \(l^{2}\mathcal {\tilde{E}}\) for some bounded, symmetric ( 0, 2)-tensor \( \mathcal {\tilde{E}}.\)
Lemma 3.3
Given any compact subset \(\mathcal {K}\subset M^{{\mathrm {reg}}},\) there is an \(l_{0}>0\) so that for all \(l\in ( 0,l_{0}) \) there is a symmetric ( 0, 2) -tensor \(\mathcal {\tilde{E}}\) and a constant \(C>0\) with the following property:

Proof
For \(x\in \mathcal {K}\subset M^{\text {reg}}\) and \(v,w\in \left. T\left( {\mathrm {orbits}}\right) \right| _{\mathcal {K}},\) using Eq. 2.3 we find
The definition of \(g_{l}\) and \(\mathrm{Ch}_{l}\) gives
So

From Eq. 3.3 we have
Combining this with Proposition 3.2 we see for small enough l, there is a bundle map
so that
and
Combining Eqs. 3.5 and 3.6 gives

where

Combining this with Proposition 3.2 and Inequality 3.7 it follows that
for some \(C>0.\) \(\square \)
Proposition 3.4
Given any compact subset \(\mathcal {K}\subset M^{{\mathrm {reg}}},\) there is an \(l_{0}>0\) so that for all \(l\in \left( 0,l_{0}\right) \) there is a ( 0, 2) -symmetric tensor \(\mathcal {E}\) and a constant \(C>0\) with the following properties. For all \(x\in \mathcal {K}\)
Proof
Since \(\Phi _{x}^{*}\left( \tilde{g}_{l}\right) \) and \(g_{{\mathrm {nh}},x}\) are G-invariant, it suffices to verify Eq. 3.8 at \(eG_{x}.\) Using Eq. 2.2 and the linearity of \(K_{M,x}\) and \(K_{G/G_{x},\,eG_{x}}^{-1},\) we see that applying \(\left( \Phi _{x}\right) ^{*} \) to Eq. gives

The result then follows by setting
and by appealing to Proposition 3.2 and the fact that \(\left| \mathcal {\tilde{E}}\right| _{C^{p}}\le C.\) \(\square \)
We are now in a position to begin the proofs of Theorems and B. First observe that the distribution orthogonal to the orbits
is the same for \(g_{l}, \tilde{g}_{l},\) and \(g_{M}.\) Also notice that for \(Z\in TG\left( x\right) ^{\perp },\)
For \(x\in \mathcal {K}\subset M^{\text {reg}}\) we set

Our next result shows that \(\tilde{g}\) is G-invariant.
Proposition 3.5
For \(y\in G(x), \left( \Phi _{x}^{-1}\right) ^{*}\left( g_{{\mathrm {nh}},x}\right) =\left( \Phi _{y}^{-1}\right) ^{*}\left( g_{{\mathrm {nh}},y}\right) \)
Proof
Let \(g_{yx}\in G\) satisfy \(g_{yx}x=y.\) Then \(g_{yx}G_{x}g_{yx}^{-1}=G_{y}\) and we have a commutative diagram

where
and \(\pi _{G_{x}}\) and \(\pi _{G_{y}}\) are the quotient maps.
It follows that
since \(L_{g_{yx}}\) is an isometry of \(\left( G\left( y\right) ,\left( \Phi _{y}^{-1}\right) ^{*}\left( g_{{\mathrm {nh}},y}\right) \right) .\) \(\square \)
Applying \(\left( \Phi _{x}^{-1}\right) ^{*}\) to both sides of Eq. 3.8, we obtain

Combining Eqs. 2.2, 3.9 and 3.11 with the inequality, \(\left| \mathcal {E}\right| _{C^{p}}\le C,\) we see that
Remark 3
Our proof does not preclude the possibility that the bounds on the higher order derivatives of \(\mathcal {E}\) depend on the order p and so does not give convergence in the \(C^{\infty }\)-topology.
The next result shows that the fibers of \(\pi ^{\text {reg}}:\left( \mathcal {U},\tilde{g}\right) \longrightarrow \mathcal {U}/G\) are totally geodesic and, combined with Inequality 3.12, completes the proofs of Theorems A and B.
Proposition 3.6
Let \(T^{g_{M}}\) and \(T^{\tilde{g}_{l}}\) be the T-tensors of the Riemannian submersions
as defined in [5]. Given any compact subset \(\mathcal {K}\subset M^{\mathrm {reg}}\) there is a constant \(C>0\) so that on \(\mathcal {K}\)
Proof
Let \(T^{g_{l}}\) be the T-tensor of the Riemannian submersion
The duality between the shape operator and the second fundamental form of the fibers implies that the norm of the T-tensor is determined by its values on just the vertical vectors.
We begin by proving Inequality 3.13 with \(T^{\tilde{g}_{l}}\) replaced by \( T^{g_{l}}\) and then we will show that \(\left| T^{\tilde{g} _{l}}\right| =\left| T^{g_{l}}\right| .\)
For \(V,W\in TG\left( x\right) \) and \(Z\in TG\left( x\right) ^{\perp },\) we lift \(\mathrm{Ch}_{l}\left( V\right) ,\) \(\mathrm{Ch}_{l}\left( W\right) ,\) and \(\mathrm{Ch}_{l}\left( Z\right) \) to \(G\times M\) and get
On the other hand if \(\left| V\right| _{g_{M}}=\left| W\right| _{g_{M}}=1,\) then
Combining the previous two displays with Proposition 3.2 we see that given any compact subset \(\mathcal {K}\subset M^{\text {reg}}\) there is a constant \(C>0\) so that
To see \(\left| T^{\tilde{g}_{l}}\right| =\left| T^{g_{l}}\right| \) we use the Koszul formula and find that
So \(\left| T^{\tilde{g}_{l}}\right| =\left| T^{g_{l}}\right| \!,\) and the result follows. \(\square \)
References
Cheeger, J.: Some examples of manifolds of non-negative curvature. J. Differ. Geom. 8, 623–628 (1973)
Gray, A.: Pseudo-Riemannian almost product manifolds and submersions. J. Math. Mech. 16, 413–443 (1967)
Hirsch, M.: Differential topology. In: Graduate Texts in Mathematics. Springer, Berlin (1994)
Müter, P.: Krümmungserhöhende Deformationen mittels Gruppenaktionen. Ph.D. thesis, University of Münster (1987)
O’Neill, B.: The fundamental equations of a submersion. Mich. Math. J. 13, 459–469 (1966)
Petersen, P., Wilhelm, F.: Examples of Riemannian manifolds with positive curvature almost everywhere. Geom. Topol. 3, 331–367 (1999)
Searle, C., Wilhelm, F.: How to lift positive Ricci curvature. Geom Topol 19, 1409–1475 (2015)
Schwachhöfer, L., Tapp, K.: Homogeneous metrics with nonnegative curvature. J. Geom. Anal. 19(4), 929–943 (2009)
Ziller, W.: On P. Müter’s Ph.D. Thesis. http://www.math.upenn.edu/~wziller/papers/SummaryMueter.pdf. (Preprint)
Acknowledgments
We are grateful to Peter Petersen, Wilderich Tuschmann, and Burkhard Wilking for stimulating conversations on this topic.
Author information
Authors and Affiliations
Corresponding author
Additional information
P. Solórzano is supported by IMPA and CAPES.
Rights and permissions
About this article
Cite this article
Searle, C., Solórzano, P. & Wilhelm, F. Regularization via Cheeger deformations. Ann Glob Anal Geom 48, 295–303 (2015). https://doi.org/10.1007/s10455-015-9471-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10455-015-9471-3





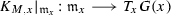 is an isomorphism that varies smoothly with x.
is an isomorphism that varies smoothly with x.