Abstract
We discuss the thermodynamics of physical adsorption of gases in porous solids. The measurement of the amount of gas adsorbed in a solid requires specialized volumetric and gravimetric techniques based upon the concept of the surface excess. Excess adsorption isotherms provide thermodynamic information about the gas-solid system but are difficult to interpret at high pressure because of peculiarities such as intersecting isotherms. Quantities such as pore density and heats of adsorption are undefined for excess isotherms at high pressure. These difficulties vanish when excess isotherms are converted to absolute adsorption. Using the proper definitions, the special features of adsorption can be incorporated into a rigorous framework of solution thermodynamics. Practical applications including mixed-gas equilibria, equations for adsorption isotherms, and methods for calculating thermodynamic properties are covered. The primary limitations of the absolute adsorption formalism arise from the need to estimate pore volumes and in the application to systems with larger mesopores or macropores at high bulk pressures and temperatures where the thermodynamic properties may be dominated by contributions from the bulk fluid. Under these circumstances a rigorous treatment of the thermodynamics requires consideration of the adsorption cell and its contents (bulk gas, porous solid and confined fluid).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The objective of this paper will be obvious to scientists and engineers working in the field of adsorption: to apply the full power of thermodynamics to the field of adsorption. Basically, thermodynamics provides quantitative relationships between seemingly unrelated phenomena such as the amount adsorbed and the heat of adsorption. Thermodynamic analysis is able to quantify the complex behavior of adsorbed mixtures in terms of the adsorption of single gases, one at a time. Thermodynamic equations enable physical chemists to explain adsorption in terms of gas-solid and gas–gas molecular interactions, while providing engineers with reliable estimates of selectivity, heats of adsorption for energy balances, and the difference between the actual and equilibrium chemical potentials which provides the driving force for mass transfer.
Experimental measurements of the amount adsorbed in porous solids are routinely done via the Gibbs adsorption excess, defined as the difference between the number of moles of gas present in the system (sample cell containing porous solid) and the number of moles that would be present if all the accessible volume in the system (both inside and outside the pores) were occupied by the adsorbate gas in its bulk state at the same temperature and pressure. A formulation of adsorption thermodynamics based upon excess properties (excess adsorption, excess enthalpy etc.) has been almost universally adopted in the thermodynamic analysis of experimental data on adsorption in porous materials even though it presents significant difficulties. Perhaps the most significant difficulty is that properties such as energy and bulk pressure are multivalued functions of the adsorption excess at sufficiently high pressure and temperature. In this paper, while recognizing the important role of the Gibbs excess in determining the amount adsorbed, we challenge the use of the excess property formulation for the determination of properties such as free energies, entropies and enthalpies. We argue that for adsorption in porous materials thermodynamics should instead focus on absolute adsorption, defined as the number of moles of gas contained in the porous material. A fully consistent thermodynamic formalism emerges by combining the focus on absolute adsorption with a treatment based on solution thermodynamics where the porous solid and adsorbed gas are treated as components in a mixture. The solution thermodynamics approach to adsorption is not new. We have argued for it previously (Myers et al. 2002) and it goes back at least to the work of Hill (1952). For adsorption of gases at low pressures the difference between adsorption excess and absolute adsorption lies within the margin of error of typical experimental measurements. However, there is increasing interest in adsorption operations where the bulk gas is dense and nonideal, such as pressure-swing-adsorption (PSA) processes and the storage of supercritical gases. Thus we think it important to set forth the case for abandoning the Gibbs excess formulation of adsorption thermodynamics in favor of an approach that does not lead to inconsistencies in this situation and offers a more rigorous treatment overall. As a bonus, the solution thermodynamics version of adsorption is relatively simple and easy to understand because it is based on standard methods developed for vapor-liquid equilibria.
Consider a solid adsorbent of mass m s that has been freshly degassed under vacuum and at high temperature to remove all traces of gas and impurities. Pack this solid into a sample cell enclosed in a temperature bath and introduce n t mol of pure gas from a dosing chamber into the sample cell. Almost all of this first dose will adsorb but a small portion of gas molecules will remain in the gas phase at equilibrium. The amount adsorbed is the total dose less the amount remaining in the gas phase. If the solid is microporous and contains a network of nanometer-sized pores, the space in the cell accessible to gas molecules is the pore volume (V p ) plus the gas volume external to the solid (V g ). If, after degassing the solid but before the experiment, n He mol of helium gas is introduced at ambient temperature \((T_{\circ})\) and pressure \((P_{\circ}),\) the so-called “dead space” (V d ) inside the sample cell can be measured using the equation of state for helium. Assuming negligible adsorption of helium and a pressure sufficiently low to justify the perfect gas law:
The standard procedure is to calculate excess adsorption using the helium dead-space correction:
The molar density of the gas phase (ρ g ) is a function of temperature and pressure as given by its PVT equation of state. Unfortunately this subtraction is an over-correction by the amount of gas that would be in the pores (ρ g V p ) if the gas were present at the density of the bulk gas. The actual or absolute amount of gas in the pores (n a ) is obtained by correcting for the previous over-correction:
where v p = V p /m s is the specific pore volume of the solid.
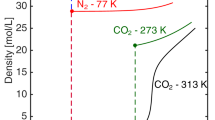
A comparison of absolute and excess isotherms related by Eq. (1.3) is shown on Fig. 1, based on a pore volume v p = 269 cm3/kg (Vyas et al. 2004). The excess isotherms exhibit maxima in the range of 30–60 bar. Thermodynamic properties calculated from these excess isotherms have bizarre behavior (Salem et al. 1998): the isosteric heat has a singularity which occurs at the maximum in excess adsorption, having a limit of \(+\infty\) approaching from the left and a limit of \(-\infty\) approaching from the right. The two excess isotherms intersect at about 110 bar; at higher pressure, the excess amount adsorbed increases with temperature at constant pressure. The excess amount adsorbed becomes negative at very high pressure (not shown on Fig. 1). The conclusion is that excess adsorption at high pressure can be measured but its thermodynamic variables are abstract and difficult to interpret.
The excess isotherms shown on Fig. 1 are typical for adsorption of supercritical gases at high pressure. For example, Specovius and Findenegg (Specovius et al. 1978) measured similar excess isotherms for adsorption of methane on graphitized carbon black. There is nothing strange or unusual about the absolute isotherms in Fig. 1. The absolute amount adsorbed increases smoothly and monotonically with pressure. Since the micropore density is the amount adsorbed divided by the pore volume, the density should increase indefinitely with pressure, as observed for a different system with a vibrating tube densimeter (Gruszkiewicz et al. 2012). Differential properties calculated from the absolute isotherms on Fig. 1 are shown on Fig. 4 of Sect. 3; the absolute differential functions are smooth functions of pressure, without the discontinuities observed for differential excess functions. Excess adsorption is abstract; absolute adsorption describes the physical phenomenon of molecules confined in porous materials.
The central thesis of this paper is that the use of the Gibbs excess formulation for calculating thermodynamic properties from adsorption isotherms is inappropriate for porous solids. To understand this argument it is useful to begin by discussing the Gibbs excess formulation as applied to planar interfaces. The concept was originally applied to the vapor-liquid interface (Rowlinson et al. 2003) where the density varies between the vapor and liquid phase in the manner shown in Fig. 2. We see that there is a region where the density smoothly varies from that of the vapor to that of the liquid. In order to focus on the properties of this interfacial region without precisely determining its extent, the Gibbs excess is introduced together with the concept of the Gibbs dividing surface, determined in this case by the condition that the Gibbs excess (\(\Upgamma\)) vanishes.
Density profile of vapor-liquid interface. z is distance measured perpendicular to the planar interface. The dashed line is the Gibbs dividing surface fixed by Eq. (1.4)
For a planar solid-fluid interface where the solid is considered inert the fluid density profile might look something like that in Fig. 3, with the detailed form of the profile depending on whether the bulk is gas or liquid and the nature of the solid-fluid and fluid-fluid interactions. Again we are dealing with a spatially varying density and an interfacial region of unknown extent. The Gibbs excess formulation is perfectly appropriate for this situation. The Gibbs dividing surface in this case is chosen as the surface of the solid.
Consider now adsorption in a porous material in contact with a bulk fluid phase. The sample morphologies encountered encompass a wide spectrum. This spectrum includes single crystals of a zeolite with adsorption mainly within the micropores of the zeolite crystal, ordered mesoporous materials like MCM-41 with fairly uniform cylindrical mesopores, and disordered materials like activated carbons or silica gels, which are collections of porous particles of various sizes with micropores and mesopores within the particles and macropores in the spaces between them (we adopt the IUPAC definition of micropores, mesopores and macropores for the purposes of this discussion). In general we have a bulk fluid (gas or liquid) in contact with another phase consisting of porous solid and adsorbed fluid. The fluid density inside the porous material is certainly locally inhomogeneous. However this does not preclude the treatment of the porous solid and adsorbed fluid as a single phase system. The situation is comparable to that encountered in the thermodynamics of bulk phases in equilibrium (vapor-liquid, solid-liquid etc.) where we can measure or compute the state of the system without inquiring as to the nature of the interface between these bulk phases. This is also appropriate for adsorption equilibrium between a bulk fluid phase and a porous solid phase containing an adsorbed fluid. For convenience we will refer to the latter as the solid phase.
Since adsorption experiments yield the Gibbs excess it is necessary to convert this quantity to absolute adsorption and we will review methods for doing this, which involve estimating the pore volume of the porous material. We also lay out the formulation of adsorption thermodynamics in terms of absolute quantities, treating each phase, bulk fluid or porous solid plus adsorbed fluid, by the equations of solution thermodynamics. The first benefit of the absolute property approach is that the fluid density is always a monotonically increasing function of the bulk pressure or chemical potential and can therefore itself be treated as an independent state variable. Consequently the concept of "isosteric" temperature derivatives of adsorption isotherms is valid under all conditions in the absolute property formulation. The equations for mixture adsorption in this formalism are quite similar to those based on the excess formalism with excess properties replaced by absolute properties. The definition of the ideal adsorbed solution is modified so that the reference state for each component is the pure adsorbed fluid at the same grand potential as the adsorbed mixture. Throughout the presentation we provide illustrative calculations using simple models and experimental data. We emphasize that the solution thermodynamics approach based on absolute quantities for adsorption in porous materials is not just an alternative to Gibbs excess thermodynamics; it is a rigorous replacement for a somewhat flawed structure. It is also evident from our presentation that quantities like surface tension or spreading pressure, concepts associated with adsorption at planar solid-fluid interfaces, need not appear in the thermodynamics of adsorption in porous materials.
We have written this paper in full recognition of the divisions in the adsorption community on the issue of excess versus absolute properties for quantifying adsorption and we do not necessarily expect to convince everyone that our view should prevail. Our intention is to provide a detailed explanation of the issues involved and to present our own conclusions. We particularly hope that this paper will assist those new to the field of adsorption in developing their own understanding of the thermodynamics.
The remainder of the paper is organized as follows. In Sect. 2 we review the methods for quantifying adsorption experimentally (Gibbs excess, net adsorption, absolute adsorption) and show how they are determined by volumetric and gravimetric measurements. Next we present the solution thermodynamics approach to adsorption in Sect. 3. Section 4 covers ideal adsorbed solutions in the framework of solution thermodynamics, including a numerical calculation. We discuss excess mixing functions and activity coefficients in Sect. 5 and liquid mixtures adsorption in Sect. 6. We consider calorimetric measurements in Sect. 7 and in Sect. 8 we briefly discuss the impact of this formalism in modeling adsorption column dynamics. We give a summary of the points raised in this paper and our conclusions in Sect. 9. The appendices provide illustrative calculations of thermodynamic properties for pure gases and their mixtures.
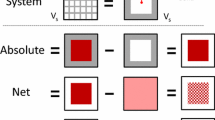
2 Quantifying adsorption
Porous adsorbents may contain pores ranging from micropores with pore diameters of less than 1 nm to macropores with diameters of 50 nm or more. The degree of order of the solid ranges from crystalline materials like zeolites to highly disordered materials such as activated carbons. Typical adsorbents are silica gel, activated carbon, zeolites, metal organic frameworks, ordered mesoporous materials [e.g. MCM-41 (Vartuli et al. 1992)], and carbon nanotubes. Regardless of the chemical composition and structure of the adsorbent, there are three definitions for the amount of gas or vapor adsorbed in the solid:
-
Gibbs excess
-
Net
-
Absolute
The first two definitions, Gibbs excess and net adsorption, are measured experimentally using macroscopic methods. A thorough discussion of net adsorption is given in a recent paper by Gumma and Talu (Gumma et al. 2010). The third definition, absolute adsorption, is the “actual” amount of gas in the solid phase. Absolute adsorption is required for thermodynamic calculations and arises naturally in theoretical models and molecular simulations. Therefore the conversion of excess or net adsorption to absolute adsorption is a crucial step toward the understanding and analysis of experimental data.
Two techniques are used for the measurement of Gibbs excess and net adsorption:
-
Volumetric
-
Gravimetric
The volumetric technique is more accurate at low pressure because almost all of the metered dose is adsorbed. The gravimetric technique has the disadvantage at low pressure that the amount adsorbed is the difference of two nearly equal numbers. At high pressure Footnote 1, the volumetric technique gives the amount adsorbed as the sum of a large number of doses with an associated cumulative error. The gravimetric technique is more accurate at high pressure because the measured amount adsorbed is referenced to the weight of the adsorbent in a vacuum. Both techniques can be automated.
2.1 Gibbs excess adsorption
2.1.1 Volumetric method
The volumetric technique is to introduce a known mass (m s ) of adsorbent into a sample cell of calibrated volume (V t ). Following desorption of the solid using high temperature and vacuum, a fixed temperature is imposed by a temperature bath and a measured dose of gas (\(\Updelta n\)) is introduced to the sample cell. After adsorption is complete, at equilibrium, the temperature (T) and pressure (P) are measured and the specific excess amount adsorbed (n e ) is defined by a mass balance:
where V d is the helium dead space of the sample cell, ρ g (T, P) is the density of the bulk gas (mol/m3) obtained from an equation of state and \(n_t = \sum_j (\Updelta n_j)\) is the total amount of gas in the sample cell. At sufficiently low pressure, the density of the bulk gas phase is given by the perfect gas law (ρ g = P/RT).
The helium dead space (V d ) is obtained from a calibration with helium gas at ambient temperature \((T_{\circ})\) and pressure \(P_{\circ}\) before starting the experiment. If the pressure is sufficiently low, the perfect gas law gives:
Equation (2.2) follows from Eq. (2.1) by setting n e equal to zero (for helium). The determination of the dead space does not depend on the perfect gas law, which can be replaced if necessary by the experimental molar density of helium (ρ He ) from an equation of state. The implicit assumption of Eq. (2.2) is that helium does not adsorb at \(P_{\circ}\) and therefore measures the pore volume of the solid as well as the volume of the bulk gas phase. The question of whether corrections should be applied for the small but finite adsorption of helium inside the pores is considered in Sect. 2.6
The total volume of the sample cell is:
V sk is the skeletal volume or “backbone” of the solid material which is inaccessible to gas molecules. The reporting of experimental adsorption isotherms should include the specific skeletal volume:
because it allows the pore volume of the solid (v p ) to be calculated from its specific volume (v s ), or the reverse:
2.1.2 Gravimetric method
A mass (m s ) of solid adsorbent is loaded into a bucket attached to a microbalance. Following desorption of the solid using high temperature and vacuum, a fixed temperature is imposed by a temperature bath and gas is admitted to the sample cell. After adsorption is complete, at equilibrium, the temperature (T) and pressure (P) are measured and the adsorption is determined from the weight of the bucket containing the solid and adsorbed gas. The weight of gas adsorbed is equal to the weight of the bucket containing the solid minus its degassed tare weight under full vacuum (\(\Updelta w\)). Using the local “g”, the corresponding mass of gas adsorbed is \(\Updelta m = \Updelta w/g\). The Gibbs excess amount adsorbed is:
where M is the molecular weight of the gas.
The second term (ρ g v sk) in Eq. (2.6) is a buoyancy correction. Since the solid is weighed while immersed in a gas, a buoyancy correction equal to the weight of bulk gas displaced is added to the weight registered by the microbalance. The Gibbs excess model is based on the pore volume being filled with gas at its bulk density, so this portion of the solid needs no buoyancy correction. The correction for buoyancy is restricted to the skeletal volume of the solid. The specific skeletal volume is determined by a helium calibration of the degassed adsorbent:
where \(\Updelta m\) is the recorded mass increase of the adsorbent in helium gas relative to its tare weight in a perfect vacuum. The molar density (ρ g ) and molecular weight (M) refer to the helium. \(\Updelta m\) is negative because the displaced helium exerts a lifting force. Eq. (2.7) follows from (2.6) by setting n e to zero (for helium).
Regardless of the experimental method, volumetric or gravimetric, the skeletal volume of the solid must be determined separately by helium calibration. The value of the skeletal volume provides useful information about absolute adsorption through Eq. (2.5).
2.2 Net adsorption
2.2.1 Volumetric method
The volumetric technique for net adsorption (n n ) is the same as for Gibbs excess but the definition (Gumma et al. 2010) is:
where V t is the total volume of the sample cell. No helium calibration is required.
2.2.2 Gravimetric method
Net adsorption (n n ) is measured gravimetrically using the procedure described for Gibbs excess but using the definition:
Consider the specific volume of the solid (v s ). This space experiences a buoyancy force from the displaced bulk gas, but the same space devoid of adsorbent experiences the same buoyancy force. Since net adsorption is relative to the space filled with gas but devoid of adsorbent, the buoyancy correction for the adsorbent cancels exactly with the buoyancy correction for the reference state. As for the volumetric method, no helium calibration is required for the determination of net adsorption.
2.3 Absolute adsorption
Absolute adsorption (n a ) is defined in terms of the volumetric method by a mass balance:
where n t is the total amount of gas introduced to the sample cell, V g is the volume of the bulk gas phase, and ρ g (P, T) is the molar density of the bulk gas phase. In other words, the adsorbed gas is the total amount of gas in the sample cell less the amount in the gas phase. Comparing Eqs. (2.1) and (2.10):
The dead space V d determined by the helium calibration is divided into two parts, a bulk gas phase V g and a pore volume V p :
Eq. (2.11) becomes:
or
where v p = V p /m s is the specific pore volume of the solid.
Determination of v p in Eq. (2.14) is essential for the use of the absolute adsorption formalism and we return to this question in Sect. 2.4
2.3.1 Comparison of absolute and excess adsorption
The difference between absolute and excess adsorption can best be understood by comparing bulk density with pore density. Referring to Eq. (2.14), the difference is negligible if:
or
but n a /v p is pore density (ρ p ) so absolute and excess adsorption may be considered equal for:
In the low-pressure region of the adsorption isotherm where Henry’s law is valid:
or
For supercritical gases, typical values of the ratio ρ p /ρ g are in the range of 104 to 105 and Eq. (2.17) is easily satisfied. This large ratio is explained by the Boltzmann factor (\(e^{-U_{1S}/k_B T}\)) for the probability of finding molecules inside the pores of the solid, as compared to the bulk gas phase, where U 1S is gas-solid potential energy.
The ratio of densities (ρ p /ρ g ) decreases as the pore density approaches a limit comparable to the density of a liquid. Referring to a bulk gas at STP, the molecular density is 0.026 nm−3. The molecular density of a liquid is ≈10 nm−3. With these numerical references in mind, Table 1 shows how the ratio varies with bulk density. The difference between excess and absolute adsorption becomes significant for ρ g > 0.1 nm−3, for which the ratio ρ p /ρ g cannot exceed 100. At a bulk density of ≈1 nm−3, the ratio of ρ p /ρ g cannot exceed 10. Under these conditions, the excess adsorption exhibits a maximum even though the absolute adsorption is increasing with bulk density (see Fig. 1). At a bulk density of ρ g = 10 nm−3, the pore density is approximately equal to the bulk density and the excess adsorption is zero.
In summary, at a bulk density less than 0.1 nm−3, the values for excess and absolute adsorption may be considered equal within experimental error. At values of bulk density exceeding 1 nm−3, the surface excess presents a misleading picture of adsorption in pores because the thermodynamic properties have multiple values and non-physical singularities. The density values in Table 1 are imprecise but provide guidance about the difference between absolute and excess adsorption.
2.3.2 Absolute adsorption from net adsorption
In the measurement of net adsorption using Eq. (2.8), the pre-calibrated total volume of the sample cell (V t ) is the sum of two macroscopic phases, the gas phase and the solid phase:
Comparing Eqs. (2.18) and (2.10) and using Eq. (2.20):
If the specific volume of the solid (v s ) is known, absolute adsorption can be calculated directly from the net adsorption by Eq. (2.21), thus bypassing entirely the measurement of surface excess using a helium calibration of the dead space.
Net adsorption isotherms have the same shape as the excess isotherms on Fig. 1 but n a > n e > n n . Excess adsorption is preferred over net adsorption because it is closer to absolute adsorption at low pressure.
Net adsorption is useful for studying the gas storage capacity of adsorbents at high pressure because the maximum in the net adsorption isotherm identifies the pressure of maximum adsorptive storage capacity compared to pure compression.
2.3.3 Absolute adsorption from molecular simulation and theory
Molecular theory and simulations of adsorption yield the absolute adsorption. For instance, absolute adsorption emerges naturally from grand canonical Monte Carlo (GCMC) simulations. The absolute amount adsorbed (n a ) is obtained as an ensemble average for fixed values of the independent variables: the chemical potential (fugacity) and temperature. The absolute differential energy is calculated from fluctuations in the energy and amount adsorbed or directly by differentiation of an isotherm of energy versus the amount adsorbed (Vuong et al. 1996). The pore volume of the solid (v p ) can be calculated for a molecular model from the ensemble average for the amount of helium in the pores at ambient temperature and low pressure, thus mimicking the actual experiment. Much of this carries over to the study of adsorption via classical density functional theory (Monson 2012). Classical density functional theory yields a prediction of the density distribution in a porous material, and again naturally yields the absolute adsorption by integration of this distribution.
2.4 Estimation of pore volume
The characterization of porous solids is a highly developed field focused on measuring the pore size distribution and other properties of adsorbent materials. Monographs are available (Lowell et al. 2006; Rouqerol et al. 1998) and an IUPAC commission has (Sing et al. 2005) provided recommendations for the measurement and analysis of adsorption data for the purposes of pore structure characterization. The most widely accepted method for pore volume estimation is the adsorption of nitrogen or argon at their respective boiling point. Plateaus in the resulting isotherms, associated with the filling of micropores and mesopores, can be used to estimate pore volumes assuming that the average density in the filled pores is equal to the bulk liquid density (Sing et al. 2005). In addition extensive databases of pore volumes calculated from structural data are available online for zeolites (First et al. 2011) (http://helios.princeton.edu/zeomics) and metal-organic-frameworks (MOF) (First et al. 2013) (http://helios.princeton.edu/mofomics).
As noted by Sing et al. (Sing et al. 2005) this method is unsuitable for macropores and perhaps also for the largest mesopores because the pore filling may occur too close to the saturation pressure, giving rise to large uncertainties in the amount adsorbed. For macropores much of the interesting molecular behavior occurs near the pore wall surface and the formation of the adsorbed layers occurs at low pressures where the distinction between absolute and excess adsorption is insignificant. For higher pressures and supercritical temperatures the overall thermodynamics may be dominated by contributions from the bulk fluid away from the pore walls.
2.5 Reporting experimental data
Experimental measurements should be reported as Gibbs excess adsorption so that the raw data can be converted by Eq. (2.14) to absolute adsorption based upon the currently accepted value for the pore volume. If published as absolute adsorption, the pore volume should be stated. For either choice, excess or absolute, the data should include the skeletal volume of the solid obtained by the helium calibration (Eq. (2.4) or Eq. (2.7)).
2.6 Helium calibration
Experimental measurement of Gibbs excess adsorption by volumetric or gravimetric methods requires a pre-calibration with helium gas to measure the dead space and skeletal volume of the solid adsorbent. This dependence of the Gibbs excess measurement upon helium calibration has led to interest in net adsorption (Gumma et al. 2010), which does not require a helium calibration for its measurement.
The standard procedure for volumetric or gravimetric determination of Gibbs excess is to measure the dead space in the system using helium gas at low pressure and at ambient temperature (≈25 °C). The assumption is that helium does not adsorb under these conditions. Adsorption of helium at ambient temperature and low pressure is very small but non-zero. This had led to the suggestion that the helium calibration be modified to account for helium adsorption (Gumma et al. 2003; Sircar 2001). The helium calibration at ambient temperature would be replaced by a more complicated procedure which requires the determination of the Henry constant for adsorption of helium. The value calculated for the dead space would decrease slightly and change slightly the value of excess adsorption. However, the value of the pore volume would decrease by the same amount so that the value obtained for absolute adsorption would be unaffected by the choice of helium calibration procedure. We do not support the recommendation that the dead space measurement be corrected for adsorption of helium because nothing is gained by the extra effort. The traditional definition of Gibbs excess as the amount adsorbed relative to “non-adsorbing” helium at ambient temperature is convenient and should be retained.
For low-temperature experiments, (e.g. 77 K), the helium calibration should be performed at ambient temperature because adsorption of helium in the pores at 77 K is not negligible. Adsorption thermodynamics is based upon the assumption that the specific volume of the solid, including its pore volume, is independent of temperature.
2.7 Treating the sample cell as the system
A concept closely related to net adsorption is the treatment of the entire sample cell as the system for the purposes of thermodynamics. This eliminates the need for both pore volume estimation and helium calibration. On the other hand Hill (Hill 1952) said in regard to this: “This is the program that must be adopted to be absolutely rigorous thermodynamically, and it is certainly important that workers in the field realize it. However, in the present writer’s opinion, if this program were actually used by experimentalists, the severe price paid, in loss of contact with molecular reality inside the container, would far exceed the value of the last ounce of exactness gained.”
For larger pores at high pressure both absolute and excess formulations are inappropriate and treating the sample cell as the system is the only rigorous way to do the thermodynamics.
2.8 Experimental methods for mixtures
Equation (2.1) for volumetric adsorption of a single gas also applies to excess adsorption of the ith component of a mixture; the density (ρ) of the bulk gas is replaced by the bulk density of the ith component. Calculation of this density requires the composition of the bulk gas inside the sample cell, which is difficult to measure without disturbing the equilibrium conditions.
Gravimetric measurements by Eq. (2.6) cannot be extended to mixtures. However, binary gas measurements of the total mass adsorbed (at constant temperature and pressure) as a function of gas-phase composition can be converted to excess adsorption for the individual components using a rigorous procedure based upon the Gibbs adsorption isotherm (Myers 1989).
Binary mixture adsorption can be calculated from simultaneous volumetric and gravimetric measurements (Keller et al. 1992). The volumetric method measures the total amount adsorbed (moles) and the gravimetric method measures the total mass adsorbed. If the molecular weights of the gases are different, the individual amounts adsorbed are obtained as solutions of a pair of linear algebraic equations.
All of these methods require the temperature, pressure, and composition of the bulk gas phase. Equilibration of mixture adsorption is a slow process due to the need to relax the composition distribution in the system. Reversibility should be checked by approaching data points from different directions.
2.9 Isotherms with hysteresis loops
In many instances adsorption isotherms exhibit hysteresis between adsorption and desorption. This is especially true for adsorption in mesoporous materials (Monson 2012), where it is associated with metastability of vapor-like and liquid-like states in the pores. Most studies of hysteresis are done for subcritical bulk gases, e.g. nitrogen at its normal boiling temperature, at low pressures where the difference between excess and absolute adsorption is small. In general it is not expected that presentation of hysteresis loops in terms of absolute adsorption rather than adsorption excess should affect the interpretation of the behavior.
3 Solution thermodynamics formulation of adsorption equilibrium in terms of absolute adsorption
For the reasons given in Sect. 1, the remainder of this paper is devoted to the application of solution thermodynamics to adsorption in terms of absolute variables. Adsorption is cast as a special case of phase equilibrium between a solid and a gas phase. Equations written in the language of solution thermodynamics are straightforward and are derived without any discussion of a dividing surface, Gibbs excess, or spreading pressure.
3.1 Conditions for equilibrium
The equilibrium conditions are the equality in both phases of temperature and the chemical potential of each gaseous component. If we restrict the treatment to inert solids (nonvolatile and incompressible) then the equality of pressure in both phases is not an equilibrium condition. The chemical species are the solid adsorbent and one or more adsorbed gases. Compositions are normally described in terms of the mole fraction of each component, but mole fractions do not apply to adsorption because the solid adsorbent has no molecular weight. The composition of the solid phase is expressed as a ratio: moles of adsorbate per kilogram of solid adsorbent (mol/kg) for each adsorbate component.
The chemical potential of the solid adsorbent varies with temperature and with the amount of gas adsorbed but it is otherwise inert. Since the adsorbent exists only in the solid phase, its chemical potential is redundant for the determination of equilibrium. The equilibrium condition for equality of chemical potential in the solid and gas phases applies only to adsorbates.
For N c gaseous components and two phases (gas and solid), there are (N c + 1) thermodynamic degrees of freedom for the system. For adsorption of a single gas there two degrees of freedom and for adsorption of a binary gas mixture, there are three degrees of freedom, e.g. {T, P, y 1}.
3.2 Properties of bulk gas phase
The driving force for adsorption of a gas is its chemical potential which it is convenient to quantify via the fugacity (f i ):
where μ i is the chemical potential, \(\mu_i^\circ\) refers to the chemical potential in the perfect-gas reference state at the same temperature and \(f_i^\circ\) ≡ 1 bar. The density of the gas phase and the fugacities of its components may be calculated from the Soave-Redlich-Kwong or Peng-Robinson equation of state, given the temperature, pressure, and composition of the gaseous mixture. Parameters needed for this calculation are the critical properties \(\{T_c \;\hbox{and}\; P_c\}\) and “acentric factor” (ω) of each component; the calculation is described in thermodynamic textbooks (Smith et al. 1996). The fugacity of a pure component is given by the pressure (f = P) and the fugacity of a component in a mixture is given by its partial pressure (f i = Py i ) provided that P < 2 bar. A 2-bar limitation for applying the perfect-gas law is only a suggestion; the range of the perfect-gas law depends upon the system and the accuracy of the experimental data.
The properties (enthalpy, entropy, etc.) of the gas phase obey the perfect-gas law at low pressure or an equation of state at higher pressure. We assume the availability of a suitable equation of state when required for high pressure so that attention in this development is focused on the solid phase.
3.3 Thermodynamics of the solid phase
The fundamental thermodynamic equation for adsorption in a solid is:
This equation applies to an open system with a differential amount dn i of adsorbate i entering the solid phase. The summation is over the gas species present, one term for each gas. The equilibrium condition is that the chemical potential of the adsorbate in the solid phase (μ i ) is equal to its chemical potential in the bulk gas phase. \(\mu_{s}^{\prime}\) in the chemical potential of the solid adsorbent and the prime symbol is intended to emphasize its mass basis of J/kg. dm s refers to differential mass of solid adsorbent. For adsorption, the solid phase is open to the adsorbates but closed to the solid material. dm s is zero but the term \(\mu_{s}^{\prime}\) dm s is retained as a reminder that the chemical potential of the solid \(\mu_{s}^{\prime}\) is altered by adsorption. Mole numbers (n i ) refer to absolute adsorption in this and subsequent sections unless stated otherwise.
The extensive properties of the solid phase are energy U in J, entropy S in J/K, volume V in m3, mass of solid m s in kg, and absolute amount n i of ith gaseous component in moles. The extensive properties (U, S, V) refer to the entire solid phase including the adsorbate. Since the function \(U(S,V,m_s,n_1,n_2,\dots)\) is homogeneous first-order in the variables S, V, m s , and amounts n i , Eq. (3.2) may be integrated directly:
The summation term is over the gases; the solid is accounted for in the \(\mu_{s}^{\prime}\) m s term.
For independent variables V, T, and n in the solid phase, the Helmholtz free energy is:
The grand potential transforms the independent variables for the gases from mole numbers (in F) to chemical potentials (in \(\Upomega\)):
The differential equations for the auxiliary functions are:
The natural thermodynamic functions for adsorption are the Helmholtz free energy and grand potential. Enthalpy and Gibbs free energy functions are less useful for the solid phase but they are well defined:
Sample values of the PV product are listed in Table 2 for a typical zeolite with a density of 2 kg/dm3 and a loading of 5 mol/kg. Since values of energy and free energy are within the range of 10–30 kJ/mol, the approximations H ≈ U and G ≈ F are valid at pressures below 10 bar.
The special character of a gas-solid mixture allows a major simplification: the volume V of the solid adsorbent is effectively constant. Although the solid may expand according to its temperature coefficient of expansion, contract according to its isothermal compressibility, or swell due to adsorption, changes in V are normally negligible. If the volume of the solid varies significantly over the range of the experiment, the principles of phase equilibrium are still valid but with the complication that the volume of the solid phase must be included as a variable in the thermodynamic equations. This complication will not be pursued here, but to do so would be straightforward.
The volume of a porous solid must be defined. Here, V is the volume of the solid including its pores, that is the skeletal volume plus its open and closed pores. This volume excludes interstitial void between the adsorbent particles. The density of the solid, which is the mass of the particle divided by this volume, is called the “effective particle density” in particle technology. If the solid is ordered and crystallographic data are available, the effective particle density is that of the unit cell. The effective particle density of a solid material is always greater than its bulk density, for which the volume includes the void space outside the particles.
Imposing the constancy of the solid volume and the fact that the system is closed for the solid material, the differential equations simplify to:
Eqations (3.10)–(3.12) exploit the advantage of the Helmholtz representation for systems of constant volume. The thermodynamic functions (\(U, S, F, \Upomega\)) refer to the entire solid phase consisting of the solid material and the gas adsorbed in its pores. What is striking about these equations is the absence of pressure and volume variables.
In preparation for a discussion of the Gibbs adsorption isotherm, Eq. (3.12) is compared term-by-term with the Gibbs-Duhem equation which plays a central role in vapor-liquid equilibrium:
For vapor-liquid equilibrium, the independent variables which define the standard states for the components of the mixture are T and P. By analogy, the standard states for mixture adsorption are determined by T and \(\Upomega\).
3.4 Gibbs adsorption isotherm for solid phase
In all equations that follow in this paper, unless stated otherwise, the extensive thermodynamic functions describing the solid phase are specific extensive functions per unit mass of solid adsorbent: U, F, and \(\Upomega\) in J/kg, S in J/(kg K), V in m3/kg, and n i in mol/kg. Equation (3.12) is unchanged:
but the extensive variables have been converted to specific quantities per unit mass of solid adsorbent. At constant temperature:
This equation, which is called the Gibbs adsorption isotherm, provides a powerful basis for describing the properties of adsorbed mixtures. In calculations, it is convenient to introduce a reduced grand potential (ψ)
Using Eqs. (3.1) and (3.15), the Gibbs adsorption isotherm is written:
The reduced grand potential ψ has units of mol/kg.
3.5 Massieu grand potential function
The grand potential in Eq. (3.13) is a double Legendre transformation of the internal energy:
The Massieu companion function (Callen 1985) is a double Legendre transformation of the entropy:
which generates the differential equation:
or, using Eq. (3.15):
This equation is used to calculate the energy by differentiating chemical potential at constant ψ, in the same way that Eq. (3.13) yields the entropy by differentiating chemical potential at constant \(\Upomega\).
3.6 Helmholtz free energy from grand potential
From Eq. (3.5):
For adsorption of a single gas:
Isothermal integration for F and \(\Upomega\) using Eqs. (3.11) and (3.12) gives:
Comparison of the two previous equations shows that the determination of F in terms of \(\Upomega\) involves an integration by parts.
3.7 Connection to statistical mechanics
Switching from the gas constant R and “moles” to the Boltzmann constant k B and “molecules”, the Helmholtz free energy is related to the canonical partition function (Q):
and the grand potential is related to the grand canonical partition function \((\Upxi)\):
The set of independent variables (V, T, μ) is matched to those of adsorption thermodynamics. GCMC methods are especially well suited to molecular simulation of adsorption. These simulations can be carried out within a sample of the solid phase using periodic boundary conditions or for a sample of the solid phase in contact with the bulk fluid (Sarkisov et al. 2000, 2001). The number of molecules adsorbed in the solid and the integral energy are obtained as ensemble averages.
Alternatively the above equations can be written in terms of Massieu functions
and
3.8 Differential properties of solid phase for adsorption of gaseous mixtures
The partial molar volume of a pure fluid is the same as its molar volume. Adsorption is distinguished from the thermodynamics of fluids in that molar integral functions for a single adsorbate are not equal to their differential values. For adsorption of amount n of a pure gas, extensive properties (Z) such as U, S, and F possess a molar integral value (z):
and an associated differential property:
but \(z \ne \overline{z}\). The integral quantity is obtained by isothermal integration of the associated differential property:
For multicomponent adsorption, each gaseous component has its own set of differential properties:
It is important to distinguish differential properties (\(\overline{z}_i\)) of the solid phase from partial molar quantities for bulk fluid phases such as, for example, the partial molar entropy of a component of a liquid mixture:
for which the entropy of the fluid mixture is given by \(S = \sum \overline{s}_i n_i \). Partial molar properties do not apply to adsorption of a gas in a porous solid material. For gases adsorbed in a solid, integral properties are the solution of a differential equation. For a binary mixture:
A path for the integration must be specified, but since Z is a state function, the value obtained for Z is independent of the path. The enormous difficulty of integrating differential equations like Eq. (3.32) using experimental data is the motivation for using excess mixing functions and activity coefficients to describe mixture behavior.
Notation for integral and differential forms is summarized in Table 3. The reference state identified by the superscript ° is the pure, perfect gas at the same temperature and at a pressure of 1 bar.
From Eq. (3.11) for the chemical potential:
The bar signifying a differential variable was omitted for μ i in Table 3 to indicate its dual status as a differential for the solid and partial molar variable for the bulk gas:
The differential energy is derived from Eq. (3.10):
From the Maxwell equation for the Helmholtz free energy, Eq. (3.11):
Substitution of Eq. (3.36) into Eq. (3.35) gives:
From Eq. (3.1):
The reference fugacity \(f_{i}^{\circ}\) is a constant equal to 1 bar. The reference chemical potential \(\mu_{i}^{\circ}\)(T) refers to the pure, perfect-gas reference state at a pressure of 1 bar. In the perfect-gas reference state:
From Eq. (3.39), the Gibbs-Helmholtz equation for the perfect-gas reference state is:
Substituting Eq. (3.1) into Eq. (3.37) and using Eqs. (3.39) and (3.40):
The differential energy of adsorption is exothermic and negative. Equation (3.41) applies to multicomponent adsorption from a real gas and provides a rigorous connection between adsorption isotherms and the differential energy of adsorption (“heats”) measured in adsorption calorimetry (see Sect. 7).
An equation similar to Eq. (3.41) for the differential entropy is derived from Eq. (3.35):
Substituting Eqs. (3.41) and (3.1) into (3.42) and using Eq. (3.39):
The differential entropy of adsorption relative to the perfect-gas reference state \((s_{i}^{\circ})\) is negative, as expected for a molecule going from the perfect-gas state to a confined state inside the pore of the adsorbent.
3.9 Differential and integral properties of solid for single-gas adsorption
The development to this point has been for multi-component adsorption. For a single gas, the subscript notation may be eliminated and from Eq. (3.41):
where \(\overline{u} \equiv (\partial U/\partial n)_T\). This equation is rigorous for single-gas adsorption. The enthalpy reference instead of energy is the consequence of using \(\upmu^{\circ}=(h^{\circ}-T\;s^{\circ})\) as the perfect-gas reference state for the chemical potential. Similarly for the differential entropy of adsorption from Eq. (3.43):
If the pressure does not exceed a few bars, the perfect gas approximation f = P may be applied:
This is arguably the most important equation of adsorption thermodynamics. \(\overline{u}\) is the differential energy in the solid phase in J/kg and n is specific absolute adsorption in mol/kg. \(h^{\circ}\) is the molar enthalpy of the gas in its perfect-gas reference state at the same temperature T. The term containing the derivative is called isosteric heat in the adsorption literature:
Heats of adsorption are discussed in Sect. 7.
For the molar integral properties, we have:
The integrals are at constant temperature and the quantities \(\{U^{\circ}, S^{\circ}, F^{\circ}\}\) refer to the clean solid under full vacuum. Note that the differential Helmholtz free energy (\(\overline{\scriptstyle F} = \overline{u} - T\overline{s}\)) is equal to the chemical potential (μ); see Table 7 in Sect. 4.
The integral properties are also given by Clapeyron-type equations. For the integral energy, it can be shown (Siperstein et al. 2001) that:
This equation seems to provide a shortcut to the integral quantities in Eqs. (3.48)–(3.50). Since the grand potential is itself an integral, differentiation at constant reduced grand potential ψ is awkward. For analysis of experimental data, it is easier to apply Eqs. (3.44) and (3.45) to the adsorption isotherm and then integrate for u and s.
3.10 Clapeyron equation
Equation (3.46) is the adsorption version of the Clapeyron equation. Let \(\Updelta v = v_g - v_s\) and let \(\lambda = h_g^\circ - \overline{u}\). Assume that the molar volume of the adsorbed gas v s is negligible compared to v g so that \(\Updelta v = RT/P\). With these perfect-gas approximations, Eq (3.46) becomes:
so the slope of the “vapor pressure” curve for adsorption at constant loading may be compared to the Clapeyron equation:
for the slope of a coexistence curve of specific latent heat L and specific volume change \(\Updelta v\). Eq. (3.52) shows the association of Eq. (3.44) to the Clapeyron equation but is not intended for calculations because of its approximations.
3.11 Properties at high pressure
Equations (3.44) and (3.45) are valid up to high pressure of the order of 100 bar without making any approximations. An example is shown on Fig. 4. Using the absolute isotherms in Fig. 1, the differential energy (\(\overline{u}\)) was calculated from Eq. (3.44) and the differential entropy (\(\overline{s}\)) from Eq. (3.45). Fugacity was estimated from the Soave-Redlich-Kwong equation of state. The differential energy is relative to the enthalpy \((h^{\circ})\) in the perfect-gas state at 285 K. The differential entropy of the adsorbed gas, which is measured relative to the entropy in the perfect-gas state at 285 K, has a limit of infinity at zero pressure. The differential energy and differential entropy intersect at a pressure of 1 bar where the chemical potential of the gas is zero (\(\mu = \overline{u} - T\overline{s}\)). \(T\overline{s}\) has a minimum of −24.4 kJ/mol, which at 285 K corresponds to an entropy of vaporization of 86 J/mol K. A rule of thumb estimate for the entropy of vaporization of a liquid at its NBP is 88 J/mol K (the Trouton constant). Even though the adsorbed methane gas is supercritical, its entropy of vaporization from a micropore at high pressure is comparable to the entropy of vaporization from its liquid state at 112 K.
4 Ideal adsorbed solutions
At the time when the theory of ideal adsorbed solutions (IAS) was developed (Myers et al. 1965), the Gibbs excess formalism was the standard approach to adsorption, as it is today. The physical picture most commonly used in thinking about such systems was quasi two-dimensional adsorption at a planar surface rather than adsorption in a three-dimensional pore network. The standard state for the definition of an ideal adsorbed solution was taken to be the pure adsorbed components at the same spreading pressure (or solid-fluid interfacial tension) as the mixture.
The application of solution thermodynamics to adsorption in porous materials leads to equations similar to those for vapor-liquid equilibria. Surface area and spreading pressure variables are eliminated. The proposed definition of an ideal solution for adsorption in porous materials is:
for the chemical potential of the ith component. This is the simplest expression for the composition dependence of the chemical potential that is consistent with the known results in the Henry’s law (low pressure) limit. It is equivalent to the definition of an ideal solution in the bulk. We will show that all results for IAS follow from this.
The chemical potential of the pure gas in its standard state (μ * i ) is determined by temperature (T) and grand potential (\(\Upomega\)). Alternatively, based on the reduced grand potential ψ from Eq. (3.15) for the standard state:
From Eq. (3.13):
From this we can write for the molar entropy:
and for IAS from Eq. (4.1):
Equation (3.20) is based on the Massieu formulation for the grand potential:
From this the molar energy is:
and for IAS from Eq. (4.2):
The Helmholtz free energy for IAS is:
with \({\scriptstyle F}_i^* = (u_i^* - T s_i^*)\).
Finally the total amount adsorbed (n) is calculated from the Gibbs adsorption isotherm, Eq. (3.14):
or
and
For an ideal solution and using the pure component version of Eq. (4.10):
so that for IAS:
Referring the chemical potential to its standard state μ * i instead of the perfect-gas reference state as in Eq. (3.1):
Comparison of Eqs. (4.15) and (4.1) gives:
Equations (4.16) and (4.14) are the working equations for an ideal adsorbed solution. In the special (and usual) case of a perfect gas, the fugacity in the bulk gas phase f i = P y i and Eq. (4.16) becomes Raoult’s law. 1/n is the mass of solid adsorbent required to adsorb one mole of the gas mixture of composition x. The reciprocal relationship in Eq. (4.14) is simply the requirement that, for an ideal solution, the mass of adsorbent needed to adsorb a mixture is the same mass required to adsorb the individual components separately in their standard states.
4.1 Statement of the adsorption equilibrium problem for mixtures
For a system of N c gases plus the solid adsorbent, there are N c + 1 components, two phases (solid and gas) and N c + 1 degrees of freedom according to the Gibbs phase rule. The system is therefore fully specified by the temperature and N c values of fugacity. These N c fugacities in the bulk gas phase are given by f i = P y i ϕ i , where the fugacity coefficient ϕ i (P, y i ) is calculated from an equation of state for the gaseous mixture, e.g., Soave-Redlich-Kwong or Peng-Robinson, as discussed in Sect. 3.2 The approximation ϕ i = 1 and f i = P y i may be used for P < 2 bar.
4.2 Simultaneous solution of equilibrium equations
We focus on a binary mixture of gases (N c = 2) with specified variables f 1, f 2, and T. From Eq. (4.16), the phase equilibrium equations are:
The gas-phase fugacities (f 1, f 2) at temperature T are the input variables. The mole fractions sum to unity:
Since x 2 = (1 − x 1), there are two Eqs. (4.17) and (4.18), and two unknowns (ψ, x 1).
The simultaneous solution of these equations obviously requires the standard-state fugacity functions f * i (ψ). If the adsorption isotherm is based upon fugacity (or pressure) for the independent variable, integration for ψ yields the function ψ(f * i ), which must be inverted to solve the fugacity equations. The model isotherm in Appendix 1 has n as independent variable so its integration yields ψ(n * i ), which is inverted to obtain n * i (ψ) as described in Appendix 3. The function required to solve the fugacity equations is then the composite function f * i [n * i (ψ)]. Solution of Eqs. (4.17) and (4.18) by Newton’s method for ψ and x 1 is described in Appendix 2. For multicomponent mixtures beyond binary solutions, each additional component adds one additional composition unknown (x i ) and one additional fugacity equation.
Solution of the phase equilibrium equations for ψ and the composition variables x i yields as a bonus the standard-state amounts adsorbed n * i . Eq. (4.14) gives the total amount adsorbed n and the individual amounts adsorbed are:
Note. Substitution of the fugacity equations into Eq. (4.19) for a binary mixture gives:
which is a single equation in a single unknown (ψ). Numerical solution of this equation is problematic because of its high degree of nonlinearity. Attempting to solve for ψ with this equation is not recommended. Simultaneous numerical solution of the fugacity equations is robust and less likely to stray outside the physical domain of ψ > 0 and 0 < x i < 1.
4.3 Energy and entropy functions
Expressions for the molar integral properties of an ideal adsorbed solution (\(u^{id}, s^{id}, {\scriptstyle F}^{id}\)) have been given in terms of the corresponding properties of the components in their standard state.
For differential energy, the task is to relate \(\overline{u}_i^{id}\) in the mixture to its value in the standard state (\(\overline{u}_i^*\)) It can be shown (Siperstein et al. 2001) that for an ideal solution:
Specifically, the differential energy of component 1 in a mixture of components 1 and 2 is:
All of the quantities on the R.H.S. of Eq. (4.22) are evaluated in the standard state (same T and ψ as the mixture). \(\overline{u}\) means differential energy and u means integral energy. The standard-state quantity \(\mathcal{G}_i^*\) is given by:
The derivative is the dimensionless slope of the adsorption isotherm of the ith component in its standard state, or \((\partial \ln n/\partial \ln P)_T\) for a perfect gas. Specifically, for Eq. (10.1), the reciprocal of the dimensionless slope is given by Eq. (10.15).
In the limit of pure adsorbate no. 1, its differential energy is the value for the standard state:
as required. At low pressure in the Henry’s law region as n → 0, the integral and differential energy functions in the mixture and in the standard state (\(u_i, \overline{u}_i, u_i^*, \overline{u}_i^*\)) are equal.
Having calculated the differential energy of adsorption (\(\overline{u}^{id}_i\)) by Eq. (4.21), the differential entropy is given by Eq. (3.42):
4.4 Numerical example for ideal adsorbed solution
This calculation uses Eq. (10.1) to fit the single-gas isotherms. Equations for standard-state properties based upon Eq. (10.1) are explicit in terms of loading (n). Eq. (10.12) provides the standard state ψ(n) and its inverse function n(ψ) generates composite functions u[n(ψ)], s[n(ψ)], f[n(ψ)] etc. for calculating standard-state properties as functions of ψ. The use of Newton’s method to invert the function ψ(n) is covered in Appendix 3.
For a binary solution, given the input variables (T, f 1, f 2), the phase equilibrium Eqs. (4.17) and (4.18) are solved for ψ and x 1. The numerical solution of the fugacity equations by Newton’s method is given in Appendix 2.
The system chosen here is a binary mixture of CO2 and C2H4 adsorbed on zeolite FAU. The experimental single-gas adsorption isotherms (Siperstein et al. 2001) are plotted on Fig. 5 and the differential energies obtained by calorimetry (Siperstein et al. 2001) are shown on Fig. 6. Constants of Eq. (10.1) for these plots are in Tables 4, 5 and 6.
Single-gas adsorption isotherms of CO2 and C2H4 on zeolite FAU at 293.15 K (Siperstein et al. 2001)
Differential energies (\(\overline{u}\)) of adsorption of CO2 and C2H4 on zeolite FAU at 298.15 K (Siperstein et al. 2001)
Consider specifically the set of input variables T = 293.15 K, f 1 = 50 kPa, f 2 = 50 kPa. In this case, the temperature of the isotherm is chosen to be the reference temperature \(T_{\circ}\) in Eq. (10.1). Based on the perfect gas law, P = 100 kPa and y 1 = y 2 = 0.5 but the input variables are the fugacities, not the pressure. Solution of Eqs. (4.17) and (4.18) gives x 1 = 0.7889 and ψ = 20.82 mol/kg. The solution procedure based on Newton’s method is described in Appendix 2. Here, Eq. (10.1) for f i (n i ) and Eq. (10.12) for ψ(n i ) are used. However, the function ψ(n i ) for the standard states must be inverted to n i (ψ) as described in Appendix 3.
Standard-state properties are given in Table 7 and the results for the mixture are listed in Table 8. The reference states for energy, entropy, and free energy are enthalpy (\(h^{\circ}\)), entropy (\(s^{\circ}\)), and chemical potential (\(\mu^{\circ}\)), respectively, in the perfect-gas state at 293.15 K.
In Table 8, T, f 1 and f 2 are input variables. ψ and x 1 are obtained by simultaneous solution of the fugacity equations. x 2 = (1 − x 1). n, n 1 and n 2 are from Eqs. (4.14) and (4.20). The differential and integral energies and entropies are from Eqs. (10.5) – (10.8). \(\mu_i = \overline{u}_i - T\overline{s}_i\) and \( {\scriptstyle F}= u - T s\).
Equation (3.21) provides an overall check of the mixture properties in Table 8:
which agrees with \( {\scriptstyle F} = u - Ts \) from Table 8.
The calculation in Table 8 is for the point at T = 293.15 K, P = 1 bar, and y 1 = 0.5. Fig. 7 shows an isobar (P = 1 bar) for individual and total amounts adsorbed at 293.15 K. Figure 8 is a plot of the isobaric energy and entropy properties for the same conditions, 293.15 K and 1 bar.
Figure 9 shows the isobaric differential energies (“heats”) relative to h ° at 293.15 K and 1 bar calculated from Eq. (4.22). The points identified by ⊙ are “infinite dilution heats”, which could be measured with a calorimeter after pre-loading the other component to its equilibrium value.
5 Excess mixing functions
Experiments (Siperstein et al. 2001) and simulations (Dunne et al. 1996) show that most adsorbed mixtures show negative deviations from ideality, which means that adsorbed-phase activity coefficients are less than unity. The cause of this behavior is understood (Myers 1983) but it is still not possible to predict the magnitude of the deviations, although attempts have been made (Myers 2005). Here, procedures are described for using experimental data to calculate thermodynamic properties by accounting for the effects of temperature, loading, and composition on activity coefficients.
Most binary liquid mixtures show positive deviations from ideality, which means that activity coefficients are greater than unity and the free energy of the solution is greater (more positive) than for an ideal solution. For sufficiently large and positive values of activity coefficients, the homogeneous solution becomes thermodynamically unstable and splits into two immiscible liquid phases. Other binary liquid mixtures exhibit negative deviations from ideality when mixture pairs form weak bonds such as hydrogen bonds; a classic example is chloroform and acetone.
For adsorption, one might expect a correlation between activity coefficients of adsorbed and liquid solutions. As it turns out, there is no correlation because the binary adsorbate interactions are overwhelmed by the stronger energy of their interactions with the solid. For adsorption in micropores, activity coefficients are either unity (ideal solution) or negative deviations from ideality.
The explanation for negative deviations from ideality (activity coefficients less than unity) for adsorbed mixtures is the segregation of components into different regions of the pore space where the local composition differs from the overall composition. Imagine an extreme case in which the adsorbent is a mixture of two different microporous materials. Suppose that each adsorbent (by itself) forms an ideal adsorbed solution but with different compositions, for example x 1 = 0.2 on one adsorbent and x 1 = 0.4 on the other adsorbent. If this heterogeneous mixture of adsorbents is treated (incorrectly) as a single adsorbent with a single (averaged) adsorbed-phase composition, then the composite system will appear to generate large negative deviations from ideality. It can be shown (Dunne et al. 1996) that segregation into regions of different composition (e.g., in different micropores) always generates negative deviations from ideality if the mixture is falsely assumed to be homogeneous.
5.1 Activity coefficients
Following the practice for vapor-liquid equilibria, activity coefficients (γ i ) for adsorption in porous materials are defined by
for the chemical potential. Expressions for all excess mixing functions follow from Eq. (5.1), which reduces to Eq. (4.1) for an ideal solution (γ i = 1).
The chemical potential of the pure adsorbate in its standard state (μ * i ) is determined by temperature (T) and grand potential (\(\Upomega\)). Alternatively, based on the reduced grand potential ψ from Eq. (3.15) for the standard state:
In terms of fugacity, Eqs. (5.1) and (5.2) are written:
or
f i is the fugacity in the bulk gas phase and f * i is the fugacity of the gas in the solid phase at the standard state.
An excess Helmholtz free energy function for the mixture is defined by:
and an excess mass m E is defined by:
The name excess mass is appropriate because reciprocal loading (1/n) has units of kg/mol. The pore volume of an adsorbent is directly proportional to its mass, so Eq. (5.6) is the adsorption equivalent of v E = v − ∑ x i v * i for the excess volume of a liquid mixture.
The terminology and notation for excess functions like m E and \( {\scriptstyle F}^E\) is copied from excess functions for liquid mixtures and has no relation to excess adsorption notation such as n e for the Gibbs surface excess discussed in Sect. 2. Here, excess notation refers to the difference between the actual mixture and an ideal solution. For example, the excess energy is defined by
Similar definitions hold for excess entropy s E, excess Helmholtz free energy f E, and excess mass m E.
As will be shown, the excess Helmholtz free energy function in Eq. (5.5) contains complete thermodynamic information about the mixture, not only activity coefficients but also excess mass, energy, entropy, etc. The natural independent variables of this “master” function are temperature (T), composition (x), and either grand potential (\(\Upgamma\)) or reduced grand potential (ψ).
The integral entropy of the mixture is obtained from Eq. (4.4):
Using Eqs. (3.13), (5.1), and (5.5):
Substituting Eq. (4.5), the excess entropy is:
The integral energy of the mixtures is obtained from Eq. (4.7):
Using Eqs. (3.20), (5.2), and (5.5):
Substituting Eq. (4.8), the excess energy is:
Recalling that \(\Omega = - RT \psi\), it is noteworthy that entropy is obtained by differentiation with respect to T at constant \(\Upomega\), but energy is obtained by differentiation with respect to T at constant ψ. We have
but \({\scriptstyle F}^E \ne {\scriptstyle F}_\gamma^E \). The function f Eγ is merely the definition in Eq. (5.5). The direct determination of f E is from Eq. (3.21):
for which the single component version is:
where the superscript * refers to a single adsorbate in its standard state at the same value of T and \(\Upomega\) as the mixture. Inserting the chemical potential from Eq. (5.1) into (5.15) and using (5.16):
where f ≡ F/n and f * i = F * i /n * i . Using Eq. (4.9) and the definitions from Eqs. (5.5) and (5.6):
where
An expression for the excess mass (m E) is derived from the Gibbs adsorption isotherm, Eq. (3.14).
and for single components in their standard states:
The remainder of the derivation is at constant T and x. From Eq. (5.1):
From Eq. (5.5):
Combination of the last four equations at constant T and x gives:
which may be written using Eq. (5.6):
Alternatively in terms of \(\psi = -\Upomega/RT\):
We have seen that excess functions (\(u^E, s^E, {\scriptstyle F}^E, m^E\)) are calculable from Eq. (5.5) by differentiation. It can be shown from Eq. (3.13) that activity coefficients are related to the \({\scriptstyle F}^E_\gamma\) function by:
5.2 Adsorption analog of Gibbs-Helmholtz equation
The Gibbs-Helmholtz equation for excess mixing functions of liquid mixtures is:
The adsorption equivalent for a binary mixture is:
which is derived from Eqs. (3.4) and (3.10).
Holding the absolute adsorption of each component of a mixture fixed while varying the temperature, either experimentally or theoretically, is awkward. For adsorption, F E = U E − TS E but the independent variables for activity coefficients are {ψ, x, T}, not {n 1, n 2, T}.
5.3 Model for activity coefficients and excess functions
In order to proceed, a model for activity coefficients and excess functions is needed. The excess functions are all zero for ideal solutions. For nonideal solutions, the simplest equation for activity coefficients (Siperstein et al. 2001) which has the proper limits and takes into account the set of independent variables {T, ψ, x} is:
There are three constants {A, B, C} for a binary mixture of gases. At the limit of low loading, ψ → 0 and f Eγ → 0. This limit enforces ideal solution behavior in the Henry’s law region. The absolute values of the excess functions reach a maximum as \(\psi \to \infty. \) The quadratic composition dependence satisfies the boundary condition that f Eγ → 0 for the pure adsorbates. More complex asymmetrical behavior can be introduced into f E at the expense of additional constants. The linearity of the excess free energy with temperature predicts a temperature-independent energy of adsorption, which is the usual approximation for adsorption over a limited range of temperature.
From Eq. (5.27) for activity coefficients:
The excess mass from Eq. (5.26) is:
The value of the excess mass at the limit of zero loading (ψ → 0) has the form (\(\infty - \infty\)) as shown by Eq. (5.6). Although the limiting value of m E from Eq. (5.33) is finite, Eq. (5.6) reduces to Eq. (4.14) as ψ → 0, as required for an ideal solution. From Eqs. (5.13), (5.10) and (5.18)
Differential properties for nonideal mixtures depend upon temperature coefficients of the activity coefficients. It can be shown (Siperstein et al. 2001) that the differential energy for a binary mixture is:
where
\(\mathcal{G}_i^*\) is defined by Eq. (4.23). The set of derivatives {d A , d B , d C , d D } vanishes for an ideal solution. For a single component, the limit from Eq. (5.37) is
which means that in the limit of single-component adsorption, the differential energy of the ith component of a mixture is equal to its differential energy in the standard state, as required.
In terms of the model from Eqs. (5.31), (5.32), and (5.33):
Note the minus signs so that \(d_D = \frac{(A + B T)}{R T}C^2 e^{-C\psi} x_1 x_2\).
5.4 Extraction of constants from experimental data
Consider a set of N experimental points for a binary mixture. For each point, the input variables are temperature and fugacities (T, f 1, f 2) and the measured variables are the loadings (n 1, n 2). Activity coefficients must be calculated indirectly. From Eq. (5.4), the activity coefficient γ i = f i /(f * i x i ) but the standard-state fugacity (f * i ) is unknown because ψ is unknown. The extraction of the constants {A,B,C} is a three-parameter optimization problem for which the objective function is the summation of error in loadings for the N data points.
The constants derived from experimental data will not fit the experimental data exactly for two reasons. First, the actual behavior of the mixture may be more complex than the three-constant model described here. Second, the experimental data may be thermodynamically inconsistent and thus incapable of being fit.
5.5 Solution procedure
Given the constants for Eq. (5.30), the calculation is similar to that for an ideal solution. The condition for equilibrium is equality of chemical potentials of the gases in the solid and gas phases, which is equivalent to equality of fugacities in both phases. For a binary mixture of gases (N c = 2) the specified variables are f 1, f 2, and T. Using Eq. (5.4) for the solid phase, the conditions for equilibrium are:
The gas-phase fugacities (f 1, f 2) at temperature T are the input variables. The mole fractions sum to unity:
Since x 2 = (1 − x 1), there are two Eqs. (5.38) and (5.39), and two unknowns (ψ, x 1). Solution of the fugacity Eqs. (5.38) and (5.39) by Newton’s method for ψ and x 1 is described in Appendix 2. The total amount adsorbed from Eq. (5.6) is:
with m E from Eq. (5.33). Individual amounts adsorbed are:
Equations (5.34) and (5.35) give the molar integral functions u and s in terms of the corresponding excess functions u E and s E and the expressions for ideal solutions, Eqs. (4.8) and (4.5). The differential energies \(\overline{u}_i\) are calculated from Eq. (5.37). Finally, the differential entropy follows from the differential energy according to Eq. (4.25).
5.6 Numerical example
Consider a binary mixture of CO2 and C2H4 adsorbed on zeolite FAU, the same system used in the calculation for an ideal solution in Sect. 4. The constants of Eq. (10.1) for the single-gas isotherms are tabulated in Tables 4, 5, 6. For the mixture, the constants determined experimentally (Siperstein et al. 2001) for Eq. (5.30) are: A = −6.5 kJ/mol, B = 0.0145 kJ/mol K, C = 0.030 kg/mol.
The numerical calculation is reproduced for the input variables T = 293.15 K and f 1 = f 2 = 50 kPa. Based upon the perfect-gas law, P = 100 kPa and y 1 = y 2 = 0.5, but the input variables are the fugacities, not the pressure. Solution of the fugacity Eqs. (5.38) and (5.39) by Newton’s method as described in Appendix 2 gives x 1 = 0.7537 and ψ = 21.23 mol/kg. The standard-state properties for this value of ψ are given in Table 9.
The mixture point calculation summarized in Table 10 is based on standard state properties in Table 9. Input variables are T, f 1 and f 2. ψ and x 1 are obtained by simultaneous solution of the fugacity Eqs. (5.38) and (5.39). x 2 = (1 − x 1). n, n 1 and n 2 are from Eqs. (5.41) – (5.43). Activity coefficients γ i are from Eqs. (5.31) and (5.32). Integral properties u and s are from Eqs. (5.34) and (5.35). Differential energies \(\overline{u}_i\) are from Eq. (5.37) and differential entropies \(\overline{s}_i\) from Eq. (4.25). Note that \(\mu_i = \overline{u}_i - T\overline{s}_i\) and \( {\scriptstyle F} = u - T s\).
Equation (3.21) provides an overall check of the calculations in Table 10:
which agrees with the value for \( {\scriptstyle F} = u - T s\) in Table 10.
This example is for the point at T = 293.15 K, P = 1 bar and y 1 = 0.5. Figure 10 shows individual and total amounts for an isobar (P = 1 bar). The solid lines are from experimental data as fit by Eq. (5.30) and the dashed lines are the prediction for an ideal solution from Fig. 7.
The differential energies (“heats”) are plotted on Fig. 11. Comparison with the values predicted for an ideal solution on Fig. 9 show that the differential properties are sensitive to deviations from Raoult’s law. The experimental values at infinite dilution identified by an ⊙ are about 8 percent lower (absolute values) than the values predicted for an ideal solution (Table 11). The dominant coefficient d Ai in Eq. (5.37) is always positive in sign so that experimental differential heats should generally be less negative (smaller in absolute value) than IAS predictions, as is the case for this mixture.
Differential energy of adsorption of CO2 and C2H4 on zeolite FAU at 293.15 K and 1 bar from calorimetric data. Compare with Fig. 9 for ideal solution. The points labeled ⊙ are values at infinite dilution
The integral properties are insensitive to deviations from ideal solution behavior. The experimental integral properties (\(u, s, {\scriptstyle F}\)) for a non-ideal mixture are nearly indistinguishable from the ideal values plotted on Fig. 8. Table 12 compares integral properties for the experimental data with those for an ideal solution. Note that the experimental standard state for ψ differs slightly from the standard state for an ideal adsorbed solution in Table 8. Having specified the independent variables {f 1, f 2, T}, the standard state (ψ) for the point depends upon the nonideality of the mixture. Excess functions for a nonideal mixture are defined by Eq. (5.7), or ψ = 21.23 kJ/mol for this particular point.
The isobar shown on Fig. 10 must satisfy the Gibbs adsorption isotherm Eq. (3.16) integrated from y 1 = 0 to y 1 = 1. Assuming a perfect gas so that f 1 = P y 1 and f 2 = P y 2:
For the single gas isotherms at 1 bar, ψ1 = 23.450, ψ2 = 17.125, and \(\Updelta\psi = 6.325\) mol/kg. The integrands for Eq. (5.44) are plotted on Fig. 12. Both integrals are 6.325 mol/kg so both the ideal solution and the experimental data satisfy the consistency test.
Obviously adsorption data can be both thermodynamically consistent and incorrect. The consistency test is most useful when it fails. For example, Fig. 13 shows linear individual isotherms for a hypothetical isobar at 1 bar and 293.15 K. (Individual isotherms are linear at low pressure). The pure component loadings agree with experiment for the CO2 − C2H4 mixture but the integral of Eq. (5.44) is \(\Updelta \psi =1.68\) mol/kg compared to the value of 6.325 mol/kg obtained from the single-gas adsorption isotherms. Thus the linear individual isotherms at 1 bar plotted on Fig. 13 are thermodynamically inconsistent and erroneous.
6 Adsorption from liquid mixtures
Immersion of a microporous material in a pure liquid causes pore filling but the amount of liquid in the pores at equilibrium is difficult to measure. However the heat of immersion or integral energy change associated with immersion of a solid in a liquid can be measured with a calorimeter.
Consider equilibrium between a microporous solid material and a binary liquid mixture. Contact of clean adsorbent with a binary liquid mixture generates a change in the composition of the liquid \((\Updelta x_1)\) from its initial value \(x^{\circ}_1\) to the equilibrium value (x ℓ1 ). This preferential adsorption of one component over another has been applied commercially to adsorptive separation of close-boiling liquid mixtures such as xylene isomers. \(\Updelta x_1\) can be related to the adsorbed liquid by a mass balance as follows:
\(n^\circ\) is the total amount before contact with the adsorbent; n ℓ is the amount in the liquid phase at equilibrium; n a is the absolute amount in the solid phase at equilibrium.
Mole fractions are defined by:
Using the mass balance for a binary liquid mixture, a quantity called excess adsorption (n e i ) is defined:
This definition of excess by a superscript e for adsorption from a liquid mixture is unrelated to the Gibbs excess adsorption from a gas (n e ) discussed in Sect. 2 It is apparent that n e1 + n e2 = 0 and the preferentially adsorbed component has a positive excess. The quantity \(n^\circ \Updelta x\) is measured by experiment without knowing either n a or x a1 . The excess terminology is appropriate because n e1 is the amount of component no. 1 in the pores (n a1 ) minus the hypothetical amount n a x ℓ1 that would be present in the pores if the composition were the same as the liquid phase.
The liquid phase is governed by the Gibbs-Duhem equation for a binary liquid mixture:
and the liquid in the pores obeys the Gibbs adsorption isotherm, Eq. (3.16):
Assuming that the v dP term in the Gibbs-Duhem equation is negligible, as is the practice in vapor-liquid equilibrium:
Using Eq. (6.6):
Since temperature is fixed, the fugacity in the liquid may be replaced by activity:
where the activity in the liquid is a ℓ i = γ ℓ i x ℓ i and γ ℓ i is the activity coefficient in the liquid phase.
Given isothermal measurements of n e1 as a function of liquid-phase composition, Eq. (6.12) may be integrated for the difference \(\Updelta \psi\):
ψ s i is the reduced grand potential for immersion of the solid in pure liquid, so the integral in Eq. (6.13) can be verified (Myers et al. 1972) by integrating the absolute adsorption isotherms of pure i vapors from zero pressure to the vapor pressure according to Eq. (10.11). Alternatively, Eq. (6.13) provides a basis for a thermodynamic consistency test which can be applied to three binary pairs of three liquids: the three differences (ψ s1 − ψ s2 ), (ψ s2 − ψ s3 ) and (ψ s3 − ψ s1 ) obtained by integrating Eq. (6.13) must sum to zero (Sircar et al. 1971).
It is interesting that Eq. (6.13) for excess adsorption from a liquid mixture was derived from a mass balance based on absolute adsorption in the solid phase.
Excess adsorption from liquids can be predicted from single-gas adsorption isotherms and vapor-liquid equilibrium data (activity coefficients) for the binary system. Given the temperature and liquid composition, the pair of fugacities in the liquid phase are given by f i = f s i γ i x ℓ i . This pair of fugacities combined with the temperature provides the input data for predicting the amounts of each component adsorbed (n a1 ,n a2 ) for an ideal adsorbed solution. The individual amounts adsorbed combined with the known liquid composition yield n E1 from Eq. (6.6).
Usually single-gas adsorption isotherms for vapors are unavailable for such calculations and the standard procedure is to measure excess adsorption directly from liquid-phase measurements of \(n^\circ\Updelta x^\ell\) according to Eq. (6.6). It can be shown that for the case of ideal solutions in both the liquid and adsorbed phase and for molecules with identical saturation capacities (m):
Substitution of Eq. (6.14) in (6.13) gives \(\Updelta\psi= m\ln s\). The quantity s is a ratio defined by the fugacity of pure saturated liquid (f s i ) and adsorption Henry constant (K i ):
The skewed quadratic Eq. (6.14) generates a maximum in n e1 at
In spite of the drastic approximations required for its derivation, Eq. (6.14) provides a qualitative fit of experimental data for ideal or nearly ideal mixtures. An example is shown on Fig. 14.
7 Heats of adsorption
The key equation of adsorption thermodynamics is Eq. (3.41)
This exact Clapeyron-type equation for multicomponent adsorption connects the differential energy with the adsorption isotherm. The differential energy is:
For binary adsorption at constant temperature, we have from the calculus and Eq. (7.2):
which provides immediately a consistency test for binary mixtures:
Equation (7.3) was used to make calorimetric measurements of differential energies in binary mixtures (Dunne et al. 1997). Focusing upon adsorption of a single pure gas, Eq. (7.1) simplifies to:
The perfect-gas enthalpy reference \((h^{\circ})\) for the differential energy is the consequence of using \(\upmu^{\circ}=h^{\circ}-T\;s^{\circ}\) as the reference state for the chemical potential.
For calorimetry, the differential heat of adsorption is defined by:
where \(\overline{u}_a\) is the differential energy in the adsorbed phase and u g is the molar energy of the equilibrium gas phase. The subscript notation is needed to distinguish the adsorbed phase (a) from the gas phase (g).
For energy balances in adsorption columns, the isosteric heat of adsorption is defined by:
The differential enthalpy and differential energy in the adsorbed phase are related by:
where (∂n/∂P) T is the slope of the adsorption isotherm. Combining Eqs. (7.5), (7.7) and (7.8):
where h R g = (h g − h ° g ) is the residual enthalpy of the gas phase, usually calculated from a PVT equation of state for the bulk gas.
The volume of the solid (V s ) is of order 1 dm3/kg and equations for the heats simplify considerably at pressures at or below 2 bar where \(\overline{h}_a \approx \overline{u}_a\) and the perfect gas approximations \(h_g=h_{g}^{\circ}\) and \(u_g=u_{g}^{\circ}=(h_{g}^{\circ}-RT)\) are valid:
The nomenclature of heats (q st and q d ) is a misnomer because heats depend upon the path and both of these quantities are the difference between state functions. The isosteric heat q st is an enthalpy difference \(\Updelta h, \) but the heat terminology is firmly established in the adsorption literature.
The isosteric and differential heats of adsorption are defined as positive quantities. Since heats of adsorption are exothermic and therefore negative in the standard thermodynamic sign convention, confusion about the sign of the heat of adsorption is unavoidable.
8 Remarks on applications to adsorption column dynamics
The choice of variables affects the basic equations for the dynamics of adsorption columns. These equations include the mass balances for each gaseous component and the energy balance for the packed column. Which variables should be used in the equations of transport which determine column dynamics: absolute or excess? Textbooks on adsorption (Ruthven 1984) ignore the difference between absolute and excess variables for heat and mass transfer.
We recommend the use of absolute variables for column design. Mass transfer between the solid and the gas is proportional to the difference between the absolute amount adsorbed in the micropores at time t and the amount that would be adsorbed at equilibrium for the prevailing temperature and fugacities (partial pressures) in the bulk gas phase.
The heat capacity needed for the accumulation term of the energy equation is the sum of the heat capacity of the bulk gas (per unit volume) and the heat capacity of the solid (per unit volume). The heat capacity of the solid phase, which includes the gas in its micropores, is the sum of the heat capacity of the clean adsorbent under full vacuum and the heat capacities of the gases in their perfect-gas state. The isosteric heat accounts for gas-gas and gas-solid interactions.
It has been argued that excess properties are suitable for the equations of adsorption column dynamics (Sircar 1985). However, at high pressure, the excess approach collapses because of the singularity in the isosteric heat when the excess amount adsorbed passes through a maximum. Even at low pressure where it makes no difference, the use of absolute variables is more intuitive than excess variables for modeling of heat and mass transport.
9 Summary and conclusions
In this paper we have discussed the thermodynamics of adsorption in porous materials. We have highlighted the difficulties with the Gibbs excess formalism for these systems and have argued that an approach based on absolute properties is a more appropriate approach to the thermodynamics. Solution thermodynamics based on absolute adsorption provides a complete description of equilibrium adsorption of pure fluids and their mixtures in porous materials without any reference to surface area, dividing surfaces, or excess variables. The equations of solution thermodynamics are rigorous, even at the highest pressures (e.g., 100 bar). One should only have confidence in the Gibbs approach for sufficiently low pressures that the difference between absolute and excess adsorption is negligible. At other conditions, the absolute formalism is necessary and this will impact many applications, e.g. mixed-gas adsorption equilibria and the differential equations describing adsorption column dynamics.
As we have noted earlier the main difficulties with the absolute approach concern the ability to determine pore volumes and the application to larger mesopores and macropores. Pore volume is a concept that is widely used in the characterization of porous materials but for small mesopores and micropores we have the issue that the accessible volume depends on the probe molecule. A similar problem arises in the determination of V d via helium pycnometry. The choice is either to accept the potential errors in absolute adsorption associated with the pore volume estimates or the clear flaws in the Gibbs excess formalism of adsorption thermodynamics.
The difficulties with application of the absolute formalism to larger mesopores and macropores stems from the large regions of the void space where the confined fluid is bulk-like. In nitrogen adsorption at 77 K pore filling will occur quite close to saturation making it difficult to estimate the pore volume. At the same time the absolute adsorption for such pores will be dominated by contributions from the bulk with the effects of adsorption and confinement heavily masked by this. Thus the absolute formalism is unsuitable for quantifying selective adsorption in large pores except at low pressures. Of course we have already shown that the excess formalism is unsuitable for such situations as well. For these pore sizes at high pressure the only sensible route to the thermodynamics is then to treat the contents of the sample cell (bulk gas, porous solid and confined fluid) as the system. This of course limits what adsorption measurements can tell us about the properties of the fluid in the pores (Hill 1952).
Notes
High pressure is defined as greater than 10 bar and low pressure is defined as less than 10 bar. The value of 10 bar is somewhat arbitrary and depends upon the gas and the temperature. See Sect. 2.3.1 where the difference between excess and absolute adsorption is related to the bulk density.
Abbreviations
- A, B, C:
-
Constants in Eq. (5.30)
- C i :
-
Power series coefficients for grand potential, Eq. (10.4)
- D i :
-
Power series coefficients for energy, Eq. (10.5)
- f :
-
Fugacity of gas, Pa
- f°:
-
Fugacity in perfect-gas reference state (=1 bar)
- f :
-
Molar integral Helmholtz free energy, J/mol
- f°:
-
Molar Helmholtz free energy in perfect-gas state, J/mol
- f E :
-
Excess Helmholtz free energy for nonideal solution, Eq. (5.18), J/mol
- f Eγ :
-
Excess Helmholtz free energy for activity coefficients, Eq. (5.5), J/mol
- F :
-
Helmholtz free energy of solid phase, J/kg; J in Sect. 3.3
- G :
-
Gibbs free energy of solid phase, J/kg; J in Sect. 3.3
- \(\mathcal{G}_i^*\) :
-
Standard-state factor for ith component, Eq. (4.23), (kg/mol)2
- h°:
-
Molar enthalpy in perfect-gas state, J/mol
- \(\overline{h}\) :
-
Differential enthalpy, J/mol
- H :
-
Enthalpy of solid phase, J/kg ; J in Sect. 3.3
- k B :
-
Boltzmann constant, \(1.3806 \!\times\! 10^{-23}\) J/K
- K :
-
Henry constant, mol/(kg-Pa)
- \(K_{\circ}\) :
-
Henry constant at ref. temp. \(T_{\circ}\)
- m :
-
Adsorbent capacity, mol/kg, Eq. (10.1)
- m s :
-
Mass of adsorbent, kg
- \(\Updelta m\) :
-
Weighed increase in mass of adsorbent, kg
- m E :
-
“Excess mass” from Eq. (5.6), kg/mol
- M :
-
Molecular weight of gas, kg/mol
- n :
-
Total absolute amount of adsorbate, mol/kg
- n a :
-
Specific absolute adsorption, mol/kg
- n e :
-
Specific excess adsorption, mol/kg
- n i :
-
Absolute amount of ith component, mol/kg; mol in Sect. 3.3
- n n :
-
Specific net adsorption, mol/kg
- n t :
-
Total amount of gas introduced to sample cell, mol
- n He :
-
Amount of He gas used for dead-space calibration, mol
- N :
-
Number of molecules
- P :
-
Pressure in gas phase, Pa
- \(P^{\circ}\) :
-
Reference pressure in perfect gas state, 1 bar
- \(P_{\circ}\) :
-
Pressure for helium calibration, Eq. (2.2), Pa
- q d :
-
Differential heat, J/mol
- q st :
-
Isosteric heat, J/mol
- Q :
-
Canonical partition function
- R :
-
Gas constant, 8.3145 J/(mol K)
- \(s^{\circ}\) :
-
Entropy in perfect-gas state, J/(mol K)
- s :
-
Molar integral entropy of solid phase, J/(mol K)
- \(\overline{s}\) :
-
Differential entropy of gas in solid, J/(mol K)
- S :
-
Entropy of solid phase, J/(kg K); J/K in Sect. 3.3
- \(S_s^{\circ}\) :
-
Entropy of degassed solid under full vacuum, J/(kg K)
- T :
-
Temperature, K
- \(T_{\circ}\) :
-
Reference temperature for Eq. (10.1) or temperature for helium calibration, Eq. (2.2), K
- \(u^{\circ}\) :
-
Molar energy in perfect-gas state, J/mol
- u :
-
Molar integral energy of solid phase, J/mol
- \(\overline{u}\) :
-
Differential energy in solid, J/mol
- U :
-
Energy of solid phase, J/kg; J in Sect. 3.3
- V :
-
Volume of solid phase, m3/kg; m3 in Sect. 3.3
- v p :
-
Specific pore volume, m3/kg
- v s :
-
Specific volume of solid, m3/kg
- v sk :
-
Specific skeletal volume of solid, m3/kg
- V a :
-
Volume of adsorbed phase, m3
- V d :
-
Volume of dead space, m3
- V g :
-
Volume of bulk gas phase, m3
- V p :
-
Pore volume, m3
- V s :
-
Volume of solid, m3
- V sk :
-
Skeletal volume of adsorbent, m3
- V t :
-
Volume of sample cell, m3
- x i :
-
Mole fraction of ith component in pores of solid
- y i :
-
Mole fraction of ith component in gas phase
- z :
-
Molar extensive property (u, s, etc.)
- \(\overline{z}\) :
-
Differential property (\(\overline{u}, \overline{s}\), etc.)
- Z :
-
Specific extensive property (U, S etc.)
- γ i :
-
Activity coefficient of ith component in adsorbed phase
- \(\Upgamma\) :
-
Gibbs excess adsorption per unit area, mol/m2
- μ:
-
Chemical potential, J/mol
- \(\upmu^{\circ}\) :
-
Chemical potential of adsorbate in perfect-gas state, J/mol
- μ s ′:
-
Chemical potential of solid, J/kg
- \(\Upxi\) :
-
Grand canonical partition function
- ρ:
-
Molecular density, m−3, Eq. (1.4)
- ρ g :
-
Molar density of bulk gas, mol/m3
- ρ p :
-
Pore density, mol/m3
- ψ:
-
Reduced grand potential (\(-\Upomega/RT\)), mol/kg
- \(\Upomega\) :
-
Grand potential, J/kg; J in Sect. 3.3
- i :
-
Refers to ith component
- *:
-
Refers to standard state for pure gas at same value of T and \(\Upomega\)
- id :
-
Refers to function for an ideal adsorbed solution
- e:
-
Refers to excess adsorption from liquid mixtures
- E :
-
Refers to excess function for deviation from ideal adsorbed solution
- °:
-
Refers to state of perfect gas
References
Callen, H.B.: Thermodynamics and an Introduction to Thermostatistics, 2nd ed. New York, NY: John Wiley & Sons, Inc. (1985)
Dunne, J.A., Myers, A.L., Kofke, David A.: Simulation of adsorption of liquid mixtures of N2 and O2 in a model faujasite cavity at 77.5 K. Adsorption 2, 41–50 (1996)
Dunne, J.A., Rao, M., Sircar, S., Gorte, R.J., Myers, A.L.: Calorimetric heats of adsorption and adsorption isotherms. 3. Mixtures of CH4 and C2H6 in silicalite and mixtures of CO2 and C2H6 in NaX. Langmuir 13, 4333–4341 (1997)
First, E.L., Gounaris, C.E., Wei, J., Floudas, C.A.: Computational characterization of zeolite porous networks: an automated approach. Phys. Chem. Chem. Phys. 13, 17339–17359 (2011)
First, E.L., Floudas, C.A.: MOFomics: computational pore characterization of metal-organic-frameworks. Microporous Mesoporous Mater. 165, 32–39 (2013)
Gruszkiewicz, M.S., Rother, G., Wesolowski, D.J., Cole, D.R., Wallacher, D.: Direct measurements of pore fluid density by vibrating tube densimetry. Langmuir 28, 5070–5078 (2012)
Gumma, S., Talu, O.: Gibbs dividing surface and helium adsorption. Adsorption 9, 17–28 (2003)
Gumma, S., Talu, O.: Net adsorption: a thermodynamic framework for supercritical gas adsorption and storage in porous solids. Langmuir 26, 17013–17023 (2010)
Hill, T.L.: Theory of physical adsorption. Adv. Catal. 211–258 (1952)
Keller, J.U., Staudt, R., Tomalla, M.: Volumetric-gravimetric measurements of binary gas adsorption equilibria. Berichte der Bunsengesellschaft fur physikalische Chemie 96, 28–32 (1992)
Lowell, S., Shields, J.E., Thomas, M.A., Thommes, M.: Characterization of Porous Solids and Powders: Surface Area, Pore Size, and Density. Springer, New York (2006)
Monson, P.A.: Understanding adsorption/desorption hysteresis for fluids in mesoporous materials using simple molecular models and classical density functional theory. Microporous Mesoporous Mater. 160, 47–66 (2012)
Myers, A.L., Prausnitz, J.M.: Thermodynamics of mixed-gas adsorption. AIChE J. 11, 121–127 (1965)
Myers, A.L., Sircar, S.: A thermodynamic consistency test for adsorption of liquids and vapors on solids. J.Phys.Chem. 76, 3412–3415 (1972)
Myers, A.L.: Activity coefficients of mixtures adsorbed on heterogeneous surfaces. AIChE J. 29, 691–693 (1983)
Myers, A.L.: Gravimetric measurements of adsorption from binary gas mixtures. Pure Appl. Chem. 61, 1949–1953 (1989)
Myers, A.L., Monson, P.: Adsorption in porous materials at high pressure: theory and experiment. Langmuir 18, 10261–10273 (2002)
Myers, A.L.: Prediction of adsorption of nonideal mixtures in nanoporous materials. Adsorption 11, 37–42 (2005)
Rouqerol, J., Rouqerol, F., Sing, K.S.W.: Adsorption by Powders and Porous Solids: Principles, Methodology and Applications. Academic Press, Waltham (1998)
Rowlinson, J.S., Widom, B.: Molecular Theory of Capillarity. Dover, New York (2003)
Ruthven, D.M.: Principles of Adsorption and Adsorption Processes. New York: Wiley, p. 275 (1984)
Salem, M.M.K., Braeuer, P., Szombathely, M.V., Heuchel, M., Harting, P., Quitzsch, K., Jaroniec, M.: Thermodynamics of high-pressure adsorption of argon, nitrogen, and methane on microporous adsorbents. Langmuir 14, 3376–3389 (1998)
Sarkisov, L., Monson, P.A.: Hysteresis in Monte Carlo and molecular dynamics simulations of adsorption in porous materials. Langmuir 16, 9857–9860 (2000)
Sarkisov, L., Monson, P.A.: Modeling of adsorption and desorption in pores of simple geometry using molecular dynamics. Langmuir 17, 7600–7604 (2001)
Sing, K.S.W., Everett, D.H., Haul, R.A.W., Moscou, L., Pierrotti, R.A., Rouquerol, J., Siemienewska, T.: Reporting physisorption data for gas/solid systems with special reference to the determination of surface area and porosity (Recommendations 1984). Pure Appl. Chem. 57, 603–619 (2005)
Siperstein, F.R., Myers, A.L.: Mixed-gas adsorption. AIChE J. 47, 1141–1159 (2001)
Sircar, S.: Excess properties and column dynamics of multicomponent gas adsorption. J. Chem. Soc. Faraday Trans. I 81, 1541–1545 (1985)
Sircar, S., Myers, A.L.: A thermodynamic consistency test for adsorption from binary liquid mixtures on solids. AIChE J. 17, 186–190 (1971)
Sircar, S.: Measurement of gibbsian surface excess. AIChE J. 47, 1169–1176 (2001)
Smith, J.M., Van Ness, H.C., Abbott, M.M.: Introduction to chemical engineering thermodynamics, 5th edn., McGraw-Hill, New York (1996), p 482
Specovius, J., Findenegg, G.H.: Physical adsorption of gases at high pressures: argon and methane onto graphitized carbon black. Berichte der Bunsengesellschaft für Physikalische Chemie 82, 174–180 (1978)
Valenzuela, D.P., Myers, A.L.: Adsorption Equilibrium Data Handbook. Prentice-Hall, Upper Saddle River, pp. 86, 261 (1989)
Vartuli, J.C., Roth, W.J., Leonowicz, M., Kresge, C.T., Schmitt, K.D., Chu, C.T-W., Olson, D.H., Sheppard, E.W., McCullen, S.B., Higgins, J.B., Schlenker, J.L.: A new family of mesoporous molecular sieves prepared with liquid crystal templates. J. Am. Chem. Soc. 114, 10834–10843 (1992)
Vuong, T., Monson, P.A.: Monte carlo simulation studies of heats of adsorption in heterogeneous solids. Langmuir 12, 5425–5432 (1996)
Vyas, R.K., Shashi, K.S.: Determination of micropore volume and surface area of zeolite molecular sieves by D-R and D-A equations: a comparative study. Indian J. Chem. Tech. 11, 704–709 (2004)
Acknowledgment
P. A. M. acknowledges support of this work at the University of Massachusetts by the National Science Foundation (Grant No: CBET-1158790). The authors are grateful to Matthias Thommes for some helpful discussions.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Illustrative calculations based on a mathematical model for absolute adsorption in microporous adsorbents
Complete thermodynamic information on the adsorption of a single gas is provided either by a series of adsorption isotherms, or by a single adsorption isotherm coupled with calorimetric measurement of its differential energy. Equation (10.1) provides a quantitative fit of data for adsorption in microporous materials (see Fig. 15) and is therefore suitable for calculating energy and entropy.
Isotherms for adsorption of pure gases are usually in the form n(P) for loading as a function of pressure. The calculation of thermodynamic properties requires a more general function n(P, T) for loading as a function of both pressure and temperature. It is apparent from Eq. (3.44) that an inverted form more useful for calculating thermodynamic properties would replace the independent variables P and T by n and T, with fugacity as the dependent variable:
For C(n) = 0, D(n) = 0, and f = P, this reduces to the (inverted) Langmuir equation. m is the saturation capacity parameter of the Langmuir equation corresponding to pore filling.
1.1 Henry constant
K is the Henry constant:
and K 0 in Eq. (10.1) is the Henry constant at reference temperature T 0. From Eqs. (10.1) and (10.2):
The Henry constant K decreases exponentially with increasing temperature.
1.2 Energy and entropy properties
The Langmuir equation accounts for molecules adsorbed singly in identical micropores and thus neglects entirely gas-gas interactions and variations in gas-solid interaction energy. The function C(n) in the exponential of Eq. (10.1) is a power series:
The exponential factor e C(n) in the adsorption equation modifies the grand potential by adding a truncated power series to the Langmuir result, as shown in Eq. (10.12). C(n) is dimensionless and its C i coefficients are measured at the reference temperature T 0. This series converges rapidly; typically termination after 3 or 4 coefficients provides quantitative agreement with experiment. Application of Eq. (3.44) to Eq. (10.1) yields the power series D(n) for the differential energy:
D(n), like the differential energy, is negative in sign with units of J/mol. The constant \(D_{\circ}\) is the differential energy at the limit of zero pressure. The assumption that the coefficients C i and D i in the power series are constants is equivalent to neglecting sensible heat in comparison to latent heat for the solid phase over a limited range of temperature. The energy \(\overline{u}\) is relative to h ° in the perfect-gas state at the reference temperature \(T_{\circ}\).
The integral energy from Eq. (3.48) and the differential and integral entropies from Eqs. (3.45) and (3.49) are:
where
C int(n), like C(n), is dimensionless. D int, like D(n), is a negative quantity with units of J/mol. The molar energy u is relative to the perfect-gas enthalpy h ° and the molar entropy s is relative to the perfect-gas entropy \(s^{\circ}\), both at the reference temperature \(T_{\circ}\) in Eq. (10.1). The reference pressure \(P^{\circ}\) = 1 bar in Eqs. (10.7) and (10.8).
1.3 Grand potential
Standard states for mixture equilibria are fixed by the reduced grand potential (ψ), which is obtained by integrating Eq. (3.16):
Substituting for the fugacity f from Eq. (10.1) followed by integration yields:
where the power series for ψ are:
C ψ(n) has units of mol/kg and D ψ(n) has units of J/kg. The domain of ψ is 0 ≤ n < m and the limit at low loading is:
1.4 Slope of adsorption isotherm
The calculation of differential energy or heat of adsorption of individual components of mixtures requires the slope of the adsorption isotherm evaluated at its standard state. From Eq. (10.1), the reciprocal of the dimensionless slope of an adsorption isotherm for a single gas is:
The standard state notation is simplified by writing f * i as f and n * i as n. \(T_{\circ}\) is the reference temperature for the determination of the C i coefficients in Eq. (10.1). The power series for Eq. (10.15) are:
C s (n) is dimensionless and D s (n) has units of J/mol. The limit at zero loading is:
1.5 Example
The first step is to select an isotherm measured at a reference temperature (\(T_{\circ}\)) suitable for extracting the constants m, \(K_{\circ}\), and the C i coefficients. Equation (4.21) written in the form:
exploits the near-linearity of \(\ln f\) versus 1/T at constant n to determine values of the differential energy, which are fit with the D i coefficients. An example is shown in Fig. 15, which compares Eq. (10.1) with adsorption isotherms measured at 25, 50 and 100 °C. The other isotherms at 0, 75, and 125 °C are interpolations and extrapolations.
Having fit the adsorption isotherms with Eq. (10.1), the thermodynamic functions are given by explicit equations. On Fig. 16 are plotted the integral and differential functions calculated from the equations in this Appendix. The functions {S, U, F} are integrals with respect to n of the differential functions \(\{\overline{s}, \overline{u}, \mu\}\). In addition, \(F = U - T S, \mu = \overline{u} - T\overline{s}\), and \((F/ n) = \mu + (\Upomega/n)\).
Properties for adsorption of ethylene on 13X molecular sieve at 298.15 K derived from experimental adsorption isotherms plotted on Fig. 15. Values of energy and entropy relative to perfect-gas state for gases and fully evacuated adsorbent for solid, both at 298.15 K. \(\mu = \overline{u} - T\overline{s}\). \(F = U - TS = \mu n + \Upomega\)
The μ function is the adsorption isotherm at 298.15 K. Equation (10.1) is based upon the simplification that U and S are independent of temperature, an approximation justified for the temperature range of the experimental data on Fig. 15.
All functions are negative in sign. Entropy and free energy functions are undefined at the limit of zero loading. The energy is finite at zero loading corresponding to the energy of a single molecule interacting with the solid. The grand potential \((\Upomega)\) has a finite value (−n R T) at zero loading, where \((\Upomega/n) = -RT = -2.48\) kJ/mol.
Appendix 2: Simultaneous solution of fugacity equations
2.1 Ideal solution
The objective is the solution of the fugacity Eq. (4.16) for ψ and composition x. For an ideal binary mixture with x 2 = (1 − x 1), we seek the simultaneous solution of the pair of fugacity equations at temperature T:
for which the Jacobian is:
The size of the Jacobian is equal to the number of gaseous components. Solution of the linear equations:
gives successive iterations according to Newton’s method:
If the single-gas isotherms obey Eq. (10.1), a suitable first guess is:
K i is the Henry constant for the ith component from Eq. (10.3).
Two pure-component functions are needed: n * i (ψ) (see Appendix 3) and the composite function f * i [n * i (ψ)].
2.2 Activity coefficients
Insertion of activity coefficients into Eq. (11.1) gives:
Using Eqs. (5.31), (5.32) and (5.33), the Jacobian is:
where:
Except for the more complicated form of the Jacobian, Eqs. (11.3)–(11.7) are unchanged.
Appendix 3: Inversion of grand potential function for mixture equilibria
Equation (10.12) is the function ψ(n) for single-gas adsorption but its inverse function is needed to fix the standard state. Define \(\mathcal{P}(n) \equiv \psi(n)\) and find the solution of the function \(\mathcal{H}(n)=0\):
Solve Eq. (12.1) by Newton’s method using:
with
A suitable first guess is n = m(1 − e −ψ/m). ψ increases monotonically with n and the iterative solution for the inverse function n(ψ) converges rapidly. The above notation for n is a simplification for n * i , the standard-state loading of single gas i. ψ and its standard-state properties (f * i , u * i , s * i ) are all explicit functions of n * i .
Rights and permissions
About this article
Cite this article
Myers, A.L., Monson, P.A. Physical adsorption of gases: the case for absolute adsorption as the basis for thermodynamic analysis. Adsorption 20, 591–622 (2014). https://doi.org/10.1007/s10450-014-9604-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10450-014-9604-1