Diffusion mechanism of CO₂ in 13X zeolite beads

Abstract

A systematic study of the diffusion mechanism of CO₂ in commercial 13X zeolite beads is presented. In order to gain a complete understanding of the diffusion process of CO₂, kinetic measurements with a zero length column (ZLC) system and a volumetric apparatus have been carried out. The ZLC experiments were carried out on a single bead of zeolite 13X at 38 °C at a partial pressure of CO₂ of 0.1 bar, conditions representative of post-combustion capture. Experiments with different carrier gases clearly show that the diffusion process is controlled by the transport inside the macropores. Volumetric measurements using a Quantachrome Autosorb system were carried out at different concentrations. These experiments are without a carrier gas and the low pressure measurements show clearly Knudsen diffusion control in both the uptake cell and the bead macropores. At increasing CO₂ concentrations the transport mechanism shifts from Knudsen diffusion in the macropores to a completely heat limited process. Both sets of experiments are consistent with independent measurements of bead void fraction and tortuosity and confirm that under the range of conditions that are typical of a carbon capture process the system is controlled by macropore diffusion mechanisms.

1 Introduction

CO₂ is the most important anthropogenic greenhouse gas, with a value of 77 % of the total anthropogenic emissions. The combustion of fossil fuels, mainly used for the production of electrical energy (but also in the cement, refining, petrochemical, iron and steel industry and transport) is responsible for the greatest part of the CO₂ emitted from anthropogenic sources (IEA 2009; Luis et al. 2012; Kuramochi et al. 2012).

Carbon capture and storage applied to large point sources, represents at the moment the most mature mitigation technology available. Pressure or vacuum swing adsorption using nanoporous adsorbents represents a possible technology which can provide the solution that can meet the requirements for good separation efficiencies satisfying both environmental and energy targets (Chou and Chen 2004; Ebner and Ritter 2009; Gomes and Yee 2002; Ishibashi et al. 1996; Kikkinides et al. 1993; Xiao et al. 2008). Several studies have indicated zeolite 13X as one of the best adsorbents available commercially for post combustion applications. For this reason it is very often used as a benchmark material for the comparison with other candidates for CO₂ separation processes (Chue et al. 1995; Harlick and Tezel 2004; Siriwardane et al. 2003; Cavenati et al. 2004; Dasgupta et al. 2012; Li et al. 2008). With this regard, most of the research work presented in the literature is focused on the uptake measurements to compare CO₂ adsorption capacities. Considerably less data are reported on the kinetic measurements of CO₂ in 13X. Onyestyák et al. (1995), Onyestyák and Rees (1999) and Onyestyák (2011) used a frequency–response technique to measure the adsorption rate of CO₂ in commercial 13X beads and found that the diffusion of CO₂ is controlled by the transport in the macropores. Knudsen diffusion was used to describe the molecular diffusion inside the macropores and a good agreement was found between the calculated and the measured values. Ahn et al. (2004) studied the CO₂ diffusion mechanism in zeolite 4A and CaX identifying clearly for CaX the presence of a macropore diffusion mechanism in the overall transport process of CO₂. Recently Giesy et al. (2012) used a new combined pressure-swing and volume-swing frequency response technique to measure the diffusivity of CO₂ in commercial 13X beads. Measurements using different bead sizes showed evidence of a Knudsen-type macropore diffusion controlled process, confirming previous literature data.

On the other hand, a recent publication of Silva et al. (2012) reported ZLC experiments on binderless beads of zeolite 13X at different temperatures and different bead sizes. The data were interpreted by the authors as a mass transfer process controlled by micropore diffusion.

The optimisation of a carbon capture process is very different for a micropore diffusion controlled system, where the overall bead size has no direct effect on the mass transfer kinetics and as a result large beads can be used to minimise column pressure drop, and for a macropore diffusion controlled process, where an optimum bead size has to be found to balance the competing effects of mass transfer kinetics and pressure drop in the column. It is therefore very important to establish unequivocally which of the two mechanisms prevails in 13X beads. To achieve this we present kinetic experiments carried out in a zero length column (ZLC) system, where CO₂ is present in a mixture with a carrier gas. In this case the experimental results allow the determination of the transport mechanism of CO₂ in the macropores through a combination of molecular diffusion in the carrier gas and Knudsen diffusion and possibly micropore diffusion of the adsorbed species. In a ZLC system external mass transfer resistances and heat effects are minimised by the high flow to particle mass ratio and the large thermal mass of the column in which a single bead is packed. In addition we also present kinetic experiments carried out with pure CO₂ in a Quantachrome Autosorb system. In this case there is no carrier gas and the experimental results allow the study of Knudsen diffusion and viscous flow resistances in the macropores and possibly micropore diffusion of the adsorbed component. The combined results allow a complete understanding of the mass transfer kinetics of CO₂ adsorption in commercial 13X beads.

2 Theory

2.1 Theory of macropore diffusion in ZLC experiments

The ZLC is a very useful chromatographic technique, originally developed for diffusivity measurements of pure gases and vapours on porous solids (Eic and Ruthven 1988). The advantage of this method is the elimination of external mass and heat transfer resistances by the use of low adsorbate concentrations, very small adsorbent sample amounts as well as high carrier flowrates during desorption. The ZLC has been developed and extensively used for diffusivity measurements in zeolite powders and in biporous materials (Brandani and Ruthven 1996; Duncan and Moller 2002; Brandani et al. 2003; Ruthven and Xu 1993).

For a macropore-controlled system, the time constant derived from the ZLC desorption curve is obtained from the particle effective diffusivity. This is easily derived starting from the mass balance in a bead:

$$ \left( {1 - \varepsilon_{P} } \right)\frac{{\partial \,\overline{q} }}{\partial \,t} + \varepsilon_{P} \frac{{\partial \,c_{P} }}{\partial \,t} = \frac{{\varepsilon_{P} }}{\tau }{\kern 1pt} D_{Macro} \frac{{\partial^{\,2} c_{P} }}{{\partial \,z^{2} }} $$

(1)

where D _Macro is the overall macropore diffusivity; ε _P is the macropore void fraction of the bead; τ is the tortuosity of the macropores. If the controlling mechanism is due to macropore diffusion, then locally the adsorbed phase in the micropores is at equilibrium with the gas in the macropores. If we make the further assumption that the isotherm is linear, i.e. q = Kc, then

$$ \left[ {\left( {1 - \varepsilon_{P} } \right)K + \varepsilon_{P} } \right]\frac{{\partial \,c_{P} }}{\partial \,t} = \frac{{\varepsilon_{P} }}{\tau }{\kern 1pt} D_{Macro} \frac{{\partial^{\,2} c_{P} }}{{\partial \,z^{2} }} $$

(2)

which can be rearranged to obtain Fick’s diffusion equation and the effective pore diffusivity

$$ \frac{{\partial \,c_{P} }}{\partial \,t} = D_{P}^{e} \frac{{\partial^{\,2} c_{P} }}{{\partial \,z^{2} }} $$

(3)

$$ D_{P}^{e} = \frac{{\varepsilon_{P} \,{{D_{Macro} } \mathord{\left/ {\vphantom {{D_{Macro} } \tau }} \right. \kern-0pt} \tau }}}{{\varepsilon_{P} + \left( {1 - \varepsilon_{P} } \right)\,K}} $$

(4)

where the denominator in Eq. 4 represents the effective bead Henry law constant.

The two diffusional time constants which should be compared are the macropore diffusion time constant, ${{R_{P}^{2} } \mathord{\left/ {\vphantom {{R_{P}^{2} } {D_{P}^{e} }}} \right. \kern-0pt} {D_{P}^{e} }}\quad$, where R _P is the bead radius (typically of the order of 1 mm), and the micropore diffusion time constant, ${{r_{c}^{2} } \mathord{\left/ {\vphantom {{r_{c}^{2} } {D_{c} }}} \right. \kern-0pt} {D_{c} }}$, where r _c is the crystal radius (typically of the order of 1 μm) and D _c is the diffusivity in the crystal’s micropores. While it is obvious that D _c is always smaller than D _Macro , what is important in determining the controlling mass transfer mechanism is the comparison of the molar fluxes, and often macropore diffusion is the controlling mechanism due to the combined effect of small crystals in relatively large beads and the large value of the effective bead Henry law constant.

When running ZLC experiments, it is possible to vary the bead radius or the molecular diffusivity, by changing carrier gas, in order to confirm that the system is controlled by macropore diffusion.

2.2 Volumetric system

The volumetric system used for the experiments is a Quantachrome Autosorb-iQ™. In the case of the transient uptake experiment, a known volume of CO₂ is injected in the sample cell and the pressure is monitored until equilibrium is reached. The analytical solution for the simplest case was developed by Crank (1956). The model assumes isothermal conditions, Fickian diffusion in spherical particles and a linear equilibrium relationship between the gas and the adsorbed phase, the governing equation is then given by:

$$ \frac{{M_{\infty } - M_{t} }}{{M_{\infty } - M_{0} }} = \sum\limits_{n = 1}^{\infty } {\frac{{6\,\alpha \left( {\alpha + 1} \right)}}{{9\alpha \, + 9 + \alpha^{2} \beta_{n}^{2} }}\exp \left( { - \beta_{n}^{2} \,\frac{D}{{R^{2} }}t} \right)} $$

(5)

where:

$$ \tan \beta_{n} = \frac{{3{\kern 1pt} \beta_{n} }}{{3 + \alpha \,\beta_{n}^{2} }} $$

(6)

$$ \alpha = \frac{3\,V}{{4\,\pi \,R^{3} \,K}} $$

(7)

In Eq. 5, M _t represent the amount adsorbed, M ₀ and M _∞ are the amounts adsorbed at time 0 and at final equilibrium, respectively. In Eq. 7, V is the volume of the uptake cell, R is the radius of the adsorbent sample, and K is defined as Δq/Δc, i.e. in the case of beads this is the effective bead Henry law constant. Kočiřík et al. (1984) extended the model for the case in which non-isothermal conditions need to be taken into account. Following the procedure adopted by Lee and Ruthven (1979), the authors developed the analytical solution for volumetric systems under non-isothermal conditions and the governing equation is given by:

$$ \frac{{M_{\infty } - M_{t} }}{{M_{\infty } - M_{0} }} = \sum\limits_{n = 1}^{\infty } {\frac{{9\,\left( {1 + K\,\frac{{V_{s} }}{{V_{g} }}} \right)\,\left[ {\frac{{Y_{n} }}{{ - \beta_{n}^{2} }}} \right]^{2} \,\exp \left( { - \beta_{n}^{2} \,\frac{D}{{R^{2} }}\,t} \right)}}{{\frac{1}{{\varphi_{n} }} + \frac{3}{2}\,\frac{\beta '}{{\varphi_{n} }}\,\left[ {\beta_{n} \,\cot \,\beta_{n} \left( {\frac{{Y_{n} }}{{\beta_{n}^{2} }}} \right) + 1} \right] + \frac{3}{2}\,K\,\frac{{V_{s} }}{{V_{g} }}\frac{1}{{\beta_{n}^{4} }}\frac{{A_{n} }}{{\varphi_{n} }}}}} $$

(8)

In which $\beta_{n}$ are the roots of:

$$ \left( { - \beta_{n}^{2} + \alpha^{'} } \right) + 3\beta^{'} \,Y_{n} - 3\,K\,\frac{{V_{s} }}{{V_{g} }}\frac{1}{{\beta_{n}^{2} }}\left( { - \beta_{n}^{2} + \alpha^{'} } \right)\,Y_{n} = 0 $$

(9)

where:

$$ Y_{n} = \beta_{n} \,\cot \,\beta_{n} - 1 $$

(10)

$$ A_{n} = Y_{n} \,\left[ {\left( {\beta_{n}^{2} - \alpha^{'} } \right)\,\beta_{n} \cot \,\beta_{n} - 2\,\alpha^{'} } \right]\, + \beta_{n}^{2} \,\left( {\beta_{n}^{2} - \alpha^{'} } \right) $$

(11)

$$ \frac{1}{{\varphi_{n} }} = \frac{1}{\beta '}\,\left( {1 - 3\,K\,\frac{{V_{s} }}{{V_{g} }}\frac{{Y_{n} }}{{\beta_{n}^{2} }}} \right) $$

(12)

$$ \alpha^{'} = \frac{h\,a}{{\rho_{s} C_{s} }}\frac{{R^{2} }}{D} $$

(13)

$$ \beta^{'} = \frac{\Updelta \,H}{{\rho_{s} C_{s} }}\left( {\frac{\partial \,q*}{\partial \,T}} \right)_{{c_{0} ,T_{0} }} $$

(14)

In Eqs. 8–14, V_s and V_g are the volume occupied by the solid and the gas, respectively; h is the overall heat-transfer coefficient; a is the external surface area divided by the volume of the adsorbent; ρ _s and C _s represent the density and the heat capacity of the sample and ΔH is the heat of adsorption.

Equation 8 reduces to the solution of the simple isothermal case, Eq. 5, in the limiting case in which either α′ → ∞ or β′ → 0 (Kočiřík et al. 1984).

What is important to note is the fact that both models assume an infinite valve constant, i.e. no pressure difference between the dosing and uptake volumes, respectively V _d and V _u (V _g  = V _d  + V _u ). This can lead to some uncertainty in converting the measured pressure in the dosing cell into the dimensionless uptake curve, especially at short times. Particular care should also be taken to define P ₀ , which is needed to calculate the dimensionless uptake curve from the experimental data.

$$ \frac{{M_{\infty } - M_{t} }}{{M_{\infty } - M_{0} }} = \frac{{P_{\infty } - P}}{{P_{\infty } - P_{0} }};\quad P_{0} = \frac{{P_{d}^{0} V_{d} + P_{u}^{0} V_{u} }}{{V_{d} + V_{u} }} $$

(15)

In the initial points, t < 5 s, since P _d  > P _u the model is only approximate and the first few experimental points should be discarded.

As in the case of the ZLC, semilog plots of the measured quantities versus time can be used to match the asymptotic decays and the physical parameters of the model. These are unaffected by the short time valve effect and should yield reliable kinetic time constants.

3 Experimental

3.1 ZLC experiments

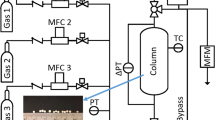
The ZLC column was packed with one 13X—APG MOLSIV™ bead (3.5 mg) from UOP, a Honeywell company, shown in Fig. 1. The average radius of the bead, 0.8 mm, was measured using an image analysis tool (GIMP) to obtain the volume of the bead.

Fig. 1

Particle size of 13X bead used in the ZLC experiments (R = 0.8 mm)

In the ZLC measurements, to avoid gas bypass the cell volume is filled with non-adsorbing rock wool and the bead. The adsorbent was thermally regenerated with a ramping rate of 1 °C/min to 300 °C and then held at this temperature for 12 h at 1 cc/min of helium purge gas. To start the experiments, the oven temperature is reduced to 38 °C. In the ZLC experiment, the sample was first equilibrated with helium containing 10 % of CO₂. At time zero, the flow was switched to a pure helium purge stream at the same flowrate. The sorbate concentration at the outlet of the ZLC can be conveniently followed using a Dycor Ametek Benchtop quadrupole mass spectrometer (MS). The MS connected to the ZLC has a modified inlet system developed in collaboration with Ametek to ensure a rapid response time with minimal inlet flow. The signal produced by the MS is continuously monitored by a computer and then converted to show the desorption curve in terms of concentration versus time. ZLC experimental runs at five different flowrates were performed in the range of 3–30 cc/min.

If the system is under macropore diffusion control it is possible to verify this conveniently using different purge gases (He and N₂) which result in different molecular diffusivities. Different bead sizes could also be used, but given that the experiment is carried out on single beads this would introduce an uncertainty due to the variable fraction of crystals (if a binder is present) between different beads and also the variable void fraction and tortuosity.

If the mass transfer rate is controlled by intracrystalline diffusion, desorption curves measured under similar conditions with different purge gases, should be identical (Eic and Ruthven 1988).

3.2 Volumetric experiment

The volumetric system used for the kinetic experiments is a Quantachrome Autosorb-iQ™. The uptake cell was filled with six closely sized 13X spherical beads with an average radius of 0.98 mm. Prior to the experiments the sample was thermally regenerated at 275 °C under vacuum for 10 h. The experiment consists in injecting a very small amount of CO₂ (0.5 cc STP) in the uptake cell at constant temperature (10 °C) while the pressure is monitored. The choice of a lower temperature for the volumetric experiments relative to the ZLC measurements is mainly dictated by the fact that the piezometric method presents severe limitations if used to measure the adsorption kinetics of fast systems or strongly adsorbed species (Brandani 1998; Schumacher et al. 1999). For the case under investigation, a lower temperature (i.e. slower kinetics) allowed to operate in the proper conditions for the determination of diffusivity.

Once equilibrium is reached a new volume of CO₂ is injected in the system and the process is repeated in small increments, which ensure linear conditions in the individual experiments, up to the final pressure. In order to verify the presence of a macropore controlled process, the same experiment, at the same conditions, was repeated on a sample with a larger bead. For this experiment a single bead with a radius of 1.95 mm was used. Both samples were characterised in terms of void fraction and tortuosity as discussed in the section that follows.

3.3 Mercury porosimetry characterisation

The correct interpretation and analysis of the results obtained through the different kinetic measurements requires the knowledge of the values of the macropore size distribution, the void fraction of the beads and the tortuosity of the sample. For this reason, independent experiments on a Quantachrome Poremaster mercury porosimeter were carried out to characterise the samples used. The experiment consists in the intrusion and extrusion of mercury in the sample up to very high pressure. In Fig. 2 the intrusion and extrusion curves obtained from the mercury porosimetry experiment for the small (R = 0.98 mm) and large (R = 1.95 mm) beads of 13X are shown. It is clear that the behaviour of the large bead is significantly different, showing a large hysteresis. Figure 3 shows the calculated pore size distribution for the small and large beads. From the pore size distribution and the volume of mercury in the macropores it is possible to calculate an average pore diameter from (Carniglia 1986):

$$ \frac{1}{{\bar{d}}} = \frac{{\sum {\frac{{\Updelta V_{i} }}{{d_{i} }}} }}{{\sum {\Updelta V_{i} } }} $$

(16)

where ΔV _i is the change in pore volume for the pore size interval i; d _i is the average diameter for the pore size interval i.

Fig. 2

Intrusion and extrusion curves for the small and big beads of 13X. Bead radius R = 0.98 mm (filled circle Intrusion, plus Extrusion); bead radius R = 1.95 mm (filled triangle Intrusion, times Extrusion)

Fig. 3

Pore size distribution for 13X beads. Bead radius R = 0.98 mm (filled circle); bead radius R = 1.95 mm (filled triangle)

The small beads sample exhibits a narrow pore size distribution with an average value of the pore radius of 0.294 μm. On the other hand the large bead shows a bimodal distribution with a small peak at about 0.45 μm (macropores) and a narrow distribution of pores with an average diameter of 0.02 μm (mesopores). Using Eq. 16 applied to the macropores only, the average pore radius is 0.516 μm.

The instrument also calculates a pore tortuosity: the values obtained are listed in Table 1. The software that accompanies the instrument calculates the tortuosity based on the extended model developed by Carniglia (1986):

$$ \tau = \left( {2.23 - 1.3\,V_{CO} \,\rho_{Hg} } \right)\,\left( {0.92\,y} \right)^{1 + E} $$

(17)

in which V _CO is the total specific pore volume that can be approximated by the volume of mercury intruded at the highest experimental pressure; ρ _Hg is the mercury density; and y is defined as:

$$ y = \frac{4}{S}\,\sum {\frac{{\Updelta V_{i} }}{{d_{i} }}} $$

(18)

S is the total surface area of the sample and E is the pore shape exponent (E = 1 for straight cylinders). We note that a value of tortuosity can be calculated also for the large bead, but the validity of an equivalent diameter and resulting simplified diffusion model for a bimodal particle is not accurate (Carniglia 1986). The results for the large bead should be considered only for qualitative comparisons.

Table 1 Fundamental properties of 13X beads from mercury porosimetry characterisation

4 Results and discussion

4.1 ZLC

The Ft plots using two different purge gases, helium and nitrogen, are presented in Figs. 4 and 5, respectively. For equilibrium-controlled processes, the response curves should be dependent only on the desorption volume, implying in this plot an overlap of curves. It is clear from Figs. 4 and 5 that the curves are diverging, so the experiments are performed under kinetic control.

Fig. 4

Experimental Ft plot of 13X (R = 0.8 mm) at 0.1 bar of CO₂ in He, 38 °C, 3.3, 5.4, 10, 20, 30 cc/min and the blank response at 20, 30 cc/min

Fig. 5

Experimental Ft plot of 13X (R = 0.8 mm) at 0.1 bar of CO₂ in N₂, 38 °C, 2.4, 4, 10, 20, 30 cc/min and the blank response at 20, 30 cc/min

Figure 6 shows the direct comparison of the high flowrate desorption curves obtained with helium and nitrogen purge gas. It can be seen that the desorption curves are dependent of the gas, with a clear effect on the long time asymptote, the slope of which is directly proportional to the effective diffusion coefficient (Eic and Ruthven 1988). This is a prima facie indication that the desorption process is macropore diffusion controlled. We also note that the area under the curves is proportional to the amount of CO₂ adsorbed and that for the two carrier gases the difference is <5 %, indicating that N₂ behaves in this case to a reasonable extent as an inert gas.

Fig. 6

Comparison of experimental ZLC response curves of 13X bead (R = 0.8 mm) at 0.1 bar of CO₂ in two different purge gas (N₂ and He), 38 °C, 20 and 30 cc/min

The traditional long time asymptote approach can be used to obtain initial estimates of the diffusivities (Eic and Ruthven 1988). The values extracted from the experimental runs are summarized in Table 2. With the relatively high CO₂ concentration used in the experiments, one of the assumptions in the model, i.e. isotherm linearity, is not fully justified. Brandani et al. (2000) analysed the effect of isotherm nonlinearity on ZLC experiments and the main effect was shown to be on the intercept of the ln (c/c₀) versus t plot and a minor effect on the slope and thus the diffusional time constant. Therefore to a first approximation the ratio of the slopes of the long-time asymptotes for different inert carrier gases should be proportional to the ratio of the macropore diffusivities. The ratio of the slopes calculated from the long-time asymptote from the ZLC curves (two different carrier gases) shown in Fig. 6 is 2.1. Since both He and N₂ behave to a good approximation as inert carriers, in taking the ratio of the slopes the effective bead Henry law constant cancels out and the value of the ratio can be compared to a theoretical value which can be calculated from the ratio of macropore diffusivities (combined molecular and Knudsen diffusivities) as defined in Eq. 19.

$$ \frac{1}{{D_{Macro} }} = \frac{1}{{D_{m} }} + \frac{1}{{D_{K} }} $$

(19)

Table 2 Parameters and calculated values from ZLC curves

In which (Bird et al. 2002):

$$ D_{m} = \frac{3}{16}\frac{{\sqrt {2\pi \,\Re T\left( {\frac{1}{{M_{1} }} + \frac{1}{{M_{2} }}} \right)} }}{{\frac{P}{kT}\sigma_{12}^{2} \Upomega_{D,12} }} $$

(20)

$$ D_{K} = \frac{2}{3}r\sqrt {\frac{8\,\Re T}{\pi \,M}} \frac{1}{\zeta } $$

(21)

where ζ is the diffuse reflection coefficient (Cunnigham and Williams 1980), which is typically assumed to be equal to unity. Some studies (Papadopoulos et al. 2007; Zalc et al. 2004) have suggested the use of the Derjaguin’s expression of the Knudsen diffusivity, which takes into account a correction factor given by (Levitz 1993):

$$ D_{KD} = D_{K} \left[ {\frac{{\left\langle {d_{p}^{2} } \right\rangle }}{{2\left\langle {d_{p} } \right\rangle^{2} }} - \frac{4}{13}} \right] \approx \frac{9}{13}D_{K} $$

(22)

We note that this form yields a smaller value of the diffusivity, which in turn will yield a smaller value of the calculated tortuosity.

The Chapman–Enskog equation (Ruthven 1984), Eq. 20, was used to calculate the molecular diffusivity of CO₂ in the carrier gas, D _m . Equations 21 and 22 were used to calculate the Knudsen diffusivity. T is the absolute temperature, M is the molecular weight of the components, and P is total pressure, $\sigma_{12}^{{}}$ is a characteristic length parameter of the binary pair and $\Upomega_{D,12}$ represents the collision integral.

With the Derjaguin’s correction, the calculated ratio of diffusivities is 2.3, while if the correction is neglected the predicted ratio is 2.55. The very small deviation from the theoretical ratio can be explained by the fact that the bead in the ZLC column may have a slightly different pore size distribution, compared to the small beads tested in the Autosorb. Given the small size of the sample in the ZLC column, it is not possible to measure directly the average pore radius, which leads to some uncertainty in the calculated Knudsen diffusivity. An additional small uncertainty is also due to the lower CO₂ capacity when N₂ is used as a carrier gas, which modifies slightly the Henry law constant in the effective diffusivity.

To obtain a more accurate description of the ZLC experiments, we also carried out direct simulations using our adsorption column simulator (Friedrich et al. 2013). With this software tool, both the effects of the column length, detector and system blank responses, isotherm nonlinearity and the slight competitive adsorption of N₂ can be considered. By linking the ZLC simulation to a Multi-Objective Genetic Algorithm (MOGA) an automated tool is created for the estimation of the kinetic and equilibrium parameters from the experimental ZLC data. The optimisation algorithm tries to minimise the least square error between the experimental data and the simulation output. In the first step the parameters of the blank system, i.e. no adsorbent in the ZLC, are fitted with experimental runs at different flowrates carried out on the system without the 13X bead. These parameters quantify the volumes of the ZLC system and the response of the detector. The second step then requires only the kinetic and equilibrium parameters in the ZLC to be fitted, i.e. the parameters of the adsorption isotherm and the effective macropore diffusivity. The combination of the adsorption simulator and the multi-objective optimisation allows us to obtain the parameters with greater certainty compared to the simplified asymptotic model, which is used to provide the initial estimate of the physical parameters. Specifically the simultaneous fitting of several experimental curves at different flowrates provides a robust estimation for both the equilibrium and kinetic parameters of the adsorbent. The regression algorithm was first used on the helium experiments. Here helium is considered non-adsorbing and the dual site Langmuir isotherm parameters for CO₂ are fitted from the low flowrate experiments. With the isotherm parameters fixed from the low flowrate experiments the effective macropore diffusivity, $D_{Macro}^{e}$ (Eq. 23), is obtained from the high flowrate experiments.

$$ D_{Macro}^{e} = \frac{{\varepsilon_{P} }}{\tau }{\kern 1pt} D_{Macro} $$

(23)

Simultaneous fits of both low and high flowrate curves are shown in Fig. 7, which includes also one of the blank curves.

Fig. 7

ZLC plot with model comparison of 13X (R = 0.8 mm) at 0.1 bar of CO₂ in He, 38 °C at different flowrates

With the CO₂ isotherm parameters and the tortuosity extracted from the helium experiments and the nitrogen isotherm from the Autosorb experiment (scaled by the ratio of the CO₂ adsorbed amounts at 0.1 bar measured on the Autosorb and the ZLC, i.e. assuming that the difference is due to a different fraction of active crystals in the samples) the nitrogen curves were predicted. The effective macropore diffusivity is calculated from the tortuosity, bead void fraction and combined Knudsen diffusivity and molecular diffusivity of CO₂ in nitrogen. Figure 8 shows the results for the nitrogen experiments and Fig. 9 shows a comparison of the predicted isotherms obtained from the fitting of the ZLC curves and the equilibrium isotherm measured on a large sample in the Autosorb apparatus. The comparison in Fig. 9 is good, considering that there is variability in the fraction of binder in the beads and small trace quantities of water will reduce the adsorbed amount in the ZLC measurements (Brandani et al. 2003).

Fig. 8

ZLC plot with model predictions of 13X (R = 0.8 mm) at 0.1 bar of CO₂ in N₂, 38 °C, at different flowrates

Fig. 9

Comparison of carbon dioxide and nitrogen isotherms from fitting ZLC runs (T = 38 °C) and measured on the volumetric system (T = 35 °C)

We note that in the simulation of the experimental data for zeolite 13X, which is an example of macropore diffusion control with a nonlinear isotherm, the model automatically includes also the variable diffusional time constant, since the effective pore diffusivity (Eq. 4) will change due to the changing slope of the equilibrium isotherm. The full model simulations show very good agreement with the experimental data for both nitrogen and helium as carrier gases, with macropore diffusion control and the same set of values for the particle void fraction and tortuosity as shown in Table 3.

Table 3 Summary of the values of diffusivity and tortuosity obtained from the ZLC fitting

4.2 Volumetric experiment

Figure 10 shows the transient uptake curves at varying pressure steps for CO₂ in 13X beads at 10 °C. The key difference from the ZLC experiments is that no inert gas is present; therefore the mechanism of mass transfer at the operating conditions is a combination of Knudsen diffusion and viscous flow in the macropores and diffusion in the micropores. In the pressure range used in these experiments, Knudsen diffusion is the prevailing mechanism for mass transfer. In an ideal isothermal case, with macropore diffusion control, for each concentration step the curves should exhibit increasing slopes by maintaining approximately the same intercept, as described by Eq. 5. This is the expected result, since, as the pressure increases, the slope of the isotherm decreases and the effective macropore diffusivity increases. Major deviation from the expected trend for the uptake curves indicates the presence of other mechanisms involved.

Fig. 10

Transient uptake curves for CO₂ in zeolite 13X at 10 °C, measured in the Autosorb system

The curve obtained from the first concentration step has clearly a very different shape if compared to the next two steps. The reason for this is explained by the Knudsen diffusion of CO₂ along the tube of the uptake cell. At the first step the uptake cell is under high vacuum and is connected to the dosing cell through a valve. At time zero the valve is opened and the CO₂ flows from the dosing volume to the sample through a 0.28 m long pipe. The resulting curve will show then an initial time region controlled by the diffusion in the connecting pipe, while in the long time region the diffusion inside the beads becomes the controlling process. The use of a model with only the macropore diffusivity yields an inaccurate prediction of the transient uptake in the short-time region. A model which includes the diffusion in the connecting pipe of the sample cell should provide an excellent prediction of the experimental curve. As a reasonable approximation to the process, we include an additional diffusional mass transfer resistance through this pipe by treating the system as a piezometric system with a valve between the dosing and uptake cells.

Figure 11 shows the experimental curve relative to the first concentration step fitted using the analytical solution of a piezometric system under isothermal conditions developed by Brandani (1998). The model considers the presence of the two volumes of the dosing and the uptake cell and the flow through the connecting valve; the solution to the governing equations is given by:

$$ \frac{{\rho_{d} }}{{\rho_{{^{d} }}^{0} }} = \frac{3\,\delta }{1 + 3\,\delta + 3\,\gamma } + \sum\limits_{n = 1}^{\infty } {\frac{{2\,\delta \,\omega^{2} \beta_{n}^{2} }}{{2\delta \,\omega^{2} \beta_{n}^{2} + \left( {\omega - \beta_{n}^{2} } \right)^{2} \left( {2\gamma \beta_{n}^{2} - z_{n} + z_{n}^{2} + \beta_{n}^{2} } \right)}}} \exp \left( { - \beta_{n}^{2} \frac{D}{{R^{2} }}t} \right) $$

(24)

in which:

$$ \beta_{n} \cot \beta_{n} = 1 + \gamma \beta_{n}^{2} + \frac{{\delta \,\omega \,\beta_{n}^{2} }}{{\left( {\omega - \beta_{n}^{2} } \right)}} = z_{n} $$

(25)

Fig. 11

Transient uptake curve at P = 0.001 bar and 10 °C fitted using the piezometric model (Eq. 24) with ω = 250

Similarly to Eq. 5, the γ and δ parameters are the ratio between the volumes of the system (uptake and dosing cell, respectively) and the CO₂ uptake; while ω represents the ratio between the kinetics of flow through the valve and the diffusional time constant. All the parameters are defined as follows:

$$ \gamma = \frac{1}{3}\frac{{V_{u} }}{{KV_{s} }};\quad \delta = \frac{1}{3}\frac{{V_{d} }}{{KV_{s} }};\quad \omega = \frac{\Re T}{{V_{d} }}\bar{X}\frac{{R^{2} }}{D}. $$

(26)

In Eq. 24, $\rho_{d}$ and $\rho_{d}^{0}$ are the dimensionless pressures defined as:

$$ \rho_{d} = \frac{{P_{d} - P_{u}^{0} }}{{P_{\infty } - P_{u}^{0} }};\quad \rho_{d}^{0} = \frac{{P_{d}^{0} - P_{u}^{0} }}{{P_{\infty } - P_{u}^{0} }} $$

(27)

In Eqs. 24–27, the subscript d, u and s refer to the dosing and the uptake cell, and the sample, respectively; V represents the volume; and $\bar{X}$ is the valve constant. With regard to the pressure, P, 0 and ∞ refer to the value of the pressure at time 0 and at equilibrium. For the case under analysis $P_{u}^{0}$ = 0 since the uptake cell was under vacuum before the start of the experiment. In order to compare the two models the solution of the piezometric model needs to be converted to 1 − (M _t  − M ₀ )/(M _∞  − M ₀ ) by simply applying a mass balance between the dosing and the uptake cell:

$$ 1 - \frac{{M_{t} - M_{0} }}{{M_{\infty } - M_{0} }} = \frac{{\rho_{u} \left( t \right)\frac{1 + 3\,\delta + 3\,\gamma }{3\,\delta } + \rho_{d} \left( t \right)\frac{1 + 3\,\delta + 3\,\gamma }{3\,\gamma } - \frac{1 + 3\,\delta + 3\,\gamma }{3\,\gamma }}}{{1 - \frac{1 + 3\,\gamma }{3\,\gamma }}} $$

(28)

As a comparison the plot in Fig. 11 presents the case with a very fast valve (i.e. limiting case of a simple volumetric system) and the one with a lower value of ω. Clearly adding a “valve” effect to approximate the flow in the connecting pipe (ω = 250) provides a much better representation in the short time region, while the slope in the long time region is related to the Knudsen diffusion of the CO₂ in the macropores of the 13X beads.

The initial part of the first pressure step will have a contribution from the Knudsen flow in the connecting pipe, and as the pressure increases there will be a transition to viscous flow. This is the reason for the clear difference between the first and subsequent steps. Viscous flow can be modelled as an equivalent diffusivity, D _v , defined as follows (Kaerger et al. 2012):

$$ D_{v} = \frac{{P\,r^{2} }}{8\,\eta }; $$

(29)

in which r is the characteristic radius of the geometry; P is the absolute pressure; and η is the viscosity. Since the viscous flow operates in parallel with the diffusive flow it is additive in the overall diffusivity:

$$ D_{pipe} = D_{k} + D_{v} $$

(30)

Apart from the initial portion of the first step, D _pipe  ≈ D _v , and will be proportional to the pressure.

Figure 12 shows the transient curve for the successive concentration step at P = 0.003 bar. As a first attempt the piezometric model was used to fit the data and since the viscous diffusivity should be three times higher for this second step, the value of ω should be at least 750. Notably the model does not represent accurately the data because of the contribution of some heat limitations. The use of the non-isothermal model, Eq. 8, provides a good prediction of the long-time asymptote but the accuracy of the prediction is lower in the short time region, which can be attributed to the diffusion resistance through the pipe. The values of the parameters used for the non-isothermal model are listed in Table 4. The high value of the α′ parameter (Eq. 13) indicates that the system is essentially controlled by the macropore diffusion, but there is also a small contribution from the heat generated during adsorption.

Fig. 12

Transient uptake curves at 10 °C, P = 0.003 bar, comparing the fitting using the piezometric model (ω = 750) and the non-isothermal model, Eqs. 8 and 28, respectively; the parameters used for the non-isothermal model are listed in Table 4

Table 4 Parameters used for the non-isothermal analysis of the uptake curves for the small beads, Eq. 8

At higher CO₂ concentrations the contribution of the heat transfer limitations is more significant: the adsorption curves exhibit a very fast initial uptake, followed by a slower adsorption rate in the long time region. The apparent diffusional time constant in the long time region is the same for the last two steps resulting in parallel curves at increasing CO₂ concentrations. Such behaviour is typical of a heat limited process in which the kinetics are initially fast, but then the slow decay is related to the dissipation of the heat generated by adsorption, resulting in additional slow uptake as the particle cools. The experimental data were then well predicted using the non-isothermal model of Kočiřík et al. (1984) and the parameters used in the model are listed in Table 4. The parameter β′ (Eq. 14) depends essentially on the heat of adsorption and the increment of adsorbed amount at equilibrium for each pressure step. This means that for a given difference in pressure the increment of adsorbed amount, Δq*, is higher at lower pressures. The expected trend of β′ assuming that the heat of adsorption does not vary significantly with loading should be increasing as the CO₂ concentration decreases. With regard to the overall heat transfer coefficient, h, this is essentially dominated by radiation in the first steps in which the concentration of CO₂ in the gas phase is extremely low. As the concentration of CO₂ increases the contribution of the conduction term becomes more important until the process is entirely controlled by conduction. This is somehow reflected by the trend of the ha/(ρ _s C _s ) group which increases with the concentration step reaching a constant value in the totally heat limited steps. The values of ha/(ρ _s C _s ) and β′ are consistent with what was reported by Ruthven et al. (1980) for a similar system.

Figure 13 displays the experimental curve relative to the higher concentration steps. Figure 14 shows the predicted and experimental curves in the short time region, in which the process is dominated by the diffusion of CO₂ inside the beads, and in the long time region in which the mechanism is controlled by heat transfer.

Fig. 13

Transient uptake curves at 10 °C and P = 0.006, 0.017, 0.042 and 0.092 bar. The curves are fitted using the non-isothermal model (Eq. 8) using the parameters listed in Table 4

Fig. 14

Transient uptake curves at 10 °C and P = 0.017, 0.042 and 0.092 bar. The curves are fitted using the non-isothermal model (Eq. 8) using the parameters listed in Table 4. On the left the short time region is shown; on the right the complete curves are plotted on a semilog diagram

The same set of experiments was carried out on a single 13X bead of larger size, R = 1.95 mm, with a mass of about 30 mg. The shape and the sequence of the adsorption curves were very similar to the ones obtained for the smaller beads.

Table 5 summarizes the values of the diffusivities obtained from the two volumetric experiments. As expected the values of the diffusional time constants are lower for the large bead, confirming the presence of a macropore diffusion controlled process, but the ratio of the diffusional time constants is lower than the ratio of R ² for the two bead sizes. The difference is mainly explained by the difference in the pore size distribution in the two beads: the small beads are unimodal, while the large bead shows a bimodal distribution and therefore the simple model used, which is based on an equivalent pore diameter is only an approximation.

Table 5 Summary of the values of the diffusivities at 10 °C obtained for CO₂ in 13X beads (R = 0.98 mm and R = 1.95 mm)

4.3 Analysis of the diffusion process

In order to understand the validity of the values of diffusivity obtained from the independent ZLC and volumetric measurements a detailed analysis of the data is needed. In the case of the volumetric system the mass transfer of CO₂ inside the macropores is governed by Knudsen diffusion and by viscous diffusion and the equivalent diffusivity is the sum of the two contributions as seen in Eq. 30. Within the range of conditions used in the experiments the viscous contribution was ~2 orders of magnitude smaller than the Knudsen contribution and was considered to be negligible. Similarly to the case described for the ZLC system, for a macropore controlled process all the diffusion terms should lump in an effective pore diffusivity term, as defined by Eq. 4:

$$ D_{P}^{e} = \frac{{\varepsilon_{P} \,{{D_{K} } \mathord{\left/ {\vphantom {{D_{K} } \tau }} \right. \kern-0pt} \tau }}}{{\varepsilon_{P} + \left( {1 - \varepsilon_{P} } \right)\,K}} $$

(31)

Clearly from the expression of Eqs. 4 and 31 it can be seen that even though the mechanisms are different for the two types of experiment they are related to the same physical properties of the sample: the void fraction and the tortuosity. This means that the values of diffusivities experimentally measured with the two different techniques can be validated if they lead to similar values of pore tortuosity.

By rearranging with respect to τ, the following expressions are obtained for the volumetric experiment

$$ \tau = \frac{{\varepsilon_{P} \,D_{K} }}{{D_{P}^{e} \,\left( {\varepsilon_{P} + \left( {1 - \varepsilon_{P} } \right)\,K} \right)}} $$

(32)

and the ZLC experiment

$$ \tau = \frac{{\varepsilon_{P} \,D_{Macro} }}{{D_{Macro}^{e} }} $$

(33)

since the data regression algorithm used to fit the ZLC experiments automatically decouples the effective macropore diffusivity (Eq. 23) from the effective pore diffusivity (Eq. 4).

Using the values of the bead void fraction and average pore radius from the small beads, it is possible to calculate a tortuosity of 2.89 from the ZLC data, using Derjaguin’s correction in the calculation of the Knudsen contribution. For the volumetric experiment, K _bead  = ε _p  + (1 − ε _p )K = Δq/Δc, is measured directly from the initial and final pressure at each step. Table 6 includes all the terms used for the calculation of the tortuosity. Since the contribution of the viscous flow is negligible compared to the Knudsen diffusion, it is clear that the main contribution to the increase of the effective diffusivity comes from the equilibrium K value. For the small beads the average tortuosity calculated is 2.45, which is in very good agreement with the value of 2.62 obtained from the mercury porosimetry experiments.

Table 6 Summary of the values used for the calculation of the tortuosity assuming r = 0.294 μm and r = 0.516 μm for the small and big beads, respectively

Overall we find consistency across the two different experimental techniques and find similar results for both molecular and Knudsen transport regimes, if the Derjaguin correction is applied.

With regard to the large bead experiment, the average value of tortuosity obtained is 2.17, which is lower than the one measured from the porosimetry experiment. This is probably a result of the bimodal pore size distribution and the qualitative nature of the comparison, given that the tortuosity is obtained from a diffusivity based on a single equivalent pore radius.

5 Conclusions

A detailed study of the diffusion mechanism of CO₂ in zeolite 13X beads was carried out. Independent ZLC measurements and volumetric experiments confirmed that the process is clearly macropore diffusion controlled.

The ZLC measurements recently published by Silva et al. (2012) and interpreted as micropore diffusion controlled are very likely to be a result of an equilibrium controlled process. In this case the curvature in the short-time region of the reported ZLC curves would be due to the non-linearity of the isotherm and would not be related to a diffusion process.

In this paper we described a methodology that, through the combination of kinetic experiments and porosity characterisation, allows a coherent determination of the tortuosity of the beads. This methodology, by relating the diffusivity measured to a physical property of the sample, allows also to double check the validity of the diffusivity values obtained. The tortuosity obtained from the volumetric and the ZLC experiments were consistent with the values measured by the porosimeter. Very similar results are obtained for both Knudsen diffusion (for beads with a single peak in the pore size distribution) and molecular diffusion processes studied in the two kinetic experiments.

Further refinements of the models for the interpretation of the volumetric system should be developed. This will allow a more accurate determination of the kinetic processes at very low pressures, where diffusion through the connecting pipe can be described more accurately than with the lumped resistance model used here. This would not change the main result reported here, i.e. that carbon dioxide in 13X is macropore diffusion controlled, both under Knudsen and molecular diffusion regimes, and has therefore not been investigated further in detail. A refined dynamic model would also allow to study in greater detail the mechanisms for mass transfer in the bead with a bimodal pore size distribution.