1 Introduction

Unmatched interface problems are increasingly common because it is difficult to satisfy the connectivity of elements for complex domains and the transition between coarse and fine meshes often results in distorted elements that reduce the accuracy of the solution in transition regions. For example, there is a growing need to perform combined analyzes of complex structures, as an airplane or a ship, using sub-structural numerical models created independently by teams of engineers using different software and collaborating remotely. Frequently the meshes of these numerical models are incompatible at the interfaces, therefore all the sub-structural models must be joined to build the entire structure. Even within the same team, discretizing problems in regions, dividing them into sub-structural models, and then using a coupling technique to connect their mismatched interfaces, can be a winning strategy.

Many different methodologies have proposed for non-matched interface problems [1,2,3,4,5,6,7,8]. Most of them use Lagrange multipliers with a negative result that the resulting system of equations is not definite positive. A possible fix is to enforce the interface constraints via a penalty method, the following advantages are obtained: a formulation that can be easily implemented in commercial codes, a positive-definite and banded stiffness matrix and a reduced number of DOFs. Therefore, the penalty approach should greatly improve the computational efficiency. However, specific procedures are required for the selection of an appropriate value of the penalty parameter. A rule for selecting the penalty parameter in the framework of the cohesive element for non-matched interface problems has been developed by Pantano and Averill [9, 10].

More and more often the sub-structural models that must be united to build the entire structure, or parts of it, are made of composite materials, of which it is important to simulate possible risks of delamination. The penalty-based cohesive element can also be effectively used to model delamination in composite materials or adhesive failure in composite-composite or metal-composite bonding.

To describe the delamination, many authors started from the basics of Linear Elastic Fracture Mechanics (LEFM) and from the concept of energy release rate, G, the energy released for crack advance unit [11,12,13]. It is clear from the literature that this magnitude has often been measured using the technique known as Virtual Crack Closure Technique (VCCT). Since this technique is based on the principles of LEFM, it is only appropriate if the crack propagates in a fragile way along a predefined path. In other words, if the LEFM theory is valid, then it is true that the necessary and sufficient condition for delamination is G > Gc, where Gc is the energy needed to break the internal bonds of the material and create two new surfaces of unit area and it is called the critical strain energy release rate. The substantial advantage of this technique is that of calculating the energy contributions through a single analysis and that the calculation is based on energy and not on the stresses, however there are several limitations. VCCT requires that the points where the propagation is triggered are identified a priori, it is necessary to define an initial delamination, but this operation is largely influenced by the type of geometry and by the acting loads, which can make it difficult to determine the initial position of the delamination front.

In order to overcome some of the difficulties related to VCCT (or other different techniques, but always deriving from the LEFM approach), over time other theories have been developed for the simulation of delamination starting from different fields. Among these, that of the cohesive finite elements is the one that perhaps has been more successful in recent decades and that today is the subject of an ever increasing number of researches.

The cohesive finite element theory is based on the so-called Cohesive Zone Model (or process zone, or also Cohesive Zone Model (CZM)) developed at the beginning of the sixties [14, 15]. These models combine aspects of strength-based analysis to predict the onset of damage at the interface between laminae and fracture mechanics to predict delamination propagation. Since the cohesive zone can still transfer load after the onset of damage, a softening model is required that describes how the stiffness is gradually reduced to zero after the interfacial stress exceeds the interlaminar tensile strength. The relation between the traction and separation that are normal to the fracture surfaces is considered. The cohesive models were later extended to the mode II fracture process, in which the tangential traction and separation are considered instead. The main advantage in the use of cohesive finite elements lies in the ability to describe both the activation and the propagation of delamination without knowing a priori neither the position of the crack nor the direction of propagation. Cohesive models to the determination of the delamination growth has been adopted by several authors [16,17,18,19,20,21,22,23,24,25,26].

In this article the penalty-based cohesive element technology previously developed [9, 10] is reviewed, subsequently new applications of the cohesive element for predicting delamination crack growth in laminated structures are introduced.

2 Formulation of the Cohesive Element

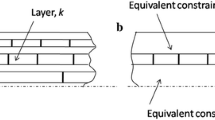
A cohesive element can act as a “glue” in the common interface of two subdomains Ω1 and Ω2 modeled independently, as shown in Fig. 1. The nodes of the cohesive element are independent of the interface nodes in the two subdomains. The cohesive element has a “stiffness” matrix, which includes the coupling terms and it is assembled as usual with the other stiffness matrices.

Fig. 1
figure 1

Interface element configurations

Full size image

The sub-domain Ωj has nodal displacements identified by \( {q}_j^o \) and \( {q}_j^i \). The degrees of freedom (DOFs) that are not on the interfaces are denoted with the superscript o, while i represents DOFs that are on the interfaces. The interface displacement field uj is function of the unknown nodal displacements \( {q}_j^i \) of the sub-domain Ωj. The displacement field of the cohesive element, identified as V, is approximated in terms of unknown nodal displacements qs.

$$ {u}_j={N}_j\ {q}_j^i\kern0.50em \ \ \ \ \ \ V=T\ {q}_s $$
(1)

where Nj can be the matrices of interpolation functions and T is a matrix of cubic spline interpolation functions. Two vectors of penalty parameters, γ1 and γ2, are used to enforce the displacement continuity constraint in a least squares sense. Therefore the total potential energy of the system takes the form:

$$ \pi ={\pi}_{\varOmega_1}+{\pi}_{\varOmega_2}+\frac{\gamma_1}{2}\underset{S}{\int }{\left(V-{u}_1\right)}^2 ds+\frac{\gamma_2}{2}\underset{S}{\int }{\left(V-{u}_2\right)}^2 ds $$
(2)

By taking the first variation of π respect to all the DOFs, with the exception of the vectors of penalty parameters γ1 and γ2 that are preset constants, the equilibrium configuration is found.

$$ {\left.\delta \pi \right|}_{q_1^o,{q}_1^i,{q}_S,{q}_2^o,{q}_2^i}=0 $$
(3)

The global system of equations method assumes the following form:

$$ \left[\begin{array}{ccccc}{K}_1^{oo}& {K}_1^{oi}& 0& 0& 0\\ {}{K}_1^{io}& {K}_1^{ii}+{G}_1^{ii}& -{G}_1^{is}& 0& 0\\ {}0& -{G}_1^{si}& {G}_1^{ss}+{G}_2^{ss}& -{G}_2^{si}& 0\\ {}0& 0& -{G}_2^{is}& {K}_2^{ii}+{G}_2^{ii}& {K}_2^{io}\\ {}0& 0& 0& {K}_2^{oi}& {K}_2^{oo}\end{array}\right]\left\{\begin{array}{c}{q}_1^o\\ {}{q}_1^i\\ {}{q}_s\\ {}{q}_2^i\\ {}{q}_2^o\end{array}\right\}=\left\{\begin{array}{c}{f}_1^o\\ {}{f}_1^i\\ {}0\\ {}{f}_2^i\\ {}{f}_2^o\end{array}\right\} $$
(4)

where:

$$ {G}_j^{ii}={\gamma}_j\underset{S}{\int}\left({N}_j^T\;{N}_j\right) ds,{G}_j^{is}={\gamma}_j\underset{S}{\int}\left({N}_j^T\;{T}_j\right) ds,{G}_j^{si}={\left[{G}_j^{is}\right]}^T,{G}_j^{ss}={\gamma}_j\underset{S}{\int}\left({T}_j^T{T}_j\right) ds $$
(5)

This global stiffness matrix is symmetric, banded and positive definite (after imposing boundary conditions). Thus the cohesive element can be associated with a “stiffness” matrix and a generalized vector of unknown displacements:

$$ \left[\begin{array}{ccc}{G}_1^{ii}& -{G}_1^{is}& 0\\ {}-{G}_1^{si}& {G}_1^{ss}+{G}_2^{ss}& -{G}_2^{si}\\ {}0& -{G}_2^{is}& {G}_2^{ii}\end{array}\right]\left\{\begin{array}{c}{q}_1^i\\ {}{q}_s\\ {}{q}_2^i\end{array}\right\}=\left\{\begin{array}{c}0\\ {}0\\ {}0\end{array}\right\} $$
(6)

For a detailed description of the cohesive element formulation, see [9, 10].

2.1 Automatic Calculation of the Proper Penalty Parameters

In the penalty method, the displacement continuity constraint is imposed through penalty parameters, a set of predetermined constants. The FE solution obtained with the penalty method is approximate, and the value of the penalty parameters used determines its accuracy. The penalty parameter should be function of the material and geometric properties of the two sub-regions. It is known that there exists a relationship between the penalty parameter and the corresponding Lagrange multiplier that enforces the same constraint. If the Lagrange multiplier method is used the continuity constraint is enforced exactly; thus it can be a reference value to assess the accuracy of the penalty method. If simple models are studied is easier to find relations among the penalty parameter and the geometrical and material properties of the model under examination.

A broad variety of one-dimensional, two-dimensional and three-dimensional problems have been solved with both the Lagrange multiplier method and the penalty method. Finite elements studied are of the following types: conventionally formulated and reduced integrated Timoshenko beam elements, plane stress quadrilateral elements and plate elements based on the first order shear deformation theory (FSDT), or Mindlin plate theory, tetrahedral and hexahedral elements.

Different penalty parameters are needed for the various nodal DOFs of each finite element formulation. Since each degree of freedom can be associated in different ways with the material and geometric properties of the model, the penalty parameters must be chosen independently. If we consider Timoshenko’s beam element as an example, it has three independent nodal DOFs: the axial displacement u, the transverse displacement w and the rotation ψ. Thus the interface continuity constraints on the three DOFs requires three different penalty parameters γu, γw and γψ to be enforced.

The approach adopted can be summarized as follow. A simple model of one or two elements is considered and the most common load cases for the FE type studied are applied separately. Both the Lagrange multiplier method and the penalty method are used to find the solutions in terms of displacements, then they are compared individually for each degree of freedom. The ratio between the two solutions is expressed in the form:

$$ \frac{u^{penalty}}{u^{Lagrange}}=1+\frac{f}{\gamma } $$
(7)

where f = f (material properties, element geometric properties, and loads).

If the penalty parameter γ is set equal to γ = βf, the ratio between the solutions is independent of geometrical and material properties:

$$ \frac{u^{penalty}}{u^{Lagrange}}=1+\frac{1}{\beta } $$
(8)

The parameter β determines the accuracy of the solution, however it cannot be indefinitely increased since round off amplification error would rise. A reasonable compromise between constraint representation error and the round off error is required. Once a value of β is identified, the same level of accuracy can be achieved for every combination of material and geometrical properties. It should be underlined that an exact value of the penalty parameter is not required. Rather, a value that is of the right order of magnitude is sufficient. In fact, even in the most complex FE analysis, there exists a range of values for this parameter for which the numerical outcomes change very little. This range can equal as much as 12 orders of magnitude for simple analyses, but usually is not less than two orders of magnitude in most situations.

An automatic control of the round-off error has been developed in previous works [9, 10] as summarized in the following lines. Due to finite precision in floating-point arithmetic used when the cohesive element stiffness matrix is numerically integrated, the stiffness coefficients are always approximated. However, in order to be imposed correctly (and to contribute no energy to the system), the displacement continuity constraint (V − u) requires the sum of the terms in every row of its stiffness matrix (6) to be zero. This condition usually cannot be achieved, due to the round-off error, and the resulting inaccuracy grows with the value of the penalty parameter. Precisely, the important measure is the ratio between the order of magnitude of the cohesive element stiffness matrix rows’ imbalance and the element stiffness. If Kn is the stiffness associated to the n-th nodal DOF, it is sufficient to consider the ratio:

$$ {Q}_n=\frac{E{R}_n}{K_n} $$
(9)

where ERn is the unbalance in the cohesive element stiffness matrix row related to the DOF n.

$$ E{R}_n=\sum \limits_j{K}_{nj} $$
(10)

When the value of Qn exceeds about 1 ⋅ 10−4, errors in the solution may become appreciable. The discussed row imbalance is proportional to the value of the penalty parameter,ERn ∝ γ. It is also approximately true that:

$$ E{R}_n\propto \gamma \propto \beta \cdot {K}_n\Rightarrow {Q}_n\propto \beta $$
(11)

Accordingly, an algorithm has been developed to control the round-off error. Its steps can be summarized as follows:

  • Stiffness terms for every nodal DOF in the cohesive element are computed from known geometrical and material properties.

  • For each row in the stiffness matrix:

    • The highest stiffness term is selected and assigned to a variable K

    • The row imbalance of the stiffness matrix is stored in a variable ER

    • \( Q=\frac{ER}{K} \) is evaluated

  • The highest Q found is compared to a given constant value C. Typically C = 1 ⋅ 10−7is used.

  • If Q > C, the parameter β is reduced according to: \( {\beta}^{new}=\frac{C}{Q}\cdot \beta \)

  • The cohesive element stiffness matrix is recalculated using the new value β = βnew.

This approach reduces the risk that round-off errors could adversely affect the solution. Thus, the initial value of β can be increased, in order to get a higher degree of accuracy, knowing that it will be automatically reduced if rounding errors don’t allow that precision to be realized.

2.2 Interface Technology for Modeling Delamination

The cohesive element technology [9, 10], in addition to being used to connect non-matching meshes, has several advantages over conventional FE one in disconnecting two regions of a model during crack growth. The most important is the ability to release portion of the interface that are smaller than the local finite element length. This is possible since the extreme values of the interval of integration of the cohesive element can be freely modified, moreover it is possible to reduce the value of the penalty parameter for a part of that interval. So the growth of delamination is not limited to advancing by releasing nodes or elements of the FE model, which is a common limitation to delamination techniques found in literature.

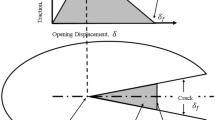
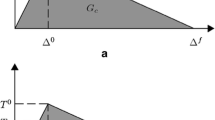
A frequently used damage model with bilinear softening has been implemented, combining strength of materials and fracture mechanics approaches, see Fig. 2. In single-mode delamination, when the load grows, the relative displacement δ the two joined FE meshes increases proportionally to the value of the penalty stiffness γ. Once δ0 is reached the stress is equal to the maximum stress level possible, the interfacial tensile strength σt. As displacements are further increased the interface accumulates damage and its capability to withstand stress decreases progressively. The model would unload to the origin after δ0 has been exceeded, but δF has not been reached. The interface is fully debonded when δ exceeds δF. For example, if from point K, see Fig. 2, the load is reduced, the model follows the line KO. If the load is reapplied, the stress grows with the relative displacement along the same line KO.

Fig. 2
figure 2

Bilinear interfacial constitutive damage model

Full size image

This damage model works by acting on the penalty stiffness γ. A parameter D controls the damage accumulated at the interface:

$$ \sigma =\left(1-D\right)\gamma \delta $$
(12)

The damage parameter D, whose initial value is zero, starts growing when δ ≥ δ0 and reaches the value 1 when δ ≥ δF. From geometry is possible to compute the value of D to be:

$$ D\left(\delta \right)=\frac{\delta_F\left(\delta -{\delta}_0\right)}{\delta \left({\delta}_F-{\delta}_0\right)} $$
(13)

To define the interfacial constitutive model when two among the following four properties are known: Gc, σt, δ0 and δF, where Gc is the critical strain energy release rate, which is equal to the area under the σ-δ curve in Fig. 2.

Among these parameters two relations exist:

$$ {G}_c=\frac{\delta_F{\sigma}_t}{2} $$
(14)
$$ {\delta}_0=\frac{\sigma_t}{\gamma } $$
(15)

The cohesive model keeps together a sub-region of the interface between the two meshes. More are the sub-regions in which the interface is divided the higher is the accuracy of the prediction. The common implementation of the damage model with bilinear softening requires it to be applied along the length of one finite element. In this case the crack can only advance by weakening and releasing at a time a length of the interface equal to one element. Thus a refined finite element mesh is needed. Instead, if the previously presented cohesive element is adopted the damage evolution is effectively mesh-independent.

The present cohesive model is applied to a desired fraction of the interface by dividing the cohesive element into a given number of intervals n, this means that the total potential energy of the system is modified as follows:

$$ \pi ={\pi}_{\varOmega_1}+{\pi}_{\varOmega_2}+\frac{1}{2}\sum \limits_{i=1}^n\left(1-{D}_i\right){\gamma}_1{\int}_{L_{i-1}}^{L_i}{\left(V-{u}_1\right)}^2 ds+\sum \limits_{i=1}^n\left(1-{D}_i\right){\gamma}_2{\int}_{L_{i-1}}^{L_i}{\left(V-{u}_2\right)}^2 ds $$
(16)

where Di is the damage parameter associated with the interval i, and the interval i is defined over the range (Li-1, Li). Li is the value of the interface coordinate L at the end of the ith interval. Thus, each interval i will obey the rules of the failure model independently from the others. The value of the relative displacement δ is evaluated at the center of the interval i. By allowing crack advance in a more continuous manner, greater accuracy of the simulation can be obtained.

For a given problem, it is necessary to perform a convergence study progressively reducing the size of the intervals in which the cohesive element is divided. This study does not require many simulations because the convergence rate is generally high and the familiarity in choosing the length of the intervals from similar simulations can be applied to new calculations.

The other important convergence study regards the number of increments in which the given load/displacement is progressively applied. This study is required for the great majority of the FE approaches to crack growth simulations, because if the increase in applied load or displacement is too high, the bilinear softening model cannot work properly and the results will be not be accurate.

2.3 Mixed Mode Failure

The definition of the damage model for crack initiation and propagation in mixed-mode I/II requires the interlaminar tensile and shear strengths T and S, the penalty parameter γ, and the critical strain energy release rates GIc and GIIc. For simplicity, we assume the same material behavior for both tensile and compressive loading.

At a given load increment the FE solution gives δx and δz for each interval of the cohesive element. It is known:

$$ {\delta}_{z0}=\frac{T}{\gamma } $$
(17)
$$ {\delta}_{x0}=\frac{S}{\gamma } $$
(18)
$$ {\sigma}_z=\gamma {\delta}_z $$
(19)
$$ {\tau}_{xz}=\gamma {\delta}_x $$
(20)

A quadratic interface failure criterion takes the following forms:

$$ {\left(\frac{\sigma_z}{T}\right)}^2+{\left(\frac{\tau_{xz}}{S}\right)}^2=1 $$
(21)
$$ {\left(\frac{\delta_z}{\delta_{z0}}\right)}^2+{\left(\frac{\delta_x}{\delta_{x0}}\right)}^2=1 $$
(22)

If the condition (22) is not satisfied, it is not necessary to do anything. Else the following ratio is assumed:

$$ \frac{\left(\frac{\delta_z}{\delta_{z0}}\right)}{\left(\frac{\delta_x}{\delta_{x0}}\right)}={C}_1 $$
(23)

to be the same as it was when the failure condition (22) was satisfied first (see Fig. 3).

Fig. 3
figure 3

Quadratic failure envelope

Full size image

If small load steps are used, the assumption is rather accurate. Then it is possible to determine the value of the relative displacements δx’ and δz’, corresponding to point F in Fig. 3.

$$ {\delta}_x\hbox{'}={\delta}_{x0}\frac{\left(\frac{\delta_x}{\delta_{x0}}\right)}{\sqrt{{\left(\frac{\delta_z}{\delta_{z0}}\right)}^2+{\left(\frac{\delta_x}{\delta_{x0}}\right)}^2}} $$
(24)
$$ {\delta}_z\hbox{'}={\delta}_{z0}\frac{\left(\frac{\delta_z}{\delta_{z0}}\right)}{\sqrt{{\left(\frac{\delta_z}{\delta_{z0}}\right)}^2+{\left(\frac{\delta_x}{\delta_{x0}}\right)}^2}} $$
(25)

The interfacial models is now modified for both modes I and II by setting δx0’ = δx’ and δz0’ = δz’, see Figs. 4 and 5. The interlayer tensile strengths T and S are modified consequently:

$$ T\hbox{'}={\gamma}_z\cdot \delta {\hbox{'}}_{z0} $$
(26)
$$ S\hbox{'}={\gamma}_x\cdot \delta {\hbox{'}}_{x0} $$
(27)
Fig. 4
figure 4

Updated interfacial constitutive model for mode I

Full size image
Fig. 5
figure 5

Updated interfacial constitutive model for mode II

Full size image

Note that the following inequalities hold.

$$ {\delta}_{x0}\hbox{'}\le {\delta}_{x0},\kern0.75em {\delta}_{z0}\hbox{'}\le {\delta}_{z0},\kern0.5em {\delta}_x\ge {\delta}_{x0}\hbox{'},\kern1em {\delta}_z\ge {\delta}_{z0}\hbox{'} $$
(28)

The quadratic interaction criterion forecasts reaching the final failure when the following condition is met:

$$ {\left(\frac{G_I}{G_{Ic}}\right)}^2+{\left(\frac{G_{II}}{G_{II c}}\right)}^2=1 $$
(29)

In a similar way to the previous one, the ratio between (GII/GIIc) and (GI/GIc) is assumed not to change as the work of separation grows, as shown in Fig. 6

Fig. 6
figure 6

Quadratic final failure surface

Full size image
$$ \frac{\left(\frac{G_{II}}{G_{II c}}\right)}{\left(\frac{G_I}{G_{Ic}}\right)}={C}_2 $$
(30)

Delamination researches commonly use specimens that, for a given configuration (geometry and loads), have a ratio between the strain energy release rates for modes I and II, GI/GII, that does not change appreciably during the entire test, e.g. [27]. This fact provides a valid basis for our assumption. Consequently, it is possible to determine the value of the strain energy release rate GI’ and GII’ corresponding to point F in Fig. 6.

From geometry, the value of the (GI/GIc)’ at F is:

$$ {G}_I\hbox{'}={G}_{Ic}\frac{\left(\frac{G_I}{G_{Ic}}\right)}{\sqrt{{\left(\frac{G_I}{G_{Ic}}\right)}^2+{\left(\frac{G_{II}}{G_{II c}}\right)}^2}} $$
(31)

To evaluate this expression we must determine the value of GI divided by GIc, see Fig. 7.

$$ {G}_{Ic}=\frac{T\hbox{'}\cdot {\delta}_{zF}\hbox{'}}{2}=\frac{\delta_{z0}\hbox{'}\cdot {\gamma}_z\cdot {\delta}_{zF}\hbox{'}}{2} $$
(32)
$$ {G}_I={G}_{Ic}-\left(\mathrm{Area}\kern0.17em \mathrm{Triangle}\; OBK\right)=\frac{\delta_{z0}\hbox{'}\cdot {\gamma}_z\cdot {\delta}_{zF}\hbox{'}}{2}-\frac{\left[{\delta}_z\left(1-{D}_z\right){\gamma}_z\right]\cdot {\delta}_{zF}\hbox{'}}{2} $$
(33)
$$ \left(\frac{G_I}{G_{Ic}}\right)=\frac{\frac{\delta_{z0}\hbox{'}\cdot {\gamma}_z\cdot {\delta}_{zF}\hbox{'}}{2}-\frac{\left[{\delta}_z\left(1-{D}_z\right){\gamma}_z\right]\cdot {\delta}_{zF}\hbox{'}}{2}}{\frac{\delta_{z0}\hbox{'}\cdot {\gamma}_z\cdot {\delta}_{zF}\hbox{'}}{2}}=1-\frac{\delta_z}{\delta_{z0}\hbox{'}}\left(1-{D}_z\right) $$
(34)
Fig. 7
figure 7

Final interfacial constitutive model for mode I delamination

Full size image

In the same way, we have:

$$ \left(\frac{G_{II}}{G_{II c}}\right)=\frac{\frac{\delta_{x0}\hbox{'}\cdot {\gamma}_x\cdot {\delta}_{xF}\hbox{'}}{2}-\frac{\left[{\delta}_x\left(1-{D}_x\right){\gamma}_x\right]\cdot {\delta}_{xF}\hbox{'}}{2}}{\frac{\delta_{x0}\hbox{'}\cdot {\gamma}_x\cdot {\delta}_{xF}\hbox{'}}{2}}=1-\frac{\delta_x}{\delta_{x0}\hbox{'}}\left(1-{D}_x\right) $$
(35)

Now, the updated state of the interfacial models can be completed for both modes I and II by setting GIc’ = GI’ and GIIc’ = GII’. The final form of the interfacial constitutive models is reported in Figs. 7 and 8. Note that the models have different penalty and damage parameters.

Fig. 8
figure 8

Final interfacial constitutive model for mode II delamination

Full size image

2.4 Friction Model

A friction model has been implemented in the cohesive element, since friction can be required for an accurate simulation when, after complete failure, the two meshes remain in contact, e.g. ELS test specimen. The friction model can also be used for cohesive elements whose only purpose is to avoid overlapping and to enforce friction. Interface forces can be evaluated for a portion of the interface length by changing the extreme values of the interval of integration and they do not depend on the compatibility of the interface meshes.

For each of the intervals in the interface, the normal force Fn can be computed as function of the normal relative displacement δn:

$$ {F}_n=\frac{1}{2}{\gamma}_n\underset{s}{\int }{\delta}_n ds $$
(36)

The tangential force Ft needed to generate the friction phenomenon is:

$$ {F}_t=\frac{1}{2}{\gamma}_t\left(1-{D}_t\right)\underset{s}{\int }{\delta}_t ds=\mu {F}_n $$
(37)

where μ is the friction coefficient and δt is the tangential relative displacement. Before failure Dt was used as a damage parameter, now employed as a scale factor able to decrease the value of the penalty parameter for the tangential DOF. From equality (35), the required damage parameter \( {D}_t^{\ast } \) related to the tangential relative displacement δt, which generate the right amount of friction, can be determined from the following relation:

$$ {D}_t^{\ast }=1-\frac{2\mu {F}_n}{\gamma_t\underset{s}{\int }{\delta}_t ds} $$
(38)

3 Numerical Results

3.1 Mode I, Mode II, and Mixed-Modes I and II Delamination Growth

The experimental considered for the validation of the numerical model are taken from the works of Camanho and Dávila [18]. The available data concern the displacement load curves of five delamination tests: a DCB test, an ENF test and 3 MMB tests respectively with a mixed mode coefficient κ = 20%, 50% and 80%. The Mixed Mode Bending (MMB) test, see Fig. 9, allows to perform mixed I / II delamination tests in unidirectional FRP laminated specimens, including the DCB test, which is a pure Mode I, and the ENF tests, which is a pure Mode II, that are two special cases. The test was designed by Reeder and Crews in the late 1980s [28], improved by the same authors over the years and finally regulated by ASTM International in 2014 [29]. The main advantages of the MMB test method are the possibility of using virtually the same specimen configuration for the I mode tests and the possibility of obtaining different mixed-mode ratios, ranging from pure I to II modes, changing the length c of the loading lever shown in Fig. 9. The unidirectional FRP laminated specimens are 24-ply unidirectional AS4/PEEK (APC2) carbon fibre reinforced composites, mechanical properties of the material of the specimens are listed in Tables 1 and 2. The specimens dimensions, with reference to Fig. 9, are reported in Table 3. The initial delamination length of the specimens (a0) for the different experiments are shown in Table 4, while the length c of the loading lever for the three MMB tests are listed in Table 5.

Fig. 9
figure 9

Loading, geometry and boundary conditions for the Mixed Mode Bending test

Full size image
Table 1 Mechanical properties of the material, AS4/PEEK, of the specimens [18]
Full size table
Table 2 Properties for AS4/PEEK [18]
Full size table
Table 3 Specimen geometry
Full size table
Table 4 Experimental data: initial delamination length [18]
Full size table
Table 5 Length of rigid lever c
Full size table

Models able to simulate the DCB, ENF and MMB test cases and using cohesive elements along the length of the specimens were built. Two independent meshes compose the finite element models of the upper and lower part of the specimens; they are joined by several cohesive elements. Along the initial delamination length of the specimens (a0), whose lengths are indicated in Table 4, the cohesive elements used do not connect the two faces but only avoid overlap. Three different convergence analyses of the solutions have been performed to set up accurate finite element models: convergence with the number of elements along the length of the specimens, convergence with the number of load increments, convergence with number of cohesive elements and with the intervals in which the cohesive elements are divided. For a high degree of accuracy, as result of the convergence study, 510 elements were used along the length of the specimens for the mesh of the two domains connected by the cohesive elements. The predictions from coarse meshes contain many local “bumps”, this phenomenon was analyzed by Mi et al. [30], concluding that coarse meshes can induce these “false instabilities”.

The convergence study proved that a good level precision can be reached with 400 load increments, however for the maximum accuracy 800 load increments were used. For the discretization of the interface each cohesive element connects six elements, three for each side of the two domains to be connected. As discussed previously, the damage technique implemented in our model allows portions of the interface, intervals, much smaller than the finite element length, to be released. A convergence study was performed progressively reducing the size of the n intervals in which the cohesive element is divided, 8 intervals were used for maximum precision.

The experimental results relate the load to the displacement of the point of application of the load P in the lever, see Fig. 9. A comparison among the numerical and experimental results for the DCB test, ENF test and 3 MMB tests are shows in Fig. 10. A good agreement was found between the numerical predictions and the experimental results. Figures 11, 12, 13, 14 and 15 show the maps of the von Mises stresses of the 5 tests in the final deformed configuration of the simulations. For the MMB tests, at the end of the analysis, the point of application of the load P in the lever c are equal to: 10.5 mm for the 20% MMB test (Fig. 12), 7 mm for the 50% MMB test (Fig. 13), 6 mm for the 80% MMB test (Fig. 14). For the DCB test in the final deformed configuration, Fig. 11, the total opening at the end of the specimen is 7 mm. For the ENF test in the final phase of the simulation, Fig. 15, the displacement of the load applied to the center on the top of the sample is 4.2 mm. The insets in Figs. 11, 12, 13, 14 and 15 show a magnification of the area where the crack tip is located.

Fig. 10
figure 10

Numerical and experimental load-displacement results for the DCB test, ENF test and 3 MMB tests

Full size image
Fig. 11
figure 11

Map of von Mises stresses of the DCB test in the final deformed configuration of the numerical simulation. The inset shows a magnification of the area where the crack tip is located

Full size image
Fig. 12
figure 12

Map of von Mises stresses of the MMB 20% test in the final deformed configuration of the numerical simulation. The inset shows a magnification of the area where the crack tip is located

Full size image
Fig. 13
figure 13

Map of von Mises stresses of the MMB 50% test in the final deformed configuration of the numerical simulation. The inset shows a magnification of the area where the crack tip is located

Full size image
Fig. 14
figure 14

Map of von Mises stresses of the MMB 80% test in the final deformed configuration of the numerical simulation. The inset shows a magnification of the area where the crack tip is located

Full size image
Fig. 15
figure 15

Map of von Mises stresses of the ENF test in the final deformed configuration of the numerical simulation. The inset shows a magnification of the area where the crack tip is located

Full size image

4 Conclusions

A cohesive element capable of joining and simulating crack growth between independently modeled finite element subdomains with non-matching meshes was presented and validated. It can be effectively used to model delamination in composite materials or adhesive failure in composite-composite or metal-composite joints. The approach is based on: penalty constraints, an automatic choice of the penalty parameter, a displacement-based damage parameter applied in a model with bilinear softening law, and a novel method for modeling the crack growth in mixed mode I + II conditions. The approach has several advantages over conventional FE one, the most important is the ability to release sub-regions of the interface surface whose length is smaller than that of the finite elements, thereby allowing for a mesh-independent tracking of the crack front. Furthermore, it is possible to vary the penalty parameter within the cohesive element, allowing to apply the damage model to a chosen fraction of the interface between the two meshes. This formulation leads to a very efficient computational approach that is completely compatible with existing commercial software. The proposed methodology has been validated by comparing numerical simulations with experimental data from DCB, ENF and MMB tests. The results indicate that the method is able to accurately predict the growth of delamination.

Acknowlodgements

In the past this research was sponsored by NASA Langley Research Center under grant NAG-1-2213 and by the State of Michigan Research Excellence Fund.