1 Introduction

Composite materials are being used for structural applications due to their high strength-to-weight ratio and flexibility in obtaining desired material properties by intelligently combining different materials. This issue becomes critical when structural applications require mechanical properties that are not available with currently used or known materials. However, the lack of plasticity mechanisms leading to premature failure is a major downfall of structural composites when used for blast resistance [1, 2]. This limitation may be overcome if the composite material is designed in such a way that the weak phases are allowed to fail while the strong phases take over the stress via stress redistribution so that the overall composite does not fail. Micro and nano-synthesis may be used to reinforce the weak phases with the strong phases. Blast resistance may also be increased in laminated composites by adjusting the stiffness of the composite layers such that the stress evolution in the composite material does not result in failure of the weak layer. This concept may be realized via multi-objective topological optimization using the microstructural homogenization method.

Topology optimization is of great interest to the aerospace and automobile industries. It allows for the design of structures with holes or cavities that reduce weight while maintaining desired stiffness. The introduction of homogenization techniques by Bendsoe and Kikuchi [3] reintroduced topology optimization to structural design. Topology optimization has been successfully applied to optimize structural geometry like trusses and frames [3, 4], and to composite plates and membranes [5, 6]. The objective functions in topology optimization are typically compliance and/or weight, but other objectives such as dynamic response and thermoelastic characteristics have also been considered [7, 8]. The idea of enhancing the elastic structural response has been examined with different methods in the past. The automotive industry has examined using shape optimization and topology optimization for mechanical design of automobile parts [9]. Size and shape optimization were demonstrated incapable of solving topology problems for either discrete or continuous structures [10]. A limitation of shape optimization is having domains with free boundaries, whereas topology optimization sets a range of possible material alternatives and chooses the optimal material alternative for given constraints and conditions. The topology optimization must be formulated correctly to ensure that the problem is not ill posed [10].

Homogenization theory achieved a breakthrough for simulation of composite structures. It enables deriving macro field equations from micro field equations. Sanchez-Palencia examined wave propagation in heterogeneous media using homogenization theory [11]. Keller studied the flux through a porous media using techniques in homogenization [12]. Bakhvalov and Panasenko introduced some of the first numerical techniques for solving the homogenization equations [13]. De Kruijf et al. [14] presented an optimization algorithm for material design in two dimensions while considering multiple objectives. The optimization algorithm was formulated as a minimization problem that was subject to volume and symmetry constraints. A Pareto front of optimal solutions was obtained by using the multi-objective weighted sum method to address both stiffness and thermal conductivity criteria [14]. Guedes and Kikuchi introduced an adaptive finite element technique for elasticity representation in homogenization of composites [15].

The accurate simulation of explosive dynamic behavior is necessary when optimizing composite laminates for blast resistance. A blast event is an event where a considerable amount of energy is released over an extremely short time period. A pressure wave represents the layer of compressed air that travels in front of the hot gases that are created during the reaction. This wave contains most of the energy released during the explosion. The time history of the blast wave is described by the positive and negative pressure impulses and the magnitude of the value of the peak overpressure [16]. The simulation of blast events is extremely complicated and requires a detailed knowledge of the pressure time history, structural transient response, fluid–structure interaction and structural behavior under high strain rates [17]. The multi-physics environment requires coupling of methods to realistically simulate the transfer of the pressure wave to the composite plate. Therefore, Computational Fluid dynamics (CFD) is suggested for simulating fluid–structure interaction during blast events [18].

The remainder of the paper is structured as follows: Methods used in this paper are explained in Section 2. A case study is demonstrated in Section 3, in which two materials, Aluminum and Titanium, are distributed in a varying microstructure of a two-layer composite plate. The layers are also assigned different thicknesses to obtain optimal blast resistance of the composite laminate. Section 4 focuses on results, followed by conclusions in Section 5.

2 Methods

2.1 Homogenization

The homogenization method is used to calculate the average constitutive parameters of a composite material. This is necessary for analysis of inhomogeneous material because the elasticity tensor E ijkl varies at the microscopic scale. This method may be applied to periodic composites in which the composite consists of a periodic unit cell that is repeated as shown in Fig. 1a. An assumption must be made in which the microstructure is much smaller than the part or structure that will be used in a particular application. We consider a periodic composite body as shown in Fig. 1a. The material behavior at the macroscopic scale is described by coordinate system X while the microscopic scale is defined by coordinate system Y. Using the homogenization method for elasticity one can consider:

Fig. 1
figure 1

Periodic composite and modeling of a discretized unit cell

Full size image
$$ Y = \left[ {0,Y1} \right],[0,Y2],[0,Y3]\;\quad \quad \left( {3 - D} \right) $$
(1)
$$ Y = \left[ {0,Y1} \right],[0,Y2]\quad \quad \quad \;\quad \quad \left( {2 - D} \right) $$
(2)

Y1 is the horizontal length, Y2 is the vertical length, and Y3 is the depth of the unit cell. For an inhomogeneous material the microscopic displacement u may asymptotically be expanded with relation to the base cell size η [19].

$$ u = {u^0}\left( {x,y} \right) + \eta \;{u^1}\left( {x,y} \right) + {\eta^2}\;{u^2}\left( {x,y} \right) + \cdots $$
(3)
$$ y = x/\eta $$
(4)

Considering Eq. (3), only the first order terms of the asymptotic expansion are used to calculate the strain fields. The strain field can be broken down into two different components when using only first order terms from Eq. (3) as follows:

$$ \varepsilon_{{ij}}^0 = 1/2\;\left( {{{{{{\delta u_i^0}} \left/ {{\delta x}} \right.}}_j} + {{{{{\delta u_j^0}} \left/ {{\delta x}} \right.}}_i}} \right) $$
(5)
$$ \varepsilon_{{ij}}^{*} = 1/2\;\left( {{{{{{\delta u_i^1}} \left/ {{\delta y}} \right.}}_j} + {{{{{\delta u_j^1}} \left/ {{\delta y}} \right.}}_i}} \right) $$
(6)

The overall microscopic strain field ε ij is therefore a combination of the of the strain field due to the average displacement over the unit cell ε 0 ij and the fluctuation strain ε * ij , which is due to the first order inhomogeneous nature of the composite unit cell [19]. The size of the unit cell η is allowed to go to zero. Then four linearly independent strain fields are applied to the unit cell in order to calculate the stiffness matrix for the composite. Four unit tensors are applied in 2-D and nine unit tensors are applied in 3-D. In 2-D the four unit tensors are ε 0(11) ij  = [1,0,0,0], ε 0(22) ij  = [0,1,0,0], ε 0(12) ij  = [0,0,1,0] and ε 0(21) ij  = [0,0,0,1]. The homogenized stiffness tensor may be written as:

$$E^{H}_{{ijkl}} = \frac{1}{Y}{\int\limits_Y {E_{{ijpq}} } }{\left( {\varepsilon ^{{0{\left( {kl} \right)}}}_{{pq}} - \varepsilon ^{{*{\left( {kl} \right)}}}_{{pq}} } \right)}dY$$
(7)

By applying these test strains along with the change in η to 0, the fluctuation strain is the solution to the following variation type problem.

$${\int\limits_Y {E_{{ijpq}} } }\varepsilon _{{ij}} {\left( \nu \right)}\varepsilon ^{{*{\left( {kl} \right)}}}_{{pq}} dY = {\int\limits_Y {E_{{ijpq}} } }\varepsilon _{{ijpq}} \varepsilon _{{ij}} {\left( \nu \right)}\varepsilon ^{{0{\left( {kl} \right)}}}_{{pq}} dY\forall \nu \in V$$
(8)

The four independent strain fields must be applied to Eq. (8) to calculate ε * ij . All ε * ij are then substituted into Eq. (7) to find all of the stiffness coefficients in the homogenized stiffness tensor E H ijkl . The stiffness matrix is symmetric such that E ijkl  = E jikl  = E ijlk  = E klij . This symmetry reduces the number of required test strain fields to 3 for 2-D and 6 for 3-D [19].

2.2 Blast Load Simulation Using CFD

CFD modeling may be used to realistically model the pressure wave generated due to a point explosion of conventional high explosive material. The model allows for the input of parameters such as burial of explosive material (if modeling underground generated blasts), height from surface or explosive material, radial distance from explosive charge as well as the TNT equivalent or weight in kilograms of explosive. CFD modeling typically integrates finite elements, finite difference and finite volume methods to model fluid dynamics. Due to the number of different material interactions, a Lagrangian frame of reference is used for solid modeling while an Eulerian frame of reference is used for modeling fluid dynamics [20].

2.3 Finite Element Simulation

The blast loading upon the composite plate is simulated using the finite element method. The Finite Element Analysis (FEA) method is used to discretize the plate into finite elements that are based upon the material properties of the given layers. The problem of interest requires a dynamic model to simulate the effects of a nonlinear blast wave due to high explosives upon the two-layer plate. A transient analysis is used to calculate the stresses and strains as a function of both position and time. The Newton–Raphson method is used to solve the nonlinear problem of the iterative transient analysis. The direct integration method is used to solve the equation of motion. At each step or sub-step, the equation of motion is integrated using Newmark method [21], then the groups of static equilibrium equations are solved simultaneously.

2.4 Multi-objective Genetic Optimization

Classical optimization approaches have always considered a single objective function while dealing with all other objectives as constraints. The fundamental difference between single-objective and multi-objective optimization is the ability of multi-objective optimization to avoid the artificial fixes needed for single-objective optimization methods to address trade-offs between different objectives. This is achieved by getting candidate designs to lie in the Pareto front, typically known as Pareto-optimal solutions [22].

Two categories of multi-objective optimization methods are identified in the literature [23]. The first category utilizes classical single objective optimization methods while reformulating the problem to address multi-objectives considering preferences [24]. Methods in the first category include techniques such as the weighted sum method, the ε-constraint method and the hierarchical optimization method [24]. The second category of multi-objective optimization methods establishes an optimization method that is multi-objective in nature. Rosenberg [25] suggests using genetic search to simulate the behavior of single celled organisms with multiple objectives. The multi-objective genetic algorithm (MOGA) allows for the formulation of multi-objective optimization problems without the need to specify weights on the various objective function values. This is achieved by considering the concept of non-dominant solutions (analogous to Pareto optimal solution) suggested by Deb [26]. MOGA directly identifies non-dominated design points that lie on the Pareto front. The advantage of the MOGA method over the conventional weighted-sum method, is that MOGA finds multiple points along the entire Pareto front whereas the weighted-sum method produces only a single point on the Pareto front. Moreover, MOGA is more capable of finding points on the Pareto front when the Pareto front is non-convex. However, the use of a genetic algorithm (GA) search method in MOGA causes the MOGA method to be much more computationally expensive than conventional derivative based multi-objective optimization algorithms. Srinivas and Deb [27] proposed non-dominated sorting genetic algorithms (NSGA). NSGA basically finds the non-dominated set of points (which constitute the first front) and gives them a large fitness value. This process continues until the entire population is classified into several domination fronts by giving smaller fitness values for the new fronts. Multiple techniques have been suggested to reduce computational time by considering rules to preserve diversity and keep the elite [28, 29]. MOGA has been successfully applied to many problems including topology optimization [30, 31].

3 Case Study

The case study considers the design of blast resistant two-layer composite plate in which two materials, Aluminum and Titanium, are distributed in each layer. The mechanical properties of Aluminum include yield strength (55 MPa), ultimate tensile strength (115 MPa), density (2,700 kg/m3), Young’s modulus of Elasticity (70 GPa) and Poisson’s ratio (0.33). For Titanium, its properties include yield strength (170 MPa), ultimate tensile strength (234 MPa), density (4,500 kg/m3), Young’s modulus of Elasticity (116 GPa) and Poisson’s ratio (0.34). The composite plate is a two-layer cylindrical plate with a 250 mm radius and a thickness that can range between 10 and 30 mm per layer. The plate is subjected to an under soil buried explosive.

3.1 Homogenization Method Applied to the Two-layer Composite

The process of determining the properties for a given layer of the composite for a single iteration is discussed here. This process is repeated for all iterations during the optimization procedure. A unit cell of the composite material is used for determining the properties of each layer. The unit cell is discretized into 3 × 3 sub cells as shown in Fig. 1b. The unit cell consists of 9 total elements. Each of the elements is then assigned either the material properties of Aluminum or Titanium. Since this is a 2-D problem, only three independent unit strain fields need to be applied to the model in order to extract the material properties. The three strain fields are shown in Fig. 2. There are a total of 16 nodes in each unit cell model. After the displacements are applied, the FEA model is solved for the unknown stresses at all nodal locations. The homogenization method allows for the calculation of the averaged properties of the unit cell. The four independent components of the stiffness matrix can be calculated as:

Fig. 2
figure 2

Three load cases showing unit strain in (a) radial direction, (b) y direction and (c) shear

Full size image
$$ {S_{{11}}} = \frac{1}{{{E_1}}},{S_{{12}}} = \frac{{ - {\nu_{{12}}}}}{{{E_1}}},{S_{{22}}} = \frac{1}{{{E_2}}}\ and\ {S_{{66}}} = \frac{1}{{{G_{{12}}}}}\,{\text{given}}\,\left\{ {\matrix{{*{20}{c}} {{\varepsilon_1}} \\ {{\varepsilon_2}} \\ {{\gamma_{{12}}}} \\ } } \right\} = \left[ {\matrix{{*{20}{c}} {{S_{{11}}}} & {{S_{{12}}}} & 0 \\ {{S_{{12}}}} & {{S_{{22}}}} & 0 \\ 0 & 0 & {{S_{{66}}}} \\ } } \right]\left\{ {\matrix{{*{20}{c}} {{\sigma_1}} \\ {{\sigma_2}} \\ {{\tau_{{12}}}} \\ } } \right\} $$
(9)

Then the stresses are summed for each direction and divided by the number of total nodes. This new stress value represents the average stress for the homogenized unit cell. The homogenized properties of the unit cell are then calculated as:

$$ \nu = \frac{{{\sigma_{{11}}}{\sigma_{{12}}}}}{{\left( {{\sigma_{{11}}}{\sigma_{{22}}} + {\sigma_{{12}}}\left( {{\sigma_{{12}}} - {\sigma_{{21}}}} \right)} \right)}},{E_1} = \frac{{{\sigma_{{11}}}\left( {{\sigma_{{11}}}{\sigma_{{22}}} - {\sigma_{{12}}}{\sigma_{{21}}}} \right)}}{{\left( {{\sigma_{{11}}}{\sigma_{{22}}} + {\sigma_{{12}}}\left( {{\sigma_{{12}}} - {\sigma_{{21}}}} \right)} \right)}},{E_2} = \frac{{\left( {{\sigma_{{11}}}{\sigma_{{22}}} - {\sigma_{{12}}}{\sigma_{{21}}}} \right)}}{{{\sigma_{{11}}}}},{G_{{12}}} = {\tau_{{123}}} $$
(10)

Where the subscript numbers on the left hand side of Eq. (10) represent the modulus direction, the subscript numbers on the average stress values (σij) represent the load case number and the stress direction respectively and τ123 is the average shear stress from load case 3.

3.2 CFD Model

CFD allows for modeling of the transient solid and fluid interactions. The model consists of 2 kg of TNT that is detonated at a location 150 mm below the soil surface. The explosion is simulated and the pressure transfer to the composite plate is monitored for 1 ms. The composite plate is centered above the explosive material at a height of 260 mm above the soil surface as shown in Fig. 3. The model is simulated in a 2-D plane in which quadrilateral elements are used for discretizing the simulation space. ANSYS-AUTODYN was used to simulate the pressure wave generated by the high explosive material [32]. Five materials were used in the simulation process: air, sand, TNT, Aluminum and Titanium. The gas dynamics are calculated using the Euler algorithm, while the solid dynamics are simulated with the Lagrangian algorithm [32]. The air was simulated as an ideal gas. The Jones-Wilkins-Lee equation of state is used to simulate the explosion of the TNT [32]. The time history of the pressure wave was recorded by placing gauges along the lower surface of the composite plate where the blast will first impact the composite plate. The pressure of the blast wave was then used in modeling the transient structural behavior of the plate in finite element analysis. The gauges were placed every 25 mm along the surface of the plate.

Fig. 3
figure 3

Mesh of CFD model showing buried TNT and composite plate

Full size image

3.3 FEA Model

The FEA model is simulated using ANSYS. The composite plate was modeled as a 2-D axisymmetric model using transient analysis. As discussed above, the homogenization method was used to determine the properties of the composite plate. The properties used by the FEA model are the modulus of elasticity in the radial direction, the modulus of elasticity in the y direction, Poisson’s ratio and the shear modulus. The density of the layers is calculated using the rule of mixtures method. The thickness of each layer of the composite plate is a design variable. This necessitates the use of an automatic meshing routine in the FEA. Eight node Plane 82 elements are used for meshing the two-layer composite plate. Plane 82 elements have two degrees of freedom per node and have the capability to simulate plasticity, creep, stress stiffening, large displacement and large strain. A zero y displacement boundary condition is forced upon the upper right node to restrain the model. This is the equivalent boundary condition to constraining a 3-D cylinder from moving in the y direction along its circumference. A 3-D expansion of the 2-D mesh is shown in Fig. 4a. At each load step in the FEA, a specific load profile output from the CFD simulation is applied to the bottom layer of the composite plate. The load profile shown in Fig. 4b is an example of a specific profile used at a given time for analysis. It may also be observed that location of maximum pressure does not occur at the center of the plate, nor is the blast wave uniform. The FEA solution is obtained using the Newton–Raphson method. For each time step, the stress distribution in both layers of the composite plate is saved for post processing.

Fig. 4
figure 4

a Finite element model showing the two-layer composite plate considered in the case study with ¼ removed for clarity and b pressure distribution at t = 0.35 ms

Full size image

3.4 MOGA

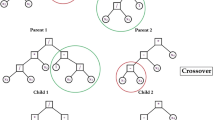
NSGA was used with the steps shown schematically in Fig. 5. A population size of 50 is selected and generated randomly without duplicates. Binary representation is used. For crossover and mutation, design variables are selected randomly from two parents to produce two children. Crossover rate is selected as 0.8, while mutation rate is selected as 0.1. Domination-based fitness assessment is used to force the algorithm to move towards the non-dominated frontier. All non-dominated designs are assigned a layer of 0, then from what remains, all the non-dominated ones are assigned a layer of 1, and so on until all designs have been assigned a layer. Then, these values are negated for the higher-is-better fitness convention. For replacement elitist strategy is used where most fit members are selected and the rest are discarded.

Fig. 5
figure 5

Flowchart showing optimization method and its integration with the blast simulation

Full size image

Niche pressure is applied to prevent the algorithm from converging to a single solution. The solutions that are too close to the current design are removed except the ones that are defined as the maximal or minimal in all but one objective dimension. A distance of 0.01 and 0.1 for stress-to-strength ratio and weight, respectively, are selected. Test for convergence includes the tests for how the expanse of the front is changing, density of the non-dominated front and goodness of the non-dominated front. The maximum number of function evaluations is set to 100.

Two objective functions representing the maximum stress-to-strength ratio and the weight of the composite denoted as f 1 and f 2 are defined as:

$$ {f_1} = {\max{_{1 \leqslant \,m\, \leqslant \,n}}}\left\{ {\frac{{\max \left( {\sigma_m^T} \right)}}{{\sigma_m^{{UT}}}},\frac{{\max \left( {\sigma_m^C} \right)}}{{\sigma_m^{{UC}}}}} \right\}\,\\\ \&\ \ {f_2} = \sum\limits_{{m = 1}}^N {\pi \;{r^2}\;{T_m}\;{\rho_m}} $$
(11)

In this formulation, f 1 is the maximum stress-to-strength ratio in all individual layers and f 2 is the weight of the composite. N is the total number of layers in the composite; \( \max \left( {\sigma_m^T} \right) \) is the maximum tensile stress observed in the m th layer due to the applied stress wave; \( \sigma_m^{{UT}} \)is the ultimate tensile strength of the m th layer; \( \max \left( {\sigma_m^C} \right) \) is the maximum compressive stress observed in the m th layer due to the applied stress wave; \( \sigma_m^{{UC}} \)is the ultimate compressive strength of the m th layer. r is the radius of the composite plate, T m is the thickness of the m th layer and ρ m is the density of the m th layer calculated using the rule of mixtures based on the unit cell of that layer. The optimization problem is formulated as a multi-objective nonlinear optimization that targets to minimize the maximum stress-to-strength ratio and to minimize weight of the composite while meeting the bounds for layer thicknesses as follows:

$$ {\text{Minimize}}\quad {f_1},{f_2}\ \ {\text{Subject}}\ {\text{to}}\quad T_m^{{\min }} \leqslant {T_m} \leqslant T_m^{{\max }}\quad \quad 1 \leqslant m \leqslant N $$
(12)

For our case study, we have a two-layer (N = 2) axisymmetric composite plate with r = 250 mm. The thicknesses of each layer in the model may vary between \( T_m^{{\min }} = 10\;mm \) and \( T_m^{{\max }} = 30\;mm \). The layers are given elastic properties that vary between 116 GPa for Titanium and 70 GPa for Aluminum. These bounds are the extreme limits of the design space for a given layer.

There are a total of 20 design variables, 18 of which are the elastic properties and 2 of the design variables are the thickness of each layer. In the optimization process the vector of design variables (DV) is passed by the optimization environment to the simulation algorithm to compute the objective function values: maximum stress-to-strength ratio overall layers and the weight of the composite plate. The optimization finishes when the stopping criteria is met and the final design variables are then saved.

4 Results and Discussions

The optimization process allowed identifying Pareto-optimal solutions for the material microstructures across the two layers to minimize the stress-to-strength ratio and weight. The MOGA method produced a Pareto front in which each Pareto point represents a microstructure for layer 1 with thickness 1 and a microstructure for layer 2 with thickness 2. The results of the MOGA optimization are presented in Fig. 6 and in Table 1. Figure 6 shows microstructure and thickness of each layer for four example solutions along the Pareto front. The black represents the Titanium phase and the white represents the Aluminum phase. Each of the points shown in Fig. 6 represents an optimal solution. Table 1 presents ten solutions some of which are labeled along the Pareto front.

Fig. 6
figure 6

Pareto front for weight and stress-to-strength ratio as two objective functions with different material microstructures and thicknesses per layer

Full size image
Table 1 Summary of results presenting ten Pareto solutions
Full size table

As it can be observed from Fig. 6, the solutions with lower stress-to-strength ratios such as point 1 have the highest overall composite weight. On the other hand, solutions like point 9 have a low composite weight but a relatively high stress-to-strength ratio. Any composite structures that exhibited stress-to-strength ratios above 1.0 are excluded. Those solutions with stress-to-strength ratios below 1.0 are all viable solutions and should have a good blast resistance. It may also be observed from Fig. 6 that the amount of Titanium used in the composite is greatly reduced when moving from low stress-to-strength ratios to high ones approaching 1.0 with a relatively low weight. This is important because Titanium is a much heavier metal and more expensive to process than Aluminum. By considering other constraints such as cost, a solution may be chosen from any of those solutions on the Pareto front. It is obvious from Fig. 6 and Table 1 that changes in the material’s microstructure as well as the two layers’ thicknesses allow for changing the stiffness distribution across the composite plate and therefore producing stresses in the composite lower than the material strength of each layer. Some of the non-dominated solutions produced stress-to-strength ratios around 0.6 while reducing the overall weight to close to 60% of the maximum possible weight using only titanium in each layer. The overall stress was reduced even further by allowing the thickness to change between 10 and 30 mm per layer.

A unit cell of 3 × 3 for each layer was chosen for the simulation environment because discretizing the solution space increases the number of required calculations exponentially. Using MOGA, 1,000 evaluations resulted in 67 solutions. 16 of these solutions were infeasible because they yielded a stress-to-strength ratio greater than 1.0. For the 3 × 3 case 1,000 evaluations is only about 0.38% of the total solution space. In order to cover 0.38% of the 4 × 4 case would require 16,384,000 evaluations. Currently, the run time is 43.7 h, while increasing the unit cell to 4 × 4 would require 7.16 e5 hours. The exponential growth of the solution space and run time is the reason why the 3 × 3 arrangement is the smallest microstructure that will yield useful information regarding the composite layup, while being able to solve in a reasonable amount of time. Unless a parallel computing approach is considered, which can significantly reduce the computational time, a 3 × 3 microstructure is the most suitable formulation of the problem. Further work is underway to re-formulate the optimization algorithm considering parallel computing capabilities.

Although gradient based methods may require less computational time, a decision was made to use MOGA based on our preliminary investigation. By using MOGA for the multi-objective optimization, artificial fixes were avoided. Moreover, using the binary encoding, artificial filters were avoided, which would normally be required if gradient based optimization was used. Based on the weights chosen and the seeding point the gradient based optimization methods might converge to a very good solution. However, given the ability of MOGA to converge independent of the types of weights chosen and the seeding point, it clearly surpasses gradient based methods for the problem considered in this paper. Moreover, another advantage of the MOGA method is that it finds multiple points along the entire Pareto front whereas the weighted-sum method or other conventional methods would produce only a single point on the Pareto front.

A major limitation of the above work is its use of implicit method to model the transfer of the blast wave to the composite plate. Future work will include an explicit blast model that is used to simulate the blast process every time the material properties of the layers are changed. This will increase the accuracy of the optimization results while yielding a more realistic blast simulation problem. Explicit blast modeling is necessary because when a blast wave encounters a solid object the pressure is transferred to the object surface and causes the object to deform based on the stiffness of the material. This means that the stiffness of the plate affects the magnitude and shape of the pressure transfer. Currently, the pressure transfer is assumed to be the same for all microstructures. As the pressure transfer changes, the stress distribution will simultaneously change requiring a different optimal microstructure than when assuming the same pressure wave. The blast model may also be modified to account for different soil properties, which might alter the blast pressure. Finally, composite plate optimization can be extended to incorporate probabilistic definition of safety using reliability theory [30].

5 Conclusions

The fundamental problem of design optimization of a two-layer blast resistant composite plate is examined. A composite plate subjected to a non-uniform blast load is considered. CFD is used to obtain spatial and temporal distributions of the blast load. FEA is used to calculate the stress evolution in the plate due to the blast load. The design optimization process was performed where both material microstructure and thickness were concurrently optimized. A multi-objective genetic algorithm optimization method is developed and used. A case study of a two-layer axisymmetric Aluminum and Titanium composite plate subjected to blast is discussed. The results show that several microstructures and thickness alternatives can be used. It is demonstrated that the use of the homogenization method can provide design alternatives for blast resistant composites that are not available using classical design methods.