1 Introduction

Explicit cracks simulation is nowadays one of the most challenging tasks in computational fracture mechanics, especially for three-dimensional composite structures. Even in two-dimensional structures, the presence of multiple cracks could be a weighty task to perform. Moreover methods based on classical fracture mechanics are not always able to explain the physical process of initiation. Therefore, methods that rely just on the physics of the problem rather than only the geometry of the fracture would be in this perspective highly desirable. The main tasks in simulations of cracks are initiation and propagation. The first one is usually based on the strength of materials theory and employs stress criteria normally based on point or average stress, while propagation is modeled with fracture mechanics tools based on the evaluation of the energy release rate G.

Cohesive models are based on the Dudgale–Barenblatt [1] cohesive zone approach, subsequently extended by Hillerborg [2] and Needleman [3], which gives a physical explanations of the failure process, whereas classical fracture mechanics lacks of a physics-based description [4].

In the cohesive zone model, it is postulated the existence of a narrow band of vanishing thickness ahead of a crack tip which represents the fracture process zone. The bonding of the surfaces of the zone is obtained by cohesive traction, which follows a cohesive constitutive law. Many different constitutive laws exist, for example the exponential or the bilinear softening model. These laws are typically regulated by both strength of material parameters (like the tensile strength) and fracture mechanics based parameters like the critical fracture energies for the considered fracture mode. Crack growth occurs when a critical value is reached at which cohesive traction disappears.

Conversely to classical fracture mechanics, the cohesive zone modeling approach does not involve crack tip stress singularities and failure is regulated by relative displacements and stresses.

Standard finite elements have the major disadvantage that crack path is highly dependent on the mesh structure, since discontinuities must follow inter-element boundaries, therefore capturing of a propagating discontinuity is achieved by constant re-meshing of the structure. This procedure is costly not to mention the degradation of the accuracy of the solution.

An important progress in this sense has been recently obtained with the introduction of partition of unity-based methods (PUM) [5] like extended finite element (XFEM) [6–9] and meshless methods like Element-Free Galerkin [10] or Reproducing Kernel Particle Method (RKPM) [11].

In the papers of [12] and [13], a new method called cohesive segments method is introduced.

In [12] the PUM idea is applied in the context of cohesive cracks. A full non-linear model is developed, with tractions acting on the cohesive surfaces. These tractions are depending on the opening displacement (or discontinuous displacement) and used to model crack propagation in three-points bending test and single edge notched beam.

In [13] these segments are introduced under a FE framework, similarly to the Extended Finite Element Method (XFEM). Using a particular instance of a PUM , a continuous crack is approximated by a set of segments, each one of them split the domain in two parts. At each of these interfaces, a cohesive model is used in order to simulate the debonding of the parts. It can be shown that by doing so, the total displacement is enriched by a sum of Heaviside functions that can effectively represent the discontinuity. In this way, additional unknowns are introduced to the final algebraic system of equations. These segments can be introduced at any time of the calculation, whenever a stress-based failure criteria is satisfied, and the orientation of the onset cohesive segment is given by the principal direction of the stress. In this way, no explicit representation of the crack surface is needed allowing to model arbitrary crack growth, which is extremely useful when the crack propagation path is not known a priori. The drawback of this method is that additional unknowns are introduced at each crack segment. The unknowns are localized to the nodes of the elements cut by the discontinuity.

In [14] the same approach is used to efficiently simulate dynamic crack propagation.

A first application of the cohesive segments combined with meshless methods rather than FE, can be found in [15].

When the crack path is known a priori, like in the case of single mode delamination, the same approach can be used without adding additional unknowns. In this case, the domain can be decomposed in two parts connected by a penalty parameter, as also suggested in [16] and the cohesive segments are located at the edges of the subdomains.

The variational problem is formulated for each sub-domain, then a coupling term between their displacements is introduced. The coupling term derives from the application of the cohesive model at the separation, resulting in a final nonlinear set of equations that must be solved iteratively.

The coupling term is nothing else than a penalty factor defined on the whole contact segment. Penalty terms are well-known in the meshfree community since, conversely to FE, the shape functions do not posses the Kronecker condition [17]. This condition allows in FE to directly impose essential boundary conditions on the nodes located on the constrained boundaries. For simple constraints, though, a constant penalty factor is sufficient throughout the whole boundary. The same approach can be used to connect or disconnect two or more objects.

2 Equations of Equilibrium

Assuming that there are no body or inertia forces, the strong form of the equilibrium equations along with the boundary conditions can be written as

$$ \nabla \cdot \mathbf{\sigma} = 0 \qquad {\mathbf{x}} \in \Omega \label{strong_diffeq} \\[-2pt] $$
(1)
$$ \mathbf{n}_t \cdot \mathbf{\sigma} = \bar{\mathbf{t}} \qquad {\mathbf{x}} \in \Gamma_t \label{strong_nat_BC}\\[-2pt] $$
(2)
$$ \mathbf{u} = \bar{\mathbf{u}} \qquad {\mathbf{x}} \in \Gamma_u \label{strong_ess_BC} \\[-2pt] $$
(3)
$$ \label{strong_contact} \mathbf{n}_c \cdot \mathbf{\sigma} = {\tau}(\mathbf{v}) \qquad {\mathbf{x}} \in \Gamma_c $$
(4)

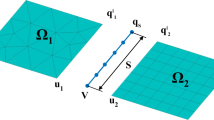
where Ω is the entire domain, σ is the Cauchy stress tensor, n t is the normal unity vector of the boundary Γ t where the traction \(\bar{\mathbf{t}}\) is prescribed, n c is the normal unity vector of the boundary Γ c where the traction τ(v) is prescribed and Γ u is the boundary where the displacement \(\bar{\mathbf{u}}\) is imposed.

The traction τ depends on the displacement jump v on the cohesive segment Γ c , which divides Ω in two sub-domains Ω1 and Ω2 as in Fig. 1. The displacement jump v( x) is defined as follows

$$ \label{displ_jump} \mathbf{v}({\mathbf{x}}) = \mathbf{u}_1({\mathbf{x}})-\mathbf{u}_2({\mathbf{x}}) \qquad {\mathbf{x}} \in \Gamma_c $$
(5)

where u 1(x) is the displacement of sub-domain Ω1 and u 2(x) is the displacement of sub-domain Ω2.

Fig. 1
figure 1

Description of the problem

Full size image

Using displacement u as test function for Eqs. 1, 2 and displacement jump v as test function for Eq. 4, the variational principle can be written as

$$\begin{array}{lll}\label{weak_form} &&{\kern-6pt} \int_{\Omega_1} \delta {\varepsilon}^T\mathbf{\sigma} d\Omega_1 + \int_{\Omega_2} \delta {\varepsilon}^T\mathbf{\sigma} d\Omega_2 - \int_{\Gamma_{t1}}\delta\mathbf{u}^T\bar{\mathbf{t}} d\Gamma_{t1} - \int_{\Gamma_{t2}}\delta\mathbf{u}^T\bar{\mathbf{t}} d\Gamma_{t2} \\ && +\, \frac{\alpha}{2} \delta \int_{\Gamma_{u1}}\big(\mathbf{u}-\bar{\mathbf{u}}\big)^2 d\Gamma_{u1} + \frac{\alpha}{2} \delta \int_{\Gamma_{u2}}\big(\mathbf{u}-\bar{\mathbf{u}}\big)^2 d\Gamma_{u2} + \int_{\Gamma_c} \delta \mathbf{v}^T{\tau} d\Gamma_c = 0 \end{array} $$
(6)

where the penalty method is used to enforce essential boundary conditions (Eq. 3) and α is called penalty parameter, which is usually a very large number. In all the computations, an arbitrarily large value of the penalty factor of 1e15 has been used. If the penalty factor is too low, then constraints are not imposed efficiently, leading to inexact results, while a penalty factor too high can lead to undesired instabilities during the numerical solution.

Varying this number it is possible to loosen or tighten a certain constraint. This will be useful in the next sections with the application of the cohesive model at the crack interface Γ c . In Eq. 6 Γ t1 and Γ u1 refer to the part of boundaries Γ u and Γ t that belong to sub-domain Ω1, whereas Γ t2 and Γ u2 the ones that belong to Ω2.

3 Reproducing Kernel Particle Method

A brief review of the construction of Reproducing Kernel Particle Method (RKPM) shape functions is reported in this section. For further details please refer to [17] and [18].

In meshfree methods, the shape functions are derived only by relying on nodes rather than elements, as in FE. Therefore, in theory, no mesh is needed to construct the shape functions.

The approximation u h(x) of a generic function u(x) can be written as

$$\label{approx} u^h(\mathbf{x}) = \sum\limits_{I=1}^N \phi_I(\mathbf{x})U_I $$
(7)

where φ I :Ω→ℝ are the shape functions (Fig. 2) and U I is the i-th nodal value located at the position x I where I = 1, ..., N where N is the total number of nodes.

Fig. 2
figure 2

One-dimensional shape functions in RKPM

Full size image

The I-th shape function is given in RKPM by the formula

$$\label{RKPMshape} \phi_I(\mathbf{x}) = C_I(\mathbf{x}) w\left(\frac{\mathbf{x}_I-\mathbf{x}}{\rho}\right) \Delta V_I $$
(8)

where C(x) is a corrective term that restore the shape function capability of reproducing all the terms contained in the basis function p(x). For polynomial basis, for example

$$\label{1Dbasis} \mathbf{p}^T(x) = \big(1,x,x^2,\ldots,x^n\big) $$
(9)

in 1D case or

$$\label{2dbasis} \mathbf{p}^T(\mathbf{x}) = \big(1,x,y,x^2,xy,y^2\big) $$
(10)

in 2D case. The corrective term C(x) is

$$\label{RKPMcorr} \underbrace{C_I(\mathbf{x})}_{1 \text{x} 1} = \underbrace{\mathbf{p}^T(\mathbf{0})}_{1 \text{x} k}\underbrace{\mathbf{M}(\mathbf{x})^{-1}}_{k \text{x} k}\underbrace{\mathbf{p}^T \left(\frac{\mathbf{x}_I-\mathbf{x}}{\rho}\right) }_{k \text{x} 1} $$
(11)

where k is the number of functions in the basis. Note that the corrective term is normally evaluated in a scaled and translated version to prevent ill-conditioning of the moment matrix M(x)

$$\label{rkpmomentsmatrixsctr} \mathbf{M}(\mathbf{x}) = \sum\limits_{I=1}^N \mathbf{p}\left( \frac{\mathbf{x}_I-\mathbf{x}}{\rho}\right) \mathbf{p}^T \left(\frac{\mathbf{x}_I-\mathbf{x}}{\rho}\right) w\left(\frac{\mathbf{x}_I-\mathbf{x}}{\rho}\right) \Delta V_I $$
(12)

The function w(x) is called kernel function having compact support, which means that they are zero outside and on the boundary of a ball ω I centered in x I . The radius of this support is given by a parameter called dilatation parameter or smoothing length which can be found indicated in literature as ρ or d I or a to avoid confusion with the mass density. According to the norm considered, the shape of the support may vary, for example could be a circle but also a rectangle. The fact of being compact basically guarantees that the stiffness matrix in a Galerkin formulation is sparse and band, which is particularly useful for the computer algorithms of storage and matrix inversion. Examples of kernel functions are the 3rd order spline

$$\label{cubicspline} w({\xi}) = \begin{cases} \dfrac{2}{3} - 4{\xi}^2 + 4{\xi}^3 & \qquad 0\leq {\xi} \leq \dfrac{1}{2} \\[6pt] \dfrac{4}{3} - 4{\xi} + 4{\xi}^2 - \dfrac{4}{3}{\xi}^3 & \qquad \dfrac{1}{2}< {\xi} \leq 1 \\[6pt] 0 & \qquad {\xi}>1 \end{cases} $$
(13)

which is C 2 or more generally the 2k-th order spline (Fig. 3)

$$\label{2kthspline} w({\xi}) = \begin{cases} \big(1-{\xi}^2\big)^k & \qquad 0\leq {\xi} \leq 1 \\ 0 & \qquad {\xi}>1 \end{cases} $$
(14)

which is C k − 1.

Fig. 3
figure 3

Example of kernel: 2k − th order spline for different k

Full size image

The order of continuity of a kernel function is important because it influences the order of continuity of the shape functions.

Equation 8 derives from a numerical discretization of an integral, therefore the term ΔV I is some measure (i.e. length, area or volume) of ω I . It has been reported in [17] that choosing ΔV I  ≠ 1 has no effects on the evaluation of the shape functions. It could be shown that choosing ΔV I  = 1 leads to another type of approximation known as Moving Least Squares (MLS), which is a quite popular choice of shape functions in other meshless methods like, for example, the EFG method. Since RKPM is substantially a least squares method, shape functions do not satisfy the Kronecker condition,

$$\label{kronecker} \mathbf{\phi}_I\big(\mathbf{x}_J\big) \neq \delta_{IJ}\qquad \forall I,J=1\ldots N $$
(15)

This means that essential boundary conditions cannot directly being imposed on the nodes. Thus, a penalty method is needed for enforcing boundary conditions on displacements.

4 Cohesive Law

As mentioned in Section 1, a cohesive model is implemented as a stress–displacement relationship τ(v), where τ is the traction at Γ c and v(x) is the displacement jumps defined in Eq. 5.

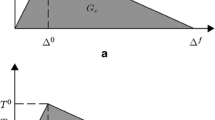
The bilinear stress relative displacement curve is divided into three main parts (Fig. 4) and the constitutive equations are the following:

  • v ≤ v0: elastic part: traction across the interface increases until it reaches a maximum, and the stress is linked to the relative displacement via the interface stiffness K0 :

    $$\label{tau_linear} \tau(v) = K_0 v $$
    (16)

  • v0 < v ≤ v F : softening part: the traction across the interface decreases until it becomes equal to zero: the two layers begin to separate. The damage accumulated at the interface is represented by a variable D, which is equal to zero when there is no damage and reaches 1 when the material is fully damaged:

    $$\label{tau_soft} \tau(v) = (1 - D(v))K_0 v $$
    (17)

  • v > v F : decohesion part: decohesion of the two layers is complete: there is no more bond between the two layers, the traction across the interface is null

The shaded area in Fig. 4 is the energy dissipated per unit area G for a particular mode, when v = v f the area of the whole triangle is the critical energy dissipated per unit area G c . It can be shown [19] that in this case cohesive zone approaches can be related to Griffiths theory of fracture. Moreover [20] showed that when v 0 = v f (which means abrupt load fall to zero) a perfectly brittle fracture can be simulated.

Fig. 4
figure 4

Bilinear softening model

Full size image

Two independent parameters are necessary to define a bilinear softening model, i.e. the interfacial maximum strength τ m and the critical energy dissipated per unit area G c , since the following relations hold

$$G_c = \frac{\tau_m v_f}{2} \label{frac_rel}\\ $$
(18)
$$\tau_m = K_0 v_0 \label{interf_strength} $$
(19)

where K 0 is an arbitrary initial penalty stiffness (dimensionally N/m 3) which is usually set as a large number. Then, once derived v 0 and v f , the variable damage D can be calculated as

$$ \label{damage_var} D(v) = \begin{cases} 0 & \qquad v \leq v_0 \\[6pt] \dfrac{v_f\big(v-v_0\big)}{v\big(v_f-v_0\big)} & \qquad \mbox{if} \ v_0 < v \leq v_F \\[6pt] 1 & \qquad v>v_F \end{cases} $$
(20)

5 Discretized Equations of Equilibrium

In general, for a two-dimensional case, (but similar argument can be conducted in the three-dimensional case), naming t the tangential direction the cohesive segment and n the normal direction, the stress–relative displacement relationship can be formulated as

$$\label{cohesive_law} {\tau} = \begin{bmatrix} \tau_t\\ \tau_n \end{bmatrix} = \begin{bmatrix} K_t\big(v_t\big) & 0 \\[3pt] 0 & K_n\big(v_t\big) \end{bmatrix} \begin{bmatrix} v_t \\ v_n \end{bmatrix} = \begin{bmatrix} \big(1-D_t\big(v_t\big)\big)K_{0t} & 0 \\[3pt] 0 & \big(1-D_n\big(v_n\big)\big)K_{0n} \end{bmatrix} \begin{bmatrix} v_t \\ v_n \end{bmatrix} $$
(21)

If a given loading mode has reached 1, the damage variable corresponding to the other loading mode is set to 1 as well to avoid that the material would still be able to carry tractions.

In this paper the only cohesive segment is located at the mid-plane, so t corresponds to axis x and n to axis y. For arbitrary orientations, a transformation matrix would be necessary to express displacements from the global reference frame to the local one.

Displacement jump in Eq. 5 can be then expressed as

$$\label{displ_jump_shape} \mathbf{v} = \begin{bmatrix} v_x \\ v_y \end{bmatrix} = \begin{bmatrix} \mathbf{\phi}_{1c}^T \mathbf{U}_1 - \mathbf{\phi}_{2c}^T \mathbf{U}_2 \\[3pt] \mathbf{\phi}_{1c}^T \mathbf{V}_1 - \mathbf{\phi}_{2c}^T \mathbf{V}_2 \end{bmatrix} = \begin{bmatrix} \mathbf{\phi}_{1c}^T & 0 & -\mathbf{\phi}_{2c}^T & 0 \\[3pt] 0 & \mathbf{\phi}_{1c}^T & 0 & -\mathbf{\phi}_{2c}^T \end{bmatrix} \begin{bmatrix} \mathbf{U}_1 \\ \mathbf{V}_1 \\ \mathbf{U}_2 \\ \mathbf{V}_2 \end{bmatrix} = {\tilde{\mathbf{\phi}}}^T {\mathbf{R}} $$
(22)

where

$$\label{phi1c} \mathbf{\phi}_{1c} = \mathbf{\phi}_1({\mathbf{x}}) \qquad {\mathbf{x}} \in \Gamma_c $$
(23)

where φ 1(x) are the shape functions of sub-domain Ω1, whereas

$$\label{phi2c} \mathbf{\phi}_{2c} = \mathbf{\phi}_2({\mathbf{x}}) \qquad {\mathbf{x}} \in \Gamma_c $$
(24)

are the shape functions belonging to sub-domain Ω2

$$\label{phitilde} {\tilde{\mathbf{\phi}}}^T = \begin{bmatrix} \mathbf{\phi}_{1c}^T & 0 & -\mathbf{\phi}_{2c}^T & 0 \\[3pt] 0 & \mathbf{\phi}_{1c}^T & 0 & -\mathbf{\phi}_{2c}^T\\ \end{bmatrix} $$
(25)

and \({\mathbf{R}}_1^T = \begin{bmatrix} \mathbf{U}_1^{ T}\;\; \mathbf{V}_1^{ T} \end{bmatrix}\) is the displacement vector for nodes located in Ω1 whereas \({\mathbf{R}}_2^T = \begin{bmatrix} \mathbf{U}_2^{ T} \;\; \mathbf{V}_2^{ T} \\ \end{bmatrix}\) is the displacement vector for nodes located in Ω2 and \({\mathbf{R}}^{T} = \begin{bmatrix} {\mathbf{R}}_1^{ T} \;\;{\mathbf{R}}_2^{ T} \end{bmatrix}\) is the total displacement vector. Substituting Eqs. 7 and 22 in the variational principle 6

$$\begin{array}{lll}\label{var_pri} &&{\kern-6pt} \delta {\mathbf{R}}_1^T \mathbf{K}_1 {\mathbf{R}}_1 + \delta {\mathbf{R}}_2^T \mathbf{K}_2 {\mathbf{R}}_2 - \delta {\mathbf{R}}_1^T \mathbf{F}_{1t} - \delta {\mathbf{R}}_2^T \mathbf{F}_{2t} + \alpha \delta {\mathbf{R}}_1^T \mathbf{V}_1 {\mathbf{R}}_1 - \alpha \delta {\mathbf{R}}_1^T \mathbf{F}_{1u} +\alpha \delta {\mathbf{R}}_2^T \mathbf{V}_2 {\mathbf{R}}_2 \\ && -\, \alpha \delta {\mathbf{R}}_2^T \mathbf{F}_{2u} + \delta {\mathbf{R}}_1^T \big(\mathbf{K}_{11}^{\delta} {\mathbf{R}}_1 - \mathbf{K}_{12}^{\delta} {\mathbf{R}}_2\big) + \delta {\mathbf{R}}_2^T \big(-\mathbf{K}_{12}^{\delta} {\mathbf{R}}_1 + \mathbf{K}_{22}^{\delta} {\mathbf{R}}_1\big) = 0 \end{array} $$
(26)

where

$$\label{Ki} \mathbf{K}_i = \int_{\Omega_i} \mathbf{B}\mathbf{D}\mathbf{B}^T d \Omega_i \qquad i=1,2 $$
(27)

where D is the stress–strain relationship matrix, B is the differential strain operator matrix

$$\label{Vinc1} \mathbf{V}_i = \int_{\Gamma_{ui}} \mathbf{\phi} \mathbf{\phi}^T d \Gamma_{ui} \qquad i=1,2 $$
(28)
$$\label{forces2displ} \mathbf{F}_{iu} = \int_{\Gamma_{ui}} \mathbf{\phi}\bar{\mathbf{u}} d \Gamma_{ui} \qquad i=1,2 $$
(29)
$$\label{forces2} \mathbf{F}_{it} = \int_{\Gamma_{ti}} \mathbf{\phi}\bar{\mathbf{t}} d \Gamma_{ti} \qquad i=1,2 $$
(30)
$$\label{K11d} \mathbf{K}_{11}^{\delta} = \begin{bmatrix} \mathbf{K}_{11}^{\delta u } & 0 \\ 0 & \mathbf{K}_{11}^{\delta v } \end{bmatrix} $$
(31)
$$\label{K12d} \mathbf{K}_{12}^{\delta} = \begin{bmatrix} \mathbf{K}_{12}^{\delta u } & 0 \\ 0 & \mathbf{K}_{12}^{\delta v } \end{bmatrix} $$
(32)
$$\label{K22d} \mathbf{K}_{22}^{\delta} = \begin{bmatrix} \mathbf{K}_{22}^{\delta u } & 0 \\ 0 & \mathbf{K}_{22}^{\delta v } \end{bmatrix} $$
(33)

and

$$\label{Kijx} \mathbf{K}_{ij}^{\delta u} = \int_{\Gamma_c} \mathbf{\phi}_{ic} \ K_x\big(v_x\big) \ \mathbf{\phi}_{jc} d\Gamma_c \qquad i,j = 1,2 $$
(34)

and

$$\label{Kijy} \mathbf{K}_{ij}^{\delta v} = \int_{\Gamma_c} \mathbf{\phi}_{ic} \ K_y\big(v_y\big) \ \mathbf{\phi}_{jc} d\Gamma_c \qquad i,j = 1,2 $$
(35)

Finally the following nonlinear set of equations can be obtained

$$ \label{matrix_nonlinear_eq} \left[ \mathbf{K} + \alpha \mathbf{V} + \mathbf{K}^{\delta}({\mathbf{R}}) \right] {\mathbf{R}} - \mathbf{F} - \alpha \mathbf{F}_{\bar{u}} = \mathbf{f}({\mathbf{R}}) = 0 $$
(36)

where

$$\label{stiffness} \mathbf{K} = \begin{bmatrix} \mathbf{K}_1 & 0 \\ 0 & \mathbf{K}_2 \end{bmatrix} $$
(37)

and

$$\label{penalty_constr} \mathbf{V} = \begin{bmatrix} \mathbf{V}_1 & 0 \\ 0 & \mathbf{V}_2 \end{bmatrix} $$
(38)
$$\label{forces} \mathbf{F} = \begin{bmatrix} \mathbf{F}_{1t} \\ \mathbf{F}_{2t} \end{bmatrix} $$
(39)
$$\label{applied_displ} \mathbf{F}_{\bar{u}} = \begin{bmatrix} \mathbf{F}_{1u} \\ \mathbf{F}_{2u} \end{bmatrix} $$
(40)
$$\label{coupling} \mathbf{K}_{\delta} = \begin{bmatrix} \mathbf{K}_{11}^{\delta} & -\mathbf{K}_{12}^{\delta} \\[3pt] -\mathbf{K}_{12}^{\delta \ T} & \mathbf{K}_{22}^{\delta} \end{bmatrix} $$
(41)

Equation 36 must be solved iteratively. A commonly used scheme is the Newton–Rhapson method where the iteration n + 1 at a generic load step is obtained from iteration n by the formula

$$\label{Newton-Raps} {\mathbf{R}}^{(n+1)} = {\mathbf{R}}^{(n)}-\left(\mathbf{J}^{(n)}\right)^{-1} \mathbf{f}\big({\mathbf{R}}^{(n)}\big) $$
(42)

where

$$\label{jacobian} \mathbf{J} = \dfrac{\partial \mathbf{f}}{\partial \mathbf{R}} $$
(43)

In order to obtain the Jacobian matrix J, a linearization of Eq. 21 is needed.

$$\label{linearization} {\tau}^{(n+1)} = {\tau}^{(n)} + \dfrac{\partial {\tau}}{\partial \mathbf{\mathbf{v}}} \left( \mathbf{v}^{(n+1)}- \mathbf{v}^{(n)}\right) = {\tau}^{(n)} + \mathbf{T} \left( \mathbf{v}^{(n+1)}- \mathbf{v}^{(n)}\right) $$
(44)

where

$$\label{tangent_stiffness} \mathbf{T} = \dfrac{\partial {\tau}}{\partial \mathbf{v}} = \begin{bmatrix} \dfrac{\partial K_x}{\partial v_x} & 0 \\ 0 & \dfrac{\partial K_y}{\partial v_y} \end{bmatrix} = \begin{bmatrix} -\dfrac{\partial D_x}{\partial v_x} K_{0x} & 0 \\ 0 & -\dfrac{\partial D_y}{\partial v_y} K_{0y} \end{bmatrix} $$
(45)

Deriving Eq. 20

$$\label{der_dam} \dfrac{\partial D}{\partial v} = \frac{v_f v_0}{v^2(v_f-v_0)} $$
(46)

Substituting Eq. 45 into Eq. 6, the expression of the Jacobian 43 can be obtained as

$$\label{expreJac} \mathbf{J} = \mathbf{K} + \alpha \mathbf{V} + \mathbf{K}_T $$
(47)

where

$$\label{TangentStiffnessMatrix} \mathbf{K}_T = \begin{bmatrix} \mathbf{K}_{T11} & \mathbf{K}_{T12}\\ \mathbf{K}_{T12}^T & \mathbf{K}_{T22} \end{bmatrix} $$
(48)

where

$$\label{K11t} \mathbf{K}_{T11} = \begin{bmatrix} \mathbf{K}_{T11x} & 0 \\ 0 & \mathbf{K}_{T11y} \end{bmatrix} $$
(49)
$$\label{K12t} \mathbf{K}_{T12} = \begin{bmatrix} \mathbf{K}_{T12x}& 0 \\ 0 & \mathbf{K}_{T12y} \end{bmatrix} $$
(50)
$$\label{K22t} \mathbf{K}_{T22} = \begin{bmatrix} \mathbf{K}_{T22x} & 0 \\ 0 & \mathbf{K}_{T22y} \end{bmatrix} $$
(51)
$$\label{Kijxt} \mathbf{K}_{Tijl} = \int_{\Gamma_c} \mathbf{\phi}_{ic} \ \left(K_l\big(v_l\big)-K_{l0}\frac{v_f v_0}{v_l\big(v_f-v_0\big)}\right) \ \mathbf{\phi}_{jc} d\Gamma_c \qquad i,j = 1,2 \qquad l = x,y $$
(52)

As reported in [21] and [22], such numerical scheme could fail to converge due to the softening nature of the cohesive model. Moreover, the choice of the penalty values is important since it could lead to large unbalanced forces and shoot the iteration beyond its radius of convergence.

One of the remedies for the overshoot can be a damping loop inside the Newton–Rhapson iteration, i.e. reduce the step-length by a power of 2 until satisfactory reduction of the residual is achieved. Even though this approach is quite efficient, it might be too slow, since a key factor in obtaining an accurate solution is the choice of sufficiently short load increments. This means that the solution of most problems could be computationally inconvenient.

In order to accelerate the Newton process, a cubic polynomial line search (LS) algorithm has been used [23]. Another drawback of the Newton–Rhapson algorithms is that their (quadratic) convergence is guaranteed only if the guess solution is close enough to the real solution. LS algorithms are instead globally convergent, since they may converge independently from the starting point.

6 Numerical Results

Five numerical applications regarding single mode delamination are presented in this section. The fracture modes studied are mode I with two Double Cantilevered Beam (DCB) tests (Fig. 5) and mode II with an End Loaded Split test (ELS) (Fig. 6) and an End Notched Flexure (ENF) test. (Fig. 7). In Table 2, for the DCB tests, G c  = G Ic the critical energy release rate is related to mode I and τ m is the maximum interlaminar traction stress, while for the ELS and ENF tests, G c  = G IIc related to mode II and τ m is the maximum interlaminar shear stress. For mode II loading, the interfaces are here supposed frictionless. All the specimens are subjected to a variable vertical applied displacement v, at each load step a nonlinear problem has been solved according to the scheme in Eq. 42. A reaction force F has been calculated when the algorithm satisfied convergence criteria. In order to simulate an initial delamination (indicated with a 0), penalty stiffnesses were set to zero at the pre-crack. A plane strain of tension is supposed.for all the cases. A rectangular grid of nodes is used for all the cases. The numerical quadrature employed is the Gaussian quadrature and three Gaussian points per triangular element were used. The simulations were carried out using an in-house meshfree code.

Fig. 5
figure 5

Double cantileverd beam: geometry and boundary conditions

Full size image
Fig. 6
figure 6

End loaded split: geometry and boundary conditions

Full size image
Fig. 7
figure 7

End notched flexure: geometry and boundary conditions

Full size image

6.1 Mode I Double Cantilevered Beam: First Test

The first case is a DCB test from [21] for a \((0^{\circ}_{ \ 24})\) T300/977-2 carbon fiber-reinforced epoxy laminate. Elastic properties and geometry along with interface parameters are resumed in Tables 1 and 2 (where w is the plate width).

Table 1 Elastic properties of the specimens
Full size table
Table 2 Geometry and inteface properties of the specimens
Full size table

A comparison with the experimental test is shown in Fig. 9, as it can be observed the numerical model can predict the applied relative displacement at which the delamination starts (around 5 mm) and the correspondent maximum reaction force (62 N). Once reached the critical opening displacement, the delamination propagates through the mid-plane (Figs. 8 and 9).

Fig. 8
figure 8

Delamination stages for DCB test T300/977-2: transverse stress σ y plot

Full size image
Fig. 9
figure 9

Reaction force for DCB test T300/977-2: continuous line: numerical; squared line: experimental

Full size image

6.2 Mode I Double Cantilevered Beam: Second Test

The second DCB case is from [20] for a XAS-913C carbon-fiber epoxy composite. The properties and the initial conditions are reported in Tables 1 and 2. The plate has been modeled as Fig. 5 and there is only a slight difference between the experimental test and the numerical results regarding the reaction force (Fig. 10). In Fig.  11 are depicted the stress color plot for the longitudinal stress σ x (Fig. 11a) and the shear stress τ xy (Fig. 11b). As expected, it could be noted that each delaminated arm behaves like a cantilevered beam in bending constrained at the delamination tip. The same distribution can be identified in the next examples.

Fig. 10
figure 10

Reaction force for DCB test XAS-913C: continuous line: numerical; squared line: experimental

Full size image
Fig. 11
figure 11

Delamination stress plot for DCB test XAS-913C

Full size image

6.3 Mode II End Loaded Split

Delamination of mode II (sliding mode) has been modeled as in Fig. 6 with a loading displacement applied at the free end of the bottom plate. Properties and geometry are summarized in Tables 1 and 2. Experimental results are taken from [24]. From Fig. 12 it can be observed that the model can capture the trend with a minor difference from the experimental test. The critical opening displacement is around 15 mm, after that the delamination advances quite rapidly (Figs. 13 and 14 ). The delamination is complete (split) for a displacement of 21 mm, after that the two beams respond separately to the loads.

Fig. 12
figure 12

Reaction force for ELS test: continuous line: numerical; squared line: experimental

Full size image
Fig. 13
figure 13

Delamination stages for ELS test: longitudinal stress σ x plot

Full size image
Fig. 14
figure 14

Delamination stages for ELS test: longitudinal stress τ xy plot

Full size image

6.4 Mode II End Notched Flexure: First Test

Another example of Mode II loading is an ENF test where a displacement is applied in the middle of a simply supported beam with an initial delamination length (three-point bending). Experimental results are taken from [21] and geometry and properties (AS4/PEEK) are resumed in Tables 1 and 2. Once again a good agreement can be observed between the experimental and the numerical results (Fig. 15). The critical opening displacement is perfectly predicted with a difference in the resulting reaction force. Delamination phases can be observed from Fig. 16.

Fig. 15
figure 15

Reaction force for ENF test: continuous line: numerical; dashed line: experimental

Full size image
Fig. 16
figure 16

Delamination stages for ENF test: longitudinal stress σ x plot

Full size image

6.5 Mode II End Notched Flexure: Second Test

Final example is a ENF test for a graphite/epoxy material T300/977-2 (same specimen of DCB test in Subsection 6.1 but with different width) taken from [25] whose elastic and interface properties are resumed in Tables 1 and 2.

The Fig. 17 shows a comparison with FE decohesion elements which has been the most widely used technique for delamination modeling. As it can seen, results are very similar. Moreover the curve is much smoother than the previous case. This is mainly due to convergence issues as mentioned in the previous Section 5. As in FE, these problems can be overcome when relatively ”small” load increments are applied and when the nodes distribution is globally refined. The measure of the refinement and the choice of load increments can really depend on the problem. Moreover, an iterative process known as modified arc-length can be used to accurately choose the load increments. Such method assumes the load level (in this case the value of the reaction force) as an additional unknown.

Fig. 17
figure 17

Reaction force for ENF test: continuous thick line: RKPM; continuous thin line: FE decohesion

Full size image

7 Conclusions

In this paper a penalty-based approach to delamination has been proposed. Delamination is modeled considering two different sub-domains connected (or disconnected) with cohesive forces. Using the cohesive model, a variable penalty factor along the crack line consented to loosen or tight the two parts according to their relative displacements.

A two-dimensional meshfree method (RKPM) has been used to discretized the laminate. Conversely to FE approaches, meshfree techniques consent to effectively treat the contact between the parts without interface elements or conforming meshes. Arbitrary crack propagation path can be as well modeled with additional cohesive segments and therefore more unknowns.

Nevertheless when the path is known, the RKPM approximation consents to couple the parts without adding additional unknowns. Results showed very good agreement with experimental evidences for single-mode delamination under mode I and mode II loading.