1 Introduction

Heroin, as an opiate drug, has been used widely and become prevalent all over the world, such as in Europe, Ireland and China [4, 10, 12]. Due to the dependence and abuse, heroin users are more susceptible to become addicted. According to the survey in [7], the most frequent routes of drug administration were intravenous injection and inhalation. The dramatic increase in illicit drug abuse severely affects the development of society and economy. At the same time, treatment of heroin users also produces a major burden on the health system of any country. Thus, more progress needs to be made towards reducing the number of heroin users and its impacts on society, understanding heroin addition problems and aiding specialist teams in devising treatment strategies. The spread of heroin habituation and addiction exhibits many features of epidemics, such as infectiousness, rapid diffusion and clear geographic boundaries. Thus, mathematical modeling methods can be applied to describe such problems. Based on the theory of compartmental epidemics models [11], these models can be referred as heroin epidemic models.

During recent years, mathematical modeling of heroin epidemic dynamics has becoming an important subject of research. These models are governed by systems of ordinary differential equations (ODEs), delay differential equations (DDEs) or hybrid systems of both. In these models, the total population is divided into three disjoint subpopulations, namely, susceptible, heroin drug users not in treatment, and heroin drug users undergoing treatment, where the density of each subpopulation at time \(t\) is denoted as \(S(t)\), \(U_{1}(t)\) and \(U_{2}(t)\), respectively. These models are very important and useful in providing insights for establishing heroin epidemic parameters. In the aspect of ODEs models, White et al. [25] presented a heroin epidemic model with standard incidence rate. Furthermore, Mulone et al. [19] revisited this ODEs model and showed that the steady state of the model in [25] is globally asymptotically stable by using eigenvalue equations and Poincare-Bendixson theory. In the aspect of DDEs models, Samanta [22] obtained sufficient conditions for permanence and global asymptotic stability for a delayed nonautonomous heroin epidemic model. Liu et al. [14] established a heroin epidemic model with distributed delays and analyzed the local stability of endemic equilibrium, while its global stability was solved by Huang et al. [8] by means of constructing a suitable Lyapunov functional in a subsequent work.

However, all these models do not include many relevant factors, for example, the level of susceptibility and relapse. Liu and Wang [13] studied a multi-group heroin epidemic model with nonlinear incidence rate and relapse delays for the drug users undergoing treatment. In fact, the susceptibility of individuals varies significantly during their life time, which firstly was accused by the development of the immune system. Moreover, the changes in the life style can also influence the number of contacts, and hence influence susceptibility of individuals, which may depend on age. To emphasize this point, Melnik and Korobeinikov [18] proposed two models with age-dependent susceptibility, which were described by systems of ODEs and partial differential equations (PDEs), and established the global stability of the systems by using the direct Lyapunov method with Volterra type Lyapunov functionals. On the other hand, relapse, as an important factor in the spread of heroin, is more closely with the relapse age (the time of heroin users in treatment). We are interested to study whether the relapse age affects the global stability of heroin epidemic model or not.

Motivated by recent work [18] and considering relapse age, we propose a heroin epidemic model with age-dependent susceptibility and relapse. The aim of this paper is to obtain the global stability of the system incorporated with ODEs and PDEs, which is the most important feature of mathematical models. It is increasingly important that a heroin epidemic model has a threshold parameter that determines whether the heroin users will remain endemic or get extinct. From the application point of view, it is particularly relevant to study the stability and attractivity of equilibrium of the system, if it exists. Questions such as the existence of equilibrium, asymptotic smoothness of solutions, uniform persistence, local stability and global stability of the model will be addressed. It is shown that the basic reproduction ratio is a threshold condition, which completely determines the global behaviors of the model by constructing suitable Lyapunov functionals.

This paper proceeds as follows. In Sect. 2, we formulate an age-structured heroin epidemic model, establish the basic reproduction ratio and then state the main results of this paper. We present some preliminary results and uniform persistence of the system in Sect. 3. In Sect. 4, we prove the main results by means of LaSalle’s invariance principle and constructing suitable Lyapunov functionals. Finally, we present brief conclusions and discussions in Sect. 5. And the proofs of our preliminary theorems are given in the Appendices.

2 Model Formulation and Main Results

In this section, we formulate an age-structured heroin epidemic model, and present the basic reproduction ratio and the existence of equilibria, and state the main results of this paper.

The total population is divided into three subpopulations. The individuals who are healthy but can contact the heroin users, form the susceptible subpopulation. The influx of this subpopulation is \(\varLambda\). The susceptible age \(a\) denotes the duration time spent in this subpopulation. Thus, the distribution of the susceptible individuals with respect to the susceptible age \(a\) at time \(t\) is denoted by \(S(t,a)\), and the total density of individuals in susceptible subpopulation at time \(t\) is \(S(t)=\int_{0}^{\infty}S(t,a)da\). The susceptible individuals become heroin users at a rate \(\beta(a)\) and remove this subpopulation at a rate \(\mu\), where \(\beta(a)\) is the age-dependent transmission rate. Then, the change rate of \(S(t,a)\) at time \(t\) and age \(a\) is

$$\begin{aligned} \textstyle\begin{cases} S(t,0)=\varLambda, \\ (\frac{\partial}{\partial t}+\frac{\partial}{\partial a}) S(t,a)=- [\beta(a)U_{1}(t)+\mu ] S(t,a), \end{cases}\displaystyle \end{aligned}$$
(1)

where \(U_{1}(t)\) denotes the density of individuals who are heroin users but not in treatment, and is called the heroin users not in treatment subpopulation. The total rate of individuals moving from the susceptible subpopulation to the heroin users not in treatment subpopulation at time \(t\) is

$$ U_{1}(t) \int_{0}^{\infty}\beta(a)S(t,a)da. $$

The heroin users remove this subpopulation at rates \(\mu+\delta_{1}+p\), where \(\mu\) is the per capita natural death rate, \(\delta_{1}\) is a removal rate for heroin users that includes heroin-related death of users not in treatment and a spontaneous recovery rate, and \(p\) is the treatment rate. Note that the heroin users in treatment may relapse into heroin users not in treatment subpopulation. This phenomenon of relapsing is related to the duration time undergone treatment. We call this time as relapse age, denoted by \(\theta\). The distribution of drug users in treatment subpopulation with respect to the relapse age \(\theta\) at time \(t\) is denoted by \(U_{2}(t,\theta)\). The total density of individuals in this subpopulation at time \(t\) is \(U_{2}(t)=\int_{0}^{\infty}U_{2}(t,\theta)d\theta\). The heroin users in treatment remove this subpopulation at rates \(\delta_{2}(\theta)+ \mu\), where \(\delta_{2}(\theta)\) is age-dependent death rate due to treatment failure. The relapse rate from this subpopulation is given by \(\gamma(\theta)\). The total density of individuals moving from the treatment subpopulation to the heroin users not in treatment subpopulation at time \(t\) is

$$ \int_{0}^{\infty}\gamma(\theta)U_{2}(t,\theta)d \theta. $$

Thus, the change rate of \(U_{1}(t)\) with time \(t\) is

$$ \frac{d U_{1}(t)}{dt}= U_{1}(t) \int_{0}^{\infty}\beta(a)S(t,a)da-( \mu+ \delta_{1}+p)U_{1}(t)+ \int_{0}^{\infty}\gamma(\theta)U_{2}(t, \theta)d\theta. $$
(2)

Furthermore, the change rate of \(U_{2}(t,\theta)\) with time \(t\) and age \(\theta\) is

$$\begin{aligned} \textstyle\begin{cases} U_{2}(t,0)=pU_{1}(t), \\ (\frac{\partial}{\partial t}+\frac{\partial}{\partial\theta}) U _{2}(t,\theta)=- [\gamma(\theta)+\delta_{2}(\theta)+\mu ]U _{2}(t,\theta). \end{cases}\displaystyle \end{aligned}$$
(3)

Equations (1)–(3) formulate an age-structured heroin epidemic model as the following form

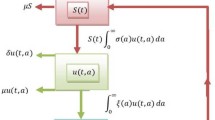
$$\begin{aligned} \textstyle\begin{cases} (\frac{\partial}{\partial t}+\frac{\partial}{\partial a}) S(t,a)= - [\beta(a)U_{1}(t)+\mu ] S(t,a), \\ \frac{d U_{1}(t)}{dt}= U_{1}(t)\int_{0}^{\infty}\beta(a)S(t,a)da-( \mu+\delta_{1}+p)U_{1}(t)+\int_{0}^{\infty}\gamma(\theta)U_{2}(t, \theta)d\theta, \\ (\frac{\partial}{\partial t}+\frac{\partial}{\partial\theta}) U _{2}(t,\theta)=- [\gamma(\theta)+\delta_{2}(\theta)+\mu ]U _{2}(t,\theta), \\ S(t,0)=\varLambda,\qquad U_{2}(t,0)=pU_{1}(t), \\ S(0,a)=S_{0}(a),\qquad U_{1}(0)=U_{1}^{0},\qquad U_{2}(0,\theta)=U_{2}^{0}( \theta). \end{cases}\displaystyle \end{aligned}$$
(4)

Figure 1 shows the schematic flow diagram of system (4). Note that \(U_{1}^{0}\in\mathbb{R}^{+}\) and \(S_{0}(a), U_{2}^{0}( \theta)\in L_{+}^{1}(0,\infty)\), where \(L_{+}^{1}(0,\infty)\) is the space of functions on \([0,\infty)\) that are nonnegative and Lebesgue integrable. For two given ages \(a_{1}\) and \(a_{2}\) satisfying \(0\leq a_{1}\leq a_{2}\leq\infty\), denote \([a_{1},a_{2}]\) be the age-interval of heroin users, i.e., an individual with the age outside that interval can not use heroin. Thus, the density of the susceptible subpopulation with age \(a\in[a_{1},a_{2}]\) at time \(t\) is

$$ \int_{a_{1}}^{a_{2}}S(t,a)da. $$

Similarly, let \([\theta_{1},\theta_{2}]\) be the age-interval of heroin users in treatment. The density of heroin users in treatment subpopulation with age \(\theta\in[\theta_{1},\theta _{2}]\) at time \(t\) is

$$ \int_{\theta_{1}}^{\theta_{2}}U_{2}(t,\theta)d\theta. $$

We will assume that \(\int_{0}^{\infty}\beta(a)da=\infty\) and \(\int_{0}^{\infty}\gamma(\theta)d\theta=\infty\), so that for all time \(t\),

$$ \lim_{a\rightarrow\infty}S(t,a)=0,\qquad \lim_{\theta\rightarrow\infty}U_{2}(t, \theta)=0. $$

We make the following assumption on the age-dependent variables. To be specific, we have the following assumption.

Fig. 1
figure 1

The schematic flow diagram of system (4). Here, the terms \([\beta S]\) and \([\gamma U_{2}]\) stand for \(\int_{0}^{\infty}\beta(a)S(t,a)da\) and \(\int_{0}^{\infty}\gamma( \theta)r(t,\theta)d\theta\)

Full size image

Assumption 1

Consider system (4), the parameters satisfy that \(\beta(a), \gamma(\theta),\delta_{2}(\theta)\in L_{+}^{1}(0,\infty)\) with respective essential upper bounds \(\bar{\beta},\bar{\gamma},\bar{ \delta_{2}}\), i.e.,

$$\begin{aligned} \bar{\beta}={\mathop{\mathrm{ess.\,sup}}_{a\in[0,\infty)}}\beta(a)< + \infty,\qquad \bar{\gamma}={\mathop{\mathrm{ess.\,sup}}_{\theta \in[0,\infty)}}\gamma(\theta)< +\infty, \qquad\bar{\delta_{2}}= {\mathop{\mathrm{ess.\,sup}}_{\theta\in[0,\infty)}} \delta_{2}( \theta)< +\infty. \end{aligned}$$

To simplify the notations and without loss of generality, in what follows, we denote that

$$\begin{aligned} &\sigma(t,a)=\beta(a)U_{1}(t)+\mu,\qquad\kappa=\mu+ \delta_{1}+p, \qquad\alpha(\theta)=\gamma(\theta)+\delta_{2}( \theta)+\mu, \\ &\rho(t,a)=e^{-\int_{0}^{a}\sigma(t-a+s,s)ds}, \qquad \varrho(\theta)=e^{-\int_{0}^{\theta}\alpha(s)ds}, \qquad \phi= \int _{0}^{\infty}\gamma(\theta)\varrho(\theta)d\theta. \end{aligned}$$

Consequently, we have for \(U_{1}(t)\geq0\), then

$$\begin{aligned} \begin{aligned} &\sigma(t,a)\geq\mu, \quad 0\leq\rho(t,a)\leq e^{-\mu a}, \qquad \frac{\partial}{\partial a}\rho(t,a)=-\sigma(t,a)\rho(t,a), \\ &\alpha(\theta)\geq\mu, \quad 0\leq\varrho(\theta)\leq e^{-\mu\theta}, \qquad \frac{d\varrho(\theta)}{d\theta}=-\alpha(\theta)\varrho( \theta). \end{aligned} \end{aligned}$$
(5)

Following [24], we can solve the first equation of system (4) and obtain (by integration along the characteristic line \(t-a=const.\)) that

$$ S(t,a)=S(t-a,0)e^{-\int_{0}^{a}\sigma(t-a+s,s)ds}=S(t-a,0)\rho(t,a) $$

for almost all \(t> a\geq0\) and

$$\begin{aligned} S(t,a)=S_{0}(a-t)e^{-\int_{0}^{t}\sigma(s,a-t+s)ds} =S_{0}(a-t)e^{- \int_{a-t}^{a}\sigma(t-a+s,s)ds} \end{aligned}$$

for almost all \(a\geq t\geq0\). Then we have

$$\begin{aligned} S(t,a)= \textstyle\begin{cases} \varLambda\rho(t,a), &t> a\geq0; \\ S_{0}(a-t)\frac{\rho(t,a)}{\rho(t,a-t)}, &a\geq t\geq0. \end{cases}\displaystyle \end{aligned}$$
(6)

Similarly,

$$\begin{aligned} U_{2}(t,\theta)= \textstyle\begin{cases} pU_{1}(t-\theta)\varrho(\theta), &t>\theta\geq0; \\ U_{2}^{0}(\theta-t)\frac{\varrho(\theta)}{\varrho(\theta-t)}, &\theta\geq t\geq0. \end{cases}\displaystyle \end{aligned}$$
(7)

Note that the average time in the heroin users not in treatment subpopulation on the first pass is \(1/\kappa\) and the probability of entering treatment subpopulation is \(p/\kappa\). Since \(\phi\) is the probability of relapsing into the heroin users not in treatment subpopulation, the total average time in heroin users not in treatment subpopulation (on multiple passes) is

$$\begin{aligned} \frac{1}{\kappa} \biggl[1+\frac{p\phi}{\kappa}+ \biggl( \frac{p\phi}{ \kappa} \biggr)^{2}+\cdots \biggr] =\frac{1}{\kappa-p\phi}. \end{aligned}$$
(8)

Multiplying (8) by \(\varLambda\int_{0}^{\infty}\beta(a)e ^{-\mu a}da\) gives

$$\begin{aligned} \Re_{0}=\frac{\varLambda}{\kappa-p\phi} \int_{0}^{\infty}\beta(a) e ^{-\mu a}da, \end{aligned}$$
(9)

or the equivalent form (36). \(\Re_{0}\) has a clearly biological interpretation and denotes the average density of new heroin users produced by one drug user not in treatment introduced into a susceptible subpopulation.

Now, we are able to state the result on the existence of equilibria for system (4).

Theorem 1

Let\(\Re_{0}\)be defined as in (9). For system (4), the following results hold true.

  1. (i)

    System (4) always has a heroin-free equilibrium\(E_{0}=(S_{0}^{*}(\cdot),0,0)\);

  2. (ii)

    System (4) has a unique heroin-spread equilibrium\(E_{*}=(S^{*}(\cdot), U_{1}^{*}, U_{2}^{*}(\cdot))\)when\(\Re_{0}>1\).

For the proof of Theorem 1, please see Appendix A. In order to state the main results of the paper, we set

$$ \bar{a}=\inf \biggl\{ a: \int_{a}^{\infty}\beta(s)ds=0 \biggr\} , \qquad\bar{ \theta}=\inf \biggl\{ \theta: \int_{\theta}^{\infty} \gamma(s)ds=0 \biggr\} . $$

Since the functions \(\beta(a),\gamma(\theta)\in L_{+}^{1}(0,\infty )\), we have \(\bar{a},\bar{\theta}>0\). Furthermore, we let

$$ Y=L^{1}(0,\infty)\times\mathbb{R}\times L^{1}(0,\infty), \qquad Y _{+}=L^{1}_{+}(0,\infty)\times \mathbb{R}^{+}\times L^{1}_{+}(0, \infty). $$

We need to partition \(Y_{+}\) as \(Y_{+}=Y_{+}^{0}\cup\partial Y_{+} ^{0}\), where

$$\begin{aligned} Y_{+}^{0} &= \biggl\{ (S,U_{1},U_{2})^{T} \in Y_{+}: \int_{0}^{\bar{a}}S(t,a)da+U _{1}(t)+ \int_{0}^{\bar{\theta}}U_{2}(t,\theta)d\theta>0 \biggr\} . \end{aligned}$$

Now, we are in the position to state the main results of this paper.

Theorem 2

If\(\Re_{0}<1\), then the heroin-free equilibrium\(E_{0}\)is the unique equilibrium of system (4), and it is globally asymptotically stable.

Theorem 3

Assume that\(\Re_{0}>1\), then the heroin-free equilibrium\(E_{0}\)is globally asymptotically stable in\(\partial Y_{+}^{0}\), and the unique heroin-spread equilibrium\(E_{*}\)of system (4) is globally asymptotically stable in\(Y_{+}^{0}\).

3 Preliminary Results and Uniform Persistence

In this section, we first show the asymptotic smoothness of the semi-flow generated by system (4), and then present some results about uniform persistence and the existence of global attractors by using the persistence theory for continuous dynamical system.

Now, the space of functions \(Y_{+}\) is equipped with the norm

$$ \|(y_{1},y_{2},y_{3})\|_{Y_{+}}= \int_{0}^{\infty}|y_{1}(a)|da+|y_{2}|+ \int_{0}^{\infty}|y_{3}(\theta)|d\theta. $$

The initial conditions that belong to the positive cone \(Y_{+}\) can be rewritten as

$$\begin{aligned} y_{0}=\bigl(S_{0}(\cdot),U_{1}^{0},U_{2}^{0}( \cdot)\bigr)\in Y_{+}. \end{aligned}$$
(10)

By the standard theory of functional differential equations [5], it can be verified that system (4) with the initial condition (10) has a unique nonnegative solution. Thus, we can obtain a continuous semi-flow \(\pi:\mathbb{R}^{+}\times Y_{+}\rightarrow Y_{+}\) defined by system (4) such that

$$ \pi(t,y_{0})=\pi_{t}(y_{0})=\bigl(S(t, \cdot),U_{1}(t),U_{2}(t,\cdot)\bigr), \quad t\in \mathbb{R}^{+},\ y_{0}\in Y_{+} $$

with the norm

$$ \|\pi_{t}(y_{0}){\|}_{Y_{+}}=\bigl\| \bigl(S(t, \cdot),U_{1}(t),U_{2}(t,\cdot)\bigr) \bigr\| _{Y_{+}} = \int_{0}^{\infty}|S(t,a)|da+|U_{1}(t)|+ \int_{0}^{ \infty}|U_{2}(t,\theta)|d\theta. $$

Therefore, the following theorem holds true.

Theorem 4

Consider system (4), we define

$$ \varOmega= \biggl\{ (S,U_{1},U_{2})\in Y_{+}: \int_{0}^{\infty}S(t,a)da+U _{1}(t)+ \int_{0}^{\infty}U_{2}(t,\theta)d\theta\leq \frac{\varLambda }{\mu} \biggr\} . $$

Then, \(\varOmega\)is positively invariant for\(\pi\), that is, \(\pi_{t}(y_{0})\in\varOmega\), for all\(t\in\mathbb{R}^{+}\)and\(y_{0}\in\varOmega\). Furthermore, \(\pi\)is point dissipative and\(\varOmega\)attracts all points in\(Y_{+}\).

For the proof of Theorem 4, please see Appendix B. Combining Assumption 1 and Theorem 4, the following proposition holds true.

Proposition 1

If\(y_{0}\in Y_{+}\)and\(\|y_{0}\|_{Y_{+}}\leq L\)for some constant\(L\geq\varLambda/\mu\), then the following statement holds true for\(t\geq0\):

$$ 0\leq \int_{0}^{\infty}S(t,a)da,U_{1}(t), \int_{0}^{\infty}U_{2}(t, \theta)d\theta\leq L. $$

In order to obtain global behaviors of system (4), it is important to prove that the semi-flow \(\{\pi(t)\}_{t\in\mathbb{R} ^{+}}\) is asymptotically smooth. Now, we give some definitions and lemmas which are useful for proving asymptotic smoothness.

Definition 1

([6])

A semi-flow \(\pi_{t}(y_{0}): Y_{+}\rightarrow Y_{+}\) is said to be asymptotically smooth, if, for any nonempty, closed bounded set \(B\subset Y_{+}\) for which \(\pi_{t}(B)\subset B\), there is a compact set \(B_{0}\subset B\) such that \(B_{0}\) attracts \(B\).

The following lemma will be used to prove the asymptotic smoothness of \(\{\pi(t)\}_{t\in\mathbb{R}^{+}}\).

Lemma 1

([6])

If the following two conditions hold, then the semi-flow\(\pi_{t}(y _{0})=\hat{\pi}_{t}(y_{0})+\check{\pi}_{t}(y_{0}):\mathbb{R}^{+} \times Y_{+}\rightarrow Y_{+}\)is asymptotically smooth in\(Y_{+}\).

  1. (i)

    There exists a continuous function\(\varphi:\mathbb{R}^{+} \times\mathbb{R}^{+}\rightarrow\mathbb{R}^{+}\)such that\(\varphi(t,r) \rightarrow0\)as\(t\rightarrow\infty\)and\(\| \hat{\pi}_{t}(y_{0})\|_{Y _{+}}\leq\varphi(t,r)\)if\(\|y_{0}\|_{Y_{+}}\leq r\).

  2. (ii)

    For\(t\geq0\), \(\check{\pi}_{t}(y_{0})\)is completely continuous.

Since \(Y_{+}\) is the infinite dimensional Banach space and \(L_{+}^{1}(0, \infty)\) is a component of \(Y_{+}\), then a notion of compactness in \(L_{+}^{1}(0,\infty)\) is needed. Note that being an infinite dimensional space, boundedness does not imply precompactness. Thus, the following definition and lemma are required.

Definition 2

A semi-flow \(\check{\pi}_{t}(y_{0}):\mathbb{R}^{+}\times Y_{+}\rightarrow Y_{+}\) is said to be completely continuous if for each \(t>0\) and each bounded set \(B\subset Y_{+}\), we have \(\{\check{\pi}_{r}(B)\}_{0 \leq r\leq t}\) is bounded and \(\{\check{\pi}_{t}(B)\}_{t\in \mathbb{R}^{+}}\) is precompact.

Lemma 2

([1])

Let\(K\subset L^{p}(0,\infty)\)be closed and bounded where\(p\geq1\). Then\(K\)is compact if the following conditions hold:

  1. (i)

    \(\lim_{h\rightarrow0}\int_{0}^{\infty}|u(z+h)-u(z)|^{p}dz=0\)uniformly for\(u\in K\). (\(u(z + h)=0\)if\(z+h<0\)).

  2. (ii)

    \(\lim_{h\rightarrow\infty}\int_{h}^{\infty}|u(z)|^{p}dz=0\)uniformly for\(u\in K\).

Based on Lemmas 1–2, the semi-flow \(\{\pi(t)\}_{t \in\mathbb{R}^{+}}\) satisfies the following theorem.

Theorem 5

The semi-flow\(\{\pi(t)\}_{t\in\mathbb{R}^{+}}\), generated by (4), is asymptotically smooth. Furthermore, the semi-flow\(\{\pi(t)\}_{t\in\mathbb{R}^{+}}\)has a global attractor\(\mathcal{T}\)contained in\(Y_{+}\), which attracts the bound sets of\(Y_{+}\).

For the proof of Theorem 5, please see Appendix C. Following [16], the following lemma and theorem are necessary for the proof of the uniform persistence.

Lemma 3

([2])

Consider the following scalar Volterra integro-differential equations:

$$\begin{aligned} \frac{dy(t)}{dt}= \int_{0}^{\infty}h(a)y(t-a)da-cy(t),\quad y(0)>0, \end{aligned}$$

where\(h(\cdot)\in L_{+}^{1}(0,\infty)\), \(c>0\)and\(\int_{0}^{ \infty}h(a)da>c\). There is a unique solution\(y(t)\)which is unbounded.

Theorem 6

The subsets\(Y_{+}^{0}\)and\(\partial Y_{+}^{0}\)are both positively invariant under the semi-flow\(\{\pi(t)\}_{t\in\mathbb{R}^{+}}\). Furthermore, the heroin-free equilibrium\(E_{0}\)is globally asymptotically stable for the semi-flow\(\{\pi(t)\}_{t\in \mathbb{R^{+}}}\)restricted to\(\partial Y_{+}^{0}\).

For the proof of Theorem 6, please see Appendix D. Now, we are able to show the uniform persistence.

Theorem 7

Assume that\(\Re_{0}>1\). The semi-flow\(\{\pi(t)\}_{t\in\mathbb{R} ^{+}}\)is uniformly persistent with respect to\((Y_{+}^{0},\partial Y _{+}^{0})\), i.e., there exists\(\varepsilon>0\)which is independent of initial values such that\(\lim_{t\rightarrow\infty}\|\pi_{t}(y)\|_{Y _{+}}\geq\varepsilon\)for\(y\in Y_{+}^{0}\). Moreover, there exists a compact subset\(\mathcal{T}_{0}\)of\(Y_{+}^{0}\)which is a global attractor for\(\{\pi(t)\}_{t\in\mathbb{R}^{+}}\)in\(Y_{+}^{0}\).

For the proof of Theorem 7, please see Appendix E.

4 Proofs of the Main Results

In this section, Theorems 2–3 are proved via analyzing the corresponding characteristic equations and constructing suitable Lyapunov functionals. Before proving our main results, we define the following functions which will be important in our proofs.

We define a Volterra type Lyapunov function with the form

$$\begin{aligned} g(y)=y-1-\ln y \end{aligned}$$
(11)

and a positive function with the form

$$\begin{aligned} \omega(\theta)= \int_{\theta}^{\infty}\gamma(s)\exp\biggl\{ - \int_{ \theta}^{s}\alpha(\tau)d\tau\biggr\} ds. \end{aligned}$$
(12)

Clearly, \(g(y)\) is positive-definite for all \(y>0\) and \(g(y)\) has its unique global minimum at \(y=1\) with \(g(1)=0\). Furthermore, \(g'(y)=1-1/y\). This type function is widely used in the proofs of global stability, see [8, 9, 18]. It can be easily checked that \(\omega(\theta)>0\) for \(\theta\in[0,+\infty)\) and \(\omega(0)=\phi\). The derivative of \(\omega(\theta)\) satisfies that

$$\begin{aligned} \frac{d\omega(\theta)}{d\theta}=\omega(\theta)\alpha(\theta)- \gamma(\theta). \end{aligned}$$
(13)

Now, we give proofs of the main results in this paper.

4.1 Proof of Theorem 2

Firstly, we show the local stability of the heroin-free equilibrium \(E_{0}\). Introducing the perturbation variables

$$ x_{1}(t,a)=S(t,a)-S_{0}^{*}(a),\qquad x_{2}(t)=U_{1}(t),\qquad x_{3}(t, \theta)=U_{2}(t,\theta), $$

and linearizing system (4) at the equilibrium \(E_{0}\) takes the following form

$$\begin{aligned} \textstyle\begin{cases} (\frac{\partial}{\partial t}+\frac{\partial}{\partial a})x_{1}(t,a)=- \mu x_{1}(t,a)-\beta(a)\sigma^{*}(a)x_{2}(t), \\ \frac{dx_{2}(t)}{dt}=x_{2}(t)\int_{0}^{\infty}\beta(a)S_{0}^{*}(a)da- \kappa x_{2}(t)+\int_{0}^{\infty}\gamma(\theta)x_{3}(t,\theta)d \theta, \\ (\frac{\partial}{\partial t}+\frac{\partial}{\partial\theta})x _{3}(t,\theta)=-\alpha(\theta) x_{3}(t,\theta), \\ x_{1}(t,0)=0,\qquad x_{3}(t,0)=px_{2}(t), \\ x_{1}(0,a)=S_{0}(a),\qquad x_{2}(0)=U_{1}^{0},\qquad x_{3}(0,\theta)=U _{2}^{0}(\theta). \end{cases}\displaystyle \end{aligned}$$
(14)

In order to get the characteristic equation of \(E_{0}\), we set the following kind of solution of system (14)

$$\begin{aligned} x_{1}(t,a)=x_{1}^{0}(a)e^{\lambda t}, \qquad x_{2}(t)=x_{2}^{0}e^{ \lambda t},\qquad x_{3}(t,\theta)=x_{3}^{0}(\theta)e^{\lambda t}, \end{aligned}$$
(15)

where \(x_{1}^{0}(a),x_{2}^{0},x_{3}^{0}(\theta)\) will be determined later. Inserting (15) into (14), we get

$$\begin{aligned} &\left \{ \textstyle\begin{array}{ll} \lambda x_{1}^{0}(a)+\frac{dx_{1}^{0}(a)}{da}=-\mu x_{1}^{0}(a)- \beta(a)\sigma^{*}(a)x_{2}^{0}, \\ x_{1}^{0}(0)=0, \end{array}\displaystyle \right . \end{aligned}$$
(16)
$$\begin{aligned} &\lambda x_{2}^{0}=x_{2}^{0} \int_{0}^{\infty}\beta(a)S_{0}^{*}(a)da- \kappa x_{2}^{0}+ \int_{0}^{\infty}\gamma(\theta)x_{3}^{0}( \theta)d \theta, \end{aligned}$$
(17)
$$\begin{aligned} & \left \{ \textstyle\begin{array}{ll} \lambda x_{3}^{0}(\theta)+\frac{dx_{3}^{0}(\theta)}{d\theta}=- \alpha(\theta)x_{3}^{0}(\theta), \\ x_{3}^{0}(0)=px_{2}^{0}. \end{array}\displaystyle \right . \end{aligned}$$
(18)

Integrating the first equation of (18) from 0 to \(\theta\) yields

$$\begin{aligned} x_{3}^{0}(\theta)=px_{2}^{0}e^{-\int_{0}^{\theta} (\lambda+ \alpha(s) )ds}. \end{aligned}$$
(19)

Substituting (19) into (17) and solving (17), we obtain the following characteristic equation corresponding to the equilibrium \(E_{0}\)

$$ 0= \int_{0}^{\infty}\beta(a)S_{0}^{*}(a)da -\kappa+p \int_{0}^{ \infty}\gamma(\theta)e^{-\int_{0}^{\theta} (\lambda+\alpha (s) )ds}d\theta- \lambda. $$
(20)

Denoting the right hand side of (20) as \(\mathcal{L}_{0}( \lambda)\). Obviously, \(\mathcal{L}_{0}(\lambda)\) is a continuously differential function with \(\lim_{\lambda\rightarrow+\infty }\mathcal{L}_{0} (\lambda) =-\infty, \lim _{\lambda\rightarrow-\infty}\mathcal{L}_{0}(\lambda)=+ \infty\), and \(\mathcal{L}_{0}' (\lambda) < 0\). Thus, Eq. (20) has a unique real root \(\lambda^{*}\). Note that

$$ \mathcal{L}_{0}(0)= (\kappa-p\phi) (\Re_{0}-1). $$

Then, we have \(\lambda^{*}<0\) if \(\Re_{0}<1\), and \(\lambda^{*}>0\) if \(\Re_{0}>1\). Let \(\lambda=x^{0}+y^{0} i\) be an arbitrary complex root to Eq. (20) with \(x^{0}\geq 0\). Then

$$\begin{aligned} \mathbf{Re}\bigl(\mathcal{L}_{0}\bigl(x^{0}+y^{0}i \bigr)\bigr) &= \int_{0}^{\infty}\beta (a)S_{0}^{*}(a)da -\kappa+p \int_{0}^{\infty}\gamma(\theta)e^{-x ^{0}\theta}\cos \bigl(y^{0}\theta\bigr)e^{-\int_{0}^{\theta}\alpha(s)ds}d \theta-x^{0} \\ &\leq \int_{0}^{\infty}\beta(a)S_{0}^{*}(a)da -\kappa+p \int_{0} ^{\infty}\gamma(\theta)e^{-x^{0}\theta}e^{-\int_{0}^{\theta} \alpha(s)ds}d \theta-x^{0} \\ &=\mathcal{L}_{0}\bigl(x^{0}\bigr). \end{aligned}$$

Thus,

$$ 0=|\mathcal{L}_{0}(\lambda)| =\mathbf{Re}\bigl(\mathcal{L} _{0}\bigl(x^{0}+y^{0}i\bigr)\bigr)\leq \mathcal{L}_{0}\bigl(x^{0}\bigr), $$

which implies that \(x^{0}\leq\lambda^{*}<0\). Thus, all the roots of Eq. (20) have negative real parts if and only if \(\Re_{0} < 1\). Therefore, the heroin-free equilibrium \(E_{0}\) is locally asymptotically stable if \(\Re_{0} < 1\).

Now, we consider the global stability of \(E_{0}\). Set the Lyapunov functional as

$$ V_{0}(t)= \int_{0}^{\infty}S^{*}_{0}(a)g \biggl( \frac{S(t,a)}{S^{*}_{0}(a)} \biggr)da+U_{1}(t) + \int_{0}^{\infty} \omega(\theta)U_{2}(t, \theta)d\theta. $$

The derivative of \(V_{0}(t)\) along with the solutions of system (4) is

$$\begin{aligned} \frac{d V_{0}(t)}{dt} ={}& \int_{0}^{\infty}S^{*}_{0}(a) \biggl( \frac{1}{S ^{*}_{0}(a)}-\frac{1}{S(t,a)} \biggr) \frac{\partial}{\partial t} S(t,a)da+ \frac{dU _{1}(t)}{dt} + \int_{0}^{\infty}\omega(\theta)\frac{\partial}{ \partial t}U_{2}(t, \theta)d\theta \\ ={}&- \int_{0}^{\infty}S^{*}_{0}(a) \biggl( \frac{S(t,a)}{S^{*}_{0}(a)}-1 \biggr) \biggl(\frac{S_{a}(t,a)}{S(t,a)}+\sigma(t,a) \biggr)da \\ &+U_{1}(t) \int_{0}^{\infty}\beta(a)S(t,a)da-\kappa U_{1}(t)+ \int_{0}^{\infty}\gamma(\theta)U_{2}(t,\theta)d \theta \\ &- \int_{0}^{\infty}\omega(\theta)\frac{\partial}{\partial t}U_{2}(t, \theta)d\theta, \end{aligned}$$

where \(S_{a}(t,a)\) denotes \(\frac{\partial}{\partial a}S(t,a)\). Note that

$$ \frac{\partial}{\partial a}g \biggl(\frac{S(t,a)}{S^{*}_{0}(a)} \biggr) = \biggl( \frac{S(t,a)}{S^{*}_{0}(a)}-1 \biggr) \biggl( \frac{S_{a}(t,a)}{S(t,a)}+\mu \biggr) $$

and

$$ \frac{dS^{*}_{0}(a)}{da}=-\mu S^{*}_{0}(a). $$

Hence, using integration by parts, we have

$$\begin{aligned} \frac{d V_{0}(t)}{dt} ={}& -S^{*}_{0}(a)g \biggl( \frac{S(t,a)}{S^{*}_{0}(a)} \biggr) \bigg|_{a=0}^{a=\infty} + \int_{0} ^{\infty}g \biggl(\frac{S(t,a)}{S^{*}_{0}(a)} \biggr) \frac{dS^{*}_{0}(a)}{da}da \\ &+U_{1}(t) \int_{0}^{\infty}\beta(a)S^{*}_{0}(a)da -\kappa U _{1}(t) -\omega(\theta)U_{2}(t,\theta) |_{\theta=0}^{\theta= \infty} \\ ={}&S^{*}_{0}(0)g \biggl(\frac{S(t,0)}{S^{*}_{0}(0)} \biggr) - \int_{0}^{ \infty}\mu S^{*}_{0}(a)g \biggl(\frac{S(t,a)}{S^{*}_{0}(a)} \biggr)da +U_{1}(t) \int_{0}^{\infty}\beta(a)S^{*}_{0}(a)da \\ &-\kappa U_{1}(t)+\omega(0)U_{2}(t,0). \end{aligned}$$

Recalling that \(S^{*}_{0}(0)=S(t,0)=\varLambda\), \(\omega(0)=\phi\) and \(U_{2}(t,0)=pU_{1}(t)\). Then, one has \(g ( \frac{S(t,0)}{S^{*}_{0}(0)} )=0\). Thus, we obtain that

$$\begin{aligned} \frac{d V_{0}(t)}{dt}= - \int_{0}^{\infty}\mu S^{*}_{0}(a)g \biggl(\frac{S(t,a)}{S ^{*}_{0}(a)} \biggr)da +U_{1}(t) (\kappa-p\phi ) ( \Re_{0}-1) \end{aligned}$$
(21)

holds since \(\Re_{0}<1\) and \(g(y)\geq0\) for all \(y>0\). Moreover, \({d V_{0}(t)}/{dt}=0\) if and only if \({S(t,a)}={S^{*}_{0}(a)}\) and \(U_{1}(t)=0\). When \({S(t,a)}={S^{*}_{0}(a)}\) and \(U_{1}(t)=0\), system (4) has the unique solution \(E_{0}\). Thus, \(M_{0}=\{E_{0}\} \subset\varOmega\) is the largest invariant subset of \(\{(S,U_{1},U_{2}): {d V_{0}(t)}/{dt}=0\}\). By the Lyapunov-LaSalle invariance principle [15], the heroin-free equilibrium \(E_{0}\) is globally asymptotically stable provided \(\Re_{0}<1\). The proof is completed.

4.2 Proof of Theorem 3

Firstly, let us consider that the unique heroin-spread equilibrium \(E_{*}\) is locally asymptotically stable. Introducing the perturbation variables

$$\begin{aligned} \breve{x}_{1}(t,a)=S(t,a)-S^{*}(a),\qquad \breve{x}_{2}(t)=U_{1}(t)-U _{1}^{*}, \qquad\breve{x}_{3}(t,\theta)=U_{2}(t,\theta)-U_{2}^{*}( \theta), \end{aligned}$$

and linearizing system (4) at \(E_{*}\) yields

$$\begin{aligned} \textstyle\begin{cases} (\frac{\partial}{\partial t}+\frac{\partial}{\partial a})\breve{x} _{1}(t,a)=-\sigma^{*}(a) \breve{x}_{1}(t,a)-\beta(a)S^{*}(a) \breve{x}_{2}(t), \\ \frac{d\breve{x}_{2}(t)}{dt}=\breve{x}_{2}(t)\int_{0}^{\infty} \beta(a)S^{*}(a)da +U_{1}^{*}\int_{0}^{\infty}\beta(a)\breve{x} _{1}(t,a)da-\kappa\breve{x}_{2}(t) \\ \phantom{\frac{d\breve{x}_{2}(t)}{dt}=} +\int_{0}^{\infty}\gamma(\theta)\breve{x}_{3}(t,\theta)d\theta, \\ (\frac{\partial}{\partial t}+\frac{\partial}{\partial\theta}) \breve{x}_{3}(t,\theta)=-\alpha(\theta) \breve{x}_{3}(t,\theta), \\ \breve{x}_{1}(t,0)=0,\qquad\breve{x}_{3}(t,0)=p\breve{x}_{2}(t), \\ \breve{x}_{1}(0,a)=S_{0}(a),\qquad\breve{x}_{2}(0)=U_{1}^{0},\qquad \breve{x}_{3}(0,\theta)=U_{2}^{0}(\theta). \end{cases}\displaystyle \end{aligned}$$
(22)

Let

$$\begin{aligned} \breve{x}_{1}(t,a)=\breve{x}_{1}^{0}(a)e^{\lambda t}, \qquad\breve{x} _{2}(t)=\breve{x}_{2}^{0}e^{\lambda t}, \qquad\breve{x}_{3}(t,\theta)= \breve{x}_{3}^{0}( \theta)e^{\lambda t}, \end{aligned}$$
(23)

where \(\breve{x}_{1}^{0}(a),\breve{x}_{2}^{0},\breve{x}_{3}^{0}( \theta)\) will be determined later. Substituting (23) into (22), we have

$$\begin{aligned} &\left \{ \textstyle\begin{array}{ll} \lambda\breve{x}_{1}^{0}(a)+\frac{d\breve{x}_{1}^{0}(a)}{da}=-\sigma ^{*}(a) \breve{x}_{1}^{0}(a)-\beta(a)S^{*}(a)\breve{x}_{2}^{0}, \\ \breve{x}_{1}^{0}(0)=0, \end{array}\displaystyle \right . \end{aligned}$$
(24)
$$\begin{aligned} &\lambda\breve{x}_{2}^{0}= \breve{x}_{2}^{0} \int_{0}^{\infty}\beta(a)S ^{*}(a)da+U_{1}^{*} \int_{0}^{\infty}\beta(a)\breve{x}_{1}^{0}(a)da- \kappa\breve{x}_{2}^{0}+ \int_{0}^{\infty}\gamma(\theta)\breve{x} _{3}^{0}(\theta)d\theta, \end{aligned}$$
(25)
$$\begin{aligned} & \left \{ \textstyle\begin{array}{ll} \lambda\breve{x}_{3}^{0}(\theta)+\frac{d\breve{x}_{3}^{0}(\theta)}{d \theta}=-\alpha(\theta) \breve{x}_{3}^{0}(\theta), \\ \breve{x}_{3}^{0}(0)=p\breve{x}_{2}^{0}. \end{array}\displaystyle \right . \end{aligned}$$
(26)

Integrating the first equation of (24) and (26) from 0 to \(a\) and from 0 to \(\theta\), together with the boundary conditions, yields

$$\begin{aligned} &\breve{x}_{1}^{0}(a)=- \breve{x}_{2}^{0} e^{-\int_{0}^{a}(\lambda+ \sigma^{*}(s))ds} \int_{0}^{a}\beta(\tau)S^{*}( \tau)e^{\int_{0} ^{\tau}(\lambda+\sigma^{*}(s))ds}d\tau, \end{aligned}$$
(27)
$$\begin{aligned} &\breve{x}_{3}^{0}(\theta)=p\breve{x}_{2}^{0}e^{-\int_{0}^{\theta}( \lambda+\alpha(s))ds}. \end{aligned}$$
(28)

Substituting the above two equations into (25) and solving (25), we obtain the following characteristic equation

$$\begin{aligned} &\lambda+\kappa+U_{1}^{*} \int_{0}^{\infty}\beta(a)e^{-\int_{0} ^{a}(\lambda+\sigma^{*}(s))ds} \int_{0}^{a}\beta(\tau)S^{*}(\tau)e ^{\int_{0}^{\tau}(\lambda+\sigma^{*}(s))ds}d\tau da \\ &\quad= \int_{0}^{\infty}\beta(a)S^{*}(a)da +p \int_{0}^{\infty} \gamma(\theta)e^{-\int_{0}^{\theta}(\lambda+\alpha(s))ds}d\theta . \end{aligned}$$
(29)

Suppose that (29) has a root \(\lambda\) with \(\mathbf{Re}(\lambda)\geq0\). Since \(\int_{0}^{\infty}\beta(a)S ^{*}(a)da=\kappa-p\phi\) and \(\phi=\int_{0}^{\infty} \gamma(\theta)e^{-\int_{0}^{\theta}\alpha(s)ds}d\theta\), we have

$$\begin{aligned} & \biggl\vert \int_{0}^{\infty}\beta(a)S^{*}(a)da +p \int_{0}^{\infty} \gamma(\theta)e^{-\int_{0}^{\theta}(\lambda+\alpha(s))ds}d\theta \biggr\vert \\ &\quad\leq \int_{0}^{\infty}\beta(a)S^{*}(a)da +p \int_{0}^{\infty }\gamma(\theta)e^{-\int_{0}^{\theta}\alpha(s)ds}d\theta \\ &\quad= \kappa \end{aligned}$$

On the other hand, obviously

$$ \biggl\vert \lambda+\kappa+U_{1}^{*} \int_{0}^{\infty}\beta(a)e^{-\int _{0}^{a}(\lambda+\sigma^{*}(s))ds} \int_{0}^{a}\beta(\tau)S^{*}( \tau)e^{\int_{0}^{\tau}(\lambda+\sigma^{*}(s))ds}d\tau da \biggr\vert > \kappa, $$

which contradicts to (29). This means that all the roots of Eq. (29) have negative real parts. Consequently, the heroin-spread equilibrium \(E_{*}\) of system (4) is locally asymptotically stable if \(\Re_{0}>1\).

In the following, we show that \(E_{*}\) is globally asymptotically stable by constructing a Lyapunov functional as follows

$$ V_{*}(t)= \int_{0}^{\infty}S^{*}(a)g \biggl( \frac{S(t,a)}{S^{*}(a)} \biggr)da +U_{1}^{*}g \biggl( \frac{U_{1}(t)}{U_{1}^{*}} \biggr) + \int_{0} ^{\infty}\omega(\theta)U_{2}^{*}( \theta)g \biggl(\frac{U_{2}(t, \theta)}{U_{2}^{*}(\theta)} \biggr)d\theta. $$

The derivative of \(V_{*}(t)\) along with the solutions of system (4) satisfies that

$$\begin{aligned} \frac{d V_{*}(t)}{dt} ={}& \int_{0}^{\infty}S^{*}(a) \biggl( \frac{1}{S^{*}(a)}-\frac{1}{S(t,a)} \biggr) \frac{\partial}{\partial t} S(t,a)da + \biggl(1- \frac{U_{1}^{*}}{U_{1}(t)} \biggr)\frac{dU_{1}(t)}{dt} \\ &+ \int_{0}^{\infty}\omega(\theta)U_{2}^{*}( \theta)\frac{ \partial}{\partial t}g \biggl(\frac{U_{2}(t,\theta)}{U_{2}^{*}(\theta )} \biggr)d\theta \\ ={}&- \int_{0}^{\infty}S^{*}(a) \biggl( \frac{S(t,a)}{S^{*}(a)}-1 \biggr) \biggl(\frac{S_{a}(t,a)}{S(t,a)}+\sigma(t,a) \biggr)da \\ &+ \biggl(1-\frac{U_{1}^{*}}{U_{1}(t)} \biggr) \biggl(U_{1}(t) \int _{0}^{\infty}\beta(a)S(t,a)da-\kappa U_{1}(t)+ \int_{0}^{\infty} \gamma(\theta)U_{2}(t, \theta)d\theta \biggr) \\ &- \int_{0}^{\infty}\omega(\theta)U_{2}^{*}( \theta) \biggl(\frac{U _{2}(t,\theta)}{U_{2}^{*}(\theta)}-1 \biggr) \biggl(\frac{U_{2\theta}(t, \theta)}{U_{2}(t,\theta)}+\alpha( \theta) \biggr)d\theta, \end{aligned}$$

where \({U_{2\theta}(t,\theta)}\) denotes \(\frac{\partial}{\partial \theta} U_{2}(t,\theta)\). Note that

$$\begin{aligned} \frac{\partial}{\partial a}g \biggl(\frac{S(t,a)}{S^{*}(a)} \biggr) &= \biggl( \frac{S(t,a)}{S^{*}(a)}-1 \biggr) \biggl(\frac{S_{a}(t,a)}{S(t,a)}+ \mu \biggr), \\ \frac{\partial}{\partial a}g \biggl(\frac{U_{2}(t,\theta)}{U_{2}^{*}( \theta)} \biggr) &= \biggl( \frac{U_{2}(t,\theta)}{U_{2}^{*}(\theta)}-1 \biggr) \biggl(\frac{U_{2\theta}(t,\theta)}{U_{2}(t,\theta)}+\alpha (\theta) \biggr) \end{aligned}$$

and

$$ \frac{d S^{*}(a)}{da}=-\sigma^{*}(a)S^{*}(a),\qquad \frac{d U_{2}^{*}( \theta)}{d\theta}=-\alpha(\theta)U_{2}^{*}(\theta). $$

Hence, using integration by parts, we have

$$\begin{aligned} \frac{d V_{*}(t)}{dt} ={}& -S^{*}(a)g \biggl(\frac{S(t,a)}{S^{*}(a)} \biggr) \bigg|_{a=0}^{a=\infty} - \int_{0}^{\infty}\sigma^{*}(a) S^{*}(a)g \biggl(\frac{S(t,a)}{S^{*}(a)} \biggr)da \\ &+ \int_{0}^{\infty}\gamma(\theta)U_{2}^{*}( \theta) \biggl(\frac{U _{2}(t,\theta)}{U_{2}^{*}(\theta)}-\frac{U_{1}(t)}{U_{1}^{*}}-\frac{U _{1}^{*}U_{2}(t,\theta)}{U_{1}(t)U_{2}^{*}(\theta)}+1 \biggr)d \theta \\ &-\omega(\theta)U_{2}^{*}(\theta)g \biggl( \frac{U_{2}(t, \theta)}{U_{2}^{*}(\theta)} \biggr) \bigg|_{\theta=0}^{\theta=\infty } - \int_{0}^{\infty}\gamma(\theta)U_{2}^{*}( \theta)g \biggl(\frac{U _{2}(t,\theta)}{U_{2}^{*}(\theta)} \biggr)d\theta \\ ={}&S^{*}(0)g \biggl(\frac{S(t,0)}{S^{*}(0)} \biggr) - \int_{0}^{\infty} \sigma^{*}(a) S^{*}(a)g \biggl(\frac{S(t,a)}{S^{*}(a)} \biggr)da +\omega (0)U_{2}^{*}(0)g \biggl(\frac{U_{2}(t,0)}{U_{2}^{*}(0)} \biggr) \\ &+ \int_{0}^{\infty}\gamma(\theta)U_{2}^{*}( \theta) \biggl(-\frac{U _{1}(t)}{U_{1}^{*}}-\frac{U_{1}^{*}U_{2}(t,\theta)}{U_{1}(t)U_{2} ^{*}(\theta)}+1+1+\ln\frac{U_{2}(t,\theta)}{U_{2}^{*}(\theta)} \biggr)d\theta. \end{aligned}$$

Note that \(S^{*}(0)=S(t,0)=\varLambda\), \(\omega(0)=\phi\), \(U_{2}^{*}(0)=pU _{1}^{*}\) and \(U_{2}(t,0)=pU_{1}(t)\). Then \(g (\frac{S(t,0)}{S ^{*}(0)} )=0\) and \(g (\frac{U_{2}(t,0)}{U_{2}^{*}(0)} )=g (\frac{U_{1}(t)}{U_{1}^{*}} )\). Furthermore, since

$$ \ln\frac{U_{2}(t,\theta)}{U_{2}^{*}(\theta)}=\ln\frac{U_{1}^{*}U _{2}(t,\theta)}{U_{1}(t)U_{2}^{*}(\theta)}+\ln\frac{U_{1}(t)}{U _{1}^{*}} $$

and \(p\phi U_{1}^{*}=\int_{0}^{\infty}\gamma(\theta)\varrho( \theta)pU_{1}^{*}d\theta=\int_{0}^{\infty}\gamma(\theta)U_{2} ^{*}(\theta)d\theta\) hold, we obtain that

$$\begin{aligned} \frac{d V_{*}(t)}{dt} ={}&- \int_{0}^{\infty}\sigma^{*}(a) S^{*}(a)g \biggl(\frac{S(t,a)}{S^{*}(a)} \biggr)da +p\phi U_{1}^{*}g \biggl(\frac{U _{1}(t)}{U_{1}^{*}} \biggr) \\ &- \int_{0}^{\infty}\gamma(\theta)U_{2}^{*}( \theta)g \biggl(\frac{U _{1}(t)}{U_{1}^{*}} \biggr)d\theta- \int_{0}^{\infty}\gamma(\theta)U _{2}^{*}( \theta)g \biggl(\frac{U_{1}^{*}U_{2}(t,\theta)}{U_{1}(t)U _{2}^{*}(\theta)} \biggr)d\theta \\ ={}&- \int_{0}^{\infty}\sigma^{*}(a)S^{*}(a)g \biggl( \frac{S(t,a)}{S^{*}(a)} \biggr)da - \int_{0}^{\infty}\gamma(\theta)U _{2}^{*}( \theta)g \biggl(\frac{U_{1}^{*}U_{2}(t,\theta)}{U_{1}(t)U _{2}^{*}(\theta)} \biggr)d\theta, \end{aligned}$$

which implies that \({d V_{*}(t)}/{dt}\leq0\) holds due to \(g(y)\geq0\) for all \(y>0\). What’s more, \({d V_{*}(t)}/{dt}=0\) if and only if \({S(t,a)}={S^{*}(a)}\), \(U_{2}(t,\theta)=U_{2}^{*}(\theta)\) and \(U_{1}^{*}U_{2}(t,\theta)=U_{1}(t)U_{2}^{*}(\theta)\), thus, \(U_{1}(t)=U_{1}^{*}\) holds. When \({S(t,a)}={S^{*}(a)}\) and \(U_{1}(t)=U _{1}^{*}\), system (4) has the unique solution \(E_{*}\). Hence, \(M_{*}=\{E_{*}\}\subset\varOmega\) is the largest invariant subset of \(\{(S,U_{1},U_{2}):{d V_{*}(t)}/{dt}=0\}\). By the Lyapunov-LaSalle invariance principle [15], \(E_{*}\) is globally asymptotically stable when \(\Re_{0}>1\). This finishes the proof.

5 Conclusions and Discussions

This paper investigates the global behaviors of an age-structured heroin epidemic model which includes two age-dependent variables describing the susceptibility of individuals and the relapse of heroin users in treatment. We establish that the global behaviors are completely determined by the basic reproduction ratio \(\Re_{0}\). If \(\Re_{0}<1\), then the heroin users eventually are under control in the sense that the heroin-free equilibrium is globally asymptotically stable (see Fig. 2); while if \(\Re_{0}>1\), then there exists a unique heroin-spread equilibrium and it is globally asymptotically stable (see Fig. 3). Clearly, the age-dependent susceptibility and relapse always influence the basic reproduction ratio, thus, influence the global behaviors of heroin epidemic model. Here, it should be noted that it is necessary to show the asymptotic smoothness of the family of solutions and uniform persistence of the system which are two major aspects in applying the means of Lyapunov functionals and LaSalle’s invariance principle. To illustrate the main theoretical results, we take the constant parameter values in Table 1 and the remaining age-dependent functions as

$$\begin{aligned} &\beta(a)=\frac{3}{100} \biggl(1+\sin\frac{(a-30)\pi}{60} \biggr), \qquad \delta_{2}(\theta)=\frac{1}{10} \biggl(1+\sin\frac{(\theta-20) \pi}{40} \biggr), \\ &\gamma(\theta)=\frac{1}{65} \biggl(1+\sin \frac{(\theta-1)\pi}{2} \biggr). \end{aligned}$$

Here, we assume that the maximum life times of susceptible and relapsing individuals are 60 and 40 years, respectively. In general, the treatment time is 2 years and the average treatment time is 1 year. The average values of \(\beta(a)\), \(\delta_{2}(\theta)\) and \(\gamma(\theta)\) are \(3/100\), \(1/10\) and \(1/65\), which are the same with those values given in [26].

Fig. 2
figure 2

The global asymptotically stability of the heroin-free equilibrium. Take \(\varLambda=1\) and \(\Re_{0}=0.28<1\)

Full size image
Fig. 3
figure 3

The global asymptotically stability of the heroin-present equilibrium. Take \(\varLambda=13\) and \(\Re_{0}=3.59>1\)

Full size image
Table 1 The biological meanings for parameter values of system (4)
Full size table

Furthermore, we can provide a special case of model (4) when the age-dependent variables \(\gamma(\theta)\) and \(\delta_{2}(\theta)\) are taken as positive constants, i.e., \(\gamma(\theta)=\gamma_{0}\) and \(\delta_{2}(\theta)=\delta_{2}\). Then, model (4) is equivalent to the following model

$$ \textstyle\begin{cases} (\frac{\partial}{\partial t}+\frac{\partial}{\partial a}) S(t,a)=- [\beta(a)U_{1}(t)+\mu ] S(t,a), \\ \frac{d U_{1}(t)}{dt}=U_{1}(t)\int_{0}^{\infty}\beta(a)S(t,a)da-( \mu+\delta_{1}+p)U_{1}(t)+\gamma_{0}U_{2}(t), \\ \frac{d U_{2}(t)}{dt}=pU_{1}(t)-(\mu+\delta_{2})U_{2}(t)-\gamma_{0}U _{2}(t), \\ S(t,0)=\varLambda, \\ S(0,a)=S_{0}(a),\qquad U_{1}(0)=U_{1}^{0},\qquad U_{2}(0)=U_{2}^{0}. \end{cases} $$
(30)

Model (30) describes a heroin epidemic model with age-dependent susceptibility. In fact, if we relabel \(U_{1}(t), U_{2}(t)\) as \(I(t), R(t)\) and don’t consider the relapse of disease \((\gamma_{0}=0)\), then model (30) is just that investigated in [18]. Moreover, if the age-dependent variable \(\beta(a)\) is taken as positive constant, i.e., \(\beta(a)= \beta_{0}\). Then, the specific model of model (4) is

$$ \textstyle\begin{cases} S(t)=\varLambda-\beta_{0}U_{1}(t)S(t)-\mu S(t), \\ \frac{d U_{1}(t)}{dt}=\beta_{0}U_{1}(t)S(t)-(\mu+\delta_{1}+p)U_{1}(t)+ \int_{0}^{\infty}\gamma(\theta)U_{2}(t,\theta)d\theta, \\ (\frac{\partial}{\partial t}+\frac{\partial}{\partial a}){ U_{2}(t,a)}=-( \gamma(\theta)+\delta_{2}(\theta)+\mu)U_{2}(t,a), \\ U_{2}(t,0)=pU_{1}(t), \\ S(0)=S_{0},\qquad U_{1}(0)=U_{1}^{0},\qquad U_{2}(0,a)=U_{2}^{0}(a), \end{cases} $$
(31)

which is just that investigated in [26]. According to Theorems 2–3, the global behaviors of models (30)–(31) are completely determined by the basic reproduction ratio.

Finally, to control the spread of heroin, several related strategies should be made to reduce the reproduction number to below unity. Note that the basic reproduction ratio has the form

$$\begin{aligned} \Re_{0}=\frac{\varLambda}{(\mu+\delta_{1}+p)-p\phi} \int_{0}^{\infty }\beta(a)e^{-\mu a}da. \end{aligned}$$

Directly computing shows that

$$\begin{aligned} &\frac{\partial\Re_{0}}{\partial\varLambda} =\frac{1}{(\mu+\delta _{1}+p)-p\phi} \int_{0}^{\infty}\beta(a) e^{-\mu a}da>0, \\ &\frac{\partial\Re_{0}}{\partial\delta_{1}}=-\frac{1}{((\mu+\delta _{1}+p)-p\phi)^{2}} \int_{0}^{\infty}\beta(a) e^{-\mu a}da< 0, \\ &\frac{\partial\Re_{0}}{\partial p}=-\frac{1-\phi}{((\mu+\delta _{1}+p)-p\phi)^{2}} \int_{0}^{\infty}\beta(a) e^{-\mu a}da< 0. \end{aligned}$$

Hence, the efficient methods of controlling the spread of heroin include reducing the input rate and improving the treatment rate. Besides, the numerical simulation shows the influences of \(\varLambda\) and \(p\) on \(\Re_{0}\) (see Fig. 4). It follows from the form of the basic reproduction ratio that it is affected by the age-dependent susceptibility and relapse. Specifically,

$$\begin{aligned} \frac{\partial\Re_{0}}{\partial\phi}=\frac{p\varLambda}{((\mu+\delta _{1}+p)-p\phi)^{2}} \int_{0}^{\infty}\beta(a)e^{-\mu a}da>0, \end{aligned}$$

which implies that \(\Re_{0}\) is an increasing function of \(\phi\). Furthermore, \(\phi\) is an increasing function of relapse rate \(\gamma(\theta)\). Thus, reducing the relapse of heroin users in treatment is benefit for controlling the spread of heroin. Moreover, decreasing the number of contacts, and hence the susceptibility of individuals, is also helpful for the reduction of the value of the basic reproduction ratio. Those may provide the theoretical basis for the health workers to design feasible control strategies.

Fig. 4
figure 4

The effects of treatment rate and birth rate on the basic reproduction ratio

Full size image