In classical thermodynamics, the mathematical description of a gas is based on the conservation laws of mass, momentum and energy [1, 2]. The closure of such equations is performed through the well-known Navier–Stokes and Fourier laws, which impose that the viscous stress tensor and the heat flux are proportional to the gradients of the velocity and of the temperature, respectively.

Following the extended thermodynamics [3] assumptions, the viscous stress tensor, the heat flux and, if necessary, other non-equilibrium quantities are considered as independent field variables. And appropriate balance laws for such quantities are taken into the theory.

Classical and extended thermodynamics models differ from each other not only in the physical approach, but also in the mathematical structure of the basic equations. In fact, the classical PDE system is of parabolic type, while the extended thermodynamics one is of hyperbolic type.

In the last twenty years the two theories have been mutually compared and tested in many different physical situations in order to understand their validity limits and their differences. Starting about ten years ago, several studies of the heat transfer problem were made to check if the substantial differences of their predictions can be detected in this simple non-equilibrium problem. The pioneering work on this subject [4] shows that, in a monatomic gas composed of single constituent at rest confined between two coaxial cylinders or two concentric spheres, some shear stress tensor components do not vanish, in contrast with predictions by the classical thermodynamics theory. Moreover, it was shown that this effect can affect also the temperature profile inside the bounded domain. Afterwards, similar results were observed for single monoatomic gases enclosed in non-planar bounded domain [5–7] and also for gas mixtures both in planar [8–10] and non-planar geometries [11]. At least for mixtures between two parallel plates, the results were also successfully compared with the Monte Carlo predictions [8].

Up to now, several authors worked on extended thermodynamics theories for polyatomic and/or dense gases [12–17]. However, these theories have some inherent difficulties. Recently a new theory gives rise to a promising model [18, 19], which was also derived for rarefied polyatomic gases through the kinetic moment equations with the maximum entropy principle [20]. In this paper, we will adopt the system of field equations proposed in [18]. The usefulness of the new theory was confirmed by the fact that the dispersion relation for ultrasonic sound in rarefied diatomic gases agrees well with the experimental data even in the high frequency range where the classical theory is no more valid [21]. Moreover, the shock wave structure in a polyatomic gas observed by experiments can be well explained by the theory [22, 23]. It is also proved [24, 25] that the theory can be regarded as a generalization of the Meixner theory of relaxation processes [26, 27].

In the case of a rarefied polyatomic gas confined between two parallel plates [28], it was found that relevant differences between classical and extended models are predicted if the specific heat at constant volume c V of the gas is not constant with respect to the temperature. In fact, for the first time, it was predicted non-vanishing non-equilibrium pressure (dynamic pressure) and non-vanishing viscous stress tensor components in a single gas at rest between two parallel plates. While, in the case of polyatomic gases with constant specific heat, differences between the two theories are observable only in the radial geometry and are restricted to the viscous stress tensor components.

In the present paper we will focus our attention on the stationary heat transfer problem in a van der Waals gas in the case of a constant specific heat c V , which is a typical model of realistic gases characterized by the following caloric and thermal equations of state:

$$\begin{aligned} p = \frac{k}{m} \frac{T \rho}{1 - b\rho} - a\rho^2, \qquad \varepsilon= \frac{D}{2}\frac{k}{m}T - a\rho, \end{aligned}$$
(1)

where p is the pressure, k the Boltzmann constant, m the mass of a molecule, T the absolute temperature, and ρ the mass density. The material-dependent constants a and b represent, respectively, a measure of the attraction between the constituent molecules and the effective volume (or exclusion volume) of a molecule [2]. Finally, D represents the degrees of freedom of a molecule.

If we assume that the gas is at rest in the gap between two plane parallel plates, we will find out a surprising result. In fact, although we take into account a temperature range for which the specific heat c V is constant, the non-equilibrium pressure and the viscous stress tensor cannot vanish. To our knowledge this is the first case in which such a phenomenon is described and, under the previous assumptions, differences between classical and extended thermodynamics are predicted. Unfortunately, the effect is very small, at least at a low or room temperature. Due to this fact, the experimental detection of the differences may be quite difficult.

1 Field Equations

In what follows we will adopt the system of field equations for a van der Waals gas prescribed in [18] appropriate to a planar one-dimensional problem. We assume that all field variables depend only on spatial coordinate x (orthogonal to the two plates) and, furthermore, that the gas velocity v vanishes, we obtain the following system of six field equations, where the quadratic terms in the non-equilibrium variables are neglected:Footnote 1

$$ \begin{aligned} \frac{\mathrm{d}}{\mathrm{d}x} [ p+\varPi-S_{\langle 11\rangle} ] &=0, \\ \frac{\mathrm{d}q}{\mathrm{d}x}&=0,\quad\Rightarrow\quad q=Q_0, \\ -\frac{2}{3}q\frac{\mathrm{d}K}{\mathrm{d}x}&=-\frac{S_{\langle 11\rangle}}{\tau _{S}}, \\ \frac{1}{3}q\frac{\mathrm{d}K}{\mathrm{d}x}&=-\frac{S_{\langle 22\rangle}}{\tau _{S}}, \\ q\frac{\mathrm{d}L}{\mathrm{d}x}&=-\frac{\varPi}{\tau_{\varPi}}, \end{aligned} $$
(2)

and

$$\begin{aligned} &-\frac{h_{4}}{2T^{2}}\frac{\mathrm{d}T}{\mathrm{d}x}+\frac{\mathrm{d}}{\mathrm{d}x} \biggl[ \frac{h_{4}}{4h_{2}} \biggl( L-\frac{2}{D ( 1-b\rho ) } \biggr) \varPi \biggr] - \frac{\mathrm{d}}{\mathrm{d}x} \biggl[ \frac {h_{4}}{4h_{3}}KS_{\langle 11\rangle} \biggr] \\ &\quad{}+ \biggl[ -\frac{k}{m}\frac{T}{\rho ( 1-b\rho ) }\frac{\mathrm{d}\rho }{\mathrm{d}x}+ \frac{D}{2}\frac{k}{m}\frac{\mathrm{d}T}{\mathrm{d}x} \biggr] ( \varPi-S_{\langle 11\rangle} ) =-\frac{q}{\tau_{q}}. \end{aligned}$$
(3)

The six variables are the temperature T, the mass density ρ, the dynamic pressure Π, the two traceless parts of the viscous stress tensor S 〈11〉 and S 〈22〉, and the x-component of the heat flux q.

The other functions in (2) and (3) are L=5K/6 and

$$ \begin{aligned} K&=4\frac{\frac{k}{m}T+\frac{a}{b^{2}\rho} ( 1-b\rho ) [ b\rho+\log ( 1-b\rho ) ] }{ ( D+2 ) \frac {k}{m}T-D ( 1-b\rho ) a\rho}, \\ h_{2}&=-\frac{T}{6} \biggl[ \frac{k}{m} \frac{ ( 2 ( D-3 ) -5Db\rho ) \rho T}{D ( 1-b\rho ) ^{2}}+a\rho^{2} \biggr] , \\ h_{3}&=-T \biggl( \frac{k}{m}\frac{\rho T}{1-b\rho}-a \rho^{2} \biggr) , \qquad h_{4}=-\frac{k}{m}T^{2} \biggl( \frac{\frac{k}{m} ( D+2 ) \rho T}{1-b\rho}-Da\rho^{2} \biggr), \end{aligned} $$
(4)

while, the relaxation times are defined as

$$ \tau_{S}=-\frac{2h_{3}}{\sigma},\qquad \tau_{\varPi}=- \frac{2h_{2}}{\varsigma},\qquad \tau_{q}=-\frac {2h_{4}}{\tau}, $$
(5)

with σ, ς and τ constants that depend on the material.

It is easy to see that (2)1,2 represent respectively the conservation laws of momentum and energy, while the other equations are the balance laws for the two components of the viscous stress and the heat flux. The conservation law of mass is identically satisfied and therefore it is omitted.

One can deduce from (2)3–5 that, even in the planar case and for v=0, the viscous stress is not zero if a van der Waals gas is considered. Moreover, there exists a non-vanishing dynamic pressure Π. Clearly, it is interesting to determine its form and its order of magnitude. For this reason, in the next section we will integrate numerically the field equations (2) and (3).

In order to make our study concise, we introduce the following dimensionless quantities:

$$ \begin{aligned} &\hat{x}=\frac{x}{d},\qquad \hat{T}=\frac{T}{T_{\mathrm{C}}}, \qquad \hat{\varPi}=\frac{\varPi}{P_{\mathrm{C}}}, \\ &\hat{S}_{\langle ij\rangle}=\frac{S_{\langle ij\rangle}}{P_{\mathrm{C}}},\qquad \hat{q}=\frac{q}{P_{\mathrm{C}}\sqrt{\frac{k}{m}T_{\mathrm{C}}}}, \qquad \hat{\rho}=\frac{\rho}{\rho_{\mathrm{C}}}, \end{aligned} $$
(6)

where d is the distance between the two plates, and

$$ \rho_{\mathrm{C}}=\frac{1}{3b},\qquad P_{\mathrm{C}}= \frac{a}{27b^{2}},\qquad T_{\mathrm{C}}=\frac{8a}{27\frac{k}{m}b}, $$
(7)

are the critical values of the density, pressure and temperature, respectively.

According to the van der Waals model, the critical temperature T C is the value of the temperature above which no phase transition is allowed; the critical pressure is the pressure below which metastable and coexistence states are allowed, and the critical density is the density of the state characterized by the critical temperature and pressure following the thermal equation of state (1)1. Usually, the field variables are reduced in this dimensionless form [2], so that the equations of state can be rewritten in a form independent of the material constants a and b.

Referring to these new variables, the field equations read

$$ \begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\hat{x}} [ \hat{p}+\hat{\varPi}-\hat {S}_{\langle 11\rangle} ] &=0, \\ \frac{\mathrm{d}\hat{q}}{\mathrm{d}\hat{x}}&=0,\quad\Rightarrow\quad\hat{q}=\hat{Q }_0, \\ -\frac{2}{3}\hat{q}\frac{\mathrm{d}K}{\mathrm{d}\hat{x}}&=-\frac{\hat {S}_{\langle 11\rangle}}{\hat{\tau}_{S}}, \\ \frac{1}{3}\hat{q}\frac{\mathrm{d}K}{\mathrm{d}\hat{x}}&=-\frac{\hat {S}_{\langle 22\rangle}}{\hat{\tau}_{S}} \quad\Rightarrow \quad \hat{S}_{\langle 22\rangle}=-2\hat{S}_{\langle 11\rangle}, \\ \hat{q}\frac{\mathrm{d}L}{\mathrm{d}\hat{x}}&=-\frac{\hat{\varPi }}{\hat{\tau}_{\varPi}} \quad\Rightarrow\quad\hat{ \varPi}=-\frac{5}{4}\frac{\hat{\tau }_{\varPi}}{\hat{\tau}_{S}}\hat{S}_{\langle 11\rangle}, \end{aligned} $$
(8)

and

$$\begin{aligned} &-\frac{\hat{h}_{4}}{2\hat{T}^{2}}\frac{\mathrm{d}\hat{T}}{\mathrm{d}x}+\frac{\mathrm{d}}{\mathrm{d}\hat{x}} \biggl[ \frac{\hat{h}_{4}}{4\hat {h}_{2}} \biggl( L-\frac{2}{D ( 1-\hat{b}\hat{\rho} ) } \biggr) \hat{\varPi} \biggr] - \frac{\mathrm{d}}{\mathrm{d}\hat{x}} \biggl[ \frac{\hat {h}_{4}}{4\hat{h}_{3}}K\hat{S}_{\langle 11\rangle} \biggr] \\ &\quad{}+ \biggl[ -\frac{\hat{T}}{\hat{\rho} ( 1-\hat{b}\hat{\rho} ) }\frac{\mathrm{d}\hat{\rho}}{\mathrm{d}\hat{x}}+\frac{D}{2} \frac{\mathrm{d}\hat{T}}{\mathrm{d}\hat{x}} \biggr] ( \hat{\varPi}-\hat {S}_{\langle 11\rangle} ) =- \frac{\hat{q}}{\hat{\tau}_{q}}, \end{aligned}$$
(9)

where \(\hat{Q}_{0}\) denotes a constant dimensionless heat flux, and we have

$$ \begin{aligned} \hat{p}&=\frac{p}{P_{\mathrm{C}}}=8\frac{\hat{\rho}\hat{T}}{3-\hat{\rho }}-3\hat{ \rho}^{2}, &\quad& \hat{a}=\frac{aP_{\mathrm{C}}}{ ( \frac{k}{m}T_{\mathrm{C}} ) ^{2}}=\frac{27}{64}, \\ K&=4\frac{\hat{T}+\frac{8}{3}\frac{\hat{a}}{\hat{b}^{2}\hat{\rho}} ( 1-\hat{b}\hat{\rho} ) [ \hat{b}\hat{\rho}+\log ( 1-\hat{b}\hat{\rho} ) ] }{ ( D+2 ) \hat {T}-\frac{8}{3}D ( 1-\hat{b}\hat{\rho} ) \hat{a}\hat{\rho}}, &\quad& \hat{b}=b\rho_{\mathrm{C}}=\frac{1}{3}, \\ \hat{h}_{2}&=\frac{h_{2}}{P_{\mathrm{C}}T_{\mathrm{C}}}=-\frac{4\hat {T}}{9} \biggl[ \frac{2 ( D-3 ) -5D\hat{b}\hat{\rho}}{D ( 1-\hat{b}\hat{\rho} ) ^{2}}\hat{\rho}\hat{T}+\frac{8}{3}\hat{a}\hat { \rho}^{2} \biggr] , &\quad& L=\frac{5}{6}K, \\ \hat{h}_{3}&=\frac{h_{3}}{P_{\mathrm{C}}T_{\mathrm{C}}}=-\frac{8}{3}\hat {T} \biggl( \frac{\hat{\rho}\hat{T}}{1-\hat{b}\hat{\rho}}-\frac{8}{3}\hat {a}\hat{\rho}^{2} \biggr) , & \quad& \frac{1}{\hat{\tau}_{S}}=\frac{d}{\tau_{S}\sqrt{\frac{k}{m}T_{\mathrm{C}}}}=-\frac{\hat{\sigma}}{2\hat{h}_{3}}, \\ \hat{h}_{4}&=\frac{h_{4}}{P_{\mathrm{C}}\frac{k}{m}T_{\mathrm{C}}^{2}}=-\frac{8}{3} \hat{T}^{2} \biggl( \frac{ ( D+2 ) \hat {\rho}\hat{T}}{1-\hat{b}\hat{\rho}}-\frac{8}{3}D\hat{a}\hat{ \rho }^{2} \biggr) , &\quad& \frac{1}{\hat{\tau}_{\varPi}}=\frac{d}{\tau_{\varPi}\sqrt{\frac {k}{m}T_{\mathrm{C}}}}=- \frac{\hat{\varsigma}}{2\hat{h}_{2}}, \\ \frac{1}{\hat{\tau}q}&=\frac{d}{\tau_{q}\sqrt{\frac{k}{m}T_{\mathrm{C}}}}=-\frac{\hat{\tau}}{2\hat{h}_{4}}, &\quad& \hat{ \sigma}=\frac{\sigma d}{P_{\mathrm{C}}T_{\mathrm{C}}\sqrt{\frac {k}{m}T_{\mathrm{C}}}}, \\ \hat{\varsigma}&=\frac{\varsigma d}{P_{\mathrm{C}}T_{\mathrm{C}}\sqrt{\frac {k}{m}T_{\mathrm{C}}}}, &\quad& \hat{\tau}=\frac{\tau d}{P_{\mathrm{C}}\frac{k}{m}T_{\mathrm{C}}^{2}\sqrt {\frac{k}{m}T_{\mathrm{C}}}}. \end{aligned} $$
(10)

It is clearly verified that the (8) and (9) constitute a non-linear ordinary differential system of the fourth order in the four independent field variables \(\hat{T}\), \(\hat{\rho}\), \(\hat {\varPi}\) and \(\hat{q}\). The remaining quantities \(\hat{S}_{\langle 11\rangle}\) and \(\hat{S}_{\langle 22\rangle}\) can be algebraically determined in terms of the others. Unfortunately, the system cannot be easily rewritten in the normal form and so we will integrate it through an implicit method. In [18] it is recalled that the non-stationary extended thermodynamics system for a van der Waals gas is symmetric hyperbolic in the neighborhood of equilibrium, if the concavity of the entropy density holds. The concavity condition is expressed through the following four inequalities:

$$ \begin{aligned} &\frac{8\hat{T}\hat{\rho}}{3-\hat{\rho}}-3\hat{\rho}^2>0, &\quad& \frac{8 \hat{T}}{(3-\hat{\rho})^2}-2\hat{\rho}>0, \\ &\frac{18+D(5\hat{\rho}-6)}{D(\hat{\rho}-3)^2}\hat{T}^2\hat{\rho}-\frac {3}{8}\hat{T} \hat{\rho}^2<0, &\quad& \frac{8(D+2)\hat{T}+3D(\hat{\rho }-3)\rho}{\rho-3}\hat{T}^2\hat{ \rho}<0. \end{aligned} $$
(11)

Then, although we will focus our attention on the stationary case, which is described by an ODE system, in what follows we will consider only solutions that satisfy the concavity condition (11).

What about the corresponding classical thermodynamics equations? As said before, the classical theory assumes that the non-equilibrium pressure and the viscous stress are proportional to the velocity gradient, which for a gas at rest obviously vanish. Therefore, in classical approximations, the system of (8) and (9) reduces to the following third order system of equations:

$$ \begin{aligned} \frac{\mathrm{d}\hat{p}}{\mathrm{d}\hat{x}} &=0, \\ \frac{\mathrm{d}\hat{q}}{\mathrm{d}\hat{x}}&=0 \quad \Rightarrow\quad \hat {q}=\hat{Q}_0, \\ \hat{S}_{\langle 11\rangle}&=0, \\ \hat{S}_{\langle 22\rangle}&=0, \\ \hat{\varPi}=0, \\ -\frac{\hat{h}_{4}}{2\hat{T}^{2}}\frac{\mathrm{d}\hat{T}}{\mathrm{d}x}&=-\frac{\hat{q}}{\hat{\tau}_{q}}. \end{aligned} $$
(12)

The classical and extended thermodynamics systems contain material parameters that are \(\hat{\sigma}\), \(\hat{\varsigma}\) and \(\hat{\tau}\). These parameters should be determined through experimental data before the integration of the two systems. This will be the subject of the next section.

2 Estimation of the Parameters

In the reference [18], it was shown that the three relaxation times are related to the shear viscosity μ, bulk viscosity ν and heat conductivity κ by

$$ \mu=p\tau_{S},\qquad \nu=-\frac{2h_2}{T}\tau_{\varPi}, \qquad \kappa=-\frac {h_4}{2T^2}\tau_{q}. $$
(13)

These relations together with the relations (5) can be used to evaluate the three material constants σ, ς and τ, when the shear viscosity, the bulk viscosity and the heat conductivity are known at least for particular choices of the physical parameters. Unfortunately, there are very few experimental results about the bulk viscosity, so very few materials and very few temperature ranges can be completely investigated. For this reason we will assume, for simplicity of the present analysis, that σ, ς and τ remain constant within the range of temperature values of the heat transfer problem. Of course, this is a rough approximation, but at the moment this is the simplest approach in order to evaluate the role of Π and S 〈ii〉.

As an example, we consider the case of a diatomic gas: Nitrogen (N2), so that D=5, m=28 (atomic mass unit), T C=126.19 K, p C=33.96 bar and ρ C=313.3 Kg/m3. To evaluate \(\hat{\sigma}\), \(\hat{\varsigma}\) and \(\hat{\tau}\), we refer to the values for the viscosities and the heat conductivity of [29] (Table 1 second line T=180 K for which it seems that p=1 bar). Then, for a very small distance between the two plates of the order of 10−3 m, it follows that \(\hat{\sigma} \simeq2839\), \(\hat{\varsigma}\simeq173\) and \(\hat{\tau} \simeq21116\). These are the coefficients that we will use for the numerical integrations of the two systems (8) and (9), and (12).

3 Boundary Values

We already said that the system of (8) and (9) can be reduced through algebraic relations to an ordinary differential system of the fourth order. Which boundary conditions can be physically assigned?

We will consider the gas confined between a permeable plate and an impermeable one. For the sake of simplicity, we assume that the permeable wall is the one at \(\hat{x}=0\) and it is also kept at a fixed temperature. In this way, at \(\hat{x}=0\) we can prescribe both the density ρ 0 and the temperature T 0 of the gas. At the impermeable wall (at \(\hat{x}=1\)), a fixed heat flux Q 0 is applied, so that the gas is at rest and we know the value of the constant heat flux.

These data are sufficient to determine completely the solution of the classical system (12), but one more condition is required for the integration of the extended thermodynamics system of (8) and (9). Unfortunately, no other data can be assigned referring to the physics of the problem: once more we are dealing with non-controllable boundary data! This problem is well-known in the literature and in the last years several approaches were introduced to overcome it.

In the present case, we have started assigning different values of the non-equilibrium pressure at one boundary and we found that the corresponding solutions, after a very steep boundary layer (very close to a vertical line), will sweep into the same single function. Although there is no proof of that, it seems that the “correct” boundary value is the one for which no boundary layers are observed. A similar phenomenon was already observed in a different context [30].

Of course, the same considerations are valid also for S 〈11〉, since it is related to Π by an algebraic relation. On the contrary, not relevant differences can be observed for the temperature and the mass density when the boundary values for Π are varied within the range of validity of the entropy concavity.

4 Numerical Examples

In this section, we present the results obtained by the numerical integration of the field equations for nitrogen with the values of the parameters and the boundary conditions previously introduced.

In particular, we are interested in the profiles of the non-equilibrium variables S 〈11〉 and Π, and their order of magnitude. Comparison between classical and extended thermodynamics predictions will also be made.

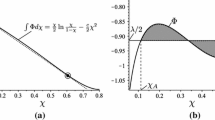
For N2 enclosed between two parallel plates we consider the case in which \(\hat{T_{0}}=1.008\), \(\hat{\rho}_{0}=0.5\), \(\hat{Q}_{0}=-0.005\). The results are illustrated in Fig. 1, where the classical solution is drawn in dashed lines, while the solid lines correspond to the extended thermodynamic fields. The variables \(\hat{\rho}\) and \(\hat{T}\) obtained from the classical and extended theories coincide with each other at least at the plot precision. For that reason we present also the plot of the differences between extended and classical thermodynamics predictions. On the contrary, the non-equilibrium variables \(\hat{\varPi}\), \(\hat{S}_{\langle 11\rangle}\) and \(\hat{S}_{\langle 22\rangle}=-2\hat{S}_{\langle 11\rangle}\) differ from the corresponding vanishing ones, predicted by the classical approximations. The order of magnitude of \(\hat{\varPi}\) and \(\hat{S}_{\langle ii\rangle}\) is very small in both cases. In Fig. 1, the non equilibrium variables \(\hat{\varPi}\) and \(\hat{S}_{\langle ii\rangle}\) seem to be zero at the right boundary. This is due only to the small plot precision. In fact, an accurate analysis of the field variables and a comparison with the numerical integration precision show that the dynamic pressure and the stress tensor do not vanish at \(\hat{x}=1\). These considerations about non-equilibrium variables are also valid in Fig. 2.

Fig. 1
figure 1

The solutions of the heat transfer problem in N2, as predicted by the extended (solid lines) and classical (dashed lines) theory. For mass density and temperature the differences between classical and extended thermodynamics are also presented in solid line

Full size image
Fig. 2
figure 2

The solutions of the heat transfer problem in N2, as predicted by extended thermodynamics, for different values of the assigned heat flux

Full size image

In Fig. 2, we assign the same values of the temperature and of the mass density at \(\hat{x}=0\) as in Fig. 1 and vary the heat flux value (\(\hat{Q}_{0}=-0.002, -0.005, -0.01\)). The higher is the value of \(\hat{Q}_{0}\), the higher is also the magnitude order of \(\hat{S}_{\langle 11\rangle}\) and \(\hat{\varPi}\). This result is in agreement with the idea that the role of dynamic pressure and stress tensor becomes more relevant as the solution is further from equilibrium.

5 Conclusions and Final Remarks

We have shown that the extended thermodynamics model for van der Waals gases, that is, typical real gases, describes the presence of the non-vanishing dynamic pressure and the viscous stress tensor, even in the simplest case of heat transfer in a gas at rest confined between two parallel plates. To our knowledge, such an effect is predicted here for the first time in the literature. In the last section, we have also verified that for gases at or below the room temperature this effect is very small and does not affect significantly the behaviors of the temperature and of the mass density. Consequently, the difference between classical and extended thermodynamics cannot be easily detected in experiments.

We did not consider solutions very far from equilibrium or at very high temperature, since in those cases no experimental datum was available for the parameter determination. Moreover, we have assumed the constant coefficients as a rough approximation. With a more accurate description or for a solution further from equilibrium, is it possible to observe more evident differences in the temperature and density fields? The question about the possible detection of the effect through experiments remains still open, and suggests, once more, the necessity of detailed experimental investigations of the heat transfer problem in gases.

The last point worthy of remark is the following. In the present paper, we have analyzed the case of dense gases with the constant specific heat c V as a first step of our study. However, in the case of dense gases with non-constant specific heat c V , we can expect much larger effects of the non-equilibrium quantities on the temperature and density profiles in a heat transfer problem. Indeed such effects have recently been found out in rarefied polyatomic gases [28] as remarked in the introduction. This is the next subject we are now planning to study.