Abstract
This paper is devoted to the classification of analytic integrable cases of two families of degenerate planar vector fields with a monodromic singular point at the origin. This study falls in the still open degenerate center problem. This classification can be done using the formal normal form theory and knowing a suitable normal form of any differential systems associated to each family.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the most important problems in the study of a planar differential system
where P and Q are analytic in a neighborhood at the origin and coprimes, is to determine when it has a local analytic first integral defined in a neighborhood of a singular point. Other open problem is to characterize when a monodromic singular point is a center. Of course, when the linear part is of center type, i.e., with imaginary eigenvalues and when the linear part is degenerate but not identically zero the characterization is well-known, [8, 18, 19, 21]. However, when the linear part is identically zero, i.e. for a degenerate center the characterization is not known and only some generic cases are solved, see for instance [2, 4–7, 13, 15, 17] and references therein.
One form to characterize the center problem for a nondegenerate singular point is through the existence of an analytic first integral in a neighborhood of the origin, see [9, 16, 18, 21]. However, the existence of this analytic first integral is only a sufficient condition to have a center for a nilpotent or a degenerate singular point, see [10–12]. Therefore there are nilpotent and degenerate centers not characterized by the existence of a local analytic first integral, see for instance [13, 15, 17, 20, 22, 24] and references therein.
For nilpotent singular points, the orbital normal form of the centers with analytic first integral was obtained in [23]. The result is the following:
Theorem 1.1
Any nilpotent center has a local analytic first integral if, and only if, it is analytically orbital equivalent to the Hamiltonian system
with k>1.
Nowadays the integrability problem for non-monodromic nilpotent systems is not solved. The problem of recognizing what degenerate singular points have an analytic first integral is still open, although some partial result have been achieved recently. In [6] the analytic integrability problem for a large family of degenerate planar system was studied. More specifically it was studied the degenerate systems of the form
and the following result was established:
Theorem 1.2
System (1.3) is analytically integrable if, and only if, it is formally equivalent to \(\dot{x}=y^{3}+3\mu x^{2} y\), \(\dot{y}= - x^{3}-3\mu x y^{2}\).
This result is equivalent to Theorem 1.1 but for degenerate systems of the form (1.3). The result was obtained by means of the normal form theory.
In [7] it is investigated if similar results for the family of degenerate systems of the form
can be obtained where the dots means terms of higher order than the first component in the quasi-homogeneous order (see definition below). However the results for systems (1.4) are different to the ones obtained for family (1.3). In fact systems (1.4) with an analytic first integral are not formally equivalent to their Hamiltonian leading part as the following result shows and this is the first family in which this phenomenon is observed.
Theorem 1.3
System (1.4) is analytically integrable if, and only if, it is formally equivalent to \(\dot{x}=y^{3}+2a x^{3} y- 2 \beta_{9} x^{4}y\), \(\dot{y} = -x^{5}-3a x^{2} y^{2}+ 4\beta_{9} x^{3} y^{2}\), where β 9 depends on the parameters of the first three quasi-homogeneous components.
This result shows that the analytic integrability problem is a difficult problem and requires further studies to find the complete solution for any degenerate differential system. In [14] such type of degenerate systems were called generalized nilpotent systems.
In this work and by means of the normal form theory we obtain necessary and sufficient conditions for the analytic integrability of some families of degenerate planar vector fields. More specifically for the family (3.3) and the family (4.3) (see these families along the work). These families are considered because are the easiest cases of monodromic families where we can apply the formal normal form and as a test bed for future studies in the analytic integrability problem for degenerate singular points. The paper is organized as follows: in Sect. 2 we give some preliminary definitions and results, in Sects. 3 and 4 using the formal normal forms theory, we compute the analytic integrability cases for these polynomial families of the type (1.3) and (1.4), respectively.
In our analysis, we use some definitions and terminology, related to the quasi-homogeneous expansions of planar vector fields. In the next section we summarize these results.
2 Preliminary Definitions and Results
A scalar function f is quasi-homogeneous of type \({\mathbf{t}}=(t_{1},t_{2})\in\mathbb{N}^{2}\) and degree k if
The vector space of quasi-homogeneous scalar function of type t and degree k is denoted by  . A vector field F=(P,Q)T is quasi-homogeneous of type t and degree k if
. A vector field F=(P,Q)T is quasi-homogeneous of type t and degree k if  and
and  . The vector space of quasi-homogeneous vector field of type t and degree k is denoted by \(\mathcal{Q}_{k}^{\mathbf{t}}\).
. The vector space of quasi-homogeneous vector field of type t and degree k is denoted by \(\mathcal{Q}_{k}^{\mathbf{t}}\).
Given a vector field F, we can formally write it as a quasi-homogeneous expansion corresponding to a fixed type t:
where each term F k is a quasi-homogeneous vector field of type t and degree k.
Given a scalar function μ, to obtain its quasi-homogeneous expansion μ=∑
k
μ
k
, with  , it is enough to collect the terms of its Taylor expansion whose exponents lie in the straightline t
1
x+t
2
y=k, for each k. The expansion in quasi-homogeneous terms of a vector field F=(P,Q)T is obtained easily from the ones of the components P, Q. If we select the type t=(1,1), we are using in fact the Taylor expansion, but in general, each term in the above expansion involves monomials with different degrees. We give some definitions and properties, see for instance [1, 2].
, it is enough to collect the terms of its Taylor expansion whose exponents lie in the straightline t
1
x+t
2
y=k, for each k. The expansion in quasi-homogeneous terms of a vector field F=(P,Q)T is obtained easily from the ones of the components P, Q. If we select the type t=(1,1), we are using in fact the Taylor expansion, but in general, each term in the above expansion involves monomials with different degrees. We give some definitions and properties, see for instance [1, 2].
-
We denote by X h the Hamiltonian vector field associated to Hamiltonian h, that is, \({\mathbf{X}}_{h}=(-\frac{\partial h}{\partial y},\frac{\partial h}{\partial x})^{T}\). It is easy to check that \({\mathbf{X}}_{h}\in\mathcal{Q}_{k}^{\mathbf{t}}\) if, and only if,
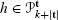 , (here |t|:=t
1+t
2 denotes the modulus of t).
, (here |t|:=t
1+t
2 denotes the modulus of t). -
The divergence of a vector field F=(P,Q)T is \(\operatorname{div}({\mathbf{F}})=\frac{\partial P}{\partial x}+\frac {\partial Q}{\partial y}\). For all \({\mathbf{F}}\in\mathcal {Q}_{k}^{\mathbf{t}}\), we have
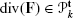 .
. -
The wedge product of two vector fields F=(P,Q)T and G=(R,S)T is the scalar function F∧G=PS−QR. If we take \({\mathbf{F}}\in\mathcal{Q}_{k}^{\mathbf{t}}\) and \({\mathbf{G}}\in\mathcal{Q}_{l}^{\mathbf{t}}\) then
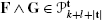 .
. -
The Lie bracket of two vector fields F and G is [F,G]=D FG−D GF. If \({\mathbf{F}}\in\mathcal{Q}_{k}^{\mathbf{t}}\) and \({\mathbf{G}}\in\mathcal{Q}_{l}^{\mathbf{t}}\) then \([{\mathbf{F}},{\mathbf{G}}]\in\mathcal{Q}_{k+l}^{\mathbf{t}}\).
-
We denote \({{\mathbf{D}}_{0}}=(t_{1}x,t_{2}y)^{T}\in\mathcal {Q}_{0}^{\mathbf{t}}\). Observe that it is a radial vector field. For any
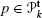 we have ∇p⋅D
0=kp (Euler’s Theorem for quasi-homogeneous vector fields).
we have ∇p⋅D
0=kp (Euler’s Theorem for quasi-homogeneous vector fields).
A key fact, which can be found in [2, 3], is the following. Any planar quasi-homogeneous vector field can be decomposed uniquely as the sum of two quasi-homogeneous vector fields, one of them having zero divergence (conservative part) and the other one with divergence equal to the original vector field (dissipative part).
Lemma 2.1
Let us consider a quasi-homogeneous planar vector field
\({\mathbf{F}}_{k}\in\mathcal{Q}_{k}^{\mathbf{t}}\). Then, there exists a unique couple of quasi-homogeneous polynomials:  ,
,  , such that
, such that
3 The Integrability of a Family of Systems (1.3)
In this section we consider system (1.3) which we write of the form
In this case the homogeneous principal part is of degree 2 respect to type t=(1,1) given by F
2=X
h
, where  and D
0=(x,y)T.
and D
0=(x,y)T.
In [6] the following results are established.
Lemma 3.1
The origin of system (3.1) with \(\mu\neq-{{\frac{1}{3}}}\) is monodromic if, and only if, \(-{{\frac{1}{3}}}<\mu\).
Theorem 3.2
System (3.1) with \(\mu\neq\pm{{\frac{1}{3}}}\) is formally equivalent to:
where \(\alpha_{4l+j}^{(i)}\) are the invariant values of the normal form which are polynomials on the parameters a ij and b ij and the first invariant values are
where
Remark
In the family of system (3.1) there exist centers without analytic first integral. For instance, \((\dot{x},\dot {y})^{T}=(y^{3},-x^{3})^{T}+x^{2}y h {{\mathbf{D}}_{0}}\), has a center at the origin because the origin is monodromic and the vector field is reversible with respect to the involution σ 2(x,y)=(x,−y). From Theorems 3.2 and 1.2 this system has not analytic first integral.
Now we apply these previous results to a particular family of polynomial vector fields. More specifically, we consider the system given by
System (3.3) has μ=0 and from Lemma 3.1 we know that system (3.3) has a monodromic singular point at the origin, that is, the singular point is a focus or a center. Therefore if system (3.3) is analytically integrable then it has a center at the origin. We recall that not all the nilpotent and degenerate centers have an analytic first integral at the origin, for instance \((\dot{x},\dot {y})^{T}=(y+x^{2},-x^{3})^{T}\) is monodromic and invariant to the change (x,y,t)→(−x,y,−t), therefore, it has a center at the origin but it is easy to prove that it is not analytically integrable, see [10]. Hence, the center problem for the system (3.3) is still open.
For simplicity we divide the study of this family into two different cases which are studied in Theorem 3.3 and Theorem 3.5, respectively.
Theorem 3.3
System (3.3) with (a 1+4b 0)(4a 4+b 3)=0 is analytically integrable in a neighborhood of the origin if, and only if, one of the following conditions is verified
-
(a)
a 1+4b 0=2a 2+3b 1=3a 3+2b 2=4a 4+b 3=0. (Hamiltonian case).
-
(b)
a 0=a 2=a 3=a 4=b 1=b 2=b 3=0 and (a 1+4b 0)≠0. (Reversible with respect to the involution σ 2(x,y)=(x,−y).)
-
(c)
\(a_{0}=a_{2}=b_{1}=3a_{3}+2b_{2}=4a_{4}+b_{3}=a_{4}+b_{4}=2a_{1}-4b_{0}+5a_{3}=a_{4}(2b_{0}- 5a_{3})+3a_{3}^{2}=0\), and (a 1+4b 0)(b 2−a 3)≠0. (Reversible with respect to the involution σ 2(x,y)=(x,−y).)
-
(d)
a 1=a 2=a 3=b 0=b 1=b 2=b 4=0, and 4a 4+b 3≠0. (Reversible with respect to the involution σ 1(x,y)=(−x,y).)
-
(e)
\(a_{3}=b_{2}=b_{4}=2a_{2}+3b_{1}=a_{1}+4b_{0}=a_{0}+b_{0}=4a_{4}-2b_{3}-5b_{1}=b_{0}(2a_{4}- 5b_{1})+3b_{1}^{2}=0\), and (4a 4+b 3)(b 1−a 2)≠0. (Reversible with respect to the involution σ 1(x,y)=(−x,y).)
Proof
Using the conservative-dissipative decomposition, see Lemma 2.1, system (3.3) can be written into the form
with
To achieve the integrability conditions we transform system (3.4) into its normal form (3.2) computing its invariant values of the normal form \(\alpha_{4l+j}^{(i)}\). From Theorem 1.2 the vanishing of these invariant values \(\alpha_{4l+j}^{(i)}\) is a necessary and sufficient condition to have analytic integrability. In practice we only compute some of them in order to obtain some necessary conditions. The sufficiency will be given by the classical alternative methods, i.e., to detect that the system is Hamiltonian or showing that it has an inverse integrating factor V(x,y) with V(0,0)≠0 or applying the box-flow theorem after desingularizing the singular point.
The first integrability obstructions are \(\alpha_{3}^{(1)}=d_{1}\), and \(\alpha_{3}^{(2)}=d_{2}\). Imposing the vanishing of these conditions, we obtain the following invariant values:
The case (a 1+4b 0)(4a 4+b 3)=0 implies d 0 d 3=0. Therefore we divide the study in 3 cases:
-
(i)
If d 0=d 3=0, we obtain the Hamiltonian case described in (a).
-
(ii)
If d 0≠0 and d 3=0 then we have \(\alpha _{4}^{(2)}=d_{0}c_{2}\), and \(\alpha_{4}^{(1)}=d_{0}(c_{4}+5c_{0})\). The vanishing of these coefficients is equivalent to c 2=0 and c 4=−5c 0. In this case, the next invariant values are:
$$\begin{aligned} \alpha_5^{(1)} =&c_0(d_0+c_1+10c_5), \\ \alpha_5^{(2)} =&2c_3(d_0+6c_1+5c_5)+125c_0^2. \end{aligned}$$-
(ii.1)
If c 0=0 then \(\alpha_{5}^{(1)}=0\) and \(\alpha_{5}^{(2)}=0\) is equivalent to either c 3=0 or d 0=−6c 1−5c 5.
-
(ii.1.1)
If c 0=c 3=0 then d 1=d 2=d 3=c 2=c 0=c 3=c 4=0, d 0≠0. System (3.3) becomes
$$\begin{aligned} \left ( \begin{array}{c} \dot{x} \\ \dot{y} \end{array} \right )=\left ( \begin{array}{c} y^3 \\ - x^3 \end{array} \right ) + \left ( \begin{array}{c} {{\frac{d_0-4c_1}{5}}}xy^3 \\ { {\frac{d_0+c_1}{5}}}y^4+c_5x^4 \end{array} \right ), \end{aligned}$$which is reversible under the involution σ 2(x,y)=(x,−y). Applying the singular change of variables x=u, y 4=v, and scaling the time by dτ=y 3 dt, we get
$$\begin{aligned} u' =&1+{{\frac{d_0-4c_1}{5}}}u, \\ v' =&- 4u^3 +4{{\frac{d_0+c_1}{5}}}v+4c_5u^4, \end{aligned}$$which is analytically integrable using the box-flow theorem. This case corresponds to (b).
-
(ii.1.2)
If c 3≠0 and d 0=−6c 1−5c 3 then \(\alpha_{6}^{(2)}=6c_{3}^{2}-25c_{1}c_{5}\) is zero if \(c_{5}=6c_{3}^{2}/(25c_{1})\) otherwise if c 1=0 implies c 3=0 and this is a contradiction. In this case, system (3.3) becomes
$$\begin{aligned} \left ( \begin{array}{c} \dot{x} \\ \dot{y} \end{array} \right )=\left ( \begin{array}{c} y^3 \\ - x^3 \end{array} \right ) + \left ( \begin{array}{c} -{{\frac{2}{25}}}{{\frac {25c_1^2+3c_3^2}{c_1}}}xy^3-{{\frac{2}{5}}}c_3x^3y \\ -{{\frac{1}{25}}}{{\frac {6c_3^2+25c_1^2}{c_1}}}y^4+{{\frac {3}{5}}}c_3x^2y^2+{{\frac{6}{25}}}{{\frac {c_3^2}{c_1}}}x^4 \end{array} \right ). \end{aligned}$$It is easy to see that this system has an inverse integrating factor given by V A where \(A={{\frac {15(5c_{1}^{2}+c_{3}^{2})}{6c_{3}^{2}+25c_{1}^{2}}}}\) and \(V=1+{{\frac {2}{625}}}{{\frac {25c_{1}^{2}+6c_{3}^{2}}{c_{1}^{2}}}}(-25c_{1}x+5c_{3}c_{1}y^{2}+3c_{3}^{2}x^{2})\). This case corresponds to (c).
-
(ii.1.1)
-
(ii.2)
If d 0=−c 1−10c 5≠0 and c 0≠0, we have \(\alpha_{5}^{(2)}=d_{0}(2c_{3}(c_{5}-c_{1})-25c_{0}^{2})\). Taking into account that c 3≠0 we get that \(\alpha_{5}^{(2)}\) is null if, and only if, \(c_{5}=c_{1}+ (25c_{0}^{2}) /(2c_{3})\). The next invariant value is \(\alpha_{6}^{(3)}=c_{0}d_{0}(3c_{1}c_{3}+50c_{0}^{2})\). Therefore \(c_{1}=-50c_{0}^{2}/ (3c_{3})\) and, in this case, \(\alpha_{6}^{(1)}\) and \(\alpha _{6}^{(2)}\) do not vanish simultaneously.
-
(ii.1)
-
(iii)
If d 0=0 and d 3≠0 doing the change x→y, y→x, dt→−dt, d i →−d 3−i for i=0,1,2,3 and c i →c 5−i for i=0,1,2,3,4,5, this case is transformed into (ii.1.1) or (ii.1.2). These two cases correspond to the cases (d) and (e), respectively. □
Remark
Notice that system (3.3) is invariant with respect to the change (x,y,t,a i ,b i )↔(−x,y,−t,−b 4−i ,−a 4−i ), i=0,…,4. Therefore, any integrability condition of system (3.3) is invariant by the change of parameters:
It is easy to see that the condition (a) of Theorem 3.3 is invariant by the change (3.5). Moreover, the conditions (d) and (e) are symmetric with respect to the conditions (b) and (c) by the change (3.5), respectively.
The following result simplifies system (3.3), for the case (a 1+4b 0)(4a 4+b 3)≠0.
Lemma 3.4
System (3.3) with (a 1+4b 0)(4a 4+b 3)≠0 is equivalent to
where \(c_{0}=-{{\frac {a_{0}(4a_{4}+b_{3})^{1/3}}{(a_{1}+4b_{0})^{4/3}}}}\), \(c_{1}={ {\frac{b_{0}-a_{1}}{a_{1}+4b_{0}}}}\), \(c_{2}={{\frac {b_{1}-a_{2}}{(a_{1}+4b_{0})^{2/3}(4a_{4}+b_{3})^{1/3}}}}\), \(c_{3}={{\frac {b_{2}-a_{3}}{(a_{1}+4b_{0})^{1/3}(4a_{4}+b_{3})^{2/3}}}}\), \(c_{4}={{\frac{b_{3}-a_{4}}{4a_{4}+b_{3}}}}\), \(c_{5}={ {\frac{b_{4}(a_{1}+4b_{0})^{1/3}}{(4a_{4}+b_{3})^{4/3}}}}\), \(d_{1}={{\frac {2a_{2}+3b_{1}}{(4a_{4}+b_{3})^{1/3}(a_{1}+4b_{0})^{2/3}}}}\), \(d_{2}={ {\frac{3a_{3}+2b_{2}}{(4a_{4}+b_{3})^{2/3}(a_{1}+4b_{0})^{1/3}}}}\) and \(S= {{\frac{(a_{1}+4b_{0})^{4/3}}{(4a_{4}+b_{3})^{4/3}}}}\).
Proof
The upscaling in the state variables and time \(x \rightarrow{{\frac{1}{a_{1}+4b_{0}}}}x\), \(y \rightarrow{{\frac {(4a_{4}+b_{3})^{1/3}}{(a_{1}+4b_{0})^{4/3}}}}y\), \(dt={ {\frac{(a_{1}+4b_{0})^{3}}{4a_{4}+b_{3}}}}d\tau\) transforms system (3.3) into the conservative-dissipative system (3.6). □
Theorem 3.5
System (3.6) is analytically integrable in a neighborhood of the origin if, and only if, one of the following conditions is verified
-
(a)
d 1=d 2=0, c 3=−Sc 2, \(c_{5}=-{{\frac {1}{5}}}S(5c_{0}S+c_{1}+c_{4})\), \(c_{1}=-{{\frac {5S^{2}c_{0}+2c_{2}}{5S}}}\), \(c_{4}={{\frac{(5S^{3}-1)c_{2}+10S^{2}c_{0}}{10S}}}\).
-
(b)
d 1=d 2=0, c 3=−c 2, c 4=−c 1, c 5=−c 0, c 1=10c 0−2c 2−1, S=1, \(9c_{2}^{2}-225c_{0}^{2}-30c_{0}c_{2}+5c_{2}+25c_{0}=0\), c 2(8c 2+5−55c 0)≠0.
-
(c)
d 1=d 2=c 2=c 3=c 4=c 5=0, c 1=−1, \(c_{0}={ {\frac{1}{5S}}}\).
-
(d)
d 1=d 2=c 2=c 3=c 0=c 1=0, c 4=1, \(c_{5}=-{ {\frac{S}{5}}}\).
-
(e)
d 1=d 2=c 2=c 3=c 0=c 5=0, c 4=1, c 1=−1.
-
(f)
d 1=d 2=c 2=c 3=0, \(c_{5}=-{{\frac{S}{9}}}\), \(c_{4}=-{{\frac{1}{9}}}\), \(c_{1}={{\frac{1}{9}}}\), \(c_{0}={{\frac{1}{9S}}}\).
Proof
The first integrability obstructions are \(\alpha _{3}^{(1)}=d_{1}\), and \(\alpha_{3}^{(2)}=d_{2}\). Imposing the vanishing of these conditions we obtain the following invariant values \(\alpha_{4}^{(2)}=c_{3}+Sc_{2}\), \(\alpha_{4}^{(1)}=5c_{5}+S(5c_{0}S+c_{1}+c_{4})\). The vanishing of these coefficients is equivalent to
In this case the next invariant values are \(\alpha_{5}^{(1)}\) and \(\alpha_{5}^{(2)}\), where
We define C 4:=c 4+10S(c 0−Sc 2)−1. Now we divide the study in two cases (i) C 4≠0 and (ii) C 4=0.
-
(i)
For C 4≠0, we get \(\alpha_{5}^{(2)}=0\) taking
$$\begin{aligned} c_1 =&{{\frac {4S(1+95S^3)c_2^2+2S^2(39C_4+20-220Sc_0)c_2+C_4(4C_4+4-45Sc_0)}{C_4}}}, \end{aligned}$$and
$$\begin{aligned} \alpha_5^{(1)} =& \bigl[40S^3c_2^2 \bigl(10S+\bigl(1+95S^3\bigr)c_2\bigr)+10S^2c_2 \bigl(136S^2c_2+9\bigr)C_4+ \bigl(5+158S^2c_2\bigr)C_4^2 \\ &{}+6C_4^3-55S\bigl(C_4+10S^2c_2\bigr) \bigl(C_4+8S^2c_2\bigr)c_0 \bigr]\\ &{}\times \bigl[10S(C_4+1)+\bigl(95S^3+1\bigr)c_2-110S^2c_0 \bigr]. \end{aligned}$$For vanishing \(\alpha_{5}^{(1)}\) we distinguish two cases (i.1) 10S(C 4+1)+(95S 3+1)c 2−110S 2 c 0=0 and (i.2) 10S(C 4+1)+(95S 3+1)c 2−110S 2 c 0≠0.
-
(i.1)
If 10S(C 4+1)+(95S 3+1)c 2−110S 2 c 0=0, then \(C_{4}=-{{\frac{(95S^{3}+1)c_{2}+10S(1-11Sc_{0})}{10S}}}\neq0\). In this case we obtain
$$\begin{aligned} \dot{x} =&y^3+{{\frac {2S}{5}}}c_2x^3y-{ {\frac {(5S^3-1)c_2+10S(Sc_0-1)}{50S}}}x^4-{{\frac {3c_2}{5}}}x^2y^2 \\ &{}+{{\frac{20S^2c_0+5S+8c_2}{25S}}}xy^3-c_0y^4, \\ \dot{y} =&-Sx^3+{{\frac {2(5S^3-1)c_2+5S(1+4Sc_0)}{25S}}}x^3y-{ {\frac {(S^3-1)c_2+10S^2c_0}{10}}}x^4 \\ &{}-{{\frac{3Sc_2}{5}}}x^2y^2+{{\frac{2c_2}{5}}}xy^3-{{ \frac {5S(Sc_0-1)+2c_2}{25S}}}y^4. \end{aligned}$$This system has an inverse integrating factor given by V A where \(V=1+{{\frac{1}{A}}}x-{{\frac{1}{AS}}}y\) and \(A={{\frac{25S}{5S(4Sc_{0}+1)-2c_{2}}}}\). If \(c_{2}={ {\frac{5S(4Sc_{0}+1)}{2}}}\), this system has an inverse integrating factor given by \(\exp(x-{{\frac{1}{S}}}y)\). This case corresponds to (a) with the additional condition (95S 3+1)c 2+10S(1−11Sc 0)≠0.
-
(i.2)
If 10S(C 4+1)+(95S 3+1)c 2−110S 2 c 0≠0, then we divide the study in three cases: (i.2.1) C 4+8S 2 c 2=0, (i.2.2) C 4+10S 2 c 2=0, c 2≠0 and (i.2.3) (C 4+10S 2 c 2)(C 4+8S 2 c 2)≠0.
-
(i.2.1)
If C 4=−8S 2 c 2, then c 2≠0 and (15S 3+1)c 2−10S(11Sc 0−1)≠0, otherwise C 4=0 and 10S(C 4+1)+(95S 3+1)c 2−110S 2 c 0=0, respectively. We obtain
$$\begin{aligned} \alpha_5^{(1)} =&(S-1)c_2\bigl(S^2+S+1 \bigr) \bigl[\bigl(15S^3+1\bigr)c_2-10S(11Sc_0-1) \bigr], \end{aligned}$$and S=1 is the only possibility to vanish this constant. In this case we obtain \(\alpha_{6}^{(2)}=0\) and
$$\begin{aligned} \alpha_6^{(1)}=\alpha_6^{(3)}= \overbrace{(8c_2+5-55c_0)}^{\neq 0} \bigl(9c_2^2+5c_2-30c_0c_2-225c_0^2+25c_0 \bigr). \end{aligned}$$Taking \(9c_{2}^{2}+5c_{2}-30c_{0}c_{2}-225c_{0}^{2}+25c_{0}=0\), we obtain
$$\begin{aligned} \dot{x} =&y^3-{{\frac {3}{5}}}c_2x^2y^2+{ {\frac {5+8(c_2-5c_0)}{5}}}xy^3+{{\frac {2}{5}}}c_2x^3y-c_0y^4\\ &{}-2{ {\frac{c_2-5c_0}{5}}}x^4, \\ \dot{y} =&-x^3-{{\frac{3}{5}}}c_2x^2y^2+{ {\frac {2}{5}}}c_2xy^3+{{ \frac {5+8(c_2-5c_0)}{5}}}x^3y\\ &{}-2{{\frac{c_2-5c_0}{5}}}y^4-c_0x^4. \end{aligned}$$This system has an inverse integrating factor given by V β where
$$V=1-{{\frac{1}{\beta}}} \biggl[y-x+{{\frac {c_2-5c_0}{10}}} \bigl(x^2+y^2\bigr)+2{{\frac {7c_2-50c_0+5}{10}}}xy \biggr], $$and \(\beta={{\frac{1}{c_{2}-7c_{0}+1}}}\). Moreover if c 2=7c 0−1, this system has an inverse integrating factor given by \(V= \exp (x-y+{{\frac {1}{10}}}(1-2c_{0})(x^{2}+y^{2})+{{\frac{1}{5}}}(c_{0}+ 2)xy )\). This case corresponds to (b).
-
(i.2.2)
If C 4=−10S 2 c 2 then c 2≠0 and (5S 3−1)c 2+10S(11Sc 0−1)≠0, otherwise C 4=0 and 10S(C 4+1)+(95S 3+1)c 2−110S 2 c 0=0, respectively. We obtain
$$\begin{aligned} \alpha_5^{(1)} =&c_2 \bigl[\bigl(5S^3-1 \bigr)c_2+10S(11Sc_0-1) \bigr]\neq0. \end{aligned}$$ -
(i.2.3)
If [10S(C 4+1)+(95S 3+1)c 2−110S 2 c 0](C 4+10S 2 c 2)(C 4+8S 2 c 2)≠0, then we get \(\alpha_{5}^{(1)}=0\) taking
$$\begin{aligned} c_0 =&{{\frac {40S^3c_2^2(10S+(1+95S^3)c_2)+10S^2c_2(136S^2c_2+9)C_4+(5+158S^2c_2)C_4^2+6C_4^3}{55S(C_4+10S^2c_2)(C_4+8S^2c_2)}}}. \end{aligned}$$Therefore,
$$\begin{aligned} \alpha_6^{(1)} =&p(C_4,c_2,S)q_1(C_4,c_2,S), \\ \alpha_6^{(2)} =&p(C_4,c_2,S)q_2(C_4,c_2,S), \\ \alpha_6^{(3)} =&c_2p(C_4,c_2,S)q_3(C_4,c_2,S), \end{aligned}$$where \(p(C_{4},c_{2},S)=2SC_{4}^{2}+(41S^{3}-1)c_{2}C4+6S^{2}(35S^{3}-3)c_{2}^{2}= [C_{4}+{{\frac{41S^{3}-1}{4S}}}c_{2} ]^{2} -{{\frac{S^{6}+62S^{3}+1}{16S^{2}}}}c_{2}^{2}\), and q i (C 4,c 2,S), i=1,2,3, are polynomials in the variables C 4, c 2 and S. To vanish \(\alpha_{6}^{(3)}\) we distinguish three cases (i.2.3.1) c 2=0, (i.2.3.2) p(C 4,c 2,S)=0, c 2≠0 and (i.2.3.3) c 2 p(C 4,c 2,S)≠0.
-
(i.2.3.1)
If c 2=0, then we obtain \(\alpha_{6}^{(3)}=0\) and
$$\begin{aligned} \alpha_6^{(1)} =&C_4(C_4-1) (9C_4+2), \\ \alpha_6^{(2)} =&C_4(C_4-1) (6C_4+5). \end{aligned}$$Then, C 4=1 is the only possibility to cancel both constants. In this case, we obtain the system
$$\begin{aligned} \dot{x} =&y^3+{{\frac {1}{5}}}x^4+xy^3-{ {\frac{1}{5S}}}y^4, \\ \dot{y} =&-Sx^3+{{\frac{1}{5}}}x^3y. \end{aligned}$$This system has an inverse integrating factor given by \(V=(1- {{\frac{y}{5S}}})^{4}(1+x-{{\frac{y}{5S}}})\). This case corresponds to (c).
-
(i.2.3.2)
Case p(C 4,c 2,S)=0, (C 4+10S 2 c 2)(C 4+8S 2 c 2)c 2≠0. In this case, we obtain 10S(C 4+1)+(95S 3+1)c 2−110S 2 c 0=0, that is contradictory.
-
(i.2.3.3)
Case c 2(C 4+10S 2 c 2)(C 4+8S 2 c 2)p(C 4,c 2,S)≠0. In this case, the resultant of polynomials q 1(C 4,c 2,S) and q 3(C 4,c 2,S) with respect the variable C 4 gives
$$\begin{aligned} R:=\bigl(998001S^2c_2^4-120925c_2^2S+2500 \bigr) \bigl(7644c_2^2S-125\bigr), \end{aligned}$$and no solution of R=0 vanishes the remaining conditions.
-
(i.2.3.1)
-
(i.2.1)
-
(i.1)
-
(ii)
If C 4=0, then c 4=−10S(c 0−Sc 2)+1 and
$$\begin{aligned} \alpha _5^{(1)} =&5S(c_1+1-10Sc_0) (c_1+Sc_0)+10\bigl(1+10S^3c_1+S \bigl(10S^3-11\bigr)c_0\bigr)c_2 \\ &{}+116S^2c_2^2, \\ \alpha_5^{(2)} =&c_2 \bigl[c_2 \bigl(95S^3+1\bigr)-10S(11Sc_0-1) \bigr]. \end{aligned}$$To vanish \(\alpha_{5}^{(2)}\) we distinguish two cases (ii.1) c 2(95S 3+1)−10S(11Sc 0−1)=0 and (ii.2) c 2=0, 11Sc 0−1≠0.
-
(ii.1)
If c 2(95S 3+1)−10S(11Sc 0−1)=0, we get \(c_{0}={{\frac{1}{110S^{2}}}}(95S^{3}c_{2}+c_{2}+10S)\). In this case, we obtain
$$\begin{aligned} \alpha _5^{(1)} =&\bigl(22Sc_1+9c_2+2S+19S^3c_2 \bigr) \bigl(55Sc_1-27c_2+5S+625S^3c_2 \bigr), \end{aligned}$$we divide the study in two cases:
-
(ii.1.1)
If \(c_{1}= -{{\frac{(19S^{3}+9)c_{2}+2S}{22S}}}\), then we have
$$\begin{aligned} \dot{x} =&y^3+{{\frac {10S-c_2(15S^3-1)}{55S}}}x^4-{ {\frac {3}{5}}}c_2x^2y^2-{ {\frac{2c_2(19S^3+9)+15S}{55S}}}xy^3 \\ &{}+{{\frac{2S}{5}}}c_2x^3y -{{ \frac {c_2(95S^3+1)+10S}{110S^2}}}y^4, \\ \dot{y} =&- Sx^3-{{\frac {c_2(53S^3-5)+5S}{55}}}x^4-{ {\frac {3S}{5}}}c_2x^2y^2+{ {\frac{2}{5}}}c_2xy^3 \\ &{}-{{\frac{4c_2(15S^3-1)+15S}{55S}}}x^3y-{{ \frac {c_2(19S^3+9)-20S}{110S}}}y^4. \end{aligned}$$It is easy to prove that this system, if 2c 2(19S 3−2)+15S≠0, has an inverse integrating factor given by V A where \(A={ {\frac{55S}{2c_{2}(19S^{3}-2)+15S}}}\) and \(V=1+{{\frac {1}{A}}} (x-{{\frac{1}{S}}}y )\). If \(c_{2}=-{{\frac{15S}{2(19S^{3}-2)}}}\) then this system has an inverse integrating factor given by \(\exp(x-{{\frac {1}{S}}}y)\). This case corresponds to case (a) with the additional condition (95S 3+1)c 2+10S(1−11Sc 0)=0.
-
(ii.1.2)
Case \(c_{1}=-{{\frac {(625S^{3}-27)c_{2}+5S}{55S}}}\neq-{{\frac {(19S^{3}+9)c_{2}+2S}{22S}}}\), i.e., c 2(35S 3−3)≠0 and \(c_{1}=-{{\frac{(625S^{3}-27)c_{2}+5S}{55S}}}\). In this case \(\alpha_{6}^{(1)}\), \(\alpha_{6}^{(2)}\) and \(\alpha_{6}^{(3)}\) do not vanish simultaneously.
-
(ii.1.1)
-
(ii.2)
If c 2=0, 11Sc 0−1≠0, then \(\alpha _{5}^{(1)}=(c_{1}+Sc_{0})(c_{1}+1-10Sc_{0})\).
-
(ii.2.1)
Case c 1=−Sc 0. In this case, we get \(\alpha_{6}^{(1)}=0\), \(\alpha_{6}^{(2)}=c_{0}(11Sc_{0}- 1) (6Sc_{0}- 1)\), \(\alpha _{6}^{(3)}=c_{0}(11Sc_{0}-1)(9Sc_{0}-1)\).
c 0=0 is the only possibility to vanish both constants. In this case, we have the system
$$\begin{aligned} \left ( \begin{array}{c} \dot{x} \\ \dot{y} \end{array} \right ) =&\left ( \begin{array}{c} y^3 \\ -Sx^3 \end{array} \right )+\left ( \begin{array}{c} {{\frac{1}{5}}}xy^3 \\ -{{\frac {S}{5}}}x^4+x^3y+{{\frac{1}{5}}}y^4 \end{array} \right ). \end{aligned}$$This system has an inverse integrating factor given by \(V=(1+{{\frac{x}{5}}})^{4}(1+{{\frac {x}{5}}}-{{\frac{y}{S}}})\). This case corresponds to (d).
-
(ii.2.2)
If c 1=10Sc 0−1, then we have \(\alpha_{6}^{(1)}=\alpha _{5}^{(3)}=c_{0}(9Sc_{0}-1)(11Sc_{0}-1)\), therefore we study two different cases.
-
(ii.2.2.1)
In the case c 0=0 system (3.6) becomes
$$\begin{aligned} \left ( \begin{array}{c} \dot{x} \\ \dot{y} \end{array} \right )=\left ( \begin{array}{c} y^3 \\ -Sx^3 \end{array} \right )+\left ( \begin{array}{c} xy^3 \\ x^3y \end{array} \right ), \end{aligned}$$and this system has an integrating factor given by \(V=(1+ x) (1-{{\frac{1}{S}}}y )\). This case corresponds to (e).
-
(ii.2.2.2)
In the case \(c_{0}={{\frac{1}{9S}}}\) we have
$$\begin{aligned} \left ( \begin{array}{c} \dot{x} \\ \dot{y} \end{array} \right ) =&\left ( \begin{array}{c} y^3 \\ -Sx^3 \end{array} \right )+\left ( \begin{array}{c} {{\frac{2}{9}}}x^4+{{\frac {1}{9}}}xy^3-{{\frac{1}{9S}}}y^4 \\ -{{\frac {S}{9}}}x^4+{{\frac{1}{9}}}x^3y+{{\frac {2}{9}}}y^4 \end{array} \right ), \end{aligned}$$which has an inverse integrating factor given by V A where \(A= {{\frac{9}{2}}}\) and \(V=1+{{\frac {2}{9}}}(x-{{\frac{1}{S}}}y)+{{\frac {1}{81}}}(x+{{\frac{1}{S}}}y)^{2}\). This case corresponds to (f). □
-
(ii.2.2.1)
-
(ii.2.1)
-
(ii.1)
Remark
Notice that the conditions (a), (b), (e) and (f) of Theorem 3.5 are invariant by the change (3.5) rewrite in terms of c i and d i , and (d) is symmetric by the change (3.5) of (c).
4 The Integrability of a Family of Systems (1.4)
We consider the following differential planar system
\({\mathbf{F}}_{8}=(a_{50}x^{5}+a_{22}x^{2}y^{2},b_{41}x^{4}y+b_{13}xy^{3})^{T}\in \mathcal{Q}_{8}^{(2,3)}\), \({\mathbf{F}}_{9}=(a_{41}x^{4}y+a_{13}xy^{3},b_{60}x^{6}+b_{32}x^{3}y^{2}+b_{04}y^{4})^{T}\in \mathcal{Q}_{9}^{(2,3)}\) and the dots represent quasihomogeneous terms of degree higher than nine.
In this case we choose the type t=(2,3), then D 0=(2x,3y)T and the quasi-homogeneous principal part is of degree 7 given by
where

In [7] the following results are stated.
Lemma 4.1
The origin of system (4.1) is monodromic if and only if \(-{{\frac{1}{\sqrt{6}}}}< a< {{\frac{1}{\sqrt{6}}}}\).
Theorem 4.2
System (4.1) with 6a 2−1≠0, is formally equivalent to:
where \(\alpha_{12l+j}^{(i)}\) are the invariant values of the normal form which are polynomials on the parameters a ij and b ij and the first invariant values are
where
Notice that the value β 9 in (4.2) is univocally determined therefore it is an invariant of system (4.1).
Now we apply the results given in this section to a concrete family of polynomial vector fields. More specifically, we consider the system given by
If \(-{{\frac{1}{\sqrt{6}}}}< a< {{\frac {1}{\sqrt{6}}}}\), Lemma 4.1 proves that system (4.3) has a monodromic singular point at the origin. Therefore if system (4.3) is analytic integrable then it has a center at the origin.
Theorem 4.3
System (4.3) is analytically integrable in a neighborhood of the origin if and only if one of the following conditions is satisfied
-
(a)
5a 0+b 1=b 2+2a 1=b 3+a 2=2b 4+a 3=a 4+5b 5=0, (Hamiltonian case).
-
(b)
\(5a_{0}+b_{1}=b_{2}+2a_{1}=b_{3}+a_{2}=a=a_{4}+5b_{5}-2a_{0}a_{3}-4a_{0}b_{4}=a_{2}-6a_{1}a_{0}+20a_{0}^{3}=b_{5}-4a_{0}^{3}a_{1}-a_{0}b_{4}+16a_{0}^{5} =a_{5}+(a_{1}+4a_{0}^{2})(b_{4}-a_{3}+2(a_{1}+4a_{0}^{2})(a_{1}+10a_{0}^{2}))=0\) and 2b 4+a 3≠0.
Proof
To get the integrability conditions we transform system (4.3) into its normal form (4.2) computing the invariant values of the normal form \(\alpha_{12l+j}^{(i)}\). From Theorem 1.3 the vanishing of these invariant values \(\alpha_{12l+j}^{(i)}\) is a necessary and sufficient condition to have analytic integrability. In practice we only compute some of them in order to obtain some necessary conditions.
The first integrability obstructions are \(\alpha_{8}^{(1)}=5a_{0}+b_{1}\), and \(\alpha_{8}^{(2)}=0\). Imposing the vanishing of these conditions, we obtain that the following invariant value is
In this case α 10=b 3+a 2, and α 11=a(2b 4+a 3). Therefore we divide the study in 2 cases:
-
(i)
If 2b 4+a 3=0, we obtain \(\alpha _{12}^{(1)}=12(a_{4}+5b_{5})\) and \(\alpha_{12}^{(2)}=2a(a_{4}+5b_{5})\). Therefore if we impose a 4+5b 5=0, we obtain the Hamiltonian case described in (a).
-
(ii)
If a=0 and 2b 4+a 3≠0 then we have \(\alpha _{12}^{(1)}={{\frac{12}{5}}}(a_{4}+5b_{5}-2a_{0}a_{3}-4a_{0}b_{4})\) and \(\alpha_{12}^{(2)}=0\). In this case we obtain \(\alpha _{14}^{(2)}=-2(a_{2}-6a_{1}a_{0}+20a_{0}^{3})(2b_{4}+a_{3})\), and \(\alpha_{14}^{(1)}=0\). From the vanishing of these coefficients is deduced that α 15=0 and \(\alpha_{16}={{\frac {40}{3}}}(b_{5}-4a_{0}^{3}a_{1}-a_{0}b_{4}+16a_{0}^{5})(a_{3}+2b_{4})\). In this case, the next invariant values are
$$\begin{aligned} \alpha_{17} =&-{{\frac {24}{5}}}(2b_4+a_3) \bigl(a_5+\bigl(a_1+4a_0^2 \bigr) \bigl(b_4-a_3+2\bigl(a_1+4a_0^2 \bigr) \bigl(a_1+10a_0^2\bigr)\bigr)\bigr). \end{aligned}$$Under such conditions system (4.3) becomes
$$\begin{aligned} \dot{x} =&y^3 +a_0x^5+a_1x^4y+2a_0 \bigl(3a_1-10a_0^2\bigr)x^3y^2+a_3x^2y^3 \\ &{}-a_0\bigl(b_4-2a_3+20a_0^2a_1-80a_0^4 \bigr)xy^4\\ &{}+\bigl(a_1-4a_0^2 \bigr) \bigl(a_3-b_4+16a_0^4+4a_0^2a_1-2a_1^2 \bigr)y^5, \\ \dot{y} =&- x^5-5a_0x^4y-2a_1x^3y^2-2a_0 \bigl(3a_1-10a_0^2\bigr)x^2y^3 \\ &{}+b_4xy^4+a_0\bigl(b_4+4a_0^2a_1-16a_0^4 \bigr)y^5. \end{aligned}$$It is easy to see that this system has an inverse integrating factor given by V A where \(A={{\frac {2b_{4}+a_{3}}{a_{3}+8a_{0}^{2}a_{1}-2a_{1}^{2}}}}\) and \(V=1+(a_{3}+8a_{0}^{2}a_{1}-2a_{1}^{2})(x^{2}+2a_{0}xy+(a_{1}-4a_{0}^{2})y^{2})\) and if \(a_{3}+8a_{0}^{2}a_{1}-2a_{1}^{2}=0\) then this system has an inverse integrating factor given by e W where \(W=2(b_{4}-4a_{0}^{2}a_{1}+a_{1}^{2})(x^{2}+2a_{0}xy+(a_{1}+4a_{0}^{2})y^{2})\). This case corresponds to (b).
This completes the proof of the theorem. □
Remark 1
Family (4.3) was also studied in [14] where such type of degenerate systems were called generalized nilpotent systems. However the results obtained there do not coincide with the ones given in this work. This is because in [14] only were found the analytic integrable systems that have a first integral of the form H(x,y)=y 4+f 5(x)y 5+⋯, which is restrictive because the first integral can be of the form H(x,y)=y 4+f 5(x,y)+⋯, where f i (x,y) are homogeneous polynomials of degree i.
References
Algaba, A., Freire, E., Gamero, E., García, C.: Quasi-homogeneous normal forms. J. Comput. Appl. Math. 150, 193–216 (2003)
Algaba, A., Gamero, E., García, C.: The integrability problem for a class of planar systems. Nonlinearity 22(2), 395–420 (2009)
Algaba, A., García, C., Reyes, M.: Like-linearizations of vector fields. Bull. Sci. Math. 133, 806–816 (2009)
Algaba, A., García, C., Reyes, M.: Integrability of two dimensional quasi-homogeneous polynomial differential systems. Rocky Mt. J. Math. 41(1), 1–22 (2011)
Algaba, A., Fuentes, N., García, C.: Centers of quasi-homogeneous polynomial planar systems. Nonlinear Anal., Real World Appl. 13, 419–431 (2012)
Algaba, A., García, C., Giné, J.: Analytic integrability for some degenerate planar systems. Commun. Pure Appl. Anal. 12(6), 2797–2809 (2013)
Algaba, A., García, C., Giné, J.: Analytic integrability for some degenerate planar vector fields. J. Differ. Equ. 257(2), 549–565 (2014)
Berthier, M., Moussu, R.: Réversibilité et classification des centres nilpotents. Ann. Inst. Fourier (Grenoble) 44, 465–494 (1994)
Chavarriga, J., Giacomini, H., Giné, J., Llibre, J.: On the integrability of two-dimensional flows. J. Differ. Equ. 157(1), 163–182 (1999)
Chavarriga, J., Giacomini, H., Giné, J., Llibre, J.: Local analytic integrability for nilpotent centers. Ergod. Theory Dyn. Syst. 23, 417–428 (2003)
Giacomini, H., Giné, J., Llibre, J.: The problem of distinguishing between a center and a focus for nilpotent and degenerate analytic systems. J. Differ. Equ. 227(2), 406–426 (2006)
Giacomini, H., Giné, J., Llibre, J.: Corrigendum to: “The problem of distinguishing between a center and a focus for nilpotent and degenerate analytic systems”. J. Differ. Equ. 232(2), 702 (2007)
Giné, J.: Sufficient conditions for a center at a completely degenerate critical point. Int. J. Bifurc. Chaos Appl. Sci. Eng. 12(7), 1659–1666 (2002)
Giné, J.: Analytic integrability and characterization of centers for generalized nilpotent singular points. Appl. Math. Comput. 148(3), 849–868 (2004)
Giné, J.: On the centers of planar analytic differential systems. Int. J. Bifurc. Chaos Appl. Sci. Eng. 17(9), 3061–3070 (2007)
Giné, J.: On some open problems in planar differential systems and Hilbert’s 16th problem. Chaos Solitons Fractals 31(5), 1118–1134 (2007)
Giné, J.: On the degenerate center problem. Int. J. Bifurc. Chaos Appl. Sci. Eng. 21(5), 1383–1392 (2011)
Li, J.: Hilbert’s 16th problem and bifurcations of planar polynomial vector fields. Int. J. Bifurc. Chaos Appl. Sci. Eng. 13(1), 47–106 (2003)
Moussu, R.: Symetrie et forme normale des centres et foyers degeneres. Ergod. Theory Dyn. Syst. 2, 241–251 (1982)
Pearson, J.M., Lloyd, N.G., Christopher, C.J.: Algorithmic derivation of centre conditions. SIAM Rev. 38(4), 619–636 (1996)
Poincaré, H.: Mémoire sur les courbes définies par les équations différentielles. J. Math. 37, 375–422 (1881); 8, 251–296 (1882); Oeuvres de Henri Poincaré, vol. I, pp. 3–84. Gauthier-Villars, Paris (1951)
Romanovski, V.G., Shafer, D.S.: The Center and Cyclicity Problems: A Computational Algebra Approach. Birkhäuser, Boston (2009)
Strózyna, E., Żoładek, H.: The analytic and normal form for the nilpotent singularity. J. Differ. Equ. 179, 479–537 (2002)
Teixeira, M.A., Yang, J.: The center-focus problem and reversibility. J. Differ. Equ. 174, 237–251 (2001)
Acknowledgements
The authors are grateful to the referees for their valuable remarks which helped to improve the manuscript. The first and second authors are supported by a MINECO/FEDER grant number MTM2010-20907-C02-02 and by the Consejería de Educación y Ciencia de la Junta de Andalucía (projects P12-FQM-1658; TIC-130 and FQM-276). The third author is partially supported by a MINECO/FEDER grant number MTM2011-22877 and by an AGAUR (Generalitat de Catalunya) grant number 2014SGR 1204.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Algaba, A., García, C. & Giné, J. Analytic Integrability of Some Examples of Degenerate Planar Vector Fields. Acta Appl Math 141, 1–15 (2016). https://doi.org/10.1007/s10440-014-0001-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10440-014-0001-2



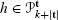 , (here |t|:=t
1+t
2 denotes the modulus of t).
, (here |t|:=t
1+t
2 denotes the modulus of t).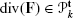 .
.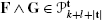 .
.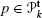 we have ∇p⋅D
0=kp (Euler’s Theorem for quasi-homogeneous vector fields).
we have ∇p⋅D
0=kp (Euler’s Theorem for quasi-homogeneous vector fields).