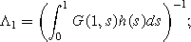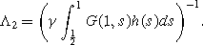Existence Theory for an Arbitrary Order Fractional Differential Equation with Deviating Argument

Abstract

In this paper, we are concerned with the existence criteria for positive solutions of the following nonlinear arbitrary order fractional differential equations with deviating argument

$$\left \{\begin{array}{l@{\quad}l}D_{0^+}^{\alpha}u(t)+h(t)f(u(\theta(t)))=0, & t\in ( 0,1 ),\ n-1<\alpha\leq n,\\[3pt]u^{(i)}(0)=0, & i=0,1,2,\ldots,n-2,\\[3pt][D_{0^+}^{\beta} u(t)]_{t=1}=0, & 1\leq\beta\leq n-2,\end{array} \right .$$

where n>3 (n∈ℕ), $D_{0^{+}}^{\alpha}$ is the standard Riemann-Liouville fractional derivative of order α,f:[0,∞)→[0,∞), h(t):[0,1]→(0,∞) and θ:(0,1)→(0,1] are continuous functions. Some novel sufficient conditions are obtained for the existence of at least one or two positive solutions by using the Krasnosel’skii’s fixed point theorem, and some other new sufficient conditions are derived for the existence of at least triple positive solutions by using the fixed point theorems developed by Leggett and Williams etc. In particular, the existence of at least n or 2n−1 distinct positive solutions is established by using the solution intervals and local properties. From the viewpoint of applications, two examples are given to illustrate the effectiveness of our results.

1 Introduction

Fractional differential equations have attracted much attention from several scientific areas in the past several decades. They are generalizations of ordinary differential equations to an arbitrary (non-integer) order and are widely applied because of their ability to model complex phenomena. These equations capture nonlocal relations in space and time with power-law memory kernels. Due to the extensive applications of fractional differential equations in engineering and science, research in this area has grown significantly, especially in areas of physics, biology, chemistry and dynamical control, etc. For details, we refer the reader to [1–5] and the references therein.

Hereafter comes from the work of Bai and Lü [6], Kaufmann and Mboumi [7] and Goodrich [8], which enlighten us on the nonlinear arbitrary order fractional differential equations with deviating argument.

For the two-point fractional differential equation

$$\left \{\begin{array}{l}D_{0^+}^{\alpha}u(t)+f(t,u(t))=0,\quad t\in ( 0,1 ),\\[3pt]u(0)=u(1)=0,\end{array} \right .$$

where $D_{0^{+}}^{\alpha}$ is the standard Riemann-Liouville fractional derivative of order 1<α≤2 and f:[0,1]×[0,∞)→[0,∞) is continuous. Bai and Lü [6] established the existence theory for at least one or three positive solutions of the above equation by using the Krasnosel’skii’s fixed point theorem [9] and the Leggett-Williams fixed point theorem [10].

In [7], Kaufmann and Mboumi considered fractional order differential equation

$$\left \{\begin{array}{l}D_{0^+}^{\alpha}u(t)+h(t)f(u(t))=0,\quad t\in ( 0,1 ),\\[3pt]u(0)=u'(1)=0,\end{array} \right .$$

where $D_{0^{+}}^{\alpha}$ is the standard Riemann-Liouville fractional derivative of order 1<α<2 and f:[0,∞)→[0,∞) is continuous.

In [8], Goodrich studied the following fractional differential equations

$$\left \{\begin{array}{l@{\quad}l}D_{0^+}^{\alpha}u(t)+h(t)f(t,u(t))=0,& t\in ( 0,1 ),\\[4pt]u^{(i)}(0)=0, & i=0,1,2,\ldots,n-2,\\[4pt][D_{0^+}^{\beta}u(t) ]_{t=1}=0, & 1\leq\beta\leq n-2,\end{array} \right .$$

where $D_{0^{+}}^{\alpha}$ is the standard Riemann-Liouville fractional derivative of order n−1<α≤n. Here u ⁽ⁱ⁾ represents the ith derivative of u and n>3 (n∈ℕ). Under certain conditions, the existence criteria are considered for at least one positive solutions by the Krasnosel’skii’s fixed point theorem too.

It is well-known that the theory of integer order differential equation with deviating arguments has quite many applications in realistic mathematical modelling of various practical situations [11–13]. Since, in the description of properties of various real materials, fractional order models are more accurate than integer order models. In other words, the study of fractional order differential equations with deviating arguments is of significance theoretically and practically. However, to the best of our acknowledge, very few literature resources are available regarding positive solutions of fractional differential equations with deviating arguments. It is also noted that the results mentioned in [6, 7] are not obtained for the case of arbitrary order fractional differential equations and no deviating arguments are involved. Therefore, it is quite necessary to make study in depth on the existence for positive solutions of arbitrary order fractional differential equations with deviating arguments in all respects.

In the present paper, we mainly focus on the following nonlinear arbitrary order fractional differential equation with deviating argument

$$\left \{\begin{array}{l@{\quad}l}D_{0^+}^{\alpha}u(t)+h(t)f(u(\theta(t)))=0, & t\in ( 0,1 ), \\[3pt]u^{(i)}(0)=0, & i=0,1,2,\ldots,n-2,\\[3pt][D_{0^+}^{\beta}u(t) ]_{t=1}=0, & 1\leq\beta\leq n-2,\end{array} \right . $$

(1.1)

where u ⁽ⁱ⁾ represents the ith derivative of u,n>3 (n∈ℕ), $D_{0^{+}}^{\alpha}$ is the standard Riemann-Liouville fractional derivative of order n−1<α≤n,f:[0,∞)→[0,∞), h(t):[0,1]→(0,∞) and θ:(0,1)→(0,1] are continuous functions. Some novel sufficient conditions are obtained for the existence of at least one or two positive solutions by using the Krasnosel’skii’s fixed point theorem, and some other new sufficient conditions are established for the existence of at least triple positive solutions by applying the fixed point theorems developed by Leggett and Williams etc. [10, 14, 15]. In particular, the existence of at least arbitrary n or 2n−1 distinct positive solutions are gained by using the solution intervals and local properties.

The rest of this paper is organized as follows. In Sect. 2, we present several definitions and lemmas which are preliminary and necessary for our main results, and then state several fixed point results. In Sect. 3, by using the Krasnosel’skii’s fixed point theorem, some sufficient conditions are demonstrated for the existence of at least one or two positive solutions of fractional differential equation (1.1). In Sect. 4, the existence criteria are explored for at least three or arbitrary odd positive solutions of fractional differential equation (1.1). Section 5 illustrates two examples.

In order to present our results in a straightforward manner, we assume that

(S1):

h∈C([0,1], [0,+∞)) and it does not vanish identically on any subinterval;

(S2):

The deviating argument θ satisfies t≤θ(t)≤1, where t∈(0,1).

2 Some Lemmas

To make the paper sufficiently self-contained, in this section we introduce several preliminary definitions and technical lemmas from fractional calculus theory which can be found in the recent literature.

Definition 2.1

[16]

The Riemann-Liouville fractional integral of order a>0 of a function y:(0,∞)→ℝ is given by

$$I_{0^+}^{\alpha}y(t)=\frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-s)^{\alpha-1}y(s)ds,$$

provided that the right side is pointwise defined on (0,∞).

Definition 2.2

[16]

The Riemann-Liouville fractional derivative of order a>0 of a function y:(0,∞)→ℝ is given by

$$D_{0^+}^{\alpha}y(t)=\frac{1}{\Gamma(n-\alpha)} \biggl(\frac{d}{dt}\biggr)^{n}\int_{0}^{t}(t-s)^{n-\alpha-1}y(s)ds,$$

provided that the right side is pointwise defined on (0,∞), where n=[α]+1.

To obtain our main results, we need the following two lemmas.

Lemma 2.3

[8]

Assume that y(t)∈C[0,1], then the following fractional differential equation

$$\left \{\begin{array}{l@{\quad}l}D_{0^+}^{\alpha}u(t)+y(t)=0, & t\in ( 0,1 ),\ n-1<\alpha\leq n,\\[4pt]u^{(i)}(0)=0, & i=0,1,2,\ldots,n-2,\\[4pt][D_{0^+}^{\beta}u(t) ]_{t=1}=0,&1\leq\beta\leq n-2,\end{array} \right .$$

has the unique solution

$$u(t)=\int_0^1G(t,s)y(s)ds,$$

where

$$G(t,s)=\left \{ \begin{array}{l@{\quad}l}\frac{t^{\alpha-1}(1-s)^{\alpha-\beta-1}-(t-s)^{\alpha-1}}{\Gamma(\alpha)}, & 0\leq s \leq t \leq 1, \\[4pt]\frac{t^{\alpha-1}(1-s)^{\alpha-\beta-1}}{\Gamma(\alpha)}, & 0\leq t \leq s \leq 1.\end{array} \right . $$

(2.1)

Lemma 2.4

[8]

Let G(t,s) be given as (2.1), then we have

• (1) G(t,s) is a continuous function on the unit square [0,1]×[0,1];

• (2) G(t,s)≥0 for (t,s)∈[0,1]×[0,1];

• (3) max _t∈[0,1] G(t,s)=G(1,s) for each s∈[0,1];

• (4) there exists a constant γ∈(0,1) such that

  $$\min_{t\in [\frac{1}{2},1 ]}G(t,s)\geq \gamma\max_{t\in [0,1]}G(t,s)=\gamma G(1,s).$$

Remark 2.5

In fact, γ has the expression [8]

$$\gamma=\min \biggl\{\frac{ (\frac{1}{2} )^{\alpha-\beta-1}}{2^{\beta}-1}, \biggl(\frac{1}{2}\biggr)^{\alpha-1} \biggr\}. $$

Let the Banach space E=C[0,1] be equipped with the norm ∥u∥=max _t∈[0,1]|u(t)|, and define the cone P⊂E by

$$P= \Bigl\{u\in E \vert u\in C[0,1],u\geq 0, \min_{t\in [\frac{1}{2},1 ]} u \bigl(\theta(t) \bigr)\geq \gamma \|u\| \Bigr\},$$

where γ∈(0,1).

Define the operator A:E→E by

$$Au=\int_0^1G(t,s)h(s)f\bigl(u\bigl(\theta(s)\bigr)\bigr) d s. $$

(2.2)

Applying Lemma 2.3 with y(t)=h(t)f(u(θ(t))), we obtain that fractional differential equation (1.1) has a solution if and only if the operator A has a fixed point.

Let u∈P, by Lemma 2.4, then we have

which implies AP⊂P. By means of the Ascoli-Arzelá theorem, it is easy to prove that T:P→P is completely continuous.

Now, we present some useful theorems regarding the theory of cones in Banach spaces [17, 18], and state several fixed point theorems which are needed to establish the existence of positive solutions of fractional differential equation (1.1).

Definition 2.6

A map α is said to be a nonnegative continuous concave (convex) functional on a cone P of a real Banach space E if α:P→[0,∞) is continuous and α(tx+(1−t)y)≥tα(x)+(1−t)α(y) (β(tx+(1−t)y)≤tβ(x)+(1−t)β(y)) for all x,y∈P and t∈[0,1].

We introduce the Krasnosel’skii’s fixed point theorem.

Lemma 2.7

[18]

Let P be a cone in a Banach space E. Assume Ω₁ and Ω₂ are open subsets of E with 0∈Ω₁ and $\overline{\Omega}_{1}\subset \Omega_{2}$. If $A:P\cap (\overline{\Omega}_{2}\backslash \Omega_{1})\rightarrow P$ is a completely continuous operator such that either

• (i) ∥Ax∥≤∥x∥,∀x∈P∩∂Ω₁ and ∥Ax∥≥∥x∥,∀x∈P∩∂Ω₂, or

• (ii) ∥Ax∥≥∥x∥,∀x∈P∩∂Ω₁ and ∥Ax∥≤∥x∥,∀x∈P∩∂Ω₂.

Then A has a fixed point in $P\cap (\overline{\Omega_{2}}\backslash \Omega_{1})$.

Let P _c ={u∈P:∥u∥<c}, P(q,b,d)={u∈P:b≤q(u),∥u∥≤d} and the map q is a nonnegative continuous concave functional on P. Next, we state the fixed-point theorem due to Leggett and Williams [10].

Lemma 2.8

Suppose that $A : \overline{P}_{c} \rightarrow \overline{P}_{c}$ is completely continuous and there exists a concave positive functional q on P such that q(u)≤∥u∥ for $u \in \overline{P}_{c}$. Suppose that there exist constants 0<a<b<d≤c such that

• (i) {u∈P(q,b,d):q(u)>b}≠∅ and q(Tu)>b if u∈P(q,b,d);

• (ii) ∥Tu∥<a if u∈P _a ;

• (iii) q(Tu)>b for u∈P(q,b,c) with ∥Tu∥>d.

Then A has at least three fixed points u ₁,u ₂ and u ₃ such that

$$\|u_1\| < a,\quad b < q(u_2)\quad\text{\textit{and}}\quad u_3 > a \quad\text{\textit{with} }q(u_3) < b.$$

Given a nonnegative continuous functional γ on a cone P of a real Banach space E, for each d>0, we let P(γ,d)={x∈P:γ(x)<d}. The following fixed-point theorem is developed in [19], which is initially motivated by Avery and Henderson’s double fixed-point theorem [15].

Lemma 2.9

Let P be a cone in a real Banach space E. Let α,β and γ be increasing, nonnegative continuous functionals on P such that for some c>0 and H>0, γ(x)≤β(x)≤α(x) and ∥x∥≤Hγ(x) for all $x\in \overline{P}(\gamma ,c)$. Suppose that there exist positive numbers a and b with a<b<c, and $A:\overline{P}(\gamma ,c)\rightarrow P$ is a completely continuous operator such that:

• (i) γ(Ax)<c for all x∈∂P(γ,c);

• (ii) β(Ax)>b for all x∈∂P(β,b);

• (iii) P(α,a)≠∅ and α(Ax)<a for x∈∂P(α,a).

Then A has at least three fixed points x ₁, x ₂ and x ₃ belonging to $\overline{P}(\gamma ,c)$ such that

$$0\leq \alpha (x_1)<a<\alpha (x_2)\quad\text{\textit{with} }\beta (x_2)<b<\beta(x_3) \quad \text{\textit{and}} \quad \gamma (x_3)<c.$$

Lemma 2.10

[20, 21]

Let P be a cone in a real Banach space E. Let α,β and γ be increasing, nonnegative continuous functionals on P such that for some c>0 and H>0, γ(x)≤β(x)≤α(x) and ∥x∥≤Hγ(x) for all $x\in \overline{P}(\gamma ,c)$. Suppose that there exist positive numbers a and b with a<b<c, and $A:\overline{P}(\gamma ,c)\rightarrow P$ is a completely continuous operator such that:

• (i) γ(Ax)>c for all x∈∂P(γ,c);

• (ii) β(Ax)<b for all x∈∂P(β,b);

• (iii) P(α,a)≠∅ and α(Ax)>a for x∈∂P(α,a).

Then A has at least three fixed points x ₁, x ₂ and x ₃ belonging to $\overline{P}(\gamma ,c)$ such that

$$0\leq \alpha (x_1)<a<\alpha (x_2)\quad\text{\textit{with} }\beta (x_2)<b<\beta(x_3)\quad\text{\textit{and}}\quad\gamma (x_3)<c.$$

Let β and ϕ be nonnegative continuous convex functionals on P, λ be a nonnegative continuous concave functional on P and φ be a nonnegative continuous functional on P, respectively. We define the following convex sets:

and a closed set

Finally, we introduce the following fixed point theorem due to Avery and Peterson [14].

Lemma 2.11

Let P be a cone in a real Banach space E and β, ϕ, λ, φ be defined as the above. Moreover, φ satisfies φ(λ′x)≤λ′φ(x) for 0≤λ′≤1 such that, for some positive numbers h and d,

$$\lambda (x)\leq \varphi (x)\quad\text{\textit{and}}\quad \Vert x\Vert \leq h\phi (x) ,$$

(2.3)

holds for all $x\in \overline{P(\phi ,d)}$. Suppose $A:\overline{P(\phi ,d)}\rightarrow \overline{P(\phi ,d)}$ is completely continuous and there exist positive real numbers a,b,c, with a<b such that:

• (i) {x∈P(ϕ,β,λ,b,c,d):λ(x)>b}≠∅ and λ(A(x))>b for x∈P(ϕ,β,λ,b,c,d);

• (ii) λ(A(x))>b for x∈P(ϕ,λ,b,d) with β(A(x))>c;

• (iii) 0∉R(ϕ,φ,a,d) and λ(A(x))<a for all x∈R(ϕ,φ,a,d) with φ(x)=a.

Then A has at least three fixed points $x_{1},x_{2},x_{3}\in \overline{P(\phi ,d)}$ such that

$$\phi(x_i)\leq d \quad\text{\textit{for} } i=1,2,3,\quad b<\lambda (x_1), \quad a<\varphi (x_2)\quad\text{\textit{and}}\quad \lambda (x_2)<b \quad\text{\textit{with} }\varphi(x_3)<a.$$

3 Single or Twin Solutions

For u∈P, we define

Following [22], we let the sign of i ₀ stand for the number of zeros in the set {f ₀,f _∞} and i _∞ stand for the number of infinities in the set {f ₀,f _∞}. Clearly, i ₀, i _∞=0, 1, or 2, and there exist six possible cases: (i) i ₀=1 and i _∞=1; (ii) i ₀=0 and i _∞=0; (iii) i ₀=0 and i _∞=1; (iv) i ₀=0 and i _∞=2; (v) i ₀=1 and i _∞=0; and (vi) i ₀=2 and i _∞=0. In the following, according to the Krasnosel’skii’s fixed point theorem in a cone, we may first consider the existence for at least one or two positive solutions of fractional differential equation (1.1) under the above six possible cases.

3.1 The Case of i ₀=1 and i _∞=1

In this subsection, we discuss the existence for at least single positive solution of fractional differential equation (1.1) only under i ₀=1 and i _∞=1, and obtain

Theorem 3.1

Fractional differential equation (1.1) has at least one positive solution in the case of i ₀=1 and i _∞=1.

Proof of Theorem 3.1

We divide the proof into two steps:

Step (i): f ₀=0 and f _∞=∞.

According to f ₀=0, there exists a constant r ₁>0 such that for 0<u≤r ₁ it holds f(u)≤εu, where ε>0 and satisfies

$$\varepsilon\int_0^1G(1,s)h(s) d s \leq 1.$$

For u∈P with ∥u∥=r ₁, by (2.2) we have

So if let $\Omega_{r_{1}}= \{ u\in P:\Vert u\Vert <r_{1} \}$, we have ∥Au∥≤∥u∥ for $u\in P\cap \partial \Omega_{r_{1}}$.

It follows from f _∞=∞ that there exists a constant r ₂>0 such that f(u)≥ku for u≥r ₂, where k>0 satisfies the following inequality

$$\gamma^{2}k \int_\frac{1}{2}^1G(1,s)h(s)d s \geq 1. $$

(3.1)

Set

$$\begin{array}{l}r_2>r_1 \quad\text{and}\quad \Omega_{r_2}= \{ u\in P:\Vert u\Vert <r_2 \} .\end{array}$$

Since t≤θ(t)≤1, t∈(0,1) and $u(t)=\int_{0}^{1}G(t,s)y(s) d s$, in view of Lemma 2.4, one has

(3.2)

If u∈P with ∥u∥=r ₂, in terms of (3.1) and (3.2), we get

(3.3)

Thus, by virtue of Lemma 2.7, fractional differential equation (1.1) has at least a single positive solution $u\in P\cap (\overline{\Omega }_{r_{2}}\backslash \Omega_{r_{1}})$ with r ₁≤∥u∥≤r ₂.

Step (ii): f ₀=∞ and f _∞=0.

Since f ₀=∞, there exists an r ₃>0 such that f(u)≥mu for 0<u≤r ₃, where m satisfies

$$\gamma^{2}m \int_\frac{1}{2}^1G(1,s)h(s)d s \geq 1. $$

(3.4)

For u∈P with ∥u∥=r ₃, according to (3.2) and (3.4), one has

(3.5)

Taking $\Omega_{r_{3}}= \{ u\in E:\Vert u\Vert <r_{3} \}$, we have ∥Au∥≥∥u∥ for $u\in P\cap \partial \Omega_{r_{3}}$.

Now, we consider f _∞=0. By the definition, there exists r ₄>r ₃ such that

$$ f(u)\leq \delta u\quad\text{for }u\geq r_4,$$

(3.6)

where δ>0 satisfies

$$\delta\int_0^1G(1,s)h(s) d s \leq 1. $$

(3.7)

Suppose that f is bounded, then we have f(u)≤φ _p (K) for all u∈[0,∞) and some constant K>0. Choose

If u∈P with ∥u∥=r ₄, we get

If f is unbounded, from f∈C([0,1], [0,+∞)), there exists a constant C>0 such that

$$f(u)\leq C\quad\text{for }u\in [0,r_{4} ].$$

Making use of (3.6) we have

$$f \bigl(u \bigl(\theta(t) \bigr) \bigr)\leq \max \{C, \delta u \}\quad\text{for }t\in [0,1].$$

Let

$$r_4>\max \biggl\{\frac{C}{\delta}, 2r_3 \biggr\}. $$

(3.8)

Assume that u∈P with ∥u∥=r ₄, then using (3.6), (3.7) and (3.8), we deduce

Apparently, in either case, taking $\Omega_{r_{4}}= \{ u\in P:\Vert u\Vert <r_{4} \}$, for $u\in P\cap \partial \Omega_{r_{4}}$, one has ∥Au∥≤∥u∥. Consequently, it follows from condition (ii) of Lemma 2.7 that fractional differential equation (1.1) has at least a single positive solution $u\in P\cap (\overline{\Omega }_{r_{4}}\backslash \Omega_{r_{3}})$ with r ₃≤∥u∥≤r ₄. □

3.2 The Case i ₀=0 and i _∞=0

In this subsection, we discuss the existence for the positive solution to fractional differential equation (1.1) under the case of i ₀=0 and i _∞=0, and obtain

Theorem 3.2

Assume that the following conditions are satisfied:

• (i) there exists a constant p>0 such that f(u)≤pΛ₁ for u∈[0,p], where

  

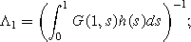
• (ii) there exists another constant q>0 (p≠q) such that f(u)≥qΛ₂ for u∈[0,q], where

  

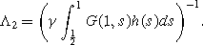
  Then fractional differential equation (1.1) has at least one positive solution u such that ∥u∥ lies between p and q.

Proof of Theorem 3.2

Without loss of generality, we may assume that p<q.

Let Ω _p ={u∈E:∥u∥<p}. For any u∈P∩∂Ω _p , it follows from condition (i) that

(3.9)

which implies

$$ \Vert Au\Vert \leq \Vert u\Vert \quad\text{for }u\in P\cap \partial \Omega_{p}.$$

Similarly, let Ω _q ={u∈E:∥u∥<q}. For u∈P∩∂Ω _q , it follows from condition (ii) that

So, letting Ω _q ={u∈E:∥u∥<q}, we have

$$ \Vert Au\Vert \geq \Vert u\Vert ,\quad u\in P\cap \partial \Omega_{q}.$$

Thus, it follows from part (i) of Lemma 2.7 that fractional differential equation (1.1) has at least one positive solution $u\in P\cap (\overline{\Omega }_{q}\backslash \Omega_{p})$. □

Theorem 3.3

Assume that $f_{0}\in (\frac{\Lambda_{2}}{\gamma} ,\infty )$ and f _∞∈(0,Λ₁) are satisfied. Then fractional differential equation (1.1) has at least one positive solution.

Proof of Theorem 3.3

On the one hand, let $\varepsilon_{1}=f_{0}-\frac{\Lambda_{2}}{\gamma}>0$, then there exists a sufficiently small constant q′>0 such that

$$\frac{f(u)}{u}\geq f_0-\varepsilon_{1} =\frac{\Lambda_2}{\gamma} \quad\text{for }u\in (0,q'].$$

If u∈[0,q′], then f(u)≥γΛ₂ u, which implies that

So, letting Ω _q′={u∈E:∥u∥<q′}, we derive

$$\Vert Au\Vert \geq \Vert u\Vert ,\quad u\in P\cap \partial \Omega_{q'}.$$

On the other hand, for ε ₂=Λ₁−f _∞>0, there exists a p″ (>q′) such that

$$\frac{f(u)}{u}\leq f_\infty +\varepsilon_{2} =\Lambda_1 \quad\text{for }u\in [p'',\infty ). $$

(3.10)

There are two cases here.

Case (i): if f is bounded. That is, there exists a constant K ₁>0 satisfying f(u)≤K ₁ for u∈[0,∞). Then we choose p′ such that p′≥max{K ₁/Λ₁, p″} and

$$f(u)\leq K_1\leq \Lambda_1p'\quad\text{for }u \in \bigl[0,\,p' \bigr],$$

which implies that condition (i) of Theorem 3.2 holds.

Case (ii): if f is unbounded. Since f∈C([0,1], [0,∞)), there exists $p_{1}^{*}>p'$ such that $f(u)\leq f(p_{1}^{*})$ for $u\in [0,p_{1}^{*}]$. By the assumption p′≥max{K ₁/Λ₁, p″}, it follows from (3.10) that

$$f\bigl(p_1^*\bigr)\leq \Lambda_1p_1^*,$$

and

$$f(u)\leq f \bigl(p_1^* \bigr)\leq \Lambda_1p_1^*\quad\text{for }u\in \bigl[0,p_1^* \bigr].$$

This implies that condition (i) of Theorem 3.2 is fulfilled. Letting

$$\Omega_{p_1*}= \bigl\{ u\in E:\Vert u\Vert <p_1^* \bigr \} ,$$

we have

$$\Vert Au\Vert \leq \Vert u\Vert \quad\text{for }u\in P\cap \partial \Omega_{p_1^*}.$$

So, we have completed the proof. □

Theorem 3.4

Assume that f ₀∈(0,Λ₁) and f _∞∈(Λ₂,∞) are satisfied. Then fractional differential equation (1.1) has at least one positive solution.

Under the above assumptions, it is easy to prove in a similar way that conditions (i) and (ii) in Theorem 3.2 are satisfied. So we omit the proof.

3.3 The Case i ₀=1 and i _∞=0 or i ₀=0 and i _∞=1

In this subsection, we discuss the existence of at least single positive solution to fractional differential equation (1.1) under conditions i ₀=1 and i _∞=0 or i ₀=0 and i _∞=1, respectively.

Theorem 3.5

Suppose that f ₀∈(0,Λ₁) and f _∞=∞ hold. Then fractional differential equation (1.1) has at least one positive solution.

Proof of Theorem 3.5

Since f _∞=∞, it follows from inequality (3.3) that

$$\Vert Au\Vert \geq \Vert u\Vert \quad\text{for }u\in P\cap \partial \Omega_{r_2}.$$

For any ε ₃=Λ₁−f ₀>0, according to f ₀∈(0,Λ₁), there exists a sufficiently small $p_{2}'\in (0,r_{2})$ which satisfies

$$f(u)\leq (f_0+\varepsilon_3 )u= \Lambda_1u\leq \Lambda_1p_2'\quad\text{for }u\in \bigl[0,p_2' \bigr].$$

This implies that part (i) of Theorem 3.2 holds. It is directly deduced that

$$\Vert Au\Vert \leq \Vert u\Vert \quad \text{for }u\in P\cap \partial \Omega_{p_2'}.$$

So the proof is complete. □

Theorem 3.6

Assume that f ₀=∞ and f _∞∈(0,Λ₁) hold. Then fractional differential equation (1.1) has at least one positive solution.

Proof of Theorem 3.6

Firstly, since f ₀=∞, in view of inequality (3.5), we have

$$\Vert Au\Vert \geq \Vert u\Vert ,\quad u\in P\cap \partial \Omega_{r_3}.$$

Secondly, since f _∞∈(0,Λ₁), using a similar technique to the second part of the proof in Theorem 3.3, we obtain that condition (i) of Theorem 3.2 holds. That is, inequality (3.9) is fulfilled, which leads to

$$\Vert Au\Vert \leq \Vert u\Vert ,\quad u\in P\cap \partial \Omega_{p'},$$

where p′>r ₃. Hence, fractional differential equation (1.1) has at least one positive solution. □

By virtue of Theorems 3.5 and 3.6, respectively, we can easily have the following two corollaries.

Corollary 3.7

Assume that one of the following two conditions holds

• (i) f _∞=∞ or f ₀=∞, and condition (i) in Theorem 3.2 is satisfied;

• (ii) f ₀=0 or f _∞=0, and condition (ii) in Theorem 3.2 is satisfied.

Then fractional differential equation (1.1) has at least one positive solution.

Thus, it is straightforward to obtain the following result.

Theorem 3.8

Assume that one of the following two conditions holds:

• (i) f ₀∈(Λ₂,∞) and f _∞=0;

• (ii) f ₀=0 and f _∞∈(Λ₂,∞).

Then fractional differential equation (1.1) has at least one positive solution.

3.4 The Case i ₀=0 and i _∞=2 or i ₀=2 and i _∞=0

In this subsection, we present the existence of at least two positive solutions for fractional differential equation (1.1) under i ₀=0 and i _∞=2 or i ₀=2 and i _∞=0.

Combining Theorems 3.1 and 3.2, we can obtain the following theorem immediately.

Theorem 3.9

• (i) Assume that i ₀=0 and i _∞=2, and condition (i) of Theorem 3.2 holds, then fractional differential equation (1.1) has at least two distinct positive solutions u ₁ and u ₂∈P such that 0<∥u ₁∥<p<∥u ₂∥.

• (ii) Assume that i ₀=2 and i _∞=0, and condition (ii) of Theorem 3.2 holds, then fractional differential equation (1.1) has at least two distinct positive solutions u ₁ and u ₂∈P such that 0<∥u ₁∥<q<∥u ₂∥.

4 Triple or Multiple Solutions

We have established some existence results of at least one or two positive solutions to fractional differential equation (1.1) in the preceding section. In this section, we will further discuss the existence of positive solutions to fractional differential equation (1.1) by using three different methods.

For the notational convenience, we denote

4.1 Three Solutions

In this subsection, we discuss the existence of at least three positive solutions to (1.1).

Theorem 4.1

Let a,b and c be constants such that $0 <a < b < \frac{N}{L}c$. In addition, if the following conditions are satisfied.

• (i) $f(u(\theta(t))) < \frac{a}{L}$ for (t,u)∈[0,1]×[0,a];

• (ii) $f(u(\theta(t))) > \frac{b}{N}$ for $(t, u) \in [ \frac{1 }{2} , 1 ] \times [b, c]$;

• (iii) $f(u(\theta(t)))\leq \frac{c}{L}$ for (t,u)∈[0,1]×[0,c].

Then (1.1) has at least triple positive solutions u ₁,u ₂,u ₃∈P such that

$$0< \|u_1\| < a,\quad b < \inf_{t\in [\frac{1}{2},1 ]}u_2, \quad a<u_3 \quad\text{\textit{with} } \inf_{t\in [\frac{1}{2},1 ]}u_3 <b.$$

Proof of Theorem 4.1

For $u\in \overline{P}$, let $q(u) =\inf_{t\in [\frac{1}{2},\,1 ]}u$. It is obvious that q(u) is a nonnegative concave function and satisfies

$$q(u) \leq \|u\|\quad\text{for } u \in P_c.$$

In the following, we shall show that all the conditions of Lemma 2.8 hold with respect to the operator A.

For u∈P _c , which reduces to u∈[0,c], by condition (iii) we have

(4.1)

which implies $A : \overline{P}_{c} \rightarrow \overline{P}_{c}$.

If u∈P _a , we have u∈[0,a]. This indicates that condition (ii) of Lemma 2.8 is satisfied. Let d be a fixed constant such that b<d≤c, namely, q(d)=d>b and ∥d∥=d, so we find P(q,b,d)≠∅. For any u∈P(q,b,d), we have

$$\|u\| \leq d\quad\text{and}\quad q(u) = \inf_{t\in [\frac{1}{2},1 ]}u \geq b,$$

and

Thus, condition (i) of Lemma 2.8 is satisfied.

Finally, using an analogous argument, for any u∈P(q,b,c) with ∥Au∥>d, we can derive that ∥u∥≤c, $\inf_{t\in [\frac{1}{2},1 ]}u\geq b$, and q(Au)>b, which indicates that condition (iii) holds.

Consequently, it follows from Lemma 2.8 that (1.1) has at least three solutions such that

$$0< \|u_1\| < a,\quad b < \inf_{t\in [\frac{1}{2},1 ]}u_2,\quad a <u_3 \quad\text{with } \inf_{t\in [\frac{1}{2},1 ]}u_3 < b.$$

 □

Note that condition (iii) in Theorem 4.1 can be replaced by the following condition:

$$\bigl(\mathrm{iii}'\bigr) \quad \lim_{u\rightarrow \infty }\frac{f(u)}{u}\leq \frac{1}{L} \quad\text{for } u\in P.$$

Corollary 4.2

If condition (iii) in Theorem 4.1 is replaced by (iii′), then the conclusion of Theorem 4.1 also holds.

Proof of Corollary 4.2

From Theorem 4.1, we only need to prove that condition (iii′) implies condition (iii). That is, if (iii′) holds, then there exists a number

$$c\geq L\max \Bigl\{\max_{u\in[0,c]}|f(u)|,b \Bigr\},$$

such that $f(u)\leq \frac{c}{L}$ for u∈[0,c].

On the contrary, suppose that for any c≥Lmax{max _u∈[0,c]|f(u)|,b}, there exists u _c ∈[0,c] such that $f(u_{c})> \frac{c}{L}$. If we take c _n >b (n=1,2,…) with c _n →∞, there exists u _n ∈[0,c _n ] such that

$$ f(u_n)> \frac{c_n}{L},$$

(4.2)

which implies

$$ \lim_{n\rightarrow \infty }f(u_n)=\infty.$$

(4.3)

Since condition (iii′) holds, there exists τ>0 such that

$$ f(u)\leq \frac{u}{L},\quad u>\tau.$$

(4.4)

Hence, we have u _n ≤τ. Otherwise, if u _n >τ, according to (4.4), we find

$$f(u_n)\leq \frac{u_n}{L} \leq \frac{c_n}{L} ,$$

which yields a contradiction with (4.2).

Let W=max _u∈[0,τ] f(u), so it has f(u _n )≤W (n=1,2,…), which also contradicts with (4.3). Consequently, the proof is complete. □

4.2 Arbitrary n Solutions

In this subsection, by using the fixed-point theorem generalized by Avery and Henderson [19], the existence criteria for at least three or arbitrary n positive solutions of fractional differential equation (1.1) are considered.

For u∈P, we define the nonnegative, increasing, continuous functionals γ ₁, β ₁ and α ₁ by

$$\gamma_1 (u)= \beta_1(u)=\inf_{t\in [\frac{1}{2},1 ]}u ,\quad \quad \alpha_1 (u)=\sup_{t\in [0,1 ]}u.$$

It is easily seen that

$$\gamma_1 (u)=\beta_1 (u)\leq \alpha_1 (u)\quad\text{for each } u\in P.$$

According to (3.2), we further have

$$\Vert u\Vert \leq \frac{1}{\gamma}\gamma_1(u)\quad\text{for all }u\in P.$$

Now we present the following main result on three distinct positive solutions in this subsection.

Theorem 4.3

Assume that there exist real numbers a′,b′,c′ such that 0<a′<b′<γc′, and f(u(θ(t))) satisfies the following three conditions

• (i) $f(u(\theta(t)))<\frac{c'}{M}$ for $(t,u)\in [\frac{1}{2} ,1 ]\times [c',\frac{1}{\gamma}c' ]$;

• (ii) $f(u(\theta(t)))>\frac{b'}{N}$ for $(t,u)\in [\frac{1}{2} ,1 ]\times [b',\frac{1}{\gamma}b' ]$;

• (iii) $f(u(\theta(t)))<\frac{a'}{L}$ for (t,u)∈[0,1]×[0,a′].

Then (1.1) has at least three distinct positive solutions $u_{1} , u_{2} ,u_{3}\in \overline{P}(\gamma,c')$ such that

Proof of Theorem 4.3

It suffices to prove that all the conditions of Lemma 2.9 hold with respect to the operator A. By using a closely similar way to the derivation of (4.1), it is not difficult to see that $A: \overline{P}(\gamma_{1},c)\rightarrow P$.

Firstly, assume that u∈∂P(γ ₁,c′), then we have $\gamma_{1} (u)=\inf_{t\in [\frac{1}{2},1 ]}u=c'$. Inequality (3.2) implies that $\Vert u\Vert \leq \frac{1}{\gamma }\gamma_{1} (u)=\frac{1}{\gamma }c'$, which gives $c'\leq u\leq \frac{1}{\gamma }c'$, $t\in [\frac{1}{2},1 ]$.

Thus, it follows from condition (i) that

which implies γ ₁(Au)<c′ for u∈∂P(γ ₁,c′).

Secondly, for u∈∂P(β ₁,b′), we have $\beta_{1}(u)=\inf_{t\in [\frac{1}{2},1 ]}u=b'$. Inequality (3.2) implies that $\Vert u\Vert \leq \frac{1}{\gamma }\beta_{1} (u)=\frac{1}{\gamma }b'$, namely, $b'\leq u\leq \frac{1}{\gamma }b'$, $t\in [\frac{1}{2} ,1 ]$. By means of condition (ii), we deduce

This means that β ₁(Au)>b′ for u∈∂P(β ₁,b′).

Finally, we show that P(α ₁,a′)≠∅ and α ₁(Au)<a′ for all u∈∂P(α ₁,a′). Since $\frac{a'}{2}\in P(\alpha_{1} ,a')$, for u∈∂P(α ₁,a′), we have α ₁(u)=sup _t∈[0,1] u=a′, which gives 0≤u≤a′ for t∈[0,1]. According to condition (iii), we derive

Hence, conditions (i)–(iii) in Lemma 2.9 are satisfied. By virtue of assumptions (S1) and (S2), we obtain that the solution of (1.1) does not vanish identically on any closed subinterval of [0,1]. Consequently, (1.1) has at least three distinct positive solutions u ₁, u ₂ and u ₃, which belong to $\overline{P}(\gamma_{1} ,c')$ and satisfy

Therefore, we have completed the proof. □

The following result can be considered as a corollary of Theorem 4.3.

Corollary 4.4

Assume that f satisfies the following two conditions:

• (i) f ₀=0 and f _∞=0;

• (ii) there exists c ₀>0 such that $f(u)>\frac{\gamma c_{0} }{N}$ for $(t,u)\in [\frac{1}{2},1 ]\times [\gamma c_{0},c_{0} ]$.

Then (1.1) has at least three distinct positive solutions.

Proof of Corollary 4.4

According to condition (ii), letting b′=γc ₀, we have

which implies that condition (ii) of Theorem 4.3 is satisfied.

Choose a sufficiently small constant K ₁>0 such that

$$K_1L=K_1 \biggl(\int_0^1G(1,s)h(s)d s \biggr) <1. $$

(4.5)

Since f ₀=0, there exists another sufficiently small constant k ₁>0 such that

$$f(u)\leq K_1 u\quad\text{for }(t,u)\in[0,1]\times [0,k_1]. $$

(4.6)

Without loss of generality, we suppose that k ₁=a′<b′. For 0≤u≤a′, we have u≤k ₁. Thus, it follow from (4.5) and (4.6) that

$$f(u)\leq K_1u\leq K_1a'< \frac{a'}{L}\quad\text{for }0\leq u\leq a'.$$

This implies that condition (iii) of Theorem 4.3 holds.

Again, choose another sufficiently small K ₂ such that

$$\frac{K_2}{\gamma}M=\frac{K_2}{\gamma} \biggl(\int_\frac{1}{2}^1G(1,s)h(s)d s \biggr) <1.$$

Since f _∞=0, there exists a sufficiently large value k ₂>0 such that

$$f(u)\leq K_2u\quad\text{for }u\geq k_2.$$

Without loss of generality, we may suppose $k_{2}>\frac{b'}{\gamma}$ and choose c′=k ₂, and find

$$f(u)\leq K_2u\leq K_2\frac{c'}{\gamma}<\frac{ c'}{M}\quad\text{for }c'\leq u\leq \frac{1}{\gamma }c'.$$

This means that condition (i) of Theorem 4.3 holds.

Combining the above discussions, we obtain 0<a′<b′<γc′. Hence, it follows from Theorem 4.3 that (1.1) has at least three distinct positive solutions. □

Extending the idea in the proof of Theorem 4.3, we can prove the existence for multiple positive solutions to (1.1) when conditions (i)–(iii) are modified and imposed appropriately on f.

Theorem 4.5

Assume that there exist constant numbers $a_{ i}', b_{i}', c_{ i}'$ such that

(4.7)

where i=1,2,…,n. Assume that f(u(θ(t))) satisfies the following three conditions:

• (i) $f(u(\theta(t)))<\frac{c_{i}'}{M}$ for $(t,u)\in [\frac{1}{2} ,1 ]\times [c_{i}',\frac{1}{\gamma}c_{i}' ]$;

• (ii) $f(u(\theta(t)))>\frac{b_{i}'}{N}$ for $(t,u)\in [\frac{1}{2} ,1 ]\times [b_{i}',\frac{1}{\gamma}b_{i}' ]$;

• (iii) $f(u(\theta(t)))<\frac{a_{i}'}{L}$ for $(t,u)\in [\frac{1}{2} ,1 ]\times [0,a_{i}' ]$.

Then (1.1) has at least n distinct positive solutions.

Proof of Theorem 4.5

If n=1, it follows from condition (iii) that

$$A: \overline{P}_{a_1'}\rightarrow P_{a_1'}\subset \overline{P}_{a_1'}.$$

This means that A has at least one fixed point $u_{01}\in \overline{P}_{a_{1}'}$ by the Schauder fixed point theorem.

If i=2, it is clear that Theorem 4.3 holds with $a'=a'_{1},\, b'=b'_{1}$ and $c'=c'_{1}$. Then we can obtain at least three positive solutions u ₁₁, u ₁₂ and u ₁₃ satisfying

which implies that (1.1) has at least 2 distinct positive solutions.

Using the mathematical induction, when n=k−1, we assume that (1.1) has at least k−1 distinct positive solutions, denoted by u _i . It follows from the solution position and local properties that

$$0<\inf_{t\in [\frac{1}{2},1]}u_{i}<c_{k-1}',\quad i=1,2, \ldots,k-1. $$

(4.8)

When n=k, it is easy to see that Theorem 4.3 holds with $a'=a'_{k},\,b'=b'_{k}$ and $c'=c'_{k}$. So there exist at least three distinct positive solutions u _k1, u _k2 and u _k3 satisfying

$$0< \|u_{k1}\|<a_k'<\|u_{k2}\|\quad \text{and}\quad\inf_{t\in [\frac{1}{2},1]}u_{k2}<b_k'<\inf_{t\in [\frac{1}{2},1]}u_{k3}<c_k'. $$

(4.9)

According to (4.7), (4.8) and (4.9), we have

$$u_{i}\neq u_{k3},\quad i=1,2,\ldots,k-1.$$

Hence, (1.1) has at least n distinct positive solutions. So the proof is completed. □

In terms of Lemma 2.10, we can obtain the following result by using the similar way as to the proof of Theorem 4.3.

Theorem 4.6

Assume that there exist positive numbers a′,b′,c′ such that a′<b′<γc′. In addition, f(u(θ(t))) satisfies the following conditions:

• (i) $f(u(\theta(t)))>\frac{c'}{N}$ for $(t,u)\in [\frac{1}{2} ,1 ]\times [c',\frac{1}{\gamma}c' ]$;

• (ii) $f(u(\theta(t)))<\frac{b'}{M}$ for $(t,u)\in [\frac{1}{2} ,1 ]\times [b',\frac{1}{\gamma}b' ]$;

• (iii) $f(u(\theta(t)))>\frac{a'}{N}$ for (t,u)∈[0,1]×[0,a′].

Then (1.1) has at least three distinct positive solutions $u_{1}, u_{2} ,u_{3}\in \overline{P}(\gamma,c')$ such that

It follows from Theorem 4.3 that we can obtain the following corollary and theorem immediately.

Corollary 4.7

Assume that f satisfies conditions

• (i) f ₀=∞ and f _∞=∞;

• (ii) there exists c ₀>0 such that $f(u)<\frac{\gamma }{M}c_{0}$ for $(t,u)\in [\frac{1}{2},1 ]\times[\gamma c_{0}, c_{0}]$.

Then (1.1) has at least three distinct positive solutions.

Theorem 4.8

Suppose that there are positive numbers $a_{i}',b_{i}',c_{i}'$ such that

where i=1,2,…,n. In addition, f(u(θ(t))) satisfies the following conditions:

• (i) $f(u(\theta(t)))>\frac{c_{i}'}{N}$ for $(t,u)\in [\frac{1}{2} ,1 ]\times [c_{i}',\frac{1}{\gamma}c_{i}' ]$;

• (ii) $f(u(\theta(t)))<\frac{b_{i}'}{M}$ for $(t,u)\in [\frac{1}{2} ,1 ]\times [b_{i}',\frac{1}{\gamma}b_{i}' ]$;

• (iii) $f(u(\theta(t)))>\frac{a_{i}'}{N}$ for $(t,u)\in [0 ,1 ]\times [0,a_{i}' ]$.

Then (1.1) has at least n distinct positive solutions.

4.3 Arbitrary 2n−1 Solutions

In this subsection, the existence of at least three or arbitrary odd positive solutions to (1.1) are established by using the Avery-Peterson fixed point theorem [14].

Define the nonnegative continuous convex functionals ϕ and β, concave functional λ and functional φ on P by

Theorem 4.9

Suppose that there exist constants a ^∗,b ^∗,d ^∗ such that $0<a^{*}<b^{*}<\frac{M}{L}d^{*}$, and f satisfies the following conditions:

• (i) $f(u(\theta(t)))\leq\frac{d^{*}}{L}$ for all (t,u)∈[0,1]×[0,d ^∗];

• (ii) $f(u(\theta(t)))>\frac{b^{*}}{N}$ for all $(t,u)\in [\frac{1}{2},1 ]\times [b^{*}, d^{*}]$;

• (iii) $f(u(\theta(t)))<\frac {a^{*}}{M}$ for all $(t,u)\in [\frac{1}{2},1 ]\times [a^{*}, d^{*}]$.

Then (1.1) has at least three distinct positive solutions u ₁, u ₂, u ₃ such that

Proof of Theorem 4.9

According to the definition of completely continuous operator A, it suffices to prove that all the conditions of Lemma 2.11 hold with respect to operator A. For all u∈P, we have λ(u)=φ(u) and ∥u∥=ϕ(u). So inequality (2.3) holds in this case.

Firstly, we show that $A:\overline{P(\phi ,d^{*})}\rightarrow\overline{P(\phi ,d^{*})}$.

For arbitrary $u\in\overline{P(\phi ,d^{*})}$, it follow from ϕ(u)=∥u∥≤d ^∗ and the assumption (i) that

It remains to show that assumptions (i)–(iii) of Lemma 2.11 are satisfied with respect to operator A.

Secondly, we verify that condition (i) of Lemma 2.11 is true. Let u≡kb ^∗ with $k=\frac{L}{M}$. From the definitions of L, M and β(u), respectively, it is easy to see that u=kb ^∗>b ^∗ and β(u)=kb ^∗. According to $b^{*}<\frac{M}{L}d^{*}$, we get ϕ(u)=kb ^∗<d ^∗. Hence, we have

$$\bigl\{ u\in P\bigl(\phi ,\beta ,\lambda ,b^*,kb^*,d^*\bigr):\lambda (x)>b^*\bigr\} \neq \emptyset .$$

For any u∈P(ϕ,β,λ,b ^∗,kb ^∗,d ^∗), we have b ^∗≤u≤d ^∗ for all $t\in [\frac{1}{2},1 ]$. According to assumption (ii), it gives

which implies that condition (i) of Lemma 2.11 is true.

Thirdly, we show that condition (ii) of Lemma 2.11 holds. For any u∈P(ϕ,λ,b ^∗,d ^∗) with β(Au)>kb ^∗, we have b ^∗≤u≤d ^∗ for $t\in [\frac{1}{2},1 ]$, and

This implies that condition (ii) of Lemma 2.11 is satisfied.

Finally, we check on condition (iii) of Lemma 2.11. Clearly, since φ(0)=0<a ^∗, we have 0∉R(ϕ,φ,a ^∗,d ^∗). If u∈R(ϕ,φ,a ^∗,d ^∗) with $\varphi (u) =\inf_{t\in [ \frac{1}{2},1 ]}u=a^{*}$, this yields a ^∗≤u≤d ^∗ for all $t\in [\frac{1}{2},1 ]$. Hence, we have

Consequently, all the conditions of Lemma 2.11 are fulfilled. The proof is completed. □

Note that condition (i) in Theorem 4.9 can be replaced by the following condition (i′):

$$\lim_{u\rightarrow \infty }\frac{f(u)}{u}\leq \frac{1}{L} \quad\text{for } t\in [0,1].$$

The proof is similar to that of Corollary 4.2.

Theorem 4.10

Suppose that there exist constants $a_{i}^{*},b_{i}^{*},d_{i}^{*}$ such that

$$0<a_1^{*}<b_1^{*}<\frac{M}{L}d_1^{*} <a_2^{*}<b_2^{*}<\frac{M}{L}d_2^{*}<a_3^{*} <\cdots<a_n^{*},\quad n\in \mathbb{N},$$

where i=1,2,…,n. In addition, f satisfies the following conditions:

• (i) $f(u(\theta(t)))\leq\frac{d_{i}^{*}}{L}$ for all $(t,u)\in[0,1]\times [0, d_{i}^{*}]$;

• (ii) $f(u(\theta(t)))>\frac{b_{i}^{*}}{N}$ for all $(t,u)\in[0,1]\times [b_{i}^{*}, d_{i}^{*}]$;

• (iii) $f(u(\theta(t)))<\frac {a_{i}^{*}}{M}$ for all $(t,u)\in [\frac{1}{2},1 ]\times [a_{i}^{*}, d_{i}^{*}]$.

Then (1.1) has at least 2n−1 positive solutions.

Proof of Theorem 4.10

If n=1, we find from condition (iii) that $A:\overline{P}_{a_{1}^{*}}\rightarrow P_{a_{1}^{*}}\subset \overline{P}_{a_{1}^{*}}$, which means that A has at least one fixed point $u_{01}\in \overline{P}_{a_{1}^{*}}$ by the Schauder fixed point theorem.

If i=2, it is clear that Theorem 4.3 holds with $a^{*}=a^{*}_{1},\,b^{*}=b^{*}_{1}$ and $d^{*}=d^{*}_{1}$. Then we can obtain at least three positive solutions u ₁₁, u ₁₂ and u ₁₃ which satisfy

So (1.1) has at least three distinct positive solutions.

By the mathematical induction, assume that when n=k−1, (1.1) has at least 2k−3 positive solutions, denoted by u _i . It follows from the solution position and local properties that

$$\|u_{i}\|<d_{k-1}^*,\quad i=1,2,\ldots,k-1. $$

(4.10)

When n=k, it is easy to see that Theorem 4.9 holds with $a'=a'_{k},\,b'=b'_{k}$ and $c'=c'_{k}$. So there exist at least three positive solutions u _k1, u _k2 and u _k3 satisfying

(4.11)

By virtue of (4.10) and (4.11), we have

$$u_{i}\neq u_{k1}\neq u_{k2},\quad i=1,2,\ldots,k-1.$$

Consequently, (1.1) has at least 2k−1 distinct positive solutions. □

5 Examples

In this section, we give two examples to illustrate our main results.

Example 5.1

Consider the fractional differential equation with deviating arguments

$$\left \{\begin{array}{l@{\quad}l}D_{0^+}^{\alpha}u(t)+\Gamma(\alpha)(1-t)f(u(\theta(t)))=0, & t\in ( 0,1 ), n-1<\alpha\leq n,\\[4pt]u^{(i)}(0)=0, & i=0,1,2,\ldots,n-2,\\[4pt][D_{0^+}^{\beta}u(t) ]_{t=1}=0, & 1\leq\beta\leq n-2,\end{array} \right . $$

(5.1)

where θ(t)=t ^ν for (t,ν)∈(0,1)×(0,∞) and

$$f(u)=\left \{\begin{array}{l@{\quad}l}u^3 &\text{for } u\in [0,1],\\[4pt]e^{u-1} &\text{for } u\in (1,+\infty).\end{array} \right .$$

It is easy to find that f ₀=0 and f _∞=∞. By virtue of Theorem 3.1, we have that fractional differential equation (5.1) has at least positive solution.

Example 5.2

Consider the following fractional differential equation with deviating arguments

$$\left \{\begin{array}{l}D_{0^+}^{\frac{7}{2}}u(t)+\Gamma (\frac{7}{2} )(1-t)f(u(\theta(t)))=0,\quad t\in ( 0,1 ),\\[4pt]u(0)=u^{(1)}(0)=0,\\[4pt][D_{0^+}^{2}u(t) ]_{t=1}=0,\end{array} \right . $$

(5.2)

where θ(t)=t ^ν for (t,ν)∈(0,1)×(0,∞) and

$$f(u)=\left \{\begin{array}{l@{\quad}l}2 &\text{for } u\in [0,1),\\[3pt]p(u) &\text{for } u\in [1,2],\\[3pt]195 &\text{for } u\in (2,\infty).\end{array} \right .$$

Here p(u) is continuous and p(1)=2, p(2)=195.

Note that $\alpha=\frac{7}{2}$ and β=2. A direct calculation gives

$$N =\gamma\int_\frac{1}{2}^1G(1,s)h(s)d s\approx0.1768\int_{\frac{1}{2}}^1(1-s)^{\frac{1}{2}}ds-0.1768\int_{\frac{1}{2}}^1(1-s)^{\frac{5}{2}}ds\approx3.7207\times 10^{-2},$$

and

$$L\approx0.3910.$$

If we take a=1, b=2 and c=100, then we find that $0<a<b<\frac{N}{L}c$ and

and

$$f(u)<\frac{c}{L}=\frac{100}{ 0.17778}\approx 262.5\quad\text{for } u\in[0,100].$$

It follows from Theorem 4.1 that fractional differential equation (5.2) has at least three distinct positive solutions such that

$$0< \|u_1\| < 1,\quad 2 < \inf_{t\in [\frac{1}{2},1 ]}u_2,\quad 1<u_3 \quad\text{with } \inf_{t\in [\frac{1}{2},1 ]}u_3 < 2.$$