Introduction

Annually worldwide, more than 280,000 patients undergo surgery to replace their diseased valves, nearly all of them are mitral or aortic, with prosthetic ones, which can be either mechanical or bioprosthetic.6,28,38,43 Bileaflet mechanical heart valves (BMHV), the subject of the current study, are composed of two semicircular disks attached to a rigid valve ring by hinges. Due to their durability and favorable flow characteristics when compared to other mechanical valves, these are the most commonly implanted prosthetic heart valves in the world. However, all current BMHVs are subject to a number of clinical complications including thrombus formation,20,33 regurgitation,7 structural failure of the leaflets,8 cavitation,17,23 and noise.3,18 These complications are closely related to the valve design and the complex, non-physiological blood flow characteristics induced by BMHVs.

BMHVs are used for both aortic and mitral valve replacements.6,28,43 However, patients with mitral valve replacements have a higher risk of thromboembolism than those with an aortic valve replacement37; cumulative mortality for mitral valve replacement is also higher than that for aortic valve replacement6; and the mitral valve appears to be the determinant of long-term survival for combined aortic and mitral valve replacement.22 Thus, a better understanding of BMHVs in the mitral position would be useful for clinical cardiology as well as the further development of these prostheses. Past studies of BMHV mitral valves have either been in vivo 21,35 or experimental,2,23,29 and have provided some insights into the dynamics of leaflets with different valve orientations as well as ventricular flow patterns and shear stresses induced by these prostheses. However, these experiments mostly employ one or two-dimensional imaging and more importantly, are unable to measure the intraventricular pressure field; this limits the quantitative analysis of some key aspects of prosthesis performance.

In the current study, we develop a model for the left ventricular blood flow and flow-structure interaction of a bileaflet mechanical heart valve in the mitral position in order to investigate the dynamics of mechanical valve leaflets, as well as the effect of these valves on the ventricular blood flow. We demonstrate that this computational model can provide unique data and insights that are difficult to obtain from in vivo studies or laboratory experiments. Simulations are performed for three locations of the valve hinge and two valve orientations in order to determine how these key design and deployment features affect important factors such as leaflet motion, mitral regurgitation, and mechanical energy loss.

Methods

Immersed Boundary Method for Flow Simulation

Blood flow in the left ventricle can be assumed as an incompressible Newtonian fluid, and its motion is governed by the Navier–Stokes equations:

$$ \nabla \cdot \varvec{u}{ = }0,\,\rho \left[ {\frac{{\partial \varvec{u}}}{\partial t} + (\varvec{u} \cdot \nabla \varvec{u})} \right] = - \nabla p + \mu \nabla^{2} \varvec{u} $$
(1)

where u is the velocity vector, p is the pressure, and ρ and µ are the density and the viscosity of the blood, respectively. The above equations are solved by a fractional step method,10,24 and all the spatial derivatives are discretized by a second-order central differencing scheme. The discretized equations are solved on a non-body conformal Cartesian grid and complex, moving boundaries are treated by a sharp-interface immersed boundary (IB) method.24,25 Briefly, the surface of each immersed boundary is represented by an unstructured mesh with triangular elements, and this is immersed into a Cartesian volume grid. The IB method employs a multi-dimensional ghost-cell methodology to impose the boundary conditions on the surface to second-order accuracy. The details of this method including validation studies can be found in Mittal et al.25

Left Ventricle Model

We employ a simple geometrical and kinematical model of the left ventricle (LV) presented in Vedula et al.36 which is taken from experiments.9,29 The in vitro left ventricle in these experiments was constructed of a flexible, transparent sack made of silicon rubber, and the ventricle was place inside a rectangular chamber filled with water. The volume of the ventricle was changed by actuating a piston connected to the ventricular assembly. A high-speed digital camera captured the time-evolution of the ventricular dynamics. The acquired images were subsequently analyzed, and the left ventricle reconstructed by an unstructured surface mesh with 124,340 triangular elements.36

A schematic of the LV, without valve leaflets, at the end-systolic and end-diastolic phases is shown in Fig. 1a. The generated computational surface model is immersed in a Cartesian grid (Fig. 1b), and the flow dynamics is obtained by solving the incompressible Navier–Stokes equation using the immersed boundary method.24,25 The volume change of the left ventricle with respect to the end-systolic volume is taken from the experiments9,29 and shown in Fig. 1c. The flow rate through the mitral annulus during diastole and through the aorta during systole is shown in Fig. 1d where positive values of the flow rate represent inflow into the ventricle and negative values represent outflow from the ventricle. The pulsatile characteristics of cardiac flows can be represented by the Reynolds number and the Womersley number. In the current study, the Reynolds number, \( \text{Re} = \frac{{\rho \bar{U}_{\text{m}} D_{\text{m}} }}{\mu } = 3475 \) and the Womersley number, \( {\text{Wo}} = \sqrt {\frac{{\rho D_{\text{m}}^{2} }}{\mu T}} = 9.8 \), where D m is the mitral orifice diameter, \( \bar{U}_{\text{m}} \) is the peak average velocity through mitral orifice, and T is the period of the entire cardiac cycle. These values are chosen in accordance with the experiment,9,13,29 and are the same as the previous numerical study.36

Figure 1
figure 1

The model left ventricle. (a) Schematic of the left ventricle shown at end-diastolic phase (\( t/T = 0.8 \)) and at end-systolic phase (\( t/T = 1.0 \)). (b) The LV model with triangulated surface elements is immersed in a Cartesian volume grid for the flow simulation with an immersed boundary method. (c) Volume change of the left ventricle with respect to the end-systolic volume. (d) Time variation of flow rate in the left ventricle during one cardiac cycle. Positive values of the flow rate represent inflow into the ventricle and negative values represent outflow from the ventricle

Full size image

BMHV Model

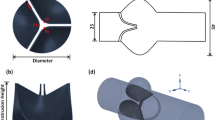
In this work, two semicircular disks are used to represent the bileaflet heart valve.2,28 The shape of a leaflet is shown in Fig. 2a. The blue dots and the dashed line in Fig. 2a represent two hinge pivots. The radius of the leaflet is R, and the location of hinge axis from the center of a valve is denoted by h = d/R. Note that the hinge axis is parallel to the diameter line of the leaflet, and the thickness of the leaflet is chosen to be 0.1R. The objective here is to study the dynamics of prosthetic mitral bileaflet valves and associated flow in the left ventricle with respect to valve orientation and hinge location. The valve orientation in Fig. 3a is referred to as the “anatomical orientation” (AO) since this more closely approximates the orientation of natural mitral valve leaflets. The valve orientation in Fig. 3b is correspondingly referred to as the “anti-anatomical orientation” (AAO). The orientation of the implant is chosen by the surgeon based on patient-specific conditions as well as the past experience of the surgeon. Experience has shown that valve orientation can have a significant effect on clinical outcome,4,7,12 but the mechanisms underlying this effect are not well understood and motivate the current study of valve orientation. The hinge location h determines the area of the central orifice between the two leaflets and the dynamics of leaflets which can influence energy losses across the valve and mitral regurgitation. However, the effect of hinge location on valve performance has yet to be explored in a systematic manner. For the investigation of the design features stated, numerical simulations are carried out for two different valve orientations and for three hinge locations varying from h = 0.1 to 0.3. This wide range of parameters covers most current valve designs and surgical practices in valve implantation.

Figure 2
figure 2

(a) Geometry of one leaflet of the bileaflet valve. The blue dots and the dashed line represent two hinge pivots. The radius of the leaflet is R, and the location of hinge axis from the center of a valve is d. (b) Freebody diagram of single leaflet. M is the net hydrodynamic torque acting on the leaflet due to the surrounding fluid and ω is the rotational speed of the leaflet

Full size image
Figure 3
figure 3

Valve implantation orientation and the definition of leaflet opening angle. (a) Anatomical orientation. (b) Anti-anatomical orientation. (c) Definition of the leaflet opening angle ϕ measured from the plane of mitral annulus. (d) A control volume surrounding the bileaflet mitral valve

Full size image

Mechanical valve leaflets are made of biocompatible materials such as pyrolytic carbon, polyester, alumina, titanium, stainless steel, etc. and the density ratio of these materials to blood ranges from about 1.5 to about 10.26,32 In the current study, we choose a density ratio of 10 which is representative of heavy metals. Using Fig. 2b as reference, the angular momentum equation around the hinge axis is

$$ I\frac{d\omega }{dt} = M = \int {\left( {{\mathbf{r}} \times ( - p{\mathbf{n}} + {\varvec{\upsigma}} \cdot {\mathbf{n}})} \right)} \cdot {\hat{\mathbf{a}}} \, dS , $$
(2)

where I is the moment of inertia around the hinge axis, ω is the rotational speed of leaflet, M is the net hydrodynamic torque acting on the leaflet due to the surrounding fluid, n is the unit normal vector on the leaflet surface S, r is the position vector from the hinge axis to the surface element dS, \( {\varvec{\upsigma}} = \mu \left( {\nabla \varvec{u + }\nabla \varvec{u}^{\varvec{T}} } \right) \) is the deviatoric stress tensor of the surrounding incompressible fluid, and \( {\hat{\mathbf{a}}} \) is the unit vector aligned with the hinge axis. The effect of the leaflet weight is not included in the current study. Once the torque acting on the leaflet is computed from the fluid pressure and viscous stress, the angular speed of the leaflet can be obtained from Eq. (2). Then, the leaflet angle θ is updated from the kinematic equation dθ/dt = ω. The coupling between the fluid and the leaflet equation (Eq. (2)) is explicit, i.e. the flow is marched one step with the current position and velocity of the leaflet as the boundary condition, and this is followed by an update of the leaflet position using Eq. (2). This method is accurate and stable for the cases simulated here and further analysis of the stability of such schemes can be found in Zheng et al.39

The motion of the valve leaflets is characterized by the leaflet opening angle θ, which is defined as the angle from the mitral annulus to each leaflet of the valve (Fig. 3c). Small values of θ represent closure or near closure of the leaflets, and large θ values represent open leaflets. In the current study, the leaflet motion is kinematically restricted to the range \( 5^\circ \le \theta \le 75^\circ \), which is within a realistic range for these prostheses.2,28 When a leaflet reaches its maximum or minimum angle, it stops instantaneously and behaves as if it is stationary; then if the direction of torque acting on the leaflet changes, the leaflet rotates again by following Eq. (2).

Boundary Conditions

The flow rate into and out of the ventricle is driven by the expansion and contraction of the LV, and the motion of endocardial surface obtained from experiments9,29 is prescribed by applying a no-slip, no-penetration boundary condition using the multi-dimensional ghost-cell methodology.24 Since the focus here is on the dynamics of the prosthetic mitral valve, the opening and closing of the aortic valve is realized by changing the boundary conditions at the far end of the aortic annulus.36 During diastole, the aortic orifice is closed by imposing a Dirichlet (u = 0) boundary condition; conversely, during systole, the aorta is opened by imposing a Neumann (\( {{\partial \varvec{u}} \mathord{\left/ {\vphantom {{\partial \varvec{u}} {\partial {\mathbf{n}}}}} \right. \kern-0pt} {\partial {\mathbf{n}}}}\varvec{ = 0} \)) boundary condition. A Neumann boundary condition is imposed on the inflow boundary of the mitral annulus during the entire cardiac cycle since the flow rate through this annulus is controlled by the dynamics of the bileaflet mechanical valve. For the pressure, a Dirichlet boundary condition (p =0) is imposed on the mitral inlet, and a Neumann boundary condition (\( {{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial {\mathbf{n}}}}} \right. \kern-0pt} {\partial {\mathbf{n}}}}\varvec{ = 0} \)) is imposed on the aortic boundary during the entire cardiac cycle.

Metrics for Analysis of Leaflet Motion and Flow

Three indices are used to characterize the motion of the BMHV leaflets. The first metric is referred to as the diastolic opening angle index (OAI) which measures the average opening angle of the valve during diastole, and is defined as \( {\text{OAI}} = \frac{1}{0.8T}\int_{0}^{0.8T} {\frac{{\theta_{1} + \theta_{2} - 2\theta_{\hbox{min} } }}{{2\theta_{\hbox{max} } }} \, } dt \), where θ 1 and θ 2 represent the opening angles of the corresponding leaflets and θ min and θ max are the minimum and maximum opening angles, and the values of this metric range between 0 (valve fully closed) and 1 (valve fully open). An effectively functioning valve should stay open during diastole in order to minimize the obstruction to the diastolic flow. The second metric, referred to here as the leaflet asymmetry index (LAI) is given by \( {\text{LAI}} = \sqrt {\frac{1}{0.8T}\int_{0}^{0.8T} {\left( {\frac{{\theta_{1} - \theta_{2} }}{{\theta_{\hbox{max} } }}} \right)^{2} } dt} \), and it provides a normalized measure of asymmetry in the motion of the two leaflets. The value of LAI ranges between 0 (perfectly symmetric) and 1 (most asymmetric). The third metric, referred to here as the diastolic unsteadiness index (DUI) quantifies the unsteady (or fluttering) motion of the leaflets during diastole and is computed as \( {\text{DUI}} = \sqrt {\frac{1}{0.65T}\int_{0.15T}^{0.8T} {\left( {\frac{{(\theta_{1} - \bar{\theta }_{1} ) + (\theta_{2} - \bar{\theta }_{2} )}}{{2\theta_{\hbox{max} } }}} \right)^{2} } dt} \), where \( \bar{\theta } = \frac{1}{0.65T}\int_{0.15T}^{0.8T} {\theta \, } dt \) is the average opening angle of a leaflet during the time interval \( 0.15T \le t \le 0.8T \). This index measures the degree of unsteadiness in the motion of the leaflets during diastole, and using the time interval \( 0.15T \le t \le 0.8T \) eliminates the initial opening of the leaflets during diastole from the DUI calculation. Excessive unsteady motion of the leaflets during diastole would tend to enhance turbulence in the flow and also increase the pressure losses across the mitral valve.

The efficiency of the mitral valve can be quantified via the regurgitation fraction, \( {\text{RF}} = V_{\text{m}} /SV \),42 where V m is the volume of blood regurgitated into the atrium through the mitral valve during systole and SV is the stroke volume. The generation of vorticity at the mitral valve and the organization of this vorticity into identifiable vortices is a key feature of intraventricular flows.14,27 In the current study, vortical structures are defined via iso-surfaces of swirl-strength II,16 which is the second invariant of the velocity gradient.

While regurgitation is one key metric of valvular efficiency, the minimization of transvalvular mechanical energy losses during diastole is also important in mitral valve function. In case of a patient with a prosthetic mitral valve, a large loss of mechanical energy in the flow across the valve will likely be compensated by an increase in cardiac effort,1,19 and could eventually lead to cardiac dysfunction. The loss of fluid mechanical energy inside any control volume V is equal to the sum of work done on boundaries and viscous energy dissipation in the control volume.15,19 In order to quantify the transvalvular mechanical energy loss, a cylindrical control volume encompassing the BMHV is considered in the current study (see Fig. 3d). The rate of fluid mechanical energy loss non-dimensionalized by \( \mu \bar{U}_{m}^{2} D_{m} \) is given by

$$ \phi = \left[ {\int\limits_{{S_{L1} , \, S_{L2} }} {( - p{\mathbf{n}} + {\mathbf{n}} \cdot {\varvec{\upsigma}})} \cdot \varvec{u} \, dS + \int\limits_{{{\text{C}} . {\text{V}} .}} {{\varvec{\upsigma}}:\nabla \varvec{u}} \, dV} \right]/\mu \bar{U}_{m}^{2} D_{m} , $$
(3)

where \( S_{L1} \) and \( S_{L2} \) represent the surface of the two leaflets. The net rate of mechanical energy loss ϕ shown above can be split into three components: the rate of work done on the leaflets due to fluid pressure, \( \phi_{1} = \int\limits_{{S_{L1} , \, S_{L2} }} { - p{\mathbf{n}}} \cdot \varvec{u} \, dS/\mu \bar{U}_{m}^{2} D_{m} \) and by the shear stress, \( \phi_{2} = \int\limits_{{S_{L1} , \, S_{L2} }} {{\mathbf{n}} \cdot {\varvec{\upsigma}}} \cdot \varvec{u} \, dS/\mu \bar{U}_{m}^{2} D_{m} \), and the rate of viscous dissipation, \( \phi_{3} = \int\limits_{{{\text{C}} . {\text{V}} .}} {{\varvec{\upsigma}}:\nabla \varvec{u}} \, dV/\mu \bar{U}_{m}^{2} D_{m} \). The net loss of mechanical energy during diastole is estimated as \( E = \int_{0}^{0.8T} \phi \, dt \).

Verification and Validation of the Model

The immersed boundary method employed in the current computational study has been tested extensively for stationary and moving boundary problems including solid bodies and immersed membranes.24,25 Furthermore, extensive validations against experimental data of this solver for a variety of biological flows with complex immersed boundaries have been reported in previous publications.11,40,41 The flow-structure interaction (FSI) capability that is employed here to model the leaflet dynamics has also been subjected to careful benchmarking for the well-established case of the flow-induced vibration of a flexible leaflet mounted behind a bluff body,5 and the FSI solver has also been used to simulate flow-induced vibrations of the vocal folds during phonation.39 These cases share a number of similarities with the leaflet of a BMHV and provide strong evidence that such simulations can be successfully carried out with our solver. The solver has also been used to successfully model cardiac flows.30,31

The LV model employed here was recently used to validate our flow solver by direct comparison with a corresponding experiment.9,29 Briefly, the validation effort employed the LV model without leaflets and focused on a quantitative comparison of flow features between the experiment and simulation. In Fig. 4, the computed velocity components are compared with that of the experimental data13 at various cross-sections of the left ventricle at peak-diastolic phase (\( t/T = 0.172 \)) in the upper row and at peak-systolic phase (\( t/T = 0.84 \)) in the lower row. At each time, velocity components are compared at three vertical cross-sections (V1, V2, V3) and at three horizontal cross-sections (H1, H2, H3). The locations of the cross-sections with velocity vectors in the LV are shown in the first column of Fig. 4. In the second column, the computed vertical velocity component w at each horizontal cross-section is compared with that from experiments (black symbols); similarly, in the third column, the computed horizontal velocity component v at each vertical cross-section is compared with that from experiments. The validation study36 showed that the computational modeling procedure employed here could reproduce all the key features of the velocity and vorticity fields observed in the experiments in the diastolic as well as systolic phases of the cycle.

Figure 4
figure 4

Validation of computed ventricular velocity (solid lines) against experimental data13 (black symbols) for the case without valve leaflets at peak-diastolic phase (\( t/T = 0.172 \)) in the upper row, and at peak-systolic phase (\( t/T = 0.84 \)) in the lower row. The first column shows the velocity vectors and the locations of three vertical cross-sections (V1, V2, V3) and three horizontal cross-sections (H1, H2, H3) at each time. In the second column, the computed vertical velocity component w at each horizontal cross-section is compared with that from experiments; similarly, in the third column, the computed horizontal velocity component v at each vertical cross-section is compared with that from experiments. Simulations were found to capture experimental flow features with reasonable accuracy

Full size image

In order to ensure grid convergence for the model with the BMHV, simulations have been conducted on three different grids: coarse (64 × 64 × 64), medium (96 × 96 × 96), and fine (128 × 128 × 128) grids for the case with h = 0.2 in the anatomical orientation. Figure 5a compares the total kinetic energy of the fluid in the whole computational domain as a function of time for the three grids, and Fig. 5b shows the comparison of the non-dimensional rate-of-work done on the valve leaflets by the shear stress ϕ 2. The relative error of these quantities in L 1 norm is about 11% between the coarse and fine meshes, and about 4% between the medium and fine meshes. A reasonable convergence is therefore achieved on the fine grid in terms of the intraventricular flow field and the resulting flow-induced leaflet motion. Consequently, all the simulations presented in the present paper employ the finer 128 × 128 × 128 Cartesian grid and 5,000 time steps are solved for each cardiac cycle; this corresponds to an average CFL (Courant–Friedrichs–Lewy) number of 0.8. It is to be noted that a computation on the 128 × 128 × 128 grid for one cardiac cycle takes about 90 h on a high performance computing cluster with 256 CPUs.

Figure 5
figure 5

Results from a grid convergence study for the h = 0.2 valve in the anatomical orientation using three grids: coarse (64 × 64 × 64), medium (96 × 96 × 96), and fine (128 × 128 × 128). (a) The total kinetic energy of the fluid in the entire computational domain. (b) The non-dimensional rate of work done on the valve leaflets by the shear stress \( \phi_{2} = \int\limits_{{S_{L1} , \, S_{L2} }} {{\mathbf{n}} \cdot {\varvec{\upsigma}}} \cdot \varvec{u} \, dS/\mu \bar{U}_{m}^{2} D_{m} \)

Full size image

Results

Leaflet Dynamics

The time variation of the leaflet opening angle for all our simulations with respect to non-dimensional time \( t^{ * } = t/T \) (where T is the period of the entire cardiac cycle), is shown in Fig. 6. The red line corresponds to the leaflet shown in red in Fig. 3 and the blue line corresponds to the leaflet shown in blue in Fig. 3. For the hinge location \( h = 0.1 \) in the anatomical orientation, both leaflets open quite rapidly during early-diastole (~\( t/T = 0.1 \)5), and stay fully opened during most of the diastole. At the beginning of systole (\( t/T = 0.8 \)), both leaflets start to close rapidly, with closure complete by \( t/T = 0.85 \). The motion of the leaflets is quite symmetric for the given configuration. As the hinge distance \( h = d/R \) increases, the time during diastole over which the leaflets are fully open decreases and the motion of the leaflets becomes increasingly unsteady and asymmetric. This is particularly the case for h = 0.3, where only one leaflet fully opens for a very short duration and both leaflets flap readily during diastole. This flapping is a result of the fact that with the hinge located more centrally on the leaflet, pressure-induced forces on either side of the hinge produce competing moments on the leaflet, leading to rapid reversals in the net moment about the hinge. The motion of the leaflets in the anti-anatomical orientation follows similar trends with increasing h although this orientation presents reduced opening angles and higher levels of unsteady leaflet motion when compared to the anatomical orientation.

Figure 6
figure 6

Leaflet opening angle θ and flow rate Q at the mitral annulus. The red line is the angle corresponding to the leaflet shown in red in Fig. 3—the medial leaflet for anatomical orientation and the posterior leaflet for anti-anatomical orientation. Similarly, the blue line is the angle corresponding to the leaflet shown in blue in Fig. 3. The black line is the mitral flow rate

Full size image

The three metrics corresponding to leaflet motion are shown in Table 1. The OAI shows a monotonic decrease with increasing h for both valve orientations. For h = 0.1, the OAI shows a higher than 80% opening during diastole but this decreases to around 50% for h = 0.2. Interestingly, for h = 0.2, the anti-anatomical valve orientation shows more significant decrease in OAI than the corresponding anatomical orientation. The leaflet asymmetry index (LAI) shows that for the hinge locations h = 0.1 and 0.2, the anti-anatomical orientation generates more asymmetric and unsteady leaflet motion compared to the anatomical orientation. This is surprising since the anti-anatomical orientation actually presents a symmetric geometry to the flow whereas the anatomical valve configuration is highly asymmetric due to the eccentric placement of the mitral annulus. By contrast, for the case with h = 0.3, the anatomical orientation generates a more asymmetric motion when compared to the anti-anatomical orientation. Finally, the diastolic unsteadiness index (DUI) shows a monotonic increase with h for both orientations. However, for h = 0.1 and h = 0.2, the anatomical orientation shows a significantly lower level of unsteady leaflet motion than the corresponding anti-anatomical configurations. For h = 0.3, both orientations show similar levels of unsteady leaflet motion.

Table 1 Leaflet dynamics characterized by mean diastolic opening angle index (OAI), leaflet asymmetry index (LAI) and diastolic unsteadiness index (DUI). The opening angle index and leaflet asymmetry index is calculated for the entire diastole (\( 0 \le t/T \le 0.8 \)), and the diastolic unsteadiness index is calculated during \( 0.15 \le t/T \le 0.8 \). AO: anatomical orientation, AAO: anti-anatomical orientation
Full size table

Mitral Regurgitation

The flow rate through the mitral annulus during the cardiac cycle is shown as a black line in Fig. 6. Positive values of the flow rates represent inflow into the ventricle, and negative values represent outflow from the mitral annulus. Thus negative mitral flow rates during systole (\( t/T \ge 0.8 \)) reveal the extent of mitral regurgitation from the ventricle to the atrium. The regurgitation fractions for all our cases are shown in Table 2 and we observe that the highest regurgitation in both valve orientations is for the h = 0.1 case, a case which otherwise perform well in terms of the metrics discussed in the previous section. In fact, the RF decreases with increasing h (except the h = 0.2 case in the anatomical orientation) and reaches extremely low values (2.1–1.3%) for h = 0.3.

Table 2 Regurgitation fraction during systole, and the average opening angle of the two leaflets at the beginning of systole (\( t/T = 0.8 \))
Full size table

An examination of the leaflet opening angle indicates that the regurgitation fraction is highly dependent on the leaflet opening angle at the beginning of systole. The average opening angle of the two leaflets at the beginning of systole (\( t/T = 0.8 \)) is also shown in Table 2. For the cases indicated above, both leaflets are only partially open at the beginning of systole (\( t/T = 0.8 \)) (also see Fig. 6). This has two implications for rapid closure: first, full closure from a partially open position requires less time; and second, valves in a partially open position experience a larger pressure difference across their two surfaces than leaflets that are fully open and this results in a larger closing moment during systole. The net result of this is that partially open valves achieve full closure more rapidly leading to reduced regurgitation. By contrast, if the valve leaflets are in fully open position, or nearly so, at the beginning of systole, then the valve definitely allows more regurgitant flow into the atrium during systole. Hence for h = 0.1 and h = 0.2 in the anatomical orientation, we observe a relatively large regurgitation fraction.

Diastolic Flow Patterns and Transvalvular Mechanical Energy Loss

The transvalvular mechanical energy losses are connected with the flow patterns that are created due to the valve motion, and we first examine these intraventricular flow patterns here. Figure 7 shows the velocity vectors at the mid-plane of the valve (first row) and the 3D vortical structures (second row) at the early filling phase of \( t/T = 0.2 \) for the anatomically oriented BMHV. Similarly, the velocity vectors and the vortical structures for the anti-anatomically oriented valve are shown in the third and fourth column, respectively, in Fig. 7. We also include the case with no valve leaflets as a baseline for this comparison. The vortical structures are identified by isosurfaces of II 16 which are colored by contours of the vertical velocity component.

Figure 7
figure 7

The intraventricular flow patterns at \( t/T = 0.2 \) for different hinge locations. The case without valve is also shown here as a baseline. The upper row of figures at each valve orientation shows velocity vectors at the mid-plane of the valve. The lower row shows the 3D vortical structures defined via iso-surface of the second invariant of the velocity gradient. The vortical structures are colored by contours of the vertical velocity component

Full size image

For the case without valve leaflets, we observe a nearly uniform velocity profile at the mitral orifice and a clear vortex ring is generated near the mitral orifice. For hinge locations h = 0.1 and h = 0.2, the leaflets split the inflow into three parts: two side jets and a central jet, and the leaflets also break the vortex ring into smaller structures. We can see two vortex rings generated at the tip of the valve leaflets, and a smaller vortex ring between the two lateral vortices. For the hinge location h = 0.3, the flapping motion of the leaflets during diastole breaks down the vortex ring completely. These general trends and patterns for the anti-anatomically oriented valves are similar to those observed for the anatomical orientation. However the anti-anatomical orientation generates more asymmetric and unsteady leaflet motion for h = 0.1 and h = 0.2 as demonstrated in the previous section, and this might be related to the propagation of vortex structures.

The time variation of the rate of loss of transvalvular mechanical energy (ϕ 1, ϕ 2, and ϕ 3) for the h = 0.1 case in the anatomical orientation is shown in Fig. 8a. The figure shows that the rate of work done on the valves is significantly larger than the viscous dissipation and this is true for all the cases simulated here. The net rate of transvalvular mechanical energy loss ϕ = ϕ 1 + ϕ 2 + ϕ 3 for various hinge locations in the anatomical orientation is shown in Fig. 8b. As expected, the case without the valve has the lowest rate of transvalvular energy loss and the energy loss across the heart valve increases with increasing hinge location parameter h. Note that, for the case without valve, the net fluid energy loss in the control volume is equal to the viscous dissipation. For a fair comparison to the baseline case without the valve, the temporal variation of the viscous dissipation rate in the control volume is shown in Fig. 8c. This quantity is also found to increase with increasing hinge location parameter h. The net loss of mechanical energy (E) during diastole is shown in Table 3 for all our cases. No significant difference in this quantity between anatomical and anti-anatomical orientations is noted. Furthermore while there is a small increase in the net energy loss as h is increased from 0.1 to 0.2, the change in E as h is increased to 0.3, is nearly by a factor of 3.4 compared to h = 0.1.

Figure 8
figure 8

(a) Rate of mechanical energy loss across the valve for h = 0.1 valve in the anatomical orientation. (b) The net rate of non-dimensionalized fluid energy loss ϕ for various hinge locations in the anatomical orientation. (c) Viscous dissipation rate ϕ 3 in the control volume for a comparison to the case without valve as a baseline. (d) Rate of work done on the h = 0.1 valve by fluid shear stress ϕ 2 with valve orientations varying slightly from AO

Full size image
Table 3 The net non-dimensional transvalvular mechanical energy loss during diastole \( E = \int_{0}^{0.8T} \phi \, dt \)
Full size table

Among the terms in Eq. (3), only viscous dissipation rate is dependent on the choice of a control volume. We have tested various control volumes enclosing the valve, including the entire computational domain comprising the LV and mitral inlet. For all the case tested, the choice of a CV does not have a significant impact on the total fluid energy loss since the dominant energy loss is caused by the pressure work done on the leaflets, which is independent of the choice of CV. Furthermore, the choice of the CV does not alter the general trend seen in Fig. 8c, i.e. the viscous dissipation in a CV increases with increasing hinge location parameter h.

In order to investigate the sensitivity of valve performance to slight changes in valve orientation, the h = 0.1 valve is rotated by ±5°, ±10° and ±15° from the anatomical orientation. It is to be noted that the anti-anatomical orientation can be regarded as a 90° rotation from the anatomical orientation (see Figs. 3a, 3b). The changes caused by these slight rotations in all the metrics presented in the paper are at most 5%. For example, Fig. 8d compares the rate of work done on the valve leaflets by fluid shear stress ϕ 2 with varying valve orientations, and the differences observed are quite small.

Discussion

We have described a computational methodology for modeling the dynamics of BMHV in the mitral position and have used this method to examine the performance of a variety of BMHV designs. The focus of the study is on a comparative analysis of valve performance for different hinge locations and orientations and the computational modeling approach employed here enables us to conduct a comprehensive, multi-modal assessment of these configurations.

With respect to the hinge location, it is found that a BMHV with a more centrally located hinge (h = 0.1) generally performs better than a hinge that is significantly offset from the center (h = 0.2 and 0.3). In particular, for both valve orientations, the h = 0.1 case produces the largest average diastolic opening angle (nearly 80% of the maximum opening angle), the lowest leaflet asymmetry and the least amount of diastolic unsteady leaflet motion (Table 1). It also generates the lowest transvalvular mechanical energy loss (Table 3).

The average diastolic opening angle and the transvalvular mechanical energy loss are two related metrics of valve performance that are particularly important since they indicate the resistance presented by the valve during the filling of the ventricle. If the non-dimensional transvalvular mechanical energy loss E (Table 3) is applied to a realistic ventricle with \( \bar{U}_{\text{m}} = 0.8{\text{ m/s}} \), \( D_{\text{m}} = 2{\text{ cm}} \), and \( \mu = 4 \times 10^{ - 3} {\text{ Pa}}{\cdot}{\text{s}} \), and assuming that the typical stroke work is 700 mJ for healthy adults,30 the transvalvular energy loss is about 0.6% of the stroke work for the h = 0.1 case (4 mJ) and is about 2% of the stroke work for the h = 0.3 case (13.5 mJ). This latter number implies a non-trivial increase in the work required by the heart to maintain cardiac output, and could in the long-term, lead to cardiac dysfunction.1,19 It is to be noted that while transvalvular mechanical energy loss clearly correlates inversely with the average opening angle (i.e. a smaller average opening angle with a fixed flow rate implies more work required to open the valve), it also depends in a complex way on leaflet asymmetry and unsteady motion.

The only metric where the h = 0.1 case does not perform well is mitral regurgitation (Table 2) where it produces a higher regurgitation (RF ~ 13%) compared to the h = 0.3 case that produces regurgitation fractions at most about 2%. This seemingly anomalous behavior is found to be correlated with the opening angle of the valves at end-diastole. The h = 0.1 case has the largest (more than 70°) opening angle at the end of diastole whereas the opening angle for the h = 0.3 case is lower than 20°. A smaller opening angle at end-diastole allows the leaflets to close rapidly during systole and reduce the degree of regurgitation. Thus interestingly, for a BMHV, a better performance during diastole (i.e., larger and more sustained opening angle) is associated with a higher degree of mitral regurgitation during systole. Healthy natural mitral valves produce regurgitation fractions of about 4%.34 The regurgitation fraction of about 13% for the h = 0.1 case would be considered mild, but is still over a factor of three larger than healthy natural mitral valves. For comparison, regurgitant volumes of St. Jude Medical BMHVs at mitral position measured in vitro are in the range of 10–13 mL/beat depending on the size of the valve38; assuming an average stroke volume of 70 mL for healthy adults, this corresponds to a RF in the range 14–18%, which agrees rather well with the current simulations.

The effect of valve orientation on performance is more complex and subtle than the hinge location and this is in-line with some previous studies.21 First, the anatomically orientated valve generally outperforms the anti-anatomically orientated valve in terms of leaflet motion (OAI, LAI, and DUI in Table 1). The regurgitation in the anti-anatomical orientation is somewhat lower than that of the anatomical orientation but this is connected with the slightly lower end-diastolic opening angle of this configuration (Table 2). The transvalvular mechanical energy loss is nearly the same in both configurations. Thus, with everything else being equal, the anatomical valve orientation is slightly superior to the anti-anatomical orientation. The small differences between the two, however, can be amplified due to patient-specific conditions (LV morphology, ejection fraction, etc.) and this has indeed been borne out in clinical practice.4,7,12

The primary limitation of the current modeling approach is the use of a relatively simple ventricular model. This model has a simple ventricular shape; it lacks a true atrium and the motion of the ventricular wall is also highly simplified. Finally, the simulations lack a true aortic valve which, if included, would have its own dynamics and timing of opening and closing. These simplifications likely affect the flow and leaflet dynamics in ways that are not completely understood. However, given that all of these other features are kept the same for all the cases simulated here, it is expected that a comparison of these cases still provides useful insights into the dynamics of BMHV in the mitral position. It is also noted that while the current simulations are based on a systematic sequence of validation and verification exercises, a limitation of the current work is that the leaflet dynamics have not been subjected to direct validation against experiments.

Conclusions

A computational model of a bileaflet mechanical heart valve in the mitral position is employed to examine the performance of BMHV in the mitral position. The model incorporates a fluid–structure interaction algorithm for the numerical simulation of leaflet dynamics and cardiac hemodynamics. The geometry and kinematics of the left ventricle are based on a simple ventricular model which has been the subject of previous studies.9,29,36

In order to assess the performance of different valve configurations, simulations are carried out with three hinge locations and two primary valve orientations. The performance of the valve is compared in terms of a range of metrics that characterize the leaflet motion as well as transvalvular hemodynamics. Results indicate that a BMHV with a more centrally located hinge, and implanted in the anatomical orientation provides the best overall performance. It is, however, found that mitral regurgitation is inversely correlated with other performance metrics and the optimal configuration results in about a 13% regurgitation fraction, which is significantly larger than that of healthy natural mitral valves. The current study also demonstrates the ability of computational modeling to provide insights into prosthetic valve performance that are difficult to obtain in vivo or via experiments. Future studies will explore such models in more realistic (even patient-specific) geometries of the left ventricle, and direct validation of computations against in vivo measurements.