Linear and Nonlinear Viscoelastic Modeling of Aorta and Carotid Pressure–Area Dynamics Under In Vivo and Ex Vivo Conditions

Abstract

A better understanding of the biomechanical properties of the arterial wall provides important insight into arterial vascular biology under normal (healthy) and pathological conditions. This insight has potential to improve tracking of disease progression and to aid in vascular graft design and implementation. In this study, we use linear and nonlinear viscoelastic models to predict biomechanical properties of the thoracic descending aorta and the carotid artery under ex vivo and in vivo conditions in ovine and human arteries. Models analyzed include a four-parameter (linear) Kelvin viscoelastic model and two five-parameter nonlinear viscoelastic models (an arctangent and a sigmoid model) that relate changes in arterial blood pressure to the vessel cross-sectional area (via estimation of vessel strain). These models were developed using the framework of Quasilinear Viscoelasticity (QLV) theory and were validated using measurements from the thoracic descending aorta and the carotid artery obtained from human and ovine arteries. In vivo measurements were obtained from 10 ovine aortas and 10 human carotid arteries. Ex vivo measurements (from both locations) were made in 11 male Merino sheep. Biomechanical properties were obtained through constrained estimation of model parameters. To further investigate the parameter estimates, we computed standard errors and confidence intervals and we used analysis of variance to compare results within and between groups. Overall, our results indicate that optimal model selection depends on the artery type. Results showed that for the thoracic descending aorta (under both experimental conditions), the best predictions were obtained with the nonlinear sigmoid model, while under healthy physiological pressure loading the carotid arteries nonlinear stiffening with increasing pressure is negligible, and consequently, the linear (Kelvin) viscoelastic model better describes the pressure–area dynamics in this vessel. Results comparing biomechanical properties show that the Kelvin and sigmoid models were able to predict the zero-pressure vessel radius; that under ex vivo conditions vessels are more rigid, and comparatively, that the carotid artery is stiffer than the thoracic descending aorta; and that the viscoelastic gain and relaxation parameters do not differ significantly between vessels or experimental conditions. In conclusion, our study demonstrates that the proposed models can predict pressure–area dynamics and that model parameters can be extracted for further interpretation of biomechanical properties.

Introduction

Transport of blood through the cardiovascular system is achieved via two principal mechanisms: conduction, which facilitates transport to the microcirculation, and buffering, which dampens the pulsatility as the pulse wave is propagated from the large to the small vessels. These mechanisms are achieved by the specific design of the arterial network as well as the individual vessels. The arteries branch almost exclusively in a bifurcating manner. At each bifurcation, the cross-sectional area of each daughter vessel is smaller than that of the parent vessel, while the combined cross-sectional area of the daughter vessels exceeds that of the parent vessel.35,36 The increase in vessel area and number of vessels lead to significant damping of the volumetric flow rate. The mean pressure is dampened, but the pulse pressure is amplified as the pulse wave propagates away from the heart along the large vessels. This pulse pressure amplification is followed by significant dampening at the arteriolar level.24 The pulse pressure amplification in the large arteries is a result of pulse wave reflections generated at the bifurcations, due to tapering of the individual arteries, and from the resistance generated by the downstream vasculature.35,36 This network structure combined with compliant vascular walls allows the system to maintain an adequately high level of mean pressure and to minimize ventricular work.

Generally, the larger vessels are more “compliant" and, consequently, they exhibit both elastic and viscoelastic distentions, while the smaller vessels are more rigid, and thus for these vessels viscoelastic deformation dominates the response. The latter contributes to the preservation of the mechanical integrity of the arterial wall (auto-protection). It is believed2,3 that this dampening is essential for optimal pulse wave transmission and subsequently for adequate tissue perfusion. It has been shown2,3 that vessels with compromised high-frequency filter capacity (such as vessels subjected to acute hypertension) are more prone to vascular disease such as atherosclerosis. A better understanding of the mechanics of the high-frequency filter capacity can, in part, be achieved through consideration of viscous and nonlinear elastic distention of the arterial wall. One way to study these properties is via analysis of arterial hysteretic pressure–diameter relationships.

The main determinants of the vascular wall elastic and viscoelastic properties are elastin and collagen fibrils and smooth muscle cells. The amount and distribution of these components differ among arterial segments (e.g., thoracic descending aorta vs. carotid arteries). Elastin gives rise to elastic and viscoelastic deformation, while collagen contributes to the nonlinear stiffening with increased pressure.1,11 Smooth muscle cells are the most important contributor to viscoelastic deformation.3,5,6,7,12,13,48 It is widely known that the amount and distribution of fibrils and cells are altered in cardiovascular disease, for example, in patients with aneurysms,29 atherosclerosis,29 hypertension,2 implanted arteries,9 after pharmacological interventions,3 and in circulations with ventricular mechanical assist devices.8 In general, it is believed that changes in the interface between collagen fibrils, elastic fibers, and smooth muscle lead to changes in the viscoelasticity of the vessel wall with aging and disease.40

The constituents of the vascular wall can be analyzed using histological studies, but it is well known that these constituents behave differently under in vivo conditions. In particular, the tethering of elastin fibers as well as the arrangement and degree of activation of smooth muscle cells are impacted by excision of the vessels. Analysis of the constituents can be used to provide insight into differences between anatomical locations and species differences, but not to describe differences in dynamics observed between ex vivo and in vivo conditions. One way to analyze differences between two experimental settings is to investigate dynamic pressure–area dynamics recorded in the same vessels under ex vivo and in vivo conditions. Comparing results from several experimental settings combined with exploration using mathematical modeling can provide more insight and may have impact on how these properties are investigated clinically.

In current clinical settings, the main property analyzed is local arterial stiffness, which is typically evaluated in superficial arteries, using static analysis of vessel diameter, systolic, and diastolic arterial blood pressure.34 However, these tests cannot be used for analysis of viscoelastic damping. One way to assess viscoelastic properties is using models that capture the distention of the vessel cross-sectional diameter induced by the fluid pressure. For such studies, the differences in vessel wall viscoelastic properties can be quantified according to anatomical location and experimental conditions (e.g., ex vivo vs. in vivo).

A number of studies have investigated arterial wall properties using empirical nonlinear elastic models,28,33 hyperelastic models,26,27,29 viscoelastic models,1,8,19,25,29,37,38,46,45 and autoregressive models.21,22 However, little work has focused on using coupled dynamic models that account for both nonlinear elastic distention and the “memory” (viscoelastic) contribution to the arterial wall distention and, to our knowledge, no studies have used this information to characterize differences according to vessel type. Previous studies by our group on ex vivo ovine aortic and carotid vessels used a Kelvin viscoelastic model43,42 and revealed that the pressure–area dynamics might be better captured using a model extension that incorporates nonlinear stiffening with increasing pressure.

In this study, we compared several computationally inexpensive nonlinear elastic and viscoelastic models that couple static linear or nonlinear wall distention with a dynamic component. By combining these coupled models with parameter estimation methods, and noninvasive measurements of arterial blood pressure and vessel diameters, we showed how biomechanical properties can be inferred. Specifically, our objective is to quantify the biomechanics of the arterial wall via model-based analysis of pressure–diameter dynamics in the thoracic descending aorta (an aneurysm-susceptible artery) and the carotid artery (an atherosclerosis-susceptible artery) using blood pressure and vessel diameter time-series measurements obtained under in vivo and ex vivo experimental conditions from ovine and human vessels. We formulated the coupled elastic–viscoelastic model within the framework of Fung’s Quasilinear Viscoelasticity (QLV) theory, facilitating comparison between a linear (Kelvin) model and nonlinear models with an arctangent or a sigmoid elastic response function. All elastic response models were then paired with a single viscoelastic relaxation function.

Methods

In this section, we first describe data acquisition methods for in vivo and ex vivo experiments. Subsequently, we describe the three elastic and viscoelastic models used to analyze the data, and statistical methods used to evaluate and compare parameter estimates and model performance among experimental conditions and anatomical locations.

Experimental Procedures

All data used for this study were collected in the vascular laboratory CUiiDARTE at the Universidad de la República in Mondevideo, Uruguay. Basic data include time-series measurements of internal arterial diameter (mm) and blood pressure (mmHg) from the thoracic descending aorta and carotid artery as shown in Fig. 1. Data were collected from male Merino sheep under both in vivo and ex vivo conditions, whereas only in vivo measurements were available from human subjects.

Figure 1

Left panel Mock circulation including a pneumatic pump, a perfusion line connected to the chamber holding the vessel segment, a resistance modulator (R) and a reservoir. The chamber was filled with thermally controlled Tyrodes solution. The pressure (P) was measured with a microtransducer, and the diameter (D) was measured with a pair of ultrasonic crystals controlled by a sonomicrometer. Right panel Generic (species independent) sketch of the large arteries including the thoracic descending aorta and carotid artery

Ovine Data

Experiments in ovine arteries conformed to the European Convention for the Protection of Vertebrate Animals used for Experimental and other Scientific Purposes (Council of Europe No. 123, Strasbourg 1985). Animal data collected include in vivo and ex vivo measurements from a total of 21 male Merino Sheep.

(1) In vivo studies. Ten healthy male Merino sheep, weighting 29 ± 2 kg and aged 12 months, were included in this study. Upon arrival at the animal facility, the sheep were vaccinated against common animal diseases and were treated for skin and intestinal parasites. For 20 days before surgery, the sheep were appropriately fed and hydrated and assessed for adequate clinical status. In these sheep, blood pressure and internal vessel diameter were measured simultaneously at a sampling frequency of 500 Hz at the level of the thoracic descending aorta. The experiments were performed under general anesthesia, which was induced with sodium thiopental (20 mg/kg intravenous) and maintained with 1% halothane delivered through a Bain tube connected to a ventilator.

A pressure micro-transducer (Millar Mikro-tip, SPC 370 7F) was inserted through the femoral artery and placed at the level of the abdominal aorta to monitor arterial pressure. A sterile thoracotomy was made at the left fifth intercostal space. A solid-state pressure micro-transducer (Model P2.5, Konigsberg Instruments, Inc., Pasadena, CA, USA), previously calibrated using a mercury manometer, was inserted in the thoracic descending aorta through a small incision. To measure the internal diameter of the thoracic descending aorta, two miniature piezoelectric crystal transducers (5 MHz, 2 mm in diameter) were sutured on opposite sides into the aortic adventitia during open-chest surgery. Before repairing the thoracotomy, all cables and catheters were tunneled subcutaneously to emerge at the interscapular space. All animals were allowed to recover under veterinary care. Ampicillin (20 mg kg⁻¹ day⁻¹ per os) was given for 7 days after surgery.

Experiments were performed starting on the seventh postoperative day. Each study was performed with the sheep resting quietly on its right side in the conscious unsedated state. The internal aortic diameter signal was calibrated in millimeters using the 1-mm step calibration option of the sonomicrometer (model 120, Triton Technology, San Diego, CA). The transit time of the ultrasonic signal (velocity 1,580 m/s) was converted into distance (diameter). After completed measurements, the animals were sacrificed with an intravenous overdose of pentobarbital followed by potassium chloride. The correct position of the ultrasonic crystals was confirmed at necropsy. At the end of each experiment, a 6-cm (measured in vivo) arterial segment, was obtained, weighed, and submitted for histological analysis. For further details, see Armentano et al. 1

(2) Ex vivo studies. Eleven healthy male Merino sheep of similar weight and age to those studied in vivo were used in the ex vivo experiments. In these sheep, blood pressure and internal vessel diameter were measured simultaneously at a sampling frequency of 200 Hz at the level of the thoracic descending aorta and the common carotid artery. During artery harvesting, general anesthesia was induced and maintained with sodium thiopental (20 mg/kg, intravenous). All animals had mechanical respiratory assistance, and respiratory parameters were maintained within physiological limits. The thoracic descending aorta and carotid artery were exposed, preserving the perivascular adipose tissue. In both vessels, a solid-state pressure micro-transducer (Model P2.5, Konigsberg Instruments, Inc., Pasadena, CA, USA) was inserted through a small arterial-wall incision. Two miniature piezoelectric crystal transducers (5 MHz, 2 mm in diameter) were sutured on opposite sides of the vessel wall into the adventitia to measure the internal vessel diameter. Pressure and diameter calibration procedures were similar to those performed in vivo. Two suture stitches were used to mark a 6-cm arterial segment measured with a pair of calipers, whose measurement accuracy is within 0.5 mm. To ensure data quality, the pressure and diameter signals were visualized in real time during the experiments.

The animals were sacrificed with an intravenous overdose of sodium thiopental followed by potassium chloride, and the selected vessel segment was excised and non-traumatically mounted at the in vivo length in the mock circulation shown in Fig. 1. This set-up has previously been used by the group in Uruguay and Argentina3 and is similar to the set-up used for data analyzed in Valdez-Jasso et al. 42,43 After being placed in the specimen chamber, each arterial segment was allowed to equilibrate for 10 min under cyclic flow conditions, with a pumping rate set at 110 beats/min, maintaining a mean pressure of 85 mmHg. To ensure stability, flow was monitored with an ultrasonic flowmeter (Transonic Systems). During the ex vivo experiments, each arterial segment was kept immersed and perfused with thermally regulated (37 °C) and oxygenated Tyrodes solution (pH 7.4). After the equilibration period, the flow sensor was removed and pressure and diameter signals were recorded and saved at a sampling frequency of 200 Hz. The mock circulation was adjusted to reproduce in vivo pressure wave morphology, enabling adequate isobaric, isoflow, and isofrequency analysis. At the end of the experimental session, the segments were weighed and submitted for histological analysis.

Human Data

Ten human subjects (5 male and 5 female, age 40 ± 5 years, and body mass index of 23.3 ± 1.5 kg/m²) participated in the in vivo studies. The study was approved by the ethics committee of the Universidad de la Republica, Uruguay, and all subjects participating in the study had signed an informed consent. Internal vessel diameter and blood pressure were obtained using ultrasound and applanation tonometry. All measurements were noninvasively taken after 15 min of recumbent rest by Drs. Bia and Zócalo, who are trained in noninvasive vascular studies. For vessels that dilate symmetrically and where the surrounding tissue is significantly more compliant than the vessel studied, previous work31 showed that the applanation tonometry procedure is highly accurate and that results obtained have a high reproducibility. Before using this method, the accuracy of the probe was validated both in animal and human subjects. Previous comparisons, both in the time domain and by spectral analysis, showed excellent correspondence between tonometric and intra-arterial pressure measurements.23

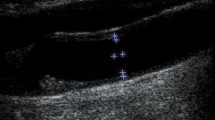
Internal arterial diameter and wall thickness were measured using real-time B-mode ultrasound echographic imaging (Portable Ultrasound System, Aloka-SSD210, Aloka Ltd., Tokyo, Japan), as shown in Fig. 2. This method has been validated against sonomicrometry, as well as against echo tracking.23 The resolution of the 7.5 MHz probes used in this study ranged from 0.2 to 0.4 mm. This resolution is not adequate for estimating the smallest changes in the diameter. However, as shown in earlier studies,16,23 this study used sub-pixel interpolation (available in the software), which enhances the resolution by a factor 5 to 10.

Figure 2

Data acquisition for the in vivo experiment in human carotid artery. Noninvasive measurements of blood pressure and internal arterial diameter at the level of the carotid artery were obtained via applanation tonometry (left) and B-mode echographic images (right), respectively. The pressure–diameter relation is then used to study the viscoelastic properties of the vessel

The left human common carotid internal artery diameter and wall thickness were examined using transverse and sagittal projections to verify the existence of walls without alterations. After that the sound beam was adjusted perpendicular to the arterial surface of the far wall of the vessel, 3 cm proximal to the bifurcation of the common carotid artery, to obtain two parallel echogenic lines corresponding to the lumen-intima and media-adventitia interfaces. Once the two parallel echogenic lines of the far wall were clearly visible on the monitor, along at least 1 cm of the segment to measure, a fixed image (end-diastolic electrocardiogram triggering) was used to assess intima-media thickness, and a sequence of images were used to determine the instantaneous waveform of arterial diameter and were acquired at a sampling rate of 30 Hz. The image analysis involved automatic detection of the anterior and posterior wall interfaces, which were used to predict the thickness of the vessel wall. This procedure was previously employed and validated against the sonomicrometric technique.23

Immediately after the echographic measurements, the pressure waveforms were measured with an applanation tonometer (Sphygmocor, AtCor Medical Inc., USA) at the same site (marked with a pen on the neck of the subject) as the diameter measurements at a sampling frequency of 125 Hz. Immediately prior to each tonometric recording, mean and diastolic brachial pressures, measured by sphygmomanometry, were recorded and used for calibration of the carotid artery pressure measurements. Calibration involved aligning the tonometric recordings of diastolic and mean pressures to those measured using spygmomanometry in the brachial artery. After calibration, data from one period of the pressure recordings were aligned with the diameter measurements, and both signals were sampled at a frequency of between 500 and 600 Hz.

Since pressure and diameter waveforms were recorded with different devices, the recorded data were resampled and interpolated to obtain sample values at the same time points. The length of the two cardiac cycles were scaled to the average length, and the waveforms were aligned using the QRS complex of the electrocardiogram. This is similar to the approach used in previous work, see DeVault et al. 18 It was assumed that the mean pressure does not change in large conduit arteries and that diastolic pressure (as opposed to systolic pressure) does not substantially differ between the brachial and the carotid artery. A surface electrocardiogram was acquired and stored together with the diameter and pressure signals.

Histological Analysis

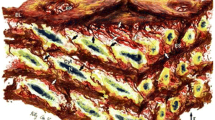
The ovine arterial segments were submitted for histological analysis. The vascular specimens were fixed by immersion in 10% formaldehyde and embedded in paraffin to obtain 7 μm transverse sections perpendicular to the longitudinal axis of the vessel. Specimens were deparaffinated and hydrated, and finally stained with the Cajal-Gallego method, which differentially stains muscle cells (yellow-green), elastin (dark red), and collagen (blue). Histological images were digitized on a square frame (630 × 1024 pixels) with an optical microscope at magnification of 400. To quantify the relative amount of each component, a procedure previously proposed by Kawasaki et al. 30 was used. In brief, after eliminating the pixels that do not correspond to vascular tissues, elastin, collagen, and smooth muscle relative contents were determined as the ratio of the number of pixels that were stained dark red (elastin), blue (collagen), and yellow-green (smooth muscle), respectively, to the total number of pixels for each image, as shown in Fig. 3.

Figure 3

Histological slices displaying a cross section of the arterial wall from an ovine thoracic descending aorta (left) and an ovine carotid artery (right). The vessels were stained with orcein using the Cajal–Gallengo method, which allows discrimination of the three main wall components that determine the arterial biomechanical behavior: smooth muscle cells (yellow), elastin (dark red), and collagen (blue)

Data Pre-processing

All data included time series measurements of blood pressure p _j and internal arterial wall diameter d _j . In the models employed, we seek to investigate the dynamics of the cross-sectional area as a function of arterial blood pressure. Consequently, we convert vessel diameter into cross-sectional area using

$$ a_j = \pi \left({\frac{d_j}{2}}\right)^2. $$

To ensure that our models are applied consistently to the experimental data, and in an effort to reduce computational cost, we applied a pre-processing step to ensure that all data were resampled (if necessary) at 200 Hz. For the animal data, we cropped the time series after four consecutive, stable cardiac cycles. In contrast, we only obtained a single cycle of data from each human subject. We therefore replicated these cycles to obtain a data segment consisting of four (identical) cycles. This was done to have sufficient data for the models to equilibrate to a dynamic steady state.

Mechanical Models

In previous studies, we have analyzed ex vivo ovine aortic and carotid wall properties using the Kelvin viscoelastic model43 and an extended two-term exponential relaxation linear viscoelastic model.42 Results from these studies revealed that the pressure–area dynamics of the vessel, especially the aorta, display nonlinear stiffening with increasing pressure. These observations served as motivation to extend the models to account for nonlinear responses in the dynamic distention. To obtain a cohesive framework for formulating and comparing models, we employed QLV theory,19 which relates the stress–strain dynamics as

$$ \varepsilon(t) = \int\limits_{-\infty}^t K(t-\gamma){\frac{d s^{(e)}[p(\gamma)]} {d\gamma}} d\gamma, $$

(1)

where ε denotes a scalar measure for vessel strain, K(t) is a creep function, and the elastic response is specified by the function s ^(e)[p]. We integrate by parts to avoid numerical differentiation of the experimental blood pressure waveform. Starting at an arbitrary time t ₀, (1) can be rewritten as

$$ \varepsilon(t) = K(0)s^{(e)}[p(t)] + \int\limits_{t_0}^t {\frac{dK(t-\gamma)} {d\gamma}}s^{(e)}[p(\gamma)] d\gamma. $$

(2)

To analyze vessel distention due to time-varying blood pressure, we consider three elastic response functions. All functions are derived under the assumption that arteries (the thoracic descending aorta and the carotid artery) can be modeled as homogeneous and isotropic thin-walled straight cylindrical vessels where $\varepsilon_{zz}, \varepsilon_{rr}\ll\varepsilon_{\theta\theta}$ and $\sigma_{zz}, \sigma_{rr}\ll\sigma_{\theta\theta}$,20 i.e., we assume that we can prescribe the elastic response s ^(e)[p] using only circumferential stress and strain components. Under equilibrium conditions in such vessels, Laplace’s law relates the circumferential stress in the vessel wall to the fluid pressure p, and the geometry of the vessel as σ_θθ = pr/h, where r is the cross-sectional radius and h is the vessel wall thickness. A circumferential strain can be expressed relative to the zero-pressure state as the normalized change in the vessel radius so that $\varepsilon_{\theta\theta}=(r-r_0)/r_0,$ where r ₀ represents the radius of the mounted, stretched vessel at zero transmural pressure. It should be noted that what we refer to as the zero-pressure state is the radius of the intact vessel at zero pressure. Note, in this study, the true residual stress is not considered, instead the unpressurized intact vessel is considered the unloaded state.

Based on the thin wall assumption, we obtain a simplified stress–strain law $\varepsilon_{\theta\theta}=\sigma_{\theta\theta}/E,$ where E is the elastic modulus. We combine these equations to obtain the strain measure ε defined as

$$ {\frac{pr}{Eh}} = {\frac{r-r_0}{r_0}}\quad \Leftrightarrow \quad p {\frac{r_0}{Eh}} = \varepsilon,\quad \hbox{where}\ \varepsilon = {\frac{r-r_0} {r}}. $$

(3)

Note that this strain measure differs from the standard measure, since it is defined relative to the deformed radius as opposed to the zero-pressure radius. The Kelvin viscoelastic (linear) model elastic response, expressed in terms of the zero-pressure cross-sectional radius, can be written as

$$ s^{(e)}[p] = {\frac{r_0}{Eh}}p. $$

(4)

In the above equation, $0<r_0<r_{\min}$ is the zero-pressure cross-sectional radius of the vessel, and Eh is the product of the wall elastic modulus and the vessel wall thickness.

We consider three elastic response functions: the linear response model in (4) and two nonlinear models that allow us to account for the stiffening of the vessel wall with increasing pressure. All three models will be incorporated within the QLV framework outlined above (2). The first nonlinear function studied was the arctangent model proposed by Langewouters et al.,33 which is an empirical model validated using data from human aortic segments measured ex vivo. This model describes the elastic response as

$$ s^{(e)}[p]=1-\sqrt{{\frac{{\frac{1}{2}}-{\frac{1} {\pi}}\tan^{-1}\left({\frac{p_0}{p_1}}\right)}{{\frac{1} {2}}+{\frac{1}{\pi}}\tan^{-1}\left({\frac{p-p_0}{p_1}}\right)}}}, $$

(5)

where p ₀ (mmHg) is the pressure at maximum slope and p ₁ (mmHg) represents the steepness of rise of the curve or half-width pressure.

The second function considered was a sigmoid function that accounts for saturation in the vessel wall distention both at high- and low-blood pressure values. This function is given by

$$ s^{(e)}[p]= 1-\sqrt{{\frac{A_0(p^k+\alpha^k)}{A_m p^k+A_0\alpha^k}}}, $$

(6)

where A _m and A ₀ (cm²) are the maximal and zero-pressure cross-sectional areas of the vessel, respectively, α (mmHg) is the characteristic pressure at which the vessel starts to saturate, and k denotes the steepness of rise of the sigmoid curve. A comparison of these models is shown in Fig. 4.

Figure 4

Illustration comparing the arctangent nonlinear model (dashed black lines) and our sigmoid nonlinear model (solid blue lines) defined in Eqs. (5) and (6). Results are given for ex vivo ovine data from the thoracic descending aorta (left panel) and carotid artery (right panel)

For all three elastic response models, we assume that the viscoelastic creep function K(t) can be characterized by a linear time-invariant dynamic term with one relaxation time b ₁ and amplitude A ₁, $K(t)=1-A_1e^{-t/b_1}.$ This creep function is derived from the Kelvin viscoelastic model (see Valdez-Jasso et al. 42 for details). Because the term A ₁ is related to spring and dashpot constants in a mechanical analog, it is constrained between zero and one, i.e., 0 < A ₁ < 1. At the lower limit $A_1\rightarrow 0,$ (4) reduces to an elastic (static) pressure–area relationship. At the upper limit $A_1\rightarrow 1,$ the Kelvin model creep function reduces to that associated with the Voigt model. Figure 5 illustrates the modeling approach, and Table 1 summarizes the models we used for the data analysis.

Figure 5

Modeling diagram, in which arterial blood pressure is used as an input, an elastic response function s ^(e)[ ] is determined and coupled with a viscoelastic creep function K(t) to predict the vessel strain ε. Finally, vessel area is predicted as a function of vessel strain as described in (2)

Table 1 Summary of models used for data analysis within the framework of the QLV theory

Parameter Estimation

The models described above relate distention of the vessel lumen to the time-varying blood pressure. Each model predicts vessel distention as a function of pressure and characterizes the mechanical properties of the vessel wall via a set of parameter values. One of the objectives of this study is to use pressure–area data to infer biomechanical properties of the vessels for individual sheep and human subjects, considering variations across location and experimental conditions. Model parameters are estimated via solution of the inverse problem minimizing the least-squares difference between computed and measured values of the cross-sectional area. Starting from a set of initial parameters ${\theta_I \in \ {\mathbb{R}}^{n_p}}$ (see Table 2), where n _p denotes the dimension of the parameter space, the inverse algorithm iteratively estimates the set of parameters θ that minimize the least-squares error between the experimental and model predicted cross-sectional area.

Table 2 Initial model parameters for the thoracic descending aorta (TDA) and carotid artery (CA)

Our formulation of the inverse problem relies on the assumption that the measurements can be described fully by an underlying dynamic model plus an error term that compensates for measurement noise. Thus, given a time series of vessel area a _j with n observations, we assume that the statistical model can be written as

$$ a_j = A(t_j;\theta)+\varepsilon_j, \quad j=1,2,\ldots, n, $$

(7)

where A(t _j ;θ) is the modeled cross-sectional area evaluated at times t _j for each data set and θ  ∈  ${{\mathbb R}^{n_p}},$ where n _p is the cardinality of the set of parameter values of the model. For this system, we assume that the measurement errors $\varepsilon_j , j = 1, 2, \ldots, n,$ are independent identically distributed (i.i.d.) random variables with mean E[ɛ _j ] = 0 and constant variance var[ɛ _j ] = σ². Given the form of the statistical model (7), we can define the objective function using the sum of squared errors, and formulate the associated least-squares estimation problem according to

$$ \hat{\theta} = \hbox{arg} \min_{\theta} J(\theta),\quad \hbox{where} \,\,J(\theta)={\frac{1} {n}}\sum_{j=1}^{n}|A(t_j;\theta)-a_j|^2. $$

(8)

To estimate model parameters, we used the Nelder–Mead simplex (direct search) method (fminsearch) implemented in Matlab (version 7.4.0, The Mathworks, Natick, MA). Our optimization was carried out in two sequential steps. First, using the parameter values presented in Table 2, we estimated the parameters associated with the elastic response of each model (Eqs. (4), (5), and (6)). Along with the input pressure, model predictions obtained with the elastic models are shown in black dashed lines in Figs. 6 and 7. We then use these parameter estimates as initial values for estimating parameters in the full viscoelastic model. Thus, in this step, we optimize the full set of parameters including both elastic and viscoelastic portion of the response. This two step algorithm gave more reliable parameter estimates than a one-step approach optimizing all parameter simultaneously. Representative results from this method are shown in Fig. 6.

Figure 6

Illustration of the model parameters estimation routine to predict area dynamics using ovine data obtained under ex vivo experimental conditions. The top row shows time varying pressure and area dynamics for the thoracic descending aorta using the sigmoid model and the bottom row shows similar graphs for the carotid artery using the Kelvin model. The black dashed lines show estimates obtained with the elastic response of the respective model, and the solid dark lines show estimates obtained with the full viscoelastic model. The light grey line is the observed data

Figure 7

Vascular cross-sectional area as a function of transmural blood pressure for the thoracic descending aorta (top two rows) and the carotid artery (bottom two rows). Experimental data are shown in gray; elastic response of each model are shown in black dashed lines; and the corresponding viscoelastic models are shown in solid black lines. Experimental data collected under ex vivo conditions are shown on the first and third rows, and the second and fourth rows show results obtained for in vivo conditions. Note that thoracic descending aorta and carotid artery ex vivo results and thoracic descending aorta in vivo results utilize ovine vessels, while in vivo carotid artery results utilizes human vessels. The results from the Kelvin model are given in the left column, results with the arctangent model are given in the middle column, and results with the sigmoid model are given in the right column. Note that blood pressure and vessel area oscillations, like those due to valve closure (dicrotic notch) or reflective pressure waves, introduce sharp features in the pressure–area plots of the in vivo experimental data. Since the ex vivo experimental measurements are from a single vessel, driven by an artificial pump, these sharp features are not present

The Nelder–Mead simplex method is an unconstrained optimization routine. However, the model parameters are constrained within given physiological limits. First, all model parameters are physical quantities that should be positive, and second, the zero-pressure radius r ₀ has to be smaller than the minimum radius observed in the data. The viscoelastic parameter A ₁ is also constrained to the interval 0 < A ₁ < 1. To ensure positive parameter values, we optimized the square root of the parameters and then squared them before the functions are evaluated. To impose bounds on r ₀ and A ₁, we introduced sigmoid functions with upper and lower limits to define the constrained parameters, and then optimized $\zeta^2.$These functions are defined as

$$ x = x_{\max} {\frac{\zeta^2}{1+\zeta^2}}, \quad \zeta > 0, $$

where x denotes the constrained parameter, i.e., $x=\{r_0,A_1\}$ and x _max denotes the bound for the two parameters, i.e., $x_{\max} = \{\min(r_j),1\}.$

To assess whether estimated parameters vary among models, experimental conditions, and anatomical locations, we make use of a two-way sample t test to determine whether there is a significant statistical difference among means of the estimated parameters. We utilized the Matlab function ttest2 for this analysis.

Results

Results analyzing the three viscoelastic models for the thoracic descending aorta and the carotid artery are shown in Fig. 7. The results displayed in this figure are obtained using one representative data set from each location for both experimental conditions. Summary statistics obtained using all available data for the estimated parameters $\hat{\theta}$ and the minimum least-squares cost values are reported in Table 3.

Table 3 Estimated model parameters obtained with the Kelvin, the arctangent, and the sigmoid models for the thoracic descending aorta (TDA) and carotid artery (CA)

Results show that all three viscoelastic models can capture the main properties of the pressure–area dynamics. For the thoracic descending aorta (under both experimental conditions), the nonlinear viscoelastic models (the arctangent model and our sigmoid model) offer significant improvement allowing excellent prediction of the nonlinear stiffening observed with increased pressure. This can be seen from the graphs in Fig. 7 as well as by inspection of the least-squares cost (J) (see Table 3), which are smaller for the nonlinear models. In contrast, for the carotid artery, the Kelvin model gives the best prediction of the pressure–area dynamics under ex vivo conditions. For the human carotid artery analyzed under in vivo conditions, the difference between the three models is less obvious, as the least-squares cost (J) does not differ significantly between the three models.

Parameter Estimates

Analysis of the standard errors and confidence intervals presented for one representative data set for each experimental condition presented in Table 6 (found in Appendix A) shows that the model parameters Eh, k, and r ₀ generate the smallest standard errors and the tightest confidence intervals indicating that these parameters are estimated with higher certainty. The remaining parameters generated larger standard errors but the confidence intervals remained fairly tight and variation of initial conditions gave almost identical parameter estimates. Consequently, these results indicate that reported parameter values are reliable and can be subject to further investigation.

One important model parameter is r ₀, which denotes the vessel radius at zero pressure. This parameter plays a role in quantifying the arterial strain (see Eq. (3)). While r ₀ can be measured under ex vivo conditions, it cannot be measured in vivo. Consequently, for all models we estimated r ₀, and then we used ex vivo measurements to verify our model predictions. The results of this analysis showed that both the Kelvin and the sigmoid models accurately predict r ₀ for the carotid artery, whereas the arctangent model under-estimateed r ₀ at both locations (compare values reported in the second column of Table 3). For the human in vivo data, we do not have similar measurements and can therefore not compare model predictions of r ₀.

Model Parameters and Biomechanical Properties

To investigate biomechanical properties, we compiled summary statistics from the histological studies and analyzed estimated model parameters. Histological results, reported in Table  4, show that the difference between smooth muscle cell content is similar between the two location, while the other two components clearly differ between the two locations: Elastin is significantly higher in the thoracic descending aorta and the level of collagen is significantly higher in the carotid artery. Model parameters cannot directly be correlated to these percentages, since the mechanical properties are a result of the interaction between the collagen fibrils, elastic fibers, and smooth muscle cells. Furthermore, it is well known that vessels display different mechanics ex vivo than in vivo, as a result of being excised from their natural environment.2,3,10,14 However, some comparisons can be made. In particular, histological results indicate that the carotid artery is stiffer than the thoracic descending aorta, while viscoelasticity may not differ significantly between location. The latter is not clear since elastin also contributes to viscoelastic dampening and that clearly differs between locations.

Table 4 Summary statistics of smooth muscle, elastin, and collagen in the ovine thoracic descending aorta (TDA) and carotid artery (CA). In addition, the summary statistics for the wall thickness h is included. Data reproduced from Zócalo47

Vessel Stiffness

At physiological pressures, the distention of the carotid artery is significantly smaller than the distention of the thoracic descending aorta when normalized to a pressure increase of 100 mmHg. Under ex vivo conditions, the cross-sectional area of the aorta distends 20%, whereas the cross-sectional area of the carotid distends only about 2%. Under in vivo conditions, the aortic distention is approximately 40%, whereas that of the human carotid artery is approximately 18%. These results show that (1) under ex vivo conditions vessels are stiffer than under in vivo conditions and (2) that the carotid artery is significantly stiffer than the thoracic descending aorta. The parameters associated with vessel stiffness are E for the Kelvin model, p ₁ in the arctangent model, and k in the sigmoid model. For the Kelvin model, the estimated parameter is Eh and, thus, using the experimentally measured values of wall thickness h shown in Table  4, we can estimate the elastic modulus. Converting these results show that E is significantly higher for the carotid artery ($7773\le E^{\rm CA}_{{\it ex \, vivo}}\le 9523$ mmHg) than for the thoracic descending aorta ($634\le E^{\rm TDA}_{{\it ex \, vivo}}\le726$ mmHg). Comparing values for thoracic descending aorta under ex vivo and in vivo conditions shows that $E_{{\it ex \, vivo}} > E_{{\it in \, vivo}}.$ For the sigmoid model, the parameter k represents vessel stiffness: a smaller value of k indicates a more rigid vessel. This model predicts that the vessel is more rigid ex vivo than in vivo ($k_{{\it ex \, vivo}} < k_{{\it in \, vivo}}$), but finds no statistically significant difference among anatomical locations (k _TDA vs. k _CA). For the arctangent model, vessel stiffness is associated with the parameter p ₁: a larger value of p ₁ denotes a stiffer vessel. Results obtained with this model indicate that vessels are stiffer ex vivo than in vivo and that the carotid artery is stiffer than the thoracic descending aorta. The observation that the carotid artery is stiffer than the thoracic descending aorta agrees with the histological analysis represented in Table 4, which shows that the carotid artery contains less elastin and more collagen than the thoracic descending aorta. Whereas the observation that vessels examined under ex vivo conditions are stiffer than those examined in vivo cannot be corroborated by the histological data, since such data can only be obtained ex vivo. Instead these observations might potentially be due to the extraction of the vessels from their support matrix.

Viscoelasticity

All three models use the same viscoelastic creep function, which is parameterized by the amplitude A ₁ and the viscoelastic relaxation time b ₁. For ex vivo estimates with the Kelvin model from the thoracic descending aorta, A ₁ is significantly larger in vivo than ex vivo. In all other cases, values for A ₁ do not differ significantly between experimental conditions or between vessel location. For most cases, A ₁ is close to 1 indicating that the Kelvin viscoelastic creep function is similar to that of a simpler viscoelastic model (Voigt model). This observed property of our parameter estimates is likely related to the dominance of a single characteristic frequency in the input pressure waveform.

For the sigmoid model, the parameter estimates for b ₁ were inconsistent between groups. This agrees with histological results for smooth muscle cells (the main contributor to viscoelasticity), which do not differ significantly between locations. For the human carotid vessels examined in vivo, we further examined significantly higher (p < 0.05) viscoelastic damping when compared with the animal data. This observation indicates human vessels contain more smooth muscle cells than ovine vessels.

To further investigate the viscoelastic properties that the vessels display and compare/identify viscoelastic characterization among the models, we analyzed the delay between peaks of the pressure and area waveforms. The delay between the pressure and diameter or area waveforms is evidence of a viscoelastic response of the arterial wall that, in turn, determines the area of hysteresis in the pressure–area relationship. However, since vessels examined here are anatomically different (the thoracic descending aorta is significantly larger than the carotid artery), it is difficult to assess viscoelasticity via comparisons of the area spanned by the hysteretic viscoelastic response. Therefore, we examined the delay, which in principle can be computed directly from data. However, noise in the measurements for vessel area makes it difficult to estimate the exact time for peak area. On the other hand, the time for maximum area is easily detected from the model predictions (compare solid light and dark lines in Fig. 6). Delays for the optimal models (the sigmoid model and the Kelvin model) are summarized in Table 5. Independent of model choice, our results show that for the thoracic descending aorta delays do not vary between in vivo and ex vivo conditions, indicating that excision of vessels does not significantly impact viscoelasticity (i.e., the smooth muscle cells and elastin). This observation agrees with results of the analysis of viscoelastic parameters discussed above. Comparing results between locations (ex vivo) indicates that the carotid artery is less viscoelastic than the thoracic descending aorta. This contradicts our results reported for the parameter b ₁, which for the sigmoid model does not differ significantly between locations. Our histological results showed no significant difference of smooth muscle cells between location, indicating that the other constitutes of the vessel wall (in particular elastin, which does differ significantly between locations) contributes to the overall viscoelastic response.

Table 5 Average delay (sec) between area and pressure peak for the Kelvin and sigmoid models

To summarize, our results indicate that viscoelasticity do not vary between experimental conditions that it may vary between location, and that differences likely exists between the two species.

Viscosity

Another comparison relates to estimates of viscosity. Viscosity can be predicted from analysis of parameters in the Kelvin model. The Kelvin model can be represented by a mechanical body with a dashpot (η), associated with viscosity, and two springs (k ₁ and k ₂). Using the mechanical body, the Kelvin model can be formulated as

$$ k_2 \varepsilon + \eta_1 \left(1 +{\frac{k_2} {k_2}}\right){\frac{d\varepsilon}{dt}} = p + {\frac{\eta_1}{k_1}} {\frac{dp}{dt}}. $$

Comparison with our formulation gives $\eta_1 = A_1 b_1 Eh/r_0$.41 This quantity is proportional to the vessel stiffness Eh, the relaxation amplitude A ₁, the relaxation time b ₁, and inversely proportional to the zero-pressure radius r ₀. Since the changes from in vivo to ex vivo conditions manifest themselves primarily in the parameter Eh, the results for viscosity follow those observed for vessel stiffness Eh in both locations. It should be emphasized though that this definition is only valid for the Kelvin model, where an analogy can be made between parameters estimated and the quantity representing viscosity. Results for the thoracic descending aorta gave η = 28.8 ex vivo and η = 15.4 in vivo. For the carotid artery we obtained η = 227 ex vivo and η = 81 in vivo.

Discussion

Results from our modeling analysis of pressure–area dynamics demonstrate that including viscoelasticity is important for capturing the loops found when relating cross-sectional area to pressure. Furthermore, it is essential to account for nonlinear stiffening when predicting, at physiological pressures, responses for the thoracic descending aorta. For the same pressure ranges, this is not essential for the carotid artery. However, histological analysis (see Table 4) shows that the carotid artery has a higher level of collagen, indicating that, for some ranges of pressure loading, accounting for nonlinear elastic behavior may also be important. Such ranges could be identified by measuring pressure–area dynamics for patients with severe hypertension or by inducing significantly higher pressures in the carotid artery under ex vivo experimental conditions.

Overall, analysis of experimental data using models reveals that the sigmoid model improves the data prediction of the arctangent model, which displays large variation in parameter estimates and consistently underestimates the zero-pressure radius r ₀. Consequently, our results support the notion that the sigmoid model is preferable for analysis of data from the thoracic descending aorta, while the Kelvin model is better for analysis of smaller and stiffer vessels, including the carotid artery. Our model analysis results show that, for the thoracic descending aorta, the nonlinear viscoelastic models can reduce the cost J by an order of magnitude under both experimental conditions. For the carotid artery, the Kelvin model produces the largest reduction in J. Overall, these specific model choices for the two vessel types consistently fit the data more precisely (give the lowest values of J) and generate parameter values within the physiological range and with the smallest confidence intervals (see Table 6) independently of the experimental conditions. All observations mentioned above are corroborated with small standard errors and overall tight confidence intervals at the 95% level.

Most results reported in this study were obtained by analysis of ovine arteries. However, results in one vessel type were obtained using human arteries. The latter was done to see if the proposed models could be applicable across species. Generally, the ovine and human cardiovascular systems differ in anatomy and physiology (e.g., the number and size of arteries, cardiac output, and blood viscosity). However, ovine- and human arteries contain the same constituents giving rise to similar mechanical behavior. These similarities support the use of ovine models to examine human cardiovascular biomechanics. For example, the ovine cardiovascular system has been shown to be an excellent model for human vascular physiology and pathology, including therapeutics (i.e., in studies analyzing the performance of vascular grafts32). Consequently, experimentalists often use ovine studies in research projects. From a modeling point of view, similarities in biomechanical behavior justify the use of the same models for analysis of ovine and human data, while differences in anatomy lead us to the expectation (as discussed below) that model parameters differ between the two species.

Vessel Stiffness

Predictions of model parameters, which relate to biomechanical properties, reveal that parameters characterizing vessel stiffness agree well with previous results reported in the literature. Our computational results showed that both vessel types (aortic and carotid) were stiffer under ex vivo conditions as compared in vivo conditions. Our results are consistent with several previous studies comparing both experimental conditions. Boutouyrie et al.10 showed, using rat aortic segments, that arterial distensibility and compliance were higher under in vivo conditions than ex vivo conditions. Similar results were reported by Wells et al.,44 who analyzed ovine artery stiffness. Wells et al. based their results on analysis of pulse wave velocity, which was found to be higher under ex vivo conditions. It is well known that pulse waves travel faster in stiff vessels than in compliant ones. Our results are also in agreement with previous experimental studies that related reductions in smooth muscle tone under ex vivo conditions to increases in elastic moduli.3 Similar results were found using ovine12 and human2 vessels.

Furthermore, our results show that the carotid artery is stiffer than the thoracic descending aorta, which was confirmed both via analysis of the estimated model parameters as well as by analysis of histological results. The latter showed that the carotid artery has less elastin and more collagen than the thoracic descending aorta, while the smooth muscle cell level did not differ significantly between the two sites.

According to our parameter estimates, the ovine carotid artery is significantly stiffer than that of humans. This observation could be investigated experimentally, by comparing histological data from the two species. However, we did not have such data available for this study. Therefore, future studies have to be conducted to test this hypothesis.

Viscoelasticity

Results showed that it is important to include viscoelasticity, without it the pressure–area hysteretic loops cannot be predicted. However, viscoelastic parameters were more difficult to compare and interpret. The models include two viscoelastic parameters: a viscoelastic gain A ₁ and a relaxation time b ₁. For the Kelvin model A ₁ < 1, while for the arctangent and the sigmoid model $A_1\rightarrow 1.$ The latter indicates that the viscoelastic response could be predicted using a Voigt model. The parameter b ₁ varied significantly (and inconsistently) for the Kelvin and arctangent models, while for the sigmoid model b ₁ did not vary significantly between experimental conditions or with vessel location. This large variation likely stems from the fact that b ₁ is the least sensitive parameter (these results are not reported here, but we refer to Valdez-Jasso41). However, even though the parameters A ₁ and b ₁ appearing in the viscoelastic creep function did not vary significantly across most data sets, it should be noted that the dynamic pressure–area characteristics are also affected by parameters in the elastic response function of the QLV formulation. In addition to analysis of viscoelastic parameters, we also analyzed the delay between pressure and area peaks, which similar to the sigmoid model showed little difference between experimental settings. While a decrease was found between the thoracic and carotid arteries, in general, these observations suggest that additional data is essential to investigate the behavior of the viscoelastic models.

The one major difference observed both for parameter predictions of A ₁ and b ₁ as well as for predictions of the delay between pressure and area peaks is that human vessels appear more viscoelastic than the corresponding ovine vessels. Again, the latter could be investigated further by comparing histological results between the two species.

Viscosity

In addition to analysis of vessel stiffness, the study by Armentano et al.2 reported a decrease in viscosity after arterial excision. This observation contradicts findings by Boutouyrie et al.,10 who reported that viscosity (assessed via evaluation of the area of the pressure–volume loop) is significantly lower in vivo. Both studies, along with a number of other studies1,2,3,5 attribute changes in viscosity to changes in smooth muscle content, arrangement, and activation. While smooth-muscle content may not differ between the experimental conditions, both the arrangement of the smooth muscle cells as well as their degree of activation may differ, thus leading to the observed differences. Our results agree with those of Boutouyrie, namely that viscosity is higher ex vivo than in vivo, but disagree with those predicted by Armentano et al. On the other hand, our results agree with results by Bia et al.,6 which showed that viscosity is higher in the carotid artery than in the thoracic descending aorta. It should be noted that modeling approaches in our studies differ from those mentioned above. Studies by Bia et al. and Armentano et al. used the Voigt model combined with analysis of a simple harmonic, while our studies used the Kelvin model and the actual pressure data to determine the value. This is again, different from the study of Boutouyrie, who assessed viscosity via prediction of the area of the pressure–volume loop. Thus, further studies are needed for more consistent prediction of this quantity. Furthermore, it should be noted that for the thoracic descending aorta, the Kelvin model did not adequately predict dynamics observed in the vessels, thus values predicted for these vessels may not accurately predict viscosity. However, we did note the same discrepancy for the carotid artery, where the Kelvin model predicted pressure–area dynamics better.

Limitations

All results discussed in this study depend on correct interpretation of the pressure–area loops, in particular, it is essential that both diameter and pressure measurements are (a) recorded simultaneously at the same location, (b) processed by circuitries having the same frequency characteristics, and (c) the signals are synchronized. Our in vivo and ex vivo methodological approaches were selected to ensure that these important methodological facts were fulfilled. The only exception is the in vivo measurements from the human subjects, where pressure and area measurements are made sequentially and then aligned to the ECG in a post hoc manner. This careful design of experiments allowed us to use the data for estimation of model parameters. Results showed significant changes within the elastic parameters, while differences in viscoelastic parameters were more subtle. It is noted that, in all our models, the same creep function K(t) was used and involved a discrete spectrum with a single relaxation term. In contrast, other studies of soft tissue viscoelasticity employ more complex creep functions, e.g. based on a continuous spectrum or a discrete spectrum approximation with multiple terms.19,25,42 However the pulsatile data considered in our study are dominated by a single frequency, thus making it challenging to characterize additional parameters in more complex viscoelastic models. In a previous study by our group, the addition of a second exponential relaxation term to the creep function resulted in no significant improvement in prediction of the experimental data.42 Future studies in which the heart is paced over a range of frequencies will contribute to more detailed characterization of the viscoelastic damping responses and, hence, to the development of a more accurate representation of the viscoelastic creep function of the arterial wall.

Another limitation of our proposed models is that we assume that arteries locally can be identified as straight cylindrical vessels. This assumption holds for both the thoracic and carotid arteries used in this study. However, our derivation of stress–strain relations does not hold if vessels are non-cylindrical. This limitation is important to keep in mind if one seeks to utilize the proposed models for vessels with a more complex geometry.

Conclusion

In conclusion, our study shows that the proposed models can predict pressure–area dynamics and can capture nonlinear stiffening of large vessels, though this phenomenon may not be important in more peripheral vessels such as the carotid artery. Results also showed that essential differences can be detected between experimental conditions, and that parameters vary with species. Our results show that the carotid arteries are stiffer than the thoracic descending aorta, that vessels are stiffer ex vivo than in vivo, and that the carotid arteries are stiffer in ovine vessels than in humans. We cannot make a similar conclusion for the thoracic descending aorta, which was only studied in sheep. Furthermore, we note that viscoelastic properties differ to a lesser degree between locations and not at all between experimental conditions. However, human carotid arteries appeared to be more viscoelastic than ovine vessels. While these results of analysis of biomechanical properties were separated between function (stiffness vs. viscoelasticity), all parameters are essential for accurate prediction of the loops apparent in pressure–area data. Further studies are required to describe, in greater detail, how changes in loop geometry are related to the damping of the pulse pressure as the pressure wave is propagated along the arteries. The latter effect is particularly important, since such results potentially can be used for analysis of impact of stents and grafts in the cardiovascular system. However, to thoroughly investigate the impact of viscoelasticity in a vessel with a stent or a graft, the models proposed in this study should be coupled with a fluid dynamics model. Today most fluid dynamics models are coupled with linear elastic models (see e.g. Olufsen35) or with simple linear viscoelastic models (see e.g., Reymond39). Thus, we propose to couple current fluid dynamics models with the nonlinear viscoelastic models developed in this study.

Appendix A: Standard errors and confidence intervals

To analyze estimates generated by each model for each subject, we compute standard errors and confidence intervals for each parameter (see Table 6). To do so, we employ the asymptotic theory of sampling distributions,4 which states that for a sufficiently large number of observations n a sampling distribution $\hat{\theta}(a)$ satisfies

$$ \hat{\theta}(a) \sim {\mathcal N}_{n_p}\left(\theta_0,\sigma_0^2 [\chi^T(\theta_0)\chi(\theta_0)]^{-1} \right) = {\mathcal N}_{n_p}(\theta_0,\Upsigma_0), $$

where θ₀ contains the true (but unknown) parameter values, σ₀ denotes the unknown variance, and χ is the sensitivity matrix defined as

$$ \chi_i(t_j,\theta_i)={\frac{d A (t_j;\theta)}{d \theta_i}} \in \ {\mathbb R}^{n\times n_p} \ , \hbox{where} \ j=1,\ldots, n \,\ \hbox{and}\, \ i=1,\ldots,n_p. $$

As discussed by Davidian et al.,17 σ₀ can be approximated using the covariance matrix $\Upsigma_0,$ evaluated at the parameter estimate $\hat{\theta},$ according to

$$ \Upsigma_0 \approx \Upsigma(\hat{\theta}) = \hat{\sigma}^2 [\chi^T(\hat{\theta})\chi(\hat{\theta})]^{-1}. $$

(9)

The adjusted variance becomes

$$ \hat{\sigma}^2 = {\frac{1} {n-n_p}}\sum_{j=1}^{n}|A(t_j;\theta)-a_j|^2, $$

where the number of model parameters n _p are taking into account to unbias the variance.

Table 6 Standard errors and confidence intervals derived for all model parameters using the thoracic descending aorta for Sheep 9 under ex vivo experimental conditions (on the left) and under in vivo conditions in Sheep 10 (on the right)

Using the approximation of the covariance (9), for each subject, we can compute the confidence intervals of the estimated parameters. In order to compute a confidence interval for each model parameter, we first calculate the standard errors according to Casella and Berger15

$$ SE_{i}(\hat{\theta}) = \sqrt{\Upsigma_{ii}(\hat{\theta})}. $$

The standard error corresponding for each estimated parameter $\hat{\theta}_i$ is thus the square root of the diagonal entries of the covariance matrix (9). The confidence intervals (at the $100\left(1-\alpha \right)\%$ level) for the estimated parameters can be calculated as

$$ [\hat{\theta}_i - t_{1-\alpha/2} SE_i(\hat{\theta}), \hat{\theta}_i + t_{1-\alpha/2} SE_i(\hat{\theta})], $$

where

$$ P\{\hat{\theta}_i - t_{1-\alpha/2} SE_i(\hat{\theta}) < {\theta_0}_i < \hat{\theta}_i + t_{1-\alpha/2} SE_i (\hat{\theta}) \} = 1-\alpha, $$

for α  ∈ [0,1] and ${t_{1-\alpha/2} \in {\mathbb R}_+}.$ To obtain 95% confidence intervals, the critical value t _1−α/2 is computed from the Student’s t distribution $t^{{n-n_{p}}}$ with n − n _p degrees of freedom. The value of t _1−α/2 is determined by P{T > t _1−α/2} = α/2 where $T \sim t^{{n-n_{p}}}.$ Given that the data set has n observations and n > 40, for all data sets considered, the degree of freedom was approximated to ∞. Thus t _1−α/2 ≈ 1.96.