Feature Extraction From Parametric Time–Frequency Representations for Heart Murmur Detection

Abstract

The detection of murmurs from phonocardiographic recordings is an interesting problem that has been addressed before using a wide variety of techniques. In this context, this article explores the capabilities of an enhanced time–frequency representation (TFR) based on a time-varying autoregressive model. The parametric technique is used to compute the TFR of the signal, which serves as a complete characterization of the process. Parametric TFRs contain a large quantity of data, including redundant and irrelevant information. In order to extract the most relevant features from TFRs, two specific approaches for dimensionality reduction are presented: feature extraction by linear decomposition, and tiling partition of the t–f plane. In the first approach, the feature extraction was carried out by means of eigenplane-based PCA and PLS techniques. Likewise, a regular partition and a refined Quadtree partition of the t–f plane were tested for the tiled-TFR approach. As a result, the feature extraction methodology presented, which searches for the most relevant information immersed on the TFR, has demonstrated to be very effective. The features extracted were used to feed a simple k-nn classifier. The experiments were carried out using 45 phonocardiographic recordings (26 normal and 19 records with murmurs), segmented to extract 548 representative individual beats. The results using these methods point out that better accuracy and flexibility can be accomplished to represent non-stationary PCG signals, showing evidences of improvement with respect to other approaches found in the literature. The best accuracy obtained was 99.06 ± 0.06%, evidencing high performance and stability. Because of its effectiveness and simplicity of implementation, the proposed methodology can be used as a simple diagnostic tool for primary health-care purposes.

Introduction

Cardiac mechanical activity is appraised by auscultation and processing of heart sound (HS) records (known as phonocardiographic signals—PCG), which is an inexpensive and non-invasive procedure. Since computer-based analysis of HS may contribute to improve diagnosis of cardiac malfunctions, PCG has preserved its importance in many medical fields of clinical practice.2,10,19 Specifically, murmurs, which are sorted into systolic or diastolic, are some of the basic signs of pathological changes to be identified, but they overlap with the cardiac beat, and these HS cannot be easily separated by the human ear, since a large amount of information in the frequency domain is below the audibility thresholds. Moreover, cardiac murmurs are non-stationary signals that exhibit sudden frequency changes and transients. Therefore, the time–frequency representations (TFRs) have been proposed before to investigate the correlation between the time–frequency (t–f) characteristics of murmurs and the underlying cardiac pathologies.19 For that matter, in the literature, both non-parametric and parametric estimations of TFR are generally employed.7,15,17 Non-parametric methods (e.g., Wigner–Villle distribution—WVD, continuous wavelet transform—CWT, etc.) are based on non-parameterized representations of the signals as a simultaneous function of time and frequency, whereas parametric methods are based on parameterized expressions of a time-dependent autoregressive modeling (or related types) and their extensions. In biomedical applications, the non-parametric methods of estimation that are commonly implemented by means of wavelet transform suffer of a trade-off between time and frequency resolution.21

Since there are large differences in the transition patterns among the individual sets of multi-frame signals, a stable estimation of the transition patterns should be carried out. In this line, and due to its intrinsic generality and its capacity to detect formant frequencies, the time-varying autoregressive (TVAR) models, in which the auto-regressive coefficients are allowed to vary with time, have provided useful empirical representations of non-stationary time series for biomedical signal analysis.6 The frequency resolution of the parametric methods is superior because of the implicit extrapolation of the autocorrelation sequence.21 Furthermore, the TVAR technique can provide a higher resolution with respect to the non-parametric estimations, and without the complication of the quadratic terms regarded to the quadratic TFR, or the need to generate a high time-resolution wavelet analysis. Despite these advantages, the selection of the model order and the methods of estimation for the parameters are the two main problems, which had discouraged the use of TVAR models to estimate the TFR.6 Explicitly, the selection of the model order has a large effect on the quality of the signal representation,15 and for pathological PCG signals it is often difficult to select a unique value correctly.12,14,16 As a result, the TVAR model may not resolve well enough the fine structure in the data. However, the methods of estimation of the TVAR parameters can help with this issue. In general, these methods should be directly coupled with the time-varying dynamics of the PCG signal. Assuming that the signal is stationary within short segments, and under the assumption that the parameters and innovations variance are independent of time,17 AR estimators can be used in short time windows. Because of the lack of resolution, this method is basically suitable for cases where the evolution in the dynamics is slow. This is the case of the PCG signals. It must be quoted that regardless of the improvement of the TVAR models for the representation of non-stationary signals, the modeling of the PCG signal to automatically detect murmurs remains still an open issue.

For the automatic detection of murmurs, the TFR-based classification methods are preferred with respect to other techniques because t–f planes have clear discriminant capabilities to separate signals belonging to different classes. In addition, even that the flexibility to form the feature vector in 2D representations is considered the main advantage of a t–f domain-based classification, this enhanced representation also tends to contain a large amount of redundant data, and hence a dimensionality reduction is required. Thus, there is a growing need for new data reduction methods that can accurately parameterize the activity in TFR of biosignals, particularly those with higher resolution, as stated in Bernat et al. 5 for the case of electroencephalographic signals. A direct approach is the use of principal component analysis (PCA) to reduce the dimensionality of the feature space resulting from the t–f plane, assuming that the information is equally distributed along with the TFR. As concluded in Englehart et al.,11 a PCA-reduced t–f representation has shown to effectively accommodate the loosely structured waveforms of some transient biological signals, when quantitative and decision-based analysis is required. PCA models each TFR as the weighted sum of base functions obtained as the components, which maximize the variability on the dataset. Nevertheless, for classification purposes, the components obtained are not always related with the most discriminative information. Thus, similar decomposition approaches, such as partial least squares (PLS), can be used as a supervised dimensionality reduction approach that yields components maximally related with labels.4

Nonetheless, as commonly known in the state-of-the-art, the methods, which classify the TFRs based on the local regions of the t–f plane, have achieved higher success rates than those based on the entire image22; and for PCG signals this supposition is more adequate, since most of the information is concentrated wherever the heart murmurs are present. But there is a noteworthy unsolved issue associated with local-based analysis, namely, the selection of the size of local relevant regions. As a result, the choice of feature extractors in the t–f domain, and the classifier, is highly dependent on the final application.19

A major motivation in this study is to generate a set of parametric TFR-based features extracted from PCG recordings, capable of detecting murmurs with higher accuracy than using static features. So, the aims of this study are (a) the calculation of TFRs using a TVAR model, taking directly into account the variability of the PCG induced by the murmurs originated by valve pathologies; (b) the evaluation of the best set of dynamic features, estimated from parametric-based TFR, and suitable for the classification of heart murmurs.

Throughout this article, the criterion followed to compare the different approaches is the classifier accuracy, obtained using the well-known k-nn approach. For the sake of comparison and for the different feature extraction techniques described, the results—in terms of accuracy—of the proposed parametric approach were compared with those obtained using two non-parametric methods, namely, WVD and CWT (estimated as explained in Quiceno-Manrique et al. 18). Moreover, the results were compared with other assumed baseline methods in the literature.8,23

The rest of this article is organized as follows: first, the time-varying representation implemented is introduced, followed by a brief description of the TVAR parameter estimation method used, computed by minimizing the mean-square error. Then, the methodology for feature extraction is described in detail (based on linear decomposition and partition schemes). Lastly, the effectiveness of a feature set based on parametric TFR representing the dynamics of the HS is applied to the detection of murmurs, comparing the results with other methods in the literature. Finally, there is a brief discussion of the results obtained.

Background

The stochastic parameters that define the TVAR model, and that are used to generate the TFRs, are briefly described in this section. Moreover, the feature extraction techniques from TFRs considered in this article are presented.

TVAR Models with Locally Stationary Assumptions

A time-variant autoregressive model of pth order, shortly TVAR(p), is described as follows

$$ x[t] = {\varvec{\uptheta}}^{\text{T}} [t]{\mathbf{h}}[t - 1] + e[t];\quad e[t] \sim N(0,\sigma_{e}^{2} [t]) $$

(1)

where ${\mathbf{h}}[t] = \{ x[t - i]:i = 1, \ldots ,p\} ,\quad {\mathbf{h}} \subset {\mathbb{R}}^{p}$ is a non-stationary (real-valued vector) processes to be modeled, e[t] is an unobservable and uncorrelated Gaussian sequence with zero mean and time-dependent variance σ ² _e [t] (or innovations variance) and ${\varvec{\uptheta}}[t] = \{ \theta_{i} [t]\} ,\quad {\varvec{\uptheta}} \subset {\mathbb{R}}^{p}$ are the parameters of the TVAR model. The order of a stationary model can be used as starting point to set the TVAR model order,1 but a more accurate estimation can be achieved by trial-and-error procedures using a fitting function such as Bayesian information criterion (BIC).17

The vector of parameters, θ[t], and the innovations variance, σ ² _e [t], for a given value of the sampling frequency, f _s is related to the spectral content of x[t] by21:

$$ {\mathbf{S}}_{x} (t,f) = {\frac{{\sigma_{e}^{2} [t]}}{{\left| {1 + \sum\nolimits_{i = 1}^{p} \theta_{i} [t]e^{{ - j\omega it/f_{\text{s}} }} } \right|^{2} }}},\quad {\mathbf{S}}_{x} (t,f) \subset {\mathbb{R}}^{T \times F}$$

(2)

that can be assumed as the time-varying power spectral density (i.e., the TFR) of the signal if the system were stationary at the time instant t. The dimension of the TFR is given by the time and frequency resolution (T for time, and F for frequency).

TVAR representations differ from their conventional stationary counterparts in that they are time-dependent. The methods upon them provide a set of potential advantages listed in Poulimenos and Fassois,17 namely, (a) its simplicity of representation, since these models may be potentially specified by a limited number of parameters; (b) improved accuracy; (c) better resolution; (d) better tracking of the time-varying dynamics; (e) flexibility of analysis, since the parametric methods are capable of directly capturing the underlying structural dynamics regarded to the non-stationary behavior.

The TVAR model of Eq. (1) is completed specifying the evolution of {θ _i [t]} and σ ² _e [t]. These two parameters will take a value at the time instant t for each window of analysis. Nonetheless, if the coefficients at each time are assumed to be independent, then the number of parameters needed becomes usually greater that the amount of data. In the context of biological signal processing and to overcome this problem, the stochastic regression approach is likely more suitable.6 Specifically, in a locally stationary method for TVAR model estimation (referred as LS-TVAR), the parameters, θ[t], are commonly computed by minimizing the mean-square error within a window of size M:

$$ \widehat{{\varvec{\uptheta}}}[t] = \arg \mathop {\min }\limits_{{\varvec{\uptheta}}} \sum\limits_{\tau = t - M}^{t} \left( {x[t] - {\varvec{\uptheta}}^{\text{T}} [t]{\mathbf{h}}[t - 1]} \right)^{2} $$

(3)

leading to the Yule-Walker equations that can be solved by any of the standard algorithms such as Burg’s one.21 The tracking ability of the LS-TVAR algorithm is prescribed by either the size of a window or the value of a fading rate, but conditioning the limitation of this approach: if the process evolves too quickly, the algorithm will not properly track the evolution of the coefficients, unless the window becomes very short which in turn degrades the spectral resolution.7 Consequently, for the LS-TVAR approach (Eq. 3), only a coarse adjustment of the tracking properties can be carried out,13 which is enough for the slowly changing dynamics of the PCG signals.

In order to complete the LS-TVAR model, the variance of the observation noise σ ² _e [t] must be estimated. A sliding window on the square of estimation error21 can be used:

$$ \sigma_{e}^{2} [t] = \frac{1}{M}\sum\limits_{\tau = t - M}^{t} {w[\tau ,\alpha ]e^{2} [t]} $$

(4)

where w[τ, α] is a smoothing Gaussian window with aperture of value α and length M which determines the quantity of data considered in the window.

Feature Extraction From the Enhanced t–f Planes

The TFR can be represented as a matrix, ${\mathbf{S}}_{x} (t,f) \subset {\mathbb{R}}^{T \times F} ,$ with T time and F frequency points. This matrix can be used to characterize the dynamics of the PCG signals, but contain a large amount of information difficulting further processing. Thus, the problem stands on how to reduce the large amount of information and redundancies of the TFRs, but keeping most of the relevant information. The goal is to reduce the original TFR, S _x (t, f), into a set of features, ${\varvec{\upxi}} \subset {\mathbb{R}}^{n} ,$ with a smaller dimension but containing the most important information available in the former dataset. The main drawback is that TFRs lie on a bidimensional space, ${\mathbb{R}}^{T \times F} ,$ while a set of features amenable for a simple classifier should reside on an unidimensional space ${ \mathbb{R}}^{n} .$

A simple approach for manipulating the TFR matrix is reducing its dimension by downsampling or even decimating the time and frequency resolution. However, this method has not been considered, since it removes some important information from the TFR. An alternative approach to reduce the dimensionality would be to divide the two-dimensional TFR in two-dimensional bins with similar characteristics, characterizing each bin with an average of the energy contained within it. The bigger the area of these bins, the smaller the final feature space, but the lower the resolution. These bins could be equally distributed or defined according to the amount of information present in each part of the TFR. On the other hand, as quoted before, another direct approach for feature extraction would be the use of a linear decomposition method (e.g., PCA, 2D-PCA, PLS) to decrease the dimensionality projecting the whole TFR into a smaller subspace but keeping the most relevant information. The feature extraction approaches used throughout this study have been grouped into two subsections: (a) tiled-TFR approaches; and (b) linear decomposition-based approaches.

Tiled-TFR Approaches

A straightforward approach for 2D feature extraction is to divide a given t–f plane into tiles evaluating their informativity (the lower the probability of the dynamic occurrence, the higher the tile informativity). The informativity can be carried out computing a statistic operator, $\mathcal{L}\{ \cdot\} ,$ over a determined tile of the t–f plane S _x (Δt, Δf) such as the variance var{·}:

$$ {\varvec{\upxi}} = {\text{var}}\{ {\mathbf{S}}_{x} (\Delta t_{i} ,\Delta f_{j} )\} ;\quad i = 1, \ldots , \, N_{\Delta t} ;\; \, j = 1, \ldots ,N_{\Delta f} $$

(5)

where Δt _i stands for the ith time segment; Δf _j is for the jth frequency bin; N _Δf stands for the number of frequency bins; and N _Δt is the number of time segments. Therefore, it is expected that the feature set extracted from Eq. (5), ξ, holds enough information related to the non-stationary properties of the signal.

In the beginning, the t–f tiles can be made up of fixed size frameworks, so that the feature vector can be described as ${\varvec{\upxi}} = \left\{ {\xi_{i} :i = 1, \ldots , \, N_{b} ;\quad \xi_{i} \in {\mathbb{R}}^{1} } \right\},\quad {\varvec{\upxi}} \in {\mathbb{R}}^{{N_{b} }} ,$ where $N_{b} = N_{\Delta f} \cdot N_{\Delta t}$ is the number of tiles. Both, N _Δf and N _Δt can be determined empirically.9,22 Time and frequency partitions are defined as:

$$ \begin{gathered} \Delta t_{i} = \left[ {\begin{array}{*{20}c} {t_{i - 1} } & {t_{i} } \\ \end{array} } \right],\quad {\text{where }}t_{i} = {\frac{i \cdot T}{{N_{\Delta t} }}},\quad \forall i = 1, \ldots ,N_{\Delta t} \hfill \\ \Delta f_{j} = \left[ {\begin{array}{*{20}c} {f_{j - 1} } & {f_{j} } \\ \end{array} } \right],\quad {\text{where }}f_{j} = {\frac{j \cdot F}{{N_{\Delta f} }}},\quad \forall j = 1, \ldots ,N_{\Delta f} \hfill \\ \end{gathered} $$

(6)

This regular configuration of time windows and frequency bins assumes that the information content is equally distributed along the t–f plane. However, for PCG signals, this assumption might be inadequate, since most of the information is concentrated around the HS,¹ S1, and S2, and eventually between them, in the systole and diastole, wherever the heart murmurs are present.

Thus, a more efficient representation might be reached using unfixed and adaptive size frameworks: for instance, using adaptive multiscale representations via the Quadtree decomposition that splits the t–f domain into four equally sized tiles, where each tile can be successively decomposed into four new tiles.20 The root of the tree is the initial TFR.

Linear Decomposition-Based Approaches

The PCA and the PLS methods were used throughout this article as unsupervised and supervised methods, respectively, to perform dimensionality reduction in the TFRs. Moreover, a two-dimensional extension of PCA was used to represent the reduced feature space.

PCA Decomposition

Let X = {χ _i : i = 1,…,N _r } be a set of N _r objects generated by m random variables. Thus, for the ith object, the respective data set ${\varvec{\upchi}}_{i} = \left[ {\chi_{i}^{1} ,\chi_{i}^{2} , \ldots ,\chi_{i}^{m} } \right]$ is given, and from which the centralized data matrix is built as:

$$ {\mathbf{\rm X}}_{0} = \left[ {({\varvec{\upchi}}_{1} - {\varvec{\upmu}}_{\chi } )^{\text{T}} , \, ({\varvec{\upchi}}_{2} - {\varvec{\upmu}}_{\chi } )^{\text{T}} , \ldots ,{ (}{\varvec{\upchi}}_{{N_{r} }} - {\varvec{\upmu}}_{\chi } )^{\text{T}} } \right]^{\text{T}} ,\quad {\varvec{\upmu}}_{\chi } = {\frac{1}{{N_{r} }}}\sum\limits_{{i \in N_{r} }} {{\varvec{\upchi}}_{j} } ,\quad {\mathbf{\rm X}}_{0} \in {\mathbb{R}}^{{N_{r} \times m}} $$

(7)

The conventional PCA looks for an orthogonal transformation matrix W, (being ${\mathbf{W}}^{\text{T}} {\mathbf{W}} = {\mathbf{I}}, \, {\mathbf{I}} \in {\mathbb{R}}^{n \times n} ,{\mathbf{W}} \in {\mathbb{R}}^{m \times n} ),$ to project the data onto a smaller set of variables with the maximum variance, by means of the linear transformation Y = X ₀ W, where:

$$ {\mathbf{W}} = \mathop {\arg \max {\text{tr}}}\limits_{{\mathbf{W}}} ({\mathbf{W}}^{\text{T}} {\mathbf{X}}_{0}^{\text{T}} {\mathbf{X}}_{0} {\mathbf{W}}) $$

(8)

In practice, the solution is found by setting the columns of W to the n leading eigenvectors of the covariance matrix X ^T₀ X ₀.

Now consider the case when each object is not defined as a vector but as a matrix, such as TFR matrices. Then, each object is described by a dataset ${\mathbf{S}}_{{x_{i} }} (t,f) \subset {\mathbb{R}}^{T \times F} ,$ which from now on will be denoted by S _i for shorter notation. Every variable of each set S _i is time-dependent and has been measured upon a set of T instants of time. Thus, for each object the following dataset is given $\left\{ {{\mathbf{S}}_{i}^{(j,k)} : \, i = 1, \ldots , \, N_{r} ; \, j = 1, \ldots , \, T; \, k = 1, \ldots , \, F} \right\},$ where notation S ^(j,k) _i stands for the kth point, measured for the ith object, at the instant of time j.

PCA can be carried out on these data performing the same singular value decomposition but on a data matrix of vectorized t–f domains, thus dealing with the stochastic nature of the variables by assuming that each instant of time and frequency point S ^(j,k) _i , ∀j, constitutes a new random variable. Therefore, each object can be described by

$$ {\varvec{\upchi}}_{i} = \left[ {S_{i}^{(1, \, 1)} , \ldots ,S_{i}^{(1, \, F)} , \cdots ,S_{i}^{(T, \, 1)} , \ldots ,S_{i}^{(T, \, F)} } \right],\quad {\varvec{\upchi}}_{i} \in {\mathbb{R}}^{T \times F} $$

(9)

and a linear component decomposition can be carried out over the rewritten centralized data matrix in Eq. (7). Lastly, it must be quoted that the PCA transformation provides a means of unsupervised dimensionality reduction, as no class membership qualifies the data when specifying the eigenvectors of maximum variance.

2D-PCA Decomposition

Another approach of bi-dimensional component analysis (known as 2D-PCA) is discussed in Yang et al. 24 and Avendano-Valencia et al. 3 Further refinement of the object description represented in Eq. (9) can be achieved if the vector used to represent an object, $\varvec{\chi}_{j} \in {\mathbf{X}},$ is represented by the following matrix, taking into account the variability of the whole variable set:

$$ {\varvec{\upchi}}_{i} = \left[ {\begin{array}{*{20}c} {S_{i}^{(1,1)} } & {S_{i}^{(1,2)} } & \cdots & {S_{i}^{(1,F)} } \\ {S_{i}^{(2,1)} } & {S_{i}^{(2,2)} } & \cdots & {S_{i}^{(2,F)} } \\ \vdots & \vdots & \ddots & \vdots \\ {S_{i}^{(T,1)} } & {S_{i}^{(T,2)} } & \cdots & {S_{i}^{(T,F)} } \\ \end{array} } \right],\quad {\varvec{\upchi}}_{i} \in {\mathbb{R}}^{T \times F} $$

(10)

In this case, the matrix of the data projected, ${\mathbf{Y}} = [{\varvec{\uppsi}}_{1}^{\text{T}} , \ldots ,{\varvec{\uppsi}}_{{N_{r} }}^{\text{T}} ]^{\text{T}} ,$ is described by the elementary matrices ${\varvec{\uppsi}}_{i} = {\varvec{\upchi}}_{i} {\mathbf{V}},\quad {\varvec{\uppsi}}_{i} \in {\mathbb{R}}^{{T \times n_{F} }} .$ The reduction of the model in Eq. (8) is carried out over the column of the objects, which implies that the variables projected are capturing the variability of each object in time.

Also, the description of the object in Eq. (11) can be transposed to compute a transformation matrix ${\mathbf{W}} \in {\mathbb{R}}^{{F \times n_{T} }} .$ Such matrix can reduce the dimensionality of the χ _i rows, by means of the operation ψ _i  = W ^T χ _i , where the matrix W is calculated from the matrix set {φ _i  = χ ^T _i :i = 1,…,N _r }. After the calculation of the arrangements, ${\mathbf{V}}_{{T \times n_{f} }} , \, {\mathbf{W}}_{{F \times n_{T} }} ,$ a column–row-based dimensionality reduction is carried out for each χ _j , i.e., ${\varvec{\uppsi}}_{i} = {\mathbf{W}}^{\text{T}} {\varvec{\upchi}}_{i} {\mathbf{V}},\quad {\varvec{\uppsi}}_{i} \in {\mathbb{R}}^{{n_{T} \times n_{F} }} .$ As a result, the dimensionality reduction takes into account not only the instant-by-instant variability of each random variable, given by the model represented in Eq. (9), but also checks for information variability through the frequency spectrum.

Mainly, the difference between PCA and 2D-PCA approaches is based on the form to tackle the matricial data. Both algorithms are graphically depicted in Fig. 1.

FIGURE 1

Dimensionality reduction procedure for TFR matrices; (a) PCA and vectorization; (b) 2D-PCA approach

PLS Decomposition

This regression is a recent technique that somehow generalizes features from PCA, by projecting a set of dependent variables from a set of independent variables, but preserving the asymmetry of the relationship between independent variables, represented by a (very) large set, and dependent variables, whereas PCA treats them symmetrically. Specifically, a multidimensional input TFR space X ₀, can be projected onto the basis vectors (planes), {λ _i : i = 1,…,m}, through the following transformation:

$$ {\mathbf{w}}_{i} = {\varvec{\uplambda}}_{i}^{T} {\mathbf{X}}_{0} ,\quad i = 1, \ldots ,m $$

(11)

The set of weights ${\varvec{\Upphi}} = \{ {\mathbf{w}}_{i} \}$ describes the contribution of each basis plane to the input TFR, and Eq. (11) is used as a feature vector for recognition tasks. The vector λ _i  = diag{Σ} comprises the diagonal elements of the diagonal matrix Σ, resulting after singular value decomposition of X ₀ (i.e., X ₀ = UΣV, being U ^T U = V ^T V = I the matrices of the left and right singular vectors). The PCA orthogonal decomposition of Eq. (11) remains the same for PLS, but choosing in a different way the latent vectors where additional conditions are required. So, the new basis vectors are recalculated after simultaneous decomposition: X ₀ = TP ^T + ɛ _X , with T ^T T = I, and Y = TQ ^T + ɛ _Y , being the matrices ɛ _X and ɛ _Y the error terms, assumed to be i.i.d. normal. P and Q are the weight matrices used to reveal the influence of the individual variables X ₀ and Y, respectively.

Experimental Setup

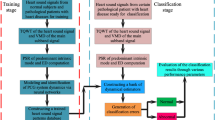
Figure 2 shows the proposed methodology for heart murmur detection appraising the next stages: (a) pre-processing; (b) estimation of the parameters of the TVAR model; (c) computing the TFRs from the TVAR parameters; (d) feature extraction and dimensionality reduction of the t–f planes; and (e) training and validation.

FIGURE 2

Experimental outline of murmur detection, and the methods subject to investigation

Database Acquisition and Pre-Processing

The database used in this study is made up of 45 adult subjects, who gave their informed consent approved by an ethical committee, and underwent a medical examination. A diagnosis was carried out for each patient and the severity of the valve lesion was evaluated by cardiologists according to clinical routine. A set of 26 patients were labeled as normal, while 19 were tagged as pathological with evidence of systolic and diastolic murmurs caused by valve disorders. Furthermore, eight phonocardiographic recordings corresponding to the four traditional focuses of auscultation (mitral, tricuspid, aortic, and pulmonary areas) were taken per patient in the phase of postexpiratory and postinspiratory apnea. Every recording lasted 12 s approximately, and was obtained from the patient standing in dorsal decubitus position. Next, after visual and audio inspection by cardiologists, some of the eight signals were removed because of artifacts and undesired noise; moreover, it was taken into consideration that most of the time murmurs do not necessary show up for all focuses at once, unless they are very intense (which is evidence of their harmfulness). An electronic stethoscope (WelchAllyn^® Meditron model) was used to acquire the PCG simultaneously with a standard 3-lead ECG (since the QRS complex is clearly determined, DII derivation is synchronized as a time reference). Both signals were sampled with 44.1 kHz rate and amplitude resolution of 16 bits. Tailored software was developed for recording, monitoring, and editing the HS and ECG signals.

Preprocessing was carried out as in Quiceno-Manrique et al.,18 and consists on downsampling at 4000 Hz, amplitude normalization and inter-beat segmentation. Finally, the database holds 548 HS beats in total: 274 with murmurs (73 of diastolic class and 201 systolic), and 274 that were labeled as normal. The selection of the 548 beats used for training and validation was carried out by expert cardiologists, who choose the most representative beats of normal and pathologic patients (with murmurs). Table 1 summarizes the records stored in the database.

Table 1 Recordings stored in the database

Although the database discriminates among normal, systolic, and diastolic murmurs, the objective in this study consists on the detection of heart murmurs for screening purposes.

Methods to Adjust the Parameters of the TFR Enhancement Techniques

Estimation of the TVAR Model Order

As stated before, an improved TFR estimation of non-stationary signals can be achieved by a locally stationary TVAR model (LS-TVAR), defined by the model order p. The literature reports that a large order of the linear predictor (e.g., 28) is necessary to model the PCG signal over its full frequency range.16 Nevertheless, the use of parametric TVAR modeling allows representing the process with a lower quantity of components.17 But, as explained in Poulimenos A, Fassois,17 a more accurate selection of the model order can be achieved based on the minimization of a fitness function. Specifically, the fitness function is estimated for each HS (i.e., heart beat) by means of the BIC. As suggested in Poulimenos A, Fassois,17 the approach consists on evaluating BIC for every family of parameters, e[t] and σ _e [t], obtained for a given order of the model p:

$$ {\text{BIC}}(p) = - \sum\limits_{t = 1}^{N} {\left( {\ln \sigma_{e}^{2} [t] + {\frac{{e^{2} [t]}}{{\sigma_{e}^{2} [t]}}}} \right)} $$

(12)

where N is the number of signal samples. The BIC curves were computed for different cut-off frequencies (raw signal, 500 and 1000 Hz), and ranging the model order from 1 to 15 (Fig. 3a). Likewise, the respective histograms are depicted in Fig. 3b for all the records in the database. The optimum model order is the one that minimizes the mean BIC function (i.e., the elbow of the curve). The figure shows that the lower the cut-off frequency signal the smaller the order selected for the model. Initially, the model order selected is p = 6, in line with the order reported in Güler et al. 12 and Kanai et al. 14 for time-varying AR modeling of HS.

FIGURE 3

Estimation of model order for parametric TVAR model; (a) mean BIC curves; (b) histogram of minimum BIC values

Later, in the “Results” section, a finer empirical adjustment is presented ranging p from 1 to 15 and trying to maximize the classifier accuracy.

Estimation of the Parameters of the TVAR Model

The parameters of the autoregressive model with smoothness priors were estimated by means of the aforementioned LS-TVAR approach (Eq. 3). Under the assumption that the AR parameters do not change quickly, the PCG recordings were divided initially into windows of short duration (100 samples). The coefficients of the LS-TVAR model were found using the Burg Algorithm.

Once the parameters of the TVAR model were estimated, the TFRs were computed by means of Eq. (2). Figure 4 illustrates an enhanced TFR for normal and pathologic HS, estimated using non-parametric methods (WVD and CWT which were estimated as explained in Quiceno-Manrique et al. 18), and the LS-TVAR parametric method used in this study. The TFRs shown in Fig. 4 are the matrices of dimension T × F, where F is the number of spectral components of the PCG signal, f = [0, 400] Hz; and T is the number of discrete-time samples of each recording. This arrangement is intended to cover the full-time range and a broad range of frequencies.

FIGURE 4

Examples of enhanced TFR for the methods of estimation considered: WVD, CWT, and LS-TVAR. (a) Normal recording; (b) PCG signal with systolic murmur

Methods to Adjust the Feature Extraction Algorithms

The next three sections describe the criteria and methods followed to adjust the aforementioned feature extraction and dimensionality reduction algorithms: (a) First of all, it is described the procedure to remove the area of the spectral surface that does not contain relevant information; (b) Secondly, and regarding the feature extraction for the tiled-based approach, it is defined empirically the size and distribution of the t–f bins that divide the TFR; (c) Third, the methods to adjust empirically the size of the projected space with the linear decomposition methods (e.g., PCA, 2D-PCA, PLS) are described. The criterion used to adjust the feature extraction algorithms was the maximization of the classifier performance. A simple k-nn classifier was used in order to assess the goodness of the feature extraction methods.

Estimation of the Relevant Area of the TFRs

A straightforward observation of the TFR in Fig. 5 suggests that there are large areas of the spectral surface that do not contain relevant information for the detection of murmurs. Thus, the irregular concentration of information suggests cropping nil content areas that lie adjacent to the border of the t–f plane. Thus, a coarse estimation of the relevant area can be accomplished computing the complement set of any measure of informativity, given in Eq. (5):

$$ \arg \left\{ {\max \dim \left\{ {{\text{var}}\left( {{\mathbf{S}}_{x}^{(0)} } \right) \cup {\text{var}}\left( {{\mathbf{S}}_{x}^{(1)} } \right)} \right\}} \right\} \ge \delta $$

(13)

where ${\text{var}}({\mathbf{S}}_{x}^{(k)} ),\;k \in \{ 0,1\}$ stands for the variance matrix of both TFR classes: normal and pathologic, respectively. The threshold, δ _min, is assumed to be the minimum value of the relevant variability. Figure 5 depicts different complement sets of variances depending on the value δ; the lower the threshold, the wider the relevant area.

FIGURE 5

Computing the relevant area of the TFR. The different contours appraise the changes of the threshold δ

The relevant area was empirically calculated evaluating the average variability of the classifier performance within the interval δ = [0.01, 0.08]. In this article, the relevant surface of the TFR was allocated within the framework described by the time interval 0 ≤ t ≤ 0.8 s and the frequency band 0 ≤ f ≤ 400 Hz.

Tuning of the Tile-Based Dimensionality Reduction

On the other hand, the tiled-based approach described in the “Tiled-TFR approaches” section was carried out extracting several features from the TFR that estimates the normalized energy on each specific t–f framework. These features were used only for partitioning the TFR, but were not used for the posterior classification. For this purpose, two partition schemes were tested in the time and frequency domains: (a) First, dividing the time and frequency axes into equally spaced intervals, as suggested in Tzallas et al. 22; (b) Second, performing a Quadtree partition scheme upon the TFR surface based on the pixel variance estimates, thus making smaller those t–f tiles with more information.

The Quadtree algorithm for computing the t–f framework (shown in Fig. 6a) is summarized next.

FIGURE 6

Computation of the Quadtree algorithm. (a) partition of the TFR information matrix; (b) number of partitions vs. framework variability

• 1. Using all the signals in the dataset used for training the system, compute the pixel variance matrix of every TFR surface, S ^(i,j)₀  = var{S _x (Δt _i , Δf _j )}, which is defined as the root of the tree decomposition.

• 2. Define an information threshold ς_min and a maximum number of quad decomposition iterations N _d . Otherwise, it leads to intractable computational load.

• 3. Divide S ^(i,j)₀ into four equally sized submatrixes ${\mathbf{S}}_{{_{1} }}^{(i, \, j)} = {\text{var}}\{ {\mathbf{S}}_{0} (\Delta t_{i} , \, \Delta f_{j} )\}$ partitioning time and frequency axes in equal segments.

• 4. Compute the pixel variance in each submatrix S ^(i,j)₁ . If ${\text{var}}\{ {\mathbf{S}}_{{_{1} }}^{(i, \, j)} \} > \varsigma_{\min } ,\forall i,j,$ then repeat steps 3 and 4 for further splitting of quad submatrixes, but not exceeding the number of iterations N _d . Otherwise, the values of Δt _i and Δf _j are retrieved.

The tuning of the tile size for each one of the configurations considered was carried out by estimating the average variability of the classifier performance while changing the information threshold ς_min, which ranges within the interval ς_min = [0.01, 0.1]. Specifically, Fig. 6b shows the outcomes with respect to the tile size, evidencing that a low value of ς_min improves the accuracy of the classifier but increases the computational load.

Tuning of the Linear Decomposition Methods

The normalized matrix assessing the relevant area of the TFR is the basis for the following feature extraction. An obvious question is how to find the number of latent variables needed to obtain the best generalization for the prediction of new observations. The amount of relevant latent components, n, was chosen as follows: for PCA, this value is based on the number of breaks in the plot of the singular values, whereas for PLS, the same value is achieved by cross-validation techniques.

The n latent variables are often interpreted by plotting them in a TFR plane (as shown in Fig. 7 with n = 4), for systolic and diastolic murmurs, and for both decompositions considered: PCA and PLS. For PCA, considering just the first principal component it can be noticed the strong influence of the S1 event; the S2 event showed less variability. A more detailed scrutiny of the PCA-based average reconstruction corroborates that most of the information is concentrated around the S1 and S2 events, which may be explained not only because of the instantaneous power of the PCG recordings, but also due to the irregularity of the cardiac rhythm (specially, for pathological cases). This fact becomes evident looking at the way that the intensity of S2 diminishes as n increases. At the same time, it can be noted that the influence of systole and diastole (i.e., wherever the heart murmurs are present) occurs in a different way. The presence of systolic murmurs (see Fig. 7a) becomes more evident as the number of components increase, starting from weak values. In the case of diastolic murmurs, their presence can be clustered into two types: (a) Murmurs with weak but spread power concentrated in the lowest spectral band (e.g., mitral stenosis, aortic insufficiency, pulmonary regurgitation; noted in Fig. 7b as type 1); (b) Those with a remarkable spectral variance, and allocated in the upper part of the spectrum (e.g., aortic valve regurgitation; noted in Fig. 7c as type 2). It can be noticed that their influence vanishes as the number of components increases. A different situation is observed for the PLS decomposition: if n = 1, there is a great influence of S1 and S2 events, but at the same time the presence of systolic and diastolic murmurs become quite evident.

FIGURE 7

First four principal vectors obtained after PCA and PLS linear decompositions multiplied by TFRs corresponding to different types of murmurs: (a) systolic murmur; (b) diastolic murmur (type 1); (c) diastolic murmur (type 2)

Results

In order to illustrate the problem addressed, and its difficultness, Fig. 8 shows several PCG waveforms belonging to normal and pathological states along with their respective TFR estimated by means of the LS-TVAR algorithm. Figure 8 shows that there are some normal signals whose waveform looks like pathological: waveforms x ₁ and x ₅ in Fig. 8a are very similar to murmurs, whereas x ₁, x ₃, and x ₅ in Fig. 8b, at first sight, resemble normal signals.

FIGURE 8

Examples of enhanced TFR for several PCG recordings. (a) normal; (b) heart murmurs

For the sake of comparison, the feature extraction algorithms proposed were also applied to two non-parametric TFR estimations: CWT and WVD.

As commented before, the criterion used to adjust the aforementioned procedures was the maximization of the average accuracy for the detection of murmurs, given by the following definition:

$$ {\text{Accuracy }}(\% ) = {\frac{{N_{\text{C}} }}{{N_{\text{T}} }}} \times 100 $$

(14)

where N _C is the number of correctly classified patterns, and N _T is the total number of feeding patterns to the classifier. Moreover, the sensitivity and specificity measures are defined to assess the performance of the detector:

$$ {\text{Sensitivity }}(\% ) = {\frac{{N_{\text{TP}} }}{{N_{\text{TP}} + N_{\text{FN}} }}} \times 100;\quad {\text{Specificity }}(\% ) = {\frac{{N_{\text{TN}} }}{{N_{\text{TN}} + N_{\text{FP}} }}} \times 100 $$

(15)

where N _TP is the number of true positives (murmurs accurately classified as murmur), N _FN is the number of false negatives (murmurs classified as normal signals), N _TN is the number of true negatives (normal signals accurately classified as normal signals), and N _FP is the number of false positives (normal signals classified as murmurs). The accuracy was evaluated with a simple k-nn classifier using a cross-validation strategy. The cross-validation was carried out generating 11 independent sets (i.e., folds) from the database with records randomly selected. Each fold contains the same number of records from both classes (i.e., normal and pathological). Ten sets were used for training while the remaining one was used for validation. The performance was calculated averaging the results for each fold. Moreover, the standard deviation was calculated.

After filtering and length normalization of the heart beat sounds the classification was carried out in accordance to the following training stages:

• Tuning of the k-nn classifier: By stepwise increasing of neighbor number, the optimal value of k is determined for the best classifier accuracy. Figure 9 illustrates the outcomes for each one of feature sets used. The figure shows that the classifier performance decreases as the number of neighbors increases. Therefore, and in order to ensure the computational stability, a value of k = 3 was selected.

  FIGURE 9

  

  Number of neighbors vs. accuracy for the different feature extraction approaches used

• Tuning of the linear decomposition methods to reduce the dimensionality. For PCA, the information threshold and the number of components (base vectors) were the first parameters to adjust. Once again, a stepwise calculation of these parameters allowed selecting the optimum values. Figure 10a depicts the estimation of the parameter δ_min (see Eq. 13) using PCA, evidencing a large fluctuation of the estimates. For the PLS classifier the performance was better and more stable. Nevertheless, the value of the threshold was chosen to be δ_min = 0.07. Figure 10b illustrates the classifier accuracy vs. the number of relevant components selected for the different schemes tested. The performance shows an asymptotic behavior starting from 8 to 10 components for both PCA and PLS techniques. However, the PLS components achieved a better performance faster than for the PCA technique. In addition, the tuning of the 2D-PCA approach was assessed by computing the accuracy for a different number of components (see Fig. 10c), which was evaluated separately for rows and columns. In the first approach, a high performance can be achieved for a low number of components (n = 6–8), while for the column-based approach a steady value of performance was reached just around (n = 10–14). During the dimensionality reduction stage, the performance was recomputed to tune the parameters of the model. Figure 10d shows that PLS and 2D-PCA provided better accuracies.

  FIGURE 10

  

  Performance of the linear decomposition approaches tested; (a) performance vs. variance threshold for PCA and PLS; (b) performance vs. number of components of PCA and PLS; (c) performance vs. number of rows and columns for the 2D-PCA approach; (d) performance of the classifier for PCA, PLS and 2D-PCA after tuning

• Tuning the tiled-based feature extraction methods. For a regular tiling partition, the parameter to be adjusted is the number of sub-bands (Fig. 11a); in this case, the classifier performance remains even, but the computational load increases. Regarding the Quadtree technique, the parameter to be adjusted is the threshold ς_min (Fig. 11b).

  FIGURE 11

  

  Tuning of the dimensionality reduction techniques; (a) number of time segments for the regular tiling; (b) information threshold for the Quadtree partition algorithm

• Adjusting the parameters of the TVAR model: As shown in Fig. 12, there is a slight improvement in the accuracy as the order of the LS-TVAR model increases, but above p = 6–8 the performance reached a steady value. The evaluation of the accuracy with respect to the window length is shown in Fig. 13. A value of M = 100 can be assumed as steady. Moreover, Fig. 14 shows that the classification accuracy achieves the best performance when α = 1, where the mean value and variance reached the best values.

  FIGURE 12

  

  Order of the LS-TVAR model with respect to the accuracy for the different feature extraction methods used

  FIGURE 13

  

  Sensibility to the window length of the LS-TVAR model to the classification accuracy

  FIGURE 14

  

  Sensibility of the classification accuracy to the aperture of the window used to estimate σ _e [t]

In summary, the number of neighbors of the k-nn classifier was set to 3, and the parameters of the TVAR model were fixed to:

• The order of the TVAR model was fixed to 6.

• The window length of the LS-TVAR model was fixed to M = 100.

• The value of the window aperture used to calculate the variance estimator was fixed to α = 1.

Once the dimensionality reduction was accomplished, the assemble of features used to train the system is summarized in Table 2.

Table 2 Summary of the features extracted for each scheme proposed

These sets of features were used to train different k-nn classifiers with three neighbors. Table 3 summarizes the classifier performance for the different approaches tested. The accuracies were calculated averaging for each fold of the cross-validation strategy. The proposed methodology evidences a high accuracy (ranging from 97 to 99%), but with no remarkable differences among all the configurations considered. This fact is also supported in view of the estimates for sensitivity, and specificity.

Table 3 Summary of the classification performance using the proposed methodology

The results evidence the effectiveness, stability, and dimensionality reduction capabilities of the proposed dimensionality reduction approach based on PLS applied to LS-TVAR TFR. In order to evaluate the robustness of this methodology against noise, it was tested under different conditions, adding artificial white Gaussian noise with signal-to-noise ratios (SNR) ranging from 0 to 30 dBs, with steps of 5 dBs. The results are shown in Fig. 15, where SNR = Inf, represents clean signals. The figure evidences a good stability of this methodology with respect to the presence of an additive white Gaussian noise: in the worst case, with SNR = 0 dB, the accuracy decreased only five absolute points.

FIGURE 15

Accuracy of the PLS dimensionality reduction approach for different values of SNR

Finally, Table 4 shows a comparison of the results achieved with the proposed methodology and other results reported in literature. The accuracy obtained with the methods described in Wang et al. 23 was obtained with the same database used in this study. The results obtained using the methods in Delgado-Trejos et al. 8 and Quiceno-Manrique et al. 18 were carried out using a subset of the database used in this study that did not contain diastolic murmurs.

Table 4 Comparison with other works in the literature

Discussion

The classification accuracy remains stable as the order of the TVAR model changes. This means that the model order can take values lower than those suggested in the literature. This fact lead us to think that most PCG signals from the database are mono-component, which are successfully represented with a TVAR(2) model. Anyway, increasing the order complements the information given by the first two parameters modeling the noise components present in the PCG signal.

Regarding the linear decomposition, an eigenplane-based PCA technique (as simplest implementation) and a PLS technique (as more sophisticated) were considered. Likewise, the regular partition and a refined Quadtree partition were examined for the tiled-TFR approach. As shown in Table 3, the accuracy of the regular tiling outperforms the rest of techniques. However, this brute-strength approach has a higher computational load, exceeding that of the methods based on linear decomposition. Concerning to the improved object representation with PCA, 2D-PCA shows a light improvement, and reached a similar accuracy than for PLS, but with a significant reduction of the computational load. The PLS technique also evidenced a good behavior against additive white Gaussian noise.

Regarding the tuning of the feature extraction procedures it must be quoted that the computational stability of the tiled TFR-based techniques is mostly guaranteed for actual matrix sizes of HS. But for linear decomposition-based techniques, it is strongly convenient to choose a confined area of relevance on the t–f plane to achieve a stable dimension reduction, and anyhow diminishing resolution of the TFR.

For the sake of comparison, the feature extraction methodology discussed in this article was also extended to two non-parametric TFRs: WVD and CWT. A slight degradation is observed using CWT, whereas WVD shows an equivalent performance to the proposed TVAR estimation techniques (Table 3). Furthermore, in terms of computational load and tuning of working parameters can be stated that parametric and non-parametric TFR are alike to enhance the resolution of non-stationary PCG signals.

Conclusions

In this article, the ability of an enhanced TFR and two approaches for dimensionality reduction are explored for the detection of murmurs. The enhancement of the TFR resolution is carried out by means of a parametric TVAR model-based estimation technique, allowing an improvement of the representation capabilities of the HS, and hence to a better detection of murmurs. The parametric TFR are more suitable for capturing the time-varying dynamics of the PCG signals than the common non-parametric approaches, because the resolution and distortion issues are worked out. Nonetheless, the emergent problems of this parametric approach (i.e., the selection of the model order and the estimation of the parameters) are effectively solved using locally stationary assumptions.

For the PCG signals, since the enhanced TFR tends to hold a lot of redundant data, a considerable dimensionality reduction was required. Specifically, two methods of feature extraction were analyzed: linear decomposition and tiling partition of t–f plane. The results indicate that a similar accuracy can be accomplished with both methodologies. The main difference lies on the effectiveness of the dimensionality reduction and the interpretability of the components obtained using the linear decomposition methods.

Because of the simplicity of implementation and worthy improvement of the representation capabilities determining the details of the pathological changes to identify, the suggested TFR-based feature extraction methodology appears to be very effective providing a high accuracy for the detection of murmurs. Therefore, in future studies, this framework could be applied to the recognition among different kinds of murmurs, and to the detection of pathologies for different types of non-stationary biomedical signals.

In contrast, a serious drawback of the proposed methodology is that these TFR-based feature extraction techniques require fixed length recordings (i.e., duration), so the HS must be chopped to a predetermined duration. This fact could limit the possibility to extrapolate the results to other databases, leading us to be cautious, although optimistic with the results obtained. A possibility to overcome this problem was suggested in Quiceno-Manrique et al.,18 where dynamic time warping techniques were used to normalize the duration of each HS.