Introduction

Blood flow through small vessels behaves as a non-Newtonian fluid. The apparent blood viscosity depends on the vessel diameter, which is known as the Fahraeus–Lindqvist effect. Since Fahraeus and Lindqvist11 first observed the significant decrease of apparent blood viscosity as the vessel diameter decreases, many investigators confirmed this effect through vitro experiments.5,20,41 Since the invention of the microscope it was suspected that red blood cells (RBCs) in small blood vessels migrate away from the wall. The formation of a cell-free layer near the wall reduces the apparent blood viscosity and hence the pressure-drop through the narrow blood vessels.8,18 This multiphase fluid nature of blood is the physical reason behind the Fahraeus–Lindqvist effect. Pries et al.36 have presented an empirical correlation for blood viscosity in terms of tube diameter and hematocrit. An objective of this study is to present a theory for the Fahraeus–Lindqvist effect.

Migration of neutrally buoyant particles in liquids from the wall toward the center has also been observed for a long time. It is known as the shear induced diffusion, as explained by Phillips et al.35 and others, by postulating a driving force due to a gradient of shear. The migration of RBCs away from the wall of the vessels may also arise due to the deformation of RBCs.1,17,19 There still exists no comprehensive theory for this effect. Sharan and Popel39 used a two-phase model for the blood flow in narrow tubes to investigate the Fahraeus–Lindqvist effect. They considered a central core of suspended erythrocytes surrounded by a cell-free layer.

The kinetic theory of granular flow invented by Savage37 and others, as reviewed by Gidaspow,12 explains the particle migration. The wall-shear-produced random oscillations of particles cause their random kinetic energy per unit mass, called granular temperature, to rise near the wall. This granular temperature is the driving force for migration, like thermal diffusion in gases.23 In flow of heavy particles in liquids, however, the particles migrate toward the wall and create a core-annular flow in vertical pipes, like the particles suspended in gases.28 Bishop et al.4 measured the granular temperature as the standard deviation of velocity to explore its effect on RBCs aggregation and shear rate.

The successful use of kinetic theory based multiphase model in the blood flow through narrow vessels will provide a basis for the medical applications, such as atherosclerosis. Shear-dependent mass transfer plays an important role in atherosclerosis.10,34 Computational fluid dynamic (CFD) models for blood flow have generally considered blood to be a single phase fluid with a viscosity of about three centipoises.16,21,22,33,42 Only in the last few years has blood flow been modeled using a two-phase flow hydrodynamic model with a shear dependent viscosity as an input.26,27 In the present study the blood viscosity is not an empirical input into the model. It is computed from the theoretical expressions obtained from the kinetic theory of granular flow. The theory used here for one particle size (RBCs) has been extended to multi-size mixtures.30,31 Benyahia2 has written a computer code for mixtures of particles. Huang has shown how to compute the transport of low density lipoprotein (LDL), high density lipoprotein (HDL), and platelets in blood flow using this theory in her 2009 PhD thesis.

The new model matches the experimental data for red blood cell concentrations in narrow tubes by Taylor44 and computes the observed blood viscosity. A CFD solution and a simplified model for Poiseuille flow both produce the Fahraeus–Lindqvist effect in agreement with experiments.

Methods

Geometry

The geometry for the 2-D model of RBCs suspension flowing in a narrow tube was constructed according to the experimental setup by Taylor.44 Table 1 gives the relevant dimensions. The diameter of the tube was 0.19 mm. The total length of the tube was 14.4 cm. The RBCs flowed through the straight narrow tube with plasma. A mesh was generated using GAMBIT software (from FLUENT Inc.) for our multiphase 2-D simulation. The total number of cells generated was 10,000. The convergence criteria was set to be 10−5 for mass and momentum balances.

Table 1 Simulation conditions and system properties
Full size table

Multiphase Navier–Stokes Equations

The two-phase model consists of the continuous plasma phase and the dispersed red blood cell phase which is treated as a continuum. The basic balances are the conservation of mass and momentum for each phase. The surface stresses are assumed to be a function of the symmetrical gradient of velocity for each phase, giving rise to two Navier–Stokes equations, coupled through the drag. This two-phase model gives rise to a new dependent variable, the volume fraction of the red blood cells, not found in single phase Navier–Stokes equations. This model was used by Jung et al.26,27 to compute flow in a right coronary artery and in other geometries. In their studies the viscosity was an input into the model. In the kinetic theory model presented here the red blood cell viscosity is computed using an equation for the random kinetic energy of the red blood cells, called granular temperature. The basic derivations based on the kinetic theory of granular flow are given in the texts by Gidaspow12 and Jackson24 and earlier in a review paper by Savage.37 The basic two-phase flow equations have been programmed into FLUENT, a commercial CFD code. Gidaspow et al.15 reviewed the fluidization literature using kinetic theory of granular flow. The experiments have shown that the particulate viscosity expression obtained from the kinetic theory gives the same values as that measured by classical methods. The CFD simulations by several groups throughout the world have shown the success of predicting transient and time averaged behavior of gas–solid flow.

The basic mass and momentum balances for the plasma and the red blood cells are as follows (f = plasma, s = RBCs).

Fluid mass balance:

$$ {\frac{{\partial \left( {\rho_{\text{f}} \varepsilon_{\text{f}} } \right)}}{\partial t}} + \nabla \cdot \left( {\rho_{\text{f}} \varepsilon_{\text{f}} \vec{\upsilon }_{\text{f}} } \right) = 0 $$
(1)

Solid mass balance:

$$ {\frac{{\partial \left( {\rho_{\text{s}} \varepsilon_{\text{s}} } \right)}}{\partial t}} + \nabla \cdot \left( {\rho_{\text{s}} \varepsilon_{\text{s}} \vec{\upsilon }_{\text{s}} } \right) = 0 $$
(2)

where ρ is density, ε is volume fraction, t is time, \( \vec{\upsilon } \) is velocity vector with the subscript indicating the phase.

The mass balances differ from those in transport phenomena texts3 by the presence of the volume fractions of solids and fluid. The volume fraction variation may introduce cohesion-like hydrodynamic forces which give rise to the phenomena, such as clustering. Such clustering phenomena have been computed using the equations given in this study.45

Fluid momentum balance:

$$ {\frac{{\partial \left( {\rho_{\text{f}} \varepsilon_{\text{f}} \vec{\upsilon }_{\text{f}} } \right)}}{\partial t}} + \nabla \cdot \left( {\rho_{\text{f}} \varepsilon_{\text{f}} \vec{\upsilon }_{\text{f}} \vec{\upsilon }_{\text{f}} } \right) = \varepsilon_{\text{f}} \rho_{\text{f}} \vec{g} - \varepsilon_{\text{f}} \nabla P + \nabla \cdot \vec{\vec{\tau }}_{\text{f}} + \beta \left( {\vec{\upsilon }_{\text{s}} - \vec{\upsilon }_{\text{f}} } \right) $$
(3)

Solid momentum balance:

$$ {\frac{{\partial \left( {\rho_{\text{s}} \varepsilon_{\text{s}} \vec{\upsilon }_{\text{s}} } \right)}}{\partial t}} + \nabla \cdot \left( {\rho_{\text{s}} \varepsilon_{\text{s}} \vec{\upsilon }_{\text{s}} \vec{\upsilon }_{\text{s}} } \right) = \varepsilon_{\text{s}} \rho_{\text{s}} \vec{g} - \varepsilon_{\text{s}} \nabla P - \nabla P_{\text{s}} + \nabla \cdot \vec{\vec{\tau }}_{\text{s}} + \beta \left( {\vec{\upsilon }_{\text{f}} - \vec{\upsilon }_{\text{s}} } \right) $$
(4)

where P is fluid pressure, P s is granular pressure, \( \vec{g} \) is gravity acceleration, \( \vec{\vec{\tau }} \) is stress tensor, and β is the interface momentum exchange coefficient. The momentum balances are those found in the commercial code FLUENT. These normally ill-posed equations are stabilized by means of the gradient of solids pressure and viscosity, as discussed by Gidaspow.12

The volume fractions for each phase are summed to be one:

$$ \varepsilon_{\text{f}} + \varepsilon_{\text{s}} = 1 $$
(5)

The random kinetic energy equation for RBCs is expressed as:

$$ \begin{gathered} {\frac{3}{2}}\left[ {{\frac{{\partial \left( {\rho_{\text{s}} \varepsilon_{\text{s}} \theta } \right)}}{\partial t}} + \nabla \cdot \left( {\rho_{\text{s}} \varepsilon_{\text{s}} \theta \vec{\upsilon }_{\text{s}} } \right)} \right] = \left( { - P_{\text{s}} \vec{\vec{\rm I}} + \vec{\vec{\tau }}_{\text{s}} } \right){:}\nabla \vec{\upsilon }_{\text{s}} + \nabla \cdot \left( {k_{\text{s}} \nabla \theta } \right) - \gamma \hfill \\ {\text{Accmulation}} + {\text{Net outflow}} = {\text{Production}} + {\text{Conduction}} - {\text{Dissipation}} \hfill \\ \end{gathered} $$
(6)

where θ is granular temperature which is defined as the mean of the squares of particle velocity fluctuation, k s is granular conductivity, and γ is the collisional energy dissipation. The granular temperature is a measure of the random particle kinetic energy per unit mass. It is produced due to “viscous type dissipation” and consumed due to inelastic collisions.

Several constitutive equations are required to close the set of Eqs. (1)–(5).

The stress tensor for each phase is given by a Newtonian type viscous approximation, as:

$$ \vec{\vec{\tau }}_{\text{f}} = \varepsilon_{\text{f}} \mu_{\text{f}} \left( {\nabla \vec{\upsilon }_{\text{f}} + \nabla \vec{\upsilon }_{\text{f}}^{\text{T}} } \right) - {\frac{2}{3}}\varepsilon_{\text{f}} \mu_{\text{f}} \nabla \cdot \vec{\upsilon }_{\text{f}} \vec{\vec{\rm I}} $$
(7)
$$ \vec{\vec{\tau }}_{\text{s}} = \mu_{\text{s}} \left( {\nabla \vec{\upsilon }_{\text{s}} + \nabla \vec{\upsilon }_{\text{s}}^{\text{T}} } \right) + \left( {\xi_{\text{s}} - {\frac{2}{3}}\mu_{\text{s}} } \right)\nabla \cdot \vec{\upsilon }_{\text{s}} \vec{\vec{\rm I}} $$
(8)

RBC pressure, P s, shear viscosity, μ s, and bulk viscosity, ξ s, are expressed as a function of granular temperature based on the kinetic theory model12

$$ P_{\text{s}} = \varepsilon_{\text{s}} \rho_{\text{s}} \theta + 2\rho_{\text{s}} \left( {1 + e} \right)\varepsilon_{\text{s}}^{2} g_{0} \theta $$
(9)
$$ \mu_{\text{s}} = {\frac{4}{5}}\varepsilon_{\text{s}}^{2} \rho_{\text{s}} d_{\text{p}} g_{0} \left( {1 + e} \right)\left( {{\frac{\theta }{\pi }}} \right)^{1/2} + {\frac{{10\rho_{\text{s}} d_{\text{p}} \varepsilon_{\text{s}} \sqrt {\theta \pi } }}{{96\left( {1 + e} \right)g_{0} }}}\left[ {1 + {\frac{4}{5}}g_{0} \varepsilon_{\text{s}} \left( {1 + e} \right)} \right]^{2} $$
(10)
$$ \xi_{\text{s}} = {\frac{4}{3}}\varepsilon_{\text{s}}^{2} \rho_{\text{s}} d_{\text{p}} g_{0} \left( {1 + e} \right)\left( {{\frac{\theta }{\pi }}} \right)^{1/2} $$
(11)

where d p is the diameter of RBC, g 0 is the radial distribution function, and e is the restitution coefficient, which is a measure of the elasticity of the particle collisions. It is defined as the ratio of rebound velocity of particle to its velocity before impact. The radial distribution function expressing the statistics of the spatial arrangement of the particles is given by a geometric approximation, the Bagnold’s equation, as

$$ g_{0} = \left[ {1 - \left( {{\frac{{\varepsilon_{\text{s}} }}{{\varepsilon_{{{\text{s}},\max }} }}}} \right)^{1/3} } \right]^{ - 1} $$
(12)

The granular conductivity, k s, consists of the kinetic part from dilute kinetic theory of gases7 and the collisional part due to inelastic collision of particles, as reviewed by Gidaspow.12

$$ k_{\text{s}} = {\frac{{150\rho_{\text{s}} d_{\text{p}} \varepsilon_{\text{s}} \sqrt {\theta \pi } }}{{384\left( {1 + e} \right)g_{0} }}}\left[ {1 + {\frac{6}{5}}\varepsilon_{\text{s}} g_{0} \left( {1 + e} \right)} \right]^{2} + 2\rho_{\text{s}} \varepsilon_{\text{s}}^{2} d_{\text{p}} \left( {1 + e} \right)g_{0} \sqrt {{\frac{\theta }{\pi }}} $$
(13)

The energy dissipation due to inelastic collision of particles, first evaluated by Savage and his colleagues, is given by

$$ \gamma = {\frac{{12\left( {1 - e^{2} } \right)g_{0} }}{{d_{\text{p}} \sqrt \pi }}}\rho_{\text{s}} \varepsilon_{\text{s}}^{2} \theta^{3/2} $$
(14)

In our analysis, it is assumed that the interaction force between plasma and RBCs is only due to drag. The interphase momentum exchange coefficient is given by the Wen and Yu46 model for the dilute flow and by the Ergun equation for dense flow, as reviewed by Gidaspow.12

$$ \beta = 150{\frac{{\varepsilon_{\text{s}} \left( {1 - \varepsilon_{\text{f}} } \right)\mu_{\text{f}} }}{{\varepsilon_{\text{f}} d_{\text{p}}^{2} }}} + 1.75{\frac{{\rho_{\text{f}} \varepsilon_{\text{s}} \left| {\vec{\upsilon }_{\text{s}} - \vec{\upsilon }_{\text{f}} } \right|}}{{d_{\text{p}} }}}\quad {\text{for}}\,\varepsilon_{\text{f}} \le 0.8 $$
(15)
$$ \beta = {\frac{3}{4}}C_{\text{D}} {\frac{{\varepsilon_{\text{s}} \varepsilon_{\text{f}} \rho_{\text{f}} \left| {\vec{\upsilon }_{\text{s}} - \vec{\upsilon }_{\text{f}} } \right|}}{{d_{\text{p}} }}}\varepsilon_{\text{f}}^{ - 2.65} \quad {\text{for}}\,\varepsilon_{\text{f}} > 0.8 $$
(16)

with the drag coefficient, C D, given by

$$ C_{\text{D}} = {\frac{24}{{\varepsilon_{\text{f}} Re_{\text{p}} }}}\left[ {1 + 0.15\left( {\varepsilon_{\text{f}} Re_{\text{p}} } \right)^{0.687} } \right] $$
(17)

where

$$ Re_{\text{p}} = {\frac{{\rho_{\text{l}} d_{\text{p}} \left| {\upsilon_{\text{s}} - \upsilon_{\text{f}} } \right|}}{{\mu_{\text{f}} }}} $$
(18)

Simulation Conditions

The simulation conditions are for the experiment in a narrow tube by Taylor.44 Table 1 gives the simulation conditions. RBCs were assumed to be rigid spherical particles. The effect of RBCs deformation associated with the kinetic energy dissipation is considered in the restitution coefficient, e, in the model in the FLUENT simulation. Initially, the whole tube was full of the mixture of plasma and RBCs with uniform RBC volume fractions of 24% and 57% and RBC granular temperature of 0.0001 m2 s−2. The axial velocities of plasma and RBCs were set to be 0.01 m s−1 and radial velocities of both phases were zero for our initial condition. Pressures were prescribed at inlet and outlet to simulate the pressure driven flow in the narrow tube.

No slip boundary conditions were used for plasma phase at the wall and Johnson and Jackson25 boundary condition was used for RBCs. The boundary condition for the RBCs velocity at the wall was derived by equating the limit of the shear stress in RBCs phase when approaching the wall to the transfer rate of momentum to the wall by RBCs when colliding with the wall.

$$ \upsilon_{\text{s,w}} = - {\frac{{6\mu_{\text{s}} \varepsilon_{{{\text{s}},\max }} }}{{\sqrt 3 \pi \phi \rho_{\text{s}} \varepsilon_{\text{s}} g_{0} \sqrt \theta }}}{\frac{{\partial \upsilon_{\text{s,w}} }}{\partial n}} $$
(19)

The boundary condition for the random kinetic energy flux at the wall was obtained by equating the flux of particles at the wall to its dissipation.40

$$ \theta_{\text{w}} = - {\frac{\kappa \theta }{{\gamma_{\text{w}} }}}{\frac{{\partial \theta_{\text{w}} }}{\partial n}} + {\frac{{\sqrt 3 \pi \phi \rho_{\text{s}} \varepsilon_{\text{s}} \upsilon_{\text{s,slip}}^{2} g_{0} \theta^{3/2} }}{{6\varepsilon_{{{\text{s}},\max }} \gamma_{\text{w}} }}} $$
(20)

where

$$ \gamma_{\text{w}} = {\frac{{\sqrt 3 \pi \left( {1 - e_{\text{w}}^{2} } \right)\varepsilon_{\text{s}} \rho_{\text{s}} g_{0} \theta^{3/2} }}{{4\varepsilon_{{{\text{s}},\max }} }}} $$
(21)

and υ s,slip is the slip velocity parallel to the wall, n is the normal component to the wall, υ s,w is the RBC velocity in the direction parallel to the wall, γ w is the energy dissipation due to inelastic collisions between particles and the wall, e w is the wall restitution coefficient, θ w is the granular temperature at the wall, and ϕ is the specularity coefficient.

Poiseuille Flow Approximation

Poiseuille flow has been traditionally used as a first approximation for blood flow. For the blood flow experiment of Taylor,44 it is a good approximation, since the flow is steady and the tube is long. Due to the large drag between the red blood cells and the plasma, the flow is nearly homogeneous. Since the maximum velocity is about 0.2 m s−1, homogeneous flow can be used as a first approximation.

The velocity is given by

$$ \upsilon_{{{\text{s}}z}} = \upsilon_{z,\max } \left[ {1 - \left( {{\frac{x}{R}}} \right)^{2} } \right] $$
(22)

The random kinetic energy equation for fully developed flow, Eq. (6) becomes as follows:

$$ \begin{gathered} {\frac{\partial q}{\partial x}} + \tau_{rz} {\frac{{\partial \upsilon_{{{\text{s}}z}} }}{\partial x}} + \gamma = 0 \hfill \\ {\text{Conduction}} + {\text{Production of Oscillations}} - {\text{Dissipation}} = 0\hfill \\ \end{gathered} $$
(23)

i.e.,

$$ \begin{gathered} \mu_{\text{s}} \left( {{\frac{{d\upsilon_{{{\text{s}}z}} }}{dx}}} \right)^{2} + {\frac{d}{dx}}\left( {\kappa_{\text{s}} {\frac{d\theta }{dx}}} \right) - {\frac{{12\rho_{\text{s}} g_{0} \left( {1 - e^{2} } \right)\varepsilon_{\text{s}}^{2} \theta^{3/2} }}{{d_{\text{p}} \sqrt \pi }}} = 0 \hfill \\ {\text{Production of Oscillations}} + {\text{Conduction}} - {\text{Dissipation}} = 0\hfill \\ \end{gathered} $$
(24)

where \( \kappa_{\text{s}} = \kappa_{s}^{\prime } \theta^{1/2} \)and

$$ \kappa_{s}^{\prime } = {\frac{{150\sqrt \pi \rho_{\text{s}} \varepsilon_{\text{s}} d_{\text{p}} }}{{384\left( {1 + e} \right)g_{0} }}}\left[ {1 + {\frac{6}{5}}\left( {1 + e} \right)g_{0} \varepsilon_{\text{s}} } \right]^{2} + {\frac{{2\varepsilon_{\text{s}}^{2} \rho_{\text{s}} d_{\text{p}} \left( {1 + e} \right)g_{0} }}{\sqrt \pi }} $$
(25)

For constant \( \kappa_{s}^{\prime } , \) Eq. (24) takes the form

$$ {\frac{{\mu_{\text{s}} }}{{\kappa_{\text{s}} }}}\left( {{\frac{{d\upsilon_{{{\text{s}}z}} }}{dx}}} \right)^{2} + {\frac{1}{2\theta }}\left( {{\frac{d\theta }{dx}}} \right)^{2} + {\frac{{d^{2} \theta }}{{dx^{2} }}} - {\frac{{12\rho_{\text{s}} g_{0} \left( {1 - e^{2} } \right)\varepsilon_{\text{s}}^{2} \theta }}{{\kappa_{\text{s}}^{\prime } d_{\text{p}} \sqrt \pi }}} = 0 $$
(26)

Using the parabolic axial RBCs velocity distribution of Eq. (22), Eq. (26) in dimensionless form becomes as follows

$$ {\frac{{d^{2} \theta^{\prime } }}{{dr^{2} }}} + {\frac{1}{{2\theta^{\prime } }}}\left( {{\frac{{d\theta^{\prime } }}{dr}}} \right)^{2} - a\theta^{\prime } = - r^{2} $$
(27)

where \( a = {\frac{{12\rho_{\text{s}} g_{0} \left( {1 - e^{2} } \right)\varepsilon_{\text{s}}^{2} R^{2} }}{{\kappa_{\text{s}}^{\prime } d_{\text{p}} \sqrt \pi }}},\,\theta^{\prime } = {\frac{\theta }{{4{\frac{{\mu_{\text{s}} }}{{\kappa_{\text{s}} }}}\upsilon_{{{\text{s}},\max }}^{2} }}},\,r = {\frac{x}{R}}. \)

The parameter “a” measures the dissipation due to inelastic collision with the restitution coefficient, e. Because of the deformability of RBCs in the blood flow, the restitution coefficient will change with the elasticity of RBCs themselves and the deformation degree of RBCs. Hence the effect of deformation of RBCs was included in the empirical restitution coefficient, e. The scale factor for granular temperature is the square of the maximum velocity times the ratio of the granular viscosity to conductivity for granular temperature. The radius of the tube is the natural scale factor for length.

The boundary condition of granular temperature at the wall is given as

$$ \theta_{\text{w}} = - B_{1} \left. {{\frac{\partial \theta }{\partial n}}} \right|_{\text{wall}} $$

where \( B_{1} = {\frac{{\kappa_{\text{s}} \theta }}{{\gamma_{\text{w}} }}}\;{\text{and}}\;\gamma_{\text{w}} = {\frac{{\sqrt 3 \pi \left( {1 - e_{\text{w}}^{2} } \right)\varepsilon_{\text{s}} \rho_{\text{s}} g_{0} \theta^{3/2} }}{{4\varepsilon_{{{\text{s}},\max }} }}} \) i.e.,

$$ \theta_{\text{w}}^{\prime } = - B_{1}^{\prime } \left. {{\frac{{\partial \theta^{\prime } }}{\partial r}}} \right|_{\text{wall}} $$
(28)

where \( B_{1}^{\prime } = {\frac{{B_{1} }}{R}}. \)

The dimensionless parameter \( B_{1}^{\prime } \) is an inverse measure of the dissipation at the wall. For elastic particles, \( B_{1}^{\prime } \) is infinite and the gradient of granular temperature is zero. For zero \( B_{1}^{\prime } \), the granular temperature at the wall is zero.

The ordinary differential Eq. (27) can be solved with the boundary condition listed in Eq. (28) using a boundary value solver, such as found in MATLAB.

In developed flow the solid pressure, P s, is not a function of radial position. Using the particle equation of state, Eq. (9), the RBC volume fraction for fully developed flow can be calculated.

Concentrations from Taylor’s Data

In Taylor’s44 experiments, the light intensity at a succession of points across the tube was read. It indicated the variation of holdup across the tube. In order to compare the simulation results with Taylor’s44 experimental data, light intensity readings were converted into concentration values. In the conversion, we assume the illumination is parallel and the refraction is neglected. The optical density is given by the Lambert–Beer formula:

$$ D = \int {2k{\frac{{\rho_{\text{s}} \varepsilon_{\text{s}} }}{{M_{\text{s}} }}}} dl $$
(29)

where D is the optical density, k is the extinction coefficient of the absorbing medium, l is the length of light passing through the tube, M s is the molecular weight of RBC, and ε s is the volume fraction of RBCs.

The data of Taylor44 were converted into concentrations by solving Eq. (29). The unknown parameter, \( {\frac{{k\rho_{\text{s}} }}{{M_{\text{s}} }}}, \) was determined by equating the average RBCs volume fraction to the hematocrit value.

Results

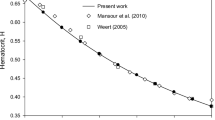
The computed time averaged RBCs volume fraction radial distributions are shown in Fig. 1, the hematocrit values being, respectively, 24 and 57 p.c. Both the computational results using FLUENT and the Poiseuille flow approximation for developed flow show that the RBCs have the highest volume fraction at the center. Near the walls of the blood vessel, the RBCs volume fractions are smaller as measured by Taylor44 and others.6 There is a small increase of the RBCs volume fraction near the wall, due to the use of the Johnson–Jackson boundary condition which accounts for the inelasticity of the wall. Figure 1 confirms the Fahraeus–Lindqvist effect, the migration of RBCs from the wall to the center.

Figure 1
figure 1

The Fahraeus–Linqvist effect: migration of RBCs from the wall to the center. A comparison of RBCs volume fractions simulated using the multiphase kinetic theory model in FLUENT (Simulation Result), developed flow described in the section of Poiseuille flow approximation (Developed Flow), and the experiment of Taylor44 for (a) Hct = 0.24, (b) Hct = 0.57. Experimental data are from light intensity measurements

Full size image

Figure 1 shows a quantitative agreement of the computational RBC volume fraction profiles with the experimental data. The two phase kinetic theory model predicts the low RBC volume fractions near the wall and the high values at the center. Near the wall, there is a small disagreement between the experiment and the theories due to the use of an inaccurate wall boundary condition for the partially flexible tube and the unknown restitution coefficient.

The computed time averaged RBC axial velocities have a parabolic distribution shown in Fig. 2. The axial velocities have the maximum values at the center. The velocity profile with hematocrit of 57% was more blunt than that with hematocrit of 24%. This result is consistent with Lyon and Leal’s32 observation, in which an increase in bulk particle concentration resulted in a more pronounced blunting of velocity profile.

Figure 2
figure 2

Parabolic RBC axial velocities for hematocrits of 0.24 and 0.57 computed in FLUENT using the multiphase kinetic theory model described in the section of multiphase Navier–Stokes equations

Full size image

The granular temperature, similar to the thermodynamics temperature for gases, was defined as a measure of the fluctuating energy of velocity of particles. Figure 3 shows the time averaged radial profile of granular temperature. Simulated granular temperatures near the wall, where the RBCs are more dilute, are larger than those in the denser center area. Also there is an increase of the near-wall maximum with decreasing RBCs volume fraction. The granular temperature with a higher hematocrit was smaller than that with the smaller hematocrit due to the smaller mean free path in the denser region.

Figure 3
figure 3

Granular temperatures for hematocrits of 0.24 and 0.57 computed in FLUENT using the multiphase kinetic theory model listed in the section of multiphase Navier–Stokes equations. Granular temperature behavior of RBCs: high near the wall due to production by shear and low at the center due to dissipation. Note that the high granular temperature near the walls causes the dip in the RBC volume fractions in Fig. 1

Full size image

Figure 4 shows the RBC viscosity distribution, with μ s calculated from the computed granular temperature by the kinetic theory model in Eq. (10). The core of the tube with rich RBCs has a higher local viscosity than near the wall, which is accordance with the results of Damiano et al.,9 Long et al.,29 and Sharan and Popel.39 The higher viscosity at the center is due to the higher RBCs concentration, in agreement with the Pries et al. 36 correlation for viscosity. The increasing viscosity towards the center area produced more resistance to the flow in the center area than near the wall, which arises due to the decreased RBCs flow rate in the center area in real parabolic flow. The axial velocity profile was shown in Fig. 2. The difference between the maximum value and the minimum value of RBCs viscosity for the case of hematocrit Hct = 0.57 was about 40 times larger than for the case of hematocrit Hct = 0.24, which gives rise to the greater resistance discrepancy between the center area and near the wall area and the phenomena of more blunt axial velocity distribution for the dense case.

Figure 4
figure 4

RBCs viscosities for hematocrits of 0.24 and 0.57 computed in FLUENT using the multiphase kinetic theory model described in the section of multiphase Navier–Stokes equations

Full size image

For the case of hematocrit Hct = 0.57, Fig. 5 shows the comparison of granular temperature using the Poiseuille flow approximation for fully developed flow with the computed granular temperature using the complete two-phase kinetic theory model. Figure 6 shows the corresponding comparison of RBC viscosity for fully developed flow to the FLUENT model. For Poiseuille flow approximation, the variations of RBCs volume fraction, viscosity, and granular temperature from the center area to the near wall maximum and minimum values were smaller than the simulation results using the complete two-phase kinetic theory model. The position for the minimum and maximum values of RBCs volume fraction, viscosity and granular temperature near the wall were closer to the wall for the Poiseuille flow approximation than the simulation results using complete two-phase kinetic theory model. The shear contributes to the momentum balance for RBC phase by a second order differential of the velocity. The assumption of parabolic axial velocity distribution used in the Poiseuille flow approximation gives a constant shear contribution to the momentum. The aggregation effect arising from the uneven resistance to the flow by viscosity distribution produced lower values in the center area and higher values near the wall. The overestimated shear production in the center area and the underestimated shear production near the wall in the Poiseuille flow approximation is the reason for the discrepancy between the FLUENT simulation results and the Poiseuille flow approximation.

Figure 5
figure 5

A comparison of granular temperatures for fully developed flow computed using the Poiseuille flow approximation with FLUENT multiphase kinetic theory model described in the section on multiphase Navier–Stokes equations, for hematocrit Hct = 0.57

Full size image
Figure 6
figure 6

A comparison of computed RBCs viscosities using Poiseuille flow approximation with the computation using complete two-phase kinetic theory model listed in the section of multiphase Navier–Stokes equations for hematocrit Hct = 0.57

Full size image

Discussion

Boundary Layer Development

Figure 7 shows the computed boundary layer development of the RBC volume fractions and granular temperatures using FLUENT. Due to the long length of the tube, the boundary layers have developed quickly. Figure 7 shows that RBC volume fraction has a constant high value at the center in the second half of the tube. The granular temperature reached the developed value in a much shorter length. Qualitatively, the boundary layers behave similarly to single phase flow.38 The granular temperature boundary layer is analogous to the thermal boundary layer with viscous heat generation. For an adiabatic wall, there exists an approximate analytical solutions, but not for the boundary condition used in this study.

Figure 7
figure 7

Computed boundary layer development of RBCs concentration and granular temperature using the FLUENT multiphase kinetic theory model listed in the section on multiphase Navier–Stokes equations

Full size image

For RBCs phase in a steady state, the pressure drop equals the weight of the bed and buoyancy is balanced by the drag. For the case of blood flow, the RBCs volume fraction did not change much, as can be seen from Fig. 1. For a simplified analysis, assuming constant RBCs volume fraction, the boundary layer equations for RBCs phase are:

$$ {\frac{\partial u}{\partial x}} + {\frac{\partial \upsilon }{\partial y}} = 0 $$
(30)
$$ u{\frac{\partial \upsilon }{\partial x}} + \upsilon {\frac{\partial \upsilon }{\partial y}} = \nu {\frac{{\partial^{2} \upsilon }}{{\partial x^{2} }}} $$
(31)
$$ u{\frac{\partial \theta }{\partial x}} + \upsilon {\frac{\partial \theta }{\partial y}} = {\frac{{\kappa_{\text{s}} }}{{1.5\rho_{\text{s}} \varepsilon_{\text{s}} }}}{\frac{{\partial^{2} \theta }}{{\partial x^{2} }}} + {\frac{{\mu_{\text{s}} }}{{1.5\rho_{\text{s}} \varepsilon_{\text{s}} }}}\left( {{\frac{\partial \upsilon }{\partial x}}} \right)^{2} $$
(32)

The similarity solutions for the velocity field was derived by Schlichting38 and other researchers. The ordinary differential equation for the random kinetic energy is obtained, employing the similarity variables, as:

$$ \eta = y\sqrt {{\frac{{U_{\infty } }}{\nu x}}},\quad f = {\frac{\psi }{{\sqrt {\nu U_{\infty } x} }}},\quad \Uptheta = {\frac{{\theta - \theta_{0} }}{{{\frac{1}{3}}U_{\infty } }}} $$
(33)

where ψ is the stream function of the RBCs flow:

$$ u = {\frac{\partial \psi }{\partial y}},\quad {\text{and}}\quad \upsilon = - {\frac{\partial \psi }{\partial x}} $$
(34)

Then the random kinetic energy Eq. (32) reduces to an ordinary differential equation:

$$ {\frac{{d^{2} \Uptheta }}{{d\eta^{2} }}} + {\frac{\Pr }{2}}f{\frac{d\Uptheta }{d\eta }} + 2\Pr \left( {{\frac{{d^{2} f}}{{d\eta^{2} }}}} \right)^{2} = 0 $$
(35)

where \( \Pr = {\frac{{3\mu_{\text{s}} \varepsilon_{\text{s}} }}{{2k_{\text{s}} }}} \) is the Prandtl number for RBCs phase.

For the particular case of an adiabatic wall, the boundary conditions are:

$$ \Uptheta \left( \infty \right) = 0\quad {\frac{\partial \Uptheta \left( 0 \right)}{\partial \eta }} = 0 $$
(36)

Then the wall granular temperature under adiabatic wall conditions is as follows:

$$ \Uptheta_{\text{w}} = \int\limits_{0}^{\infty } {\left[ {{\frac{{\int_{0}^{\eta } {\exp \left( {\int_{0}^{\eta } {{\frac{Pr }{2}}fd\eta } } \right)} 2 Pr \left( {f^{\prime \prime } } \right)^{2} d\eta }}{{\exp \left( {\int_{0}^{\eta } {{\frac{Pr }{2}}fd\eta } } \right)}}}} \right]} d\eta $$
(37)

Equation (37) can be readily integrated numerically, employing f(η) from Schlichting.38 For the case of hematocrit of 57%, the surface dimensionless granular temperature was calculated to be 0.5904. The main stream velocity is U ∞ ≈ 0.16 m s−1, and the granular temperature at the center is θ 0 ≈ 0.000127 m2 s−2. Then the wall granular temperature θ w ≈ 0.00516 m2 s−2. This is larger than the simulated wall granular temperature using FLUENT of ≈ 0.000372 m2 s−2. Such a larger value is expected due to additional dissipation at the wall in the Johnson-Jackson boundary condition. The FLUENT computations in Fig. 7 and the approximate boundary layer analysis allow us to estimate the entrance length. Figure 7 shows that this entrance length is short. Beyond the entrance length the approximate Poiseuille flow solution is valid.

Effect of Restitution Coefficients

In the two-phase kinetic theory model, the restitution coefficient between RBC particles, e, and the restitution coefficient between the RBC particle and the wall are the only empirical inputs in the model.

From equations of (27) and boundary condition (28), we can see that the granular temperature for fully developed flow is a function of dimensionless groups “a” and \( B_{1}^{\prime } \). The dimensionless group of “a” is the ratio of dissipation over the diffusive flux of random kinetic energy. Calculated granular temperature radial distributions for different numbers of “a” were shown in Fig. 8. With the increase of “a”, granular temperatures decrease because the dissipation of random kinetic energy becomes more dominant. For the case of a = 0, there is no random kinetic energy dissipation and the production of kinetic energy by shear was completely balanced by diffusive flux. For elastic particle collisions, Eq. (24) reduces itself to43

$$ \kappa_{\text{s}} {\frac{{d^{2} \theta }}{{dx^{2} }}} = - \mu_{\text{s}} \left( {{\frac{{d\upsilon_{{{\text{s}}z}} }}{dx}}} \right)^{2} $$
(38)
Figure 8
figure 8

Effect of inelastic dissipation on fully developed flow granular temperatures. “a” is a measure of inelasticity of particles. As the RBCs become more inelastic, the dimensionless group of “a” increases and the granular temperatures decrease. The dimensionless granular temperatures were computed using the Poiseuille flow approximation

Full size image

Using the parabolic axial RBCs velocity Eq. (22) and conversion to dimensionless form gives

$$ {\frac{{d^{2} \theta^{\prime } }}{{dr^{2} }}} = - r^{2} $$
(39)
$$ \theta_{\text{w}}^{\prime } = {\frac{{\theta_{\text{w}} }}{{4{\frac{{\mu_{\text{s}} }}{{\kappa_{\text{s}} }}}\upsilon_{{{\text{s}},\max }}^{2} }}}. $$
(40)

As already shown by Tartan and Gidaspow,43 Eq. (39) gives a fourth-power dependence of granular temperature on radial position.

$$ \theta^{\prime} - \theta_{\text{w}}^{\prime } = {\frac{1}{12}}\left( {1 - r^{4} } \right) $$
(41)

A comparison of the analytical solution for the elastic case and the more general developed flow approximation is shown in Fig. 9. The granular temperatures at the center are higher than those near the wall.

Figure 9
figure 9

A comparison of granular temperature distributions for developed flow computed using the Poiseuille flow approximation with the analytical solution for elastic particles with prescribed wall temperature computed using Eq. (41)

Full size image

The dimensionless group, \( B_{1}^{\prime } = {\frac{{\kappa_{\text{s}} \theta }}{{\gamma_{\text{w}} R}}}, \) in the boundary condition quantifies the importance of random kinetic energy diffusive flux and dissipation by inelastic collision between RBCs and wall. Calculated granular temperature radial distributions for different values of \( B_{1}^{\prime } \) were shown in Fig. 10. The values of \( B_{1}^{\prime } \) have much more effects on the granular temperature near the wall than that at the center. With \( B_{1}^{\prime } \) increasing, the diffusive flux of random kinetic energy becomes more important than inelastic dissipation.

Figure 10
figure 10

Effect of wall inelasticity on the granular temperatures. \( B_{1}^{\prime } \) is an inverse measure of wall inelasticity. As the dimensionless group \( B_{1}^{\prime } \) decreases, the granular temperatures near the wall decrease. The dimensionless granular temperatures were computed using the Poiseuille flow approximation

Full size image

Order of Magnitude Estimate of Fahraeus–Lindqvist Effect

An understanding of the change of the blood viscosity flowing in tubes of diameter between 10 to 1000 micrometers can be obtained by making some reasonable crude approximations. The general granular temperature equation can be simplified by neglecting conduction and assuming constant shear. Then a balance between production of oscillations due to shear and dissipation due to inelasticity of particles gives the approximate expression.12

$$ \begin{gathered} \theta \propto \left( {{\frac{{\partial \upsilon_{z} }}{\partial x}}d_{\text{p}} } \right)^{2} \hfill \\ {\text{Granular temperature}} = \theta = ( {\text{shear gradient}} \times {\text{particle diameter)}}^{2} \hfill \\ \end{gathered} $$
(42)

Then for constant shear the granular temperature can be approximated as follows:

$$ \begin{gathered} \theta \propto \left( {{\frac{{\upsilon_{z,\max } d_{\text{p}} }}{R}}} \right)^{2} \hfill \\ {\text{Granular temperature}} = ( {\text{max.}} {\text{ fluid velocity}} \times {\text{particle diameter/2}} \times {\text{tube diameter)}}^{2} \hfill \\ \end{gathered} $$
(43)

For developed flow there is no radial flow. Hence the particle pressure gradient is constant. Using an ideal equation of state as a crude approximation,

$$ P_{\text{s}} = \varepsilon_{\text{s}} \rho_{\text{s}} \theta $$
(44)

an expression for the blood solids volume fraction, hematocrit is then as follows.

$$ \begin{gathered} {\text{Hct}} = c\left( {{\frac{R}{{d_{\text{p}} \upsilon_{z,\max } }}}} \right)^{2} \hfill \\ {\text{Hematocrit}} = ( {\text{tube diameter/red blood cell diameter)}}^{2} /(\max. {\text{fluid velocity}})^{2} \times {\text{constants}} \hfill \\ \end{gathered} $$
(45)

The above equation approximately gives the hematocrit observed dependence on tube diameter, fluid velocity, and the particle size. The relative blood viscosity can then be given by the semi-theoretical expression below.

$$ \eta = 1 + 0.127{\text{Hct}}^{1/3} g_{0}^{0.8} $$
(46)

for 20 micrometer tube diameter in agreement with the empirical equation of Pries et al.36 shown in Fig. 11, where Hct is the hematocrit and g 0 is radial distribution function at contact using the Bagnold equation in Eq. (12). The one-third dependence is obtained from the following approximation:

Figure 11
figure 11

A comparison of the computed relative apparent viscosity of blood for 20 μm tube diameter using expression (46) and the kinetic theory model with a packing limit correlation for RBCs to the empirical correlation of Pries et al.36 as a function of hematocrit

Full size image

In the dilute regime the mixture density is proportional to the 3/2 power of granular temperature. Hence the viscosity which varies with the square root of the granular temperature is proportional to the one-third power of the volume fraction. The radial distribution function corrects for the dense region. For uniform packing limit of RBCs, computed relative apparent viscosities have a sharp increase when hematocrit is near 0.55, which is the result of RBCs deformation in dense region. The greater deviation from the spherical shape of RBCs, the denser is the packing. We assume that the packing limit of RBCs has a linear relationship with hematocrit to take account of the RBCs deformation in the dense regime:

$$ \varepsilon_{{{\text{s}},\max }} = 0.6686{\text{Hct}} + 0.3084\quad {\text{for}}\quad {\text{Hct}} \ge 0.55 $$
(47)

Figure 12 shows a comparison of the FLUENT calculation of the relative apparent viscosity dependence on the tube diameter and hematocrit, with the empirical equation given by Pries et al.36

Figure 12
figure 12

A comparison of the computed relative apparent viscosity of blood using the multiphase kinetic theory model in FLUENT (e = 0.95, e w = 0.6) and the Poiseulle flow approximation model to the empirical equation by Pries et al.,36 with error bars, for two values of hematocrit

Full size image

Conclusions

  1. 1.

    A complete and an approximate kinetic theory based two-phase flow models were used to explain the Fahraeus–Lindqvist effect,18 the migration of red blood cells from the wall to the center in narrow tubes. This type of migration is known to be due to shear induced diffusion in the two-phase flow literature. Here it is explained using a kinetic theory based model already found in FLUENT, a commercial code. This migration is caused by a decrease of granular temperature at the center of the tube due to inelastic collisions. The granular temperature is the driving force for migration. The magnitude of the inelasticity is the only significant empirical parameter in the model. The dip in the granular temperature at the center gives rise to the increased red blood cell concentration.

  2. 2.

    The kinetic theory model computes the red blood cell viscosity, similar to the computation of particle viscosity in gas fluidization.13

The computed viscosity agrees with the measurements of blood viscosity.36 In this computation the radial distribution function of statistical mechanics was approximated by a geometric type approximation, called the Bagnold equation, long used in the estimation of liquid–solid viscosities.35 For a better estimate, direct measurements are needed, as was done for gas-particle systems using a particle image velocity technique.14