Methods for Quantifying Three-Dimensional Deformation of Arteries due to Pulsatile and Nonpulsatile Forces: Implications for the Design of Stents and Stent Grafts

Abstract

The knowledge of dynamic changes in the vascular system has become increasingly important in ensuring the safety and efficacy of endovascular devices. We developed new methods for quantifying in vivo three-dimensional (3D) arterial deformation due to pulsatile and nonpulsatile forces. A two-dimensional threshold segmentation technique combined with a level set method enabled calculation of the consistent centroid of the cross-sectional vessel lumen, whereas an optimal Fourier smoothing technique was developed to eliminate spurious irregularities of the centerline connecting the centroids. Longitudinal strain and novel metrics for axial twist and curvature change were utilized to characterize 3D deformations of the abdominal aorta, common iliac artery, and superficial femoral artery (SFA) due to musculoskeletal motion and deformations of the coronary artery due to cardiac pulsatile motion. These illustrative applications show the significance of each deformation metric, revealing significant longitudinal strain and axial twist in the SFA and coronary artery, and pronounced changes in vessel curvature in the coronary artery and in the inferior region of the SFA. The proposed methods may aid in designing preclinical tests aimed at replicating dynamic in vivo conditions in the arterial tree for the purpose of developing more durable endovascular devices including stents and stent grafts.

Introduction

The introduction of minimally invasive endovascular therapies, such as coronary, carotid, and peripheral artery stenting and aortic stent grafting, has radically changed the treatment of cardiovascular diseases.8,19,22,32,54 The engineering challenges associated with these devices are considerable and include issues related to biocompatibility, deliverability, efficacy, safety, and durability.17,21,24,47,51 Efficacy of the device in treating cardiovascular disease must be balanced with safety considerations. Implanted devices simultaneously alter the biochemical and biomechanical environment of the cardiovascular system, triggering acute and chronic changes, and are in turn inherently affected by the physiologic environment of the body.

While biocompatibility issues related to device safety and efficacy have received considerable attention, the in vivo forces imparted to endovascular devices are not as well understood, despite the acknowledged importance of this information for designing durable endoluminal devices. Recent reports on device failures in the coronary,11 carotid,12 renal,2,16,36,38 aorta,4,25,26 iliac,37 popliteal,46 and superficial femoral arteries (SFA),1,18,39 have been a source of great concern in the medical device industry, among physicians and for regulatory agencies, stimulating research on the characterization of in vivo arterial deformation. A lack of knowledge of the in vivo biomechanical environment may lead to devices that are designed for deformations that are arguably much less important than others. For example, many of the stents that have been implanted in the SFA have been nitinol biliary stents used off-label. Although the stents were evaluated by means of radial pulsatile fatigue tests, they have experienced a high fracture rate in vivo when implanted in the SFA, likely due to dynamic changes of curvature and longitudinal strain in the femoral and popliteal region caused by hip and knee flexion.10,39

Presently, quantification of in vivo forces on devices has been limited to fluid shear and pressure imparted by the blood stream directly to the device or via the cyclic radial force imparted by the blood vessel due to the pressure pulse. Quantification of pulsatile longitudinal and bending forces imparted by the vessel wall to the device and nonpulsatile forces imparted to the device due to musculoskeletal motion has received far less attention. For good reason, such forces are extraordinarily difficult to measure in vivo. Fortunately, some information related to the nature of these forces can be gained by studying the consequences of these forces, namely the in vivo deformation of the blood vessels themselves. Quantification of in vivo deformation of blood vessels has only recently become feasible with the advent of three-dimensional (3D) imaging modalities, especially bi-plane angiography, magnetic resonance imaging (MRI), and computed tomography (CT).

In addition to the need to quantify in vivo deformation for purposes of device design, quantifying vessel geometry and the pulsatile and nonpulsatile deformation of arteries is important for understanding the pathogenesis of cardiovascular diseases.40–42 The curvature and torsion of the vasculature are of interest because of the resultant impact on hemodynamic conditions and disease localization.6,34,42,44,50,53

Various methods and quantification metrics have been proposed to characterize the aforementioned types of in vivo arterial deformations.5,7,9,10,14,20,28,29,33,41–44,49,50,53 For example, the “distance factor,” which is defined as the ratio between the vessel path length and the distance between two endpoints, is a simple metric commonly used to measure nonlinearity of vessels, i.e., tortuosity.7,53 This metric lumps 3D information into a one-dimensional (1D) metric and hence does not clearly differentiate local curvature changes, especially when the vessel maintains the same distance factor. The well-known Frenet formula has been widely used to describe the curvature and torsion of a vessel. According to this formula, curvature and torsion are defined as $\kappa = {\left\| {\varvec{\alpha}^\prime \times {\varvec{\alpha} }\ifmmode{''}\else$''$\fi } \right\|}/{\left\| {{\varvec{\alpha} }\ifmmode{'}\else$'$\fi } \right\|}^{3}$ and $\tau = ({\varvec{\alpha} }\ifmmode{'}\else$'$\fi \times {\varvec{\alpha} }\ifmmode{''}\else$''$\fi) \cdot {\varvec{\alpha} }\ifmmode{'''}\else$'''$\fi/{\left\| {{\varvec{\alpha} }\ifmmode{'}\else$'$\fi \times {\varvec{\alpha}}\ifmmode{''}\else$''$\fi } \right\|}^{2}$, respectively, where α indicates a position vector in space.9,28,29,33,35,53 By definition, this curvature metric measures an infinitesimal rate of change in the tangent vector at each point of the curve, whereas the torsion metric measures the infinitesimal rate of change in the orientation (binormal vector of the curve) of the osculating plane. While curvature is well appreciated because of its reciprocal relation to the radius of curvature, the torsion metric is less frequently used in practice because of its susceptibility to error in calculations associated with higher-order derivatives.

Moreover, despite the precise mathematical definition that the Frenet formula provides in a continuous space, the discrete data points require finite differentiation methods, or best-fit polynomials for calculating derivatives. As a result, curvature and torsion metrics calculated with this method may not represent the global characteristics of vessel morphology because the metric is highly sensitive to noise, commonly found in medical imaging data. In addition, variations in curvature or torsion that occur on a scale smaller than the vessel radius are arguably insignificant for purposes of designing implantable devices. Although arithmetic averaging of the curvature, the so-called mean curvature, has been commonly employed to report the curvature,29,33,53 this approach may cause excessive smoothing resulting in the underestimation of the curvature in the region of interest. Therefore, the averaging span needs to be determined judiciously so as not to lose spatially varying characteristics.

In our view, the lack of explicit methods for generating a centerline path is the most critical hindrance in determining reliable quantitative measures of arterial deformation in order to design practical benchtop tests. Generally, centerline paths of vessels are employed to represent 3D volumetric vessel trees because of the ease of measuring geometric parameters based on the coordinates of these paths. Extracting centroid coordinates from segmentations of the cross-sectional lumen boundaries of the vessel, or directly from 3D geometry, has become a more common practice with increased computing power and the development of more efficient segmentation algorithms.5 Consequently, the irregularity of centroids generated by segmentation of the lumen boundaries, caused by the voxel size- or noise-limited segmentation process, introduces a need for a smoothing operation. Although least-squares polynomial fitting has been employed to smooth irregularities in the vessel path,33 higher-order polynomials which may be necessary for representing kinked segments of vessel, may introduce spurious oscillations. Moreover, there has not been a systematic method of determining the optimal level of smoothness of the curve representing the vessel. Furthermore, the presence of branch vessels adversely affects the consistent calculation of centroids along a vessel. Thus, segmentations around the branch ostia have been generally excluded in determining the centerline path,33 and the effect of the branches on the centroid calculation of the main vessel has received little attention. Finally, vessel twisting has not been comprehensively investigated in previous studies although significant twisting deformations may occur due to muscle deformations observed in the myocardium55 or thigh.3,10

In this paper, we propose a general approach and novel metrics for quantifying dynamic arterial deformation due to pulsatile and nonpulsatile forces. More specifically, we introduce a systematic framework for generating the centerline path of the vessel by utilizing 2D threshold and level set segmentation techniques. The proposed framework includes centroid calculations for representation of vessel paths and a Fourier smoothing method to eliminate the irregularity of these centroid-based centerlines. In order to determine optimal smoothness of the centerline, we introduce a cost function using the degree of the Fourier smoothing mode as an argument variable. These steps enable us to find consistent centroids of a main vessel, even in the vicinity of branch vessels, with minimal operator dependency. After generating the centerline path, we then describe methods for quantifying longitudinal strain, axial twist, and curvature change to characterize changes in vessel geometry. Moreover, these methods are validated on software phantoms. Finally, to illustrate the application of these methods, we analyze deformations of the coronary artery, abdominal aorta, common iliac artery, and SFA, since these arteries are predisposed to cardiovascular disease and hence are frequent sites of endovascular stenting or stent grafting procedures.

Methods

Imaging Protocol

Magnetic resonance imaging and computed tomography were used to acquire 3D in vivo geometric data of the arterial tree. Depending upon the anatomic locations and resolution, the imaging sequence and parameters were optimized to capture changes in vessel morphology, as follows.

MRI

The study protocol was approved by the Stanford University Panel on Human Subjects in Medical Research, and written informed consent was obtained from each volunteer. We performed Gadolinium-enhanced magnetic resonance angiography (MRA) using a General Electric Signa Excite 1.5T scanner (GE Medical Systems, Milwaukee, WI, USA) to image the SFA of one healthy subject (56 years old). Two static supine and bent-leg positions were imaged to induce arterial deformation within the constraint of the MRI bore. A time-resolved MRA pulse sequence (GE-TRICKS) was performed for approximately 4 min in each position with the following parameters: 8 ms repetition time, 1.6 ms echo time, 45° flip angle, 512 × 224 acquisition matrix per each slice, 2.6 mm slice thickness with 1.3 mm overlap, and approximately 19 s temporal resolution. The voxel size of the reconstructed image was 0.8 × 0.8 × 1.3 mm³.

In addition, we imaged the abdominal aorta and common iliac arteries of one healthy subject (39 years old) with the same magnet in order to investigate the characteristics of nonpulsatile deformation in larger vessels. As with the SFA experiment, two different positions—supine and fetal—were prescribed to induce nonpulsatile arterial deformation. Each scan lasted approximately 30 s and was performed during a breath hold to eliminate respiratory motion. The image volume was approximately 30 × 30 × 10 cm³ with a reconstructed matrix of 512 × 512 × 72 pixels, resulting in voxel size of 0.6 × 0.6 × 1.4 mm³. Using proprietary software (GE Medical Systems, Milwaukee, WI, USA), we corrected each volume of MRA data for known gradient nonlinearities which can cause distortion in the slice-selection direction.15

CT

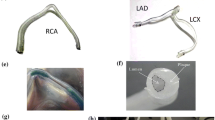
A pre-existing 64-row multi-detector CT image of the coronary arteries was obtained from the Picture Archiving and Communications System (PACS) at the Stanford Hospital and Clinics and was de-identified. With retrospective ECG gating, ten individual cardiac cycles were used to generate one image data set of a cardiac cycle. Thus, each frame represents 1/10th of the cardiac cycle. The field of view was 20 × 20 × 20 cm³ with a reconstructed matrix size of 512 × 512 × 405 and voxel size of 0.4 × 0.4 × 0.5 mm³. In order to quantify pulsatile deformation of the coronary artery, the peak-systolic (maximum diameter of the aorta) and end-diastolic (minimum diameter of the aorta) phases were identified and compared.31

Image-Based Anatomic Model Construction

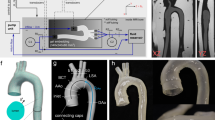
Significant morphological changes observed in the coronary artery (Fig. 1), abdominal aorta, common iliac artery, and SFA (Fig. 2) due to pulsatile and nonpulsatile forces motivated the development of the quantification methods. We analyzed each 3D image volume to construct the centerline path of vessels and branch locations using custom software.52

FIGURE 1

Geometric changes in human coronary arteries due to cardiac pulsatile motion (Green: diastole, Red: systole)

FIGURE 2

Geometric changes in human arteries due to hip and knee flexion. Geometric solid models of major arteries in the thigh of a 56-year-old healthy male subject are shown together with a slice plane from the magnetic resonance imaging data obtained under the (a) supine and (b) bent-leg positions. Note the pronounced changes in vessel curvature in the inferior region of the model. Also shown are the geometric solid models extracted from a 39-year-old healthy female subject in the (c) supine and (d) fetal positions. Note the changes in curvature of the aorta and the common iliac arteries with maximal hip and knee flexion

Centerline Path Generation

The most critical step in quantifying vessel geometric changes is the generation of the centerline path. Volumetric vessels were represented by 3D space curves based on medical imaging data as follows. First, an initial centerline path was generated by an interpolated cubic hermite spline from hand-picked points selected along the center of the artery. Along this initial centerline path, a two-dimensional (2D) threshold segmentation technique was used to find the lumen boundaries of the vessel at spline coordinates approximately 1 mm apart. In order to compensate for the intensity variation in the MRI data down the length of a vessel, linearly interpolated threshold values were used on the basis of sampled locations along the artery.

Next, the centroid of the lumen cross section was computed and used to construct a revised centerline path of the vessel. Segmentations in the vicinity of the branch vessels need special attention because the ostia of the branch vessels perturb the centroids of the main vessel (Fig. 3a and c). Particularly large branch vessels, such as the celiac, superior mesenteric (SMA), renal, and inferior mesenteric arteries (IMA) cause slowly varying perturbations of the centroid path (Fig. 3c), which render Fourier smoothing on the centroid-based path ineffective (Fig. 3e). Thus, we excluded branch structures by using a 2D level set method based on a curvature constraint.48 The control over the curvature of the lumen boundary effectively prevented the level set segmentation from advancing towards the ostia of the branching vessel (Fig. 3b). Prior to the calculation of the centroids, a Fourier smoothing operation was performed on the segmentation contours to eliminate artificial irregularities as well as to provide evenly spaced coordinates on the lumen boundary.

FIGURE 3

Effect of the branch vessels on the centroid of the abdominal aorta dataset. (a) Original 2D threshold segmentations were generated. (b) The corrupted segmentations in the vicinity of the celiac artery, SMA, renal arteries and IMA were corrected by a 2D level set method, and 5-mode Fourier smoothing was performed on the lumen contour. Centroids of all segmentations along the aorta were calculated for the (c) original segmentation, and the (d) corrected segmentation. A 15-mode Fourier smoothing was performed on the centerlines connecting each centroid for the (e) original segmentation and the (f) corrected segmentation. Note that Fourier smoothing was not effective in removing low frequency perturbation, as shown in (e), whereas it was effective in generating a smooth centerline path by removing high frequency perturbation, as shown in (f)

Since the centerline connecting the centroids of the main vessel is inherently irregular (Fig. 3d) because of various random factors including the pixel size and noise in the image, the resultant centroid set needs additional post processing before further calculations. These random factors essentially cause calculated centroids to deviate from the true, but yet unmeasurable, position within the cross-sectional lumen boundary. This was more apparent when segmentations were more closely spaced as the smoothness of the vessel centroid path was diminished. Thus, Fourier smoothing was performed on the centerline connecting the calculated centroids in order to remove spurious high spatial frequency components in the centerline path (Fig. 3f). This algorithm takes the original set of coordinates and generates a newly allocated set of evenly spaced coordinate points by linear interpolation. A 1D fast Fourier transform is then independently performed on each x-, y-, and z-coordinate that is mirrored to ensure periodicity prior to use of the Fourier transform. Next, only a small number of modes (q), to be determined, are preserved for reconstructing smoothed coordinates by inverse Fourier transform. Finally, half of the smoothed coordinates are selected since the data sets were mirrored. As a result of the q-mode Fourier smoothing, the vessel’s centerline path retains lower modes of spatial frequency (2πk/L, where k = 1,...,q and L = vessel length).

In order to develop a systematic method for determining the optimal number of modes (q), we investigated the characteristics of smoothing operations and conventional methods to determine the level of smoothness as follows. The centerline connecting the centroids is the best representation of the vessel in view of the infinitesimal exactness, but the worst in view of the global smoothness, as shown in Fig. 4a. In contrast, when a small number of Fourier smoothing modes is used to eliminate the spurious irregularities, the global smoothness of the centerline path increases, whereas the exactness of the vessel representation is compromised. To illustrate this, a 10-mode smoothing generates a highly smooth centerline path while compromising the exact representation of the vessel curvature (Fig. 4b). As the number of Fourier modes increases, the centerline path represents a more accurate vessel geometry while the smoothness decreases because the curve approaches a set of irregularly positioned centroids (Fig. 4b–f). Indeed, since a smoothing operation inevitably compromises the exactness, the minimal Fourier smoothing mode that maintains a sufficient exactness, but avoids image noise related fluctuations should be chosen.

FIGURE 4

Algorithm to determine the optimal Fourier smoothing mode and the effect of Fourier smoothing on the vessel centerline paths. (a) An initial irregular centerline, connecting the centroids of the cross-sectional lumen boundaries of the SFA was generated and was followed by Fourier smoothing with (b) 10 modes, (c) 20 modes, (d) 30 modes, (e) 40 modes, and (f) 50 modes. As the number of Fourier modes increases, the difference between centerlines becomes negligible and visually indistinctive. On the basis of this observation, the convergence rate cost was defined by the maximum distance between centerlines in successive Fourier smoothing. As shown in (g), the convergence rate cost decreases to a limit as the number of Fourier mode increases and the threshold value of 0.1 determines the optimal Fourier mode as 48

Conventionally, the level of smoothness is determined by visual inspection of the exactness of the smoothed centerline. For example, in the lower range of smoothing modes, the difference between the smoothed curve and the true geometry is visually distinctive, which requires an operator to increase the number of modes (Fig. 4b and c). Infinitesimal adjustment then occurs in the higher range of modes (Fig. 4d–f). Therefore, an operator would choose an estimate of the smoothness between 40 and 50 modes (Fig. 4e and f) because the difference between the two curves is not visually observable, which implies “convergence.” In summary, the conventional methods can be decomposed into two steps: exactness observation and convergence determination, which involve a large degree of subjectivity in determining the “optimal” number of smoothing modes.

The analysis of the characteristics of the smoothing process and the conventional methods motivated the development of a systematic framework to identify the optimal level of smoothness. Fundamentally, this framework transformed the conventional methods based on empirical observation into a systematic method with quantitative criteria as follows. For comparison of two 3D curves generated by successive q − 1 and q mode Fourier smoothing, points with half of the vessel radius intervals were first sampled along the q − 1 mode smoothed curve $( \ifmmode\expandafter\tilde\else\expandafter\sim \fi{X}(q - 1))$. Next, distances from the sampled points to the q mode curve $( \ifmmode\expandafter\tilde\else\expandafter\sim \fi{X}(q))$ were calculated. The convergence rate cost was then defined by the maximum distance among the distances at sampled locations as follows:

$$ C_{{{\text{convergence}}\,\,{\text{rate}}}} (q) = {\mathop {\max }\limits_i }{\left\| { \ifmmode\expandafter\tilde\else\expandafter\sim \fi{X}_{i} (q) - \ifmmode\expandafter\tilde\else\expandafter\sim \fi{X}_{i} (q - 1)} \right\|}, $$

(1)

where $\ifmmode\expandafter\tilde\else\expandafter\sim \fi{X}_{i} (q - 1)$ represents the ith sampled coordinate in the q − 1 mode Fourier smoothed curve, and $\ifmmode\expandafter\tilde\else\expandafter\sim \fi{X}_{i} (q)$ represents the closest spline coordinate of q mode smoothed curve to $\ifmmode\expandafter\tilde\else\expandafter\sim \fi{X}_{i} (q - 1)$. The maximum distance, instead of mean distance, was used to penalize the worst pair of points, as is the case for visual inspection. As the number of Fourier modes increases, the convergence rate cost decreases to a limit because the smoothed curve eventually approaches the irregularly positioned centroids (Fig. 4g). This property enabled us to construct criteria to determine when to stop further smoothing, and we found that 0.1 mm could be used as a consistent upper bound of the convergence rate cost for a stopping criterion. In short, the proposed methods to determine the optimal number of Fourier smoothing modes are simply represented by

$$ {\text{minimize}}\,\,q\,\,{\text{subject to }}C_{{{\text{convergence}}\,\,{\text{rate}}}} (q) \le 0.1\;{\text{mm}}\; for \;\forall \;{q}. $$

(2)

In order to ensure sufficient exactness and smoothness of the converged curve, we additionally examined the approximation error and the noise ratio of the resultant curve. The approximation error was defined by the mean distance from the original irregularly positioned centroids to the resultant smoothed centerline and the noise ratio was measured by the proportion of the curvature values that were higher than the inverse of the vessel radius, which is a geometrically admissible maximum curvature. The Frenet curvature formula was used to effectively detect spurious high curvature caused by any infinitesimal irregularities.

To illustrate these steps, as shown in Fig. 4g for the SFA in the bent-leg, the convergence rate cost evaluated at more than 47 modes was found to be smaller than the threshold, and hence 48 modes was selected as the optimal number of Fourier modes, satisfying Eq. (2). The approximation error of the smoothed centerline was 0.2 mm (25% of the pixel size) and the noise ratio was 0% as compared with 34% for the original centroid sets prior to smoothing operation. These measurements showed that the smoothed centerline was sufficiently accurate and high spatial frequency noise was effectively removed by 48-mode Fourier smoothing. Finally, the smoothed centerline path was again interpolated by a cubic hermite spline and subsequently used for the calculations of longitudinal strain, curvature change, and axial twist.

Identification of the Ostia

In order to acquire spatially resolved information, the ostia of several branches along the main vessel were used as landmarks for a Lagrangian material point in different image volumes. Detecting the ostium consistently in different image volumes is important because this information will be directly used in the calculations of each deformation metric. We thus defined the branch’s starting point by the centroid of the segmentation at the ostium, as illustrated in Fig. 5 for a muscular artery branching off the SFA. For this example, we first determined a line slicing across the ostium and another line slicing through the midpoint of the ostium on the axial plane of the main vessel to generate sagittal and coronal planes, respectively (Fig. 5a). Then, 2D threshold segmentations were generated on sagittal slice planes through the ostium (Fig. 5b). Of these sagittal segmentations, a contour slicing through the midpoint of the ostium was selected to help determine the segmentation of the ostium in the coronal plane. For the final segmentation of the ostium, we selected a contour that began to exhibit the actual contour of the ostium without perturbation of the main vessel (Fig. 5c). Intervals between segmentations were on the order of the sub-pixel size, e.g., 0.4 mm for this example, to avoid missing the true ostium. After the centroid of the ostium was identified, it was projected onto the main artery by calculation of the minimum distance to the centerline path (Fig. 5d). Finally, the branch projection point provided a Lagrangian landmark to compute the following deformation metrics.

FIGURE 5

Identification of the ostium of a branch vessel. (a) A line slicing across the ostium and another line slicing through the midpoint of the ostium were determined on the axial plane of the main vessel. (b) 2D threshold segmentations were generated on the sagittal slice planes through the ostium. A contour slicing through the midpoint of the ostium was selected to help determine the segmentation of the ostium. (c) 2D threshold segmentations were generated on the coronal slice planes. A contour that began to exhibit the actual contour of the ostium without perturbation of the main vessel was selected as a final segmentation of the ostium. (d) The centroid of the ostium was projected onto the main artery

Deformation Metrics

On the basis of the centerline path and branch projection points, the longitudinal strain of the vessel was readily computed. In addition, metrics for axial twist, and curvature change were defined to further quantify the vessel deformation.

Longitudinal Strain

Longitudinal strain was defined by the change in the arc length of a segment between branches divided by its original length as follows:

$$ \varepsilon _{l} = \frac{{l - L}} {L}, $$

(3)

where L is the length in the reference configuration, and l is the length in the current configuration. The branch projection points were used as landmarks to determine the corresponding range of segments between branch vessels in different configurations. As the value for L decreases, the limitations of image resolution can compromise the accuracy of the strain value. Moreover, since the length of stents and stent grafts significantly exceeds the diameter of the devices, changes in length of segments that are shorter than the vessel diameter scale are less useful for designing preclinical tests. Therefore, the approximate order of the vessel diameter was used as a minimum distance between branches to ensure measurement robustness by limiting error potentially produced by the finite pixel size. Specifically, starting with well-recognized branch vessels, e.g., the profunda femoris for the SFA and left circumflex coronary artery (LCX) for the left anterior descending coronary artery (LAD), we identified next branch vessels distal to the first branch vessel by more than its diameter distance. For example, muscular branches <7 mm apart from the profunda femoris were ignored in the SFA analysis since the vessel diameter was approximately 7 mm.

Curvature Change

Changes in vessel curvature can occur because of a bending moment due to pulsatile or nonpulsatile forces. Surrounding tissue support and vessel compliance can affect the amount of curvature change. Geometrically, the curvature is the inverse of the radius of the osculating circle. In a discrete domain, the osculating circle can be approximated by a circumscribed circle around three points on the vessel centerline path, as illustrated in Fig. 6.27

FIGURE 6

Method to calculate vessel curvature. (a) A window size of the vessel diameter was moved down along the centerline path incrementally to identify three adjacent points on the centerline path for the curvature calculation. (b) A circumscribed circle through three points was used to compute the curvature of the vessel along its length

In order to characterize the global curvature rather than the infinitesimal curvature, we computed the radius of the circumscribed circle through three sequential centerline coordinates within the range of a window size ω (discussed subsequently), at each evenly spaced coordinate. Specifically, as illustrated in Fig. 6b, the curvature at P _i was defined as the inverse of the radius of the circumscribed circle around the three coordinates P _a , P _i , and P _b , where P _a and P _b have equal distance of $\omega /2$ to P _i along the vessel curve.

As the window size, ω, decreases to an infinitesimal value, the curvature estimation approaches the true curvature. From a practical perspective, however, ω should be limited to a finite length. We chose the diameter of the vessel as a window size for measuring curvature in order to eliminate spurious changes in curvature due to the imaging or segmentation process, while simultaneously preserving true changes in the local curvature caused by vessel bending or buckling. The choice of the diameter as a window size can be further rationalized as follows. In a perfect arc vessel, as illustrated in Fig. 6b, the maximum deviation (δ _i ) of the interpolated line from the original vessel centerline is represented by Taylor series expansion with the assumption of ${R/(2\rho _{i} )} \ll 1$, as follows:

$$ \delta _{i} = \rho _{i} {\left( {1 - \cos \frac{{\theta _{i} }} {2}} \right)} = \rho _{i} {\left( {1 - \cos \frac{R} {{2\rho _{i} }}} \right)} \approx \frac{{R^{2} }} {{8\rho _{i} }}, $$

(4)

where θ _i is the central angle of the arc P _a P _i and P _i P _b , R is the radius of a vessel, and ρ _i is the radius of curvature (Fig. 6b). Assuming the vessel undergoes smooth deformation (e.g., centerline path ∈ C ²), which is a physiologically reasonable assumption considering the internal blood pressure and elastic nature of healthy blood vessels, the minimum possible radius of curvature is the vessel radius itself. Therefore, the admissible radius of curvature is always larger than the vessel radius (ρ _i  > R), and hence the maximum deviation is always limited by the following inequality:

$$ \delta _{i} < \frac{1} {8}R. $$

(5)

In real image data, the upper bound (right hand side of the inequality (5)) is more likely to be much smaller than the above calculation (R/8), since the radius of curvature is generally much larger than the vessel radius. In this respect, choosing the vessel diameter as a window size guarantees that global characteristics of vessels can be effectively captured without spurious curvature spikes that might be observed in segments shorter than the vessel radius.

Finally, curvature changes between two different configurations can be calculated by comparison of local curvature values for corresponding points in the two configurations. In many cases, however, branch vessels, i.e., landmarks, are located in a limited region that may not necessarily include the region of interest for curvature comparison. For example, as shown in Fig. 1, branch vessels from the distal LAD near the apex of the heart are either nonexistent or invisible although curvature changes are more pronounced in that region. Therefore, for curvature comparison beyond the landmarks, we extrapolated corresponding points by calculating an equivalent length of the vessel in the current configuration to that in the reference configuration. The strain measurement (ε _l ) between the identified landmarks, and the relationship of s _current = s _reference (1 + ε _l ) were used for the extrapolation.

From the perspective of designing preclinical tests, the maximum cyclic change in the curvature would be the most important measure for extreme bending deformation. The comparison between curvature values for two configurations can be evaluated at the linearly interpolated locations between the landmarks and at the extrapolated locations beyond the landmarks. However, a nonuniform longitudinal deformation in the interpolated and the extrapolated regions may result in misregistration of corresponding points. Therefore, we calculated maxima of curvature in each configuration and then identified maximum difference in corresponding “nearby” maxima, instead of piecewise comparison, as follows:

$$ \Updelta \kappa ^{*}_{{\max }} \, = \,\,\max {\left| {\kappa ^{*}_{{{\text{current}}}} - \,\kappa ^{*}_{{{\text{reference}}}} } \right|}, $$

(6)

where $\kappa ^{*}_{{{\text{current}}}}$ and $\kappa ^{*}_{{{\text{reference}}}}$ represent corresponding maxima, and “nearby” was defined as a distance within the vessel radius (R) along the vessel length. This approximate measure of maximum change in curvature was based on the assumption of a “±R” misregistration between two configurations.

In addition, change in mean curvature was also calculated to characterize the difference in curvature change along the vessel length, after the vessel was divided into two or three equal segments depending upon the curvature variations along the length as follows:

$$ \Updelta \ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }\, = \,\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{current}}}} - \,\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{reference}}}} , $$

(7)

where $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa } = (1/N){\sum\nolimits_{i = 1}^N{\kappa _{i} } }$, and N represents the total number of sampled curvature values in each subdivided segment. For example, the LAD was divided into two segments and change in mean curvature during cardiac phases was measured in the proximal and distal segments, respectively.

Verification of the Algorithm to Calculate Curvature

The curvature calculation algorithm was verified by means of an analytic space curve based on the following modified helix curve (Fig. 7a):

$$ \begin{aligned}{} & x(s) = \frac{\kappa } {{\kappa ^{2} + \tau ^{2} }}\cos {\left( {\frac{s} {L}} \right)} \\ & y(s) = \frac{\kappa } {{\kappa ^{2} + \tau ^{2} }}\sin {\left( {\frac{s} {L}} \right)} \\ & z(s) = \frac{\tau } {{\kappa ^{2} + \tau ^{2} }}\frac{s} {L}e^{{ - \lambda s}} \\ \end{aligned} $$

(8)

FIGURE 7

Software phantom used to verify new curvature metric. (a) A helix curve was modified to mimic the kinked shape of the SFA for the bent-leg position. (b) On the basis of 6.6 mm window size reflecting the SFA diameter, curvature was measured by the proposed methods and was plotted with analytic curvature by use of Frenet formula as a gold standard. The difference between the two metrics was plotted and was found to be relatively small

The Frenet formula was employed to compute the analytic curvature, $\kappa _{{{\text{analytic}}}} (s)$ as:

$$ \kappa _{{{\text{analytic}}}} (s) = \frac{{\kappa (\kappa ^{2} + \tau ^{2} )}} {{\kappa ^{2} + \tau ^{2} (1 - \lambda s)^{2} e^{{ - 2\lambda s}} }}{\sqrt {\frac{{\kappa ^{2} + \tau ^{2} e^{{ - 2\lambda s}} (L^{2} \lambda ^{2} (2 - \lambda s)^{2} + (1 - \lambda s)^{2} )}} {{\kappa ^{2} + \tau ^{2} e^{{ - 2\lambda s}} (1 - \lambda s)^{2} }}} }, $$

(9)

which served as a gold standard for computing the difference. In the case of λ = 0, coefficients κ and τ represent the curvature and torsion of a helix, respectively. In the example of Eq. (9), λ in the exponent of z(s) generates spatially varying curvature and torsion, resulting in a kinked shape, while L is a scaling factor. Those coefficients were adjusted to mimic the geometric shape observed in the MRI study of SFA deformations, which exhibited significant changes in local curvature, as will be further discussed in the “Results” section.

In order to investigate the accuracy of the curvature estimation, the difference between the estimated curvature and the analytic curvature was evaluated as follows:

$$ \eta (s) = \kappa _{{{\text{estimate}}}} (s) - \kappa _{{{\text{analytic}}}} (s). $$

(10)

The curvature variation and error estimation along the parametric arc length of the phantom are shown in Fig. 7b. When the diameter of the SFA (6.6 mm) was used for the window size, the maximum error of −0.0046 mm⁻¹ (−4.0%) occurred at the location of the maximum curvature due to the finite window size, resulting in underestimation of the true curvature. The difference in the corresponding radius of curvature was 0.36 mm. The root-mean-square of the absolute value of η(s) over the entire length was 0.00002 mm⁻¹ (0.03%). This analysis shows that the proposed algorithm can effectively measure the local curvature when a global scale of the vessel diameter is used as a window size.

Axial Twist

Musculoskeletal motion or cardiac pulsatility can induce torsional moments that result in axial twist of the vessel. The twisting of the vessel is a volumetric quantity that cannot be derived by one centerline path in one configuration. For example, a straight cylinder can twist axially without variation of curvature or torsion, as shown in Fig. 8a. In this sense, the axial twist is different from the aforementioned Frenet torsion metric. To overcome the limitations of the Frenet formula for describing axial twist, we developed a new twisting metric that more completely measures 3D characteristics of the vessel geometry. Specifically, we defined a new metric, which we refer to as the “angle of separation,” as the angle between adjacent branches. Axial twist is determined by the difference between the angle of separation of a current configuration θ and that of a reference configuration Θ. In the simplest case, illustrated in Fig. 8a, the vessel is straight in both configurations, and hence the twisting angle is θ − Θ.

FIGURE 8

Methods for quantifying axial twisting of blood vessels. (a) Twisting angle calculation algorithm was applied to a straight vessel. (b) Angle of separation calculation algorithm was applied to a vessel with non-zero torsion. A vessel was divided into small segments such that each segment can be assumed to be planar

During vessel deformation, however, bending and twisting effects are superimposed, and the vessels are not necessarily coplanar. Therefore, the bending component was separated from the total deformation to obtain a pure twisting component as follows. First, the centerline of the vessel was divided into small segments such that each subdivided segment of the centerline could be assumed to be planar. Second, a datum curve from the first branch to the next branch was found by means of the rotation axis $\ifmmode\expandafter\vec\else\expandafter\vec\fi{\omega }_{i} = {\ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{i} \times \ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{{i + 1}} } \mathord{\left/ {\vphantom {{\ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{i} \times \ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{{i + 1}} } {{\left\| {\ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{i} \times \ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{{i + 1}} } \right\|}}}} \right. \kern-\nulldelimiterspace} {{\left\| {\ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{i} \times \ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{{i + 1}} } \right\|}}$ and rotation angle $\psi _{i} = \cos ^{{ - 1}} {\left( {{\ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{i} \cdot \ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{{i + 1}} } \mathord{\left/ {\vphantom {{\ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{i} \cdot \ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{{i + 1}} } {{\left( {{\left\| {\ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{i} } \right\|} \cdot {\left\| {\ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{{i + 1}} } \right\|}} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {{\left\| {\ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{i} } \right\|} \cdot {\left\| {\ifmmode\expandafter\vec\else\expandafter\vec\fi{n}_{{i + 1}} } \right\|}} \right)}}} \right)}$ in each segment (Fig. 8b). Specifically, the datum points B _i were calculated as follows:

$$ {\overrightarrow{{P_{{i + 1}} B}}} _{{i + 1}} = Rot(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\omega } _{i} ,\psi _{i} ) \cdot {\overrightarrow{{P_{i} B}}} _{i} , $$

(11)

where

$$ Rot(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\omega } _{i} ,\psi _{i} ) = e^{{[\ifmmode\expandafter\vec\else\expandafter\vec\fi{\omega }_{i} ]\psi _{i} }} \quad \hbox{and} \quad [\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\omega } _{i} ] = {\left( {\begin{array}{*{20}c} {0} & {{ - \omega _{{iz}} }} & {{\omega _{{iy}} }} \\ {{\omega _{{iz}} }} & {0} & {{ - \omega _{{ix}} }} \\ {{ - \omega _{{iy}} }} & {{\omega _{{ix}} }} & {0} \\ \end{array} } \right)} $$

Third, the angle of separation, Θ, was determined in a reference configuration by means of the identified datum curve. A counterclockwise position of the distal branch origin relative to the proximal branch origin was considered as a “positive” angle of separation. This algorithm was applied to a second dataset to get the angle of separation in a different position, θ, and then the twisting angle was calculated by subtraction of those angles of separation, θ − Θ. With the same sign convention as the angle of separation, a counterclockwise twisting angle was considered positive. Lastly, the axial twist rate was determined by division of the twisting angle over the segment length.

Verification of the Algorithm to Calculate the Angle of Separation

The proposed algorithm for quantifying the twisting angle was verified by means of a software phantom. The angle of separation was quantified in a vessel of known geometric configuration with high torsion. The analytic vessel comprised two planar arcs that were connected with a 90° angle, as shown in Fig. 9a. The upper arc was located on the z–x plane, while the lower arc was on the y–z plane (Fig. 9b and c). Six branches had known angles of separation (−30°, −60°, 180°, 150°, 120°) with respect to the first branch.

FIGURE 9

Software phantom used to verify new metric to quantify axial twisting of vessels. Geometry consists of two perpendicular arcs at the midpoint, as illustrated in (a) 3D view, (b) z–x plane view, and (c) y–z plane view

The verification test cases consisted of evaluating the angle of separation between the first branch and the five subsequent branches. Geometrically, the segments between Branch 1 and Branch 5, and Branch 1 and Branch 6 have high torsion because the segment between Branch 5 and Branch 6 is located on the y–z plane whereas Branch 1 is located on the z–x plane. For these test cases, the estimated angles of separation were −30.0°, −60.0°, 179.2°, 150.1°, 120.2°, which resulted in an estimation error of 0.2 ± 0.3°. This analysis shows that the proposed algorithm to quantify the angle of separation in the vessel is robust and accurate for these test cases with high torsion.

Results

To demonstrate the methods described in this paper, we quantified deformations in examples of the abdominal aorta, common iliac artery, SFA, and LAD. These vessels were chosen to demonstrate applicability of the methods for a variety of vessel sizes.

Generation of the Centerline Path using Fourier Smoothing

For the SFA in the bent-leg position, 48-mode Fourier smoothing was optimal for the approximately 500 centroids defined at 0.7 mm intervals. The 48-mode smoothing process satisfied the convergence rate criteria established, effectively representing both the low and high curvature region. A 35-mode Fourier smoothing was used for the SFA in the supine position. For the abdominal aorta in the fetal position, 15-mode smoothing for the approximately 300 centroids at 0.5 mm intervals was enough because its shape is inherently quite smooth. A 35-mode smoothing was required for the common iliac artery in the fetal position. For the supine position, 16- and 15-mode Fourier smoothing was used for the abdominal aorta and the iliac artery, respectively. For the coronary artery in systole, 38-mode smoothing for the approximately 370 centroids at 0.3 mm intervals was optimal to effectively represent the local curvature variations of the LAD. In diastole, 34-mode Fourier smoothing was used for the coronary artery. Next, longitudinal strain, axial twist, and curvature change were calculated in each example.

Deformation Metrics for the Coronary Artery

The geometry of the LAD (diameter: 2.5 ± 0.8 mm) at the peak-systolic and end-diastolic phases of the cardiac cycle was quantified to investigate the effect of the pulsatile cardiac motion on the artery (Fig. 1). Ostia of two branch vessels including the LCX were used as fiducial landmarks between the two cardiac phases (Fig. 10a). Although a short segment was used for the strain calculation due to the location of the side branches, an approximately 110-mm-long segment was used for the curvature comparison beyond the landmarks. From the end-diastolic to peak-systolic phases, the LAD shortened by 6.7% (diastole: 19.2 mm, systole: 17.9 mm), twisted clockwise by 6.0° (twist rate: 0.3°/mm), and the curvature increased by 0.077 ± 0.14 mm⁻¹ on average (diastole: 0.10 ± 0.08 mm⁻¹, systole: 0.18 ± 0.15 mm⁻¹). When changes in mean curvature were compared, the distal half of the LAD ($\Updelta \ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{distal}}}}$: 0.14 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{diastole}}}}$: 0.13 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{systole}}}}$:0.27 mm⁻¹) exhibited approximately four times higher curvature change than the proximal half of the LAD ($\Updelta \ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{proximal}}}}$: 0.03 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{diastole}}}}$: 0.07 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{systole}}}}$: 0.10 mm⁻¹). For the local curvature change, as shown in Fig. 11a, the maximum curvature change $(\Updelta \kappa ^{*}_{{\max }} )$ was 0.75 mm⁻¹ ($\kappa^{{\text{*}}}_{{{\text{diastole}}}}$: 0.05 mm⁻¹, $\kappa ^{*}_{{{\text{systole}}}}$: 0.80 mm⁻¹). For geometric interpretation, locations at the LAD corresponding to the maxima of the curvature graph are illustrated in Fig. 11b.

FIGURE 10

Selected segments of each artery for quantifying the vessel deformation. (a) Left anterior descending coronary artery, (b) infrarenal aorta and left common iliac artery, and (c) left superficial femoral artery were used for geometric analysis

FIGURE 11

Local variation of curvature change along the vessel length. (a) Curvature variation for the LAD coronary artery was plotted and maxima of the curvature, labeled as C₁–C₈, were identified in the systolic phase. (b) Geometric locations of the corresponding maxima were labeled as well in the solid model of the coronary artery. (c) Curvature variation for the left SFA was plotted along the vessel length. (d) Circumscribed circle at the maximum curvature was illustrated for geometric interpretation of the curvature

Deformation Metrics for the Abdominal Aorta

The deformation of the infrarenal abdominal aorta (diameter: 16.3 ± 1.3 mm) was quantified among two different body positions: supine and fetal positions (Fig. 2c and d). The renal arteries and aortic bifurcation were used as fiducial landmarks (Fig. 10b). Although the lumbar arteries were visible in the image, they were not used for the landmarks because of small intervals of their locations and ambiguous ostia. For this subject, 13.4° clockwise axial twisting (twist rate: 0.14°/mm) and −4.1% longitudinal strain (supine: 97.9 mm, fetal: 93.8 mm) were observed. On average, from the supine to fetal positions, the curvature increased by 0.0007 ± 0.0047 mm⁻¹ (supine: 0.0086 ± 0.0030 mm⁻¹, fetal: 0.0093 ± 0.0043 mm⁻¹). Distinctive local changes in mean curvature along the length were not observed in the abdominal aorta on the basis of the measurement at the proximal half ($\Updelta \ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{proximal}}}}$: 0.002 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{supine}}}}$: 0.006 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{fetal}}}}$: 0.008 mm⁻¹) and the distal half ($\Updelta \ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{distal}}}}$: 0.001 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{supine}}}}$: 0.011 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{fetal}}}}$:0.010 mm⁻¹). For the local curvature change, the maximum curvature change $(\Updelta \kappa ^{*}_{{\max }} )$ was 0.008 mm⁻¹ ($\kappa ^{*}_{{{\text{supine}}}}$: 0.007 mm⁻¹, $\kappa ^{*}_{{{\text{fetal}}}}$: 0.015 mm⁻¹).

Deformation Metrics for the Common Iliac Artery

Deformation of the left common iliac artery (diameter: 8.4 ± 1.6 mm) was quantified over a segment between the aortic bifurcation and the internal iliac artery (Fig. 2c and d). The origin of the common iliac artery was defined as the intersection between the aortic bifurcation plane and the centerline of the iliac artery (Fig. 10b). Then the arc length change of the common iliac artery centerline between its origin and the internal iliac artery was measured. From the supine to fetal positions, the iliac artery segment shortened by 2.2% (supine: 66.6 mm, fetal: 65.2 mm) and twisted counterclockwise by 1.5° (twist rate: 0.023°/mm). The curvature increased by 0.010 ± 0.012 mm⁻¹, on average (supine: 0.020 ± 0.010 mm⁻¹, fetal: 0.031 ± 0.013 mm⁻¹) although distinctive local changes were not observed in the iliac artery on the basis of the mean curvatures at the proximal half ($\Updelta \ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{proximal}}}}$: 0.011 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{supine}}}}$: 0.018 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{fetal}}}}$: 0.029 mm⁻¹) and the distal half ($\Updelta \ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{distal}}}}$: 0.010 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{supine}}}}$: 0.023 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{fetal}}}}$: 0.033 mm⁻¹). For the local curvature change, the maximum curvature change $(\Updelta \kappa ^{*}_{{\max }} )$ was 0.020 mm⁻¹ ($\kappa ^{{\text{*}}}_{{{\text{supine}}}}$: 0.017 mm⁻¹, $\kappa ^{{\text{*}}}_{{{\text{fetal}}}}$: 0.037 mm⁻¹).

Deformation Metrics for the Superficial Femoral Artery

Deformation of the left SFA (average diameter: 6.6 ± 0.6 mm) caused by body change from the supine to the bent-leg positions was measured (Fig. 2a and b). The profunda femoris and five muscular branches, including the descending genicular arteries defined five segments of the SFA, as illustrated in Fig. 10c. For this subject, SFA shortening of 8.8 ± 4.4% was observed from the supine (71.9 ± 50.0 mm) to bent-leg (65.4 ± 46.4 mm) positions. For axial twisting angle, the absolute value was taken in each segment, resulting in the average twisting of 0.8 ± 0.4°/mm. On average, curvature increased by 0.014 ± 0.022 mm⁻¹ (supine: 0.008 ± 0.005 mm⁻¹, bent-leg: 0.022 ± 0.024 mm⁻¹) while the changes in curvature between the supine and bent-leg positions were more pronounced in the distal portion of the SFA ($\Updelta \ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{distal}}}}$: 0.031 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{supine}}}}$: 0.008 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{bent}}}}$: 0.039 mm⁻¹) compared with the proximal ($\Updelta \ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{proximal}}}}$: 0.007 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{supine}}}}$: 0.009 mm⁻¹, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\kappa }_{{{\text{bent}}}}$: 0.016 mm⁻¹) and middle (${\Updelta \overline{\kappa } _{{{\text{middle}}}}}$: 0.006 mm⁻¹, $\overline{\kappa } _{{{\text{supine}}}}$: 0.006 mm⁻¹, $\overline{\kappa } _{{{\text{bent}}}}$: 0.012 mm⁻¹) portions of the SFA. Curvature variation for both positions along the SFA is shown in Fig. 11c., and the maximum curvature change $(\Updelta \kappa ^{*}_{{\max }} )$ was 0.14 mm⁻¹ ($\kappa ^{*}_{{{\text{supine}}}}$: 0.01 mm⁻¹, $\kappa^{*}_{{{\text{bent}}}}$: 0.15 mm⁻¹). In addition, a circumscribed circle at the maximum curvature is plotted on the curvature plane with the vessel intensity view for geometric interpretation, as shown in Fig. 11d.

Discussion

As more innovative endovascular devices are developed, the knowledge of dynamic changes in the vascular system will become increasingly important in ensuring the safety and efficacy of these devices. Regulatory agencies require specific benchtop testing of devices in a manner reflecting the in vivo environment in terms of the duty cycle and number of cycles. The superficial femoral and iliac arteries are particularly susceptible to multi-modal deformations due to repetitive hip and knee flexion, which can occur, for example, during walking. The coronary arteries experience dynamic forces due to cardiac motion, and the aortic motion can be induced by cardiac, respiratory, and musculoskeletal motion. Understanding these cyclic changes in arterial geometry is essential for understanding device fatigue. Therefore, more complete and practical methods are needed to quantify 3D arterial deformation. There is also a need to make these metrics readily accessible to device manufacturers and clinicians.

We have developed a systematic framework, with reduced operator dependency, for generating the centerline path of a vessel by employing Fourier smoothing. To do so, we generated a reference centerline path of the vessel by calculating the centroid of the segmented lumen cross section. This irregularly positioned centerline connecting the centroids was then gradually smoothed by an increasing number of Fourier smoothing modes. Due to the competing characteristics of the exactness and smoothness as a result of the smoothing operation, exactness constraints would provide a lower limit of the smoothing mode, whereas the smoothness constraints would provide an upper limit of the smoothing mode. Moreover, since the minimal Fourier smoothing mode is desirable provided that a sufficient exactness is guaranteed, we used the convergence criteria, which were a stricter condition than the exactness criteria, for identifying the optimal Fourier smoothing mode. Although the smoothness criteria were not employed in developing these methods, we confirmed the smoothness of the resultant centerline by means of the noise ratio while examining whether the maximum curvature was geometrically admissible.

More importantly, we developed a consistent criterion for different arterial centerlines when determining the level of smoothness by employing the maximum distance between two successive smoothed centerlines as the convergence rate cost. Although the cost ideally would converge to zero in the limit, the finite interval between spline points resulted in residuals (Fig. 4g). Since the criteria are required to be robust to random factors including the image resolution, noise in the image, number of centroids, as well as the vessel size, the original irregularly positioned centroids, which involve maximum randomness, were not directly used to construct the cost. The use of smoothed centerlines, instead of the irregular centroid set, for establishing quantitative criteria allowed us to find a consistent criterion that could be applied to all image data sets, studied herein. Essentially, the process of examining convergence criteria for determining the optimal Fourier mode is equivalent to the visual comparison of successive centerlines in conventional methods.

The application of this method to various vessels of different size and image resolution illustrates a sufficient performance in terms of the exactness and smoothness of the centerline path, measured by the approximation error and the noise ratio. The SFA, especially for the bent-leg position, was one of the most challenging applications of smoothing because of its large variation in the curvature along the length: minimum curvature was as low as 0.0003 mm⁻¹, whereas maximum curvature was 0.15 mm⁻¹ at the distal portion of the SFA. The noise ratio for the original centroid data set was 34% with a maximum Frenet curvature of 2.0 mm⁻¹. For the SFA in the supine position, the noise ratio was 15% and the maximum Frenet curvature was as high as 20.8 mm⁻¹, undoubtedly resulting from the noise. On the contrary, the maximum Frenet curvature of the smoothed centerline significantly decreased to 0.03 and 0.17 mm⁻¹ for the supine and bent-leg positions, respectively, resulting in 0% noise ratio. Consequently, the Fourier smoothing method on the basis of the identified optimal mode enabled an effective elimination of spurious high spatial frequencies while preserving a wide spectrum of real curvature. Overall, for all smoothed centerlines, the approximation error was 0.22 ± 0.08 mm (38 ± 13% of the pixel size) and the noise ratio was 0.04 ± 0.07% as compared with 51 ± 30% for the original irregular centroid sets. The small noise ratio was caused by one coordinate for the smoothed aorta centerline (supine) and two coordinates for the coronary (systole) that exhibited spurious high Frenet curvature larger than the inverse of the vessel radius. However, when the proposed curvature metric based on the diameter-window size was used, the curvature values were within a reasonable range.

While Fourier smoothing could effectively reduce sharp perturbations—high spatial frequencies—of the centroids caused by small branch vessels or image noise, segmentations at the ostia of relatively large vessels such as the celiac, renal and SMA required a different segmentation algorithm in order to eliminate the effect of segmentation “leaking” (Fig. 3a and b). A curvature-based 2D level set segmentation technique enabled us to detect consistent centroids of the main vessel without perturbation by the branch vessels (Fig 3f).

The vessel length between branches was determined by projecting the centroid of the ostia of the branches onto the centerline path of the main artery. This definition was essential for detecting consistent branch location between different image volumes. Detection of branch vessels for longitudinal strain calculations was performed such that the interval distance between identified branches was longer than the vessel diameter ensuring robustness to the measurement error inherent in a finite voxel size. In a pilot study applying these methods, we observed shortening of the SFA caused by musculoskeletal movement. The anatomic location of the SFA, which continues down the thigh from anterior to posterior with respect to the femur, may induce compression of the SFA caused by hip and knee flexion. The shortening of the SFA from the supine to flexed positions is consistent with our previous in vivo study10 (−13 ± 11%), and a cadaver study45 (mid SFA: −5%, distal SFA: −14%). However, the smaller strain in this study as compared to our previous in vivo study may be related to less elastic vessels of the older subject and a smaller hip flexion angle although a larger study is needed. Coronary artery shortening was observed from the diastolic to systolic phases, likely related to the changes in ventricular volume. The observed strain of the LAD was similar to the value reported in a previous study13 (4.0 ± 1.8%) despite the difference in analysis methods and subjects. Further investigations will be required to quantify coronary longitudinal strain and achieve statistically significant results.

The skeletonizing process of the volumetric vessel into a centerline path may add spurious curvature because of noise in the image data or segmentation error inherent in data processing. Consequently, curvature can be overestimated if an infinitesimal segment is used for the measurement. In an attempt to avoid these limitations, we have proposed that a vessel diameter is an appropriate window size for curvature calculation based on the geometric definition of curvature—the inverse of the radius of a circumscribed circle around sampled points. The verification study with an analytic space curve showed that this algorithm was accurate enough to detect global characteristics of the vessel curvature. When this method was applied to actual image data, pronounced curvature change in the SFA occurred in the distal portion of the SFA, approximately at the level of the adductor hiatus. This finding is consistent with that of a previous study.1 Moreover, the average curvature value in the supine position was in the similar range of that in the literature53 (0.006 ± 0.009 mm⁻¹).

The circumscribed circle at the maximum curvature helped us to understand the geometric interpretation of the curvature. For the coronary artery, curvature range of the LAD in this study was within those reported in previous studies13,23,28 although individual anatomic variation along the length would have a greater effect on the numerical values. We also observed a greater curvature change in the distal LAD than the proximal portion which is consistent with the literature.28 However, a much larger curvature and cyclic curvature change may be related to our subject’s anatomic specificity in the distal LAD, as illustrated in Fig. 11a and b.

A significant increase in curvature of the common iliac artery was observed from the supine to fetal positions (0.020 ± 0.010 mm⁻¹, 0.031 ± 0.013 mm⁻¹), which was strongly related to the anatomic location of the common iliac artery adjacent to the hip joint. The curvature in the abdominal aorta also increased from the supine to fetal positions (0.0086 ± 0.0030 mm⁻¹, 0.0093 ± 0.0043 mm⁻¹). This increase in curvature may be attributed to the curvature change of the common iliac arteries due to hip flexion or the spine influencing the shape of the abdominal aorta via the lumbar arteries, although further statistical study among a larger subject population is required to confirm these results. Curvature of the common iliac artery and abdominal aorta measured in this study was in a similar range compared with those in a previous study33 (iliac: 0.022 ± 0.008 mm⁻¹, aorta: 0.014 ± 0.003 mm⁻¹).

For quantifying the axial twisting angle, we developed a new method that can be applied to any geometric shapes of vessels without losing 3D information. The proposed algorithm is unique in that it quantifies the axial twisting of the object with varying curvature and torsion. We verified this algorithm by using software phantoms and found it to be valid in all segments with various kinds of torsion. Compared with our previous in vivo results10 (60 ± 34°, 0.28 ± 0.17°/mm), significantly larger twisting of the SFA was observed in this most recent study. Besides the variations in population or methods to calculate the twisting angle, we think this difference resulted from the fact that local changes along the SFA were ignored in the previous study. If only the profunda femoris and the most distal branch were used, the twisting angle between those branches was −39.4° (−0.11°/mm), which showed a similar result to our previous study.

This present study had several limitations. First, the quantification methods depend inherently upon the limitation of the imaging modalities despite significant improvements in image resolution that have been made in recent years. For example, the inhomogeneous gradient field in MRI may induce spurious deformation of the imaged vessel. Thus gradient-warp correction for the MRI is essential prior to geometric quantification. With regard to the cardiac-gated CT, misregistration of the images during a cardiac cycle potentially caused by the irregular heartbeat may also cause spurious deformation of the vessel. In addition, small vessels such as those in the distal portion of the coronary arteries may limit the exactness of the vessel representation due to an insufficient number of pixels across the vessel diameter. These types of limitations can be minimized as more reliable and accurate medical imaging systems are developed. Second, although manual processing was significantly reduced in the proposed framework, minimal user intervention was necessary in detecting the ostia or in removing the branch structure for the centerline generation. Direct 3D segmentation methods may help to improve the consistency of geometric analysis. Third, all of the metrics were calculated from centerline paths of volumetric blood vessels. Thus the proposed metrics do not reveal any information about the deformation of the surface of the vessel, which may be important especially for large vessels such as the thoracic or abdominal aorta. There is also an inherent limitation of Fourier smoothing used for generating centerline paths.30 Mirroring of the nonperiodic centroid sets was employed to ensure periodicity since vessel centerlines are generally open space curves. Fourth, we assumed circular vessel cross sections, which are not necessarily accurate for diseased vessels. Further studies are required to quantify deformations of blood vessels with atherosclerosis or aneurysmal degeneration. Lastly, the data used in the longitudinal strain and twisting metrics required determination of branch locations. The strain and twisting angle metrics were discontinuous measurements since we used a finite number of branches as fiducial landmarks to compare different configurations. Thus, there is no information available in the segment between branches. Although the curvature is a continuous variable along the vessel, the strict comparison between different configurations is only possible at the branch locations. The comparison between segments is an approximate evaluation at the linearly interpolated locations between identified branches. More fiducial markers, such as calcification, will help improve the limited amount of spatial information that can be obtained.

While we presented four examples at different anatomic locations (the SFA, abdominal aorta, common iliac artery, and coronary artery), we believe that the methods described herein are applicable to quantification of many other 3D vessel deformations. For the clinical implications, measured parameters of longitudinal strain, twisting angle, or curvature change can be studied as dynamic factors indicative of stimulants for vascular remodeling or sites predisposed to occlusive disease. Moreover, deformation metrics obtained with these methods can be directly used to design benchtop testing parameters for cyclic longitudinal compression (or tension), axial twisting, and bending tests.

Conclusions

We have developed general methods to quantify 3D vessel deformations due to pulsatile and nonpulsatile forces. We illustrated these methods by applying them to examples including the deformation of the SFA, abdominal aorta, and common iliac artery caused by hip and knee-flexion and to the deformation of the coronary artery due to cardiac pulsatility.

On the basis of these examples, we believe these metrics for longitudinal strain, axial twist, and curvature change can be applied to many other examples beyond those illustrated herein. In addition, the proposed metrics have proven to be practical and straightforward to implement for benchtop tests aimed at replicating the in vivo condition and developing more durable endovascular devices. Further studies will be required to characterize deformation of diseased vessels that have asymmetric cross sections and nonuniform vessel properties.