Branching Morphology of the Rat Hepatic Portal Vein Tree: A Micro-CT Study

 

In contrast to the lung and the myocardium, the liver is a relatively homogeneous organ with fewer anatomic constraints on vascular branching. Hence, we hypothesize that the hepatic vasculature could more closely follow optimization of branching geometry than is the case in other organs. The geometrical and fractal properties of the rat hepatic portal vein tree were investigated, with the aid of three-dimensional micro-computed tomography data. Frequency distributions of vessel radii were obtained at three different voxel resolutions and fitted to a theoretical model of dichotomous branching. The model predicted an average junction exponent of 3.09. Hemodynamic model calculations showed that with generation, relative shear stress decreases. Branching angles were found to oscillate between those predicted by two optimality principles of minimum power loss and volume, and of minimum shear stress and surface. The liver shows a variation in branching morphology similar to that of other organs. Therefore, we conclude that anatomic constraints do not have a major perturbing impact.

INTRODUCTION

Thorough analysis of blood flow in vascular trees is ideally performed using the measured geometry of intact trees. A tree synthesized from statistical assumptions of a population of trees is a reasonable interim approach, because detailed data on the morphology of intact vascular trees are scarce. Vascular trees have been previously described in terms of the properties of so-called segments, which are defined as the vessel parts between two bifurcations in a tree.4 ^, 20 After establishing the geometry of the network of segments, it can be further analyzed using physical laws of fluid dynamics to predict distributions of blood flow and pressure throughout the branching system under investigation. Such studies may give important insight in the mechanisms through which particular organs are reperfused in normal physiological conditions or during pathology.

To date, a plethora of theoretical and numerical models on vascular branching has been published.1 ^, 2 ^, 9 ^, 11 ^, 15 ^, 16 Most of these studies report theoretical analyses of the relationship between the anatomical structure of the tree and one or more hemodynamic variables, such as shear stress,16 drag and power loss,15 and perfusion volume.9 Unfortunately, the bulk of these models are not well supported by empirical data. Previously, Kassab et al. built a statistical representation of the morphology of the pig coronary artery,4 ^, 10 which has been used in further studies in an attempt to explain its design.22 Zamir also used data on the human coronary arteries to investigate the fractal behavior of vascular networks.20 ^, 21 A problem with coronary and pulmonary arterial trees (the most commonly investigated trees) is that their branching structure may well be constrained by anatomic structures such as the bronchi or shell-like geometry of the myocardium. Moreover, these organs cyclically deform over a relatively large range and, hence, the vascular geometry is also dynamic. This means that any one ‘snapshot’ may not be representative of the average behavior of the tree.

The aim of this paper is to quantitatively describe the branching properties of the rat hepatic portal vein tree. The liver vascular network was chosen since its branching morphology is minimally affected by anatomic constraints or deformations. The three-dimensional (3D) vascular geometry is most conveniently obtained by 3D tomographic image methods, such as X-ray computer tomography (CT) and magnetic resonance imaging (MRI). Although these imaging methods have limited spatial resolution, actual segment diameters down to a certain dimension can be used with confidence. The 3D images were segmented and skeletonized. In addition to segment lengths and radii, junction exponents were calculated at the bifurcations, and a simple model of dichotomous branching was fitted to the data. As our 3D μ-CT images of the rat hepatic portal vein tree were obtained at three different levels of image resolution, the effect of resolution of the imaging system was also investigated. Additionally, we report data on angles at the bifurcations, which govern the efficacy of volume-filling and may play a key role in the mechanism of distribution of blood flow.

MATERIALS AND METHODS

Experiments

Specimen Acquisition

Male Sprague-Dawley rats weighing about 250 g were used. The study was approved by the Institutional Animal Care and Use Committee. The rats were anesthetized with an intraperitonial injection of 50 mg/kg Nembutal. A midline abdominal incision was used to expose the portal vein and canulated with polyethylene tubing. Heparin was injected to prevent blood clotting. The suprahepatic portion of the inferior vena cava was cut to allow exanguination. The liver venous system was then flushed with heparinized saline until the liver blanched uniformly. Subsequently radiopaque Microfil^® (MV-122; Flow Tech Inc Carver MA, USA), a Pb containing silicon polymer, was injected manually until the liver was uniformly colored to its edges, but before the Microfil^® emerged from the hepatic vein. Following this the portal vein and hepatic artery were ligated and the body placed in a refrigerator for two hours to permit polymerization. The liver was resected, divided into individual lobes and fixed in 10% neutral buffered formalin. The liver was then immersed in a sequence of 30, 50, 75 and 100% glycerin solutions, each for 24 h. The liver lobe was then suspended in a close-fitting thin-walled plastic tube and immersed in bioplastic (Aldon Corp. Avon, NY, USA). This set into a hard cylinder. The specimen was then scanned in the μ-CT scanner.

Image Reconstruction

Specimens were scanned intact at two resolutions by the Mayo μ-CT system as described previously.3 Briefly, it consists of a spectroscopy X-ray source with a molybdenum anode and zirconium foil filter so that the Kalpha radiation (17.5 keV) photons predominate the emitted X-ray spectrum. The specimen's X-ray image was converted to a light image in a thin Cesium Iodide (Thallium doped) crystal and this image was recorded on a Charge Coupled Device (CCD) array, consisting of $1024\times 1024$ pixels. The electronic signal from the CCD was recorded digitally and stored in a computer. This image was generated at each of 721 equispaced angles of view around 360°. These digital data were then used to reconstruct the 3D image using a modified Feldkamp reconstruction algorithm. The lens that focused the light image onto the CCD array was adjusted to generate 20 μm or 5.9 μm on-a-side pixels, and there-by reduced the volume imaged proportionality. The 20 μm voxel image was also converted into a 40 μm image.

The resulting 3D images were displayed and regions of interest were extracted using image analysis software (Analyze^® 7.0; Biomedical Imaging Resource, Mayo Clinic, Rochester, MN). Subsequently, the images were segmented and skeletonized with software developed in collaboration with our group (Tree Analyzer 2.2, The Multidimensional Image Processing Lab, Penn State University, University Park, PA). A detailed description of that model-based vascular tree analysis software was previously published.18 The obtained information included the mean cross-sectional area A of the segments, the segment length L, the segment coordinates, as well as the connection to the parent segment. The segment radius (r) was calculated via $r = (A/\pi)^{\frac{1}{2}}$. Segment volume V was calculated as $V = A \cdot L$. The angle θ between two branch segments with vectors $\bf{v}_1$ and $\bf{v}_2$ was computed via:

$$\cos \theta = \frac {\bf{v}_1 \cdot \bf{v}_2}{|\bf{v}_1| |\bf{v}_2|} .$$

(1)

Effect of Image Resolution

Because of the finite image resolution due to X-ray transmission image blurring and partial volume effects, segments with radii below a certain cut-off radius $r_{\it c}$ were removed from the further numerical data analysis. The values for $r_{\it c}$ were determined to be that radius at which the maximum of the probability histograms of the radii occurred. Bin sizes equal to 0.5 and 10 times the image resolution were taken for the segment radii and lengths, respectively. For the radii, the downslope of the probability histograms were alligned, to visualize the effect of image resolution in quantitation of number of segments of different diameters. The probabilities of the segment lengths were normalized with respect to the maximal probability for each data set.

Analysis

Once the essential geometrical characteristics of the tree (i.e. radii, lengths and volumes of segments, and branching angles) are determined, one can analyze the branching morphology in terms of theoretical models. In the following, we will consider a simple model based on the assumption of dichotomous branching and characterization by an average bifurcation index and junction exponent. Furthermore, we will analyze branching with respect to various optimality principles as applied to branching angles, and so called structure-structure relationships22 between cumulative volumes, lengths and the radius of the root segment of the tree. We will also consider a model for relative shear stress, based on the resistance determined from Poiseuille's law. Finally, we analyze our tree with respect to its fractal dimension as defined by Zamir.21

Dichotomous Branching Model

Assuming only bifurcations, the following relationship between the radius of the mother segment ($r_0$) and the radii of the daughter segments ($r_1$ and $r_2$) can be established:

$$\label{junction}r^k_0 = r^k_1 + r^k_2 ,$$

(2)

where k is the junction exponent. The above equation is a generalized formulation of Murray's cube law, in which case k = 3. For any combination $(r_0, r_1, r_2)$, such that $r_1,r_2 < r_0$, Eq. (2) has a unique solution with respect to k. To further characterize the bifurcation, one can also use the bifurcation index λ, defined as:

$$\label{lambda}\lambda = \frac{r_2}{r_1}, r_2\leq r_1 .$$

(3)

Using Eqs. (2) and (3), the following relations between the mother and daughter radii were established:

$$\label{lambdak}r_1=(1+\lambda^k)^{-\frac{1}{k}}r_0 ,$$

(4a)

$$\label{lambdak}r_2=\lambda (1+\lambda^k )^{-\frac{1}{k}}r_0 .$$

(4b)

Furthermore, it was assumed that the entire tree could be represented by an average λ and k. Together with Eqs. (4a) and (4b), this constitutes a model of a branching tree, which we will refer to as the ($\lambda, k$)-model. Using this model, the mean radius $\bar{r}_n$ of segments belonging to the $n^{{\rm th}}$ generation of bifurcations was derived (see Appendix):

$$\label{barrn}\bar{r}_n=\frac{(1+\lambda)^n}{2^n}(1+\lambda^k)^{-\frac{n}{k}}r_0 .$$

(5)

Under the assumption that segments continue to branch into two daughter segments, the number of segments N at generation n is given by $N = 2^n$. Writing Eq. (5) in terms of N resulted in:

$$\label{dichmodel}\ln N = \beta (\ln r_0 - \ln \bar{r}_n) ,$$

(6)

where

$$\beta = \frac{k\ln2}{k\ln2-k\ln(1+\lambda)+\ln(1+\lambda^k)} .\label{beta}$$

(7)

Equation (6) was fitted to the experimental data to obtain parameter β.

Branching Angles

At each bifurcation, the angle $\theta_0$ between the two daughters was computed. In addition, the angles between mother and daughter segments were calculated. These were denoted as $\theta_1$ and $\theta_2$, where $\theta_1 \leq \theta_2$. Based on the definitions of k (Eq. (2)), and λ (Eq. (3)), optimal values for the branching angles at the bifurcations can be calculated.15 Minimization of lumen volume and pumping power results in:

$$\label{princ1}\cos \theta_0 = \frac{(1+\lambda^k)^{4/k}-\lambda^4-1}{2\lambda^2} ,$$

(8)

whereas minimization of lumen surface and total shear force on the endothelium gives:

$$\label{princ2}\cos \theta_0 = \frac{(1+\lambda^k)^{2/k}-\lambda^2-1}{2\lambda} .$$

(9)

These angles were calculated and validated using the experimental data.

Structure-Structure Relationships

Murray derived his cube law (k = 3 in Eq. (2)) via minimization of a cost function consisting of a term for viscous power dissipation and a term for metabolic power dissipation. In an effort to generalize Murray's law for an entire vascular tree, Zhou et al. (1999) proposed an empirical relation for the equivalent resistance to flow in a subtree. In their model, this resistance is dependent on the cumulative volume $V_c$ and cumulative length $L_c$ of a subtree. After subsequent minimization of the energy cost function, the model predicted the following structure-structure relationships:

$$\label{VL}\frac{V_{c}}{V_{{c},\max}} = \left(\frac{L_{c}}{L_{{c},\max}}\right)^\frac{5}{\epsilon'+1}$$

(10a)

$$\label{VL}\frac{V_{c}}{V_{{c},\max}} =\left(\frac{r_0}{r_{0,\max}}\right)^\frac{20}{3\epsilon'-2} .$$

(10b)

Here $V_{{c},\max}$ and $L_{{c},\max}$ are volume and length of the total tree under consideration, whereas $r_{0,\max}$ is the radius of the root segment of the entire tree. The parameter $\epsilon'$ is the ratio of metabolic (i.e. cost of making and maintaining blood volume) to viscous power loss.8

A relation between the cumulative volume $V_{c}$ of a subtree and the radius of the root segment $r_0$ was also derived from the proposed ($\lambda,k$)-model. Assuming λ = 1 and k = 3, the number of branches N at generation n equals:

$$N r_n^3=r_0^3 ,$$

(11)

Under the assumption that segment length is proportional to the segment radius with proportionality constant α ($L_n = \alpha r_n$), the total volume $V_n$ of a generation of segments is given by:

$$\label{genvol}V_n=N \pi r_n^2 L_n = \alpha \pi N r_n^3 =\alpha \pi r_0^3 .$$

(12)

Hence, Eq. (12) implies the total volume in each generation is the same. Since there are $n = \log_2 N$ generations, the total volume of a subtree is given by:

$$\label{cumvol}V_{c}=n V_n = 3 \alpha \pi r_0^3 \log_2\frac{r_0}{r_n} .$$

(13)

We subsituted $r_n$ by the minimal resolvable radius, and tested Eq. (13) against the experimental data.

Relative Shear Stress

Fluid shear stress acting on the vascular wall has been proposed to be a major determinant of vascular structural adaptation. Therefore, we investigated the distribution of relative wall shear stress in the network using previously published flow simulations.6 ^, 12 For this analysis, it was assumed that the conductance $G_{ij}$ in a segment between nodes i and j is given by Poiseuille's law:

$$G_{ij}=\frac{\pi r_{ij}^4}{8\mu L_{ij}},$$

(14)

where μ is the blood viscosity. The pressure difference over the segment ($\Delta P_{ij} = P_i - P_j$) is related to the flow$Q_{ij}$ via the conductance:

$$\Delta P_{ij} G_{ij}= Q_{ij} .\label{ohm}$$

(15)

The flow into a node was considered to be positive, whereas the flow out of a node was considered to be negative. By the law of conservation of mass, the sum of flows through the M nodes i must be equal to zero:

$$\sum_{j=1}^3 Q_{ij} = 0, (i = 1,2,\ldots,M)\label{kirchhoff}$$

(16)

Furthermore, it was assumed that the terminal branches were all at the same pressure. Given an inlet pressure, Eqs. (15) and (16) form a set of linear equations with the nodal pressures as unknowns:

$${\bf G} {\bf P}={\bf GP}_{\bf b},$$

(17)

where $\bf{G}$ is an $M \times M$ matrix containing the segment conductances, $\bf{P}$ is a $1 \times M$ vector with unknown pressures, and ${\bf GP}_{\bf b}$ is a $1 \times M$ column vector of conductances times pressures at the boundaries (terminals and root). This matrix equation was solved using singular value decomposition. The relative shear stress $\tau_{ij}$ in each segment was calculated from the obtained pressure differences:

$$\tau_{ij} = \frac{\Delta P_{ij} r_{ij}}{2L_{ij}}.$$

(18)

The computed shear stress was then averaged for each generation.

Fractal Dimension

Zamir (2001) proposed a definition of fractal dimension based on purely hemodynamic grounds. When the area ratio at a bifurcation γ is defined as:

$$\gamma=\frac{r^2_1+r^2_2}{r^2_0} ,$$

(19)

a fractal dimension D can be formulated for the magnification of the vessel cross-sectional area from one bifurcation to the next:

$$D=\frac{\ln2}{\ln2 - \ln\gamma} .$$

(20)

Using the definitions of k (Eq. (2)) and λ (Eq. (3)), D can be written as:

$$D=\frac{\ln2}{\ln2-\ln\,(1+\lambda^2)+\ln\,(1+\lambda^k)^{\frac{2}{k}}} .\label{fractal}$$

(21)

RESULTS

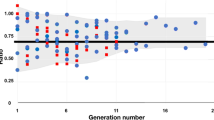
A maximum intensity projection of the 40 μm voxel resolution image is shown in Fig. 1. Figure 2A shows the probability histograms of the segment radii and lengths for the three data sets. The number of segments, radius of the root segment and the cut-off radius $r_{\it c}$ are summarized in Table 1 for each resolution. The correlation between segment length (L) and segment radius (r) is shown in Fig. 2B. Despite the considerable scatter about the regression, the slope of that regression is close to unity on a logarithmic scale. Figure 3 shows the distributions of segment radius, number and length with respect to the generation number (i.e. number of bifurcations from the root segment) for the 20 μm data set.

FIGURE 1.

Maximum intensity projection of the 3D μm-CT image of a rat hepatic portal vein tree (opacified with Microfil^®), obtained at a voxel resolution of 40 μm.

FIGURE 2.

(A) Probability histograms of the segment radii (top two panels) and segment lengths (lower panel) with voxel resolutions of 40 μm, 20 μm and 5.9 μm. (B) Log-log plot of segment length vs. segment radii of the three datasets combined. Segments with radii below a certain cut-off radius were discarded (see text for Effect of image resolution).

The probability distributions of the bifurcation index λ and the junction exponent k are shown in Fig. 4A. Mean and standard deviation found were: λ = 0.83 ± 0.14; k = 2.97 ± 2.87. The mean value for k was also calculated from the ($\lambda, k$)-model. Linear regression of Eq. (6) resulted in β = 2.97 (see Fig. 4B). Based on λ = 0.83, Eq. (7) gives k = 3.09.

The dispersion of the branching angles is shown in Fig. 5A. When the mother and two daughter segments lie within the same plane, $\theta_1 + \theta_2 = \theta_0$. We found that in 82% of the segments, the difference $|\theta_1 + \theta_2 - \theta_0|$ was less than 15°. This difference was less than 5° in 59% of the segments. Based on the mean $\lambda = 0.83$ and $k = 2.97, \theta_0$ would be 74.5° using Eq. (8) and 101.5° using Eq. (9). Interestingly, we found a mean $\theta_0 = 88.3^\circ$, which lies halfway between the angles based on the two proposed optimality principles (see Fig. 5A). The evolution of $\theta_0$ along a representative pathway in the tree is shown in Fig. 4B. Note that $\theta_0$ is oscillating between the values for the minimum surface and minimum volume models.

In regard to structure-structure relationships, the following numerical results were obtained. The ratio of metabolic to viscous power loss $\epsilon'$ was obtained from the relationship between normalized cumulative volume and normalized cumulative length ($\epsilon'$ = 3.63, $R^2$ = 0.94, see top panel Fig. 6A). This ratio has been determined in several other species and organs as recently summarized7 and ranged from 2.47 in rabbit omentum veins to 3.51 in human pulmonary artery. Linear regression of normalized cumulative volume vs. normalized radius of the root segment resulted in $\epsilon'$ = 3.07 ($R^2$ = 0.59, see lower panel Fig. 6A). In Fig. 6B, the relationship between $V_{c}$ and $r_0$ as given by the ($\lambda, k$)-model (Eq. (13)) was compared with the three data sets (α = 2.13, $R^2$ = 0.71).

TABLE 1. Statistical information of the three data sets.

The distribution of relative wall shear stress in the network is shown as a function of the number of bifurcations from the root in Fig. 7 for the 20 μm data set. The calculated wall shear stress was found to decrease about two to three orders of magnitude in the vascular network.

FIGURE 3.

Segment radius (top panel), number of segments (middle panel) and segment length (lower panel) with respect to generation. Data shown for the 20 μm data set.

FIGURE 4.

(A) Frequency histogram of the bifurcation index λ (top two panels) and junction exponent k (lower panel). (B) Plot of $\ln N$ vs. $\ln r_0 - \ln r_n$ for the combination of the three image resolutions (40 μm, 20 μm and 5.9 μm). Linear regression resulted in a slope of $\beta = 2.97$ with correlation $R^2$ = 0.94.

FIGURE 5.

(A) Top two panels: Frequency histogram of the maximum ($\theta_1$) and minimum ($\theta_2$) branching angles at a bifurcation. Means are 71.2° for $\theta_1$ and 28.4° for $\theta_2$. Lower panel: Frequency histogram of the angle $\theta_0$ between daughter segments at a bifurcation. Mean $\theta_0$: 88.3°. This value is in between theoretical angles computed from the minimum surface and minimum volume models. (B) Evolution of $\theta_0$ along a representative path in the tree. Optimum values from the minimum surface and volume models are indicated. Data shown obtained from image with 40 μm voxel resolution.

FIGURE 6.

(A) Top two panels: Relationship between normalized cumulative volume ($V_{c}/V_{{c},\max}$) and normalized cumulative length ($L_{c}/L_{{c},\max}$). Lower panel: Relationship between$V_{c}/V_{{c},\max}$ and normalized root radius ($r_0/r_{0,\max}$). (B) Relationship between cumulative volume$V_{\it c}$ and radius of the root $r_0$, based on the $(\lambda, k$)-model with $\lambda = 1$ and $k = 3$. Parameter $r_n$ is the minimal resolvable radius.

FIGURE 7.

Distribution of relative shear stress through the nextwork as calculated from the flow simulation model. Data shown are for the 20 μm data set.

The fractal dimension D was plotted against the branching parameters k and λ (see Fig. 8). Theoretical curves are shown for the mean $\lambda = 0.83$ (top panel), and for $k = 1$ and $k = 5$ (lower panel; 73% of the junction exponents are between these values). The mean and standard deviation of D was found to be $1.37 \pm 1.14$.

FIGURE 8.

Self-similarity of the vessel cross-sectional area upon branching. Top panel: Fractal dimension D vs. junction exponent k. Theoretical curve for $\lambda = 0.83$ is shown. Lower panel: Fractal dimension D vs. bifurcation index λ. Theoretical curves for $k = 1$ and $k = 5$ are shown.

DISCUSSION

In this study, we provided an overview of the distibutions and correlations of morphological and topological parameters of the rat hepatic portal vein tree. The liver was studied, because it is a relatively homogeneous organ with fewer anatomic constraints than e.g. the myocardium or the lung. Data of complete vascular trees were obtained through μ-CT imaging at three different voxel resolutions.

Because of the fractal, hierarchical nature of vascular trees, which span three orders of magnitude in scale, analysis of an entire tree at high resolution is computationally very intensive. In an attempt to deal with this problem, we used images obtained at different voxel resolutions and concatenated the data sets. Because of blurring and partial volume effects in the μ-CT data, the different data sets were pruned by discarding segments with radii below a certain cut-off radius. The results indicate that concatenation of the data sets results in a smooth transition.

Whereas segment radius is often used as an ordering parameter based on hemodynamic grounds, branching level provides a measure of the position of the segment along a pathway. The data were analyzed using both parameters. As shown in Fig. 3, the average segment radius clearly decreases with increasing generation. Our results indicate that segment length and branching level are less well correlated, which may be related to the high degree of scatter in the relation between segment length and segment radius (Fig. 2B). In agreement with measurements in the rat mesentery,12 the frequency distribution of generation numbers demonstrates the topological heterogeneity in the vascular tree.

A simple mathematical model of dichotomous branching of the vascular tree was established and applied to the experimental data. This so-called ($\lambda, k$)-model describes the relation between segment radius and the number of segments. Linear regression of the model equation resulted in an average junction exponent close to 3.0. Calculation of the junction exponents directly from the individual bifurcations yielded a relatively wide range of exponents, which is consistent with findings for the human coronary artery 20 and the pulmonary arterial tree.2 An average value of 3 is in agreement with Murray's cube law and is consistent with uniform shear stress throughout the tree. Using a junction exponent of 3, the ($\lambda, k$)-model was able to predict a relation between the radius of a segment, and the total vascular volume distal to that particular segment (see Fig. 6B).

The two branching angles between mother and daughter segments at a bifurcation were found to be asymmetric. This may reflect a distinction between vessels with a distributing function and vessels with a delivering function. A classification between delivering and distributing paths in vascular trees was earlier made for the human heart, 19 although no branching angles were reported in that study. In addition, we used our data to test two optimality principles,15 relating the branching angles at the bifurcations to the junction exponent and the bifurcation index. One principle minimizes lumen volume and pumping power, whereas the other principle minimizes lumen surface and total shear force on the endothelial tissue. We found that the mean branching angle was in between the optimal angles for minimum power loss and minimum drag. Along a pathway, the branching angle was found to be oscillating between the two angles. Therefore, it may be speculated that the design of the hepatic portal vein tree is based on a simultaneous optimization of volume, pumping power, lumen surface and shear force.

Murray's law of minimum pumping power and vessel lumen volume was generalized to be applicable to subtrees containing multiple generations of bifurcations by Zhou et al. (1999).22 Based on an empirical equation for the equivalent resistance to blood flow in an entire subtree, they derived power law relationships between cumulative tree volume, cumulative tree length, and radius of the root segment. The exponent of these structure-structure relationships (Eqs. (10a) and (10b)) depended on the ratio of metabolic to viscous power loss $\epsilon'$. In the rat hepatic portal vein tree, we calculated $\epsilon'$ to be 3.07 for the volume-radius relationship and 3.63 for the volume-length relationship. Compared to the recently published range of 2.47–3.51,8 these values are on the high side. A possible explanation could be that viscous power losses in the portal vein tree are lower than in anatomically constrained trees, such as the pulmonary arterial tree and the coronary arteries.

Murray's concept of minimal work predicts a volume flow proportional to the vessel radius cubed and is consistent with constant shear stress throughout the vascular network. In favor of this theory, the ($\lambda, k$)-model predicts that, on average, the junction exponent is close to 3. In contrast, the hemodynamic model calculations by us and others12 show that with increasing generation number, relative shear stress decreases and can vary over about two orders of magnitude, consistent with previously published measurements in a microvessel network of the rat mesentery.14 Although this may be partially explained by the fact that we assumed a constant blood viscosity in our calculations, it has been pointed out previously by Pries et al. 13 that vessels are exposed not only to shear stress, but also to transmural pressure. Design of vascular beds may therefore in part be based on a simultaneous optimization of both variables, i.e. local wall shear stress is maintained at a level dependent on the transmural pressure. The extension of Murray's original cost-function by a factor for smooth-muscle tone appears to harmonize Murray's law with the pressure-shear hypothesis.17 In addition, high-generation vessels typically lie on relatively long flow pathways, which experience low pressure gradients, and hence low wall shear stresses.

Besides reaching every part of the tissue or organ it serves, the vascular tree has to bring the flow velocity down by about three orders of magnitude, to facilitate oxygen exchange in the capillaries. Based on this hemodynamic function, it was hypothesized by Zamir that the distribution of segment cross-sectional area follows a fractal pattern.21 Analysis of the hepatic portal vein data showed a wide scatter in the distribution of this fractal dimension of hemodynamic function. Since the magnification of the cross-sectional area depends on the degree of assymetry of the bifurcation, the variability in D is related to the degree of variability of the bifurcation index and the junction exponent (Fig. 8). Zamir showed that, in human coronary arteries, the spectrum of fractal dimensions could be partially explained by the existence of a multi-fractal pattern.21

That the branching structure of vascular trees does not closely follow a simple, fixed pattern has been noted by investigators over many decades. One plausible reason for this observation is that measurements of the vascular trees are either insufficiently accurate, or the measurements are performed on a distorted representation of the vascular tree. These two possibilities would seem to have been reduced considerably by the use of high resolution μ-CT of intact rodent organs, or intact portions of large organs. Another plausible cause, which is the one we address in this current study, is the anatomic constraints placed on vascular tree branching, such as caused by the bronchi in the lung or the multi-layered shell-like structure of the myocardium, as well as their periodic distortion due to breathing and cardiac contraction. As the liver would appear to be the least affected by such constraints, we studied it, but it too shows a very similar variation to that observed in those other organs. This suggests that local anatomic constraints are not a major perturbing influence.

One variable that has not been well addressed is the fact that each organ has resting flow and increased flow to match the functional stress it occasionally experiences. The magnitude and duty-cycle of that modulation may have an impact such that a single snapshot of its vascular anatomy does not adequately reflect the functional optimization that it accomodates over time. That this modulation may be of importance is suggested by the fact that the femoral and renal arteries are of similar diameters, but that renal artery flow is relatively constant with little modulation, whereas the femoral artery accommodates a fivefold range of flow to accommodate intermittent exercise. Perhaps this means that we need to look for patterns in the branching geometry of the in situ vessels as they operate over the ususal range and duty-cycle of flows.

APPENDIX: CALCULATION OF THE MEAN RADIUS $\bar{r}_n$

When applying the ($\lambda, k$) model to a dichotomous branching tree, we can calculate the radii of each individual segment after i generations of bifurcations from the root segment. We denote by $r_{ij}, i=0,\ldots,n, j=1,2,\ldots, 2^i$ the radius of the segment $(i,j)$, and by $\bar{r}_i$ the average radius of the segments belonging to generation i. Since radii of daughter branches are given by Eq. (4) we can express the radius of any segment via $\lambda, k$ and radius of the root $r_{01}$. Radii of branches (1, 1) and (1, 2) are given by:

$$r_{11} = (1+\lambda^k)^{-\frac{1}{k}}r_{01} ,\quad r_{12} = \lambda (1+\lambda^k)^{-\frac{1}{k}}r_{01} .$$

(A.1)

Hence, the mean radius of the first generation ($\bar{r}_{1}$) is:

$$\bar{r}_{1} = \frac{(\lambda +1)}{2}(1+\lambda^k)^{-\frac{1}{k}}r_{01} .$$

(A.2)

Similarly, the segment radii for the second generation in the tree are:

$$\begin{array}{l}r_{21} = (1+\lambda^k)^{-\frac{1}{k}} r_{11} = (1+\lambda^k)^{-\frac{2}{k}} r_{01} ,\\r_{22} = \lambda (1+\lambda^k)^{-\frac{1}{k}} r_{11}= \lambda (1+\lambda^k)^{-\frac{2}{k}} r_{01} ,\\r_{23} = (1+\lambda^k)^{-\frac{1}{k}} r_{12}= \lambda (1+\lambda^k)^{-\frac{2}{k}} r_{01} ,\\r_{24} = \lambda (1+\lambda^k)^{-\frac{1}{k}} r_{12} = \lambda^2 (1+\lambda^k)^{-\frac{2}{k}} r_{01} .\end{array}$$

(A.3)

The mean radius of the second generation is:

$$\bar{r}_{2}=\frac{(\lambda^2+2\lambda+1)}{4}(1+\lambda^k)^{-\frac{1}{k}}r_{01}=\frac{(\lambda +1)^2}{2^2}(1+\lambda^k)^{-\frac{2}{k}}r_{01} .$$

(A.4)

By using mathematical induction, we found that the mean radius after n generations of bifurcations is:

$$\bar{r}_{n} = \frac{(\lambda +1)^n}{2^n}(1+\lambda^k)^{-\frac{n}{k}}r_{01} .$$

(A.5)

ACKNOWLEDGMENTS

We thank Patricia E. Beighley for preparation of the specimens, Steven M. Jorgensen and David F. Hansen for μ-CT scanning of the specimens, and Diane R. Eaker for help with the image analysis. This work was in part supported by NIH grants HL72255 and EB000305.