Symplectic perturbation series methodology for non-conservative linear Hamiltonian system with damping

Abstract

In this paper, the symplectic perturbation series methodology of the non-conservative linear Hamiltonian system is presented for the structural dynamic response with damping. Firstly, the linear Hamiltonian system is briefly introduced and its conservation law is proved based on the properties of the exterior products. Then the symplectic perturbation series methodology is proposed to deal with the non-conservative linear Hamiltonian system and its conservation law is further proved. The structural dynamic response problem with eternal load and damping is transformed as the non-conservative linear Hamiltonian system and the symplectic difference schemes for the non-conservative linear Hamiltonian system are established. The applicability and validity of the proposed method are demonstrated by three engineering examples. The results demonstrate that the presented methodology is better than the traditional Runge–Kutta algorithm in the prediction of long-time structural dynamic response under the same time step.

1 Introduction

The classical mechanics are divided into three categories, namely, Newtonian mechanics, Lagrangian mechanics, and Hamiltonian mechanics [1]. Newtonian mechanics take the particle as the object and focuses on the action relation of force. Newtonian mechanics mostly adopt an intuitive geometric method, which is more convenient and simpler than analytical mechanics in solving simple mechanical problems. Lagrangian mechanics [2] belongs to analytical mechanics. Lagrange introduced the concept of generalized coordinates and applied Darren Bell's principle to get the Lagrange equation, which is equivalent to Newton's second law. Hamiltonian mechanics [3] evolved from the Lagrangian mechanics and Hamiltonian mechanics have been widely applied in semiconductor, plasma, structural biology, and so on. Many dynamic governing equations can be derived from Hamiltonian principle [4,5,6]. The frequency-domain method [7, 8] and time-domain method [9, 10] are two common ways to solve the dynamic governing equations.

For systems with n degrees of freedom, the Hamiltonian system is represented by introducing n generalized coordinates and n generalized momentum. The energy of the system is expanded into a 2n-dimensional phase space. One of the basic characteristics of the Hamiltonian system is the symplectic structure, namely, the area of dual variables remain unchanged in the phase space. Lagrangian equation and Hamilton equation equivalently describe the same physical law while they are different in actual numerical calculation due to the difference in form. Feng and Qin [11] proposed the symplectic algorithm of the Hamiltonian system, which has the advantage of maintaining the architecture and is superior to the traditional algorithm in symmetry and conservation of spatial structure, especially in the stability and long-term tracking ability [12]. The theoretical analysis and a large number of numerical experiments illustrate that the symplectic algorithm is an effective method for medium-and long-term prediction of computational dynamics [13,14,15,16,17,18,19,20].

At present, the Hamiltonian system is mainly used to solve classical dynamic problems of plates and shells, such as vibration problems of isotropic plates and composite plates. For the vibration of isotropic thin plates, Bao et al. [21] studied the general analytical solution of free vibration of elastic thin plates under the Hamiltonian system. Zhong et al. [22] studied the free vibration of a rectangular thin plate with quadrilateral solidification and obtained the Hamiltonian analytical solution. Qing et al. [23] constructed the multi-symplectic form for the vibration of thin circular plates with central symmetry and studied the vibration of a thin circular plate under impact loading. On the vibration of medium-thickness plates, Yao et al. [24] developed the symplectic methodology to solve the problem of the Reissner plate. Bao et al. [25] studied the symplectic methodology for the Mindlin plate problems. Zhong et al. [26] established the general Hamiltonian variational principle and gave the direct method for the analytic solution of the Reissner–Mindlin plate bending problem. Wang and Tang [27] combined the Hamiltonian system with the finite element method and proposed a semi-analytic method, namely, the Hamiltonian element method, to analyze the vibration of orthotropic laminates. In other aspects, Xu et al. [28] studied the symplectic eigensolutions of viscoelastic thick-walled cylinder problems and established three symplectic methodologies of viscoelastic basic problems. Zou [29] gave the conjugate symplectic orthogonal analytical solution of the piezoelectric dielectrics electro-structure coupling problem and established the symplectic orthogonal model of ceramic materials.

In the field of non-conservative Hamiltonian system, Zhu et al. [30, 31] investigated the stationary solution of a dissipative Hamiltonian system with random excitation. Wang et al. [32] studied the non-conservative Hamilton system with non-conservative force by the Hamilton–Jacobi method. Zhang et al. [33] investigated the dissipative generalized Hamiltonian system with constraints and proposed the method for constructing the ordinary differential equation system in Euclidean space. Gao et al. [34] studied the non-smooth, non-convex and non-conservative Hamilton systems, in which the canonical dual/polar transformation methods and the associated bi-duality and triality theories are generalized into fully nonlinear dissipative dynamical systems.

Motivated by the previous work, the main contribution of this paper is to develop the symplectic perturbation series methodology is applied to deal with a non-conservative linear Hamiltonian system with damping. The non-conservative linear Hamiltonian system is expanded in power series form based on perturbation theory [35,36,37,38,39,40,41,42], and thus the non-conservative linear Hamiltonian system is transformed into a series of linear Hamiltonian canonical equations, which can be solved by the symplectic difference schemes. Besides, the non-homogeneous linear Hamiltonian system is converted to a standard linear Hamiltonian system based on linear transformation. The structural dynamic response problem with damping and external load is transformed into the non-conservative linear Hamiltonian system and thus the dynamic responses of the structure can be successfully obtained.

The remainder of this paper is organized as follows. The linear Hamiltonian system is briefly introduced and its conservation law is proved in detail in Sect. 2. In Sect. 3, the non-homogeneous linear Hamiltonian system is converted to a standard linear Hamiltonian system and the symplectic perturbation series methodology is applied to deal with the non-conservative linear Hamiltonian system with damping. In Sect. 4, the structural dynamic response problem with eternal load and damping is converted to the non-conservative linear Hamiltonian system. The symplectic difference schemes are presented for the structural dynamic response problem in Sect. 5. Three examples are accomplished to demonstrate the applicability and effectiveness of the proposed method in Sect. 6, followed by some conclusions.

2 Linear Hamiltonian system and its conservation law

Let $H$ a differentiable function of variables $z_{1} ,z_{2} , \cdots z_{n} ,z_{n + 1} , \cdots ,z_{2n}$ then the Hamiltonian system can be expressed as follows:

$$ \frac{{\text{d}{\varvec{z}}}}{{\text{d}t}} = {\varvec{J}}^{ - 1} H_{{\varvec{z}}} , $$

(1)

where

$$ {\varvec{z}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {z_{1} } \\ \vdots \\ {z_{n} } \\ \end{array} } \\ {z_{n + 1} } \\ \vdots \\ {z_{2n} } \\ \end{array} } \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} H_{{\varvec{z}}} = \left( {\begin{array}{*{20}c} {\frac{\partial H}{{\partial z_{1} }}} \\ \vdots \\ {\frac{\partial H}{{\partial z_{2n} }}} \\ \end{array} } \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varvec{J}} = \left( {\begin{array}{*{20}c} {\mathbf{0}} & {{\varvec{I}}_{n} } \\ { - {\varvec{I}}_{n} } & {\mathbf{0}} \\ \end{array} } \right), $$

(2)

in which ${\varvec{I}}_{n}$ is the $n \times n$ identity matrix; ${\varvec{J}}$ is an antisymmetric matrix satisfying ${\varvec{J}}^{ - 1} = {\varvec{J}}^{\text T} = - {\varvec{J}}$; $H({\varvec{z}})$ is named the Hamiltonian function.

Especially, if the function $H$ is a quadratic term of ${\varvec{z}}$, namely

$$ H\left( {\varvec{z}} \right) = \frac{1}{2}{\varvec{z}}^{{\text{T}}} {\varvec{Cz}}, $$

(3)

where ${\varvec{C}}$ is a symmetric matrix satisfying ${\varvec{C}}^{{\text{T}}} = {\varvec{C}}$, then the system is a linear Hamiltonian system.

The linear Hamiltonian system is expressed as follows:

$$ \frac{{{\text{d}}{\varvec{z}}}}{{{\text{d}}t}} = {\varvec{Bz}}, $$

(4)

where ${\varvec{B}} = {\varvec{J}}^{ - 1} {\varvec{C}}$ is an infinitesimal symmetric matrix.

The symplectic structure of the linear Hamiltonian system can be written as

$$ \omega = \sum\limits_{i = 1}^{n} {\text{d}z_{i} \wedge \text{d}z_{n + i} } , $$

(5)

where the notation “$\wedge$” denotes the exterior product. Equation (5) can be rewritten as

$$ \omega = \frac{1}{2}\left( {\text{d}{\varvec{z}}} \right)^{{\text{T}}} \wedge {\varvec{J}}\text{d}{\varvec{z}}\user2{.} $$

(6)

The conservation law of the linear Hamiltonian system is proved in Appendix A.

3 Symplectic structure of the non-conservative linear Hamiltonian system

3.1 Non-homogeneous linear Hamiltonian system

The non-homogeneous linear Hamiltonian system is expressed as

$$ \dot{\user2{z}} = {\varvec{Bz}} + \user2{G,} $$

(7)

where ${\varvec{B}}$ is an invertible matrix.

Let

$$ {\varvec{z}} = \tilde{\user2{z}} + {\varvec{c}}(t), $$

(8)

we can obtain

$$ \frac{{{\text{d}}{\varvec{z}}}}{{{\text{d}}t}} = \frac{{{\text{d}}\tilde{\user2{z}}}}{{{\text{d}}t}} + \frac{{{\text{d}}{\varvec{c}}}}{{{\text{d}}t}}. $$

(9)

Substituting Eq. (9) into Eq. (7) yields

$$ \frac{{{\text{d}}{\varvec{z}}}}{{{\text{d}}t}} = \frac{{{\text{d}}\tilde{\user2{z}}}}{{{\text{d}}t}} + \frac{{{\text{d}}{\varvec{c}}}}{{{\text{d}}t}} = {\varvec{B}}\left( {\tilde{\user2{z}}{ + }{\varvec{c}}} \right) + {\varvec{G}}\user2{.} $$

(10)

Make

$$ \frac{{{\text{d}}{\varvec{c}}}}{{{\text{d}}t}} = {\varvec{Bc}} + \user2{G,} $$

(11)

yields

$$ \frac{{{\text{d}}\tilde{\varvec {z}}}}{{{\text{d}}t}} = \user2{B}\tilde{\varvec {z}}. $$

(12)

Consequently, the non-homogeneous linear Hamiltonian system in Eq. (7) is transformed into a standard linear Hamilton system in Eq. (12). The conservation law of the linear Hamilton system is proved in Sect. 2.

3.2 Perturbation series expansion method for a non-conservative linear Hamiltonian system

For a non-conservative linear Hamiltonian system with damping, the matrix ${\varvec{B}}$ is no longer the infinitesimal symplectic matrix. Under such circumstances, the traditional symplectic structure, which is proved in Appendix A, is no longer maintained. In this section, the matrix ${\varvec{B}}$ in the non-conservative linear Hamiltonian system is decomposed into the infinitesimal symplectic matrix and perturbed matrix. The perturbation series expansion method is applied to deal with the perturbed matrix and the conservation law of the non-conservative linear Hamiltonian system is proved.

Firstly, the non-conservative linear Hamiltonian system is defined as follows:

$$ \dot{\user2{z}} = \left( {\tilde{\user2{B}}_{0} + \Delta {\varvec{B}}} \right){\varvec{z}}\user2{.} $$

(13)

Based on the perturbation series expansion method, the perturbed matrix $\Delta {\varvec{B}}$ can be approximated by the summation over a series of infinitesimal symplectic matrices, namely

$$ \Delta {\varvec{B}} \approx \overline{\user2{B}}_{0} + \sum\limits_{k = 1}^{\infty } {\varepsilon^{k} {\varvec{B}}_{k} } , $$

(14)

where $\overline{\user2{B}}_{0}$ and ${\varvec{B}}_{k}$ ($k = 1,2, \cdots$) are infinitesimal symplectic matrices. The detailed proof for Eq. (14) is described in Appendix B. Then the vector ${\varvec{z}}$ can be determined based on the perturbation series expansion method, namely,

$$ {\varvec{z}} = \sum\limits_{k = 0}^{\infty } {\varepsilon^{k} {\varvec{z}}_{k} } . $$

(15)

Substituting Eqs. (14) and (15) into Eq. (13) yields

$$ \frac{{\text{d}\left( {\sum\limits_{k = 0}^{\infty } {\varepsilon^{k} {\varvec{z}}_{k} } } \right)}}{{\text{d}t}} = \left( {\sum\limits_{k = 0}^{\infty } {\varepsilon^{k} {\varvec{B}}_{k} } } \right) \cdot \left( {\sum\limits_{k = 0}^{\infty } {\varepsilon^{k} {\varvec{z}}_{k} } } \right), $$

(16)

where ${\varvec{B}}_{0} = \tilde{\user2{B}}_{0} + \overline{\user2{B}}_{0}$ is an infinitesimal symplectic matrix. Expanding Eq. (16) yields

$$ \sum\limits_{k = 0}^{\infty } {\varepsilon^{k} \frac{{\text{d}{\varvec{z}}_{k} }}{{\text{d}t}}} { = }\sum\limits_{k,l = 0}^{\infty } {\varepsilon^{k + l} {\varvec{B}}_{k} {\varvec{z}}_{l} } . $$

(17)

Comparing the same terms $\varepsilon$ on each side of the Eq. (17), we can have

$$ \begin{gathered} \varepsilon^{0} :{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\text{d}{\varvec{z}}_{0} }}{{\text{d}t}} = {\varvec{B}}_{0} {\varvec{z}}_{0} , \hfill \\ \varepsilon^{1} :{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\text{d}{\varvec{z}}_{1} }}{{\text{d}t}} = {\varvec{B}}_{0} {\varvec{z}}_{1} + {\varvec{B}}_{1} {\varvec{z}}_{0} , \hfill \\ \varepsilon^{2} :{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\text{d}{\varvec{z}}_{2} }}{{\text{d}t}} = {\varvec{B}}_{0} {\varvec{z}}_{2} + {\varvec{B}}_{1} {\varvec{z}}_{1} + {\varvec{B}}_{2} {\varvec{z}}_{0} , \hfill \\ \cdots \hfill \\ \varepsilon^{n} :{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\text{d}{\varvec{z}}_{n} }}{{\text{d}t}} = \sum\limits_{i = 0}^{n} {{\varvec{B}}_{i} {\varvec{z}}_{n - i} } , \hfill \\ \ldots \hfill \\ \end{gathered} $$

(18)

The nominal value of ${\varvec{z}}$, i.e., ${\varvec{z}}_{0}$ can be determined based on the first formula in Eq. (18). On this basis, the first-order perturbation of ${\varvec{z}}$, i.e., ${\varvec{z}}_{1}$ is determined by the second formula in Eq. (18). Similarly, ${\varvec{z}}_{i}$ can be determined based on Eq. (18). Consequently, ${\varvec{z}}$ can be obtained by

$${\varvec{z}} = {\varvec{z}}_{0} + \varepsilon {\varvec{z}}_{1} + \varepsilon^{2} {\varvec{z}}_{2} + \cdots + \varepsilon^{n} {\varvec{z}}_{n} + \cdots.$$

(19)

The conservation law of the non-conservative linear Hamiltonian system is conducted in Appendix C.

4 Non-conservative linear Hamiltonian system for structural dynamic response problem

Considering the n-dimensional second order differential equations set for dynamic response of structures with eternal load and damping as follows

$$ \user2{M}\ddot{\user2{x}} + \user2{D}\dot{\user2{x}} + \user2{K}\user2{x} = {\user2{F}}({t}),$$

(20)

where ${\varvec{M}}$, ${\varvec{D}}$ and ${\varvec{K}}$ denote the mass matrix, damping matrix and stiffness matrix respectively; ${\varvec{x}}$ represents the structural displacements vector which is the function of $t$. ${\varvec{F}}(t)$ is the eternal loads acting on the structure; Generally, ${\varvec{M}}$ and ${\varvec{K}}$ are symmetric matrixes satisfying

$$ {\varvec{M}}^{\text{T}} = {\varvec{M}},{\varvec{K}}^{\text{T}} = {\varvec{K}}\user2{.} $$

(21)

To solve the Eq. (20), a generalized dual variables vector is defined as follows:

$$ \user2{y} = {\mathbf{M}}\dot{\user2{x}}.$$

(22)

Solving the velocity vector $\dot{\user2{x}}$ from Eq. (22) yields

$$ \dot{\user2{x}} = {\varvec{M}}^{ - 1} {\varvec{y}}\user2{.} $$

(23)

The derivative of generalized dual variables to $t$ can be denoted by

$$ \dot{\user2{y}} = \user2{M}\ddot{\user2{x}}.$$

(24)

Substituting Eq. (20) into Eq. (24) yields

$$ \dot{\user2{y}} = - \user2{D}\dot{\user2{x}} - \user2{K}\user2{x} + \user2{F}({t}). $$

(25)

Based on Eqs. (23) and (25), the original second-order differential equations set in Eq. (20) can be rewritten as

$$ \left( {\begin{array}{*{20}c} {\dot{\user2{x}}} \\ {\dot{\user2{y}}} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\mathbf{0}} & {{\varvec{M}}^{ - 1} } \\ { - {\varvec{K}}} & { - {\varvec{DM}}^{ - 1} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\varvec{x}} \\ {\varvec{y}} \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\varvec{F}}(t)} \\ \end{array} } \right). $$

(26)

Considering the perturbation form of Eq. (26) we can obtain

$$ \left( {\begin{array}{*{20}c} {\dot{\user2{x}}} \\ {\dot{\user2{y}}} \\ \end{array} } \right) = \left[ {\left( {\begin{array}{*{20}c} {\mathbf{0}} & {{\varvec{M}}^{ - 1} } \\ { - {\varvec{K}}} & {\mathbf{0}} \\ \end{array} } \right){ + }\left( {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & { - {\varvec{DM}}^{ - 1} } \\ \end{array} } \right)} \right]\left( {\begin{array}{*{20}c} {\varvec{x}} \\ {\varvec{y}} \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\varvec{F}}(t)} \\ \end{array} } \right). $$

(27)

The nominal equations set of Eq. (27) is expressed as follows:

$$ \left( {\begin{array}{*{20}c} {\dot{\user2{x}}} \\ {\dot{\user2{y}}} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\mathbf{0}} & {{\varvec{M}}^{ - 1} } \\ { - {\varvec{K}}} & {\mathbf{0}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\varvec{x}} \\ {\varvec{y}} \\ \end{array} } \right). $$

(28)

The nominal equations set is a standard linear Hamiltonian system, which can be expressed by

$$ \frac{{{\text{d}}{\varvec{z}}}}{{{\text{d}}t}} = {\varvec{Bz}}, $$

(29)

where

$$ {\varvec{z}} = \left( {\begin{array}{*{20}c} {\varvec{x}} \\ {\varvec{y}} \\ \end{array} } \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varvec{B}} = \left( {\begin{array}{*{20}c} {\mathbf{0}} & {{\varvec{M}}^{ - 1} } \\ { - {\varvec{K}}} & {\mathbf{0}} \\ \end{array} } \right). $$

(30)

The Hamilton function $H({\varvec{z}})$ can be expressed as

$$ H({\varvec{z}}) = \frac{1}{2}{\varvec{z}}^{{\text{T}}} {\varvec{Cz}},$$

(31)

where

$$ {\varvec{C}} = {\varvec{JB}} = \left( {\begin{array}{*{20}c} {\mathbf{0}} & {\varvec{I}} \\ { - {\varvec{I}}} & {\mathbf{0}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\mathbf{0}} & {{\varvec{M}}^{ - 1} } \\ { - {\varvec{K}}} & {\mathbf{0}} \\ \end{array} } \right)\user2{ = }\left( {\begin{array}{*{20}c} { - {\varvec{K}}} & {\mathbf{0}} \\ {\mathbf{0}} & { - {\varvec{M}}^{ - 1} } \\ \end{array} } \right).$$

(32)

The matrix ${\varvec{C}}$ is a symmetric matrix satisfying ${\varvec{C}}^{\text{T}} = {\varvec{C}}$. Consequently, the non-conservative linear Hamiltonian system for structural dynamic equations set is expressed as follows:

$$ \dot{\user2{z}} = \left( {{\varvec{B}} + \Delta {\varvec{B}}} \right){\varvec{z}} + {\varvec{G}}(t), $$

(33)

where

$$ \Delta {\varvec{B}} = \left( {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & { - {\varvec{DM}}^{ - 1} } \\ \end{array} } \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varvec{G}}(t) = \left( {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\varvec{F}}(t)} \\ \end{array} } \right). $$

(34)

5 Symplectic difference schemes for a non-conservative linear Hamiltonian system

As the non-homogeneous linear Hamiltonian system can be transformed into a standard linear Hamiltonian system, the symplectic difference schemes for the non-conservative linear Hamiltonian system is discussed in this section. In Sect. 3, the symplectic structure of the non-conservative linear Hamiltonian system is illustrated. Therefore, symplectic difference schemes can be adopted to solve the system.

For the first equation in Eq. (18), the Euler centered scheme is expressed as follows:

$$ {\varvec{z}}_{0}^{k + 1} ={\varvec{\varGamma}}_{{\tau_{0} }} {\varvec{z}}_{0}^{k} , $$

(35)

where

$${\varvec{\varGamma}}_{{\tau_{0} }} = \left( {{\varvec{I}}_{0} - \frac{\tau }{2}{\varvec{B}}_{0} } \right)^{ - 1} \left( {{\varvec{I}}_{0} + \frac{\tau }{2}{\varvec{B}}_{0} } \right). $$

(36)

Proposition 1

If B′ is infinitesimal symmetric, and |I + B′| ≠ 0, then $\left( {{\varvec{I}} + {\varvec{B}}^{\prime } } \right)^{{ - 1}} \left( {{\varvec{I}} - {\varvec{B}}^{\prime } } \right)$ is a symplectic matrix.

As ${\varvec{B}}_{0}$ is an infinitesimal symplectic matrix, then there exists a sufficiently small number $- \frac{\tau }{2}$ to make $- \frac{\tau }{2}{\varvec{B}}_{0}$ an infinitesimal symplectic matrix and $\left| {{\varvec{I}} + \left( { - \frac{\tau }{2}{\varvec{B}}_{0} } \right)} \right| \ne 0$. According to Proposition 1, ${\varvec{\varGamma}}_{\tau_0 }$ is a symplectic matrix.

For the second equation in Eq. (18), namely

$$ {\kern 1pt} {\kern 1pt} \frac{{\text{d}{\varvec{z}}_{1} }}{{\text{d}t}} = {\varvec{B}}_{0} {\varvec{z}}_{1} + {\varvec{B}}_{1} {\varvec{z}}_{0} , $$

(37)

in which the vector ${\varvec{z}}_{1}$ is irrelevant to ${\varvec{z}}_{0}$. Therefore, Eq. (37) can be treated as the non-homogeneous linear Hamiltonian system, which can be transformed into a standard linear Hamilton system, namely

$$ \frac{{{\text{d}}\tilde{\user2{z}}_{1} }}{{{\text{d}}t}} = {\varvec{B}}_{0} \tilde{\user2{z}}_{1} , $$

(38)

where

$$ \tilde{\user2{z}}_{1} = {\varvec{z}}_{1} - {\varvec{c}}_{1} , $$

(39)

in which

$$ \frac{{{\text{d}}{\varvec{c}}_{1} }}{{{\text{d}}t}} = {\varvec{B}}_{0} {\varvec{c}}_{1} + {\varvec{B}}_{1} {\varvec{z}}_{0} . $$

(40)

Based on Proposition 1, we give the symplectic difference schemes for Eq. (38), namely,

$$ \left( {{\tilde{\varvec{z}}}_{1} } \right)^{k + 1} ={\varvec{\varGamma}}_{{\tau_{0} }} \left( {{\tilde{\varvec{z}}}_{1} } \right)^{k} , $$

(41)

where

$${\varvec{\varGamma}}_{{\tau_{0} }} = \left( {{\varvec{I}}_{0} - \frac{\tau }{2}{\varvec{B}}_{0} } \right)^{ - 1} \left( {{\varvec{I}}_{0} + \frac{\tau }{2}{\varvec{B}}_{0} } \right). $$

(42)

Similarly, the vectors ${\varvec{z}}_{2} ,{\varvec{z}}_{3} , \cdots ,{\varvec{z}}_{n} , \cdots$ can be determined in the same way. Then the dynamic structural response ${\varvec{z}}$ can be obtained according to Eq. (15).

The dynamic structural response ${\varvec{z}}$ is calculated by the sum of following series:

$$ {\varvec{z}} = {\varvec{z}}_{0} + \varepsilon {\varvec{z}}_{1} + \varepsilon^{2} {\varvec{z}}_{2} + \cdots + \varepsilon^{n} {\varvec{z}}_{n} + \cdots . $$

(43)

Firstly, ${\varvec{z}}_{0}$ can be solved by the Euler centered scheme. After ${\varvec{z}}_{0}$ is obtained, ${\varvec{z}}_{1}$ can be calculated by the proposed symplectic difference scheme. Similarly, ${\varvec{z}}_{2}$ can be solved by the symplectic difference scheme based on the results of ${\varvec{z}}_{0}$ and ${\varvec{z}}_{1}$. Then ${\varvec{z}}_{3} ,{\varvec{z}}_{4} , \cdots ,{\varvec{z}}_{n} , \cdots$ can be calculated in the same way. The computation of ${\varvec{z}}_{1}$ is nearly two times larger than the that of ${\varvec{z}}_{0}$, and the computation of ${\varvec{z}}_{2}$ is nearly three times larger than the that of ${\varvec{z}}_{0}$. The computational efficiency of the proposed method depends on the number of items selected. In the study, three items are selected and thus the computation of the proposed method is nearly six times of the traditional first order difference method under the same time step.

6 Numerical examples

6.1 Forced vibration of cantilever I-beam

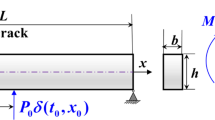
As shown in Fig. 1, a cantilever I-beam is fixed on the left side and a downward load $F = 100{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{N}$ is imposed on the beam. The I-beam is 9 m long and its section is illustrated in Fig. 1, in which $a = 0.05{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{m,}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} b = 0.04{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{m}$. The thickness of the I-beam is 0.005 m and the beam is divided into fifteen elements. The density of the beam is $7.85 \times 10^{3} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{kg}/\text{m}^{3}$ and Young’s modulus is $200{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{GPa}$.

Fig. 1

Finite element model of the cantilever beam

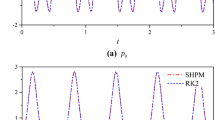
The proposed symplectic algorithm (PSA) is applied to obtain the vertical displacement of the right node of element 15 and the Runge–Kutta algorithms are also conducted for comparison. The time step is set to be $\Delta t = 0.05{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}$. The results of the vertical displacement and Hamiltonian function are shown in Figs. 2 and 5 respectively.

Fig. 2

Deflection responses of the right node of the cantilever beam obtained by PSA

From the results we can conclude that the PSA can obtain reasonable results of the vertical displacement. The symplectic properties of algorithm can be carried out by the values of Hamiltonian function with respect to time. As shown in Fig. 5, the Hamiltonian function remains a constant value ($\lg ( - H) = {1}.27 \Rightarrow H = - 18.8{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{J}$) during the numerical calculation, which illustrates the symplectic conservation of the proposed algorithm. The numerical results obtained by second order Runge–Kutta (RK2) and fourth order Runge–Kutta (RK4) with the same time step, which are shown in Figs. 3, 4, 5, are divergent. The results show that PSA is better than RK2 and RK4 in the example.

Fig. 3

Deflection responses of the right node of the cantilever beam obtained by RK2

Fig. 4

Deflection responses of the right node of the cantilever beam obtained by RK4

Fig. 5

Hamiltonian function $H$ obtained by PSA

The Butcher tableau for RK2 in the study is listed as follows:

(44)

The Butcher tableau for RK4 in the study is listed as follows:

(45)

6.2 Vibration of the rigid wing system

The second example is the forced vibration of the rigid wing system. As shown in Fig. 6, the rigid wing is supported by the wire spring $K_{h} = 1000{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{N} \cdot \text{m}$ and torsion spring $K_{a} = 100{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{N}$. The wing is affected by gravity and starts to vibrate. The distance between the leading edge of the wing segment and the bending center B is $l_{1} = 0.2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{m}$ and the distance from the bending center to trailing edge is $l_{2} = 0.3{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{m}$. The distance between the bending center B and the centroid position O is $\delta = 0.08{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{m}$. The mass of the rigid wing is $m = 8{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{kg}$ and the inertia moment around the center of gravity is $I_{0} = 0.18{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{kg} \cdot \text{m}^{2}$. To describe the motion of the rigid wing, the distance of the bend center of the wing from the static equilibrium position $h$ and the angle of the wing around the bend center $\alpha$ are selected as the generalized coordinates.

Fig. 6

Schematic diagram of the rigid wing system

The proposed symplectic algorithm is applied to obtain the dynamic response $h$ and $\alpha$. The Runge–Kutta algorithm RK1 is also conducted for comparison and the time step is set to be $\Delta t = 0.01{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}$. To make a fair comparison between PSA and RK1, the time step of PSA is also set as $\Delta t = 0.01{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}$. If the time step in RK1 is decreased, the error will be reduced. Moreover, the first order Runge–Kutta (RK1) with step size $\Delta t = 0.002{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}$ is also applied to obtain the dynamic response. The results obtained by the Runge–Kutta algorithm RK4 with time steps $\Delta t = 0.0001{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}$ are regarded as the exact solutions. The results are embodied in Figs. 7, 8, 9, in which RK1-1 represents RK1 with time step $\Delta t = 0.01{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}$ and RK1-2 denotes RK1 with time step $\Delta t = 0.002{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}$. As shown in Figs. 7 and 8, the difference between the results of the symplectic algorithm and that of the Runge–Kutta algorithm is small at the beginning, while the difference between PSA and RK1 is getting bigger and bigger as time goes on. Moreover, the results obtained by PSA coincide with that obtained by RK4, which demonstrates the applicability of PSA and its superiority towards RK1. From the results in Fig. 9, the values of Hamiltonian function obtained by PSA remain unchanged over time ($H = - 3.07328{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{J}$), which illustrates the symplectic conservation of PSA. The values of Hamiltonian function obtained by RK4 decreases very slowly ($t = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}:H = - 3.07328{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{J} \Rightarrow t = 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}:H = - 3.07319{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{J}$) while results obtained by RK1 decreases faster ($t = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}:H = - 3.07328{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{J} \Rightarrow t = 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}:H = { - }{4}{\text{.45874}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{J}$) as time goes by. The Runge–Kutta algorithm RK1 has first order accuracy, i.e., the local truncation error is the same order of the square of the step size. Therefore, the local truncation error will be reduced if the step size is decreased.

Fig. 7

Dynamic response $h$ solved by different algorithms

Fig. 8

Dynamic response $\alpha$ solved by different algorithms

Fig. 9

Hamiltonian function $H$ obtained by different algorithms in the second example

6.3 Forced vibration of a two-compartment building with openings

As shown in Fig. 10, the wind-induced internal pressure for a two-compartment building with openings is changing with time. The transient wind pressure coefficients of the windward wall, compartments 1 and 2 are $C_{PW}$, $C_{{P{\text{i}}1}}$ and $C_{{P{\text{i}}2}}$, respectively. The areas of openings 1 and 2 are $A_{o1}$ and $A_{o2}$, respectively. The internal volumes of compartments 1 and 2 are $V_{o1}$ and $V_{o2}$, respectively. The flow coefficients at the openings 1 and 2 are $c_{1}$ and $c_{2}$, respectively. The effective lengths of “air slugs” in openings 1 and 2 are $L_{e1}$ and $L_{e2}$, respectively. The displacements of “air slugs” in openings 1 and 2 are $x_{1}$ and $x_{2}$, respectively.

Fig. 10

Two-compartment building with openings

The dynamical differential equations of the two-compartment building with openings are expressed as follows:

$$ \user2{M}\ddot{\user2{x}}(t)+\user2{D}\dot{\user2{x}}(t)+\user2{K}\user2{x}(t)=\user2{F}(t), $$

(46)

where the mass matrix equals the identity matrix, namely ${\varvec{M}} = {\varvec{I}}$; the damping matrix, stiffness matrix, and load vector are expressed as:

$$ \begin{array}{*{20}c} {{\varvec{D}} = \left( {\begin{array}{*{20}c} {\frac{{c_{j1} }}{{\rho_{a} c_{1} A_{o1} L_{e1} }}} & 0 \\ 0 & {\frac{{c_{j2} }}{{\rho_{a} c_{2} A_{o2} L_{e2} }}} \\ \end{array} } \right),} & {{\varvec{K}} = \left( {\begin{array}{*{20}c} {\omega_{11}^{2} } & { - \frac{{L_{e2} }}{{L_{e1} }}\omega_{12}^{2} } \\ { - \frac{{L_{e1} }}{{L_{e2} }}\omega_{11}^{2} } & {\omega_{22}^{2} + \omega_{12}^{2} } \\ \end{array} } \right),} & {{\varvec{F}} = \left( {\begin{array}{*{20}c} {\frac{{qC_{PW} }}{{\rho_{a} L_{e1} }}} \\ 0 \\ \end{array} } \right)} \\ \end{array} . $$

(47)

$\omega_{11}$, $\omega_{22}$ and $\omega_{12}$ are determined by

$$ \begin{array}{*{20}c} {\omega_{11} = \sqrt {\frac{{\gamma P_{a} c_{1} A_{o1} }}{{\rho_{a} L_{e1} V_{o1} }}} ,} & {\omega_{22} = \sqrt {\frac{{\gamma P_{a} c_{2} A_{o2} }}{{\rho_{a} L_{e2} V_{o2} }}} ,} & {\omega_{12} = \sqrt {\frac{{\gamma P_{a} c_{2} A_{o2} }}{{\rho_{a} L_{e2} V_{o1} }}} } \\ \end{array} . $$

(48)

The values of all parameters are given in Table 1.

Table 1 Parameter values of the two-compartment building

The dynamic response results are solved by the PSA and the time step is set to be $\Delta t = 5 \times 10^{ - 3} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}$. For comparison, the RK1 is also conducted with the same time step. The exact solutions are obtained by the RK4 with the time step $\Delta t = 5 \times 10^{ - 5} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}$. Figures 11, 12, 13 embody the dynamic response results. From the results in Figs. 11 and 12, the dynamic response results based on RK1, PSA and RK4 are almost the same at the beginning, while the difference between PSA and RK1 is getting bigger and bigger over time. Moreover, the difference of results by PSA and RK4 is extremely small, which demonstrates the superiority of PSA towards RK1. As shown in Fig. 13, the values of Hamiltonian function by PSA remain constant ($H = - {172}{\text{.64937}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{J}$) as time goes by, which illustrates the symplectic property of PSA. The results obtained by RK4 decreases very slowly ($t = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}:H = - {172}{\text{.64937}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{J} \Rightarrow t = 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}:H = - {172}{\text{.64854}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{J}$) while results by RK1 decreases faster ($t = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}:H = - {172}{\text{.64937}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{J} \Rightarrow t = 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{s}:H = - {5898}{\text{.47673}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \text{J}$) over time.

Fig. 11

Dynamic response x₁ solved by different algorithms

Fig. 12

Dynamic response x₂ solved by different algorithms

Fig. 13

Hamiltonian function H obtained by different algorithms in the third example

7 Conclusions

This paper presents the symplectic perturbation series methodology of a non-conservative linear Hamiltonian system for the structural dynamic response problem with damping and external load. Based on the properties of the exterior product, the conservation law of the linear Hamiltonian system is proved. Based on the perturbation series method, the non-conservative linear Hamiltonian system is transformed into a series of linear Hamiltonian canonical equations. Moreover, the conservation law of the non-conservative linear Hamiltonian system is illustrated. By setting the dual variables, the structural dynamic response problem with eternal load and damping is transformed as the non-conservative linear Hamiltonian system. Therefore, the symplectic difference schemes can be developed to solve the structural dynamic response problem. Three examples demonstrate the applicability and validity of the proposed symplectic algorithm. The results illustrate that the presented methodology has better performance than the traditional Runge–Kutta algorithm in the prediction of structural dynamic response.

The study proposes the symplectic perturbation series methodology for non-conservative linear Hamiltonian system. Therefore, the non-conservative linear Hamiltonian system are transformed as a series of non-homogeneous linear Hamiltonian system. The non-homogeneous linear Hamiltonian system can be transformed as standard linear Hamilton system by linear transformation. In the study, the Euler centered scheme, which is symplectic, is applied to solve the standard linear Hamilton system. Similarly, the symplectic Runge–Kutta method, which may have a higher accuracy, can also be applied to solve the standard linear Hamilton system. By the symplectic perturbation series methodology and the symplectic Runge–Kutta method, the symplectic property can be achieved for the non-conservative linear Hamiltonian system.

Appendices

Appendix A: Conservation law of linear Hamiltonian System

The symplectic structure of the Hamiltonian system can be written as

$$ \omega = \sum\limits_{i = 1}^{n} {\text{d}z_{i} \wedge \text{d}z_{n + i} } , $$

(A.1)

where the notation “$\wedge$” denotes the exterior product. The matrix form of Eq. (A.1) is expressed as follows:

$$ \omega = \left( {\begin{array}{*{20}c} {\text{d}z_{1} } \\ \vdots \\ {\text{d}z_{n} } \\ \end{array} } \right)^{\text{T}} \wedge \left( {\begin{array}{*{20}c} {\text{d}z_{n + 1} } \\ \vdots \\ {\text{d}z_{2n} } \\ \end{array} } \right). $$

(A.2)

Considering $\text{d}z_{j} \wedge \text{d}z_{k} = - \text{d}z_{k} \wedge \text{d}z_{j} ,(1 \le j \le n,n + 1 \le k \le 2n)$, Eq. (A.2) is equivalent to

$$ \omega = \frac{1}{2}\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\text{d}z_{1} } \\ \vdots \\ {\text{d}z_{n} } \\ \end{array} } \\ {\text{d}z_{n + 1} } \\ \vdots \\ {\text{d}z_{2n} } \\ \end{array} } \right)^{\text{T}} \wedge \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\text{d}z_{n + 1} } \\ \vdots \\ {\text{d}z_{2n} } \\ \end{array} } \\ { - \text{d}z_{1} } \\ \vdots \\ { - \text{d}z_{n} } \\ \end{array} } \right).$$

(A.3)

Equation (A.3) can be rewritten as

$$ \omega = \frac{1}{2}\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\text{d}z_{1} } \\ \vdots \\ {\text{d}z_{n} } \\ \end{array} } \\ {\text{d}z_{n + 1} } \\ \vdots \\ {\text{d}z_{2n} } \\ \end{array} } \right)^{\text{T}} \wedge \left( {\begin{array}{*{20}c} {\mathbf{0}} & {{\varvec{I}}_{n} } \\ { - {\varvec{I}}_{n} } & {\mathbf{0}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\text{d}z_{1} } \\ \vdots \\ {\text{d}z_{n} } \\ \end{array} } \\ {\text{d}z_{n + 1} } \\ \vdots \\ {\text{d}z_{2n} } \\ \end{array} } \right) = \frac{1}{2}\left( {\text{d}{\varvec{z}}} \right)^{\text{T}} \wedge {\varvec{J}}\text{d}{\varvec{z}}\user2{.} $$

(A.4)

Let

$$ {\varvec{z}}_{t} = \frac{{\text{d}{\varvec{z}}}}{{\text{d}t}}, $$

(A.5)

then the differentiation of $\omega$ to $t$ is

$$ \frac{{\text{d}\omega }}{{\text{d}t}} = \frac{{\text{d}\left[ {\frac{1}{2}\left( {\text{d}{\varvec{z}}} \right)^{\text{T}} \wedge {\varvec{J}}\text{d}{\varvec{z}}} \right]}}{{\text{d}t}}. $$

(A.6)

Based on the property of the differential form, Eq. (A.6) can be rewritten as

$$ \frac{{\text{d}\omega }}{{\text{d}t}} = \frac{1}{2}\left( {\text{d}{\varvec{z}}_{t} } \right)^{\text{T}} \wedge {\varvec{J}}\text{d}{\varvec{z}} + \frac{1}{2}\left( {\text{d}{\varvec{z}}} \right)^{\text{T}} \wedge {\varvec{J}}\text{d}{\varvec{z}}_{t} . $$

(A.7)

Considering the right multiplication of matrix ${\varvec{J}}$ only turns the position as well as the symbols of vector elements and the product of two negative unities make one positive unity, we can have

$$ \left( {\text{d}{\varvec{z}}_{t} } \right)^{\text{T}} \wedge {\varvec{J}}\text{d}{\varvec{z}} = \left( {{\varvec{J}}\text{d}{\varvec{z}}_{t} } \right)^{\text{T}} \wedge {\varvec{J}} \cdot {\varvec{J}}\text{d}{\varvec{z}}{.} $$

(A.8)

Substituting Eq. (A.8) into Eq. (A.7) yields

$$ \frac{{\text{d}\omega }}{{\text{d}t}} = \frac{1}{2}\left( {{\varvec{J}}\text{d}{\varvec{z}}_{t} } \right)^{\text{T}} \wedge {\varvec{J}} \cdot {\varvec{J}}\text{d}{\varvec{z}} + \frac{1}{2}\left( {\text{d}{\varvec{z}}} \right)^{\text{T}} \wedge {\varvec{J}}\text{d}{\varvec{z}}_{t} . $$

(A.9)

Considering ${\varvec{J}} \cdot {\varvec{J}} = - {\varvec{J}}^{ - 1} \cdot \user2{J = } - {\varvec{I}}$, we have

$$ \frac{{\text{d}\omega }}{{\text{d}t}} = \frac{1}{2}\left( {{\varvec{J}}\text{d}{\varvec{z}}_{t} } \right)^{\text{T}} \wedge \left( { - \text{d}{\varvec{z}}} \right) + \frac{1}{2}\left( {\text{d}{\varvec{z}}} \right)^{\text{T}} \wedge {\varvec{J}}\text{d}{\varvec{z}}_{t} . $$

(A.10)

As $\left( {{\varvec{J}}\text{d}{\varvec{z}}_{t} } \right)^{\text{T}} \wedge \left( { - \text{d}{\varvec{z}}} \right) = \left( {\text{d}{\varvec{z}}} \right)^{\text{T}} \wedge \left( {{\varvec{J}}\text{d}{\varvec{z}}_{t} } \right)$, Eq. (A.10) can be transformed as

$$ \frac{{\text{d}\omega }}{{\text{d}t}} = \frac{1}{2}\left( {\text{d}{\varvec{z}}} \right)^{\text{T}} \wedge \left( {{\varvec{J}}\text{d}{\varvec{z}}_{t} } \right) + \frac{1}{2}\left( {\text{d}{\varvec{z}}} \right)^{\text{T}} \wedge {\varvec{J}}\text{d}{\varvec{z}}_{t} = \left( {\text{d}{\varvec{z}}} \right)^{\text{T}} \wedge \left( {{\varvec{J}}\text{d}{\varvec{z}}_{t} } \right). $$

(A.11)

For a linear Hamiltonian system, we can obtain

$$ \frac{{\text{d}\omega }}{{\text{d}t}} = \left( {\text{d}{\varvec{z}}} \right)^{\text{T}} \wedge \left[ {{\varvec{J}}\text{d}\left( {{\varvec{Bz}}} \right)} \right] = \left( {\text{d}{\varvec{z}}} \right)^{{\text{T}}} \wedge {\varvec{JB}}\text{d}{\varvec{z}} = \left( {\text{d}{\varvec{z}}} \right)^{{\text{T}}} \wedge {\varvec{C}}\text{d}{\varvec{z}}{.} $$

(A.12)

Let $C = \left( {C_{jk} } \right)_{2n \times 2n}$, then Eq. (A.12) can be determined by

$$ \frac{{\text{d}\omega }}{{\text{d}t}} = \sum\limits_{1 \le j,k \le 2n} {C_{jk} {\text{d}}z^{j} \wedge {\text{d}}z^{k} } . $$

(A.13)

Considering ${\text{d}}z^{j} \wedge {\text{d}}z^{k} = 0 \,(j = k)$, Eq. (A.13) can be rewritten as

$$ \frac{{\text{d}\omega }}{{\text{d}t}} = \sum\limits_{1 \le j,k \le 2n,j \ne k} {C_{jk} \text{d}z^{j} \wedge \text{d}z^{k} } . $$

(A.14)

As $C_{jk} = C_{kj} \,(k \ne j)$, we have

$$ C_{jk} \text{d}z^{j} \wedge \text{d}z^{k} + C_{kj} \text{d}z^{k} \wedge \text{d}z^{j} = C_{jk} \text{d}z^{j} \wedge \text{d}z^{k} - C_{kj} \text{d}z^{j} \wedge \text{d}z^{k} = 0 \,(k \ne j). $$

(A.15)

Substituting Eq. (A.15) into Eq. (A.14) yields

$$ \frac{{\text{d}\omega }}{{\text{d}t}} = \sum\limits_{1 \le j,k \le 2n} {C_{jk} \text{d}z^{j} \wedge \text{d}z^{k} } = 0. $$

(A.16)

Consequently, the conservation law of the linear Hamiltonian system is proved.

Appendix B: Detailed proof about that a non-infinitesimal symplectic matrix can be approximately denoted by a linear combination of an infinite series of infinitesimal symplectic matrices

Firstly, we introduce a linear function, namely

$$ f(x) = \left( {{\text{e}}^{{\alpha_{1} - \varepsilon x}} - \beta_{1} } \right){\varvec{B}}^{*} + \left( {{\text{e}}^{{\varepsilon x/n - \alpha_{2} }} - \beta_{2} } \right)\Delta \user2{B,} $$

(B.1)

where ${\varvec{B}}^{*}$ is an infinitesimal symplectic matrix while $\Delta {\varvec{B}}$ is a non infinitesimal symplectic matrix. The parameters $\alpha_{1} ,\beta_{1} ,\alpha_{2} ,\beta_{2}$ satisfy the following condition:

$$ \begin{gathered} {\text{e}}^{{\alpha_{1} }} - \beta_{1} = 1,{\text{e}}^{{\alpha_{1} - \varepsilon }} - \beta_{1} = 0 \Rightarrow \alpha_{1} = - \ln \left( {1 - {\text{e}}^{ - \varepsilon } } \right),\beta_{1} = {{{\text{e}}^{ - \varepsilon } } \mathord{\left/ {\vphantom {{{\text{e}}^{ - \varepsilon } } {(1 - {\text{e}}^{ - \varepsilon } )}}} \right. \kern-\nulldelimiterspace} {(1 - {\text{e}}^{ - \varepsilon } )}}, \hfill \\ {\text{e}}^{{ - \alpha_{2} }} - \beta_{2} = 0,{\text{e}}^{{\varepsilon /n - \alpha_{2} }} - \beta_{2} = 1 \Rightarrow \alpha_{2} = \ln \left( {{\text{e}}^{\varepsilon /n} - 1} \right),\beta_{2} = {1 \mathord{\left/ {\vphantom {1 {\left( {{\text{e}}^{\varepsilon /n} - 1} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{\text{e}}^{\varepsilon /n} - 1} \right)}}. \hfill \\ \end{gathered} $$

(B.2)

Hence, we can obtain

$$ f(0) = {\varvec{B}}^{*},\;f\;(1) = \Delta {\varvec{B}}\user2{.} $$

(B.3)

Based on the Taylor series expansion theorem, we can obtain

$$ \begin{gathered} f(1) = f(0) + f^{(1)} (0)\left( {1 - 0} \right) + \frac{1}{2}f^{(2)} (0)\left( {1 - 0} \right)^{2} + \cdots + \frac{{f^{(k)} (0)}}{k!}\left( {1 - 0} \right)^{k} + \cdots \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = f(0) + f^{(1)} (0) + \frac{1}{2}f^{(2)} (0) + \cdots + \frac{{f^{(k)} (0)}}{k!} + \cdots, \hfill \\ \end{gathered} $$

(B.4)

where $f^{(k)} (0)$ represents the k-th derivative of function $f$. Calculating $f^{(k)} (0)$ yields:

$$ f^{(k)} (0) = \left( { - \varepsilon } \right)^{k} {\text{e}}^{{\alpha_{1} }} {\varvec{B}}^{*} + \left( {\frac{\varepsilon }{n}} \right)^{k} {\text{e}}^{{ - \alpha_{2} }} \Delta {\varvec{B}}\text{ = }\varepsilon^{k} \left[ {\left( { - 1} \right)^{k} {\text{e}}^{{\alpha_{1} }} {\varvec{B}}^{*} + \left( \frac{1}{n} \right)^{k} {\text{e}}^{{ - \alpha_{2} }} \Delta {\varvec{B}}} \right]. $$

(B.5)

By choosing a large value of parameter $n$ we can obtain

$$ \left( { - 1} \right)^{k} {\text{e}}^{{\alpha_{1} }} {\varvec{B}}^{*} + \left( \frac{1}{n} \right)^{k} {\text{e}}^{{ - \alpha_{2} }} \Delta {\varvec{B}} \approx \left( { - 1} \right)^{k} {\text{e}}^{{\alpha_{1} }} {\varvec{B}}^{*} . $$

(B.6)

Therefore, we can obtain

$$ f^{(k)} (0) \approx \varepsilon^{k} \left( { - 1} \right)^{k} {\text{e}}^{{\alpha_{1} }} {\varvec{B}}^{*} . $$

(B.7)

Substituting Eq. (B.7) into Eq. (B.4) yields

$$ f(1) = \Delta {\varvec{B}} \approx {\varvec{B}}^{*} + ( - \varepsilon ){\text{e}}^{{\alpha_{1} }} {\varvec{B}}^{*} + \frac{{\varepsilon^{2} }}{2!}{\text{e}}^{{\alpha_{1} }} {\varvec{B}}^{*} + \cdots + \frac{{\left( { - \varepsilon } \right)^{k} }}{k!}{\text{e}}^{{\alpha_{1} }} {\varvec{B}}^{*} + \cdots . $$

(B.8)

Consequently, a non-infinitesimal symplectic matrix is approximately denoted by a linear combination of an infinite series of infinitesimal symplectic matrices.

Appendix C: Conservation law of non-conservative linear Hamiltonian system

The symplectic structure of the non-conservative Hamiltonian system is expressed by

$$ \omega = \frac{1}{2}\text{d}\left( {{\varvec{z}}_{0} + \varepsilon {\varvec{z}}_{1} + \varepsilon^{2} {\varvec{z}}_{2} + \cdots + \varepsilon^{n} {\varvec{z}}_{n} + \cdots } \right)^{\text{T}} \wedge {\varvec{J}}\text{d}\left( {{\varvec{z}}_{0} + \varepsilon {\varvec{z}}_{1} + \varepsilon^{2} {\varvec{z}}_{2} + \cdots + \varepsilon^{n} {\varvec{z}}_{n} + \cdots } \right). $$

(C.1)

Expanding Eq. (C.1) yields

$$ \omega = \frac{1}{2}\sum\limits_{k,l = 0}^{\infty } {\varepsilon^{k + l} \left( {{\text{d}}{\varvec{z}}_{k} } \right)^{{\text{T}}} \wedge {\varvec{J}}\text{d}{\varvec{z}}_{l} } . $$

(C.2)

Expanding $\omega$ as power series yields

$$ \omega = \sum\limits_{i = 0}^{\infty } {\varepsilon^{i} \omega_{i} } . $$

(C.3)

Based on Eq. (C.2) and Eq. (C.3) we can have

$$ \begin{gathered} \varepsilon^{0} :\omega_{0} = \frac{1}{2}\left( {{\text{d}}{\varvec{z}}_{0} } \right)^{{\text{T}}} {\varvec{J}}{\text{d}}{\varvec{z}}_{0}, \hfill \\ \varepsilon^{1} :\omega_{1} = \frac{1}{2}\left( {{\text{d}}{\varvec{z}}_{0} } \right)^{{\text{T}}} \wedge {\varvec{J}}{\text{d}}{\varvec{z}}_{1} + \frac{1}{2}\left( {{\text{d}}{\varvec{z}}_{1} } \right)^{{\text{T}}} \wedge {\varvec{J}}{\text{d}}{\varvec{z}}_{0}, \hfill \\ \varepsilon^{2} :\omega_{2} = \frac{1}{2}\left( {{\text{d}}{\varvec{z}}_{0} } \right)^{{\text{T}}} \wedge {\varvec{J}}{\text{d}}{\varvec{z}}_{2} + \frac{1}{2}\left( {{\text{d}}{\varvec{z}}_{1} } \right)^{{\text{T}}} \wedge {\varvec{J}}{\text{d}}{\varvec{z}}_{1} + \frac{1}{2}\left( {{\text{d}}{\varvec{z}}_{2} } \right)^{{\text{T}}} \wedge {\varvec{J}}{\text{d}}{\varvec{z}}_{0}, \hfill \\ \ldots \hfill \\ \varepsilon^{n} :\omega_{n} = \frac{1}{2}\sum\limits_{i = 0}^{n} {\left( {{\text{d}}{\varvec{z}}_{i} } \right)^{{\text{T}}} \wedge {\varvec{J}}{\text{d}}{\varvec{z}}_{n - i} }, \hfill \\ \cdots \hfill \\ \end{gathered} $$

(C.4)

The differentiation of $\omega$ to $t$ is expressed by

$$ \frac{{\text{d}\omega }}{{\text{d}t}} = \frac{{\text{d}\left( {\sum\limits_{i = 0}^{\infty } {\varepsilon^{i} \omega_{i} } } \right)}}{{\text{d}t}} = \sum\limits_{i = 0}^{\infty } {\varepsilon^{i} \frac{{\text{d}\omega_{i} }}{{\text{d}t}}} , $$

(C.5)

where

$$ \frac{{\text{d}\omega_{i} }}{{\text{d}t}} = \frac{1}{2}\frac{{\text{d}\left[ {\sum\limits_{j = 0}^{i} {\left( {{\text{d}}{\varvec{z}}_{j} } \right)^{{\text{T}}} \wedge {\varvec{J}}{\text{d}}{\varvec{z}}_{i - j} } } \right]}}{{\text{d}t}}. $$

(C.6)

Let

$$ {\varvec{z}}_{t}^{i} = \frac{{\text{d}{\varvec{z}}^{i} }}{{\text{d}t}}, $$

(C.7)

then Eq. (C.6) can be transformed as follows:

$$ \frac{{\text{d}\omega_{i} }}{{\text{d}t}} = \sum\limits_{j = 0}^{i} {\left( {{\text{d}}{\varvec{z}}_{j} } \right)^{{\text{T}}} \wedge {\varvec{J}}{\text{d}}{\varvec{z}}_{t}^{{_{i - j} }} } . $$

(C.8)

For $i = 0,$ it gives

$$ \frac{{\text{d}\omega_{0} }}{{\text{d}t}} = \left( {{\text{d}}{\varvec{z}}_{0} } \right)^{{\text{T}}} \wedge {\varvec{J}}{\text{d}}{\varvec{z}}_{t}^{{_{0} }} . $$

(C.9)

As ${\varvec{z}}_{0}$ corresponds to a linear Hamiltonian system, its conservation law is proved in Sect. 2.2, namely

$$ \frac{{\text{d}\omega_{0} }}{{\text{d}t}} = 0. $$

(C.10)

For $i = 1,$ we can have

$$ \frac{{\text{d}\omega_{1} }}{{\text{d}t}} = \left( {{\text{d}}{\varvec{z}}_{0} } \right)^{{\text{T}}} \wedge {\varvec{J}}{\text{d}}{\varvec{z}}_{t}^{{_{1} }} + \left( {{\text{d}}{\varvec{z}}_{1} } \right)^{{\text{T}}} \wedge {\varvec{J}}{\text{d}}{\varvec{z}}_{t}^{{_{0} }} . $$

(C.11)

Substituting Eq. (18) into Eq. (C.11) yields

$$ \frac{{\text{d}\omega_{1} }}{{\text{d}t}} = \left( {{\text{d}}{\varvec{z}}_{0} } \right)^{{\text{T}}} \wedge {\varvec{J}}{\text{d}}\left( {{\varvec{B}}_{0} {\varvec{z}}_{1} + {\varvec{B}}_{1} {\varvec{z}}_{0} } \right) + \left( {{\text{d}}{\varvec{z}}_{1} } \right)^{{\text{T}}} \wedge {\varvec{J}}{\text{d}}\left( {{\varvec{B}}_{0} {\varvec{z}}_{0} } \right). $$

(C.12)

Simplifying Eq. (C.12) we can have

$$ \frac{{\text{d}\omega_{1} }}{{\text{d}t}} = \left( {{\text{d}}{\varvec{z}}_{0} } \right)^{{\text{T}}} \wedge {\varvec{JB}}_{0} {\text{d}}{\varvec{z}}_{1} { + }\left( {{\text{d}}{\varvec{z}}_{0} } \right)^{{\text{T}}} \wedge {\varvec{JB}}_{1} {\text{d}}{\varvec{z}}_{0} + \left( {{\text{d}}{\varvec{z}}_{1} } \right)^{{\text{T}}} \wedge {\varvec{JB}}_{0} {\text{d}}{\varvec{z}}_{0} . $$

(C.13)

As ${\varvec{B}}_{0}$ and ${\varvec{B}}_{1}$ are infinitesimal symplectic matrices, we can have

$$ \begin{aligned} {\varvec{JB}}_{0} = &- {\varvec{B}}_{0}^{\text{T}} {\varvec{J}} = {\varvec{B}}_{0}^{\text{T}} {\varvec{J}}^{\text{T}} = \left( {\varvec{JB}}_{0} \right)^{\text{T}}, \\ {\varvec{JB}}_{1} =& - {\varvec{B}}_{1}^{\text{T}}{\varvec{JT}} = {\varvec{B}}_{1}^{\text{T}} {\varvec{J}}^{\text{T}} = \left( {\varvec{JB}}_{1} \right)^{\text{T}}. \end{aligned} $$

(C.14)

Let ${\varvec{C}}^{0} = \left( {C_{jk}^{0} } \right)_{2n \times 2n} = {\varvec{JB}}_{0} ,{\varvec{C}}^{1} = \left( {C_{jk}^{1} } \right)_{2n \times 2n} = {\varvec{JB}}_{1}$, then ${\varvec{C}}^{0}$ and ${\varvec{C}}^{1}$ are symmetric matrices. Simplifying Eq. (C.13) yields

$$ \frac{{\text{d}\omega_{1} }}{{\text{d}t}} = \sum\limits_{1 \le j,k \le 2n} {C_{jk}^{0} {\text{d}}z_{0}^{j} \wedge {\text{d}}z_{1}^{k} } + \sum\limits_{1 \le j,k \le 2n} {C_{jk}^{1} {\text{d}}z_{0}^{j} \wedge {\text{d}}z_{0}^{k} } + \sum\limits_{1 \le j,k \le 2n} {C_{jk}^{0} {\text{d}}z_{1}^{j} \wedge {\text{d}}z_{0}^{k} } . $$

(C.15)

As ${\text{d}}z_{0}^{j} \wedge {\text{d}}z_{1}^{k} = - {\text{d}}z_{1}^{k} \wedge {\text{d}}z_{0}^{j}$ and $C_{jk}^{0} = C_{kj}^{0}$ we can have

$$ \sum\limits_{1 \le j,k \le 2n} {C_{jk}^{0} {\text{d}}z_{0}^{j} \wedge {\text{d}}z_{1}^{k} } + \sum\limits_{1 \le j,k \le 2n} {C_{kj}^{0} {\text{d}}z_{1}^{k} \wedge {\text{d}}z_{0}^{j} } = 0. $$

(C.16)

Based on Eq. (A.16) in Appendix A, we can obtain

$$ \sum\limits_{1 \le j,k \le 2n} {C_{jk}^{1} {\text{d}}z_{0}^{j} \wedge {\text{d}}z_{0}^{k} } = 0. $$

(C.17)

Substituting Eqs. (C.16) and (C.17) into Eq. (C.15) yields

$$ \frac{{\text{d}\omega_{1} }}{{\text{d}t}} = 0. $$

(C.18)

For $i = l$, we can have

$$ \frac{{\text{d}\omega_{l} }}{{\text{d}t}} = \sum\limits_{m = 0}^{l} {\sum\limits_{n = m}^{l} {\left( {{\text{d}}{\varvec{z}}_{m} } \right)^{{\text{T}}} } } \wedge {\varvec{JB}}_{n - m} {\text{d}}{\varvec{z}}_{l - n} = \sum\limits_{m = 0}^{l} {\sum\limits_{n = m}^{l} {\left( {{\text{d}}{\varvec{z}}_{m} } \right)^{{\text{T}}} } } \wedge C^{n - m} {\text{d}}{\varvec{z}}_{l - n} .$$

(C.19)

Simplifying Eq. (C.19) yields

$$ \frac{{\text{d}\omega_{l} }}{{\text{d}t}} = \sum\limits_{m = 0}^{l} {\sum\limits_{n = m}^{l} {\left( {{\text{d}}{\varvec{z}}_{m} } \right)^{{\text{T}}} } } \wedge C^{n - m} {\text{d}}{\varvec{z}}_{l - n} = \sum\limits_{0 \le m \le n \le l}^{{}} {\left( {{\text{d}}{\varvec{z}}_{m} } \right)^{{\text{T}}} \wedge C^{n - m} {\text{d}}{\varvec{z}}_{l - n} } . $$

(C.20)

Based on Eq. (C.16), we can similarly have

$$ \left( {{\text{d}}{\varvec{z}}_{m} } \right)^{\text{T}} \wedge C^{n - m} {\text{d}}{\varvec{z}}_{l - n} + \left( {{\text{d}}{\varvec{z}}_{l - n} } \right)^{{\text{T}}} \wedge C^{n - m} {\text{d}}{\varvec{z}}_{m} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (m \ne l - n). $$

(C.21)

Substituting Eq. (C.21) into Eq. (C.20) yields

$$ \frac{{\text{d}\omega_{l} }}{{\text{d}t}} = \sum\limits_{m \le l/2}^{{}} {\left( {{\text{d}}{\varvec{z}}_{m} } \right)^{{\text{T}}} \wedge C^{l - 2m} {\text{d}}{\varvec{z}}_{m} } . $$

(C.22)

Based on Eq. (A.16) in Appendix A, we can similarly have

$$ \sum\limits_{m \le l/2}^{{}} {\left( {{\text{d}}{\varvec{z}}_{m} } \right)^{{\text{T}}} \wedge C^{l - 2m} {\text{d}}{\varvec{z}}_{m} } = 0. $$

(C.23)

Therefore, we can have

$$ \frac{{{\text{d}}\omega_{2} }}{{{\text{d}}t}} = 0, \cdots ,\frac{{{\text{d}}\omega_{n} }}{{{\text{d}}t}} = 0, \cdots . $$

(C.24)

Consequently, the conservation law of the non-conservative linear Hamiltonian system is proved.