1 Introduction

Structural topology optimization is intended to place the given material to achieve best structural performance. The pioneer work can be traced to Bendsøe and Kikuchi [1], the topology optimization has developed in a variety of directions with the emergence of substantial approaches including homogenization method, solid isotropic material with penalization (SIMP) method [2, 3], evolutionary structural optimization method [4] and bi-directional evolutionary structural optimization (BESO) method [5], level set method [6,7,8] and phase field method [9]. With the aim of establishing a direct link between topology optimization and a computer aided design (CAD) modeling system, more recently, an explicit topology optimization approach based on a moving morphable components (MMC) concept was presented by Guo et al. [10,11,12,13,14,15]. Compared with the traditional method, the MMC method can render the solution containing more geometry and mechanical information in optimized topology. Comprehensive reviews on a specific method or comparison of various methods and their applications are given in Refs. [16,17,18]. Meanwhile, topology optimization with inverse homogenization technique was proposed initially in microstructural design of porous and composite materials [19, 20]. The increasing advancement of additive manufacturing technology makes it possible to fabricate various man-made materials, such as porous material with negative Poisson’s ratio over large deformations [21], orthotropic material for negative or zero compressibility [22]. The state-of-the-art for material design via topology optimization can be referenced in Ref. [23].

To date, the mentioned research is confined to individual macrostructural optimization or micro-scale material optimization, i.e. designing the macrostructures composed of optional materials or designing the microstructures for the expected or extreme properties individually. Concurrent design of structure and material becomes one of the hardest tasks in the fields of structural engineering and materials engineering, which has attracted the attention of many researchers. Rodrigues et al. [24] firstly addressed a hierarchical optimization formulation for optimizing material distribution in both macrostructure and microstructure. Later, this hierarchical approach was extended to 3D elastic structures by Coelho et al. [25]. In their methods, optimal microstructures may vary from point to point, which leads to high computational cost and manufacture difficulties. To address these problems, Liu et al. [26] suggested a concurrent computational procedure that the porous material is uniform and periodically distributed in macrostructure. The extension of this approach for maximum primary frequency and minimum compliance of thermo-elastic structures was given by Niu et al. [27] and Deng et al. [28] successively. Then Guo et al. [29] presented a robust concurrent optimization formulation emphasized on uncertainties of loads. Optimized topologies of microstructure tend to be isotropic and Kagome structure under such uncertainties. The work of Huang et al. [30] used the BESO method for realizing the concurrent optimization design with the unambiguous configurations on both macro- and micro-scales. Nowadays, the BESO algorithm has been developed to achieve multifunctional designs [31] and to maximize natural frequency with a given mass [32]. Also, Xu et al. [33,34,35] furthered the BESO method to concurrent topology optimization in regard to material distribution in macrostructure and periodic microstructure under harmonic, transient, and random excitations. Zhang and Sun [36] revealed the size effect of materials and structures in the integrated two-scale optimization approach. More recently, Xia and Breitkopf [37, 38] proposed an \(\hbox {FE}^2\) resolution framework focused on nonlinearity for the concurrent design. The study by Jia et al. [39] presented a hierarchical design of structures and multiphase material cells. Furthermore, Long et al. [40] introduced a two-scale topology optimization method for maximizing the frequency of macrostructure that are composed of periodic composite units consisting of two isotropic materials with distinct Poisson’s ratios. The work of Chen et al. [41] presents concurrent design method based on the moving iso-surface threshold concept.

Fig. 1
figure 1

An illustration of a structure composed of periodic cellular units: a macrostructure; b periodic cellular units; c unit cell (microstructure)

Full size image

Volume or mass fraction of macrostructure or/and microstructure is taken as the constraint to improve general convergence in above concurrent optimization studies. As indicated by Sigmund and Maute [18], the volume constraint is regarded as the basic constraint for the academic interest. However, most real life applications have to meet various design demands, which come in the form of constraint in the optimization problem. Meanwhile, the minimization of the total mass would be of practical importance for the purpose of lightweight design. Compared with the existing concurrent optimization models [27, 32, 41] aiming at finding optimal configurations of macrostructures and microstructures with maximum structural stiffness or fundamental frequency, this paper aims to develop a novel concurrent optimization formulation based on the independent, continuous and mapping (ICM) method [42,43,44], in which the total mass of structure is minimized considering simultaneously load-carrying capabilities and thermal insulation properties. Structural responses at macro- and micro-levels are regarded as multiple constraints. Hence, the selection of weight coefficient in multi-objective design for multifunctional design can be avoided in previous study [28, 31]. By introducing the reciprocal variables, the objective function and constraint function can be explicitly approximated by the Taylor-series expansion method. Then the optimal problem can be effectively updated by sequential quadratic programming (SQP) algorithm, by setting up a series of sub-problems with the second-order sensitivities. Some factors and parameters affecting the macrostructure or microstructure are also investigated.

The rest of this paper is structured as follows. Section 2 formulates the concurrent topology optimization problem of minimization of total mass with multiple constraints. Section 3 describes the homogenization procedure for effective material properties and sensitivity analysis with respect to macro- and micro-scale density variables. Section 4 introduces the design variables to conduct the standard quadratic programming. Section 5 describes the filtering schemes to eliminate numerical instabilities. Section 6 presents 2D and 3D numerical examples to validate the effectiveness of the proposed optimization method. Section 7 draws the concluding remarks.

2 Concurrent topology optimization for minimization of total mass with multiple constraints

In this paper, it is assumed that the macrostructure is composed of periodic cellular units (PCUs) as indicated in Fig. 1. Both macrostructure and microstructure are discretized by finite element (FE). Each element on macro-scale or micro-scale level is assigned an exclusive density, namely macro-elemental density \(P_{i}\) \((i=1,2,\ldots ,M)\) or micro-elemental density \(r_j\) \((j=1,2,\ldots ,N)\), where M and N are the total number of FE in macrostructure and microstructure, respectively. In the PCU, \(r_{j}=1\) indicates that the jth element is occupied by base material while \(r_{j}=0\) when the jth element is void. \(P_{i}=1\) means the ith element is porous and \(P_{i}=0 \) represents the ith element is void whatever value of \(r_{j}\). In the concurrent optimization, two sets of relative densities will be integrated into one system through homogenization theory.

The total mass of the structure m can be calculated as

$$\begin{aligned} m=\sum _{i=1}^{M} m_{i}=\sum _{i=1}^{M} P_{i} V_{i} \rho _{i}^\mathrm{{H}}, \end{aligned}$$
(1)

where \(V_{i}\) is the ith elemental volume, and \(\rho _{i}^{\mathrm{H}}\) is the homogenized density in the macrostructure which is expressed as

$$\begin{aligned} \rho _{i}^\mathrm{{H}}=\frac{\sum _{j=1}^{N} V_{j} r_{j} \rho }{V_{i}}, \end{aligned}$$
(2)

where \(V_j\) denotes the jth elemental volume in the microstructure. \(\rho \) denotes the density of base material.

The FE equation of the static equilibrium can be written as

$$\begin{aligned} \varvec{KU=F}, \end{aligned}$$
(3)

where \(\varvec{U}\) and \(\varvec{F}\) represent the applied load vector and the nodal displacement vector of the macrostructure, respectively. \(\varvec{K}\) represents the global stiffness matrix of the macrostructure which can be assembled by the elemental stiffness matrix \(\varvec{K}_i\)

$$\begin{aligned} \varvec{K}=\sum _{i=1}^{M} \varvec{K}_i =\sum _{i=1}^{M} \int _{V_{i}} \varvec{B}^{\mathrm{T}} \varvec{D}^{\mathrm{MA}} \varvec{B} \text {d} V_{i}, \end{aligned}$$
(4)

where \(\varvec{B}\) is the strain-displacement matrix of the macrostructure. At the macro scale, the ith elemental elastic matrix \(\varvec{D}^\mathrm{{MA}}\) is defined by

$$\begin{aligned} \varvec{D}^{\mathrm{MA}}=P_{i}^{\alpha } \varvec{D}^{\mathrm{H}}, \end{aligned}$$
(5)

where \(\alpha \) is the exponent of penalization with the typical value \(\alpha =4\) in this paper. \(\varvec{D}^{\mathrm{H}}\) is the effective elasticity matrix which can be computed through numerical homogenization.

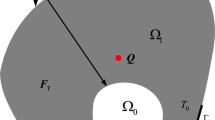
The rigidity of the macrostructure can be measured in terms of nodal displacement, which can be calculated by multiplying a unit virtual load vector \(\varvec{\varGamma }\) and displacement vector.

$$\begin{aligned} d=\varvec{\varGamma }^{\mathrm{T}} \varvec{U}. \end{aligned}$$
(6)

Then we define a auxiliary vector as

$$\begin{aligned} \varvec{\varGamma } =\left\{ 0,0,\ldots ,1,0,\ldots \right\} ^{\mathrm{T}}, \end{aligned}$$
(7)

where \(\varvec{\varGamma }\) is a vector consisting of zeros except for the position a, corresponding to the concerned d.o.f., where its value is one.

For the orthotropic material, the heat conduction capability can be evaluated in accordance with the summation of the diagonal elements in the effective thermal conductivity matrix. The thermal insulation constraint function for the 2D or 3D porous material can be stated as

$$\begin{aligned} \sum _{s=1}^{2,3} \kappa _{ss}^{\mathrm{H}} \leqslant \bar{\kappa }, \end{aligned}$$
(8)

where \(\kappa _{ss}^{\mathrm{H}}\) is the sth diagonal element in the effective thermal conductivity matrix. \(\bar{\kappa }\) is the upper bound for the final design. For anisotropic material, the non-diagonal elements can be non-zero. In this study, geometrical symmetries on both x and y axis are imposed on the microstructure for the design of orthotropic material.

In this study, the concurrent topology optimization aims at finding the minimization of total mass considering rigidity of macrostructure and thermal insulation capabilities of porous material simultaneously. The optimization problem can be mathematically stated as

$$\begin{aligned} \begin{array}{ll} \text {Minimize:} \quad &{} m=\mathop \sum \limits _{i=1}^{M} m_{i}, \quad i=1,2,\ldots ,M,\\ \text {Subject to:} \quad &{} d_{k} \leqslant \bar{d}_{k}, \quad k=1,2,\ldots ,K,\\ &{}\mathop \sum \limits _{s=1}^{2,3} \kappa _{ss}^{\mathrm{H}} \leqslant \bar{\kappa },\\ &{}0<P_{\mathrm{min}}\leqslant P_{i} \leqslant 1,\quad 0<r_{\mathrm{min}}\leqslant r_{j} \leqslant 1,\\ \end{array} \end{aligned}$$
(9)

where \(d_{k}\) and \({\bar{d}}_{k}\) denote the nodal displacement and the corresponding upper bound for the kth constraint function respectively. \(P_{\mathrm{min}} (=0.01)\) and \(r_{\mathrm{min}} (=0.01)\) are the lowest densities to ensure numerical non-singularity in FE analysis and numerical homogenization.

From Eq. (9), we can observe that the objective function of total mass depends on both the macro-scale and micro-scale density variables. The constraint functions also include both macrostructural responses \(d_k\) and effective thermal conductivity related to the microstructure. It is a typical two-scale topology optimization problem where the optimized topologies of macrostructure and microstructure should be achieved simultaneously.

3 Homogenization and sensitivity analyses on both the macro-scale and micro-scale

The micro-elemental elastic matrix and thermal conductivity matrix are interpolated by SIMP scheme as

$$\begin{aligned}&\varvec{D}^{\mathrm{MI}}=r_{j}^{\beta } \varvec{D}_{0}, \end{aligned}$$
(10a)
$$\begin{aligned}&\varvec{\kappa }^{\mathrm{MI}}=r_{j}^{\beta } \varvec{\kappa }_{0}, \end{aligned}$$
(10b)

where \(\beta \) represents the micro penalization power with the value of 4 in this work. \(\varvec{D}_{0}\) and \(\varvec{\kappa }_{0}\) denote the elasticity matrix and the thermal conductivity matrix when the corresponding element is solid. When the PCU is small enough in comparison to the size of the macrostructure, the effective elasticity matrix \(\varvec{D}^{\mathrm{H}}\) in Eq. (5) can be calculated through homogenization theory [45]

$$\begin{aligned} \varvec{D}^{\mathrm{H}}=\frac{1}{V} \int _{V} (\varvec{I}-\varvec{bu})^{\mathrm{T}} \varvec{D}^{\mathrm{MI}} (\varvec{I}-\varvec{bu}) \text {d}V, \end{aligned}$$
(11)

where \(\left| V \right| \) is the volume of PCU; \(\varvec{I}\) is identity matrix; \(\varvec{b}\) and \(\varvec{u}\) are the strain-displacement matrix and displacement vector for the microstructure, respectively.

To obtain the displacement vector \(\varvec{u}\), the PCU is analyzed by applying the periodic boundary conditions

$$\begin{aligned} \bigg (\int _{V} \varvec{b}^{\mathrm{T}} \varvec{D}^{\mathrm{MI}} \varvec{b} \text {d}V\bigg ) \varvec{u}= \int _{V} \varvec{b}^{\mathrm{T}} \varvec{D}^{\mathrm{MI}} \text {d}V. \end{aligned}$$
(12)

The right-hand side term of Eq. (12) denotes the external forces caused by the uniform strain fields, e.g. two normal unit strains in x and y directions and one shear unit strain for 2D cases.

Similarly, the homogenized heat conductivity matrix can be calculated as

$$\begin{aligned} \varvec{\kappa }^{\mathrm{H}}=\frac{1}{V} \int _{V} (\varvec{I_{s}}-\varvec{\chi })^{\mathrm{T}} \varvec{\kappa }^{\mathrm{MI}} (\varvec{I_{s}}-\varvec{\chi }) \text {d}V, \end{aligned}$$
(13)

where \(\varvec{I_{s}}\) denotes identity matrix for thermal conductivity homogenization, \(\varvec{\chi }\) represents the induced temperature gradient field, which can be computed from uniform gradient temperature.

For numerical homogenization expressed by Eqs. (11) and (13), more details on implementation can be referenced in Ref. [45].

With the aid of interpolation scheme in Eq. (10), the sensitivity of the homogenized elasticity tensor and thermal conductivity with respect to \(r_{j}\) can be conducted as

$$\begin{aligned}&\frac{\partial \varvec{D}^{\mathrm{H}}}{\partial r_{j}} =\frac{\beta r_{j}^{\beta -1}}{V} \int _{V} (\varvec{I}-\varvec{bu})^{\mathrm{T}} \varvec{D}_0 (\varvec{I}-\varvec{bu}) \text {d}V, \end{aligned}$$
(14a)
$$\begin{aligned}&\frac{\partial \varvec{\kappa }^{\mathrm{H}}}{\partial r_{j}} =\frac{\beta r_{j}^{\beta -1}}{V} \int _{V} (\varvec{I_{s}}-\varvec{\chi })^{\mathrm{T}} \varvec{\kappa }_0 (\varvec{I_s}-\varvec{\chi }) \text {d}V. \end{aligned}$$
(14b)

The sensitivities of nodal displacement with respect to the macro-density \(P_{i}\) and micro-density \(r_{j}\) are obtained through adjoint method as [46]

$$\begin{aligned} \frac{\partial d}{\partial P_i}=-\bar{\varvec{U}}^{\mathrm{T}} \frac{\partial \varvec{K}}{\partial P_i} \varvec{U}, \frac{\partial d}{\partial r_j}=-\bar{\varvec{U}}^{\mathrm{T}} \frac{\partial \varvec{K}}{\partial r_j} \varvec{U}, \end{aligned}$$
(15)

where \(\bar{\varvec{U}}\) represents the adjoint displacement vector of macrostructure, which can be obtained via solving the following adjoint equation

$$\begin{aligned} \varvec{K}\bar{\varvec{U}} =\varvec{\varGamma }. \end{aligned}$$
(16)

In Eq. (15), the sensitivities of global stiffness matrix \(\varvec{K}\) with respect to \(P_{i}\) and \(r_{j}\) can be given based on Eqs. (4), (5), (11), and (14)

$$\begin{aligned}&\frac{\partial \varvec{K}}{\partial P_i} =\alpha P_{i}^{\alpha -1} \int _{V_i} \varvec{B}^{\mathrm{T}} \varvec{D}^\mathrm{{H}} \varvec{B} \text {d} V_i, \end{aligned}$$
(17a)
$$\begin{aligned}&\frac{\partial \varvec{K}}{\partial r_j} =\sum _{i=1}^\mathrm{{M}} P_{i}^{\alpha } \int _{V_i} \varvec{B}^{\mathrm{T}} \frac{\partial \varvec{D}^{\mathrm{H}}}{\partial r_j} \varvec{B} \text {d} V_i. \end{aligned}$$
(17b)

4 Introduction of design variables and formulation of quadratic programming

We notice that multiple constraints are present in Eq. (9), which needs to be solved by a mathematical programming algorithm. In this section, we will introduce design variables to make the constraint functions linearization by means of Taylor series expansion.

In this study, the design variables are defined as the reciprocal function of density variables, i.e.

$$\begin{aligned} x_{i}=\frac{1}{P_{i}^{\alpha }}, y_{j}=\frac{1}{r_{j}^{\beta }}, ~~ i=1,2,\ldots ,M;j=1,2,\ldots ,N. \end{aligned}$$
(18)

Then we have

$$\begin{aligned}&P_{i}=x_{i}^{-1/\alpha }, r_{j}=y_{j}^{-1/\beta }, ~~ \nonumber \\&\quad i=1,2,\ldots ,M;j=1,2,\ldots ,N. \end{aligned}$$
(19)

The derivations of \(P_{i}\) or \(r_{j}\) with respect to design variables are expressed by

$$\begin{aligned}&\frac{\partial P_i}{\partial x_{i}}=-\frac{1}{\alpha } x_{i}^{-(1/\alpha +1)}, \quad i=1,2,\ldots ,M, \end{aligned}$$
(20a)
$$\begin{aligned}&\frac{\partial r_{j}}{\partial y_{j}} =-\frac{1}{\beta } y_{j}^{-(1/\beta +1)}, \quad j=1,2,\ldots ,N. \end{aligned}$$
(20b)

The approximate expression of \(d_k\) can be given using the first-order Taylor series expansion as

$$\begin{aligned} d_{k}\approx d_{k}^{(b)}+ \sum _{i=1}^{M} \frac{\partial d_{k}}{\partial x_{i}}\bigg |_b ( x_{i} -x_{i}^{(b)})+ \sum _{j=1}^{N} \frac{\partial d_{k}}{\partial y_{j}}\bigg |_b ( y_{j} -y_{j}^{(b)} ), \end{aligned}$$
(21)

where superscript (b) is the number of the optimization iteration.

In the same way, we have

$$\begin{aligned} \kappa _{ss}^\mathrm{{H}} \approx \kappa _{ss}^\mathrm{{H} (b)} + \sum _{i=1}^{M} \frac{\partial \kappa _{ss}^\mathrm{{H}}}{\partial x_{i}}\bigg |_b ( x_{i} -x_{i}^{b})+ \sum _{j=1}^{N} \frac{\partial \kappa _{ss}^{\mathrm{H}} }{\partial y_{j}}\bigg |_b ( y_{j} -y_{j}^{(b)} ). \end{aligned}$$
(22)

In Eqs. (21) and (22), the sensitivities of \(d_k\) and \(\kappa _{ss}^{\mathrm{H}}\) with respect to the design variables are calculated by the chain rule as follows

$$\begin{aligned} \frac{\partial d_{k}}{\partial x_i}&=\frac{\partial d_{k}}{\partial P_i}\cdot \frac{\partial P_i}{\partial x_i}, \frac{\partial d_{k}}{\partial y_j} =\frac{\partial d_{k}}{\partial r_j}\cdot \frac{\partial r_j}{\partial y_j},\end{aligned}$$
(23a)
$$\begin{aligned} \frac{\partial \kappa _{ss}^{\mathrm{H}} }{\partial x_i}&=0,\quad \frac{\partial \kappa _{ss}^{\mathrm{H}} }{\partial y_j} =\frac{\partial \kappa _{ss}^{\mathrm{H}}}{\partial r_j}\cdot \frac{\partial r_j}{\partial y_j}. \end{aligned}$$
(23b)

According to Eqs. (1) and (18), the total mass m can be rewritten as

$$\begin{aligned} m= & {} \sum _{i=1}^{M} m_i= \sum _{i=1}^{M} P_i \left( \sum _{j=1}^{N} V_{j} r_j \rho \right) \nonumber \\= & {} \sum _{i=1}^{M} x_{1}^{-1/\alpha } \left( \sum _{j=1}^{N} V_{j} y_{j}^{-1/\beta } \rho \right) . \end{aligned}$$
(24)

Two sets of design variables are combined as

$$\begin{aligned} \varvec{z}=\left\{ \begin{array}{c} \varvec{x} \\ \varvec{y} \\ \end{array} \right\} . \end{aligned}$$
(25)

Thus, the total mass can be rewritten as

$$\begin{aligned} m \approx m^{(b)} + \varvec{G}^{\mathrm{T}} \varvec{z}+\frac{1}{2} \varvec{z}^{\mathrm{T}} \varvec{H} \varvec{z}, \end{aligned}$$
(26)

where \(\varvec{G}\) and \(\varvec{H}\) are the first order derivative matrix and the Hessian matrix, respectively.

The first-order and second-order derivatives of the total mass with respect to design variables can be calculated as follows

$$\begin{aligned}&\frac{\partial m}{\partial x_i} =-\frac{\rho }{\alpha } x_{i}^{-(1/ \alpha +1)} \bigg (\sum _{j=1}^{N} V_{j}y_{j}^{-1/\beta }\bigg ),\end{aligned}$$
(27a)
$$\begin{aligned}&\frac{\partial m}{\partial y_j}=-\frac{\rho V_j y_{j}^{-(1/\beta +1)}}{\beta } \sum _{i=1}^{M} x_{i}^{-1/\alpha },\end{aligned}$$
(27b)
$$\begin{aligned}&\frac{\partial ^2 m}{\partial x_{i}^2}=\frac{(\alpha +1)\rho }{\alpha ^2} x_{i}^{-(1/\alpha +2)}\bigg (\sum _{j=1}^{N} V_j y_{j}^{-1/\beta }\bigg ),\end{aligned}$$
(27c)
$$\begin{aligned}&\frac{\partial ^2 m}{\partial y_{j}^2} =\frac{(\beta +1) }{\beta ^2} \rho V_{j} y_{j}^{-(1/\beta +2)} \sum _{i=1}^{M} x_{i}^{-1/\alpha },\end{aligned}$$
(27d)
$$\begin{aligned}&\frac{\partial ^2 m}{\partial x_{i} \partial y_{j}} =\frac{\rho V_j}{\alpha \beta } x_{i}^{-(1/ \alpha +1)} y_{j}^{-(1/\beta +1)}. \end{aligned}$$
(27e)

In Eq. (26), the constant \(m^{(b)}\) can be omitted for objective function. By combining Eqs. (21), (22), and (26), the mathematical optimization model determined by Eq. (9) can be rewritten as

$$\begin{aligned} \begin{array}{lll} \text {Minimize:} \quad &{}\varvec{G}^{\mathrm{T}} \varvec{z}+\frac{1}{2} \varvec{z}^{\mathrm{T}} \varvec{H}\varvec{z}, \\ \text {Subject to:}\quad &{} d_k \leqslant \bar{d}_{k}, &{}k=1,2,\ldots ,K,\\ &{}\mathop \sum \limits _{s=1}^{2,3} \kappa _{ss}^{\mathrm{H}} \leqslant \bar{\kappa },\\ &{}1\leqslant x_{i}\leqslant P_{\mathrm{min}}^{-\alpha }, &{}i=1,2,\ldots ,M,\\ &{}1\leqslant y_{j}\leqslant r_{\mathrm{min}}^{-\beta }, &{}j=1,2,\ldots ,N. \end{array} \end{aligned}$$
(28)

It is worth pointing out that Eq. (28) is in the form of a standard quadratic programming problem. Optimum values of design variables are updated by SQP algorithm efficiently. Then the macrostructure and microstructure are rebuilt by renewed densities according to Eq. (19) until the following criterion is satisfied as

$$\begin{aligned} \left| m^{(b+1)}- m^{(b)} \right| /m^{(b+1)}\leqslant \varepsilon , \end{aligned}$$
(29)

where \(\varepsilon \) is the precision of convergence.

5 Elimination of numerical instabilities

To avoid unfavorable phenomena in topology optimization, i.e. checkerboard patterns and mesh dependence, the sensitivity filter technique is widely used in topology optimization. In this paper, instead of filtering the sensitivity of the objective function in SIMP method, the first term of constraint function in Eq. (21) is taken as the filtered variable as

$$\begin{aligned} {e}_{ik,x}=\frac{\partial d_{k}}{\partial x_{i}} x_{i},\quad {e}_{jk,y}=\frac{\partial d_{k}}{\partial y_{j}} y_{j}, ~~ k=1,2,\ldots ,K. \end{aligned}$$
(30)

The filter is implemented by solving the Helmholtz partial differential equation (PDE) with Neumann boundary conditions [47]

$$\begin{aligned}&\begin{array}{c} -r_{1}^{2} \bigtriangledown ^{2} {\tilde{\varvec{e}}}_{k,x}+ \tilde{\varvec{e}}_{k,x}= \varvec{e}_{k,x}, \frac{\partial \tilde{\varvec{e}}_{k,x}}{\partial n}=0, \\ \end{array} \end{aligned}$$
(31a)
$$\begin{aligned}&\begin{array}{c} -r_{2}^{2} \bigtriangledown ^{2} {\tilde{\varvec{e}}}_{k,y}+ \tilde{\varvec{e}}_{k,y}= \varvec{e}_{k,y}, \frac{\partial \tilde{\varvec{e}}_{k,y}}{\partial n}=0, \\ \end{array} \end{aligned}$$
(31b)

where \({\tilde{\varvec{e}}}_{k,x}\) and \({\tilde{\varvec{e}}}_{k,y}\) denotes the filtered fields for \(\mathrm{e}_{ik,x}\) and \( \mathrm{e}_{jk,y}\). And \(r_1\) and \(r_2\) are PDE parameters for macrostructure and microstructure, which play a similar role as the filter radius in the original filter.

Fig. 2
figure 2

Density distribution of initial design

Full size image

It can be proved that

$$\begin{aligned} \sum _{i=1}^{M} {\tilde{\varvec{e}}}_{ik,x} =\sum _{i=1}^{M} \mathrm{e}_{ik,x}, \sum _{j=1}^{N} {\tilde{\varvec{e}}}_{jk,y} =\sum _{j=1}^{N} {e}_{jk,y}. \end{aligned}$$
(32)

From Eq. (32), the sum of filtered variables before and after filtering remains the same. The optimization procedure can benefit from such preserving feature which leads to a stable convergence. After filtering, the modified sensitivities expressed in Eq. (33) will replace the original sensitivities to update design variables.

$$\begin{aligned} \frac{\partial {\tilde{d}}_{k}}{\partial x_i}=\frac{\tilde{e}_{ik,x}}{x_i},\quad \frac{\partial {\tilde{d}}_{k}}{\partial y_j}=\frac{\tilde{e}_{jk,y}}{y_j}. \end{aligned}$$
(33)

The similar procedure can be applied for the sensitivities \(\dfrac{\partial \kappa _{ss}^{\mathrm{H}} }{\partial x_i}\) and \(\dfrac{\partial \kappa _{ss}^{\mathrm{H}} }{\partial y_j}\) , the details are omitted here for simplicity.

The filtering scheme brings blur boundary in final topologies on both macro- and micro-scales. To eliminate the immediate density, the filtering programs are terminated after convergence and the optimization procedure proceeds until meeting the condition described in Eq. (29) again. For the whole process, \(\varepsilon \) is prescribed to be 0.1% and 0.01% before and after filtering.

6 Numerical examples and discussions

It is a usual practice in macro-scale topology optimization to adopt uniformly distributed material as the initial design to avoid local optimal solutions. However, it is infeasible in the inverse homogenization because the homogeneous sensitivity field generated by periodic boundary conditions will result in the halt of the optimization procedure. Following Amsturz et al. [48], the domain of PCU is assumed to be square with the edge length l. A circular region with the diameter D composed of softer material is defined at the center of PCU as shown in Fig. 2.

To illustrate the capability and effectiveness of the proposed method, we present several numerical examples, for concurrently designing macrostructures and microstructures. The following material parameters are used for isotropic base material: Young’s modulus \(E=210\)  GPa, Poisson’s ratio \(\nu =0.3\), density \(\rho =7800\,{\hbox {kg}/\hbox {m}^3}\), and heat conductivity \(k=40 ~{\hbox {W}/(\hbox {m}\cdot \hbox {K})}\). For comparison, the normalized objective function \(m/m_{0}\) is used, in which m and \(m_{0}\) denote the total mass of the optimal structure and the initial structure full of materials, respectively. All numerical examples are run on a desktop computer with an Intel i7 2.93 GHz processor.

6.1 Example I

In the first example, a short cantilever beam is optimized to illustrate the effect of initial design on finial topologies. Figure 3 shows the admissible design domain in macrostructure with length \(L=120\) cm, height \(H=60\) cm, and thickness \(T=1\) cm undergoing a concentrated vertical load \(F=100\,\mathrm {kN}\) at the center of the right edge. The left side is fully constrained. The 2D design domain is discretized into 4-node plane strain elements with an edge length of 1 cm. The following constraints should be satisfied: (1) nodal displacement at point A in the y direction, i.e. \(u_{A} \geqslant -0.8\) cm; (2) the effective conductivity constraint, i.e. \( \sum _{s=1}^{2}\kappa _{ss}^{\mathrm{H}}\leqslant 25\,{ \hbox {W}/(\hbox {m}\cdot K)}\). Three different initial distributions of material are investigated with the diameter \(D=5l/8, l/2\), and 3l / 8. The PCU is discretized into \(80 \times 80\) 4-node quadrilateral elements. The density is distributed uniformly with the value of 0.9 and 0.45 outside and inside the circle for three initial designs. No symmetric constraints are imposed on macrostructure and microstructure in this example. The optimized macrostructure, microstructure, and the corresponding material properties are summarized in Table 1.

Fig. 3
figure 3

2D macro-structural design domain for the concurrent optimization in Example I, with the dimension: length \(L=120\,\hbox {cm}\), height \(H=60\,\hbox {cm}\) with thickness \(T=1\,\hbox {cm}\). The left side is fully constrained and a concentrate vertical load \(F=100\,\hbox {kN} \) is applied at the center of the right edge

Full size image
Table 1 Optimal results for different initial design
Full size table

From Table 1, the results give the similar macrostructure, but distinct microstructure compared to each other. As expected, optimized topologies of both macrostructure and microstructure possess geometric symmetry. In all cases, the resulting nodal displacement constraint and effective conductivity agree well with prescribed values. Three mass fractions of the final design are close to each other. Therefore, it can be inferred that optimized topologies of microstructure are affected by initial design, which has similarities to material design. Results from the first initial design provide the minimum mass and its corresponding microstructure is simpler than two others.

To illustrate the effectiveness of the proposed method, the conventional SIMP method is adopted, i.e. Eq. (9) is updated directly by the Method of Moving Asymptotes (MMA) [49]. Initial design in Table 1 with the diameter D = 5l/8 is adopted. Optimized topologies of macrostructure and microstructure shown in Fig. 4 are similar to those obtained by the proposed method. These results verify the effectiveness of the present approach.

6.2 Example II

This example is the extension of Example I, which intends to reveal the influence of the nodal displacement constraint on the final results. The effective conductivity constraint is fixed as \( \sum _{s=1}^{2}\kappa _{ss}^{\mathrm{H}}\leqslant 30\,\hbox {W}/(\hbox {m}\cdot \hbox {K})\). The low bound of nodal displacement \(\underline{u}_A\) varies from \({-}\)1.2 to \({-}\)0.6 cm. Other parameters are the same as those chosen in Example I. Figure 5 presents the mass fraction for various low bounds of nodal displacement with optimal macro and micro topologies inserted.

From Fig. 5, we can observe that optimized topologies of microstructure share similar configurations when the thermal-insulating capability of porous material is set to be a constant. In contrast, macrostructure depends obviously on different displacement constraint values imposed at point A. It is seen that a larger mass fraction can be achieved with a more strict control on the displacement of macrostructure. It is intuitively easy to understand because the structure with a larger mass fraction possesses sufficient rigidity to resist elastic deformation.

6.3 Example III

This example is also the extension of Example I, which is considered in an attempt to reveal the influence of effective conductivity constraint on the final results. The nodal displacement constraint is fixed as \(u_A \geqslant -0.5\)  cm. The upper bound for the effective conductivity varies from 36 to 48  \( \hbox {W}/(\hbox {m}\cdot \hbox {K})\). Other parameters are the same as those chosen in Example I. Figure 6 shows the mass fraction for various upper bounds of the effective thermal conductivity with typical topologies of macrostructure and microstructure inserted.

Fig. 4
figure 4

Optimized topologies obtained from MMA algorithm for: a macrostructure; b microstructure

Full size image
Fig. 5
figure 5

Evolution history of the total mass with the increasing upper bound of effective thermal conductivity and the corresponding structural evolution for Example II

Full size image
Fig. 6
figure 6

Evolution history of the total mass with the increasing low bound of nodal displacement, and the corresponding structural evolution for Example III

Full size image

In this example, we can find that optimized topologies of macrostructure share similar configurations for different conductivity constraint values when the nodal displacement constraint is fixed. However, the conductivity constraint values have a greater impact on the mass fraction of macrostructure and the volume fraction and optimal topology of microstructure. The mass fraction of macrostructure decreases monotonously with the increase of the conductivity constraint values, in contrast to the increase in the volume fraction of microstructure. Compared with results in Fig. 5, because more emphasis is placed on thermal insulating properties of porous material, more material is shifted from micro level to macro level automatically. The optimal results have demonstrated that the proposed concurrent optimization method can distribute the base material between macrostructure and microstructure to meet the requirements of lightweight design and various constraints simultaneously.

6.4 Example IV

This example optimizes the same structure as illustrated in Example I except that the concentrated vertical load is imposed on the bottom corner on the right side, aiming to further demonstrate the feasibility of the proposed method in asymmetric loading condition. We set the effective conductivity constraint as \( \sum _{s=1}^{2}\kappa _{ss}^{\mathrm{H}}\leqslant 30\,\,\hbox {W}/(\hbox {m}\cdot \hbox {K})\). The low bound of nodal displacement \(u_B\) varies from \({-}\)0.8 to \({-}\)1.4 cm. Other parameters are the same as those chosen in Example I. The symmetries in x and y directions are enforced on the microstructure for obtaining orthotropic material. Figure 7 presents the mass fraction for various low bounds of nodal displacement with optimal macro and micro topologies inserted.

Fig. 7
figure 7

Evolution history of the total mass with the increasing low bound of nodal displacement, and the corresponding structural evolution for Example IV

Full size image

From Fig. 7, it can be seen that the mass fractions for various low bounds of nodal displacement show the same tendency as that previously reported in Example 1. However, a slight difference can be found in optimized topologies of microstructure, which implies that, in spite of the same thermal insulation constraint, the microstructure may be affected by the variation of prescribed nodal displacements in macrostructure.

6.5 Example V

This example is the extension of Example II, specifically used for evaluating the effect of multiple nodal displacement constraints on optimized topologies. As depicted in Fig. 3, two concentrated loads, acting in opposite directions, are imposed on point B (downward) and point C (upward) for loading case I and II, respectively. In loading case I, the constraint value of vertical displacement on point C is prescribed as \(u_C\leqslant \,0.9\) cm as the first constraint. In loading case II, the low bound for the vertical displacement on point B are investigated which varies from \({-}\)0.8 to \({-}\)1.1 cm. The symmetries in x and y directions are enforced on the microstructure for obtaining orthotropic material. Other parameters are the same as those chosen in Example II. Figure 8 presents the mass fraction for various low bounds of nodal displacement with optimal macro and micro topologies inserted.

Fig. 8
figure 8

Evolution history of the mass fraction with the increasing low bound of nodal displacement, and the corresponding structural evolution for Example V

Full size image

Apparently, optimal topology of macrostructure is symmetric only when nodal displacement constraint is prescribed to be symmetric in different loading cases. With more stringent requirements for the stiffness concerned with the macrostructure, the mass fraction increase monotonously at the macro level while the resulting topologies of the microstructure have no significant difference from each other. Seeking for a lightweight design, both load-carrying capabilities of the macrostructure in multiple loading cases and requirement of thermal insulation related to cellular material can be balanced by the proposed method.

6.6 Example VI

This example optimizes a typical 3D structure, aiming to illustrate the feasibility of the proposed approach in 3D structure. Figure 9 shows the admissible design domain in macrostructure, which is discretized by brick elements with the size: length \(L=48\,\hbox {cm}\), width \(B=30\,\,\hbox {cm}\), and height \(H=6\,\hbox {cm}\). The size of the elements is 1 cm. The microstructure is discretized into \(26\times 26\times 26\) solid elements. The left surface is fully constrained and a concentrate force \(F=1\times 10^4\,\hbox {kN}\) is applied on the centre of the right surface.

Fig. 9
figure 9

3D macrostructural design domain for the concurrent optimization in Example VI, with the dimension: length \(L=48\,\hbox {cm}\) , width \(B=30\,\hbox { cm}\) and height \(H=6\,\hbox { cm}\). The left surface is fully constrained and a concentrate force \(F=1\times 10^4\,\hbox {kN} \) is applied on the centre of the right surface

Full size image

When we fixed the effective conductivity constraint as \( \sum _{s=1}^{3}\kappa _{ss}^{\mathrm{H}}\leqslant 30\,\,\hbox {W}/(\hbox {m}\cdot \hbox {K})\), the low bound of nodal displacement \(u_A\) can vary from \({-}\)0.4 to \({-}\)0.8 cm. Figure 10 presents the mass fraction for various low bounds of nodal displacement with optimal macro and micro topologies inserted. For easier identification, the configurations with a cross section are presented.

When we fixed the low bound of nodal displacement as \(u_A\geqslant -1.0\,\hbox {cm}\), the upper bound for the effective conductivity varies from 30 to 40  \(\hbox {W}/(\hbox {m}\cdot \hbox {K})\). Figure 11 presents the mass fraction for various upper bounds of the effective thermal conductivity with optimal macro and micro topologies inserted. The final microstructure is symmetrical.

Fig. 10
figure 10

Evolution history of the mass fraction with the increasing low bound of nodal displacement, and the corresponding structural evolution for Example VI

Full size image
Fig. 11
figure 11

Evolution history of the mass fraction with the increasing upper bound of effective thermal conductivity and the corresponding structural evolution for Example VI

Full size image

Similar to 2D cases, Figs. 10 and 11 also demonstrate that the two-scale optimal design is a compromising solution between the thermal insulation of materials and structural stiffness at macro level. The weight fractions of final design share the similar tendency as those illustrated in 2D cases.

Table 2 Iteration steps and CPU time for different FE discretization meshes
Full size table
Fig. 12
figure 12

Optimized topologies for different FE discretization meshes: a \( 22 \times 22 \times 22 \); b \( 26 \times 26 \times 26 \); c \( 30\times 30 \times 30 \); d \( 34 \times 34 \times 34 \); e \( 38 \times 38 \times 38 \); f \( 42 \times 42 \times 42 \)

Full size image

It is worth pointing out that topology optimization of 3D structure is time-consuming. In the present concurrent optimization model, there are six numerical homogenization analyses involving mechanical properties and three numerical homogenization analyses involving thermal properties for each iteration step. Table 2 provides a comparison of the iteration steps and computational cost (CPU time in seconds) for six different FE discretization meshes. The optimized topologies of microstructure for different discretization meshes are also shown in Fig. 12. As can be seen from Table 2, the CPU time increases dramatically as mesh density increases. It is normal for optimization methods to need more design iterations, when increasing the mesh density [46], especially for 3D structure. However, the presented method can provide a solution in which number of iterations is independent of discretization mesh. Figure 12 also demonstrates that optimized topologies are independent of the discretization mesh. The slight difference between these topologies is that the boundary becomes smoother with finer mesh.

7 Conclusion

In this present paper, a novel concurrent topology optimization formulation for minimization of total mass considering load bearing in macrostructure and thermal insulation of porous material simultaneously is proposed, which is distinct with the existing concurrent topology optimization approaches. For a typical two-scale optimization problem, the objective function of total mass involves the macro-scale and micro-scale density. The material properties from homogenization of microstructure are applied to macrostructural analysis, while the sensitivities of the microstructure are related to the displacement vectors of macrostructures obtained from original and adjoint load cases. With the introduction of reciprocal variables, the constraint functions are linearized while the objective function is approximated as the second order Taylor expansion. Then the established optimization model can be solved efficiently using SQP algorithm, by setting up a series of sub-problems in the form of a quadratic program with second-order sensitivities.

As highlighted in the provided numerical examples, the proposed concurrent optimization method can automatically allocate the base material between macrostructure and microstructure to meet the requirements various constraints simultaneously to achieve a lightweight design. Because of its generality, this method can be extended to the structural design considering other design requirements, such as the frequency constraints.