1 Introduction

Cell sorting is a basic and important step for medical research and clinical applications [1–5]. The traditional cell sorting principles are mainly based on the differences of the cells’ physical and/or chemical properties, such as density, charge, density magnetism, selective fluorescent markers and so on [6–10]. However, these methods are usually either complex in device configuration or need additional labels like magnetic or fluorescent markers [11, 12]. These disadvantages make the traditional methods very expensive or extremely difficult to implement. As a newly developed method, the size-dependent sorting method (SDSM) has attracted growing attention in the past few years attributed to its promising advantages of low cost, high efficiency, and label-free visualization [10, 13–18]. Four typical SDSMs have been reported, the deterministic lateral displacement (DLD) [10, 13], the pinched flow fractionation [14–16], the cross-flow filtering [17], and the inertial focusing sorting [18]. Some of them have been used to sort blood components [19–22]. Among these methods, the DLD is very attractive due to its simplicity and high efficiency [23, 24]. It simply utilizes an array of micro cylinders within a channel to precisely control the trajectory of particles with different sizes and achieve a sorting result, and can parallel sort high throughput samples with multi-sized particles.

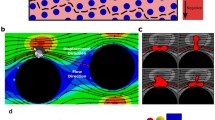
The DLD method was first proposed experimentally by Huang et al. [23], who found that particles of different sizes can be sorted by adjusting the gap width between micro columns and the column shift of adjacent rows of micro columns, as shown in Fig. 1. Two different migration modes of particles, displacement mode and zigzag mode, are observed by changing the particle size, gap width, and column shift. Two particles of different sizes can be separated if each one follows different migration modes. As an interesting application, Davis et al. [25] used a multistage micro-column matrix to separate blood cells. White blood cells (WBCs), red blood cells (RBCs) and platelets can be sorted due to their size variations. Lately, the DLD has been extensively used in enrichment and separation of large cells involved in tissue engineering, cells dyeing, labeling, and manipulation in biochemistry [26–28].

Fig. 1
figure 1

Two types of motion modes

Full size image

With the rapid development of computer science, the numerical simulation technique plays an increasing role in optimization design and the mechanism exploring of micro fluidic cell manipulation [29–36]. For example, Quek et al. [37] numerically studied the DLD migration trajectories of deformable bodies with different sizes, and a third migration mode called the dispersive mode was first reported. In the present work, a numerical model based on the immersed boundary-lattice Boltzmann method (IB-LBM) is employed to study the flexible cell sorting with the DLD method. The simulation results indicate that the cell sorting results can be significantly influenced by regulating two critical parameters, the gap width d between the micro columns and the column shift \(\Delta \lambda \) of adjacent two rows of columns, and a proper group of parameters can lead to a well concentrated cell sorting. This can provide a significant reference for optimizing the cell sorting architecture design in an experimental case.

The organization of the present paper is as follows. The numerical method, i.e., the IB-LBM, and the cell membrane mechanics are described in Sect. 2. Section 3 gives the DLD numerical model. A single flexible cell’s motional principle and the further continuous cell sorting of multiple cells are discussed and analyzed in Sect. 4. Final conclusions are given in Sect. 5.

2 Mathematics model

In this work, the fluid motion is solved by the LBM with the D2Q9 lattice model. The discrete lattice Boltzmann equation of a single relaxation time model is [38–40]

$$\begin{aligned}&g_i({\varvec{x}}+\varvec{e}_{{i}}\Delta t,t+\Delta t)-g_i({\varvec{x}},t)\nonumber \\&\quad =-\frac{1}{\tau }(g_i({\varvec{x}},t)-g_i^{\mathrm {eq}}({\varvec{x}},t))+\Delta tG_i, \end{aligned}$$
(1)

where \(g_{i}({{\varvec{x}}}, t)\) is the distribution function for particles of velocity \({{\varvec{e}}}_{i}\) at position \(\varvec{x}\) and moment t, \(\Delta t\) is the time step, \(g_i^\mathrm{eq}\) is the equilibrium distribution function, \(\tau \) is the non-dimensional relaxation time, and \(G_i\) is the body force term. \(g_i^{\mathrm {eq}}\) and \(G_i\) are calculated by [41]

$$\begin{aligned}&g_{i}^{\mathrm {eq}}({\varvec{x}},t)=\omega _i \rho \left[ 1+\frac{\varvec{e}_{{i}}\cdot {\varvec{u}}}{c_{\mathrm{s}}^{2}} +\frac{(\varvec{e}_{{i}}\cdot {\varvec{u}})^{2}}{2c_{\mathrm{s}}^{4}} -\frac{{\varvec{u}}^{2}}{2c_{\mathrm{s}}^{2}}\right] ,\end{aligned}$$
(2)
$$\begin{aligned}&G_i=\left( 1-\frac{1}{2\tau }\right) \omega _i \left( \frac{\varvec{e}_{{i}}-{\varvec{u}}}{c_{\mathrm{s}}^{2}} +\frac{\varvec{e}_{{i}}\cdot {\varvec{u}}}{c_{\mathrm{s}}^{4}}\varvec{e}_{{i}}\right) \cdot {\varvec{f}}, \end{aligned}$$
(3)

where \({{\varvec{u}}}\) is the velocity vector, \({{\varvec{f}}}\) is the body force density vector, \(\rho \) is the density, \(\omega _i\) are the weights defined by \(\omega _0= 4/9\), \(\omega _i = 1/9\) for \(i=1{-}4\) and \(\omega _i = 1/36\) for \(i=5{-}8\), and \(c_{\mathrm {s}} =\Delta x/(\sqrt{3}\Delta t)\) is the sound speed.

For the immersed boundary to model the cell membrane, its position can be updated within one time step of \(\Delta t\) through [42]

$$\begin{aligned} {\varvec{U}}(s,t)=\int _\varOmega {{\varvec{u}}(x,t)D} ({\varvec{x}}-{\varvec{X}}(s,t))\hbox {d}x, \end{aligned}$$
(4)

and

$$\begin{aligned} \frac{\partial {\varvec{X}}}{\partial t}={\varvec{U}}(s,t), \end{aligned}$$
(5)

where \({{\varvec{X}}}(s, t)\) is the position of the membrane s at moment t, \({{\varvec{U}}}(s, t)\) is the velocity of the membrane, \({{\varvec{u}}}({{\varvec{x}}}, t)\) is the velocity of the fluid, \(\text {d}x\) is the lattice side length, and \(\varOmega \) is the nearby area of the membrane controlled by a Delta function \(D(\varvec{x} - \varvec{X})\) [30, 41].

The blood cell membrane is made up of a series of solid particles connected with springs in a consecutive way. Each solid particle supports both stretching and bending forces. The stretching force of membrane \({\varvec{F}}_{\mathrm {s}} \) and the bending force \({\varvec{F}}_{\mathrm {b}} \), are derived from the Frechet derivative of the bending energy formula based on the virtual work principle:

$$\begin{aligned} {\varvec{F}}_{\mathrm{s}}= & {} \frac{\partial }{\partial s}\left[ {K_{\mathrm{s}}\left( \left| \frac{\partial {\varvec{X}}(s,t)}{\partial s}\right| -1\right) \frac{\partial {\varvec{X}}(s,t)}{\partial s}} \right] ,\end{aligned}$$
(6)
$$\begin{aligned} {\varvec{F}}_{\mathrm{b}}= & {} K_{\mathrm{b}} \frac{\partial ^{4}{\varvec{X}}(s,t)}{\partial s^{4}}, \end{aligned}$$
(7)

where \({{\varvec{X}}}\) is the position coordinate of the grid point on the membrane, s is the Lagrangian coordinate along the membrane, t is the time variable, \(K_{\mathrm{s}}\) is the elastic coefficient and \(K_{\mathrm{b}}\) is the bending coefficient. In addition, the normal force on the membrane, \({{\varvec{F}}}_{\mathrm{a}}\), which controls the cell incompressibility, and the membrane-wall extrusion acting on the cell, \({{\varvec{F}}}_{\mathrm{e}}\), are applied according to

$$\begin{aligned} {\varvec{F}}_{\mathrm {a}}= K_{\mathrm{a}}\frac{S-S_{0}}{S_{0}}{\varvec{n}}, \end{aligned}$$
(8)

and

$$\begin{aligned} {\varvec{F}}_{\mathrm{e}}=\left\{ \begin{array}{ll} K_{\mathrm{e}}\frac{{\varvec{X}}(s,t)-{\varvec{X}}_{\mathrm{w}} }{|{\varvec{X}}(s,t)-{\varvec{X}}_{\mathrm{w}} |^{3}},&{} |{\varvec{X}}(s,t)-{\varvec{X}}_{\mathrm {w}} |\leqslant r_\mathrm{c}, \\ 0,&{}|{\varvec{X}}(s,t)-{\varvec{X}}_{\mathrm {w}} |>r_\mathrm{c}. \end{array}\right. \end{aligned}$$
(9)

In Eq. (8) S is the cell area, \(S_{0}\) is the cell area in the natural state, \(K_{\mathrm{a}}\) is the volume maintenance factor, and \(K_{\mathrm{e}}\) is the repulsive force coefficient of the wall. Therefore, the cell membrane mechanics is proposed as \({{\varvec{F}}} = {{\varvec{F}}}_{\mathrm{s}} - {{\varvec{F}}}_{\mathrm{b}} + {{\varvec{F}}}_{\mathrm{a}} + {{\varvec{F}}}_{\mathrm{e}}\).

In Eq. (9), \(r_\mathrm{c}\) is the cut-off distance, \(\varvec{X}_\mathrm{w}\) are the wall boundary points nearest to the cell membrane points at moment t. This means one cell membrane point is bound to have one nearest wall boundary point at a moment, which will produce a minimal distance, then all the minimal distances are \(|\varvec{X}(s,t)-\varvec{X}_\mathrm{w}|\), and \(\varvec{n}\) is the unit vector obtained by \(\frac{\varvec{X}(s,t)-\varvec{X}_\mathrm{w}}{|\varvec{X}(s,t)-\varvec{X}_\mathrm{w}|}\).

Then the force density \({{\varvec{f}}}\) in Eq. (3) acting on the nearby fluid is calculated by

$$\begin{aligned} {\varvec{f}}({\varvec{x}},t)=\int _\varGamma {\varvec{F}}(s,t)D ({\varvec{x}}-{\varvec{X}}(s,t))\hbox {d}s. \end{aligned}$$
(10)

3 Model definition and inspection

3.1 Models and parameter settings

The numerical DLD model is established to sort WBCs and RBCs, which are distinct in size. All cells are assumed to be spherical in the natural state. They are deformable under an external force such as shear or extrusion, and the deformed cells will recover rapidly if the external force is removed.

Fig. 2
figure 2

The model of the cell sorting structure

Full size image

The two-dimensional (2-D) cell sorting structure is shown in Fig. 2, which is mainly composed of a channel and a set of micro-cylinder arrays (MCA). The channel is \(610.2\,\upmu \hbox {m}\) in length and \(319.8\,\upmu \mathrm{m}\) in width. The MCA is arranged in the following way. The radius of the cylinder is R, the horizontal and vertical distances between two adjacent cylinder centers are both \(\lambda \), the vertical shift of two adjacent cylinder centers in a horizontal direction is \(\Delta \lambda \) as marked in Fig. 2, and their ratio is denoted by \(\varepsilon =\Delta \lambda /\lambda \). Another crucial parameter is the dimension ratio \(\omega = D_{\mathrm{c}}/d\), where \(D_{\mathrm{c}}\) is the cell diameter and d is the gap width between adjacent cylinders and defined as \(\lambda -2R\). The cells to be sorted are released from a presetting position at the inlet, and get out from the channel outlet.

A parabolic velocity profile with maximum velocity of \(u_{\mathrm{m}}=2.12\times 10^{-2}\, \hbox {m/s}\) is proscribed at the inlet; free-stress is applied at the outlet; and stationary boundary condition is applied at the top and bottom walls. In the LBM application, all boundary conditions are achieved by using the non-equilibrium extrapolation scheme [43].

The computational domain is discretized by \(1017 \times 533\) Cartesian nodes, which ensures there are 20 nodes over a WBC and 12 nodes over an RBC in the natural state. The WBC and RBC membranes are divided into 68 and 38 points, respectively, which makes the initial interval of two neighboring membrane points suitable for the setting of the immersed boundary method [42]. The time step is \(9.44 \times 10^{-8}\,\hbox {s}\), and the total computation time is 0.2833 s. Simulations have been conducted to ensure that the results are independent of the mesh size and time step. Other parameters are listed in Table 1.

Table 1 Simulation parameters
Full size table

In Table 1, \(K_{\mathrm{a}}\) is chosen to ensure that the variation rate of the cell volume is less than 2 %. \(K_{\mathrm{e}}\) controls the degree of repulsive force on the cell membrane node once it is pressed to be less than \(1.2\,\upmu \mathrm{m}\) (the cut-off distance \({r}_{\mathrm{c}})\) to the wall. The value of \(K_{\mathrm{e}}\) is chosen to be large enough so that the cell membrane is located at least 1 lattice away from the wall [42]. The Reynolds number, defined by \(\textit{Re} = D_{\mathrm{rbc}}\rho u_{\mathrm{m}}/\mu _{\mathrm{p}}\), is in the range of 0.1–1. Flows in this Reynolds number regime can be tackled by the LBM [30, 40]. The geometric parameters \(\lambda , d, \varepsilon \) and the cell properties \(K_{\mathrm{s}}\) and \(K_{\mathrm{b}}\) will be varied to study their effects on cell sorting in the DLD, and will be given in Sect. 4.

3.2 Validation: the migration of a rigid circular particle

The IB-LBM used in this work has been extensively validated and verified for numerical accuracy and convergence in the filament flapping and RBC fluid–structure interaction [30–32, 38, 40]. Hence, we will not present here again the validation of the IB-LBM for flexible cells. In this section, we present the validation of the rigid particle migration in an MCA. To do this, a set of numerical cases are performed to test the migration modes of a rigid circular particle passing the cylinder array. Since the migration mode of displacement (dis) and zigzag (zig) can be predicted exactly in theory [23], this validation is able to verify our model by making a comparison between the numerical and the theoretical results.

In Ref. [44], the membrane parameters \(K_{\mathrm{s}}\) and \(K_{\mathrm{b}}\) are set to be in the range of \(0.01 \times 10^{-12}-3.0\times 10^{-12}\) N\(\cdot \)m for the normal RBC. Here, in order to simulate the high rigidity of the particle, the elastic coefficient \(K_{\mathrm{s}}\) and the bending coefficient \(K_{\mathrm{b}}\) are increased to be \(1\times 10^{-11}\) and \(5\times 10^{-12}\,{\hbox {N}}{\cdot }{\hbox {m}}\). The particle diameter is set as \(12\,\upmu \mathrm{m}\) referenced by the size of WBC. By regulating \(\varepsilon \) and \(\omega \), the results are displayed in Fig. 3, where the square and circular points are numerical results and the solid line is the theoretical division boundary according to Ref. [47]. The numerical results are found well consistent with the theoretical prediction, which illustrates that our model is effective and reliable.

Fig. 3
figure 3

Validations of dis. and zig. motion modes in the micro-cylinders array

Full size image
Fig. 4
figure 4

Schematic diagrams of cells’ trajectories for different elastic modulus \(K_{\mathrm{s}}\)

Full size image

4 Results and discussion

In this study, we consider the DLD sorting of blood cells (mainly including WBC and RBC). Compared with the rigid circular particles, the blood cells are flexible and deformable. In general, their configuration is not circular, for example, the normal RBC is biconcave. These characteristics make it challenging for modeling of the DLD sorting for blood cells. For simplicity, here all blood cells are treated as spherical, by considering the facts that the WBC is naturally spherical and that the RBC can be extended to be spherical by decreasing the concentration of the normal saline. In the present work, we focus on the effects of the cell deformability, special distribution of MCA, and initial cell–cell distance on the DLD sorting.

4.1 Effects of cell deformability

4.1.1 Single cell migration in MCA

In this section, the effects of cell deformability on DLD are studied. In the present model, we set the spatial distribution parameters as \(d = 18\,\upmu \mathrm{m}\), \(\lambda = 32.4\,\upmu \mathrm{m}\) and \(D_\mathrm{c} = 12\,\upmu \mathrm{m}\), the fraction ratio \(\varepsilon = \Delta \lambda /\lambda \) as 0.25, and \(K_{\mathrm{b}}=5\times 10^{-13}\) N\(\cdot \)m. Note that \(K_{\mathrm{b}}\) is chosen to be so small so that it does not affect the deformation of the cell, which, instead, is controlled by \(K_{\mathrm{s}}\) and \({{\varvec{F}}}_{\mathrm{a}}\). A larger \(K_{\mathrm{s}}\) can make a stiffer cell, while a smaller value corresponds to a softer cell. To exhibit the effect of cell deformability on the cell’s migration path, five numerical cases are performed by varying \(K_{\mathrm{s}}\). The setting of \(K_{\mathrm{s}}\) and the corresponding results are shown in Fig. 4. It shows that under the same conditions, different values of \(K_{\mathrm{s}}\) will result in different migrating paths. This indicates that the cell deformability is one of the critical factors affecting the DLD sorting.

4.1.2 Sorting of two types of cells

In general, RBC is much softer than WBC. In our study, \(K_{\mathrm{s}}\) of RBC is set as 10 % of WBC to distinguish the deformability approximately, where the basic \(K_{\mathrm{s}}\) of WBC is set as \(1\times 10^{-11}\) N\(\cdot \)m, the basic \(K_{\mathrm{s}}\) of RBC is \(1\times 10^{-12}\) N\(\cdot \)m. For the bending coefficient \(K_{\mathrm{b}}\), it is set as \(5\times 10^{-13}\) N\(\cdot \)m both for WBC  and  RBC. In order to study the effect of cell deformability to the cell sorting, a set of numerical cases are performed by varying \(K_{\mathrm{s}}\), which is set in order as 1, 0.4, 0.2, 0.1, and 0.05 times the basic \(K_{\mathrm{s}}\), and the corresponding cases are marked as case (1) to case (0.05). Besides the parameter setting in Sect. 3.1, the additional parameters are introduced as follows. It is found the cell sorting results are not ideal at \(d=18\,\upmu \mathrm{m}\) and \(\varepsilon =0.25\), while which can be improved by decreasing d to some extent. To focus on the effect of cell deformability on the cell sorting, here we set a smaller \(d= 12\,\upmu \mathrm{m}\), equal to the diameter of WBC. The default simulation time scope is 0.2833 s, which enables more than 35 WBCs and 35 RBCs to pass the MCA continuously. The initial cell–cell distance between the cell membranes is fixed as \(14.4\,\upmu \mathrm{m}\). For the convenience to evaluate the quality of the cell sorting results, an index \(P_{{ni}}\) is defined as \(P_{ni}=m_{ni}/m_n\times 100~\% \) where \(m_{n}\) is the total number of the n-th type of cells (\(n = 1\) for WBC and \(n = 2\) for RBC), and \(m_{ni}\) is the quantity of the n-th type of cells going through the i-th gap of the MCA outlet. The statistical simulation results of the two groups of numerical cases are shown in Fig. 5. It is found in case (1) and case (0.4) the WBC and RBC can be sorted concentratively, where WBCs leave the MCA from gap 7 and RBCs from gap 2. However, when decreasing \(K_{\mathrm{s}}\), cells get more and more scattered when leaving the MCA. This indicates that the stiffer cells are much more suitable for DLD sorting.

Fig. 5
figure 5

The statistical results of \(P_{ni}\) when varying \(K_{\mathrm{s}}\) of  WBC and RBC. The horizontal coordinates are the varying cases of \(K_{\mathrm{s}}\), the longitudinal coordinates of the axis are the gap sequence, which is defined in Fig. 2

Full size image

4.2 Effect of spatial distribution of MCA

In order to study the effect of the spatial distribution of the MCA on DLD cell sorting, the shift fraction ratio \(\varepsilon \) and the cylinder gap width d are set variable to test the blood cell sorting results. Correspondingly, two sets of numerical cases are performed. For the first set: \(d = 18\,\upmu \mathrm{m}\), \(\lambda = 32.4\,\upmu \mathrm{m}\), set \(\varepsilon \) to vary in the scope of 0.02 to 0.45 with the sequence of 0.02, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, and 0.45. In the second set: \(\varepsilon = 1/3\), \(\lambda = 32.4\,\upmu \mathrm{m}\), set d to vary from \(8.4\,\upmu \mathrm{m}\) to \(22.8\,\upmu \mathrm{m}\) with the sequence of 8.4, 10.8, 12, 13.2, 15.6, 18, 20.4, and \(22.8\,\upmu \mathrm{m}\). To express the cell deformability, in the two cases, \(K_{\mathrm{s}}\) are set to be \(4\times 10 ^{-12}\,{\hbox {N}}{\cdot }{\hbox {m}}\) for WBC and \(4\times 10^{-13}{\hbox { N}}{\cdot }{\hbox {m}}\) for RBC, which are equal to 0.4-fold the settings of the basic \(K_{\mathrm{s}}\). \(K_{\mathrm{b}}\) is fixed at \(5\times 10^{-13}\) N\(\cdot \)m both for WBC and RBC. Other parameters are listed in Table 1. The statistical simulation results of the two sets of numerical cases are given in Fig. 6a and b, respectively.

Fig. 6
figure 6

The statistical results of \(P_{ni}\) by changing the spatial distribution of MCA

Full size image

First, for the results of set 1 in Fig. 6a, it is found that both WBC and RBC are scattered when leaving the MCA, and can not be sorted entirely in all cases. These results indicate that under the setting of \(d=18\,\upmu \mathrm{m}\) and \(\lambda = 32.4\,\upmu \mathrm{m}\), turning \(\varepsilon \) up or down is not able to sort two categories of cells effectively. This is caused by the excessively large distance between two adjacent cylinders since \(d= 18\,\upmu \mathrm{m}\), which is 1.5 times of the diameter of WBC and 2.5 times RBC. In such case, the effect of MCA on flow is not prominent enough to partition the two categories of cells. Three snapshots in the sorting process under \(\varepsilon = 0.10\), 0.25, and 0.45 are shown respectively in Fig. 7a–c to display the sorting results. In these figures, the gray line is the streamline, the big circle is the WBC, and the small circle is the RBC. Combining Fig. 7a and the result of \(\varepsilon = 0.1\) in Fig. 6a, it is found WBC and RBC are not able to be sorted properly, as well as Fig. 7b and \(\varepsilon = 0.25\) in Fig. 6a. Specially, see Fig. 7c and \(\varepsilon = 0.45\) in Fig. 6a, it is found that 100 % WBCs have gone through the outlet of gap 2, and 96.2 % RBCs have passed gap 3, which means WBC and RBC are almost separated completely. This result is interesting, because both WBCs and RBCs follow the “zig” migrating mode, but almost all WBCs and RBCs can be sorted properly. From Fig. 7c, it is found that the WBCs tend to move downward while RBCs have the tendency to go upward. This may hint a feasible scheme to sort WBCs and RBCs if the scale of MCA is large enough.

Fig. 7
figure 7

Three snapshots of cell sorting at \(\varepsilon = 0.10\), 0.25, and 0.45 under \(d = 18\) \(\upmu \mathrm{m}\). a \(\varepsilon = 0.10,\, d = 18\) \(\mu \). b \( \varepsilon = 0.25,\, d = 18\) \(\mu \). c \(\varepsilon = 0.45,\) \(d = 18\) \(\mu \)

Full size image
Fig. 8
figure 8

Two snapshots of cell sorting at \(d = 10.8\) and \(13.2\,\upmu \mathrm{m}\) under \(\varepsilon = 1/3\). a \( d = 10.8\) \(\mu , \varepsilon = 1/3\). b \( d = 13.2\) \(\mu , \varepsilon = 1/3\)

Full size image

Then, for the results of set 2 in Fig. 6b, where \(\varepsilon \) is fixed at 1/3, d is changed by regulating the cylinder radius R. According to the results, WBCs and RBCs can be well concentrated for sorting at \(d= 8.4\), 10.8, 12, and \(13.2\,\upmu \mathrm{m}\). These results indicate that under \(\varepsilon = 1/3\) and \(\lambda = 32.4\,\upmu \mathrm{m}\), the regulation of d is able to sort two categories of cells. It is noted that at \(d = 8.4\) and \(10.8\,\upmu \mathrm{m}\), the WBC has to deform to get through the gap because its diameter is \(12\,\upmu \hbox {m}\), which is larger than the gap size d. Two snapshots in the sorting process under \(d = 10.8\) and \(13.2\,\upmu \mathrm{m}\) are shown in Fig. 8a and b, respectively. Combining Fig. 8a with Fig. 6b, it is found that all WBCs follow the “dis” migrating mode and finally leave the MCA from the outlet of gap 7, while all RBCs follow the “zig” migrating mode and leave from gap 2. Therefore, two categories of cells are both sorted and concentrated, and this is an ideal result for sorting the two categories of blood cells. By comparison, for the results of \(d = 13.2\,\upmu \mathrm{m}\) in Fig. 8b, where all RBCs leave the MCA from gap 2 while WBCs go out from the gaps of 5, 6, and 7, the sorted WBCs are not well concentrated.

In addition, the same sorting results take place at \(d = 8.4\), 10.8, and \(12\,\upmu \mathrm{m}\), as demonstrated in Fig. 6b. When decreasing the gap size, the flow at the gap will speed up if the flux is fixed, and the WBC will experience a larger deformation to get through the gap. These changes tend to result in higher shear and normal stresses, this may do damage to the cell. Moreover, too small a gap size is hard for the cells to pass through and such constrictive structure has a greater possibility to be blocked in experimental operations.

4.3 Effect of the initial cell–cell distance

As discussed above, the DLD cell sorting is significantly affected by the cell sizes and the flow allocation in the MCA. In this section, we will consider the effect of the cell–cell interaction on cell sorting. When we increase the releasing frequency of cells, the initial distance between two adjacent cells will decrease, and the motion of the later cells may be affected by the front ones if they are too close. Here set \(\varepsilon = 1/3\) and \(d = 12\,\upmu \hbox {m}\), \(K_{\mathrm{s}}\) and \(K_{\mathrm{b}}\) are set the same as in Sect. 4.2, five numerical cases are performed by varying the initial cell–cell distance L as 3.6, 6.3, 9, 11.7, and \(14.4\,\upmu \mathrm{m}\). The statistical results of \(P_{ni}\) are displayed in Fig. 9.

Fig. 9
figure 9

The statistical results of \(P_{ni}\) by varying the initial cell–cell distance

Full size image

From Fig. 9, it is found that in all five cases, the WBCs and RBCs can be sorted completely. However, it is also found that the cells leaving the MCA become not well concentrated at \(L = 3.6\), 6.3, 9, and \(11.7\,\upmu \mathrm{m}\). We can deduce that the sorted cells becoming scattered are caused by the cell–cell interaction produced by the decreased initial distance. This illustrates that the decreasing of the initial cell–cell distance can enhance the cell–cell interaction, which is influential for the DLD cell sorting. According to the results of Fig. 9, it is suggested that the initial cell–cell distance should be bigger or equal to \(14.4\,\upmu \mathrm{m}\), which is 1.2 times the WBC diameter.

5 Conclusions

In this paper, a DLD cell sorting scheme for the WBCs and RBCs has been proposed and investigated numerically by the IB-LBM. The migration of a rigid circular particle has been simulated to validate the numerical method used in this work. It is found that the present results agree well with the theoretical prediction. The cell deformability, the spatial distribution of cylinder arrays, and the initial cell–cell distance have been considered to study their effects on the flexible cell sorting by the DLD. The numerical results show that the cell deformability is important for the DLD cell sorting, which is attributed to the variant sizes of the cell projected diameter compared with the gap sizes. In addition, when the gap size d is set to be smaller or equal to the diameter of a WBC, well concentrated sorting results can be achieved at \(\varepsilon = 1/3\). Finally, the initial distance of two adjacent cells is suggested to be bigger or equal to 1.2 times the WBC diameter in order to obtain an ideal sorting result.