1 Introduction

Magnetic micro- and nanoparticles have been used in various microfluidic applications due to easy and flexible manipulation using magnetic forces (Suwa and Watarai 2011; Nguyen 2012). According to different external magnetic fields, two types of magnetic forces acting on magnetic particles can be generated. The one is commonly known as gradient magnetic force requiring a nonuniform magnetic field which is usually applied to trap and separate magnetic particles (Pamme 2006; Basore and Baker 2012; Sajeesh and Sen 2014), and the other is magnetic interaction force between particles in both uniform and gradient magnetic fields which can make magnetic particles tend to form multi-particle chains or clusters (Cao et al. 2014). The former force has been used more widely in biological and chemical applications (Gijs et al. 2010), while the latter force has recently attracted increasing interest in manipulation of magnetic particles with the aid of dynamic magnetic fields (Eickenberg et al. 2013; Lin et al. 2014; Gao et al. 2014). Actually, the aggregation behavior of particles due to the latter force under gradient magnetic fields could bring several interesting and challenging issues such that: (1) It can fuel separation process and this point has been demonstrated by several experimental studies, in which magnetic nanoparticles can be effectively separated just using low-gradient magnetic field, known as the low-gradient magnetophoretic separation (De Las Cuevas et al. 2008); (2) conversely, how to avoid magnetic aggregation is another interesting issue since aggregation behavior of magnetic particles will give rise to some problems in microfluidic applications. For example, nontarget objects (impurities) will be physically remained in the aggregated structures, resulting in low purity (Ramadan et al. 2010); magnetic particles with different parameters will also aggregate with each other, which will increase the separation difficulty for multiple types of particles (Mayo et al. 2011). Thus, understanding the motion behavior of magnetic particles under gradient magnetic fields and flow fields is very important for practical applications.

Typically, the particle dynamics is considered to be determined by the gradient magnetic force and hydrodynamic force induced by the relative motion between the particles and the fluid. On this basis, there are two approaches generally adopted in the simulations: The first is depicted as one-way particle–fluid coupling method, in which the fluid flow is assumed to be independent of particle motion (Furlani and Ng 2006; Wu et al. 2011); the other is named as two-way particle–fluid method, in which the coupled particle–fluid momentum interaction is considered (Modak et al. 2010; Khashan and Furlani 2012). It should be noted that the interparticle interactions are ignored in these studies and thus the obtained results could be just adaptable to the cases when these particles are in dilute suspension. With increasing particle concentration, the distance between particles will be not very large and then aggregation behavior of particles should be considered. Up to now, only a few groups have taken into account the interparticle interactions in the existing simulations. These studies have been limited in using the so-called magnetic dipole–dipole interaction models (Mikkelsen et al. 2005; Cregg et al. 2012), in which each magnetic particle is assumed as a point with dipole moment responding to the external magnetic field. However, the simple model cannot precisely capture the real dynamics of closely spaced particles, as is usual in the cases of relatively high particle concentration in microfluidic applications. Moreover, the assumption that hydrodynamic force has no concern with the distance between particles is not applicable when the distance is comparable to particle size.

In this study, the direct numerical simulation scheme known to be very accurate for solving magnetic and hydrodynamic forces is taken for strictly tackling the above problems. This scheme has been effectively applied to investigate the particle–particle interactive motion under an applied electric field (Ai and Qian 2010; Ai et al. 2014; Hossan et al. 2016) or a uniform magnetic field (Kang et al. 2008; Kang and Suh 2011). Kang and Maniyeri (2012) applied the simulation scheme to investigate both DC dielectrophoretic and magnetophoretic motions of particles under a uniform external field and found that interactive motions of particles in the two cases agree well with each other qualitatively due to very similar governing equations. To the best of our knowledge, this is the first attempt to apply the direct simulation scheme to solve particulate flows with several suspended magnetic particles under gradient magnetic fields. First, the governing mathematical equations for solving the coupled problem of magnetic field, flow field and particle motion are presented. Second, to validate the developed numerical scheme, we apply it to investigate the motion behavior of two magnetic particles under an external uniform magnetic field and then compare the results with the existing solutions for the same problem. Finally, the magnetic and hydrodynamic interactions between particles with different configurations under an external gradient magnetic field are analyzed in detail as well as their effects on the motion behavior of particles.

2 Theory and method

Figure 1 schematically illustrates several paramagnetic particles in a microcontainer filled with a nonmagnetic fluid and a permanent magnet for generating a gradient magnetic field, which is shown in a 2D Cartesian coordinate system. To calculate the magnetic field distribution generated by the permanent magnet, a computational domain of surrounding air is required and represented by the domain Ω1. The air domain should be much larger than the magnet size for not perturbing magnetic field distribution, and hence greatly larger than the sizes of microsystem and particles. Due to the excessive difference in size between air and particles, finite element meshing of the domain Ω5 cannot be finished with a desired size and thus the calculation accuracy of magnetic field distribution around particles could be very low. To solve this problem, two models are applied for magnetic field calculation: One is for calculating the magnetic field distribution in Ω3 by modeling the domains of Ω1, Ω2, Ω3 and Ω4 (without modeling the particle domain Ω5); the other is used to obtain the field distribution around particles by modeling the domains of Ω3, Ω4 and Ω5, in which the field distribution along the boundary of domain Ω3 obtained in the first model is taken as the boundary condition. This treatment should be practicable since the size of domain Ω3 is still much larger than particle size and thus the field distribution along the boundary Ω3 will remain basically unchanged in the two cases with and without domain Ω5. For the simulation of fluid field in the microcontainer, the domain Ω4 is set relatively large to not affect the fluid flow around the particles. All the particles have the same radius and are assumed to be rigid in the simulations. To investigate the dynamic behavior of these particles, governing equations for solving magnetic field, fluid field and particle motion are described in the following section.

Fig. 1
figure 1

Schematic diagram of the computation domains in a 2D view. Ω1, Ω2, Ω3, Ω4 and Ω5 denote regions of the surrounding air, the permanent magnet, the local air around microsystem, the microsystem and particles, respectively. The letter s represents the spacing between Ω2 and Ω3

Full size image

2.1 Physical equations

When permanent magnets are used as magnetic sources, the magnetic field can be expressed by the Maxwell equation without current and calculated by introducing the magnetic potential:

$$\nabla \times \left( {\frac{1}{{\mu_{r} \mu_{0} }}} \right)(\nabla \times {\mathbf{A}} - {\mathbf{B}}_{{\mathbf{r}}} ) = 0$$
(1)
$${\mathbf{H}} = \frac{1}{{\mu_{r} \mu_{0} }}\quad {\mathbf{B = }}\frac{1}{{\mu_{r} \mu_{0} }}\nabla \times {\mathbf{A}}$$
(2)

where \({\mathbf{A}}\) is the magnetic vector potential, \(\mu_{\text{0}}\) is the magnetic permeability in vacuum (\(\mu_{\text{0}}\) = 4π × 10−7 H/m), μ r is the relative permeability of the particles or the fluid and \({\mathbf{B}}_{{\mathbf{r}}}\) means the remanent flux density of materials with a value of 1 T in the domain of the permanent magnet and zero in other domains. As mentioned above, two models have been taken to calculate the magnetic field distribution around particles. Thus, two different boundary conditions will be applied:

$${\mathbf{n}} \times {\mathbf{A = 0}}$$
(3)
$${\mathbf{n}} \times {\mathbf{H = n}} \times {\mathbf{H}}_{{\text{cal}}}$$
(4)

where \({\mathbf{n}}\) is the outward normal vector and \({\mathbf{H}}_{{\text{cal}}}\) means the field distribution along the domain boundaries. For the first model, the magnetic insulation boundary condition in Eq. (3) is applied along the boundaries of domain Ω1. For the second model, the boundary condition in Eq. (4) is applied along the boundaries of domain Ω1, where the component values of magnetic field \({\mathbf{H}}_{{\text{cal}}}\) are obtained by solving the first model. After solving Eqs. (1) and (2) for obtaining the magnetic field distribution, the magnetic forces acting on the ith particle can be expressed by integrating the Maxwell stress tensor \({\mathbf{T}}_{m,i}\) on its surface:

$${\mathbf{F}}_{m,i} = \int_{{\varGamma_{i} }} {{\mathbf{T}}_{m,i} } \cdot {\mathbf{n}}dS = \int_{{\varGamma_{i} }} {\left[ {{\mathbf{HB}}^{T} - \frac{1}{2}\text{(}{\mathbf{H}} \cdot {\mathbf{B}}\text{)}{\mathbf{I}}} \right]} \cdot {\mathbf{n}}\;{\text{d}}S$$
(5)

where \({\mathbf{I}}\) denotes the identity tensor, H and B mean the magnetic field and the magnetic flux density, respectively, and p represents the pressure. Noted that the magnetic force \({\mathbf{F}}_{m,i}\) is composed of gradient magnetic force generated by the external gradient magnetic field and magnetic interaction force between particles.

The fluid field in the domain Ω4 can be expressed by the continuity equation and Navier–Stokes equation:

$$\nabla \cdot {\mathbf{u}}_{f} = 0$$
(6)
$$\rho_{f} \frac{{\partial {\mathbf{u}}_{f} }}{\partial t} + \rho_{f} \left( {{\mathbf{u}}_{f} \cdot \nabla } \right){\mathbf{u}}_{f} = \nabla \cdot \left[ { - p{\mathbf{I}} + \eta \left( {\nabla {\mathbf{u}}_{f} + (\nabla {\mathbf{u}}_{f} )^{T} } \right)} \right]$$
(7)

where η and \({\mathbf{u}}_{f}\) are the fluid dynamic viscosity and velocity vector of the fluid, respectively. No-slip boundary conditions (\({\mathbf{u}}_{f} = 0\)) are applied along the boundaries of domain Ω4. Since each particle is considered as a moving entity, a boundary condition is applied on the particle surface for reflecting the effect of its translational and rotational behavior on the flow around particles:

$${\mathbf{u}}_{b,i} = {\mathbf{u}}_{p,i} + {\varvec{\upomega}}_{p,i} \times \left( {{\mathbf{r}}_{s,i} - {\mathbf{r}}_{c,i} } \right)$$
(8)

where \({\mathbf{u}}_{b,i}\) means the fluid velocity on the ith particle surface and \({\mathbf{u}}_{p,i}\) and \({\varvec{\upomega}}_{p,i}\) are the translational and rotational velocity of the ith particle, respectively. The hydrodynamic force acting on the ith particle can be expressed by integrating the hydrodynamic stress tensor \({\mathbf{T}}_{h,i}\) on its surface:

$${\mathbf{F}}_{h,i} = \int_{{\varGamma_{i} }} {{\mathbf{T}}_{h,i} } \cdot {\mathbf{n}}dS = \int_{{\varGamma_{i} }} {\left[ { - p{\mathbf{I}} + \eta \left( {\nabla {\mathbf{u}}_{f} + \nabla {\mathbf{u}}_{f}^{T} } \right)} \right]} \cdot {\mathbf{n}}dS$$
(9)

Then, the motion behavior of the ith particle including translation and rotation can be determined by:

$$m_{p,i} \frac{{d{\mathbf{u}}_{p,i} }}{dt} = {\mathbf{F}}_{h,i} + {\mathbf{F}}_{m,i}$$
(10)

and

$$I_{p,i} \frac{{d{\varvec{\upomega}}_{p,i} }}{dt} = \int_{{\varGamma_{i} }} {({\mathbf{r}}_{s,i} - {\mathbf{r}}_{c,i} )} \times \left[ {({\mathbf{T}}_{m,i} + {\mathbf{T}}_{h,i} ) \cdot {\mathbf{n}}} \right]dS$$
(11)

where m p,i and I p,i mean the mass and the moment of inertia. Other forces including thermal kinetic force induced by Brownian motion and gravitational force are not considered in the simulations. To prevent particles from penetrating each other, the following collision strategy adopted by Glowinski et al. (1999) is taken to replace Eq. (10) by

$$m_{p,i} \frac{{d{\mathbf{u}}_{p,i} }}{dt} = {\mathbf{F}}_{h,i} + {\mathbf{F}}_{m,i} + {\mathbf{F}}_{r,i}$$
(12)

where \({\mathbf{F}}_{r,i}\) represents a short-range repulsive force exerted on the ith particle by the other particles. For the three-particle system, it is given by

$${\mathbf{F}}_{r,i} = \sum\limits_{j = 1,j \ne i}^{3} {{\mathbf{F}}_{i,j} }$$
(13)
$${\mathbf{F}}_{i,j} = \left\{ {\begin{array}{ll} {\mathbf{0}} & {\quad d_{i,j} > 2r_{p} + \delta } \\ {\frac{1}{\varepsilon }\left( {{\mathbf{r}}_{p,i} - {\mathbf{r}}_{p,j} } \right)\left( {2r_{p} + \delta - d_{i,j} } \right)} & {\quad d_{i,j} \le 2r_{p} + \delta } \\ \end{array} } \right.$$
(14)

where d i,j  = \(\left| {{\mathbf{r}}_{p,i} - {\mathbf{r}}_{p,j} } \right|\) represents the center-to-center distance between the ith and jth particles, δ is the force range and ε means a small positive stiffness parameter.

2.2 Numerical method and validation

In the particle transport process, the local magnetic field and flow field around particles will vary with particle position and velocity and in turn could affect the magnetic and hydrodynamic forces acting on the particles. Thus, to precisely reflect the strongly coupled interactions of magnetic field–fluid field–particle motion, an arbitrary Lagrangian–Eulerian (ALE) finite element method is presented in this study and numerical implementation of the above relevant mathematical equations is performed by a commercial finite element package COMSOL (version 5.0). Four physical models have been established in the simulations: (1) “global ordinary differential equations (ODEs) and differential algebraic equations (DAEs)” model, (2) “magnetic fields” model, (3) “laminar flow” and (4) “moving mesh” model, which are solved using a time-dependent fully coupled solver. The ALE method was taken to update the location of the moving particles and the shapes of mesh elements in each time step. In this process, the ALE implementation requires mesh movement, in which the mesh in the domain of fluids deforms in a free way, while the deformation for the mesh in the particle domain of particles was prescribed by particle displacement. The mesh quality will deteriorate as mesh deforms. When the mesh deformation has become so large that the mesh quality becomes less than a given limit (0.2 in our calculations), the mesh will be re-initialized according to the function of automatic re-meshing.

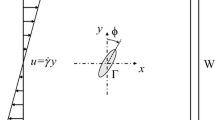
In order to validate the numerical method, we perform numerical simulations on the two-dimensional (2D) motion of two paramagnetic particles in a nonmagnetic fluid subjected to an external uniform magnetic field, and then compare the results of magnetic field and fluid field with the solutions obtained in the existing studies. First, magnetic forces between two neighboring particles in a 2D planar model are calculated and compared with the results obtained by the semi-analytical (SA) method (Suh and Kang 2011) and the one-stage method (Kang and Suh 2011). As shown in Fig. 2, two circular particles with a given center-to-center distance and an angle (D, θ) are located in a uniform magnetic field along the positive x-axis. All the variables of the magnetic problem solved for validation are dimensionless and the corresponding structural and physical dimensionless parameters are kept the same as that in Kang and Suh (2011), except for the size of the square cavity.

Fig. 2
figure 2

Schematic diagram of the computational domain with two magnetic particles in a cavity under a uniform magnetic field

Full size image

In the simulation, the sizes of mesh elements in the regions where the two particles are located are set as 0.04 and the maximum element growth rates in Ωa and Ωb are set as 1.03 and 1.05, respectively. The region Ωa is used for refining the mesh near the particles and its size L fg is given as 20 for the magnetic analysis in this section. To ensure the calculation accuracy based on the Maxwell stress tensor and finite element method (MST-FEM), magnetic particles should be far enough away from the outer boundaries and thus the effect of the size of the outer boundaries on the magnetic force distribution is first analyzed. Take the case of (D, θ) = (2.4, 45°) for example, as shown in Fig. 3, when the size of the outer square cavity L bc is larger than 120, the calculated two magnetic force components (F mx , F my ) of the particle P_1 tend to remain stable with increasing boundary size. The relative stable values of the two magnetic force components in the case of L bc  = 200 are listed in Table 1. The relative errors are presented in parenthesis with the SA results as reference values. It can be seen that the differences between these results obtained from the three methods are all very small and the maximum difference between MST-FEM and SA is only 1.24% for the two cases, which reflects that the magnetic force acting on particles with different distances can be precisely obtained by using the presented MST-FEM in the simulation.

Fig. 3
figure 3

Relationship of calculated magnetic force with the size of the outer boundary of the computational domain

Full size image
Table 1 Validation and comparison of the simulation results for magnetic force calculation in the two-particle system
Full size table

According to the above validation study, it has been found that magnetic force acting on particles under static conditions can be calculated accurately by the use of MST-FEM. Further, the computational accuracy of magnetic force by use of MST-FEM and ALE methods under dynamic conditions should also be demonstrated. For this, a simple transient process was used for testing, in which two particles in the case of θ = 0° moved toward each other with a given velocity. As shown in Fig. 4, magnetic force F mx acting on particles P_1 was calculated by two methods: ALE method and parametric sweep analysis. Different with transient analysis using ALE method, stationary solver was used for parametric sweep analysis and discrete results were obtained through changing the initial gap between particles. It can be seen that the results obtained by the two methods are in excellent agreement with each other, which indicates that the ALE method can be used to generate accurate solutions for forces acting on particles in motion.

Fig. 4
figure 4

Calculated magnetic force acting on particles by two methods

Full size image

Next, numerical simulations for quasi-static velocities of two particles suspended in a square cavity filled with water under an external uniform magnetic field (see Fig. 2) are performed and compared with the existing results by SA method (Suh and Kang 2011) and one-stage method (Kang and Suh 2011). Both the magnetic and flow problems considered for the validation are much the same as that in Kang and Suh (2011). The magnetic problem is solved in all domains in Fig. 2, and the flow problem is only solved in Ωa. For the flow field, no-slip boundary conditions are imposed on the boundaries ab, cd, ad and bc. The values of the boundaries L bc and L fg in Fig. 2 are set as 200 and 40 in this simulation, respectively. To obtain the quasi-static results, the positions of the two particles and meshes are fixed in the simulation. Meanwhile, the continuity and momentum equations are described and calculated without unsteady terms. Table 2 shows the translational and rotational velocity components of the particle P_1 obtained by MST-HST-FEM and two other numerical results obtained by the methods of SA and one-stage SP for comparison. The relative errors are presented in parenthesis with the SA results as reference values. Results indicate that all of the velocity components for (2.4, 45°) and (4, 80°) are in good agreement with the existing solutions, which further demonstrates the effectiveness of our method.

Table 2 Validation and comparison of the simulation results for velocity calculation in the two-particle system
Full size table

3 Results and discussion

In the following sections, 2D particle motion in the two- and multi-particle problems in the environment with the geometry shown in Fig. 1 will be investigated. Here, it should be noted that it is acceptable to use 2D model to capture the motion behavior of particles in 3D microfluidic systems with relatively simple structures like that in Fig. 1, which has been demonstrated in several numerical and experimental studies of the electrophoretic motion of particles (Ai et al. 2009, 2010). Especially for the 3D systems, in which the size in the direction perpendicular to the 2D model is sufficiently large, the simulation accuracy using 2D model is good enough since the variation in mass transport in this direction can be negligible (Khashan and Furlani 2014; Munir et al. 2014). The fluid used in the simulations is water with a density ρ f  = 1.0 × 103 kg m−3, a viscosity η = 1.0 × 10−3 N s m−2 and a relative permeability μ f  = 1.0. For the 2D planar model in this study, the spherical paramagnetic microparticles are treated as circular cylinder particles with a radius of 0.5 μm, a density ρ p  = 1.8 × 103 kg m−3 and a relative magnetic permeability μ p  = 3.625 and this value is assumed to be unchanged in the simulations. The square boundary sizes of Ω1, Ω2, Ω3 and Ω4 in Fig. 1 are set as 200 mm, 4 mm, 400 μm and 200 μm, respectively. The spacing between Ω2 and Ω3 (s) is 4 mm. The sizes of mesh elements in the regions where particles are located are set as 0.05 μm and the maximum element growth rates in Ω3 and Ω4 are set as 1.1 and 1.05, respectively. The time step is set as 5e−6 s in the following transient analysis. The values of δ and ε in Eq. (14) are set to be 0.5e−7 and 1e−15.

3.1 Motion behavior of two magnetic particles

In this section, the particle trajectories and interparticle distances with time for different initial configurations in Fig. 5 are investigated, in which both hydrodynamic and magnetic interactions are considered. The magnetic field distribution in the domain Ω4 is shown in Fig. 6, in which the field direction is mainly along y-axis and an obvious field gradient exists.

Fig. 5
figure 5

Particle configurations in the two-particle model for investigating a the effects of angle θ and b interparticle distance on the motion behavior of particles

Full size image
Fig. 6
figure 6

Magnetic field distribution in the domain Ω4 without particles. The arrows show the magnetic field direction

Full size image

First, to examine the particle motion affected by the angle θ between the linking line of particles and the magnetic field direction, we choose two-particle problems with four initial configurations in Fig. 5a. The particle trajectories and interparticle distances with time in the four configurations are plotted in Figs. 7 and 8, respectively. Results indicate that the two particles could form a chain aligned with the magnetic field direction in the first stage and then move together in the last stage regardless of the initial angle, except for the case with θ = 90°. For θ = 0°, the two particles are initially attracted to move toward each other without any revolution, which is because the magnetic attractive force between particles and gradient magnetic force are both along the y-axis parallel to the field direction. It also turns out the magnetic interaction force between particles is larger than the gradient magnetic force in this case according to the initial motion direction of P_1 in Fig. 7a. When the two particles collide at the time of about 0.78 ms, they become paired with each other and then start moving together with an unchanged interparticle distance (Fig. 8) toward the magnet surface under the action of gradient magnetic force. For θ = 30°, the two particles are attracted to move toward each other while revolving in the counterclockwise direction in the first stage. For θ = 60°, the two particles are repelled from the beginning and then start to move toward each other at the time of about 1.05 ms, while revolving in the counterclockwise direction in the first stage. The difference of the initial motion direction between the above two cases is due to the fact that the magnetic interaction force is either attractive or repulsive depending on the angle θ, which has been well known in the existing solutions in the case of uniform magnetic fields (Kang et al. 2008; Banerjee et al. 2012). For θ = 90°, the two particles move away from each other in the horizontal direction and move down along y-axis without any revolution because the magnetic interaction force between particles is only along x-axis. Further, the motion behavior of the two particles with different initial interparticle distances in Fig. 5b is investigated. As shown in Fig. 9, it can be seen that the time needed for particle chain formation increases significantly (from 2 to 53.4 ms) with increasing the initial interparticle distance (from 5 to 12.5 μm), which reflects that the aggregation behavior of magnetic particles is much affected by the particle concentration.

Fig. 7
figure 7

Trajectories of the two particles P_1 and P_2 at a θ = 0°, b 30°, c 60° and d 90°

Full size image
Fig. 8
figure 8

Center-to-center distances between particle P_1 and P_2 in motion with an initial distance of 5 μm for different angles

Full size image
Fig. 9
figure 9

Center-to-center distances between particle P_1 and P_2 in motion with different initial distances

Full size image

3.2 Motion behavior of three magnetic particles

In this section, the simulation studies are extended to the case with three particles and then the following two issues are further investigated: (1) effect of field direction on the particle trajectories and (2) comparison of particle velocity in three cases with different particle numbers.

Figure 11 depicts the trajectories of the three magnetic particles in Fig. 10a under two types of gradient magnetic fields generated by a permanent magnet with different magnetization directions (x-direction or y-direction). In our previous work, we have shown that the directions of gradient magnetic force in the two cases are both along the negative y-axis and their difference lies in the magnetic field direction (Cao et al. 2016), in which the magnetic field generated by the permanent magnet in Fig. 1a is along positive y-axis, while the magnetic field is along negative x-axis for the permanent magnet with magnetization along the positive x-axis. According to the results shown in Fig. 11a and b, it can be seen that the three magnetic particles are all aggregated in the long run and then move in the same direction (negative y-direction) in the two cases. However, the distributions of the formed chain-like structures are configuration dependent with the field direction, as shown in Fig. 11. These results are in qualitative agreement with the prediction results based on Monte Carlo simulations (Cao et al. 2016) and experimental results (Wise et al. 2015) in the similar studies. The obtained results should be paid more attention since they mean that the field direction could have potential impacts on the particle velocity and particle distribution in the target region, which are usually ignored in the conventional simulations and experiments.

Fig. 10
figure 10

Particle configurations in the three-particle model for investigating a the first issue and b the second issue in Sect. 3.2

Full size image
Fig. 11
figure 11

Particle trajectories of the three magnetic particles P_1, P_2 and P_3 under gradient magnetic fields. a The field direction is mainly along y-axis and b the field direction is mainly along x-axis

Full size image

Figure 12 shows the axial displacement curves of magnetic particle P_1 for single-particle model (P_1), two-particle model (P_1 and P_2) and three-particle model in Fig. 10b. Results indicate that the movement distance of particle P_1 in 10 ms increases with increasing particle numbers and the gap increases with time. The main reasons are that (1) particle velocity can be increased in the aggregation process due to the magnetic interaction force. This point is clearly shown in Fig. 13, in which the velocity curves of magnetic particle P_1 for the three models are plotted. (2) Chain-like aggregates of particles move faster than the single particle under the same conditions. As shown in Fig. 13, it can be found that neighboring magnetic particles in the two-particle and three-particle models start moving together with the same velocity after aggregation process, and the value of this velocity increases with increasing particle numbers. Take the case with a displacement of −6 μm for example, the velocities of the particle P_1 in the three models are 0.546, 0.98 and 1.32 mm s−1, respectively. This phenomenon is mainly due to that the drag on the chain-like aggregates of particles is related to the number of particles per chain, which has been investigated in similar studies. According to the work reported by Wise et al. (2015), for the case of a chain of identical spherical particles, the ratio (R a ) of the magnetophoretically induced velocity per chain to the velocity of a single-particle traveling toward a magnet can be approximately determined by the following equation:

$$R_{a} = \left\{ {\begin{array}{ll} 1 & {\quad n = 1} \\ {\frac{3}{4}\frac{{n[(2n^{2} - 1)/(n^{2} - 1)^{0.5} \ln (n + (n^{2} - 1)^{0.5} ) - n]}}{{n^{2} - 1}}} & {\quad n > 1} \\ \end{array} } \right.$$
(15)

where n means the particle number. Figure 14 shows that the ratios of the velocity of particle P_1 in the three models to that in the single-model are almost equal to the calculation results based on Eq. (15), which confirms the above argument that the velocity of n-particle chain increases with the particle numbers.

Fig. 12
figure 12

Axial displacement curves of magnetic particle P_1 in the three models

Full size image
Fig. 13
figure 13

Axial velocity curves of particles in the three models

Full size image
Fig. 14
figure 14

Calculated ratios of the velocity of particle P_1 in the three models to that in the single-model

Full size image

3.3 Motion behavior of magnetic and nonmagnetic particles

In this section, the effect of hydrodynamic interactions on motion behavior of particles is investigated. First, only one magnetic particle (P_2) and two nonmagnetic particles (P_1 and P_3) are used. The initial position coordinates of the three particles are shown in Fig. 10b. For magnetic particle P_2, it moves toward the surface of permanent magnet along the negative y-axis under the action of gradient magnetic force. As it is initially located in the central line of permanent magnet, the x-component of magnetic force is zero and thus its movement direction is mainly along y-axis, which can be seen from the trajectory of particle P_2 shown in Fig. 15. For the nonmagnetic particles P_1 and P_3, in the case without considering hydrodynamic interactions, they could remain stationary since there is no magnetic force acting on them. But when the hydrodynamic interaction is considered, the motion of magnetic particle P_2 can create a disturbance to the surrounding fluid and then will drive the nonmagnetic particles P_2 and P_3 along the streamlines, which is clearly shown in Fig. 15. This also indicates that the hydrodynamic interaction could promote the movement of surrounding particles toward the target region (magnet surface). These results are basically consistent with the existing numerical and experimental solutions (Mikkelsen et al. 2005; Leong et al. 2015), in which hydrodynamic interaction was demonstrated to be an important factor in enhancing particle capturing. Further, two magnetic particles (P_1 and P_2) and one nonmagnetic particle (P_3) are used to investigate the effect of hydrodynamic interactions on the particle aggregation behavior, in which the initial position coordinates of the three particles are also shown in Fig. 10b. Figure 16 shows the y-component of velocities of magnetic particles (P_1 and P_2) and nonmagnetic particle (P_3). For magnetic particles P_1 and P_2, they initially move in opposite directions with different velocities due to a strong magnetic interaction force and then move together with the same velocity under the action of gradient magnetic force. For the nonmagnetic particle P_3, due to the hydrodynamic interaction, it initially moves toward with a positive velocity and then moves with a negative velocity after the aggregation of particles P_1 and P_2. This means that the particle P_3 tends to move toward the region where magnetic particles are concentrated in the aggregation process, which indicates that hydrodynamic interactions between particles are also conducive to the chain formation of particles.

Fig. 15
figure 15

Particle trajectories of the magnetic particle (P_2) and nonmagnetic particles (P_1 and P_3)

Full size image
Fig. 16
figure 16

Particle velocities of the magnetic particles (P_1 and P_2) and nonmagnetic particle (P_3)

Full size image

4 Conclusion

A finite element model based on the direct simulation scheme for investigating particle motion behavior in a microsystem under an externally applied gradient magnetic field has been developed and implemented in this work. The numerical solutions of some problems in the existing studies are compared against several analytical, numerical and experimental results, showing good agreement with each other. The accuracy and efficiency of the proposed numerical method mainly arise from the ALE method for dealing with the movement of the particles and the calculation method for forces acting on particles based on the Maxwell stress tensor and hydrodynamic stress tensor. Based on this method, the transport and interaction behavior of particles with the consideration of magnetic and hydrodynamic effects can be accurately analyzed. Simulation results have illustrated the magnetic effect on the particle trajectory pattern and the importance of both the two effects on promoting the acceleration of particles due to magnetic aggregation and induced disturbance to the fluid. Remarkably, the method can be easily employed in other cases with complex geometrical configurations of microfluidic systems. For future work, we will use the developed method to simulate the diverse magnetic manipulations (e.g., focusing, trapping and separation) (Zeng et al. 2013; Zhao et al. 2016) of various particles (e.g., spherical or nonspherical, and rigid or soft) (Zhu et al. 2015; Zhou and Xuan 2016) in continuous (magnetic or nonmagnetic) fluid flows (Pamme 2006).