1 Introduction

Magnetophoresis involves the manipulation of colloidal magnetic particles using an external magnetic field. Over the past several years the interest in this phenomenon has grown dramatically, especially for applications in fields such as microbiology and biotechnology (Furlani 2010a, b; Ganguly and Puri 2010; Gijs 2004). Magnetic particles can be functionalized to selectively bind to target biomaterials such as proteins, enzymes, nucleic acids or whole cells, thereby enabling magnetophoretic control of these materials (Pankhurst et al. 2003, 2009; Moser et al. 2009; Berry 2009; Berry and Curtis 2003; Arrueboa et al. 2007; Majewski and Thierry 2007; Safarik and Safarikova 2002). This capability is being leveraged through advances in microfluidics that enable miniature biochemical laboratories to be integrated into a single microsystem, i.e. lab-on-a-chip and “micro total analysis systems” (μTAS). Such microsystems typically range in size from millimeters to the centimeters and are usually made using planar glass-, silicon- or polymer-based substrates. Fluidic structures within these systems such as mixing chambers and flow channels range from several to hundreds of microns in size. Magnetic functionality can be integrated into these systems by embedding magnetic field source elements in the substrate, in proximity to the flow channels. These elements can be magnetically passive structures such as nickel-based microbars, or active voltage-driven conductors (Choi et al. 2000, 2001; Furlani 2001; Smistrup et al. 2005 Furlani 2006; Furlani and Sahoo 2006; Furlani et al. 2007; Smistrup et al. 2008). In the former case, an external field source is used to magnetize the elements. In the latter case, circuitry is required to activate the conductors. In either case, the source elements generate a magnetic field distribution that gives rise to a magnetic force on magnetically labeled material as it flows through a microchannel, thereby enabling magnetophoretic control to sort or immobilize the material.

The fusion of magnetism and microfluidics is its infancy, but advancing rapidly (Ganguly and Puri 2010; Pamme 2006; Gijs 2004). Magnetic-based microsystems have advantages over comparable electrostatic-based systems for applications involving particle manipulation, e.g. sorting and capture. Passive magnetic systems enable on-chip manipulation of magnetically labeled material using an external field that can be provided by a permanent magnet, which requires no power consumption. This eliminates the need for a power source, drive circuitry and integrated electrodes, which are required for electrophoretic manipulation. Furthermore, since substrates and carrier fluids are usually nonmagnetic, they do not interfere with an efficient coupling between the applied field and the magnetically labeled material in the fluid. Also, magnetic systems are less sensitive to factors such as surface charge, pH and ionic concentration.

Another impetus for the development of magnetic microsystems is the availability of multifunctional magnetic particles that can selectively bind to a target biomaterial as mentioned above. Magnetic particles are finding increasing use in fields such as microbiology, biomedicine and biotechnology where they are used to label, sort and immobilize biomaterials and to deliver therapeutic drugs to a target tissue. The small size, large surface to volume ratio, biofunctionality and superparamagnetic behavior of magnetic nanoparticles makes them well suited for probing and manipulating bioparticles and biosystems such as proteins (5–50 nm), viruses (20–450 nm), genes (2 nm wide and 10–100 nm long) or whole cells (10–100 μm) (Pankhurst et al. 2003, 2009; Berry 2009; Berry and Curtis 2003). Magnetic nanoparticles are typically 1–100 nm in diameter and most commonly made from magnetite (Fe3O4). However, larger micron-sized “magnetic beads” can be fabricated by encapsulating magnetic nanoparticles within an organic (polymeric) or inorganic matrix. These magnetically loaded spherical beads can be functionalized with oligomeric compounds, which form a thin shell to which bioactive ligands such as antibodies can be linked.

To date, the most common use of magnetic particles has been for the separation of biological and chemical entities. Most applications involving magnetic separation require labeling the target material with magnetic particles through antigen–antibody interactions. However, some biomaterials such as red blood cells (RBCs) in plasma and magnetotactic bacteria do not require labeling as they exhibit an intrinsic magnetic susceptibility that is sufficient for magnetic manipulation. (Furlani 2007; Khashan and Haik 2006; Han and Frazier 2005, 2006; Haik et al. 1999; Schuler and Frankel 1999).

During the past decade, microfluidic devices for the analysis of small samples of molecular components and sub-cellular structures in living cells have emerged as a major branch of bioanalytical chemistry (Ahn et al. 1996). Biochemical assays typically make use of some form of separation to facilitate the detection and characterization of materials such as cells, proteins, genes, DNA, drugs, pathogens, toxicants and odorants. The high specificity and efficiency of magnetic separation makes it well suited for such applications. It holds special potential for applications involving continuous flow separation. In this process, a sample is continuously fed into a separation chamber where it is subjected to a separation force, typically perpendicular to the flow. The components in the sample respond differently to the force and are therefore differentially deflected from the flow direction and collected at different outlets.

Continuous flow separation has advantages over batch procedures, which require the precise injection of small sample volumes for chromatography or electrophoresis (Pamme 2007). Continuous flow separation enables a relatively high throughput of a sample and it allows for real-time monitoring of separation efficiency. The latter capability enables on-line feedback for optimization, which can be achieved by adjusting parameters such as the flow rate and the induced force. In addition, the continuous flow approach can accommodate multiple inlets and outlets for the simultaneous separation of multiple sample components. The continuous nature of the separation process lends itself to a high level of integration with other upstream or downstream process. Various mechanisms have been used to fractionate sample components in continuous flow applications including electric forces, standing ultrasonic waves and arrangements of obstacles in the flow path. Magnetic separation has also been successfully used for this process. An early commercialized magnetic cell separation system that utilized permanent magnets to generate the magnetic force was employed to separate cells labeled with biotinylated superparamagnetic ferrite-dextran beads (Miltenyi et al. 1990). Other systems using micromagnetic elements have been used for the complete separation of 1 μm magnetic particles (Smistrup et al. 2006).

The performance of continuous flow magnetophoretic microsystems for bioapplications can be modeled in advance of fabrication to determine system parameters that optimize the separation or captured efficiency of a target biomaterial (Pamme and Manz 2004; Pamme et al. 2006; Pamme and Wilhelm 2006; Peyman et al. 2008; Lehmann et al. 2006; Shikida et al. 2006; Wang et al. 2008; Tsuchiya et al. 2008). To date, several researchers have studied and modeled magnetic transport and separation at the microscale. Choi et al. (2000, 2001) analytically computed the trajectories and capture times in a microfluidic bioseparator for no-inertia particles assuming a prescribed fully developed flow. They showed that efficient separation can be achieved in a few minutes with modest power dissipation. Smistrup et al. (2005) presented experiments and simulations of the magnetic separation of magnetic beads in a microfluidic channel integrated with microfabricated electromagnets. Mikkelsen et al. (2005) analytically simulated the magnetic bead motion in the context of a linearized viscous flow using a Green’s function representing the action of a point force on the bead. Furlani (2007) employed a mathematical model for predicting the motion of both red and white blood cells under magnetic, buoyant and viscous forces. His results show that blood cells can be efficiently separated by embedded magnetic element array. Furlani has also developed transport models to study various biomedical applications including magnetic-assisted gene transfection (magnetofection) (Furlani and Ng 2008) and magnetic targeting of therapeutic drugs in the human vascular system (Furlani and Ng 2006; Furlani and Furlani 2007). Nandy et al. (2008) analytically computed capture efficiency as a function of the strength of a field-induced magnetic dipole and the particle size. In their study, the capture efficiency is parameterized using a dimensionless number that scales the particle’s magnetic–hydrodynamics force interaction. Their dimensionless number is derived independent of the magnetic field gradient and is presented specifically for an electromagnetic field that corresponds to anti-parallel current-conducting wires. It is important to note that the aforementioned theoretical studies were limited in that they are based on a one-way coupling between the particles and a prescribed fully developed flow field. Specifically, while the fluid velocity field influences the trajectories of the particles (usually through a simplified Stokes drag relation), the flow is assumed to be constant and independent of the motion of the particles. It should be noted that to date, very few authors have studied magnetic particle transport in microfluidic systems taking into account two-way particle–fluid coupling wherein momentum is transferred from the particles back to the fluid phase. Notable among such studies are the work of Modak et al. (2009, 2010). In this paper, we demonstrate that such analysis is needed for accurate predictions of capture efficiency, which is a critical metric for bioseparation systems.

In this paper, we develop a scaled fully coupled particle–fluid model for predicting the transport and capture of magnetic particles in microfluidic systems. The model involves a CFD-based Eulerian–Lagrangian analysis that includes the dominant forces on the particles and two-way momentum transfer between the moving particles and the flow field. As noted above, this is one of a very few studies of particle separation in microfluidic system that is based on fully coupled particle–fluid CFD analysis (Modak et al. 2009, 2010). Our model takes into account key magnetic variables including the size and magnetic properties of the particles and the magnetic field parameters, i.e. the magnitude and gradient of the field as well as the distance of the field source to the microchannel. It also accounts for fluidic parameters including the dimensions of the microchannel and the fluid viscosity. Several simplifying assumptions are made in the analysis. Specifically, we assume the fluid is incompressible and that the flow is laminar, which is usually the case in microfluidic devices. We further assume that the particle suspension is sufficiently dilute so that particle–particle interactions can be neglected. Particle coagulation as well as build-up and subsequent channel blockage are also neglected. The particle magnetism is assumed to be in the linear range, below saturation. We also assume that the particles enter the channel with a uniform spatial distribution.

In the development of the model we introduce two dimensionless groups that characterize particle capture, one that scales the magnetic and hydrodynamic forces on the particle and another that scales the distance to the magnetic field source. We use the model to parameterize capture efficiency with respect to the dimensionless numbers for both one-way and two-way particle–fluid coupling. For one-way coupling in which the particle motion does not alter the flow momentum, we develop correlations that provide insight into system performance towards optimization. We quantify for the first time the difference in capture efficiency predicted using one-way versus two-way coupling analysis. Our work demonstrates that one-way coupling provides a conservative estimate of capture efficiency. Specifically, it overpredicts the magnetic force needed for particle capture compared to the more rigorous fully coupled analysis as it does not account for a particle-induced modification to the flow field that enhances the capture efficiency. As such, one-way coupling can be used for rapid parametric screening of particle capture performance. However, more accurate predictions require two-way particle–fluid coupling analysis. This is especially true when considering higher capture efficiencies and/or higher particle concentrations.

Finally, it should be noted that other authors have studied a system similar to ours using a similar solution methodology and nondimensional analysis (Modak et al. 2009, 2010). However, these previous studies did not take into account inertial effects (particle acceleration), nor did they quantify the difference in capture efficiency predicted using one-way versus two-way coupling analysis, which is a key and distinguishing feature of this study.

2 Theory

The motion of a magnetic particle in a fluid under the influence of an applied field is governed by several factors. These include the applied magnetic force, fluidic drag (pressure and viscous), an increase in the effective particle mass due to an entrainment of surrounding fluid, the Basset force related to the particle’s history, the Saffman lift force due to fluid shear, the Magnus lift force due to particle rotation, particle–fluid interactions (particle-induced perturbations to the flow field), gravity, buoyancy, Brownian dynamics and interparticle effects such as magnetic dipole–dipole interactions (Furlani 2010c; Fletcher 1991; Gerber et al. 1983). A comprehensive model that takes all of these factors into account is highly complex and beyond the scope of this paper. In the following, we make simplifying assumptions as described above and develop a fully coupled particle–fluid CFD-based approach to study the transport and capture of magnetic particles in microfluidic channels.

Broadly speaking, two approaches are commonly used to model particle transport in microfluidic systems, the Eulerian and the Lagrangian approaches. In the Eulerian approach particles are modeled collectively in terms of a time-dependent spatially varying concentration. The concentration is governed by a PDE that accounts for both force-induced drift and Brownian diffusivity of the particles (Khashan et al. 2011; Furlani and Ng 2008). The Eulerian method is used to study the behavior of sub-micron particles when the Brownian diffusivity, as modeled by a Stokes–Einstein-like equation, has a significant impact on the particle transport. In this case, the particles are assumed to respond instantaneously (with a negligibly short acceleration) to a balance between the fluidic drag and magnetic forces. The particle moves at a constant terminal velocity relative to the base fluid, which is commonly referred to as the magnetophoretic velocity. This velocity adds to fluid velocity to define the overall particle motion that drives its convective flux in the Eulerian frame work. The PDE that governs the particle concentration has the same form as the fluidic momentum equations and can be solved simultaneously with these equations using almost the same numeric algorithm. Thus, an Eulerian-based particle transport model can be readily integrated into Eulerian-based CFD codes (Khashan et al. 2011).

In the Lagrangian approach, particles are treated as discrete entities and the trajectory of each particle is determined by integrating the Newtonian equations of motion. The fluid is governed by the Navier–Stokes equations and the flow field is usually considered to be incompressible. This approach is appropriate for larger particles when Brownian motion is negligible.

In this paper we use a combined Lagrangian–Eulerian CFD-based approach to model the fully coupled particle–fluid behavior of magnetic particles in a microfluidic channel under the influence of a magnetic force. We use a Lagrangian analysis to track the motion of individual particles, and we couple the particle motion to the fluid by introducing a particle force sink into the Navier–Stokes momentum equations, which are solved using an Eulerian-based CFD analysis. The application of two-way coupling is a key result of this work and distinguishes it from most other studies that consider only one-way particle–fluid coupling. We quantify for the first time the difference in capture efficiency predicted using one-way versus two-way coupling analysis as described below.

We first introduce a Lagrangian formulation for particle motion. As noted above, the total force on a particle consists of several different components. We assume that the constituent forces are linearly additive. The total force acting on a particle can then be expressed by Newton’s second law:

$$ m_{\text{p}} \frac{{{\text{d}}{\mathbf{u}}_{\text{p}} }}{{{\text{d}}t}} = \sum {{\mathbf{F}}_{\text{ext}} } $$
(1)

where m p and u p are the mass and the velocity vector of the particle, respectively, and ∑F ext represents all external force vectors exerted on the particle. The particle size is an important factor in determining its dynamics. Brownian motion, and the corresponding stochastic force can influence particle motion when the particle diameter D p is sufficiently small. Gerber et al. (1983) have developed the following criterion to estimate this diameter

$$ |{\mathbf{F}}|D_{\text{p}} \le kT $$
(2)

where |F| is the magnitude of the total force acting on the particle, k is the Boltzmann constant, and T is the absolute temperature. In order to apply Eq. 2, one needs to estimate |F|. If the magnetic field source is specified, one can estimate |F| for a given particle by taking a spatial average of the force on the particle over the region of interest. Gerber et al. (1983) studied the capture of Fe3O4 particles in water using a single magnetic wire and have estimated the critical particle diameter for this application to be D c,p ≡ kT/|F| = 40 nm (i.e. |F| = 0.1 pN). For particles with a diameter below D c,p (which is application dependent) one solves a drift–diffusion equation for the particle concentration rather than the Newtonian equation for the trajectory of a single particle (Furlani and Ng 2008). In addition, the Saffman, Basset, Magnus and added mass forces are generally negligible in comparison with the fluidic drag force. We ignore these effects and write the effective external forces on the particle as follows:

$$ \sum {{\mathbf{F}}_{\text{ext}} = 6\pi \eta a({\mathbf{u}} - {\mathbf{u}}_{\text{p}} )} + V_{\text{p}} (\rho_{\text{p}} - \rho ){\mathbf{g}} + {\mathbf{F}}_{\text{mag}} . $$
(3)

The variables u, ρ and η are the instantaneous local velocity vector, density and the molecular viscosity, respectively, of the carrier fluid ρ p, a and V p are the density, radius and volume of the particle, and g is the gravitational acceleration. The first term on the right-hand side represents the drag (viscous and pressure), as dictated by stokes’ law. For small particles in liquids, lift (buoyant) force can be significant and is considered to act in the opposite direction to the gravitational force as represented in the second term. This force depends on the mass difference of the particle and the corresponding displaced fluid. The third term presents the magnetic force as described below.

The magnetic force as applied on the magnetic particle suspended in a state of dilute suspension in a non-conducting carrier fluid can be expressed as

$$ {\mathbf{F}}_{\text{mag}} = \frac{1}{2}\mu_{0} \chi_{\text{m}} V_{\text{p}} \nabla H^{2} $$
(4)

where μ 0 is the free-space magnetic permeability and χ m (dimensionless) is the effective volume-averaged susceptibility of the linearly magnetic particle, which is estimated based on its magnetically active volume and relative to the susceptibility of the carrier fluid, i.e. the magnetic moments of the polymeric-based microparticles are derived completely from the magnetic nanocrystals encapsulated or embedded in the polymer matrix. Here H = (H · H)1/2 is the magnitude of the applied external magnetic field (A/m), which can be related to the magnetic field induction B (in T) of a particle suspended in a non-magnetic or weakly diamagnetic fluid by B = H/μ0. Both H and B can be determined from Maxwell’s field equations under magneto-static conditions. With particle mobility b defined as (6πηa)−1, the adopted particle motion takes the following form:

$$ m_{\text{p}} \frac{{{\text{d}}{\mathbf{u}}_{\text{p}} }}{{{\text{d}}t}} = b^{ - 1} ({\mathbf{u}} - {\mathbf{u}}_{\text{p}} ) + V_{\text{p}} (\rho_{\text{p}} - \rho ){\mathbf{g}} + \frac{1}{2}\mu_{0} \chi_{\text{m}} V_{\text{p}} \nabla H^{2} . $$
(5)

The trajectory equations are solved by stepwise integration over discrete time steps. Integration of time in particle motion equation yields the velocity of the particle at each point along the trajectory as

$$ \frac{{{\text{d}}{\mathbf{u}}_{\text{p}} }}{{{\text{d}}t}} = \tau^{ - 1} ({\mathbf{u}} - {\mathbf{u}}_{\text{p}} ) + {\mathbf{A}} $$
(6)

where

$$ {\mathbf{A}} = \frac{{V_{\text{p}} (\rho_{\text{p}} - \rho ){\mathbf{g}} + \frac{1}{2}\mu_{0} \chi_{\text{m}} V_{\text{p}} \nabla H^{2} }}{{m_{\text{p}} }} $$
(7)

and τ = m p b. The trajectory can be predicted using

$$ \frac{{{\text{d}}{\mathbf{x}}_{\text{p}} }}{{{\text{d}}t}} = {\mathbf{u}}_{\text{p}} . $$
(8)

The characteristic time τ (Eq. 6) is that required for a particle to respond to changes in the base fluid motion, also referred to as the particle relaxation time. Note that Eqs. 6 and 8 are a set of coupled ordinary differential equations. These can be integrated using a number of different numerical techniques. We have used a fourth-order Runge–Kutta method for our analysis (Furlani 2006; Furlani et al. 2007).

We model the fluid phase using a Eulerian approach. The fluid velocity field is described by the Eulerian incompressible Navier–Stokes equations

$$ \nabla \cdot {\mathbf{u}} = 0 $$
(9)
$$ \rho \left( {\frac{{\partial {\mathbf{u}}}}{\partial t} + {\mathbf{u}}\nabla {\mathbf{u}}} \right) = - \nabla P + \nabla \cdot (\eta \nabla {\mathbf{u}}) - {\mathbf{f}}_{\text{p}} . $$
(10)

In this study, the particle volume fraction (particle loading) is assumed to be sufficiently low so that its effect on the fluidic continuity equation and on the inertia and stress flux terms in the fluidic momentum equation can be neglected. The two-way coupling is accounted for through the particle-weighted sink term f p that represents the counter drag force density exerted by the particles (located in the continuum cells) on the fluid assuming that the suspension is dilute (Faeth 1983 and Modak et al 2009). In practice, this is realized when the volume fraction of the discrete phase is <10–12%. We use the discrete phase model (DPM) provided by ANSYS FLUENT (http://www.ANSYS.com) to predict particle–fluid coupling and to track particle motion. This model employs an Euler–Lagrange approach that treats the fluid phase as a continuum by solving the Navier–Stokes equations, while the dispersed phase is solved by tracking particle parcels, each containing particles with the same properties including diameter, velocity, injection position and trajectory.

The standard Lagrangian part of the DPM calculates the trajectory based on the translational force balance that is formulated for a representative particle as in Eq. 1. In the standard DPM, each particle represents a parcel of particles. In our case, a DPM parcel is subjected to a fluidic drag force, a magnetic force and gravity. The magnetic force is programmed based on the particle position (not the cell position) and then compiled into FLUENT using a user-defined function (UDF). The volume loading (per cell) and other variables are monitored using the same UDF. In the DPM, a particle is treated as a point mass, i.e. it does not occupy volume in the computational domain. Thus, interparticle collisions and the volume displacement of the base fluid by the discrete particles are neglected. Due to these assumptions and simplifications, the DPM is deemed to be valid for dilute fluid–particle flow with a volume loading <12%. This condition can be tracked throughout the analysis to ensure proper application of the model.

The behavior of each parcel is determined by the behavior of its constituent particles. Streams are defined for injecting the parcels in the computational domain. Specifically, n streams require n locations of parcel injections. The stream mass flow rate \( \dot{m}_{\text{stream}} \) and the number of particles in a parcel per second \( \dot{n}_{\text{parcel}} \) are related by \( \dot{n}_{\text{parcel}} = \dot{m}_{\text{stream}} /m_{\text{p}} . \) In all simulations, the total mass flow rate of the injected discrete particle is selected so that its inlet volume fraction (ϕ i) is equal to 0.3%. The injection can be uniformly scaled over the computational cell faces of the inlet plane. Accordingly, 80 cell faces can be used to inject a total of 1.0 × 10−7 kg/s via 80 streams each comprising a parcel of particles that has a mass flow rate of 1.25 × 10−9 kg/s and follow a distinct trajectory. The corresponding total particle loading is ~9.7 × 106 particles/s, which is comparable to values used by Modak et al. (2009). A variable time-step-size accuracy control routine was implemented to ensure efficiency and accuracy of the trajectory solution (Longest et al. 2004). A minimum of ten time steps is used to track the parcel trajectory as it passes a single continuum computational cell.

The flow field of the continuum phase under steady-state conditions is predicted by solving the Navier–Stokes equations, which are discretized using the finite volume approach. The QUICK scheme was used to approximate the momentum equation while the pressure–velocity coupling was realized through the SIMPLEC method.

The particle acceleration term, usually neglected in previous studies, has been retained here to quantify the effect of particle acceleration on the trajectory calculation as well as on particle capture. The effects of the particle–wall boundaries have not been included. The latter simplification is justified as long as the durations of the simulated injections do not significantly exceed the total residence time spent by the last particle to be captured or to escape the computational domain.

Another important variable that can be directly retrieved from the FLUENT analysis is the particles mass concentration per computational cell. This variable (when divided by the particle density) is used to calculate the volume loading in each cell. It is essential to monitor this to ensure that it does not exceed 12%, which is the upper limit for the validity of the DPM. It is important to recall that the DPM treats particles as mass points, disregarding the physical volume they occupy in a computational cell.

In our analysis particle streams were released at the inlet plane. The outlet was set to allow particles to escape while the walls in the channel were set to trap particles. Thus, the collection efficiency could be determined by calculating the percentage of particle streams that were trapped. However, if particles are allowed to accumulate at a capture site for an extended period of time, the volume loading could potentially exceed the maximum DPM loading value (12%) and might even reach the upper limit defined by particle packing. In our numerical studies, we imposed a “reflect” as opposed to “trap” boundary condition to investigate the evolution of volume loading build-up at a capture site.

The momentum transfer from the continuous phase to the discrete phase is determined by examining the change in momentum of a particle as it passes through each control volume. Recall that in the DPM, particles are treated as point masses. The momentum transfer (sink term in Eq. 10) is computed using

$$ - {\mathbf{F}}_{\text{p}} = \frac{1}{{m_{\text{p}} }}\sum\limits_{\text{p}} {\frac{1}{b}({\mathbf{u}}_{\text{p}} - {\mathbf{u}})\dot{m}_{\text{p}} \Updelta t} . $$
(11)

This force which takes the form of a sink term in the continuous-phase equation is equal but opposite to the force that the fluid exerts on the particles (F p). The summation is taken over all parcels that may exist in the computational cell. The variables \( \dot{m}_{\text{p}} \) and Δt are the mass flow rate of each parcel and the residence time that a parcel spends in the computational cell, respectively. The continuum flow velocity is interpolated to the moving parcel position within the cell.

As the trajectory of a particle is computed, FLUENT tracks the momentum gained or lost by a particle stream and this can be incorporated in the subsequent continuous-phase calculations. This two-way coupling is accomplished by alternately solving the discrete and continuous-phase equations until subsequent calculations agree to within a prescribed tolerance (e.g. the continuum mass imbalance falls below 10−13). Furthermore, the UDF is used to verify that concentration, momentum sources as well as the instantaneous particle velocity (and acceleration) are matching those values readily post-processed by FLUENT.

3 Dimensionless groups

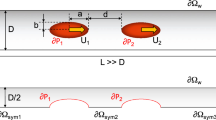
We apply the theory to the analysis of particle transport and capture in a two-dimensional microchannel shown in Fig. 1. In the following, the width of the channel (into the page) is assumed to be sufficiently large to justify a two-dimensional flow analysis, i.e. we ignore flow variation in that direction. The channel height is large enough to justify a continuum Newtonian fluid analysis and we ignore particle–wall hydrodynamic interactions. The length of the channel is sufficiently long so that hydrodynamic effects at the inlet and outlet do not impact the magnetic field-directed particle motion near the mid-length of the channel.

Fig. 1
figure 1

Microfluidic system with magnetic dipole field source

Full size image

A magnetic dipole field source in the form of a pair of anti-parallel current carrying conductors is positioned beneath the lower wall of the microchannel, midway along its length. The magnetic field at any location (r, ϕ) with respect to the virtual origin of the line dipole is given by Ganguly et al. (2004) and Modak et al. (2009):

$$ {\mathbf{H}} = \frac{p}{{{\mathbf{r}}^{2} }}(\sin (\phi )\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{r} + \cos (\phi )\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{\phi } ) $$
(12)

where \( p = \frac{Id}{2\pi }, \) I is the current in each conductor and d is the distance between the conductors.

The performance criterion for magnetic separation is defined in terms of collection efficiency, which is the percentage of incoming particles that are captured (trapped) in the microchannel by the magnetic force. A key goal of this work, aside from the comparison of particle transport and capture for one-way versus two-way coupling, is to obtain dimensionless groups that provide physical insight into the separation physics and useful parameterization with respect to the capture efficiency. Our choice of these groups was based on ensuring their broad applicability while at the same time accounting for key fluidic and magnetic variables. The key fluidic variables include channel dimensions, fluid–particulate flow interaction (mainly drag), particle size and flow conditions. Key magnetic variables include the particle’s effective susceptibility (based on its magnetic content), its magnetization and the strength and local gradient of the magnetic field. After considering many alternatives, we settled on two dimensionless groups that are found to exhibit simple, yet useful collective correlations with respect to the target capture efficiency. Our rational for this selection is as follows: first, we sought a dimensionless group that scales both the magnetic and drag force on the particles. Such a scaling can be realized as a proportionality between the downward directed magnetic force on a particle in the middle of the channel just above the magnetic source, i.e. \( (x_{\text{mag}} ,\frac{h}{2}) \) and the axial fluidic drag force at that point that acts to move the particle downstream, i.e. resisting capture,

$$ F_{{{\text{mag}},y}} \left( {x_{\text{mag}} ,\frac{h}{2}} \right) \sim F_{{{\text{drag}},x}} \left( {x_{\text{mag}} ,\frac{h}{2}} \right). $$
(13)

We normalize the analysis by choosing the average drag force on a particle to be F drag,x  ∼ 6πηau i. The magnetic force on the particle is given by

$$ {\mathbf{F}}_{\text{mag}} = - \frac{1}{2}\mu_{0} \chi V_{\text{p}} \left[ {\frac{{4p^{2} (x - x_{\text{mag}} )}}{{((x - x_{\text{mag}} )^{2} + (y - y_{\text{mag}} )^{2} )^{2} }}\hat{i} + \frac{{4p^{2} (y - y_{\text{mag}} )}}{{((x - x_{\text{mag}} )^{2} + (y - y_{\text{mag}} )^{2} )^{2} }}\hat{j}} \right]. $$
(14)

Note that y mag is negative in Eq. 14 (Fig. 1). The proportionality described above takes the form

$$ \frac{1}{2}\mu_{0} \chi V_{\text{p}} p^{2} \frac{4}{{\left( {y_{c} + \frac{h}{2}} \right)^{5} }} \sim 6\pi \eta au_{i} , $$
(15)

where y c = |y mag|. A dimensionless group that is scaled based on such proportionality would include, in addition to the drag force, the dependency of the magnetic force on the particle magnetization and the magnetic field gradient. However, it is desirable to parameterize these factors separately. For that purpose, the scaling can be more conveniently based on the following proportionality

$$ \frac{1}{2}\mu_{0} \chi V_{\text{p}} p^{2} \frac{4}{{h^{5} }}\left( {\frac{{y_{c} }}{h}} \right) \sim 6\pi \eta au_{i} . $$
(16)

Accordingly, we present the following two dimensionless groups

$$ \beta = \frac{{\frac{1}{2}\mu_{0} \chi V_{\text{p}} p^{2} }}{{6\pi \eta au_{i} h^{5} }} $$
(17)

and

$$ \gamma = \left( {\frac{{y_{c} }}{h}} \right). $$
(18)

It should be noted that β is independent of the location of the magnetic source, while γ depends on the position of the source (y c) and therefore the field gradient that it generates within the microchannel. The use of two dimensional groups is motivated by the fact that the magnetic field and its gradient decay rapidly (and in a nonlinear fashion) with distance from the source. Thus the magnetic force is much more sensitive to the placement of the source than any other system parameter. It is difficult to use a single dimensionless group that exhibits sensitivity to the field gradient that is comparable to that of the other key variables. Also, it is desired that the dimensionless number β have a realistic value that is within the same order of magnitude of unity in line of the perceived magnetic-drag force equilibrium. For magnetization below saturation, β takes the general form,

$$ \beta \sim \frac{{\frac{1}{2}\mu_{0} \chi V_{\text{p}} \left. {\frac{{\partial H^{2} }}{\partial y}} \right|_{{(x_{\text{mag}} ,h)}} }}{{ - 6\pi \eta au_{i} }} $$
(19)

where \( \left. {\frac{{\partial H^{2} }}{\partial y}} \right|_{{(x_{\text{mag}} ,h)}} \)is scaled using the height of the microchannel. Note that scaling the magnetic and fluidic forces with β directly accounts for the increased magnetic force due to larger effective particle susceptibility and size. It also account for the particle’s mobility b = (6πηa)−1, in different viscous base fluids.

4 Results

We apply the theory to the analysis of particle capture in the microchannel shown in Fig. 1. We perform a parametric analysis of this system about a base configuration in which the microchannel has a height h = 100 μm and a length L = 1,000 μm. The dipole field source is positioned at a distance y mag = −100 μm beneath the lower wall of the microchannel, midway along its length (x mag = 500 μm).

In our model, incompressible Newtonian fluid enters the channel at the left side (inlet) with a fully developed laminar flow profile in which the average velocity is u i = 200 μm/s. The outlet pressure is set to zero. Solid spherical magnetic particles are injected into the computational domain at the inlet with a uniform distribution over the entrance plane. We assume that the fluid is water, which is essentially nonmagnetic (χ f ≈ 0). The viscosity and density are η = 0.001 N s/m2 and ρ = 1,000 kg/m3, respectively. The properties of the magnetic particles are chosen to be compatible with the MyOne™ beads produced by Dynal Biotech (http://www.dynabead.com), which are widely used for bio-analytical applications. The MyOne particle has a radius a = 0.525 μm, density ρ p = 1,700 kg/m3, saturation magnetization M s = 4.3 × 104 A/m and an “effective” susceptibility χ = 1.4. The magnetization of the particles will be below saturation as long as B ≤ μ 0 M s/χ where B = |B| (Furlani et al. 2007). This will occur as long as B does not exceed 38 mT, which was the case in all simulations. The rate of the discrete phase injection at the inlet plane is set to 1 × 10−7 kg/s.

A comparison of predicted particle trajectories with one-way and two-way coupling for the base problem is shown in Fig. 2 for various values of the dipole field strength p. From this figure, we find that the one-way coupling analysis underpredicts particle capture relative to the two-way fully coupled analysis. That is, the magnetic force required to achieve a given capture efficiency is predicted to be higher using one-way coupling as compared with the fully coupled analysis. The p = 215 μAm calculations (Fig. 2d) are illustrative of this effect. Specifically, for one-way coupling, this field strength renders critical particle capture, i.e. all particles are captured, albeit some at locations beyond the dipole field source. However, it is obvious that the critical particle capture occurs at a lower field strength (i.e. for p between 192 and 215 μAm) in the two-way coupling analysis. The reason for this is because near the dipole source, the magnetic force accelerates the particles downward. This in turn, induces a downward (vertical) component in the fluid velocity due to the two-way momentum transfer between the particles and the fluid, which is proportional to the instantaneous difference between their respective velocities as indicated in Eq. 11. This effect can be seen in Fig. 3, which shows the particle trajectories superimposed with the corresponding fluid stream-lines as a function of the injected inlet volume fraction of particles ϕ i. The downward distortion of the stream-lines due to two-way particle–fluid coupling is clear and is more pronounced at higher volume fractions as expected. Note that while the inlet volume fractions used in this analysis are relatively small (<1%), the local volume fraction near the capture zone needs to be carefully monitored to ensure that it does not exceed the upper limit of viability for the DPM analysis (i.e. 12%), which was the case. The fluid velocity vectors (not shown), which are tangential to the stream lines, acquire a downward vertical component that is more profoundly sensed by two-way coupling. Once the induced vertical flow field is established, it further accelerates particles downward near the field source, thereby enhancing particle capture. Thus, two-way coupling shows a cooperative effect between the magnetic force and a particle-induced vertical fluidic force component that acts to enhance the capture efficiency. This is in contrast to one-way coupling in which the fluid velocity is purely horizontal, reflecting a fully developed flow throughout the channel. This analysis clearly shows that one-way coupling predictions of capture efficiency will be inadequate, and of little use for device design, when the combined effects of a sufficiently strong magnetic force coupled to a sufficiently high local particle concentration gives rise to a significant distortion of the stream lines near the capture zone as shown in Fig. 3c, d. Furthermore, the degree of accuracy of a one-way coupled analysis is difficult to estimate a priori as it depends on both the local force and local concentration of particles, i.e. not just the absolute volume fraction of the injected particles, which is typically used as a metric for the viability of using the one way coupled analysis. It is instructive to compare the particle acceleration for one-way versus two-way coupling as shown in Fig. 4. Note that the particle acceleration (along the fifth stream from the upper plate) in both the horizontal a x and vertical a y directions are substantially higher near the field source for two-way coupling.

Fig. 2
figure 2

Comparison of predicted particle trajectories using one-way (left) and two-way (right) coupling versus dipole strength p for the base problem (h = 100 μm, L = 1,000 μm, y c = 100 μm, x mag = 500 μm, u i = 200 μm/s, d p = 1.05 μm, ϕ i = 0.3% and χ = 1.4): a p = 64 μAm, b p = 128 μAm, c p = 192 μAm and d p = 215 μAm

Full size image
Fig. 3
figure 3

Two-way coupled particle trajectories superimposed with fluid stream lines for different inlet particle volume fractions: a ϕ i = 0.0588%, b ϕ i = 0.3%, c ϕ i = 0.588% and d ϕ i = 0.882%

Full size image
Fig. 4
figure 4

Comparison of particle acceleration for one-way versus two-way coupling analysis (ϕ i = 0.3%)

Full size image

It is worth mentioning that if the inertia were not retained (i.e. assuming equilibrium), the acceleration components would be zero throughout the whole path of the parcel. Also, Fig. 4 clearly indicates that retaining of the inertia has more pronounced effect under two-way simulation.

Based on our base problem simulation; for the last parcel to be captured, the total residence time (from injection until capture) is calculated to be 5.97 s (the average residence time for all parcels is 1.86 s). With that in mind, assume that all the parcels are injected over twice this maximum residence time (i.e. 12 s) and therefore accumulated in a confined capture site. The total volume of the corresponding captured particles will be 14 × 10−10 m3 which is <1.4% of the total computational domain. Furthermore, the particle loading in this volume is still within the DPM validity threshold. Therefore, under these assumptions, which are deemed to be conservative to cope with a worst case scenario, the blockage is marginal and any packing will be within a smaller portion of this volume. The coupled continuum flow prediction is most reliable when the actual separation process has a duration that is not significantly larger than the total residence time of the last parcel to be captured or, in case of incomplete capture, the last parcel to escape the domain. The capture efficiency based on two-coupling, which is introduced below, is recorded within the maximum residence time, which presents an early stage that precedes any significant accumulation of particles.

Next, we study the capture efficiency (CE) as a function of the dimensionless number β, where

$$ {\text{CE}} = \frac{\text{number\,of\,particles\,captured}}{\text{total number of particles}}. $$
(20)

Figure 5 shows the capture efficiency CE versus β with γ fixed (γ = 1) for one-way coupling. Note that a single curve is obtained for all variations of the inlet velocity, particle diameter, particle magnetic susceptibility and fluid viscosity as long as γ is held constant. To gain insight into the effects of magnetic capture, it is useful to decompose β into constituent terms to isolate different functional dependencies, i.e.

$$ \beta = \frac{{\frac{1}{2}\mu_{0} \chi V_{\text{p}} p^{2} }}{{6\pi \eta au_{i} h^{5} }} = \frac{{\alpha p^{2} }}{{h^{5} }}, $$
(21)

where

$$ \alpha = \frac{1}{9}\frac{{\mu_{o} \chi a^{2} }}{{\eta u_{i} }}. $$
(22)
Fig. 5
figure 5

The capture efficiency CE versus β at γ = 1.0 (one-way coupling analysis). The base problem corresponds to h = 100 μm, L = 1,000 μm, y c = 100 μm, x mag = 500 μm, u i = 200 μm/s, d p = 1.05 μm, ϕ i = 0.3%, χ = 1.4 and η = 10−3 N s/m2

Full size image

Note that α is independent of the position of the field source, the magnetic strength and the height of the microchannel. Based on this analysis, we find that the following variational relation holds for specified values of CE and γ,

$$ \frac{{\partial (\alpha p^{2} )}}{\partial p}\,{\text{d}}p + \frac{{\partial (\alpha p^{2} )}}{\partial \alpha }\,{\text{d}}\alpha = 0, $$
(23)

or

$$ \left( {\frac{\partial p}{\partial \alpha }} \right)_{{{\text{CE}},\gamma }} = \frac{ - p}{2\alpha }. $$
(24)

It is instructive to analyze the partial variational relation between p and α, which relates the ratio between a change in the former in response to a change in the latter,

$$ \left( {\frac{{p_{2} }}{{p_{1} }}} \right)_{{{\text{CE}},\gamma }} = \left( {\frac{{\alpha_{1} }}{{\alpha_{2} }}} \right)^{1/2} . $$
(25)

In this and in the following expressions, the subscripts 1 and 2 denote the initial and new value of the parameter, respectively. Extended partial variational relations between any two variables among the constituents of α and p can be written as

$$ \left( {\frac{{p_{2} }}{{p_{1} }}} \right)_{{{\text{CE}},\gamma ,\chi ,u_{i} }} = \frac{{a_{1} }}{{a_{2} }},\quad \, \left( {\frac{{p_{2} }}{{p_{1} }}} \right)_{{{\text{CE}},\gamma ,a,u_{i} }} = \left( {\frac{{\chi_{1} }}{{\chi_{2} }}} \right)^{1/2} ,\quad \, \left( {\frac{{p_{2} }}{{p_{1} }}} \right)_{{{\text{CE}},\gamma ,\chi ,a}} = \left( {\frac{{u_{i2} }}{{u_{i1} }}} \right)^{1/2} . $$
(26)

These relations indicate that the dipole strength p required for particle capture is inversely proportional to both the particle’s radius and the square root of its magnetic susceptibility χ 1/2, but directly proportional to the squared root of the inlet velocity u 1/2i . It is also inversely proportional to the fluid viscosity. Any variation in h 5 leads to a different distinct CE–p relation. As such, its partial variation with respect to p (or αp 2) does not hold, i.e. (p 2/p 1)2 ≠ (h 1/h 2)5. This is one reason we chose to exclude the variable h from the definition of α in Eq. 22. Specifically, α compromises all the system parameters that are found to follow the variational relation described above. All variations in α constituents result in a single CE–β relation at the specified γ (and not just y mag). If we had included h in α it would be difficult to isolate results using CE–β and γ only.

It should be noted that the merit of Eq. 25 is limited by the constraints under which it is derived. Knowing that α depends on the hydrodynamics and magnetization parameters of the particle, and not on the magnetic field or its gradient per se, one can state that when γ is held constant, a target capture efficiency can be obtained according to Eq. 25 by controlling the p and α values, or alternatively, p and any constituent of α according to Eq. 26. Recalling that β = αp 2/h 5, one could question the choice of using β to characterize the hydrodynamic and magnetization interactions of the particle rather than αp 2. The inclusion of h 5 can be justified as a necessary scaling constant that renders β dimensionless with values having an order of magnitude near unity (as h does in γ) and more importantly by the fact that γ includes h as well. Such an arrangement leaves β and γ with constant interdependence with respect to h in a way that does not interfere with them being physically independent variables.

We have found that a target capture efficiency can be obtained under operating conditions defined by two dimensionless groups, β and γ. A similar dependence [i.e. CE = CE(β, γ)] is obtained by Nandy et al. (2008) using an analytical solution that utilizes a prescribed fully developed velocity field. Though their solution is based on a high channel diameter to length ratio, their calculated capture efficiency directly corresponds to the normalized entry position (with respect to h) at which a particle is critically collected at the channel exit.

In our study, particles are assumed to be captured once they contact the lower plate (at y = y mag). In many cases, they are captured at locations well before the outlet as shown in Fig. 2c, and it might be more appropriate to define capture efficiency with respect to a desired target site rather than the whole length of the lower wall. This is especially the case when confined particle focusing or separation is desired. The CE–β correspondence at fixed γ is also illustrated in Fig. 4 for different values of the hydraulic channel diameter h. It is evident from the figure that the unique correspondence holds even though the inlet mass flow rate of the base fluid (∼u i h) is doubled for each γ cases.

The upward bend at the upper end close to complete capture as shown in Fig. 5 indicates that the capture efficiency CE becomes more sensitive to β so that a slight increase in β gives an abrupt rise in CE. This can be attributed to the fact that the last parcels to be captured, which were injected near the upper wall, have a significantly longer residence time since a considerable portion of their trajectory lies within slow fluid near the upper wall of the channel. With longer residence time, particles are easier to be retained and therefore captured at the lower wall. For the same reason, the steep portion of the CE–β at lower values of β (in Fig. 5) corresponds to the parcels injected near the lower wall. To further explain this, we examine the motion of five representative parcels. These parcels are injected uniformly at the inlet plane. Figure 6a shows the residence time for each parcels stream labeled consecutively, according to their injection position, from 1 near the lower wall to 5 near the upper wall. The line terminates at the total residence time and the corresponding path length. The residence time of the near-wall streams (1 and 5) is longer due to the high shear rate of the carrier fluid therein. The stream representing the last particles to be captured has a substantially longer residence time. Figure 6b shows the normalized magnitude of the slip, i.e. S = |u p − u|/u i. The figure suggests that the near-wall originated parcels were constrained from attaining high magnetophoresis motion. Though stream 5 experiences a noticeable magnetophoresis force as it leaves the high shear region, its eventual capture is mainly aided by the viscous effect once it enters the other near (lower) wall region.

Fig. 6
figure 6

One-way coupling description for representative parcels labeled sequentially with their respective injection positions from 1 to 5, where 1 labels the parcel injected close to the lower wall and 5 labels the parcel injected close to the upper wall. a Residence time, b normalized slip S = |u p − u|/u i, c normalized difference between the equilibrium-based and inertia-based axial velocity and d normalized difference between the equilibrium-based and inertia-based vertical velocity. The simulation corresponds to h = 100 μm, L = 1,000 μm, y c = 100 μm, x mag = 500 μm, u i = 200 μm/s, d p = 1.05 μm, ϕ i = 0.3%, χ = 1.4 and η = 10−3 N s/m2

Full size image

The effect of retaining the inertia term, as opposed to assuming magnetic-drag equilibrium, is illustrated by Fig. 6c and d. The normalized difference between the equilibrium-based particle velocity and that calculated with retaining the inertia is marginal (<1 and 2% for the axial and vertical velocities, respectively). This difference closely corresponds to the inertia (acceleration) of the particle (i.e. the LHS of Eq. 1).

Figure 7a shows the two-way-coupling based residence time for parcel 3 injected through the mid inlet plane and parcel 5 injected near the upper wall. The two particle loadings shown here (ϕ i = 0.3% and ϕ i = 0.5%) are calculated based on the whole inlet plane. The line terminates at the total residence time and the corresponding path length. The residence time of the near-wall streams (1 and 5) is longer due to the high shear rate of the carrier fluid therein. Increasing the particle loading increases the residence time of the last parcel slightly. It is evident that one-way-coupling analysis (as shown in the same figure) significantly overpredicts the total residence time spent by the last parcel to be captured. Figure 7b shows that the parcels experience higher slip under increased particle loading. The same figure shows that one-way coupling underpredicts the slip more clearly for the last parcels to be captures. Figure 7c and d shows the continuum cell-based counter drag forces exerted on the fluid by the particles (S x  = −f p,x *V cell and S y  = −f p,y *V cell in the last term in Eq. 10) for different parcel trajectories. Obviously, increased particle loading yields more impact on the fluid (see Fig. 3).

Fig. 7
figure 7

Two-way coupling simulation for two different particle loadings (ϕ i = 0.3% and ϕ i = 0.5%) for representative parcels labeled sequentially with their respective injection positions from 1 to 5, where 1 labels the parcel injected close to the lower wall and 5 labels the parcel injected close to the upper wall. a Residence time and b normalized slip S = |u p − u|/u i, c prevailing added axial momentum source and, d prevailing added axial momentum source. The simulation corresponds to h = 100 μm, L = 1,000 μm, y c = 100 μm, x mag = 500 μm, u i = 200 μm/s, d p = 1.05 μm, χ = 1.4 and η = 10−3 N s/m2

Full size image

Figure 8 below shows two distinct CE–β relations for γ equal to 1.0 and 0.5, respectively. These plots as obtained using one-way coupling, indicate that at smaller γ (i.e. the magnetic source closer to the microchannel), a higher capture efficiency can be obtained at smaller β. For instance, at β = 0.25, the capture efficiency is about 40 and 80%, for γ = 1 and 0.5, respectively. In fact, this explains why we chose β to be proportional to ∂H 2/∂y using p 2/h 5 rather than p 2/(|y mag| + h/2)5. The latter definition would have resulted in an intermingling of effects due to magnetic and hydrodynamic interactions with those due to the position of the field source and its field gradient. With this in mind, the figure clearly indicates that smaller β is required at smaller γ. In other words, the capture under less particle magnetization or faster throughput flow can be more easily accommodated when the magnetic source is brought closer to the microchannel.

Fig. 8
figure 8

The capture efficiency CE versus β at γ = 1.0 and 0.5 (one-way coupling analysis). The parameter α, as defined by Eq. 22 can be any value

Full size image

The plot of CE versus β, in Figs. 5 and 8 can be considered in terms of three distinct regions, each with a different functional dependencies. The simplest functional dependency, which is nearly linear, extends from CE between 0.6 and 0.95. In this region, the slope of CE–β increase as γ decreases. As such, (∂CE/∂β) ∼ 0.5 at γ = 1 and (∂CE/∂β) ∼ 1.8 at γ = 0.5. This CE range represents the region of most practical importance. A 3D regression can be used to model these practical capture efficiencies in this range (i.e. CE between 0.6 and 0.95) as

$$ {\text{CE}} \approx 2.622 - 2.4\gamma + 0.72\ln \beta + 0.62\gamma^{2} + 0.069(\ln \beta )^{2} - 0.28\gamma \ln \beta . $$
(27)

For β in the same range

$$ \beta \approx e^{2\gamma } ( - 0.1577 + 0.2753\tanh \gamma + 0.3621{\text{CE}})^{2} . $$
(28)

This regression is extracted from all CE–β variations (within the practical CE range stated above) at γ equal to 0.2, 0.25, 0.35, 0.5, 0.7, 1.0 and 1.5. Though the validity of the above regression equation is sensitive to the specified CE range (see the offset constant 2.622 in Eq. 27), it yields relative errors that are noticeably <5%. From a conservative design point of view, the regression is carefully weighted so as to never overpredict complete capture (i.e. CE = 1).

Figure 9 presents the critical β cr–γ correspondence at which complete capture CE = 1 can be achieved under the assumption of one-way coupling. A lower particle magnetization is needed when the magnetic source is brought closer to the microchannel, a condition that obviously corresponds to a higher gradient and, therefore, a higher magnetic force. Over the considered γ range, the critical β cr can be expressed in the following analytical form:

Fig. 9
figure 9

CE map with respect to γ and β (one-way coupling analysis). The shaded area below CE = 1.0 corresponds to complete particle capture

Full size image
$$ \beta_{\text{cr}} = \frac{{\alpha p_{\text{cr}}^{2} }}{{h^{5} }} \approx 1.14\gamma^{3} - 0.41\gamma^{2} + 0.5\gamma . $$
(29)

This equation provides a direct means to relate the following parameters: α (a grouping of hydrodynamics and magnetization parameters), h (the microchannel height) and p cr (the required critical dipole strength) to the parameter γ. Thus, we can use this expression to correlate the critical β and γ values at which we have complete capture. Furthermore, the definition of β indicates that this equation may be used to relate a variation in any of α, p cr or h with respect to γ at complete capture. Another important point is that this correlation, which is based on one-way coupling, when used to simulate dilute particle loading, can be used as a conservative design parameter for the more rigorous two-way coupling.

Figure 10 shows a comparison of the predicted capture efficiency using one-way versus a two-way coupling analysis for two different values of γ but under the same dilute particle loading (i.e. ϕ i = 0.3%). Note that for both values of γ the one-way and two-way coupled simulations yield approximately the same functional profile for values of β that render CE ≤ 0.6. However, the former underpredicts the latter for larger vales of β. This last result is important and is a key finding of this study. Specifically, we quantify for the first time the difference in capture efficiency predicted using one-way versus two-way coupling analysis. Specifically, we show that one-way coupling overpredicts the magnetic force needed for particle capture as compared with the more rigorous fully coupled analysis, especially at higher capture efficiencies and/or higher particle concentrations.

Fig. 10
figure 10

The capture efficiency CE versus β at γ = 1.0 and 0.5 using the one-way and two-way coupling approaches under dilute particle loading (ϕ i = 0.3%)

Full size image

5 Conclusion

In this paper, we have presented a model for predicting the field-induced capture of colloidal magnetic particles in microfluidic systems taking into account two-way particle–fluid coupling. The method involves the use a CFD-based Lagrangian–Eulerian approach to predict particle motion and its impact on the flow field. We have demonstrated the method via application to a particle capture in a two-dimensional system consisting of a microfluidic channel and a dipole field source, which is located beneath and midway along the channel. We have introduced two dimensionless groups for this system that characterized particle capture. One that scales the magnetic and hydrodynamic forces on the particle and another that scales the distance to the field source. We have used the model to parameterize capture efficiency with respect to the dimensionless numbers for both one-way and two-way particle–fluid coupling. For one-way coupling, we have developed correlations that provide insight into system performance towards optimization. We quantify for the first time the difference in capture efficiency predicted using one-way versus two-way coupling analysis. We have shown that predictions based on one-way coupling overpredict the magnetic force needed for particle capture as compared with those based on two-way coupling. Our analysis demonstrates that this is because in two-way coupling there is a cooperative effect between the magnetic force and a particle-induced fluidic force component that acts to enhance the capture efficiency. Thus, while a simplified one-way particle–fluid coupling analysis enables rapid parametric screening of novel capture systems, two-way coupling needs to be modeled for more accurate analysis, especially when considering higher particle concentrations. The reliability of the coupled continuum flow prediction is most established when the actual separation process has a duration that is not overly larger than the total residence time of the last parcel to be captured or, in case of incomplete capture, the last parcel to escape the domain. The method presented here is fundamental and should be of substantial use in the development of a broad range of novel magnetophoretic processes and devices.