Formation of vortices in long microcavities at low Reynolds number

Abstract

Microcavities are a central feature of many microflow systems ranging from sprouting capillaries during angiogenesis to various microfluidic devices. Recently, the flow and transport phenomena in microcavities have been subject of a number of studies, yet a physical picture of the flow properties at low Reynolds number, which is the relevant regime in many biological applications, has not been fully brought out. We have therefore systematically investigated, experimentally and by modeling, the flow in a long microcavity and found that the flow properties depend decisively on the depth/width ratio of the cavity. Notably, if this cavity aspect ratio is higher than approximately 0.51, counter-flow vortices emerge in the cavity even at vanishing Reynolds number. The distance of the first vortex from the cavity entrance decreases with an increasing aspect ratio as an inverse power law. In the vortex-free regime below the threshold aspect ratio, the flow velocity decays exponentially away from the cavity entrance, with a decay length that scales with the width of the cavity and depends also on the aspect ratio of its cross section. The results of our numerical simulations are supported by a theoretical analysis and are in good agreement with experimental data, acquired by optical velocimetry with optical tweezers.

1 Introduction

Microcavities have become an integral part of diverse microfluidic devices. They have been, for example, used as flow-free diffusion chambers for single-cell experiments and studies of soft biological systems (Luo et al. 2008; Liu et al. 2008; Vrhovec et al. 2011; Omar et al. 2014; Yew et al. 2013). On the other hand, microcavities have also been used for controlled formation of microvortices in applications ranging from a centrifuge on a chip (Shelby et al. 2003; Mach et al. 2011) to analysis of microorganism behavior (Stocker 2006) and cell sorting (Zhou et al. 2013; Hur et al. 2011). Interestingly, while the microcavity vortices are a central feature in some applications, they have not been observed in others. It has been noted that a high depth-to-width ratio of the cavity and a high Reynolds number contribute to the emergence of vortices (Yu et al. 2005; Stocker 2006; Fishler et al. 2013), but the flow properties, including in particular the counter-vortex position, have not been thoroughly analyzed at low Reynolds number.

In applications demanding high flow rates, the vortices have been observed in cavities of various geometries. For example, applications of high-throughput particle sorting (Zhou et al. 2013; Hur et al. 2011) and the studies of a centrifuge on a chip (Mach et al. 2011) have reported vortices at Reynolds numbers higher than approximately $Re=40$, which is consistent with recent analyses of cavity flow using microparticle image velocimetry (Shen et al. 2015). However, typical Reynolds numbers in single-cell experiments and in many biological applications are much lower, since a high flow rate could hinder accurate single-cell analysis and even result in irreversible cell damage. To put a high Reynolds number in a biologist’s perspective: since the Reynolds number is defined as $Re = \rho v_0 d/\eta$, where $\rho$ is the fluid density, $v_0$ the mean flow velocity, d the channel dimension, and $\eta$ the fluid viscosity, the flow velocity of water in a 100-μm-wide microchannel at $Re=40$ would reach 40 cm/s. In other words, at this flow rate a cell would traverse a typical 100-μm-wide microscope field of view in just 0.25 ms.

Several studies have shown that the flow velocity in a microcavity drops off rapidly with the distance from the cavity entrance (Yu et al. 2005; Vrhovec et al. 2011), with a characteristic length as small as approximately 1/4 of the cavity width (Yew et al. 2013; Shen et al. 2015). Hence, already in a cavity that is only two times longer than its width, the flow at its termination drops to $\sim \mathrm{e}^{-8}\approx 0.03\,\%$ of the entrance magnitude and in the Stokes regime becomes negligible even in comparison with diffusion. The flow pattern at the cavity entrance, however, remains important for the mass transfer into the cavity (Yew et al. 2013). Moreover, for residual flows this weak, the influence of the terminating boundary on the overall flow field in the microcavity is hardly noticeable: e.g., in the middle of the cavity it amounts to $\sim$0.03 % of the velocity magnitude there.

Hence, such long microcavities can be sensibly modeled as having infinite length. An example of a long microcavity is the diffusion chamber described in Vrhovec et al. (2011). Another example is the sprouting of capillaries during angiogenesis, a process that is essential for normal tissue development but also for tumor growth. Here, a sprout extending perpendicularly from the capillary can grow many times its diameter (Galie et al. 2014). The typical flow rates in the capillary are of the order of 10 μm/s, and its cross section is of the order of 10 μm, rendering the Reynolds number in the capillary considerably lower than 1. Because the epithelial development depends crucially on the transport of nutrients and on the shear stress exerted on the vessel walls (Galie et al. 2014), understanding the flow pattern in a microcavity is an essential step toward understanding the physiology and pathology of capillary sprouting.

In this work, we combine numerical modeling with theoretical analysis and experimental verification in order to obtain a comprehensive picture of flow in microcavities at low Reynolds number. In particular, we identify the main parameters that control the emergence and configuration of vortices and the falloff of the fluid velocity along the microcavity. We investigate the dependence of the flow morphology on the aspect ratio of the microcavity cross section and point to the existence of a well-defined aspect ratio threshold separating the flow regimes with and without counter vortices. We consider microcavities which are sufficiently long, so that the flow at the cavity ending effectively vanishes in the sense that the overall flow pattern in the cavity does not depend notably on its length any more. Moreover, in the “Appendix,” we consider the theoretical flow solutions in the limiting cases of vanishing and infinite values of the aspect ratio, focusing on the features that preserve relevance also for practical, experimentally accessible aspect ratios.

2 Methods

2.1 Problem formulation

The model microcavity in our study consists of a dead-end microchannel extending perpendicularly from the main microchannel, Fig. 1. The cavity length is a and $x=0$ corresponds to the junction, its width is b, $-b/2< y < b/2$, and the depth of all the channels is h, where $0 < z < h$. Cavities of minimum length $a\approx 2.4 b$ were used, all qualifying as long according to the above argument. The width of the main channel is the same as the width of the cavity. In the studied experiments, the Reynolds number in the main microchannel is $Re\sim 1$; however, in the microcavity, it shortly becomes much smaller as the magnitude of the velocity drops off rapidly along x.

Fig. 1

Microcavity geometry and definition of the coordinate axes. The microcavity extends perpendicularly from the main channel. The length of the microcavity is a, and its width is b ($a>b$). The depth of the cavity and the main microchannel is h

Generally, in a long microcavity, the shape of the flow can depend only on the Reynolds number and the channel cross section aspect ratio h/b, since one of the lengths b or h can be used to define the length scale of the system and then all lengths and velocities are scaled relative to it. For $Re\rightarrow 0$, the shape of the flow field does not depend on Re any more, i.e., the velocity field converges to the low-Re configuration that scales with $v_0$, while h/b is the only remaining parameter of the system. Thus, within this regime, the results presented in this paper can be, by rescaling, quantitatively applied to any Newtonian fluid and any width b or depth h of the microcavity. If the microcavity is not long, i.e., if the flow is not negligible near its end and thus communicates with the terminating boundary, then the cavity length a becomes a second parameter of the system. For the reason of lucidity, we will, however, not pursue this ramification here, as the physical essence is contained already, and primarily, in the long cavity limit.

The boundary condition at the entrance to the microcavity cannot be simply stated. It depends on the width of the main channel unless it was large compared to b and also on the exact shape of the junction (e.g., the curvature of the channel walls at the junction) as we will demonstrate. The latter certainly affects the details of the flow field; in particular, it introduces a position offset, but it leaves the behavior at large x unaltered.

2.2 Numerical modeling

We use the PDE solver package FEMLAB 3.1 (COMSOL AB) to simulate the flow in the three-dimensional experimental situation. Once the agreement with the experimental flow fields was confirmed, the numeric simulation gives us flexibility to vary the geometry of the channel and extract the studied dependencies from the computed flow fields.

2.3 Microfluidic system

Two microfluidic systems were built, a “shallow” cavity with the aspect ratio $h/b=0.38$ ($h=45$ μm, $a=290$ μm, $b=120$ μm) and a “deep” cavity with the aspect ratio $h/b=1.40$ ($h=140$  μm, $a=290$ μm, $b=100$ μm). Due to fabrication limitations, the microcavity entrance of the high-aspect-ratio system was rounded, with a curvature radius of approximately $100$ μm (Fig. 2).

The microfluidic system was fabricated by standard soft lithography techniques as described previously (Vrhovec et al. 2011). In brief, microchannels were cast in PDMS and sealed to a glass cover slide after plasma-induced surface activation. Low-aspect-ratio master molds were prepared by etching SU-8 photoresist on a glass substrate, and the high-aspect-ratio master was made in aluminum by CNC micromilling with drill radius 0.1 mm (Sodick MC 430 L, Sodick Europe Ltd).

The flow rate in the microchannels was regulated by adjusting the hydrostatic pressure difference between the inlet and outlet water reservoirs. The pressure difference needed for a mean velocity flow rate $v_0=1$ mm/s in the main channel was 25.0 mmH$_2$O (245 Pa) for the shallow design and 6.3 mmH$_2$O (62 Pa) for the deep design.

2.4 Flow measurements

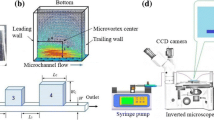
There exist a number of methods for analyzing the flow in a microfluidic system, each having its own advantages and disadvantages (Van Dinther et al. 2012), yet in a biology laboratory equipped with optical tweezers, the preferred method is optical velocimetry (Di Leonardo et al. 2006). In brief, a multi-trap AOD-steered optical tweezers (Tweez 250i, Aresis d.o.o, Ljubljana, Slovenia) with a long working distance 60$\times$ water immersion objective was used to position 5.2-μm-diameter silica microspheres along the symmetry axis of the cavity. The flow velocity at a given position is proportional to the viscous drag on the microsphere, which is measured by detecting the sphere displacement from the trap center. For relative velocity measurement, an accurate absolute trap stiffness calibration is not essential. A dynamic adjustment of the relative trap stiffness allows for accurate velocity measurements over more than one order of magnitude. If only qualitative assessment of the streamlines was needed, we tracked the flow of 100-nm fluorescent polystyrene microspheres dispersed in water.

3 Results

Fig. 2

Two flow regimes in a microcavity, as observed in experiments (a, b) and in numerical modeling (c, d). At the cavity cross section aspect ratio $h/b=0.38$, the flow is vortex free (a, c), while at the aspect ratio $h/b=1.40$ a vortex is clearly visible. In principle, in an infinitely long microcavity, the vortex regime consists of a train of alternating vortices, but since the flow velocity decreases rapidly along the microcavity, only the first vortex is observed in experiments, whereas already the second (in this case revealed by numerics) cannot be detected. The experimental images are inverted micrographs of 100-nm fluorescent microspheres dispersed in water. Traces of individual microspheres in the main channel cannot be distinguished due to their high velocity (see also Video 1 and 2 in the Supplementary Material)

In the experiments, we observe two flow regimes depending on the microcavity cross section aspect ratio. In the shallow channel (small h/b), no counter vortex is formed, Fig. 2a and Supplementary Video 1, and the flow decays monotonically along x. The flow in the deep channel, however, exhibits a counter vortex, Fig. 2b and Supplementary Video 2. Note that this phenomenon is different than the flow separation at higher Re (Shen et al. 2015)—we are strictly in the $Re\rightarrow 0$ limit. Controlling the existence of this counter vortex and in particular the exact position of the flow separatrix between the primary flow and the first counter-vortex flow is crucial for any application-oriented design of the microcavity.

The two flow regimes are nicely reproduced by numerical simulations, Fig. 2c, d. The simulations will also reveal that in principle, the vortex regime consists of a train of alternating vortices. Due to the rapidly decreasing flow velocity along the microcavity only the first vortex is typically seen in vitro even for an excessively long microcavity channel.

3.1 Vortex-free regime

It is important to realize that in this flow regime, occurring for cavity cross section aspect ratios h/b lower than the threshold aspect ratio $(h/b)_c\approx 0.51$ (which will consistently come along in Sect. 3.2), no vortices are formed even in an infinitely long microcavity. Both experimental and simulation data ($h/b=0.38$) show a monotonic exponential decrease in the velocity magnitude with x, Figs. 3 and 4. Within a shallow microcavity approximation, i.e., in the limit $h/b\ll 1$, one can show analytically (see “Appendix”) that both velocity components drop off as $\exp (- x/x_0)$, Eq. (30), where the decay length equals $x_0=b/\pi$. Moreover, the simulation shows a decrease in the decay length for increasing h/b, Fig. 5, and confirms the limit $b/\pi$ for $h/b\rightarrow 0$.

Fig. 3

Profile of the normalized velocity $v_y(x)/v_0$ at $y=0$, $z=h/2$, presented as $\ln {v_y/v_0}$ for legibility, at the aspect ratio $h/b=0.38$: experiment (squares) and numerical modeling (solid line)

Fig. 4

Numerical modeling for different values of the aspect ratio h/b in the vortex-free flow regime. Left flow streamlines at the cross section $z=h/2$. Right profiles of the normalized velocity $v_y(x)/v_0$ at $y=0$, $z=h/2$, presented as $\ln {v_y/v_0}$ for legibility

Fig. 5

Dimensionless velocity decay length, obtained by numerical modeling, as a function of the aspect ratio h/b. The vertical gray line indicates the critical aspect ratio $(h/b)_c\approx 0.51$, see Sect. 3.2. The dashed red line represents the theoretical overall decay length in the 2D lid-driven cavity (Shankar and Desphande 2000), 1/4.212, which represents the high aspect ratio (deep channel) limit of the vortex regime

3.2 Vortex regime

In the deeper cavity ($h/b=1.40$), only a single counter vortex can be observed in the experiment. The simulation in a long cavity, however, suggests that in the vortex regime, the long cavity solution in principle consists of a train of alternating vortices, Figs. 2d and 6. Such flow morphology is compatible with the analytic solution (Shankar and Desphande 2000) of the 2D ($h/b\rightarrow \infty$) lid-driven cavity problem in the Stokes ($Re\rightarrow 0$) regime, Eq. (13), Fig. 9, presented in the “Appendix”. The driven lid at $x=0$ does not correspond to the actual experimental circumstances at the junction, but this local detail becomes unimportant further down the channel (cf. Fig. 9 of “Appendix”). Moreover, further down the channel, the analytic solution is to a very good approximation dominated by the first term of the expansion Eq. (13) alone. As thus follows from the analytic solution, in an infinitely long channel of an infinite depth the flow decays exponentially with x, with a rather short decay length of b/4.212. The distance between successive vortex centers is $\sim$1.396  b, and the flow field decays by a factor $\sim 1/357$ in going from one vortex to the next (Shankar and Desphande 2000; see “Appendix”).

One must be aware, however, that the 2D analytic solution is a pertinent high aspect ratio limit only if the flow is actually restricted to the xy plane. As we will show in Sect. 3.3, in real 3D systems this is only partially fulfilled.

When the cavity cross section aspect ratio h/b decreases from infinity to experimentally accessible values ($h/b\sim 1.5$ and lower), the qualitative shape of the flow is preserved, but the flow decays somewhat faster, Fig. 5, and in particular, the separation of vortices increases, Fig. 6. We perform simulations varying h/b over the range of experimentally accessible values and extract from the computed velocity fields the position of the flow separatrix before the first vortex, i.e., the x coordinate at which $v_x$ vanishes for $y=0$. The dimensionless position of the first separatrix $s_1/b$ as a function of the cavity cross section aspect ratio h/b is shown in Fig. 7. It is well fitted with a power law,

$$\begin{aligned} \frac{s_1}{b}=a \Bigg [\frac{h}{b} - \Big (\frac{h}{b}\Big )_c\Bigg ]^{-\beta } + C. \end{aligned}$$

(1)

Moreover, we demonstrate that the separatrix position depends appreciably on the details of the junction, such as the curvature of the corners, mainly as a position offset. Apart from that, the functional dependence on h/b is not significantly affected.

Fig. 6

Numerical modeling for different values of the aspect ratio h/b in the vortex flow regime in a long microcavity. Left flow streamlines at the $z=h/2$ cross section (the middle of the microcavity). Right profiles of the normalized velocity along the microcavity $v_y(x)/v_0$ at $y=0$, $z=h/2$, presented as the logarithm $\ln {v_y/v_0}$ for legibility

Fig. 7

Dimensionless position of the first flow separatrix as a function of the aspect ratio h/b for two different types of junction corners: 90° (black squares) and rounded as in Fig. 2b (red circles). Solid lines are fits to Eq. (1), yielding $(h/b)_c=0.51 \pm 0.03$ and $\beta =0.86 \pm 0.05$. The values from 2D simulations $s_1/b=0.25$ (90°) and $s_1/b=0.67$ (rounded) are indicated by horizontal lines

Figure 7 also demonstrates that for $h/b>1$, the position of the separatrix approaches the value which can be reproduced in the 2D simulation. This is of importance as it signifies the relevance of the 2D solution (also the 2D analytic solution Eq. (13)) as the $h/b\rightarrow \infty$ limit of the real 3D system. The 2D solution is thus meaningful, in spite of the fact that further down the microcavity, the flow might escape from the xy plane (see Sect. 3.3).

Most importantly, the fits of the flow separatrix position, Fig. 7, show that there exists a critical aspect ratio

$$\begin{aligned} \left( {h/b}\right) _c \approx 0.51 \end{aligned}$$

(2)

approaching which the separatrix position is expelled to infinity and below which the flow configuration switches to the vortex-free regime. Thus, by studying the dependence of the flow separatrix position on the cavity cross section aspect ratio and finding its critical behavior, we are able to identify the two distinct $Re\rightarrow 0$ flow regimes of the microcavity. This approach enables us to rigorously distinguish between the vortex and the vortex-free regimes and determine the threshold aspect ratio very precisely.

3.3 Instability of the 2D flow

As soon as $h/b>1$, we find numerically that the flow which is originally in the xy plane near the entrance to the microcavity becomes unstable down the channel and gets reorganized. It escapes from the original xy plane becoming three dimensional. Interestingly, at larger x it settles again as a 2D flow in the xz plane, i.e., in the plane of the lower aspect ratio, where it is stable. At a high aspect ratio like the one in Fig. 8, the restructuring of the flow takes place rather shortly near the entrance, while for aspect ratios closer to unity this happens further down the cavity.

Fig. 8

Restructuring of the flow for $h/b>1$. Left escape of the flow from the xy plane into the xz plane, $h/b=5$. Right logarithm of the y and z components of the normalized velocity, i.e., $\ln (|v_y(x)|/v_0)$ and $\ln (|v_z(x)|/v_0)$ in the middle of the microcavity, $h/b=5$. In this particular example, the escape takes place at $x/b\approx 1.5$. The dashed line is a linear fit of $\ln (|v_z(x)|/v_0)$, yielding a slope of $-0.283$

Elaborating further details of this 3D flow restructuring is beyond the present scope. With this example, we have nevertheless pointed out that the flow need not be—and in general is not—restricted to the xy plane. This should not appear particularly surprising. What is probably less obvious, however, and at this point emerges as an empirical finding, is the fact that the planar flow actually is stable for $h/b<1$ and, moreover, that for $h/b>1$ it not only becomes unstable developing a full 3D form, but eventually settles in the other plane (for which the analogously defined aspect ratio is $b/h<1$). Note again that this applies to the low-Reynolds-number regime. At higher Re, the cavity flows are known to be fully three dimensional (Shankar and Desphande 2000; Shen et al. 2015).

Consequently, the solutions of the 2D lid-driven cavity or 2D microcavity linked to the main microfluidic channel, either analytic or numerical, cannot be applied to the realistic 3D cases without caution. Regarding the stability of the initial planar flow, only for $Re\rightarrow 0$ and $h/b<1$ this is not problematic—but the 2D problem is certainly not a good approximation in this case. Comparing the flow separatrix position for $h/b>1$ with the position from the 2D simulation, Fig. 7, we nevertheless learned that the 2D solution is meaningful at least in the first part of the microcavity, before the 3D restructuring of the flow takes place.

4 Discussion

Microcavities have been increasingly used in various microfluidic applications. Many such designs comprise a narrow entrance and a larger cavity with complex flow patterns (Luo et al. 2008; Liu et al. 2008; Stocker 2006). In contrast, the present study builds on the work by Yew et al. (2013) and simplifies the design of a rectangular diffusion chamber, which does not require additional numerical modeling. Namely, Fig. 5 shows the value of the decay constant ($1/x_0$) for a wide range of experimentally accessible aspect ratios. Interestingly, the fastest decay occurs near the threshold aspect ratio (with $1/x_0\approx 5.0/b$) and not in the limit $h/b\rightarrow 0$ (where $1/x_0=\pi /b$). Of note, an even faster decrease in the velocity can be accomplished by placing the microcavity at the T-junction of the main microchannel (Vrhovec et al. 2011). Another important advantage of the rectangular design is that the diffusion into a long rectangular microcavity can be modeled simply by a 1D diffusion equation (Vrhovec et al. 2011).

Relating our present work to the recent study by Shen et al. (2015), we point to a couple of important differences: (1) Unlike ours, their cavities are not in the long limit, (2) in their case the flow transformations are a result of increasing Reynolds number, whereas we have $Re\rightarrow 0$ at all times. In particular, their flow separation, which is due to the increasing Reynolds number, has little connection with our vortex regime, which emerges as a result of the increased aspect ratio at $Re\rightarrow 0$. The value of the decay constant 4.35/b presented by Shen et al. (2015) for $Re = 3$ is specific to the particular length and width of their cavity: $b/h=3.75$ and $a/h=2.5$ according to our notation. In our language, this cavity is not in the long limit, as $a/b=2/3$ only. Therefore, we cannot expect an exact agreement with our $Re\rightarrow 0$ value of the decay constant for the long cavity at the same aspect ratio $h/b = 0.267$, which is $1/x_0 \approx 3.75/b$ as read off from Fig. 5.

The aspect ratio of biological microcavities is often close to 1, i.e., in the vortex regime. Indeed, counter vortices have been observed in microfluidic cavities mimicking capillary sprouting (Forouzan et al. 2011). In this context, the formation of vortices may have an important consequence for the transport of nutrients into a growing blood vessel. A detailed study of mass transport into a microcavity has been performed in the vortex-free regime (Yew et al. 2013), yet our results indicate that in the vortex regime, the flow and a corresponding diffusion pattern can change in a qualitative way. For example, one can expect that in the vortex regime, the transition from advection- to diffusion-dominated transport may take place rather sharply at the flow separatrix, as a contrast to the vortex-free regime where this transition is gradual. This feature was indeed observed during diffusion of 100-nm microspheres into the microcavity in our experiments (see Supplementary Video 3), but further experimental, numerical and theoretical studies are needed to fully understand the mass transport into a microcavity in the vortex regime.

5 Conclusions

To summarize, we have studied, experimentally, numerically and theoretically the flow of a Newtonian fluid in a long dead-end microcavity extending perpendicularly from the main microchannel. In the Stokes (low Reynolds number) limit, we systematically addressed the role of the microcavity depth and found that the flow properties depend decisively on the depth-to-width aspect ratio h/b of the microcavity cross section. The results are presented using dimensionless units and are thus directly applicable to arbitrary widths b of the microcavity and arbitrary velocities in the main microchannel, provided that the microcavity flow is in the low-Reynolds-number regime.

Complementing the results obtained by Yew et al. (2013), which focused on the vortex-free regime, and the results obtained by Shen et al. (2015), which focused primarily on flow separation due to increased Reynolds number, we have shown that already at low Reynolds number there exist two qualitatively distinct flow configurations, i.e., the vortex and vortex-free regimes, separated by a well-defined aspect ratio threshold at $(h/b)_c\approx 0.51$. Below this threshold, in the vortex-free regime, the flow velocity decays exponentially away from the cavity entrance, with a decay length that scales linearly with the cavity width and also depends on the aspect ratio. Above this threshold, in the vortex regime, a series of counter-flow vortices emerge in the long microcavity. The first of these vortices can be readily achieved experimentally. The existence and the position of the flow separatrix between the primary flow and the first counter vortex depend solely on the cross section aspect ratio which is an important finding for microcavity design.

Appendix

An incompressible flow $\mathbf{v}(\mathbf{r})$ in the absence of external forces is described by the continuity and Navier–Stokes equations

$$\begin{aligned} \nabla \cdot \mathbf{v}= 0, \end{aligned}$$

(3)

$$\begin{aligned} \rho \left[ {\partial \mathbf{v}\over \partial t}+(\mathbf{v}\cdot \nabla )\mathbf{v}\right]= & {} -\nabla p + \eta \nabla ^2 \mathbf{v}, \end{aligned}$$

(4)

where p is the pressure and $\eta$ is the dynamic viscosity of the fluid. The continuity Eq. (3) can be satisfied by means of a velocity vector potential ${\varvec{\Psi }}$,

$$\begin{aligned} \mathbf{v}=\nabla \times {\varvec{\Psi }}. \end{aligned}$$

(5)

Taking the curl of Eq. (4) eliminates the pressure and results in the vorticity equation,

$$\begin{aligned} \rho \left[ {\partial {{\varvec{\omega }}}\over {\partial } t}+(\mathbf{v}\cdot \nabla ){{\varvec{\omega }}}\right] = \rho ({{\varvec{\omega }}}\cdot \nabla )\mathbf{v} + \eta \nabla ^2{{\varvec{\omega }}}, \end{aligned}$$

(6)

where ${\varvec{\omega }}=\nabla \times \mathbf{v}$ is the vorticity, which is by construction connected to ${\varvec{\Psi }}$ by the Poisson equation

$$\begin{aligned} \nabla ^2{\varvec{\Psi }} = -{\varvec{\omega }}. \end{aligned}$$

(7)

Here we make the restriction to steady incompressible Stokes ($Re=0$) flow. In this case, the vorticity Eq. (6) reduces to

$$\begin{aligned} \nabla ^2{\varvec{\omega }}= 0 \end{aligned}$$

(8)

and together with Eq. (7) results in the biharmonic equation

Fig. 9

Velocity streamlines in a narrow 2D cavity: numerical solutions of the lid-driven cavity (left) and the cavity connected to the main channel (middle). Right velocity field obtained from the first term of the analytic solution for the stream function, Eq. (13)

$$\begin{aligned} \nabla ^2\nabla ^2{\varvec{\Psi }} = 0. \end{aligned}$$

(9)

1.1 Analytic solution for the 2D lid-driven cavity

Worthful analytic insight is gained by invoking the 2D lid-driven cavity (Shankar and Desphande 2000) problem. One is aware that the boundary condition at the lid ($x=0$) differs from the experimental situation in which the lid is replaced by the junction with the main channel, Fig. 9. However, this local detail should not be crucial for the form of the flow field at larger distances x further down the cavity.

Let us choose the width of the cavity b as the length unit, so that its long walls are at $y=\pm 1/2$, and let the velocity of the lid be unity. For the 2D lid-driven cavity ($h\rightarrow \infty$) where

$$\begin{aligned} \mathbf{v}(x,y) &= \nabla \times \varPsi (x,y)\hat{\mathbf{e}}_z = \left( {\partial \varPsi \over \partial y},-{\partial \varPsi \over \partial x},0\right) , \end{aligned}$$

(10)

$$\begin{aligned} {\varvec{\omega }}(x,y)= \omega (x,y)\hat{\mathbf{e}}_z, \end{aligned}$$

(11)

there exist an analytic solution (Shankar and Desphande 2000) to the biharmonic Eq. (9), now reading

$$\begin{aligned} \nabla ^2\nabla ^2\varPsi =0, \end{aligned}$$

(12)

in the form of an infinite series for the stream function:

$$\begin{aligned} \varPsi (x,y) = \mathcal{R} \left[ \sum _{n=1}^\infty a_n\, \phi _n(y)\,\mathrm{e}^{-\lambda _n x}\right] , \end{aligned}$$

(13)

where $\mathcal R$ denotes the real part and

$$\begin{aligned} \phi _n(y) = y\, \sin (\lambda _n y) - {1\over 2} \tan \left( {\lambda _n\over 2}\right) \, \cos (\lambda _n y). \end{aligned}$$

(14)

To fulfill the boundary conditions $\varPsi =0$ and $\partial \varPsi /\partial n=0$ on the side walls, the eigenvalues $\lambda _n$ must satisfy the transcendental equation $\sin \lambda _n=-\lambda _n$, the roots of which are all complex (Shankar and Desphande 2000). Let $\lambda _n$ be the roots in the first quadrant, ordered by the magnitudes of their real parts. Then $-\lambda _n$, $\bar{\lambda }_n$ and $-\bar{\lambda }_n$ are also roots. The principal eigenvalue is $\lambda _1=\lambda _1^{\prime} + \mathrm{i}\lambda _1^{\prime\prime} = 4.212 + 2.251\,\mathrm{i}$. In Eq. (13) we have taken into account that the cavity is infinitely long (hence $\lambda _n$’s with negative real parts are left out) and that the real part includes the sum of terms with $\lambda _n$ and $\bar{\lambda }_n$. The coefficients $a_n$ are then determined such that the sum in Eq. (13) satisfies the boundary conditions $\varPsi =0$ and $\partial \varPsi /\partial n=-1$ on the lid.

At sufficiently large x, the solution is dominated by the principal eigenvalue $\lambda _1$, Fig. 9 right. Disregarding the modulation due to the alternating vortices, the velocity magnitude thus drops off as $\mathrm{e}^{-\lambda _1^{\prime} x}$, i.e., with the characteristic length 1/4.212 (in units of the cavity width b). The distance between successive vortex centers is $\sim \pi /\lambda _1^{\prime\prime}\sim 1.396$ and the flow field decays by a factor $\exp (-\pi \lambda _1^{\prime}/\lambda _1^{\prime\prime})\sim 1/357$ in going from one vortex center to the next.

1.2 Large but finite ($h\ll b$)

It is illuminating to encompass the qualitative behavior of the flow configuration when departing from the 2D geometry, i.e., for a large but finite cavity depth h/b. In a minimal approach, one can start with the 2D solution, Eqs. (13) and (10),

$$\begin{aligned} \mathbf{v}_0(x,y) = \left( {\partial \varPsi \over \partial y}, -{\partial \varPsi \over \partial x}\right) , \end{aligned}$$

(15)

including in $\varPsi$ only the aforementioned leading term, and decorate it with a simple z dependence and a correction depending on x,

$$\begin{aligned} \mathbf{v}(x,y,z) = \mathbf{v}_0(x,y)\, \mathrm{e}^{-\Delta \lambda \, x}\, \sin (\pi z/h), \end{aligned}$$

(16)

where the complex number $\Delta \lambda \equiv \Delta \lambda '+ \mathrm{i}\Delta \lambda ''$ is the correction to be determined. The length unit is b as in the previous section. The velocity field Eq. (16) is of course not a solution of Eq. (8), but one can minimize the norm of the deviation of $\nabla ^2{\varvec{\omega }}$ from zero,

$$\begin{aligned} {\partial \over \partial \Delta \lambda }\int \!\! \mathrm{d}x\mathrm{d}y \left| \nabla ^2\, \nabla \times \mathbf{v}\right| ^2 = 0, \end{aligned}$$

(17)

and therefrom determine the correction $\Delta \lambda$. Here $\Delta \lambda '$ represents the correction of the decay rate in the x direction with respect to the 2D solution, while $\Delta \lambda ''$ represents the correction of the wave vector, i.e., a shift of the positions of separatrices and vortex centers with respect to the 2D solution. The dependence of both corrections on h is presented in Fig. 10.

Fig. 10

The corrections $\Delta \lambda '$ and $\Delta \lambda ''$ as functions of the cavity depth h, representing the x-profile deviation of the 3D trial configuration from the 2D solution. With decreasing h/b, the decay exponent $\Delta \lambda '$ increases and the wavenumber $\Delta \lambda ''$ decreases. The latter shifts the flow separatrices to larger x

The exact functional dependence of $\Delta \lambda '(x)$ and $\Delta \lambda ''(x)$ is insignificant as it is subject to the choice of the trial function in Eq. (16). What is relevant, however, is the qualitative result: When the cavity depth decreases, the velocity decay length decreases, while the x coordinate, $s_1$, of the flow separatrix increases. Both dependences are consistent with the simulation results presented in Figs. 5, 6 and 7.

1.3 Shallow cavity limit ($h\ll b$)

Here we describe a cavity of finite depth much smaller than its width, $h\ll b$ (small microcavity aspect ratio). In this shallow limit, no counter vortex is formed down the cavity. The cavity is defined by $-b/2 < y < b/2$, $0 < z < h$, and $x>0$. The velocity lies in the xy plane.

Suggested by numeric simulations, there exist two regions with distinct flow attenuation profiles along x. In the vicinity of the lid, i.e., at distances small compared to b, the velocity decreases with a characteristic length defined by h. At larger x, however, despite the fact that the fluid is severely confined in the z direction, the characteristic decay length is defined by b, not by h as we will see, and this is dictated by the continuity requirement.

1.3.1 Near flow ($x\ll b$)

Next to the lid, at $x\ll b$, the flow can be approximated by shear, $\mathbf{v}=v(x,z)\,\hat{\mathbf{e}}_y$, for which the continuity condition is satisfied by construction and the Stokes equation reduces to

$$\begin{aligned} \nabla ^2 v = 0. \end{aligned}$$

(18)

The solution is:

$$\begin{aligned} v(x,z) = \sum _{n=1} v_n\, \sin (k_n z)\, \mathrm{e}^{-k_n x},\quad k_n = n\pi /h. \end{aligned}$$

(19)

The leading contribution ($n=1$) thus decays with the characteristic length $h/\pi$.

1.3.2 Far flow ($x\gg b$)

At $x\gg b$, one has to deal with both the continuity Eq. (3),

$$\begin{aligned} {\partial v_x\over \partial x} + {\partial v_y\over \partial y} = 0, \end{aligned}$$

(20)

and the vorticity Eq. (8), which now takes the form

$$\begin{aligned} \nabla ^2\left( -{\partial v_y\over \partial z},{\partial v_x\over \partial z},{\partial v_y\over \partial x}-{\partial v_x\over \partial y}\right) = 0. \end{aligned}$$

(21)

The Ansatz with a plausible y dependence of the velocity components, disregarding the no-slip boundary condition at $y=\pm b/2$ (which is not significant in the shallow limit because $v_x$ drops to 0 no sooner than only in a thin boundary layer $\sim h$),

$$\begin{aligned} v_x= A\,f(z) \sin (k_y y)\, \mathrm{e}^{-\lambda x},\nonumber \\ v_y= B\,f(z) \cos (k_y y)\, \mathrm{e}^{-\lambda x}, \end{aligned}$$

(22)

respects the continuity, Eq. (20), under the condition

$$\begin{aligned} \lambda A + k_y B = 0. \end{aligned}$$

(23)

In the shallow cavity limit, we neglect the xy part of the Laplacian in Eq. (21),

$$\begin{aligned} \nabla ^2 \approx {\partial ^2\over \partial z^2}, \end{aligned}$$

(24)

obtaining

$$\begin{aligned} \left( -{\partial ^3 v_y\over \partial z^3},{\partial ^3 v_x\over \partial z^3},{\partial ^2\over \partial z^2}\left[ {\partial v_y\over \partial x}-{\partial v_x\over \partial y}\right] \right) = 0. \end{aligned}$$

(25)

The first two components of Eq. (25) define the parabolic z profile of both velocity components, $f(z) = z(h-z)$. Taking this into account in the third component of Eq. (25), it then follows that

$$\begin{aligned} {\partial v_y\over \partial x}-{\partial v_x\over \partial y} = 0, \end{aligned}$$

(26)

which is also fulfilled by the Ansatz Eq. (22), provided that

$$\begin{aligned} \lambda B + k_y A = 0. \end{aligned}$$

(27)

The conditions Eqs. (23) and (27) furnish the solution

$$\begin{aligned} \lambda = \pm k_y,\quad B = \mp A. \end{aligned}$$

(28)

Satisfying the boundary condition dictated by the incompressibility, i.e., $v_y=0$ for $y=\pm b/2$, we require

$$\begin{aligned} k_y={(2n-1)\pi \over b},\quad n=1, 2, 3 ... \end{aligned}$$

(29)

Hence, the leading contribution ($n=1$) in the infinitely long cavity is

$$\begin{aligned} v_x= A\, z(h-z)\sin (k_y y)\, \mathrm{e}^{-k_y x},\nonumber \\ v_y= -A\, z(h-z)\cos (k_y y)\, \mathrm{e}^{-k_y x}, \end{aligned}$$

(30)

with $k_y=\pi /b$. In the shallow cavity limit, the characteristic decay length of the velocity magnitude in the far flow region is thus $b/\pi$.