1 Introduction

Flow separation and internal recirculation at low Reynolds numbers are well-known properties of cavity flows (Shankar and Deshpande 2000). In classic examples at the creeping flow regime where the Reynolds number is much smaller than unity (Re ≪ 1), slow internal recirculation is driven by the translation of one or more of the containing walls for closed cavities (Leong and Ottino 1989; Shankar 1993, 1997; Patil et al. 2006) or by a shear flow over the cavity’s mouth for open configurations (O’Brien 1972; Higdon 1985; Shen and Floryan 1985). Other mechanisms leading to recirculation include rotating a cylinder inside a cavity (Hellou and Coutanceau 1992), as well as the action of surface tension gradients (Rashidnia and Balasubramaniam 1991; Sznitman and Rösgen 2010) and acoustic streaming (Sznitman and Rösgen 2008).

Historically, cavity flows have been extensively characterized using analytic and numerical methods. In a seminal work, Moffatt (1964) predicted analytically a series of 2D counter-rotating eddies for Stokes flow in sharp corners. The study of separated flows was later expanded to a variety of 2D and 3D geometries. For example, O’Neill (1977) studied numerically flows in a cylindrical cavity or protrusion in a plane, and O’Brien (1972) investigated recirculating 2D flows in a rectangular cavity. For 3D flows in spherical cavities, Pozrikidis (1994) showed numerically the existence of recirculation with open streamlines that spiral into singular points. More recently, Heaton provided a detailed quantification in 2D rectangular-driven cavities for the number of eddies and the shape of the corresponding streamlines as a function of the rectangle’s aspect ratio (Heaton 2008). In all the aforementioned theoretical and numeric studies, the topologies of separated recirculating cavity flows were shown to be determined by details of the geometry.

To the best of the authors’ knowledge, the first experimental evidence for Stokes flow detachment phenomenon was reported in the pioneering visualizations of Taneda (1979) for geometries including wedge-shaped and rectangular cavities, as well as cylindrical ridges and other geometries. One intriguing aspect of low-Reynolds-number cavity flows is the development of a principal vortex coalescing from two side vortices as the geometry of the cavity changes. With further geometric alterations, the vortex then proceeds through a series of intermediate steps including “cat’s eye” three-vortex structures; this latter configuration is constructed of two vortices with a saddle point located between them and surrounded by a third vortex. Cat’s eye vortex structures have been observed in analytic and computational studies in 2D rectangular cavities (Shankar 1993; Patil et al. 2006; Shen and Floryan 1985) and in a cylindrical container featuring a moving end-wall (Shankar 1997). In contrast, a cat’s eye structure has only been qualitatively observed in large-scale experiments for flow in a rectangular tank induced by a rotating cylinder (Hellou and Coutanceau 1992). Despite some experimental evidence of their existence in the viscous regime, the full range of existing vortex configurations (e.g., number, structure, etc.) and their evolution are yet to be experimentally resolved as a function of geometry and Reynolds number.

With the advent of microfluidic devices operating at low Reynolds numbers (typically in the range of Re = 0.1–100), cavity flows have gained renewed attention because of the numerous applications of microvortices in microfluidic devices (Lim et al. 2003; Stocker 2006; Shelby et al. 2003; Zeta Tak For and Lee 2005). In particular, lab-on-a-chip assays make increasing use of microvortices and microcentrifuges for cellular and particle manipulations (Chiu 2007; Shelby and Chiu 2004; Shelby et al. 2004), high-throughput sorting (Mach et al. 2011; Hur and Mach 2011), and cell docking solutions using microwells (Cioffi et al. 2010; Khabiry et al. 2009). Yet, to successfully design devices featuring microcavities, it is preferable to implement well-defined geometries where flow phenomena are characterized thoroughly and selected beforehand. Among the existing choices of microfluidic geometries, the use of a box-shaped microcavity was investigated in depth by Zeta Tak For and Lee (2005). This setup, however, is often not ideal for lab-on-chip applications: at low Re, a vortex only forms when the channel depth is large enough compared with the cavity dimensions; conversely, an asymmetric vortex is observed at relatively high Re. As a result, alternative geometries have been advocated to realize better control flow recirculation with the use of diamond-shaped cavities (Lim et al. 2003; Shelby et al. 2003) and rectangular-shaped cavities featuring a partially closed opening (Stocker 2006). Despite such progress, there is a dearth of experimental quantitative assessments characterizing in detail cavity microrecirculation (e.g., velocity fields, predetermined flow pattern as a function of geometry and quantitative data comparing flow velocity in the channel to velocities, as well as recirculation frequencies, inside the cavity). Such knowledge would constitute a first step toward providing precise and comprehensive guidelines for designing microcavities in microfluidic applications.

In the present study, we investigate microscale cavity flow phenomena using a microfluidic screening platform featuring rectangular channels with cylindrical cavities. This simple geometry is closely related to the aforementioned configurations (Lim et al. 2003; Stocker 2006; Shelby et al. 2003) and is characterized by few geometric parameters; moreover, this geometry can easily be realized with standard soft-lithography microfabrication techniques (Duffy et al. 1998). Based on particle image velocimetry (PIV) measurements, supported by computational fluid dynamics (CFD) simulations, we provide a detailed quantitative mapping of the entire range of vortex configurations that exist within recirculating cavity flows, including side pairs of vortices and “cat’s eye” flow structures. In an effort to help lab-on-chip users in the cavity design and selection process, results are concisely presented using phase diagrams of the corresponding flow regimes (i.e., attached flow, single vortex, multivortex systems). These phase maps can be used, for example, to choose geometries that yield a single vortex and avoid attached or multivortex flow structures as desired for cell separation (Mach et al. 2011) or centrifuging (Shelby et al. 2004). To give further practical information for design of single microvortex applications, we characterize rotational frequencies of the ensuing recirculating flows as a function of Re and geometric parameters. While past attempts have highlighted some aspects of low-Re cavity flows (Khabiry et al. 2009; Leneweit and Auerbach 1999; Iwatsu et al. 1989), the scope of such studies has been generally limited to only a few representative geometries, without providing a complete roadmap for microcavity selection. Our microfluidic platform enables a rapid and systematic screening of recirculating cavity flow phenomena for design guidelines of microfluidic-based microcentrifuges and vortex mixers.

2 Methods

2.1 Geometry

A simple geometry consisting of a rectangular duct with cylindrical cavities located symmetrically on each side is chosen as the base cavity unit since it is a well-defined, vortex-promoting geometry. Figure 1a shows schematically half of the full geometry, which is symmetric along the x–z midplane. For low-Reynolds-number flows in cavities approaching the creeping regime, flows about this midplane are known to be symmetric (Leneweit and Auerbach 1999). Streamline patterns in an asymmetric geometry, where a cavity exits only on one side of the channel, yield negligible differences from a symmetric case, as verified from CFD simulations (see Fig. S1 in the Supplementary Material). Figure 1 illustrates the geometric parameters, describing the shape of the duct and cavity, which include the rectangular duct width (w), the cavity radius (r), the cavity extrusion length (ε), and the cavity height (h). The cavity’s geometry is captured by two dimensionless parameters: r/h establishes the cavity’s aspect ratio, while ε/r describes the relative extrusion of the cavity. Note that both the cavity and the main duct share the same height, h, and the opening angle (α) of the cavity mouth is directly related to ε and r (i.e., α = 2cos−1(ε/r)). Here, a negative value of ε implies that the center of the cavity is located inside the channel. For simplicity, the channel aspect ratio (w/h) was kept constant for all experiments at w/h = 3.

Fig. 1
figure 1

Schematic of model geometry unit featuring a cylindrical cavity on a rectangular duct. The gray region indicates the fluid domain. Geometric parameters include the rectangular duct width (w), the cavity radius (r), the cavity extrusion (ε), and the cavity (and duct) height (h). a, b Illustrate the range of computational geometries investigated. Geometry (a) shows half of the full geometry and the symmetry plane (dotted line indicating the x–z midplane of the full geometry) with r/h = 1.89, and ε/r = 0.995. (b) Close-up view of a cavity with r/h = 0.2, and ε/r = –0.08. The red circle indicates the curved intersection between cylinder and duct

Full size image

2.2 Microfluidic screening device

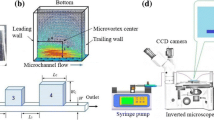
Microfluidic devices are fabricated in poly(dimethylsiloxane) (PDMS) using standard soft-lithography techniques (Duffy et al. 1998) (Fig. 2a). Our screening device is composed of eight separate horizontal channels (each with an inlet and outlet) with a fixed width-to-height ratio (as noted above), where the channel height is h = 133.8 ± 1.4 μm and the channel width is w = 401.5 ± 2.5 μm, based on imaging the channel cross section. Each channel is lined on both sides with a series of cavities characterized by a fixed radius, and a linear increase of ε spanning left to right. Intervals of ε were designed as small as possible given the microfabrication method (see Fig. 2a and Fig. S2 in the Supplementary Material). The symmetry of the geometry along the x–z midplane allows a convenient means to repeat the examination of a given cavity geometry by simply moving the field of view to the opposite side of the channel. With this setup, we effectively devise a screening matrix covering the following range of dimensionless parameters: r/h = 0.47–1.89 and ε/r = 0.33–0.98, as measured from microscopy. Note that the intersection between the cylinder and duct at the opening of a cavity has a finite curvature defined through the microfabrication process (marked by a red circle in the schematic of Fig. 1b). Namely, we measured this radius of curvature to be approximately 4 μm (0.03 h) and used this value in all our CFD simulations (see below).

Fig. 2
figure 2

a Snapshot of the microfluidic screening device. Scale bar 1 mm. b Streamline visualization of steady flow based on digital averaging over a sequence of 200 images acquired at 50 Hz (Re = 0.1, r/h = 1.14, ε/r = 0.967). Scale bar 60 μm. c Corresponding PIV velocity map. Scale bar 60 μm

Full size image

In total, the screening device features 752 individual cavities across the eight channels, where each channel is symmetric about the x–z midplane (compare Figs. 1a, 2a). To insure negligible flow interactions between neighboring cavities, the axial cavity-to-cavity separation distance was kept at a fixed value of 4r (>250 μm), well above the maximum entrance length (L e ), estimated in our study at ~202 μm for Re = 10, based on the empirical correlation for low-Reynolds-number channel flow (Shah and London 1978), where L e /D h  ~ 0.6/(1 + 0.035Re) + 0.056Re, and D h  = 201 μm is the hydraulic diameter of the duct. Here, the Reynolds number is defined as Re = ŪD h /ν, where Ū is the average velocity in the main duct, and ν is the kinematic viscosity of the fluid.

2.3 Quantitative PIV measurements

Quantitative flow visualizations inside the microfluidic device were performed using a suspension of polystyrene red fluorescent beads (d = 0.86 μm, Thermo Scientific) at three different flow conditions corresponding to Reynolds numbers of 0.1, 1 or 10. Deionised water was used as the suspending liquid for Re = 1 and Re = 10, while a 60 % (v/v) glycerol solution in water was used for Re = 0.1. In each experiment the suspension was flown through one channel at a steady flow rate (Q) using a syringe pump (PHD Ultra, Harvard Apparatus). To insure steadiness of the flow, the stream was allowed to stabilize before initiating measurements. Image sequences of the flow were visualized using a commercial microparticle image velocimetry (μPIV) system (Flow Master MITAS, LaVision GmbH) consisting of a high-speed CMOS camera (1024 × 1024 pixels), a continuous wave (CW) diode-pumped solid-state (DPSS) laser (wavelength: 532 nm, power: 2.26 W), and a custom inverted microscope with spatial resolutions ranging from 1.8 μm (10X) down to 0.5 μm (40X), depending on the specific cavity size interrogated. Experimental PIV data are depth-averaged over the effective depth of correlation, ranging from 28.7 μm (10X) to 7.7 μm (40X) using a standard analytic solution (Olsen and Adrian 2000); experimental results are to be contrasted with CFD simulations where 2D flow fields are directly extracted from the x–y midplane (described below).

For each experiment, a series of 1,000 consecutive frames were acquired at a constant rate of 50 frames per second (fps) with an exposure time of 0.02 s. For steady-state flows, 2D velocity fields were obtained using a PIV sum-of-correlation algorithm (Meinhart et al. 2000). Specifically, the vector field was iteratively calculated with two passes using a 64 × 64 pixel interrogation window with 50 % window overlap, followed by two passes using a 32 × 32 pixel interrogation window with a 75 % window overlap. The first three passes were calculated using round-Gaussian weighted interrogation windows, while the last pass implemented an adaptive interrogation window scheme (Wieneke 2010). Figure 2b shows an example of a digitally averaged image sequence of a single vortex in a cavity providing a qualitative visualization of the streamline pattern for a recirculating cavity flow; the corresponding 2D velocity vector map obtained from PIV is depicted in Fig. 2c.

To quantitatively locate steady vortex centers and saddle points, points of zero velocity were extracted from the 2D velocity fields (see for example Iwatsu et al. 1989) and tracked as a function of dimensionless geometric (i.e., r/h and ε/r) and flow (i.e., Re) parameters. Here, the average velocity in the main duct (Ū) was calculated according to the steady flow rate (Q) supplied by the syringe pump and the measured duct dimensions.

2.4 Numerical procedure

Numerical solutions of the steady-state 3D flow field were obtained via finite-element simulations of the incompressible form of the Navier–Stokes equations performed using a commercially available software (COMSOL Multiphysics, version 4.1). Simulations were conducted for a duct and cavity geometry (Fig. 1), where a constant velocity profile was imposed at the domain inlet (in the x direction) and a constant pressure of 100,000 Pa was arbitrarily set at the domain outlet. The symmetry along the x–z midplane (Figs. 1, 2a) allows a reduction in computational time by performing simulations over a computational domain corresponding to half of the physical domain. Namely, only the part of the geometry residing on one side of the symmetry plane (the x–z midplane of the full geometry, as indicated in Fig. 1a) was simulated. To insure that the simulations represent realistically the physics in half of the physical domain, a slip condition was imposed along the boundary coinciding with the symmetry plane. Here, the Reynolds number estimated in simulations is defined based on the velocity imposed at the inlet for the corresponding hydraulic diameter of the duct. As noted earlier, the maximal entrance length in our study is approximately 202 μm for Re = 10, and therefore the simulated duct length upstream of the cavity was always kept above 360 μm to insure fully developed flow conditions. The range of simulated geometries is illustrated in Fig. 1.

Tetrahedral mesh elements were used to mesh the domain, and mesh refinement studies were performed to insure that flow solutions are grid independent and converged. Namely, the maximum element size inside the cavity was reduced by 20 % below that which was eventually used. The following geometries were tested: r/h = 1.89, ε/r = 0.935; r/h = 0.771, ε/r = 0.6; r/h = 0.614, ε/r = 0.47; r/h = 0.2, ε/r = −0.05. Ultimately, the chosen mesh size inside the cavity was chosen to be 1/60 of the cavity diameter for cases where r/h = 0.771–1.889, and 1/45 of the cavity diameter for cases where r/h = 0.2–0.614. The final computational domains consisted of 1.3 × 106 to 2.2 × 106 mesh elements depending on the geometry simulated. Simulations over these domains guaranteed sufficiently accurate results such that changes in both the average flow velocity magnitude and average shear rate over the cavity mouth opening were within 1 % upon further mesh refinement. In addition, changes in the tracked coordinates of vortex centers and saddle points were within 0.5 % of r upon further mesh refinement. All numerical solutions were found to converge with residuals below 10−7.

3 Results and discussion

3.1 Cavity flow structures

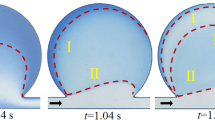
Examples of velocity maps for PIV experiments and CFD simulations are shown in Fig. 3. Streamline plots are overlaid with the color-coded, normalized velocity magnitude |u|/Ū, where |u| is the 2D velocity magnitude defined as |u| = (u x  + u y )1/2. For all plots shown here, supporting CFD data are presented for the x- and y-velocity components, extracted at the x–y midplane (Fig. 1). Results shown in Fig. 3 correspond to the most disk-like geometry investigated (r/h = 1.89) at Re = 0.1 for several values of ε/r (increasing from left to right). Note that PIV data are truncated close to the cavity mouth since large differences in flow velocities did not allow us to resolve simultaneously the flow across the entire geometry (i.e., duct and cavity) using the same acquisition frame rate. As ε/r increases, we observe that the flow pattern changes from attached flow (Fig. 3a, e) to a two-vortex configuration (Fig. 3b, f), followed by a “cat’s eye” three-vortex system (Fig. 3c, g), and finally evolving into a single vortex structure (Fig. 3d, h). In general, we find strong agreement, both qualitative and quantitative, between experimental and numerical velocity maps. Note that small changes in ε/r profoundly affect the resulting flow pattern, while the separatrix (Horner et al. 2002) (i.e., the separation line, or surface, between the ductal and cavity flow) approaches concurrently the cavity mouth for increasing values of ε/r. In previous studies (Shankar 1993, 1997; O’Brien 1972), the side vortices were reported to appear first in the corners of the cavity opposing the location of the mouth (or moving wall for a closed cavity). However, we observe here that they first arise close to the cavity mouth. The side vortices seen in our experiments are also unique in the sense that their formation is shown to be dependent on the cavity aspect ratio (r/h). As discussed below (Figs. 6 and S2, see Supplementary Material), side vortices are absent at low values of r/h (these values correspond to more tube-like geometries as schematically shown in Fig. 1b), effectively approaching the theoretical 2D case. Indeed, our observations are in agreement with the fact that a single, main vortex is observed for 2D viscous flow over a cylindrical cavity (Higdon 1985; O’Neill 1977). The three-vortex structure (Fig. 3c, g) comprises two adjacent vortices that rotate in the same direction, giving rise to a saddle point (or stagnation point) between them, where the “cat’s eye” configuration is completed with a third vortex that surrounds the two adjacent vortices. In contrast to previous studies for rectangular cavities (Shankar 1993, 1997; Patil et al. 2006) where the centers of the vortices and the saddle point are positioned closely along an imaginary line, here they are observed to form a triangular-like configuration covering the entire cavity geometry.

Fig. 3
figure 3

Normalized velocity magnitude and corresponding streamlines for PIV experiments (top row) and CFD simulations (bottom row). Values of ε/r increase from left to right (experiments: ε/r = 0.905, 0.937, 0.953, and 0.977; simulations: ε/r = 0.86, 0.92, 0.935, and 0.965). For all cases, r/h = 1.89 and Re = 0.1, and ductal flow is from left to right. With increasing ε/r, the cavity flow evolves from being attached (left) to exhibiting two side vortices that eventually give rise to a “cat’s eye” configuration, before coalescing into a single vortex (right)

Full size image
Fig. 4
figure 4

Normalized velocity magnitude and corresponding streamlines for PIV experiments (top row) and CFD simulations (bottom row) at r/h = 1.14. Results are shown for PIV at ε/r = 0.847 and for CFD at ε/r = 0.805

Full size image

Figure 4 shows a three-vortex configuration at r/h = 1.14 (i.e., a more tube-like geometry compared with Fig. 3), for different values of Re. Although flow patterns are very similar at both Re = 0.1 and Re = 1, a small inertial effect is nevertheless observed at Re = 1, resulting in a slight asymmetry in the adjacent vortices coupled with a downstream shift in the location of the saddle point. This effect is somewhat more pronounced in the simulations (Fig. 4d–f) compared with PIV results (Fig. 4a–c). Such discrepancies are thought to result from small imperfections in the fabrication process of the microcavity geometries leading to shifts in the exact location of the saddle point. A much larger inertial effect is observed at Re = 10, resulting in the disappearance of the three-vortex structure and instead the formation of a single asymmetric vortex shifted upstream (Fig. 4c, f).

Fig. 5
figure 5

1D velocity profiles for three combinations of flow and geometric parameters. Left column: r/h = 1.14, ε/r (CFD) = 0.945, ε/r (PIV) = 0.967 and Re = 0.1, middle column: r/h = 1.889, ε/r (CFD) = 0.945, ε/r (PIV) = 0.953 and Re = 1, right column: r/h = 1.51, ε/r (CFD) = 0.920, ε/r (PIV) = 0.949 and Re = 10. In the top row, u y /Ū is plotted along a line in the x-direction lying in the x–y mid-plane (indicated by a bold line in the inset). In the bottom row, u x /Ū is plotted along a line in the y-direction. The origin of the coordinate system coincides with the center location of the cavity

Full size image

A thorough understanding of how recirculatory flow structures are affected by geometry and flow conditions can be achieved by tracking the precise location of vortex centers and saddle points. Such quantitative characterization at the microscale is achieved at unprecedented detail using our microfluidic screening device. Namely, we present concise maps of the locations of vortex centers and saddle points over the range of geometric parameters and Reynolds numbers investigated (see Fig. S3 in the Supplementary material). While our discussion of flow structures is largely restricted to 2D projections of the flow at the x–y midplane (see Figs. 3, 4), streamlines away from this midplane may feature interesting 3D characteristics, as previously reported (Shankar 1997; Iwatsu et al. 1989). In particular, flows inside cavities may exhibit the formation of open streamlines that spiral into singular points, a property known to exist in 3D cavities but absent in 2D configurations (Shen and Floryan 1985; Tobak and Peake 1982). In contrast, our experimental PIV results do not capture the 3D features of the flow (and may further account for some of the discrepancies observed with simulations). However, our CFD simulations resolve such localized 3D flow phenomena (see discussion in the Supplementary Material and Fig. S4), in particular for cavities with a relatively tube-like geometry (e.g., r/h = 0.468) and an extrusion parameter just above the minimum identified for flow recirculation (ε/r = 0.33).

Finally, to quantify the relationship between velocity magnitudes in ducts and cavities, respectively, we extract 1D velocity profiles from PIV and CFD results for three characteristic cases: a single symmetric vortex at Re = 0.1 (Fig. 5a, d); a three-vortex system at Re = 1 (Fig. 5b, e); and a single asymmetric vortex at Re = 10 (Fig. 5c, f). For each of these cases, the normalized velocity component u x /Ū is plotted along a line in the y-direction crossing through the cavity center (Fig. 5d–f) while u y /Ū is plotted along a line in the x-direction crossing through the vortex (or vortices) center(s) at the x–y midplane (Fig. 5a–c). We observe that u x /Ū decreases dramatically inside the cavity and reverses its sign at a given location (i.e., at the vortex center or saddle point for symmetric flows). For the single vortex structure, reversed flow is usually found to be two orders of magnitude slower than in the main duct (Fig. 5d); for a three-vortex configuration reversed flow velocity is decreased by yet another order of magnitude as observed in Figs. 3c, g and 5e. This phenomenon can be qualitatively understood from considering mass conservation inside the cavities. Namely, streamlines crossing the y-axis between the saddle point and the cavity wall in the three-vortex configuration (Fig. 3c, g) originate from a small cross section located between the right vortex and the cavity wall. In contrast, the corresponding streamlines in the single vortex configuration (Fig. 3h) originate from a relatively wider cross section providing effectively a larger mass flow rate.

Fig. 6
figure 6

Phase diagrams of the cavity flow regimes. Flow configurations are plotted as a function of geometric parameters (r/h and ε/r) for different values of Re (0.1, 1, and 10). Color-coding represents areas obtained from CFD, while data points delineate the geometries near the phase transitions resolved experimentally

Full size image

Velocities obtained from PIV measurements are generally found to be slightly slower compared with CFD results, but the agreement remains close in particular inside the cavity domains. The most significant differences are observed in the main duct, with a factor up to approximately two (i.e., the maximum is observed in Fig. 5f, e, in the vicinity of y/r = −0.5). These discrepancies are thought to be because of inaccuracy in evaluating the mean velocity in the main channel based on the flow rate and measurements of the duct dimensions and because of the relatively large depth of field in our system. Accordingly, the average velocities in a straight channel obtained by PIV are 22, 24, and 37 % smaller for Re = 0.1, 1, and 10, respectively, compared to the average velocity in the midplane for the corresponding simulations.

3.2 Flow regimes

To establish a useful microfluidic design roadmap for microfluidic users, we map the different flow configurations as a function of geometric parameters (Khabiry et al. 2009). Figure 6 depicts such phase-diagrams for both PIV and CFD results at Re = 0.1, 1, and 10, respectively. For CFD results, the range of geometries giving rise to the different flow patterns are shown as colored regions of the map, while PIV results are depicted by data points corresponding to the geometries identified as closest to the phase transition lines. In general, Fig. 6 shows good agreement between PIV and CFD results, with a close overlap between the delimiting regions of flow regime transitions. Note that the identification of a vortex is contingent on the spatial resolution; this parameter is defined for PIV by the interrogation window size and overlap, and for CFD by the mesh density. We thus chose arbitrarily to define an incipient vortex (i.e., the first appearance of a vortex) as a flow configuration in which the distance between the vortex center and the cavity wall is greater than 10 % of the cavity radius; this definition falls well within the spatial resolution of both experiments and simulations.

From the phase diagrams (Fig. 6), it emerges that detached flows are restricted to geometries with either low r/h (i.e., tube-like geometries) or high ε/r (i.e., large cavity extrusion). In addition, for large values of r/h, the cavity geometry giving rise to an incipient vortex corresponds to high values of ε/r. Hence, to observe detached flow in shallow disk-like geometries, it is necessary to increase the relative cavity extrusion. In contrast, detached flow in cavities with small extrusion lengths is only observed for deeper, tube-like geometries. It is also apparent that the two- and three-vortex configurations are formed only across a narrow gap of geometric parameters. We note that the phase diagram does not change appreciably between Re = 0.1 and Re = 1. At Re = 10, however, incipient vortices are observed at comparatively much lower values of ε/r. Using Fig. 6, one may now identify the regimes where the evolution of a vortex follows the flow patterns initially presented in Fig. 3 (i.e., sequence of attached flow, 2 vortices, 3 vortices, and single vortex, as ε/r increases at Re = 0.1 and 1, for r/h > 0.77), and regions where a direct transition from attached flow to a three-vortex system is observed (Re = 0.1 and 1 with r/h < 0.77, and Re = 10 for all values of r/h). For Re = 10, however, our numerical simulations suggest the existence of a previously unreported phenomenon, where at r/h ≥ 1.5, a gradual increase in ε/r leads from attached flow to a single vortex, followed by three-vortices, and then back to a single vortex. Indeed, this phase transition is not observed in the absence of finite inertial effects. Our PIV results support this phenomenon observed in the CFD simulations. Given limitations in the microfabrication process, however, this phenomenon is only identified experimentally for a single configuration (see Re = 10, r/h = 1.89, ε/r = 0.929 in Fig. 6 and Fig. S3g in the Supplementary Material).

3.3 Rotation frequency

The rotation frequency (e.g., of particles, cells, etc.) inside a cavity is often an important factor in the design of microfluidic applications (Shelby et al. 2003; Shelby and Chiu 2004). Few, if any, data are readily available to select the appropriate frequencies sought in a lab-on-a-chip assay featuring microcavities. Here, we attempt to provide some quantitative insight into cavity rotation and investigate the effects of geometry and flow conditions on the rotation frequency by analyzing PIV velocity maps and the corresponding CFD results extracted at the x–y midplane. A second order Runge–Kutta integration scheme is used to calculate the recirculation time (T) defined as the time required for a fluid particle to complete a full cycle around the vortex center after being released at a distance of 0.075 h (10 μm in this case) in the y-direction from a vortex center. Here, we define the dimensionless rotation frequency as f* = 2πr/(ŪT); this parameter can be interpreted as the ratio of the particle rotation frequency near the vortex center to the rotation frequency of a cylinder of radius r rotating with maximal tangential velocity Ū. Specifically, we chose to define f* at 10 μm (or 0.075 h) from the vortex center since this length falls in the typical size range of cells (or large particles) used in microfluidic applications. In addition, this characteristic length is in most cases close enough to the cavity center, where the maximal rotation frequency is approached (see Fig. S5 in the Supplementary Material), but is still sufficiently large as to avoid inaccuracies due to the finite resolution of CFD simulations (i.e., mesh element size) and PIV (i.e., interrogation window size), respectively. Note that for Re = 10, T corresponds to twice the time required for completing half a cycle, since the streamlines quickly spiral outward (see Fig. 3), while the time required for completing a full cycle along a streamline does not reflect realistically the characteristic time for rotation near the vortex center.

Figure 7 shows the variation of f* with extrusion length (ε/r) for a selection of fixed values of the ratio r/h. Overall, we find that experimental data follow the same trends seen in the CFD results, yet these exhibit generally lower rotation frequencies compared with simulations as a result of the lower measured velocities. Note that only single vortex structures are considered here; such recirculating flows are frequently sought in microfluidic applications including microcentrifuges (Lim et al. 2003; Stocker 2006; Shelby et al. 2003, 2004; Zeta Tak For and Lee 2005; Chiu 2007; Shelby and Chiu 2004; Mach et al. 2011; Hur et al. 2011; Cioffi et al. 2010; Khabiry et al. 2009) Accordingly, only values of ε/r that are high enough to yield a single vortex are considered. Within this range of single vortices, the non-dimensional rotation frequency observed is almost identical for Re = 0.1 and Re = 1 (Fig. 7a), suggesting a negligible Re effect at low Reynolds number. Namely, the magnitude of f* increases monotonically, illustrating an exponential-like profile at low ε/r and a more linear one at higher ε/r; the slope of these curves increases with higher r/h values. Note that curves for f* span a wider range of ε/r values for a smaller r/h since recirculation is initiated for smaller ε/r under such configurations. However, f* approaches a maximum value of approximately 0.15 in the limit of ε/r = 1 for all the presented values of r/h. For Re = 10 (Fig. 7b), a local maximum or an inflection point is apparent at an intermediate ε/r value (~0.6–0.9, depending on the chosen value of r/h). This behavior is correlated to the identified locations of the vortex center (Fig. S3 g–i in the Supplementary Material), with higher values of y/r corresponding to relatively lower rotation frequencies. Nevertheless, curves illustrate an increasing trend in the magnitude of f* with larger ε/r, ultimately reaching a peak of f* = 0.12–0.13 at ε/r = 1. This result is similar to the phenomenon observed at Re = 0.1 and 1 (Fig. 7a), and emphasizes again the slow rotation speeds inside cavities. Hence, our results indicate that in the design of microcavities where a maximum rotation frequency is desired, a high value of the relative cavity extrusion should always be adopted (i.e., ε/r approaching 1).

Fig. 7
figure 7

Non-dimensional rotation frequency (f*) as a function of the extrusion length (ε/r) for a Re = 0.1 and 1, and b Re = 10

Full size image

4 Conclusions

The present study describes in detail the experiments, and supporting numeric simulations, the effects of geometry, and Reynolds number on resulting flow phenomena within cylindrical microcavities. By resolving steady-state flow fields and tracking the evolution of vortices inside cavities (i.e., number, location, center, and existence of saddle point), we are able to characterize quantitatively the entire range of intermediate flow structures that arise at low Reynolds number for the specific cylindrical geometries investigated. These findings are integrated into concise phase maps, relating flow regimes at low Re to dimensionless geometric parameters. In particular, we find that inertial effects lead to a clear break of symmetry in the shape and spatial arrangement of vortices at Re = 10, yet signs of such trends begin to appear as early as Re = 1. Moreover, our efforts provide useful quantitative insight into the resulting rotation frequencies inside cavities featuring single vortex structures, and how to maximize these for microfluidic applications.

The study provides quantitative visualizations and data characterizing extensively, and in a systematic way, the diverse range of recirculating flow patterns that may arise within microfluidic cavity devices. Namely, flow structures available for potential applications include attached or separated flows, the latter featuring single or complex multivortex systems. Our findings are anticipated to serve as a valuable and straightforward roadmap to help microfluidic users in their design of application-driven microcavities.