1 Introduction

Magnetic microparticles have been of great interest in both research and diagnostic applications. Functionalized nano and microparticles or beads offer a large specific surface for chemical binding and may be advantageously used as a “mobile substrate” for bioassays and in vivo applications (Gijs 2004). They may have various sizes ranging from a few nanometres up to tens of nanometres (Pankhurst et al. 2003). Due to the presence of magnetite (Fe3O4) or its oxidized form maghemite (γ-Fe2O3), magnetic particles are magnetized in an external magnetic field. Such external field, generated by a permanent magnet or an electromagnet, may be used to manipulate these particles through magnetophoretic forces and therefore result in migration of particles in liquids. By virtue of the size and distribution of the small embedded iron-oxide grains, particles lose their magnetic properties when the external magnetic field is removed, exhibiting superparamagnetic characteristics.

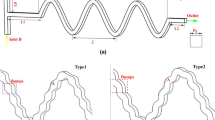
This additional advantage has been exploited for separation of desired biological entities, e.g. cell, DNA, RNA and protein, out of their native environment for subsequent analysis, where particles are used as a label for actuation. Concept of magnetic isolation protocol is depicted in Fig. 1. Prior to separation of the bio-cell/particle complex from contaminants, magnetic particles should be distributed throughout the bio-fluidic solution which contains target cells. This is done by a mixing process which helps to tag the target with particles. In the next stage, only those cells attached to magnetic particles will be isolated in the separation process, while the rest of the bio-fluidic mixture remains unaffected by the magnetic force. Separation of particles in microdevices based on magnetophoretic forces has been reported in the literature (Choi et al. 2001; Do et al. 2004; Ramadan et al. 2006).

Fig. 1
figure 1

Concept of magnetic bio-entity isolation

Full size image

Nevertheless, in micro-scale devices where the Reynolds number is often less than 1, mixing is not a trivial task due to the absence of turbulence. In such circumstances, mixing relies merely on molecular diffusion. Diffusion coefficient for a dilute solution of relatively large spheres in small, spherical molecules is estimated by Stokes–Einstein equation as follows (Mitchell 2004):

$$ D = \frac{{\kappa _{{\text{B}}} T}} {{3\pi \mu d}}, $$
(1)

where κ B is Boltzmann’s constant, Т is the absolute temperature, μ is the dynamic viscosity of the solvent, and d is the diameter of diffusing particle. The diffusion time constant τ is proportional to the diffusion distance squared (τ = L 2/D) which can be up to the order of 105 s for particles with 1 μm diameter dispersed in water solution diffusing a distance of 100 μm. Obviously, such a diffusion time is not realistic and some improving mechanisms need to be employed to facilitate the mixing process.

In order to enhance the diffusion process, (multi-)lamination with different types of feed arrangements has been used in passive micromixers (Koch et al. 1999). The idea is to reduce the diffusion length scale using narrow mixing channels. Split-and-recombine (SAR) configurations (Haverkamp et al. 1999) can also enhance mixing through splitting and later joining the streams. Such configurations create consecutive multi-laminating patterns and increase the interfacial area. However, one disadvantage of using lamination for mixing of the particle laden fluids is the high probability of clogging in narrow channels. Another approach is to generate chaotic advection either by fabrication of special geometries and structures (e.g. obstacles, Wang et al. 2002; 3D channels, Liu et al. 2000; grooves, Stroock et al. 2002) or by applying external forces (e.g. dielectrophoretic, Deval et al. 2002; electroosmotic, Lin et al. 2004; pressure Deshmukh et al. 2000; thermal fields, Tsai and Lin 2002) in passive and active devices, respectively. Chaotic advection increases interfacial area and, consequently, enhances the mixing process. Recently, in addition to separation, magnetophoretic forces are exploited to enhance the mixing of the particles in solution (Rida et al. 2003; Rong et al. 2003; Suzuki et al. 2004). The purpose of this study is to design a chaotic magnetic particle-based micromixer and develop a numerical model in order to characterize the device with different driving parameters. To this end, a combination of electromagnetic, microfluidic and particle dynamics models has been used.

2 Concept and methods

2.1 Concept of the design

In this investigation, a straight channel with two embedded serpentine conductors beneath the channel is utilized to produce the chaotic pattern in the motion of particles and intensify the capturing of bio-cells. The burst-view of the mixer is depicted in Fig. 2a. Two flows; target cells suspension and the particle laden buffer, are introduced into the channel and manipulated by pressure-driven flow (see Fig. 2b). While the cells follow the mainstream in upper half section of the channel (they are transported by convection of the suspending bio-fluid), the motion of magnetic particles is affected by both the surrounding flow field and the localized time-dependent magnetic field generated by sequential activation of two serpentine conductors (here we call the advection due to bulk flow field passive and due to magnetophoretic forces active for the sake of distinction of these phenomena). Circular form of the tip of each tooth in conductors provides an intensified magnetic field in the centre where it acts as a sink for particles. Particles from various positions in the upstream and downstream sides move across the streamlines and are attracted towards the inner edge of the nearest activated tip where the maximum magnetic force is applied. By using a proper periodical current density and structural geometry, chaotic patterns can be produced in the particles’ motion which leads to their better mixing into the bio-fluid suspension.

Fig. 2
figure 2

Concept of the micromixer design: a burst-view of the device (not to scale), b one mixer unit and one simulated unit (dimensions are in μm)

Full size image

Dimensions are shown in Fig. 2b. Channel is 150 μm wide and 50 μm deep. Conductors are 50 μm high and 25 μm wide in the section and distances between centre of circular tips of the conductors are 100 and 65 μm in x and y directions, respectively. Each row of upper and lower conductors is connected to the supply alternately. The mixing operation cycle consists of two phases. In the first half cycle, one of the conductor arrays in switched on while the other one is off. In the next half cycle, the status of conductor arrays is reversed. Each mixing unit consists of two adjacent teeth from opposite conductor arrays and the mixer is composed of a series of such mixing units which are connected together.

2.2 Magnetophoretic forces

Magnetophoretic (hereafter, magnetic) forces are generated by the conductors embedded beneath the channel, as shown in Fig. 2b. The magnetic force on particles is a function of the external magnetic field gradient and the magnetization of the particle. Before saturation, particles are linearly magnetized with their magnetic moment magnitude increasing in the direction of the external field. Beyond the saturation point, magnitude of the moment tends to a constant value. Effective magnetic moment m eff in the linear area (field intensities less than 15,120 A/m) is calculated as (Jones 1995):

$$ {\user2{m}}_{{{\text{eff}}}} = 0.5\pi d^{3} \frac{{\mu _{2} - \mu _{1} }} {{\mu _{2} + 2\mu _{1} }}H, $$
(2)

where d is the diameter of the spherical particle, H is the external magnetic field, μ 1 is permeability of the media and μ 2 is permeability of the particle. In de-ionized water, the magnetic force exerted on the particle is described by:

$$ F_{{\text{m}}} = 0.25\pi \mu _{0} d^{3} \frac{{\mu _{{\text{r}}} - 1}} {{\mu _{{\text{r}}} + 2}}\nabla H^{2} , $$
(3)

where F m is magnetic force, μ r is relative permeability of the particle and μ 0 is permeability of the vacuum. The direction of the force is parallel to the gradient of the external field and particles are attracted towards higher magnetic field regions. Magnetic properties of the reference particle used in this study (M-280, Dynabeads, Dynal, Oslo, Norway) are shown in Table 1 (Fonnum et al. 2005).

Table 1 Properties of the reference magnetic particle
Full size table

Figure 3 shows one mixing unit with its magnetic field generated near the circular tip of the conductor when a current of 750 mA is injected into one conductor array and is turned off in the opposite array during a half cycle of activation. The greyscale map represents variations in the magnetic field intensity at 10 μm above the surface of the conductor where the maximum magnitude of the field is about 6,000 A/m at the centre of the circular tip (point P).

Fig. 3
figure 3

Magnetic field near the tip of one tooth in one mixing unit during a single phase of activation (field in A/m)

Full size image

Magnetic forces exerted on one particle along line A–A (as shown in Fig. 3) are plotted in Fig. 4a showing the force at different heights above the conductor. As expected, the maximum force (5.5 pN) is applied on particles near the conductor and inside the circle of its tip (inner edge) where the gradient of magnetic field squared is at its maximum value. Although the magnetic field is maxima at the centre point P, the force on particles is relatively small at this point. This is due to the fact that the magnetic force is proportional to the gradient of the field which is almost constant in the neighbourhood of the point P. In moving away from the conductor, the force drops significantly due to a dramatic decrease in the magnetic field which in turn affects the magnetic moment. It is worth noting that the magnetic force is three-dimensional and the z component of the force is downward which together with gravity, pull the particles towards the bottom of the channel and restrict their motion to a two-dimensional pattern. In fact, this component has no contribution to the chaotic motion of the particles and is assumed not to be influential on the process of mixing. Hence, in this study, planar forces at 10 μm above the surface of the conductors are of interest as closer layers might not be practical due to fabrication restrictions. Figure 4b illustrates x and y components of the force at 10 μm above the conductor along the lines A–A and B–B.

Fig. 4
figure 4

Magnetic forces exerted on one particle: a force along line A–A (see Fig. 3) at different heights above the conductor, b x and y components of the force at 10 μm above the conductor along the lines A–A and B–B (P is the centre point of the circular tip)

Full size image

2.3 Motion of the particles in a viscous fluid

Given the magnetic forces, motion of the particles relative to the media can be assumed as a creeping flow and therefore, drag force on the particle may be evaluated by Stokes’ law (Coulson et al. 1991). The velocity of the particle due to the magnetic and drag forces can be described by Newton’s second law:

$$ m_{{\text{p}}} \frac{{\partial V}} {{\partial t}} = F_{{\text{m}}} - 3\pi \mu dV, $$
(4)

where m p is the particle mass, V is the relative velocity of the particle with respect to the fluid, μ is dynamic viscosity and d is the diameter of the particle. When magnetic force is exerted, particle accelerates and reaches the terminal velocity V m given by:

$$ V_{{\text{m}}} = \frac{{F_{{\text{m}}} }} {{3\pi \mu d}}. $$
(5)

The particle reaches this velocity in a very short time. Given the particle properties (Table 1) and viscosity of 0.001 kg/ms (characteristic of water at room temperature), particle relaxation time (τ = d 2 ρ/18 μ) is less than 100 ns. During this time, particle moves a minute distance which can be neglected in tracing the particle position. Hence, ignoring the acceleration phase, we assume particles react to magnetic forces without delay and total velocity of the particle at each moment (V p) is the sum of velocity due to fluid field (V f; passive advection) and velocity due to the magnetic field (V m; active advection):

$$ V_{{\text{p}}} = V_{{\text{f}}} + \frac{{F_{{\text{m}}} }} {{3\pi \mu d}}. $$
(6)

Neutral diffusion (Brownian motion) of particles of this size is insignificant. Diffusion rate for such a particle in water would be in the order of 10−13 m/s. Advection due to magnetic forces is approximately 105–106 times greater than the diffusion fluxes.

3 Simulations

3.1 Simulation procedure

A two-dimensional numerical simulation is carried out assuming that particles are neutrally buoyant and their motion in z direction is either zero or negligible as discussed in Sect. 2.2. Procedure consists of two steps: first, the steady-state velocity field of an incompressible Newtonian fluid (water) and time-dependent magnetic field are computed using commercial multiphysics finite element package Comsol (COMSOL, UK) and velocities of the particles due to the fluid and magnetic fields are extracted. Then trajectories of particles are evaluated by integrating the sum of velocities using Euler integration method in Matlab:

$$ r_{{\text{p}}} = {\int {V_{{\text{p}}} \, \cdot {\text{d}}t = {\int {{\left( {V_{{\text{f}}} + \frac{{F_{{\text{m}}} }} {{3\pi \mu d}}} \right)} \cdot {\text{d}}t} }} }. $$
(7)

This method of integration is adopted because the equation of motion of the particles is highly stiff due to quick changes in the magnetic field and, consequently, in magnetic forces when the signal phase change occurs. In order to obtain accurate results, a small discrete time-step (10 ms) is considered for particle tracking procedure and, where necessary, the fluid velocity and the magnetic intensity is linearly interpolated between two adjacent grids. Analysis is based on the premise that there are no magnetic or hydrodynamic interactions between particles (one-way coupling) and the motion of particles is treated as if they are moving individually. This assumption is valid for small particles at low concentration in suspension, namely less than 1015 particles/m3 (Mikkelsen and Bruus 2005). Also diffusion is neglected. In fact, particles are small enough not to agitate the flow, but large enough not to get involved with Brownian motion, moving only with the surrounding flow itself. Trajectories of cells are obtained using the same method as for magnetic particles, with the exception that cells are magnetically inactive and simply follow the mainstream in the fluid field. The size of biological entities may vary from a few nanometres (proteins) to several micrometers (cells). In this study, cells are considered to be spheres of 1 μm diameter.

For reduction of the computational domain, the smallest possible mixing unit with periodic boundary conditions must be used. For a periodic mixer like the one proposed, the flow field solution is also periodic and remains invariant in each mixing unit. This indicates that every single mixing unit contains all the information of the flow in the whole mixer system. However, the same cannot be said for the magnetic field as the generated field by neighbouring teeth affects the field in each unit. In other words, one mixer unit as shown in Fig. 2b cannot comprise the field of outer teeth if it is simulated as a stand-alone domain. Hence, one extended unit which includes adjacent teeth at both sides is used (see Fig. 2b) and field solution is extracted for inner unit. Other teeth are too far to influence the field in the inner unit and their effect is not taken into account. The bulk velocity of flow is in the order of 10 μm/s which yields a Reynolds number of the order of 10−3 meaning that the flow is laminar.

3.1.1 Chain formation

It should be noted that particles can be locally up-concentrated near the inner edge of the conductors which may result in chain formation of the particles. This phenomenon is the result of the magnetic dipole interactions between neighbouring particles. A mutual attractive force between two identical particles is estimated by (Jones 1995):

$$ F_{{{\text{mutual}}}} = K\mu _{1} \pi d^{2} H^{2} , $$
(8)

where K is the normalized factor and highly depends on the spacing (δ) between the particles and their relative permeability to the media. For δ = 0–d (d is the diameter of the reference particle), K will be in the range of 0.25–0.025. The magnetic force and hydrodynamic resistance on a chain depends on its shape and cannot be obtained by simply summarizing the forces on all individual particles. Therefore, the advection of the particles may be significantly affected and the assumption of one-way coupling will no longer be valid. Derks et al. (2006) investigated the manipulation of such chained particles and it was found that for each chain, there is a velocity enhancement factor normalized to the velocity of a single particle. Since all chains will align with the magnetic field lines (axial movement of the chains), this factor depends merely on the length of the chain (therefore, the number of the particles in the chain) and can be approximated by:

$$ K_{{vcf}} = \frac{{V_{{\text{c}}} }} {{V_{{\text{p}}} }} = 1 + 0.77 \cdot \ln \;(n), $$
(9)

where n is number of the particles and V c is velocity of the chain. While evaluating the particles trajectories in simulation procedure, the advection of individual particles is monitored constantly. A chain is assumed to be formed when the spacing between two (or more) particles is zero at the end of the time-step. Then the trajectory of the axially dragged chain is obtained by implementing Eq. 9. Particles will remain in the chain form until the phase change occurs. In that time particles are far away from the activated tip in the opposite conductor array and dipole interaction force which depends on the intensity of the magnetic field is weak (see Eq. 8). Therefore, particles advecting in streamlines with different velocities in Poiseuille flow are assumed to be separated by drag forces. Separated particles will flow individually and may join a new chain in downstream close to the next activated tip.

3.2 Simulation parameters

In order to characterize the mixing efficiency and optimize the design, effects of a large number of different parameters may be investigated. These parameters include geometry (e.g. channel dimensions, size of the conductors and spacing between them), bulk flow rate, particle characteristics, particle concentration and magnitude and frequency of the current. Nevertheless, it seems impractical to consider the effect of variation of all influential parameters simultaneously due to computational restrictions. Therefore, based on preliminary calculations, a reasonably optimized geometry for the channel and conductors (as discussed in Sect. 2.1) and a permissible current magnitude at which heat generation is not an issue (750 mA), are adopted and the effect of variation of two driving parameters; namely the bulk flow velocity and frequency of the current, has been investigated against mixing efficiency. The ratio of these driving parameters is defined as a dimensionless number St (Strouhal number):

$$ St = \frac{{fL}} {V}, $$
(10)

where f is the frequency, L is the characteristic length (here, distance between two adjacent teeth), and V is the mean velocity of the fluid.

4 Results and discussion

Figure 5 illustrates a typical effect of magnetic actuation within two mixing units. Bio-cells and magnetic particles enter the first mixing unit from the left in upper and lower halves of the section, respectively, and with the same concentration. When there is no magnetic actuation, both cells and particles remain in their initial section and follow the streamlines (continuous lines) of the parabolic velocity profile in Poiseuille flow (see Fig. 5a). In this situation, tagging might occur only in the middle of the channel along the interface between two halves. When the external field is applied, particles travel across the streamlines as well as the interface. Therefore, they find the opportunity to spread in upper section where they can meet and collect cells (see Fig. 5b).

Fig. 5
figure 5

Advection of cells and particles within two mixing units: a without external perturbation, b with magnetic perturbation (St = 0.4, V = 40 μm/s). Continuous lines represent fluid streamlines and dimensions are normalized to the characteristic length

Full size image

4.1 Basis of chaotic advection in particles

Chaotic advection increases the interfacial area and, therefore, enhances the mixing process. Chaos cannot occur in steady two-dimensional flows, but only in three-dimensional and two-dimensional time-dependent flows. In two-dimensional flow, time-dependency may be considered as an added third dimension. The key to effective mixing lies in producing stretching and folding of lines in two-dimensional (surfaces in three-dimensional) flows which can be equated with chaos. In rough terms, a necessary condition for chaos is the crossing of streamlines which must occur at different times (Ottino and Wiggins 2004).

Fig. 6
figure 6

Consecutive stretching and folding in trajectories which results in chaotic advection (St = 0.2, V = 45 μm/s)

Full size image

In order to explain the basis for chaotic advection in the proposed micromixer, trajectories of four particles (particles 1–4 in Fig. 6) are considered as typical trajectories in the mixer. Particles are released in the first mixing unit uniformly with the spacing of 10 μm when St = 0.2 and V = 45 μm/s. During the first half cycle, first array (conductor I) is on and second array (conductor II) is off. Particle 1 feels a strong magnetic force in y direction and tends to move in this direction while it is advected by the mainstream in x direction. Note that depending on its location in the channel which determines both drag force in the Poiseuille flow and magnetic force, particle 1 can have a positive or negative velocity in x direction according to Eq. 6. Particle 2 is farther from the conductor I and does not find any chance to be attracted upwards completely during the first half cycle. Therefore, two initially nearby particles diverge inducing the mechanism of stretching which is marked with a rectangle. In this phase particle 1 is exposed to the target cells across different streamlines and captures them in case on any collision.

In the following half cycle, electric current is injected into the conductor II and turned off in conductor I. In this phase, particle 1 is free to move from the previous location and is further advected by the mainstream until it approaches a region of strong enough magnetic force and, consequently, is pulled towards the centre of conductor II. Particle 2 is subject to a small magnitude of magnetic force in y direction (see Fig. 4b) but tends to move faster than the mainstream by virtue of magnetic force in x direction. In this phase, particle 2 approaches and tags the target cells, if any, along one streamline. Folding is achieved where two distant trajectories converge and even in some operating conditions cross each other. Consecutive stretching and folding can be produced in this way which is the basis of chaos.

Particles 3 and 4 which are too far from the conductor I to be attracted, are dragged downstream by the fluid and gradually move towards the upper half section of the channel. After passing a few mixing units, almost all particles penetrate to cells’ region and fluctuate in a chaotic regime confined to the tips of two conductors.

4.2 Evaluation of mixing process

In order to quantitatively evaluate the degree of mixing, two criteria are computed for the investigated range of simulation parameters. The ability to spread the magnetic particles can represent the performance of the mixer. Alternatively, a common definition of mixing quality is based on the inspection of chaotic regimes developed in the mixer and calculating the Lyapunov exponent is a standard method of investigating chaos.

4.2.1 Particle dispersion

A quantitative criterion to characterize the degree of mixing is the so-called “discrete intensity of segregation” which is extracted from statistical parameters. Intensity of segregation is the variance of the concentration distribution. In fact, this index measures the deviation of local concentration from the ideal situation (i.e. homogeneous mixture) and is defined as (Anderson et al. 2000):

$$ I_{{\text{s}}} = \frac{1} {{\overline{C} {\left( {1 - \overline{C} } \right)}}}\;\frac{1} {A}\;{\sum\limits_{i = 1}^N {{\text{(}}C_{i} - \overline{C} {\text{)}}^{2} \cdot a_{i} } }, $$
(11)
$$ \overline{C} = \frac{1} {A}\;{\sum\limits_{i = 1}^N {C_{i} \cdot a_{i} } },\quad A = {\sum\limits_{i = 1}^N {a_{i} } }, $$
(12)

where N is the number of cells, A is the total area of all cells taken into account, C i is the concentration of cell i with area a i , and(C is the mean concentration over the section. For unmixed distributions where all cells are either black (C i  = 1) or white (C i  = 0) which corresponds to complete segregation, the intensity of segregation is equal to 1. When the concentration in all cells approaches its overall average value which corresponds to optimal dispersion (perfect mixing), I s equals 0. However, for all other scenarios 0 < I s < 1. In this study distribution of the magnetic particles is used to compute the intensity of segregation. Since the dispersion of the particles in upper half of the channel where target cells exist is of interest, a regular grid of rectangle cells with equal size is considered over entire upper half as shown in Fig. 7. Therefore, Eq. 11 can be simplified to:

$$ I_{{\text{s}}} = \frac{1} {{\overline{C} {\left( {1 - \overline{C} } \right)}}}\;\frac{1} {N}\;{\sum\limits_{i = 1}^N {{\text{(}}C_{i} - \overline{C} {\text{)}}^{2} } },\quad \overline{C} = \frac{1} {N}\;{\sum\limits_{i = 1}^N {C_{i} } }. $$
(13)

A lump of 500 particles was injected in the lower half of the channel and I s was computed along the channel length at various sections. At each section, a column of the cells were taken into account, thereby assessing dispersion of the particles across the channel width.

Fig. 7
figure 7

Initial position of the particles and rectangle cells used for the computation of intensity of segregation

Full size image

Figure 8 shows the intensity of segregation for two driving parameters with the same Strouhal number. It can be noticed that in upstream, the intensity of segregation is equal to one. This is owing to the fact that none of the upper cells are occupied by the particles. As the flow passes through the channel, some of the particles penetrate into the upper half of the channel and spread across cells’ region. Consequently, the intensity of segregation declines displaying different behaviours for flows with different bulk velocities. Scrutiny of the graphs reveals that for the flow with velocity of V = 40 μm/s, I s decreases quickly continued by a slower rate of decline in the vicinity of 100 μm in the channel. This region corresponds to the position of a circular tip on the lower conductor array and is marked on both mixer and graphs in Fig. 8. This phenomenon is the result of folding of the particles by the activated conductor where particles spread across the channel width are pulled towards the tip. Therefore, particles are up-concentrated in some of the cells which may even lead to an increase in local I s. At a higher flow rate (V = 50 μm/s) a different behaviour is observed; the graph shows an almost uniform rate of decline. This is the result of larger drag forces which may prevent the clustering of the particles near the conductors. Two graphs cross each other several times where the point of each intersection represents the position of the conductor tips.

Fig. 8
figure 8

Intensity of segregation for driving parameters with different fluid velocities and the same Strouhal number

Full size image

In order to compare the results to other existing magnetic particle-based devices, two mixers reported by Grumann et al. (2005) and Rida and Gijs (2004) are considered. In the former reported mixer an efficiency of nearly 100% is achieved in the best case (beads and alternate spinning) after a mixing time of 8 s. The latter reports an efficiency of 95% using a mixing length of 400 μm and liquid flows of the order of 0.5 cm/s. Our proposed mixer shows an efficiency of 70% over the same mixing time and length but at extremely lower flow velocities of the order of 0.05 mm/s. Since the binding of the target entities to magnetic particles is of interest, such low velocities seems to be essential which may allow the chemical binding to occur. However, the main advantage of the proposed mixer in this study is the simplicity of the structure which does not require the utilization of the permanent magnets or any mechanical energy input.

The intensity of segregation was examined over a high number of mixing units for a few driving parameters and it was noticed that after almost four mixing units (channel length of 800 μm), I s eventually reaches certain minimal levels and then oscillates around that level. These oscillations are the result of the concentration fluctuations ascribed by folding of the particles near the circular tips. However, calculation of I s over such long channels calls for extensive computational time. Moreover, since a perfect mixture is described by an intensity of segregation equal to zero, the rate of its decline essentially characterize the performance of the mixer. Therefore, I s was computed over two mixing units for a wide range of driving parameters and the average value was obtained for each status. Comparison of these values allows revealing the driving parameters that perform more efficiently. The results are dealt with later is Sect. 4.2.3.

4.2.2 Lyapunov exponent

Sensitivity to initial conditions is an indication of chaos. In chaotic systems, time evolution of two initially nearby particles shows exponential divergence. Lyapunov exponent is the average exponential rate of divergence or convergence of initially neighbouring orbits in the phase space and is defined as:

$$ \lambda = {\mathop {\lim }\limits_{t \to \infty } }\frac{1} {t}\ln \frac{{{\left| {d(t)} \right|}}} {{{\left| {d(0)} \right|}}}, $$
(14)

where d(t) and d(0) are distance between two orbits at time t and initial time, respectively. Calculation of the Lyapunov exponent can be used to detect the incidence of chaos, measure its extent, and investigate the relationships between various affecting parameters and chaos. For chaotic mixing problems, Lyapunov exponent reflects the dispersion rate of the fluid particles and in this study, it is used to quantify the chaotic advection of magnetic particles. Lyapunov exponents are defined as a spectrum with n components in an n-dimensional phase space. However, normally it suffices to consider its largest component to describe the system. A positive value is the signature of chaos, while zero indicates stable properties. Here Sprott’s method (2003) is used to calculate the largest Lyapunov exponent (hereafter λl). This method utilizes the general idea of tracking two initially close particles, and calculates average logarithmic rate of separation of the two particles. The numerical procedure is shown in Fig. 9.

Fig. 9
figure 9

Schematic illustration for calculating the largest Lyapunov exponent based on Sprott’s method

Full size image

For any arbitrary particle, a virtual particle is considered with a minute distance of d(0) from the chosen particle and trajectories of these particles are tracked. At the end of each time-step, the new distance, d(t), between real and virtual particles and also ln ∣d(t)/d(0)∣are calculated. The virtual particle is then placed at distance d(0) along its connecting line to the real particle. After repeating this process for several time-steps, λl will be converged and is evaluated by:

$$ \uplambda_{{\text{l}}} = {\mathop {\lim }\limits_{n \to \infty } }\frac{1} {{n\Delta t}}{\sum\limits_{i = 1}^n {\ln \frac{{{\left| {d_{i} (t)} \right|}}} {{{\left| {d(0)} \right|}}}} }, $$
(15)

where Δt is the duration of one time-step and n is the number of steps. An appropriate choice of d(0) is one that is about 1,000 times larger than the precision of the floating point numbers that are being used (Sprott 2003). Therefore, a value of 0.01 μm will suffice for initial distance. Figure 10 shows the convergence of λl versus time for one particle with two different driving parameters and also in the absence of the external field. Without magnetic perturbation, λl convergences to zero which indicates a steady flow. At St = 0.2 and bulk fluid velocity of 35 μm/s it convergences to a constant value of about 0.45 whereas at velocity of 40 μm/s, this value is about 0.19. Hence, it can be deduced that in the former operating condition, the system exhibits a stronger chaotic behaviour. Close observation of the graphs reveals that there are some points where λl declines quickly (marked with circles). Considering the time of these incidents, it can be inferred that near the end of each phase, some particles enter the centre of tips and become trapped in these regions yielding a zero value for λl (for that specific time) and reducing the overall λl. When the driving current is switched and system is in next half cycle, particles are free to flow with the mainstream up to the point where they are re-attracted by nearby active tooth leading to an increase in λl. Examination of λl for various particles reveals that generally after a period of 20 s, λl approaches its converged value.

Fig. 10
figure 10

Convergence of the largest Lyapunov exponent for one particle

Full size image

4.2.3 Collision ratio

Since the ultimate goal of the system is to improve the attachment of cells to magnetic particles, frequency of the collision between target cells and the particles can be a supplemental criterion for investigating the mixing process. It offers the ability to examine the efficiency of the mixer versus chaotic advection and also analyse the effect of driving parameters on the probability of collision. This method uses the idea of monitoring the trajectories of cells and particles to predict their collision in the domain. Particles and cells with a uniform distribution and the same concentration (1015 particles/m3) enter the lower and upper halves of the channel, respectively. It is assumed that collision happens when the distance between the centre of circular particle and cell becomes smaller than the sum of their radii. It should be noted that merely the incident of collision between cells and particles does not warranty the formation of the chemical binding between them, as biological interactions have their own kinetics and time scale. However, the occurrence of collision can imply the probability of binding; the higher the collision ratio, the higher the rate of binding. Once a cell is collided with a particle, it will be counted and then assumed as removed. Subsequently, Collision Ratio (CR), i.e. ratio of the collided cells to the total number of entered cells, is calculated after a period of 20 s. Figure 11a illustrates variation of CR for different driving parameters (St = 0.2–1) where each graph represents the values of CR for a constant fluid velocity (V = 30–50 μm/s).

Fig. 11
figure 11

Variation of characterizing indices versus different system operating conditions: a collision ratio, b largest Lyapunov exponent, c intensity of segregation

Full size image

Moreover, in order to evaluate the effect of driving parameters on chaotic advection, 21 particles are uniformly distributed in upper half of the first mixing unit as the initial positions and λl is calculated for each individual particle using the method explained in Sect. 4.2.2. The time period is 20 s when the particles approach their constant value of λl. In order to quantify the extent of chaos over the entire domain in the upper section (where cells exist), the average of λls of 21 particles is taken. Results are shown in Fig. 11b. Also the results for the intensity of segregation over the same driving parameters are illustrated in Fig. 11c.

The global variations of λl and I s are almost identical for different bulk flow velocities. Both characterizing indices show a good agreement; an increase in chaos leads to an increase in particle dispersion in the mixer domain. The maxima for particle dispersion happens around the Strouhal number of 0.4, while the minimum occurs at St = 0.9. It should be noted that the values for the intensity of segregation are the mean values over the first two mixing units and do not represent the ultimate efficiency of the mixer. CR exhibits a similar behaviour at Strouhal numbers less than 0.6 which means that an increase in chaos leads to an increase in number of the collided cells. Maximum values for λl and CR are realized at St = 0.4 which are 0.37 and 80%, respectively. This extent of chaos is comparable to the reported chaotic strength by Suzuki et al. (2004).

At higher Strouhal numbers (namely 0.8), λl and CR show different variations. Although at high bulk flow velocities (larger than 40 μm/s) a good agreement between two indices can still be observed, in the case of lower velocities they show contradicting behaviours. At low velocities of the bulk flow, some particles are advected until they are attracted to the inner edge of one tip in the upper conductor. In the vicinity of the channel wall, flow velocity is much less than the central region as the parabolic velocity profile in Poiseuille flow is developed in the channel. Since the magnetic forces are significantly large in the central region of the conductor, these particles will be retained in this area. Even after the current is switched to the opposite array, due to low fluid velocity particles will not have the opportunity to escape from the previous conductor and come close enough to the opposite conductor. Therefore, in next period of activation, particles are again pulled back towards the same region quickly and become trapped again. For such particles, mixer is partially acting like an asymptotically stable system which results in a decrease in the Lyapunov exponent of the whole domain. High values for I s are the result of the clustering of a high number of particles in neighbouring cells. However, trapped particles play the role of nearly fixed posts which are exposed to multiple cells, thereby increasing the value of CR. Although the ratio is relatively high, in practice it is a challenging issue where trapped particles can clog the channel. Figure 12 illustrates the trajectories of such particles at St = 0.8 and V = 40 μm/s. Five particles are released in the first unit and after flowing along three and a half units, three particles (particles 1–3) are trapped and never exit the channel. Trajectories of these particles are plotted with dotted lines and locations of traps are marked with rectangles. In such operating conditions, the mixer is only partially chaotic, and the mixing is incomplete. However, when the Strouhal number is low, i.e. in case of longer time periods, particles have the chance to move away from these attractors, even though the velocity is low.

Fig. 12
figure 12

Trajectories of particles at St = 0.8 and V = 40 μm/s; rectangles indicate the location of trapped particles

Full size image

Some particles (here particles 4–5) seem to have nearly similar and close trajectories. There are two possible scenarios. First, two particles may flow along the same Lagrangian path but at different times. In this case these particles may collide with different cells if any. The other scenario occurs when operating conditions force the particles to take almost the same trajectories at the same time, despite their different initial positions. Finally, collision ratio is calculated for a mixing time of 30 s which improves the maximum ratio up to 90%. However, longer mixing times require longer channels. In fact, mixing length is a function of bulk fluid velocity as well as mixing time. For instance, 30 s of mixing process at bulk velocity of 45 μm/s can take place through 5.5 mixing units (CR = 76%) while solely three units are required for 20 s of mixing at velocity of 35 μm/s (CR = 67%). Therefore, one needs to reach the best compromise between efficiency and size of the design.

5 Concluding remarks

A two-dimensional numerical study of mixing of the magnetic particles with bio-cells is performed in order to characterize the efficiency of the micromixer. Although employed simulation techniques and developed codes allow the evaluation of the effect of various geometry configurations and particle characteristics, this study focuses on the effect of two driving parameters (i.e. the fluid velocity and frequency of magnetic activation) on the mixing quality. Intensity of segregation is used as the main index to characterize the mixer where best efficiency of 85% is obtained in a mixing length of 500 μm. Lyapunov exponent as an index of chaotic advection is found to be highly dependent on Strouhal number where the maximum chaotic strength is realized in Strouhal numbers close to 0.4, which corresponds to the Lyapunov exponent of 0.37. It is shown that collision ratio in the mixer cannot be used as a stand-alone index which might suggest operating conditions that are not practical. Thus, both indices need to be taken into account while characterizing the device. Maximum collision ratio is found to be 80% which means that more than three quarters of the existing cells will have a chance to be tagged by the particles; although this could be further increased at the cost of longer mixing time and channel length.